MP Board Class 7th Maths Solutions Chapter 11 परिमाप और क्षेत्रफल Ex 11.2
प्रश्न 1.
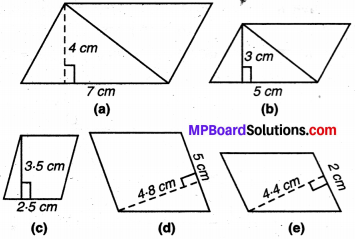
निम्न में प्रत्येक समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए:
हल:
(a) यहाँ, आधार (b) = 7 cm, ऊँचाई (h) = 4 cm
∴ समान्तर चतुर्भुज का क्षेत्रफल = b × h
= (7 × 4) cm2 = 28 cm
(b) यहाँ, आधार (b) = 5 cm, ऊँचाई (h) = 3 cm.
∴ समान्तर चतुर्भुज का क्षेत्रफल
= b × h = (5 × 3) cm2 = 15 cm2
(c) यहाँ, आधार (b) = 2.5 cm, ऊँचाई (h) = 3.5 cm
∴ समान्तर चतुर्भुज का क्षेत्रफल = b × h
= (2.5 × 3.5) cm2 = 8.75 cm2
(d) यहाँ, आधार (b) = 5 cm, ऊँचाई (h) = 4.8 cm
∴ समान्तर चतुर्भुज का क्षेत्रफल = b × h
= (5 × 4.8) cm2 = 24 cm2
(e) यहाँ, आधार (b) = 2 cm, ऊँचाई (h) = 4.4 cm
∴ समान्तर चतुर्भुज का क्षेत्रफल = b × h
= (2 × 4.4) cm2 = 8.8 cm2
![]()
प्रश्न 2.
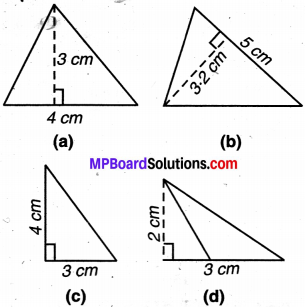
निम्न में से प्रत्येक त्रिभुज का क्षेत्रफल ज्ञात कीजिए :
हल:
(a) यहाँ, आधार (b) = 4 cm, ऊँचाई (h) = 3 cm
∴ त्रिभुज का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × b × h
= (\(\frac { 1 }{ 2 } \) × 4 × 3) cm2
= 6 cm2
(b) यहाँ, आधार (b) = 5 cm, ऊँचाई (h) = 3.2 cm
∴ त्रिभुज का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × b × h
= (\(\frac { 1 }{ 2 } \) × 5 × 32) cm2
= 8 cm2
(c) यहाँ, आधार (b) = 3 cm, ऊँचाई (h) = 4 cm
∴ त्रिभुज का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × b × h
= (\(\frac { 1 }{ 2 } \) × 3 × 4 ) cm2
= 6 cm2
(d) यहाँ, आधार (b) = 3 cm, ऊँचाई (h) = 2 cm
∴ त्रिभुज का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × b × h
= ( \(\frac { 1 }{ 2 } \) × 3 × 2) cm2
= 3 cm2
प्रश्न 3.
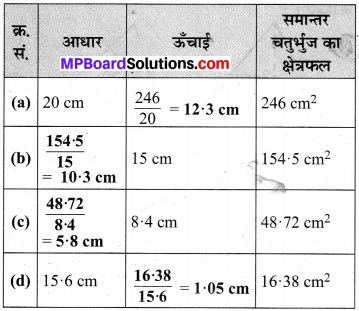
रिक्त स्थानों का मान ज्ञात कीजिए।
हल:
चूँकि हम जानते हैं कि समान्तर चतुर्भुज का क्षेत्रफल
= आधार × ऊँचाई
प्रश्न 4.
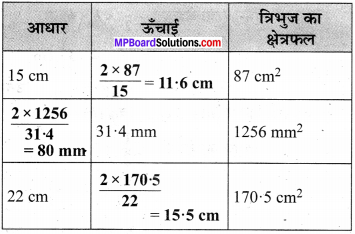
रिक्त स्थानों का मान ज्ञात कीजिए :
हल:
चूँकि हम जानते हैं कि
त्रिभुज का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × आधार × ऊँचाई
![]()
प्रश्न 5.
PQRS एक समान्तर चतुर्भुज है (संलग्न चित्र 11.17)| QM शीर्ष Q से SR तक की ऊँचाई तथा QN शीर्ष Q से PS तक की ऊँचाई है। यदि SR = 12 cm और QM = 7.6 cm, तो ज्ञात कीजिए :
(a) समान्तर चतुर्भुज PQRS का क्षेत्रफल
(b) ON यदि, PS = 8 cm
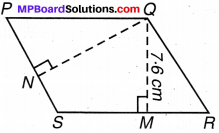
हल:
(a) यहाँ, आधार SR = 12 cm,
संगत ऊँचाई QM = 7.6 cm
समान्तर चतुर्भुज PQRS का क्षेत्रफल = b × h
= SR × QM
= (12 × 7.6) cm2
= 91.2 cm2
(b) अब, समान्तर चतुर्भुज का क्षेत्रफल
= 91.2 cm2, आधार (PS) = 8 cm
माना कि संगत ऊँचाई (QN) = h cm
b × h = 91.2
या 8 × h = 91.2
या h = \(\frac { 91.2 }{ 8 } \) = 11.4 cm
∴ QN = 11.4 cm
प्रश्न 6.
DL और BM समान्तर चतुर्भुज ABCD की क्रमशः भुजाएँ AB और AD पर लम्ब हैं(संलग्न चित्र 11.18)। यदि समान्तर चतुर्भुज का क्षेत्रफल 1470 cm2 है, AB = 35 cm, और AD = 49 cm है, तो BM तथा DL की लम्बाई ज्ञात कीजिए।
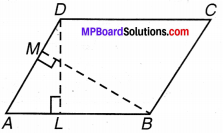
हल:
यहाँ, समान्तर चतुर्भुज ABCD का क्षेत्रफल
= 1470 cm2
आधार AB = 35 cm,
∵ समान्तर चतुर्भुज ABCD का क्षेत्रफल
= आधार × ऊँचाई = AB × DL
∴ 35 × DL = 1470
या DL = \(\frac { 1470 }{ 35 } \) = 42 cm
पुनः समान्तर चतुर्भुज का क्षेत्रफल = आधार × ऊँचाई
= AD × BM
∴ 49 × BM = 1470
या BM = \(\frac { 1470 }{ 49 } \) = 30 cm
![]()
प्रश्न 7.
त्रिभुज ABC, A पर समकोण है (संलग्न चित्र 11.19),और AD भुजा BC पर लम्ब है। यदि AB = 5cm, BC = 13 cm और AC = 12 cm है, तो ∆ABC का क्षेत्रफल ज्ञात कीजिए। AD की लम्बाई भी ज्ञात कीजिए।
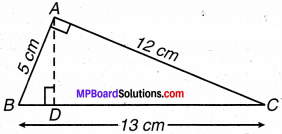
हल:
यहाँ, AB = 5 cm, BC = 13 cm, AC = 12 cm
∆ ABC का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × आधार × ऊँचाई
= \(\frac { 1 }{ 2 } \) AB × AC
= \(\frac { 1 }{ 2 } \) × 5 × 12 cm2
= 30 cm2
पुन: ∆ ABC का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × आधार × ऊँचाई
= \(\frac { 1 }{ 2 } \) BC × AD
∴ 30 = \(\frac { 1 }{ 2 } \) × 13 × AD
या AD = \(\frac{30 \times 2}{13}=\frac{60}{13}\) cm
प्रश्न 8.
∆ ABC समद्विबाहु त्रिभुज है, जिसमें AB = AC = 7.5 cm और BC = 9 cm है (संलग्न चित्र 11.20)। 4 से BC तक की ऊँचाई AD, 6 cm है। ∆ ABC का क्षेत्रफल ज्ञात कीजिए। C से AB तक की ऊँचाई, अर्थात् CE क्या होगी?
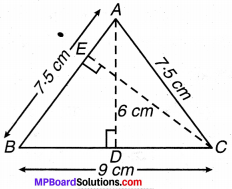
हल:
यहाँ, आधार BC = 9 cm,
संगत ऊँचाई AD = 6 cm
∴ ∆ ABC का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × आधार × ऊँचाई
= \(\frac { 1 }{ 2 } \) × BC × AD
= \(\frac { 1 }{ 2 } \) × 9 × 6 cm2
= 27 cm2
पुन: ∆ ABC का क्षेत्रफल = \(\frac { 1 }{ 2 } \) × AB × CE
= 27 cm2
या \(\frac { 1 }{ 2 } \) × 7.5 × CE = 27
या CE = \(\frac{27 \times 2}{7 \cdot 5}\) = 7.2 cm
पाठ्य-पुस्तक पृष्ठ संख्या # 236
इन्हें कीजिए
प्रश्न 1.
संलग्न चित्र 11.21 में
(a) किस वर्ग का परिमाप अधिक है ?
(b) कौन-सा अधिक है; छोटे वर्ग का परिमाप या वृत्त की परिधि?

हल:
(a) बाहरी वर्ग का परिमाप अधिक है।
(b) छोटे वर्ग के परिमाप से वृत्त की परिधि अधिक है।
प्रयास कीजिए
प्रश्न 1.
एक चौथाई प्लेट तथा एक अर्द्ध प्लेट लीजिए। प्रत्येक को टेबल की ऊपरी सतह पर एक बार घुमाइए। कौन-सी प्लेट एक पूरे चक्कर में अधिक दूरी तय करती है? कौन-सी प्लेट कम चक्कर में टेबल की ऊपरी सतह की लम्बाई को पूरा करेगी?
हल:
एक पूरे चक्कर में अर्द्ध प्लेट अधिक दूरी तय करेगी। एक चौथाई प्लेट की अपेक्षा अर्द्ध प्लेट कम चक्कर में टेबल की ऊपरी सतह की लम्बाई को पूरा करेगी।
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 237
निम्न पर विचार कीजिए
एक किसान खेत के केन्द्र पर 7 m त्रिज्या वाली एक फूलों की क्यारी खोदता है। उसे खाद को खरीदने की आवश्यकता है। यदि 1 m2 क्षेत्रफल के लिए 1 kg खाद की आवश्यकता हो, तो उसे कितने किलोग्राम खाद खरीदनी चाहिए?
हल:
यहाँ, फूलों की क्यारी की त्रिज्या r = 7 m
∵ क्यारी का क्षेत्रफल = πr2
∴ क्यारी का क्षेत्रफल = \(\frac { 22 }{ 7 } \) × 7 × 7 = 154 m2
∵ 1 वर्ग मीटर के लिए खाद चाहिए = 1 kg
∴ 154 वर्ग मीटर के लिए खाद चाहिए = 1 × 154
= 154 kg
अत: उसे 154 किलोग्राम खाद खरीदनी चाहिए।
पाठ्य-पुस्तक पृष्ठ संख्या # 238
प्रश्न 1.
₹10 प्रति m2 की दर से, 2 m त्रिज्या वाले एक वृत्ताकार टेबल के ऊपरी सतह पर पॉलिश कराने का व्यय क्या होगा?
हल:
यहाँ, टेबल की त्रिज्या r = 2 m
वृत्ताकार टेबल की ऊपरी सतह का क्षेत्रफल = πr2
= \(\frac { 22 }{ 7 } \) × 2 × 2 = \(\frac { 88 }{ 7 } \) m2
अत: ₹ 10 प्रति m2 की दर से ऊपरी सतह पर पॉलिश कराने का व्यय
= ₹ 10 × \(\frac { 88 }{ 7 } \) = ₹ \(\frac { 880 }{ 7 } \)
= ₹ 125.71 (लगभग)
![]()
पाठ्य-पुस्तक पृष्ठ संख्या # 239-240
इन्हें कीजिए
प्रश्न 1.
ग्राफ पेपर पर अलग-अलग त्रिज्याओं के वृत्तों को बनाइए। वर्गों की संख्या को गिनकर क्षेत्रफल ज्ञात कीजिए। सूत्र का प्रयोग करके भी क्षेत्रफल ज्ञात कीजिए। दोनों उत्तरों की तुलना कीजिए।
हल:
1 वर्ग सेमी के ग्राफ पर 2 सेमी तथा 3 सेमी त्रिज्या के दो वृत्त खींचे।
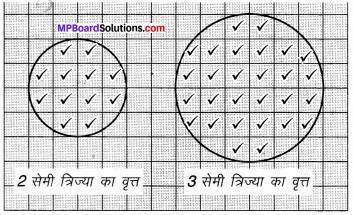
दोनों वृत्तों के पूर्ण वर्ग को गिनने पर हमें क्रमश: 12 सेमी तथा 28 सेमी2 क्षेत्रफल प्राप्त होता है।
सूत्र का प्रयोग करने पर हमें उनका क्रमशः निम्न क्षेत्रफल प्राप्त होता है।
2 सेमी त्रिज्या वाले वृत्त का क्षेत्रफल = πr2
= \(\frac { 22 }{ 7 } \) × (2)2
= \(\frac { 22 }{ 7 } \) × 4 = \(\frac { 88 }{ 7 } \) सेमी2 = 12.57 सेमी2
3 सेमी त्रिज्या वाले वृत्त का क्षेत्रफल = πr2
= \(\frac { 22 }{ 7 } \) × (3)2 = \(\frac { 22 }{ 7 } \) × 9
= \(\frac { 198 }{ 7 } \) सेमी2 = 28.28 सेमी2
यहाँ हम देखते हैं कि दोनों क्षेत्रफलों के मान भिन्न-भिन्न प्राप्त होते हैं। हालांकि यह अन्तर बहुत कम है।