MP Board Class 12th Physics Important Questions Chapter 10 Wave Optics
Wave Optics Important Questions
Wave Optics Objective Type Questions
Question 1.
Choose the correct answer of the following:
Question 1.
A light ray appears to travel in a straight path because :
(a) It is made up of tiny particles
(b) Its velocity is high
(c) Its wavelength is very small
(d) None of the above.
Answer:
(c) Its wavelength is very small
Question 2.
Which of the following phenomenon does not give evidence of wave nature of light:
(a) Refraction
(b) Reflection
(c) Interference
(d) Polarisation.
Answer:
(b) Reflection
Question 3.
Two coherent sources or light must have the same :
(a) Amplitude
(b) Phase difference
(c) Frequency
(d) Both (b) and (c).
Answer:
(c) Frequency
Question 4.
Which of the following wave can not be polarised :
(a) X – rays
(b) Radio waves
(c) Longitudinal waves
(d) Transverse waves.
Answer:
(c) Longitudinal waves
![]()
Question 5.
The intensity of central fringe in Young’s experiment is I. One slit is closed then intensity becomes I0. Which of the following is true :
(a) I = I0
(b) I = 2I0
(c) I = 4I0
(d) No relation between I and I0.
Answer:
(c) I = 4I0
Question 6.
A colourless soap solution in white light appears to be coloured because of :
(a) Reflection
(b) Refraction
(c) Interference
(d) Diffraction.
Answer:
(d) Diffraction.
Question 7.
The ratio of amplitudes of light waves is 2 : 3. Due to their interference, ratio of maximum and minimum intensity of light will be :
(a) 2 : 3
(b) 4 : 9
(c) 5 : 1
(d) 25 : 1.
Answer:
(d) 25 : 1.
Question 8.
Young’s double – slit experiment proves that:
(a) Light rays consist of particles
(b) Light rays are waves
(c) Light rays are neither particles nor waves
(d) None of these.
Answer:
(b) Light rays are waves
![]()
Question 9.
Which of the following cannot be explained by wave nature of light : (MP 2009 Set B)
(a) Polarisation
(b) Interference
(c) Diffraction
(d) Photoelectric effect.
Answer:
(d) Photoelectric effect.
Question 10.
Waves are carrier of :
(a) Energy
(b) Amplitude
(c) Wavelength
(d) Matter.
Answer:
(a) Energy
Question 2.
Fill in the blanks :
- The light is transverse wave, it is proved by ………………. of light.
- In Young’s double slit experiment, the distance between two successive bright fringes is known as ……………….
- The phase difference between two coherent sources of light is ……………….
- In constructive interference of light path difference is always ………………. multiple of \(\frac {λ}{2}\)
- Young’s double – slit experiment proves ………………. theory of light.
- Bending of waves around the comers of an obstacle is known as ……………….
- The phase difference between two points situated in the same wave front is ……………….
- At polarising angle, the angle between reflected and refracted ray is ………………. (MP 2012)
- The surface of medium at an instant of time, in which all the particles of medium vibrates with same phase is called ……………….
- To take clear photographs of clouds is used before the lens of camera. (MP 2009 Set A)
- ………………. rays are used as germs killer. (MP 2009 Set B)
- At polarising angle, the angle between the reflected ray and the refracted ray from a surface is ………………. (MP 2011,13)
- ip+ r = ………………. (MP 2013)
Answer:
- Polarisation
- Width of dark fringes
- Zero or constant
- Even
- Wave
- Diffraction
- Zero
- 90°
- Wavefront
- Polaroids
- Ultraviolet rays
- 90°
- 90°
Question 3.
Match the Columns :
I. (MP 2012)

Answer:
- (c)
- (e)
- (d)
- (b)
- (a)
II. (MP 2010)

Answer:
- (e)
- (d)
- (b)
- (c)
- (a)
Question 4.
Write the answer in one word/sentence :
- What type of wave front will emerge from a point source?
- Which phenomenon explains the colours on soap bubble?
- What is the effect on fringe width if the distance between the coherent sources is decreases?
- How is the wave front related to the direction of corresponding rays.
- What is the phase difference corresponding to a path difference of λ?
Answer:
- Spherical
- Interference
- Increases
- Perpendicular
- 2p.
Wave Optics Very Short Answer Type Questions
Question 1.
What is the phase difference between two points on a wavefront?
Answer:
Zero.
Question 2.
The line perpendicular to wavefront express the direction of what?
Answer:
Direction of propagation of wave.
Question 3.
What is the cause of colours on the thin film of liquid surface?
Answer:
Interference.
Question 4.
What should be the phase difference between two waves producing destructive interference?
Answer:
ϕ = π, 3π, 5π … (2n + 1) π.
Question 5.
Which type of light sources are required for interference of light?
Answer:
Coherent sources.
![]()
Question 6.
What should be the order of aperture of slit to obtain diffraction pattern?
Answer:
Of the order of wavelength of light.
Question 7.
Write formula of fringe width in Young’s double slit experiment.
Answer:
β = \(\frac {Dλ}{d}\)
Where
D → Distance between slit and screen
d → Separation between the slits
λ → Wavelength of light.
Question 8.
Two bulbs each of 60 W are kept very closed to each other. Will they produce interference?
Answer:
No, they will not produce interference because the bulbs are two different sources, they never be coherent.
Question 9.
What is angle between reflected ray and refracted ray at the angle of polarization?
Answer:
90°.
Question 10.
What do you mean by crossed polaroids?
Answer:
If the transmission axis of the two polaroids are perpendicular then these polaroids are called as crossed polaroids.
Question 11.
When a small circular obstacle is placed in the path of light coming from a far distance then a bright spot is observed at the centre of shadow of obstacle. Why?
Answer:
When a small circular obstacle is placed in the path of light then the diffraction takes place at its comers (edges). The diffracted wave produce the constructive interferemce at the centre of shadow. So a bright spot is observed.
Question 12.
The longitudinal waves do not show the phenomenon of polarization why?
Answer:
In the longitudinal waves the vibration of particles of medium takes place along the direction of propagation of waves. Hence they
do not show the polarization.
![]()
Question 13.
Define crossed polaroids.
Answer:
The two polaroids whose transmission axis are perpendicular to each other are called crossed polaroids.
Question 14.
For which arrangement of polarizer and analyzer in the analysis of polarized light, the intensity of light is minimum?
Answer:
When the axis of polarizer and analyser are mutually perpendicular.
Wave Optics Short Answer Type Questions
Question 1.
What is the principle of superposition of waves?
Answer:
When two or more waves reach to a point of a medium simultaneously, the particle vibrates with the resultant amplitude equal to the vector sum of the individual amplitudes.
Let n waves are reaching to a point and displacement of the particle for each wave is \(\vec { { y }_{ 1 } } \) , \(\vec { { y }_{ 2 } } \) , \(\vec { { y }_{ 3 } } \) , ………….
∴ The resultant displacement, y = \(\vec { { y }_{ 1 } } \) + \(\vec { { y }_{ 2 } } \) + \(\vec { { y }_{ 3 } } \) + …….. + \(\vec { { y }_{ n } } \)
Question 2.
When a white light is incident on the soap bubble or on a thin film of oil on f water surface, the beautiful colours are seen why? The soap bubble appears colourful why?
Answer:
When the sunlight is made to incident on a thin film whose thickness is of order of wavelength of light then some of its part gets reflected from its upper surface and remaining part of light is reflected from its lower surface.The interference of these reflected surface takes place. Since the white light is consist of seven colours, so due to interference of these reflected rays of different colours the film or soap bubble appears to be colourful.
Question 3.
In a Young’s double slit experiment the two slits are illuminated by two different lamps which are emitting the light of same wavelength. Will you observe interference pattern? Give reason.
Answer:
The sustained interference pattern will not be observed because two different source may never be coherent for sustained interference the sources should be coherent.
![]()
Question 4.
Explain, interference follows the law of conservation of energy.
Or
When two waves interfere, the energy of few particles become zero, is the energy lost?
Answer:
In the phenomenon of interference the total energy of waves remains constant, only the energy is redistributed. The energy which is lost at destructive interference is gained at the constructive interference. Hence, the energy is conserved.
Question 5.
How would you know that two sources are coherent?
Or
What are coherent sources of light? What are the conditions of two sources being coherent?
Answer:
Coherent sources:
The sources which emit the waves of same frequency with constant phase difference (zero), are called coherent sources.
Conditions:
- The frequency of both the sources should be equal.
- The phase difference should be constant or zero.
Question 6.
What do you mean by interference of light?
Or
What is interference light? Write its one example.
Answer:
When two light waves of same frequency and approximately same amplitude travel in a medium in the same direction then due to the superimposition the intensity of light changes. This phenomenon is called interference.
Example:
The soap bubble and thin film of oil on the water appear to be coloured.
Question 7.
Can the interference be obtained from white light?
Answer:
Yes, in the white light there are seven colours. The position of central bright fringe for all colours remains same. Hence the central bright fringe is white. For the different colours the positions of bright fringes are different.
Question 8.
In Young’s double slit experiment if the wavelength of monochromatic light is increased, then what will be the effect on fringe width?
Answer:
Now, we know that fringe width, β = \(\frac {λD}{d}\)
If D and d are constants, then β ∝ A.
Therefore, if wavelength is increased, fringe w’idth will also be increased.
Question 9.
In Young’s double slit experiment, what happens if screen is moved away from the slit?
Answer:
From the formula, β = \(\frac {λD}{d}\)
If λ and dare constants, then β ∝D. i.e., Fringe width will be increased.
![]()
Question 10.
If the apparatus of Young’s double slit experiment is immersed into water then what will be the effect on fringewidth ?
Answer:
From the formula β = \(\frac {λD}{d}\) it is clear that if D and d are constant then β ∝ λ .
Since the value of λ in the water decreases so the fringe width will decrease.
Question 11.
If the distance between two coherent sources is decreased then what will be the effect on fringe width ?
Answer:
Fringe width will increase because β ∝\(\frac {1}{d}\)
Question 12.
On what factors does the fringe width in Young’s double slit experiment depends? Write only name of factors.
Answer:
According to the formula β = \(\frac {λD}{d}\) the fringe width depends upon
- Wavelength of light
- Distance of slits from the screen and
- Distance between the slits.
Question 13.
What do you mean by diffraction?
Answer:
When an obstacle comes in the path of waves then waves get bent at the obstacle. The bending of the waves around the comers is called diffraction.
Question 14.
How many types of diffraction are there? Write their examples.
Answer:
Diffraction is of two types :
- Fresnel class diffraction
- Fraunhofer class diffraction.example of Fresnel class diffraction is diffraction from straight edge and example of Fraunhofer diffraction is diffraction from a single slit.
Question 15.
What do you mean by polarization?
Answer:
Polarization of light is the phenomenon in which vibrations of electric vectors are restricted in a certain direction on a plane perpendicular to the direction of propagation
Question 16.
Differentiate plane polarized light and unpolarized light.
Answer:
Difference between plane polarized and unpolarized light:
Plane polarized light:
- In plane polarized light, the electric vector vibrates in one direction, normal to the direction of propagation of light.
- When polarized light is passed through a polaroid, which is rotated about the ray, then intensity becomes maximum and minimum.
Unpolarized light:
- The electric vector vibrates in all the directions normal to the direction of propagation of light.
- When this light is passed through a polaroid and polaroid is rotated then intensity of light does not change.
Question 17.
Light waves can be polarized but sound waves can’t. Why?
Answer:
Polarization is possible only in transverse waves not in longitudinal waves. Sound waves are longitudinal waves. Since, light waves are transverse waves, hence they can be polarized.
Question 18.
How the phenomenon of polarization is different from interference and diffraction.
Answer:
Interference and diffraction can occur in transverse as well as in longitudinal wave, but the polarization can take place only in transverse waves.
Question 19.
When an aircraft is travelling at low height, then the pictures on the T.V. screen undergo vibration. Why?
Answer:
When the aircraft is travelling at a lower height, then it reflects the T.V. signals. Interference occurs between the incoming signals and the reflected signals. Hence, vibrations are seen on the pictures in the T.V. screen.
Question 20.
Write down why the sun glasses made of polaroids are much useful than the goggles.
Answer:
Light reflected from the objects are partially plane polarized. The polaroid stops the horizontal component of partially plane polarized light decreasing the dazzling effect. But goggles cannot do so.
Question 21.
What will be the effect on interference pattern in a Young’s double slit experiment if one slit is closed?
Answer:
The interference pattern will not be obtained.
![]()
Question 22.
In which of the following waves the polarization is possible why?
- X – rays
- Sound waves
- Radio waves.
Answer:
In X – rays and Radio waves polarization is possible because these are transverse waves. In sound waves polarization is not possible because they are longitudinal.
Question 23.
Write two limitations of Huygen’s wave theory.
Answer:
- With the help of this theory the photoelectric effect could not be explained.
- According to this theory there is a mediam called ‘ether’ but experimentally it could not be verified.
Question 24.
What is the shape of interference fringes in Young’s double slit experiment?
Answer:
The interference fringes in double slit experiment are like the parallel lines. These lines are parallel to the slit and are bright and dark alternately.
Question 25.
Define the following :
- Spherical wave front
- Plane wavefront
Answer:
1. Spherical wavefront : When the light source is of point type then at any instant at finite distance the locus of all the particles vibrating with same phase is a sphere. It is called spherical wavefront.
2. Plane wavefront : When the source of light is at infinite distance then the wave front formed is called plane wavefront.
Question 26.
Which type of wave do not show the polarization?
Answer:
Longitudinal waves do not show the polarization.
Question 27.
In Young’s double slit experiment if white light is used then only white and dark fringes are obtained. Is this statement true? Why?
Answer:
This statement is not true, because in this condition only central bright fringe is white while the other fringes are coloured.
Question 28.
Two persons separated by a high obstacle like a wall can hear their voice but cannot see each other. Why?
Answer:
For the diffraction of waves it is necessary that the size of obstacle should be of order of the wavelength of wave. The wavelength of sound waves is of order of size of obstacle so the sound waves are diffracted and the person can hear their voice.
The wavelength of light waves is very small while the aperture of obstacle is large so light waves are not diffrected and the persons can not see each other.
Question 29.
On what factors does the diffraction depend?
Answer:
The diffraction depends upon two factors :
- Size of aperture and
- Wavelength.
Question 30.
What is interference of light? Write the necessary conditions for it.
Or
Write any four necessary conditions for interference of light.
Answer:
Interference:
When two light waves of same frequency and approximately same amplitude travel in a medium in the same direction then due to the superimposition the intensity of light changes. This phenomenon is called interference.
Example:
The soap bubble and thin film of oil on the water appear to be coloured.
Conditions for interference:
- Frequencies of light emitted by both sources should be equal.
- Amplitudes of both waves should be almost equal.
- Both waves should move in the same direction.
- Both the sources should be placed close to each other.
- Both the light sources should be narrow.
- Phase difference of the two waves should be zero or should be constant.
- Light sources should be monochromatic.
- If light rays are polarized, then their plane of polarization should be parallel.
- Both the sources should be coherent (i.e phase difference between the two waves should be zero or constant).
Question 31.
State Huygen’s secondary wavelets theory.
Answer:
Huygen’s secondary wavelets theory : The main postulates of this theory are given below:
1. When a disturbance is created in a medium the particles of the medium starts vibrating. The surface in the medium, on which each particle vibrate in same phase is called the wavefront. If the source is like a point, at a finite distance, the wavefront is always spherical. If the source is in form of a slit at a finite distance the wavefront is cylindrical.
2. Every point of the medium on a given wavefront is a source of originating new
disturbances. These new disturbances are called secondary wavelets.
3. These secondary wavelets advances in the medium with same velocity as of original wave.
4. The common tangential surface drawn on these secondary wavelets at any instant, shows the position of new wavefront at that instant.
Question 32.
Write the path difference for constructive and destructive interference in terms of wavelength l.
Answer:
We know that
Phase difference = \(\frac {2π}{λ}\) x path difference
or ϕ = \(\frac {2π}{λ}\) x y … (1)
For constructive interference ϕ = 2nπ … (2)
From eqns. (1) and (2)
\(\frac {2π}{λ}\) = 2nπ
or
For nth bright fringe (constructive interference)
y = yn
or yn = 2n\(\frac {λ}{2}\)
Hence for constructive interference the path difference should be even multiple of \(\frac {λ}{2}\)
For minimum intensity ϕ = (2n +1 )π
or \(\frac {2π}{λ}\) y = (2n +1 )π
or y = (2n +1) \(\frac {λ}{2}\)
or y = (2n + l) \(\frac {λ}{2}\)
For nth dark fringe y = yn
or yn = (2n + 1)\(\frac {λ}{2}\)
![]()
Question 33.
What should be the path difference between the two waves
y1 = a1 sin ωt and y2 = a2 cos(ωt + ϕ)?
Answer:
For first wave y1 = a1 sin ωt
and for second wave y2 = a2 cos(ωt + ϕ)
ory2 = a2 sin (ωt + ϕ + \(\frac {π}{2}\))
The phase difference between first and second wave.

Question 34.
If the distance between the slits is doubled and distance between slit and screen is halved then what will be the effect on fringe width in Young’s double slit experiment?
Answer:
Formula : Fringe width β = \(\frac {Dλ}{2}\)
Let d’, D’ and β’ are changed values of slit separation
Distance between slits and fringe width respectively then
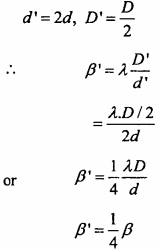
∴ Fringe width will be one fourth of its previous value.
Question 35.
If angle of polarization is 30° then find out refractive index of medium.
Solution:
Given : Angle of polarization ip = 30°
µ = tanip ⇒ µ = tan30°
µ = \(\frac { 1 }{ \sqrt { 3 } }\)
Question 36.
Define the following:
- Plane of vibration
- Plane of polarization.
Answer:
1. Plane of vibration : Plane of vibration is that plane which contains the vibra-tions of electric vector and direction of propagation of wave.
2. Plane of polarization : A plane perpendicular to the plane of vibration and which contains the direction of propagation of waves is called plane of polarization.
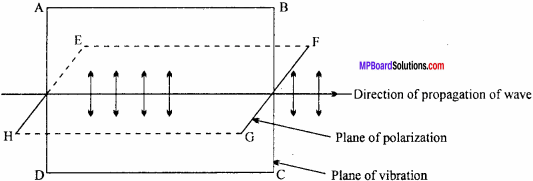
ABCD → Plane of vibration, EFGH → Plane of polarization.
Question 37.
How many types of interference are there? Explain.
Answer:
There are two types of interference.
- Constructive interference
- Destructive interference.
Interference of light:
When two light waves of same frequency and approximately same amplitude travel in a medium in the same direction then due to the superimposition the intensity of light changes. This phenomenon is called interference.
Example:
The soap bubble and thin fiLm of oil on the water appear to be coloured.
Constructive interference:
When two wave super imposed together at a point with same phase i.e. the fall on crest and trough on trough then at that point the intensity of light becomes maximum. This interference is called constructive interference.
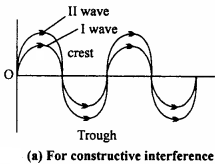
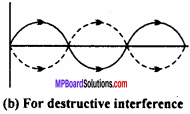
Destructive interference:
When two waves superimposed together at a point in such a way that there is a phase difference of 180° [or (2n – 1) π] then at those points the intensity of light becomes minimum or zero. This interference is called as destructive interference
Conditions:
For constructive interference the phase difference should zero or even multiple of π i.e. ϕ = 2nπ. For destructive interference the phase difference should be 180° or odd multiple of π. i.e. ϕ = (2n + 1) π, where n = 0, 1, 2, 3, ……
Question 38.
What do you mean by coherent sources? Can two independent sources of light produce interference ? How can the coherent waves be obtained?
Answer:
Coherent Sources:
The sources which emit the waves of same frequency with constant phase difference (zero), are called coherent sources.
The phase difference between the waves coming from two different sources varies with time. Hence the two different sources cannot produce interference. The coherent waves can be obtained by different methods such as Fresnel’s biprism method, Amplitude division method etc.
Question 39.
What do you mean by diffraction of light? What is essential condition to obtain diffraction? The diffraction of sound w aves is easier than that of light waves. Why?
Answer:
Diffraction of light:
When an obstacle comes in the path of waves then waves get bent at the obstacle. The bending of the waves around the comers is called diffraction.
Condition:
To obtain diffraction the size of obstacle should be of order of wave length of waves.
In case of sound waves the size of obstacle is of order of wavelength while in case of light the obstacle is usually not of order of wavelength of light so the diffraction of sound waves is easier than that of light waves.
Question 40.
What is the difference between interference and diffraction?
Answer:
Difference between interference and diffraction :
Interference:
- Interference fringes are formed when the two light rays from the coherent sources are superimposed.
- All bright fringes are equally illuminated.
- Width of all fringes are always equal.
- Minimum intensity is zero, so fringes can be distinguished very well.
Diffraction:
- Fringes are formed due to superimposition of light rays from the same source.
- Central fringe is brightest and all other fringes have intensity’ in decreasing order.
- Fringe width decreases when we move away from the centre.
- Minimum intensity fringes are not perfectly darker so it is relatively difficult to distinguish bright and dark fringes.
Question 41.
What is polaroid? State its applications in daily life.
Answer:
Polaroids are large sized manufactured polarizing films capable of producing plane polarized beam of light
Uses:
- These are used in laboratory to produce and analyse plane polarized light.
- These are used in sun glasses.
- These are used in headlights and windscreen of automobile to cut off the dazzling light.
- These are used for viewing three dimensional pictures.
Question 42.
What are polaroids? How will you obtain the plane polarized light by polaroids? How will you distinguish between unpolarized light and plane polarized light?
Answer:
Polariods:
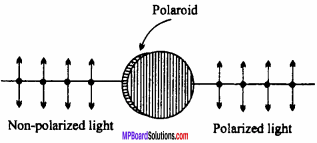
Polaroids are large sized manufactured polarizing films capable of producing plane polarized beam of light. The light obtained from an ordinary source is made to fall on polariod. The light emerging out from the polaroides is plane polarized light. To identify (or distinguish) between polarized and non – polarized light. The beam is made to incident on another polariod. If there is no change in intesity of light on rotating the Polaroid then the light is unpolarized. But if there is variation in the intensity of light then the light is plane polarized.
![]()
Question 43.
What is polaroid? Write its construction and working.
Answer:
Polaroid:
Polaroids are large sized manufactured polarizing films capable of producing plane polarized beam of light.
Construction:
It is a thin film whice is sandwiched between two glass plates. To form this film, the crystal of an organic compound ‘herapathite’ or Iodo – quinine sulphate are kept on a thin film of Nitro cellulose in such a way that the axis of all crystals are parallel to each other.
Working:
The polaroid has a characteristic plane called transmission plane. When an unpolarized light falls on it only the vibrations of electric vector, parallel to the plane of transmission get transmitted. Thus the transmitted light obtained is plane polarized.
Wave Optics Long Answer Type Questions
Question 1.
Explain Huygen’s theory of secondary wavelets.
Answer:
Huygen’s secondary wavelets theory:
1. Each point of wavefront behaves like a new source of light which emits the new waves. These are called secondary wavelets.
2. The secondary wavelets advances in the medium with the velocity same as that of the original waves.
3. The common tangential surface drawn on these secondary wave lets at any in stant shows the position of new wave front at that instant.
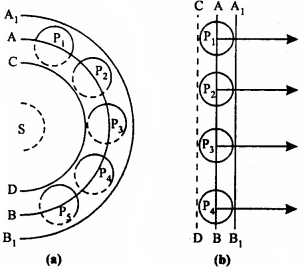
Let S is point type light source AB is a part of spherical wavefront. After time ‘t’ what will be the position of this wavefront it is to be determined. According to Huygen’s secondary wave. let theory every point of wavefront behaves like a source of light. Take points P1 P2, P3, P4, on this wavefront.
The distance travelled by secondary wavelet in time ‘t’ with velocity V be vt. Now by taking P1 P2, P3, P4, …… as centre draw circles of radius vt. Now draw a comman tangential surface A1B1 It will show the new wavefront.
Question 2.
What do you mean by wavefront? How many types of wavefront are there?
Answer:
Wavefront:
An imaginaiy plane made of medium perpendicular to the direction of propagation of waves in which each particle of medium vibrates with same phase is called wavefront. There are three types of wavefronts :
1. Spherical wavefront : When the light source is point type and at finite distance then the wavefront is called spherical wavefront
2. Cylindrical wavefront : When light source is slit type and at a finite distance then the wavefront is called as cylindrical wavefront.
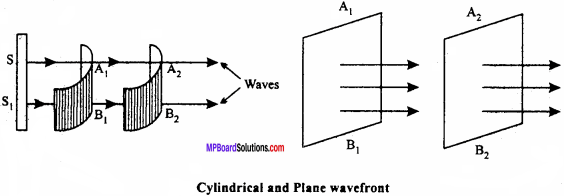
3. Plane wavefront : When light source is at infinite distance then the wavefront obtained is called plane wavefront.
Question 3.
What is interference of light? Write its essential conditions.
Or
State essential condition for interference of light.
Answer:
Interference:
When two light waves of same frequency and approximately same amplitude travel in a medium in the same direction then due to the superimposition the intensity of light changes. This phenomenon is called interference.
Example:
The soap bubble and thin film of oil on the water appear to be coloured.
Conditions for interference:
- Frequencies of light emitted by both sources should be equal.
- Amplitudes of both waves should be almost equal.
- Both waves should move in the same direction.
- Both the sources should be placed close to each other.
- Both the light sources should be narrow.
- Phase difference of the two waves should be zero or should be constant.
- Light sources should be monochromatic.
- If light rays are polarized, then their plane of polarization should be parallel.
- Both the sources should be coherent (i.e phase difference between the two waves should be zero or constant).
Question 4.
What do you mean by interference of light? Define constructive and de – structive interference and write essential conditions for it
Answer:
Interference of light:
When two light waves of same frequency and approximately same amplitude travel in a medium in the same direction then due to the superimposition the intensity of light changes. This phenomenon is called interference.
Example:
The soap bubble and thin fiLm of oil on the water appear to be coloured.
Constructive interference:
When two wave super imposed together at a point with same phase i.e. the fall on crest and trough on trough then at that point the intensity of light becomes maximum. This interference is called constructive interference.

Destructive interference:
When two waves superimposed together at a point in such a way that there is a phase difference of 180° [or (2n – 1) π] then at those points the intensity of light becomes minimum or zero. This interference is called as destructive interference
Conditions:
For constructive interference the phase difference should zero or even multiple of π i.e. ϕ = 2nπ. For destructive interference the phase difference should be 180° or odd multiple of π. i.e. ϕ = (2n + 1) π, where n = 0, 1, 2, 3, ……

Question 5.
How does the diffraction of light take place from a straight edge? Draw energy distribution curve also.
Or
Describe the diffraction of light from a straight edge under the following heads :
- Experimental arrangement
- Observation
- Energy distribution curve.
Answer:
1. Experimental arrangement:
In the fig. S is a narrow slit which is illuminated by a monochromatic light source. A straight edge is placed infront of slit S in such a way that its edge is parallel to the slit. At some distance from the obstacle AB a screen XY is placed. WW’ is a cylindrical wavefront.
2. Observation:
According to geometrical optics above the point O on the screen XY the intensity should be uniform because in this region light rays can reach without any obstruction.
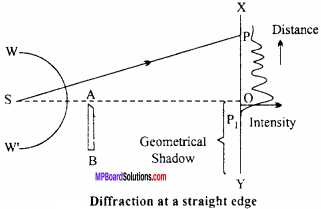
Below the point O there should be complete darkness because the light rays are obstructed by obstacle AB. But actually if not happens. Actually we get the following pattern:
(a) In the region of geometrical shadow some light is reached. The intensity of light rapidly decreases and at point P, the intensity becomes zero. Thus after point P1 complete darkness is obtained.
(b) In the illuminated region OX the dark and bright of decreasing intensity and width are obtained. Ultimately above point P the fringes vanishes and light of uniform intensity is obtained.
3. Energy distribution curve : It is shown in adjacent fig.
![]()
Question 6.
Write any four differences between interference and diffraction.
Answer:
Interference:
- Interference fringes are formed when the two light rays from the coherent sources are superimposed.
- All bright fringes are equally illuminated.
- Width of all fringes are always equal.
- Minimum intensity is zero, so fringes can be distinguished very well.
Diffraction:
- Fringes are formed due to superimposition of light rays from the same source.
- Central fringe is brightest and all other fringes have intensity’ in decreasing order.
- Fringe width decreases when we move away from the centre.
- Minimum intensity fringes are not perfectly darker so it is relatively difficult to distinguish bright and dark fringes.
Question 7.
What do you mean by polarization of light? Describe on experiment to prove that light waves are transverse in nature.
Answer:
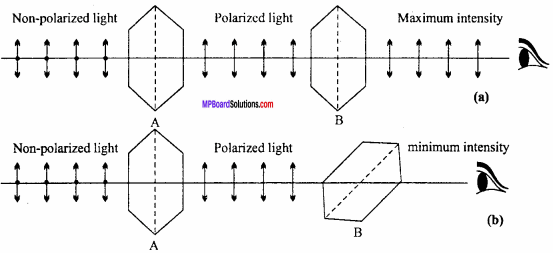
The lack of symmetry about the direction of travel of a wave is called polarization. To demonstrate that light waves are transverse we use two polaroids A and B. These polaroids are placed in such a way that their planes parallel to their vertical axis.
Now beam of light is incident normally on A and the light is seen through B from the other side. In this condition the intensity of light is maximum. Now keeping ‘A’ fixed, the B is rotated by doing this the intensity of light decreases gradually. When the axis of B becomes perpendicular to that of A then the intensity of light becomes minimum. If the ‘B’ is further rotated then the intensity again increases gradually. The intensity becomes maximum again when the axis of A and B again becomes parallel.
By this experiment it is proved that the light waves are transverse in nature
Question 8.
Explain polarization of light by reflection.
Answer:
When a beam of ordinary light is reflected from a transparent medium such as glass etc. then it get partially polarized. With increase in the value of angle of incident, at a particular value of angle of incidence the reflected light is obtained completely plane polarized. This value of angle of incidence is called as angle of polarization.
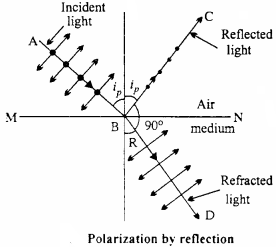
In the fig. AB is incident ray, BC is reflected ray and BD is refracted ray. MN is the interface of air and medium when the light is incident at angle ip (angle of polarization) then the reflected ray along BC is completely plane polarized. The vibrations of plane polarized light are perpendicular to the plane of paper. Hence they are expressed by dots The light obtained in the direction BD is partially polarized.
Explanation:
In a non – polarized light the electric vectors can be dissociated in two rectangular components
- Parallel to the plane of incidence
- Perpendicular to the plane of incidence
These are expressed in the fig. by dots and arrows. When the light falls on refracting surface then its electrons vibrates in the two directions. At the angle of polarization the reflected ray and refracted rays are mutually perpendicular. The vibration parallel to the plane of incidence are along the wave. Hence they can not produce transverse waves along the reflected light. As a result the electric vectors vibrates in a plane perpendicular to the plane of incidence and the completely plane polarized light is obtained.
Question 9.
State Brewster’s law. Prove that at angle of polarization, reflected rays and refracted rays are mutually perpendicular.
Or
What is Brewster’s law? Prove that for light incident on a transparent surface at Brewster’s angle the reflected and refracted rays are normal to each other.
Answer:
Brewster’s law:
The refractive index of a medium is equal to the tangent of angle of polarization, i.e.,
μ = tan ip
Let a light ray is incident at the angle of polarization ip, to the medium of refractive index μ.
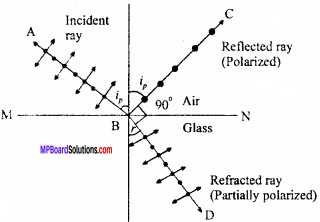
By Snell’s law, μ = \(\frac { sin{ i }_{ p } }{ sinr }\)
Where, r is the angle of refraction. But, μ = tan ip
From eqns. (1) and (2), we get
tan ip = \(\frac { sin{ i }_{ p } }{ sinr }\)
or \(\frac { sin{ i }_{ p } }{ cos{ i }_{ p } }\) = \(\frac { sin{ i }_{ p } }{ sinr }\)
∴ cos ip = sinr
or sin(90°- ip) = sinr
or 90° – ip = r
or ip + r = 90°
But we have, ip + r + ∠CBD = 180°
or 90°+∠CBD = 180°
or ∠CBD = 180°
Thus, reflected ray and refracted ray are mutually perpendicular.
Question 10.
What do you mean by polarization of light? Why the light get polarized by scattering? Explain.
Answer:
Polarization of light:
In plane polarized light, the electric vector vibrates in one direction, normal to the direction of propagation of light. When polarized light is passed through a polaroid, which is rotated about the ray, then intensity becomes maximum and minimurp.
Explanation of polarization by scattering:
It is observed that the sun light is scattered by the molecules of gases in the atmosphere. Due to scattering light rays gets polarized in the adjacent fig. the polarization of light by scattering due to nitrogen molecule is shown.
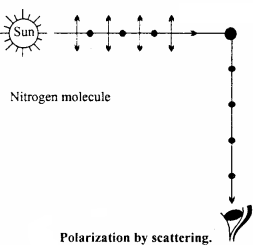
Light incident from sun is unpolarized in which electric field vector can vibrate in all possible directions perpendicular to the direction of propagation of incident light. All these vibrations can be resolved into two components :
- Paralled to plane of paper shown by double arrowed lines.
- Perpendicular to plane of papers shown by dots.
When light waves falls on nitrogen molecules then electrons of molecule start vibrating in their perpendicular directions. The vibration parallel to the plane of paper are along the observer. Therefore these vibrations cannot produce transverse waves in the direction of observer. The vibrations perpendicular to the plane of paper can only produce transverse wave in the direction of the observer. Thus the light entering the eye of observer is plane polarized light.
Question 11.
What are polaroids? Write its construction, working and uses?
Answer:
Polaroids are large sized manufactured polarizing films capable of producing plane polarized beam of light
Uses:
- These are used in laboratory to produce and analyse plane polarized light.
- These are used in sun glasses.
- These are used in headlights and windscreen of automobile to cut off the dazzling light.
- These are used for viewing three dimensional pictures.
Construction:
It is a thin film whice is sandwiched between two glass plates. To form this film, the crystal of an organic compound ‘herapathite’ or Iodo – quinine sulphate are kept on a thin film of Nitro cellulose in such a way that the axis of all crystals are parallel to each other.
Working:
The polaroid has a characteristic plane called transmission plane. When an unpolarized light falls on it only the vibrations of electric vector, parallel to the plane of transmission get transmitted. Thus the transmitted light obtained is plane polarized.
Question 12.
Obtain the conditions for maximum and minimum intensity of light in Young’s double slit experiment
Or
Find out the conditions for constructive and destructive interference of two waves theoriticaily.
Or
What do you mean by interference of light? Two waves having amplitudes a1, a2 and angular frequencies co are superimposed together. Find out intensity in the constructive and destructive interference.
Answer:
Interference:
When two light waves of same frequency and approximately same amplitude travel in a medium in the same direction then due to the superimposition the intensity of light changes. This phenomenon is called interference.
Example:
The soap bubble and thin film of oil on the water appear to be coloured.
Let two waves having same frequency are propagating in same direction in same medium. Their equation are
y1 = a1Sinωt … (1)
and y2 = a2 sin (ωt + ϕ) … (2)
Where, a1 and a2 are their amplitudes and ϕ is phase difference between them.
If both the wave are superimposed together then by the principle of superposition of waves,
\(\vec { y }\) = \(\vec { { y }_{ 1 } } \) + \(\vec { { y }_{ 1 } } \)
or \(\vec { y }\) = a1 sinωt + a2 sinωt (ωt + ϕ)
or y = a1 sinωt + a2 sinωt cosϕ + a2 cosωt sinϕ
or y = (a1 + a2 cosϕ)sinωt + a2ϕ cosωt … (3)
Now let
a1 = a2 cosϕ = R cosϕ … (4)
and a2 sinϕ = R sinθ … (5)
Where, R and θ are constants
Then by eqn. (3),
y = R cosθ sinωt + R sinθcosωt
or y = R sin(ωt + θ) … (6)
Equation (6) shows the resultant wave. Its amplitude is R
Squaring and adding equations (4) and (5)
R2 cos2θ + R2 sin2θ = (a1 + a2 cosϕ)2 + (a2 sinϕ)2
or R2 (cos2θ + sin2) = a1 + 2a1a2 cosϕ + a22 cos2ϕ + a22 sin2ϕ
or R2 = a12 + 2a1a2 cosϕ + a22
or R2 = a12 + a12+ 2a1a2 cosϕ
∵ Intensity is proportional to the R2
I = K(a12 + a12 + 2a1a2 cosϕ) … (7)
Where K is a proportionality constant.
From equation (7) it is clear that the resultant intensity depends upon the phase difference between the two waves.
Condition for constructive interference : from equation (7) it is clear that for maximum intensity
cosϕ= 1
or ϕ = 2nπ, (where, n = 0, 1,2, 3, )
At the points where the waves with same phase are superimposed, the intensity becomes maximum.
Thus Imax = K(a12 + a12 + 2a1a2)
= K(a1 + a2)2
If the path difference for constructive interference is ∆x, then
∆x = \(\frac {λ}{2π}\) x ϕ
∆x = \(\frac {λ}{2π}\) x 2nπ
∆x = 2n x \(\frac {λ}{2}\) = even mul of \(\frac {λ}{2}\)
Condition for destructive interference : From equation (7) it is clear that for minimum intensity
cosϕ = -1
ϕ = (2n -1)π (where, n = 1,2,3, ……… )
or
Hence if the waves are opposite in phase then the destructive interference takes place. If the path difference for destructive interference is ∆x, then
∆x = \(\frac {λ}{2π}\) x ϕ
∆x = \(\frac {λ}{2π}\)(2n – 1)π
∆x = (2n – 1)\(\frac {λ}{2}\) = odd multiple of \(\frac {λ}{2}\)
Expression for intensity in the constructive interference In equation (7) putting cosϕ = 1
I = K(a12 + a12 + 2a1a2 ) = K(a1 + a2)2
If a1 = a1 = a, then
I = K(a + a)2 or I = 4Ka2.
Expression for intensity in destructive interference
Putting cosϕ= -1 in equation (7)
I = K(a12 + a22 + 2a1a2) = K(a1-a2)2
If a1 = a2 = a, then
If a1 = a1 = a, then
I = K(a – a)2 = 0
Question 13.
Derive formula for the width of fringe in Young’s double – slit experiment.
Or
Prove that β = \(\frac { λD}{d}\), where symbols have their usual meanings.
Answer:
Let S is a source which is illuminated with monochromatic light. S1 and S2 are the two slits placed close to each other which are parallel and equidistant from S. Therefore, Si and S2 behave as coherent sources.
Suppose that S1 S2 = d
Screen is placed at distance D from the sources S1 S2 on which interference fringes are formed.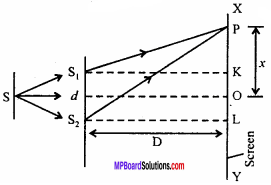
Path difference at point O on screen is
S1O – S2O = 0
∴Intensity at point O will be maximum and will be central fringe.
Let a point P on the screen XY at distance x from the centre.
From S1, drop perpendicular S1K on screen and from S2L, drop perpendicular S2L on screen.
In right angled ∆S1KP,

Now, for the bright fringe,
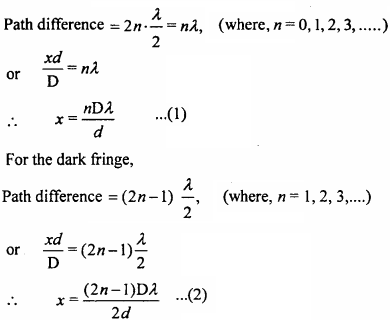
If distances of nth and (n + 1)th fringes from the centre are xn and xn+x, therefore from equation (1),
xn = \(\frac {nDλ}{d}\)
and xn+1 = \(\frac {(n+1)Dλ}{d}\)
Distance between the two consecutive bright fringes or width of the dark fringe,
xn+1 – xn = \(\frac {(n+1)Dλ}{d}\) – \(\frac {nDλ}{d}\)
and xn+1 – xn = \(\frac {Dλ}{d}\) … (3)
Similarly, distance of nth and (n + l)th dark fringes from the point O are xn and xn+1, therefore from equation (2),
xn = \(\frac {(2n – 1)Dλ}{2d}\)
and xn+1 = \(\frac {(2n + 1)Dλ}{2d}\)
Distance between the two consecutive dark fringes or width of the bright fringe,
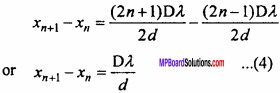
Hence, it is clear from equations (3) and (4), that the width of the fringes are always equal and is given by
β = \(\frac {Dλ}{d}\)
Question 14.
State law of malus and explain it.
Answer:
Malus law:
If a beam of completely plane polarized light is incident on an analyser, then the resultant intensity (I) of light transmitted from the analyser varies directly as the square of the cosine of the angle between the transmission direction of polariser and analyser. i.e., I ∝ cos2θ

Derivation:
Let OP and OA are the pass axes of polarizer and analyser respectively. Let the angle between OP and OA be θ and a be the B amplitude of emergent light from polarizer along axis OP. Amplitude a can be resolved in two components :
- acosθ along pass axis OA of analyzer
- asinθ along pass axis OB of polarizer
Component acos0 only emerges out of analyzer. Therefore intensity of light emerging out from analyzer
I ∝ (acosθ)2
or I = Ka2 cos2θ
Where, K is proportionality constant
or I = I0 cos2θ
Where I0 = ka2 … (1)
∴ I ∝ cos2θ
This is law of malus.
Wave Optics Numerical Questions
Question 1.
What is the Brewster’s angle for transmission from air to glass? (µ = 1.5) (NCERT)
Solution:
Given µ = 1.5
∵µ = tan ip
∴ 1.5 = tan ip
0r ip = tan-1(1.5) = 56.4°.
Question 2.
In a Young’s double slit experiment of the fringe width is 4 mm. Obtain distance of third dark fringe from central bright fringe.
Solution:
Given: β = 4mm = 4 x 10-3 m
For third dark fringe n = 3
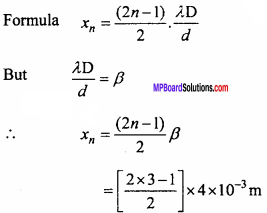
⇒ xn =10 x 10-3 m
= 10-2 m
= 10 mm.
![]()
Question 3.
The angle of polarization for a transparent medium is 60°. Find the angle of refraction and refractive index of medium.
Solution:
Given : Angle of polarization ip = 60°
∴ ip + r = 90°
∴ 60° + r = 90°
r = 90° – 60°
∴ r = 30°.
Again by Brewster’s Law
µ = tan ip = tan 60°
µ = 1.73.
Question 4.
In a Young’s experiment the distance of slits from the screen is 2m. A light of 6000 A is incident on the slits. (i) If the fringe width is 2mm then find distance between the slits. (ii) If the light of wavelenght 4800 Å is incident then find fringe width.
Solution:
Given D = 2m, λ= 6000Å = 6000 x 10-10m = 6 x 10-7m
