MP Board Class 11th Physics Solutions Chapter 5 गति के नियम
गति के नियम अभ्यास के प्रश्न एवं उनके उत्तर
प्रश्न 5.1.
निम्नलिखित पर कार्यरत नेट बल का परिमाण व उसकी दिशा लिखिए:
- एकसमान चाल से नीचे गिरती वर्षा की कोई बूँद।
- जल में तैरता 10 g संहति का कोई कार्क।
- कुशलता से आकाश में स्थिर रोकी गई कोई पतंग।
- 30 km h-1 के एकसमान वेग से ऊबड़ – खाबड़ सड़क पर गतिशील कोई कार।
- सभी गुरुत्वीय पिण्डों से दूर तथा वैद्युत और चुंबकीय क्षेत्रों से मुक्त, अंतरिक्ष में तीव्र चाल वाला इलेक्ट्रॉन।
उत्तर:
- न्यूटन के प्रथम नियमानुसार कोई नेट बल नहीं लगता है।
- न्यूटन के प्रथम नियमानुसार कोई नेट बल नहीं लगता है।
- न्यूटन के प्रथम नियमानुसार कोई नेट बल नहीं लगता है।
- न्यूटन के प्रथम नियमानुसार कोई नेट बल नहीं लगता है।
- चूँकि यह वैद्युत चुम्बकीय एवम् गुरुत्वीय बल उत्पन्न करने वाली भौतिक एजेंसियों से काफी दूर है। अत: कोई बल कार्य नहीं करता है।
प्रश्न 5.2.
0.05 kg संहति का कोई कंकड़ ऊर्ध्वाधर ऊपर फेंका गया है। नीचे दी गई प्रत्येक परिस्थिति में कंकड़ पर लग रहे नेट बल का परिमाण व उसकी दिशा लिखिए:
- उपरिमुखी गति के समय।
- अधोमुखी गति के समय।
- उच्चतम बिंदु पर जहाँ क्षण भर के लिए यह विराम में रहता है। यदि कंकड़ को क्षैतिज दिशा से 45° कोण पर फेंका – जाए, तो क्या आपके उत्तर में कोई परिवर्तन होगा? वायु – प्रतिरोध को उपेक्षणीय मानिए।
उत्तर:
चूँकि उपरोक्त तीनों स्थितियों में, वायु के प्रभाव को नगण्य मानते हुए कंकड़ पर केवल एक ही बल (गुरुत्व बल) 0.5 न्यूटन ऊर्ध्वाधरतः, अधोमुखी लगता है यदि कंकड़ की गति ऊर्ध्वाधर की ओर नहीं है तब भी उत्तर अपरिवर्तित रहता है। कंकड़ उच्चतम बिन्दु पर विराम में नहीं है। इसकी समस्त गति की अवधि में इस पर वेग का एकसमान क्षैतिज घटक कार्यरत रहता है।
![]()
प्रश्न 5.3.
0.1 kg संहति के पत्थर पर कार्यरत नेट बल का परिमाण व उसकी दिशा निम्नलिखित परिस्थितियों में ज्ञात कीजिए:
- पत्थर को स्थिर रेलगाड़ी की खिड़की से गिराने के तुरन्त पश्चात्।
- पत्थर को 36 km h-1 के एकसमान वेग से गतिशील किसी रेलगाड़ी की खिड़की से गिराने के तुरन्त पश्चात्।
- पत्थर को 1ms-2 के त्वरण से गतिशील किसी रेलगाड़ी की खिड़की से गिराने के तुरंत पश्चात्।
- पत्थर 1 ms-2 के त्वरण से गतिशील किसी रेलगाड़ी के फर्श पर पड़ा है तथा वह रेलगाड़ी के सापेक्ष विराम में है। उपरोक्त सभी स्थितियों में वायु का प्रतिरोध उपेक्षणीय मानिए।
उत्तर:
- स्थिर रेलगाड़ी की खिड़की से गिराने पर, पत्थर पर एक मात्र बल उसका भार नीचे की ओर कार्य करेगा। पत्थर पर बल (mg) = 0.1 x 10 = 1 न्यूटन नीचे की ओर।
- इस स्थिति में गाड़ी से गिराने के पश्चात् गाड़ी की गति का उस पर कार्य करने वाले बल पर कोई प्रभाव नहीं होगा तथा पत्थर पर बल उसका भार नीचे की ओर कार्य करेगा। अतः पत्थर बल पर = 1 न्यूटन नीचे की ओर।
- इस स्थिति में (b) के समान बल नीचे की ओर कार्य करेगा।
- पत्थर रेलगाड़ी के सापेक्ष विरामावस्था में है।
∴ पत्थर पर त्वरण = रेलगाड़ी का त्वरण = 1 मीटर/सेकण्ड
∴ पत्थर पर गाड़ी की त्वरित गति के कारण नेट बल।
F = ma = 0.1 x 1 = 0.1 न्यूटन क्षैतिज दिशा में।
प्रश्न 5.4.
l लंबाई की एक डोरी का एक सिरा m संहति के किसी कण से तथा दूसरा सिरा चिकनी क्षैतिज मेज पर लगी खूटी से बँधा है। यदि कण ” चाल से वृत्त में गति करता है तो कण पर (केंद्र की ओर निर्देशित) नेट बल है:
- T
- T – \(\frac { mv^{ 2 } }{ l }\)
- T + \(\frac { mv^{ 2 } }{ l }\)
- 0
T डोरी में तनाव है। (सही विकल्प चुनिए)
उत्तर:
विकल्प
- सही है।
प्रश्न 5.5.
15 ms-1 की आरंभिक चाल से गतिशील 20 kg संहति के किसी पिण्ड पर 50 N का स्थाई मंदन बल आरोपित किया गया है। पिण्ड को रुकने में कितना समय लगेगा?
उत्तर:
दिया है:
u = 15 मीटर/सेकण्ड,
m = 20 किग्रा, मंदन बल,
F = 50 न्यूटन,
v = 0, समय (t) = ?
गति के द्वितीय नियम से,
a = \(\frac{F}{M}\) = \(\frac{50}{20}\) = 2.5 मीटर/सेकण्ड2
सूत्र, v = u + at से,
0 = 15 + ( – 2.5) x t
∴t = \(\frac{15}{2.5}\)
= 6 सेकण्ड
![]()
प्रश्न 5.6.
3.0 kg संहति के किसी पिण्ड पर आरोपित कोई बल 25 s में उसकी चाल को 2.0 ms-1 से 3.5 ms-1 कर देता है। पिण्ड की गति की दिशा अपरिवर्तित रहती है। बल का परिमाण व दिशा क्या है?
उत्तर:
दिया है:
m = 3 किग्रा,
µ = 2 मीटर/सेकण्ड,
t = 25 सेकण्ड,
v = 3.5 मीटर/सेकण्ड, बल का परिणाम
F = ?, बल की दिशा = ?
न्यूटन के गति विषयक द्वितीय नियम से,
पिण्ड पर लगा बल, F = संवेग परिवर्तन की दर
\(\frac{mv – mu}{t}\) = \(\frac{m(v – u)}{t}\)
= \(\frac{3(3.5 – 2)}{25}\) = \(\frac{3 x 1.5}{25}\)
= 1.8 न्यूटन
बल पिण्ड की गति की दिशा में ही लगेगा।
प्रश्न 5.7.
5.0 kg संहति के किसी पिण्ड पर 8 N व 6 N के दो लंबवत् बल आरोपित हैं। पिण्ड के त्वरण का परिमाण व दिशा ज्ञात कीजिए।
उत्तर:
दिया है: m =5 किग्रा,
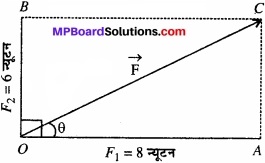
F1 = 8 न्यूटन
F2 = 6 न्यूटन
त्वरण = ?, त्वरण की दिशा = ?
बलों के समान्तर चतुर्भुज नियम से,
पिण्ड पर लगने वाला परिणामी बल,
F = \(\sqrt { F_{ 1 }+F_{ 2 } } \)
= \(\sqrt { 8^{ 2 }\quad +\quad 6^{ 2 }\quad } \)
=10 न्यूटन
परिणामी बल द्वारा F, से बना कोण,
θ = tan-1 \(\frac { F^{ 2 } }{ F_{ 1 } }\)
= tan-1 \(\frac{6}{8}\)
= 37°
पिण्ड पर त्वरण,
a = \(\frac{F}{M}\) = \(\frac{10}{5}\)
= 2 मीटर/सेकण्ड2
प्रश्न 5.8.
36 km h-1 की चाल से गतिमान किसी ऑटो रिक्शा का चालक सड़क के बीच एक बच्चे को खड़ा देखकर अपने वाहन को ठीक 4.0s में रोककर उस बच्चे को बचा लेता है। यदि ऑटो रिक्शा बच्चे के ठीक निकट रुकता है, तो वाहन पर लगा औसत मंदन बल क्या है? ऑटो रिक्शा तथा चालक की संहतियाँ क्रमशः 400 kg और 65 kg हैं।
उत्तर:
दिया है: ऑटो रिक्शा की प्रा० चाल, u = 36 किमी/घण्टा =10 मीटर/सेकण्ड
ऑटो रिक्शा की अन्तिम चाल v = 0, t = 4 सेकण्ड औसत मंदन बल, F = ?
कुल द्रव्यमान = ऑटो रिक्शा का द्रव्यमान + चालक का द्रव्यमान
= 400 + 65 = 465 किग्रा
समी० u = y + at से,
θ = \(\frac{v – u}{t}\) = \(\frac{0 – 10}{4}\)
= -2.5 मीटर/सेकण्ड2
अतः मंदन बल, F = ma = 465 x 2.5
= 1.16 x 103 1.2 x 103 न्यूटन
![]()
प्रश्न 5.9.
20,000 kg उत्थापन संहति के किसी रॉकेट में 5 ms-2 के आरंभिक त्वरण के साथ ऊपर की ओर स्फोट किया जाता है। स्फोट का आरंभिक प्रणोद (बल) परिकलित कीजिए।
उत्तर:
दिया है:
रॉकेट का द्रव्यमान, m = 20,000 किग्रा त्वरण, a = 5 मीटर/सेकण्ड2 माना रॉकेट पर ऊपर की ओर लगने वाला आरम्भिक प्रणोद F है।
यहाँ रॉकेट पर दो बल लगते हैं –
- प्रणोद (F) ऊपर की ओर तथा
- रॉकेट का भार (mg) नीचे की ओर
चूँकि रॉकेट ऊपर उठ रहा है। अतः रॉकेट पर ऊपर की ओर लगने वाला बल,
F1 = F – mg, F1 = ma
∴ ma = F – mg
∴ F = mg + ma
= m (g + a)
= 20,000 (10 + 5)
= 20,000 x 15
= 300,000 x 3 x 105 न्यूटन।

प्रश्न 5.10.
उत्तर की ओर 10 ms-1 की एकसमान आरंभिक चाल से गतिमान 0.40 kg mg संहति के किसी पिण्ड पर दक्षिण दिशा के अनुदिश 8.0 N का स्थाई बल 30 s के लिए आरोपित किया गया है। जिस क्षण बल आरोपित किया गया उसे t =0, तथा उस समय पिण्ड की स्थिति x = 0 लीजिए। t = – 5 s, 25 s, 100 s पर इस कण की स्थति क्या होगी?
उत्तर:
दिया है: प्रारम्भिक वेग, u = 10 मीटर/सेकण्ड, उत्तर दिशा की ओर
आरोपित बल F = 8 न्यूटन, दक्षिण की ओर
m = 0.4 किग्रा, t = 30 सेकण्ड
t = 0 तथा x = 0 पर बल आरोपित किया जाता है।
t = – 5 सेकण्ड पर,
चूँकि t = 0 से पूर्व पिण्ड पर कोई बल आरोपित नहीं था।
अतः इस समयान्तराल में पिण्ड एकसमान वेग से गतिशील होगा।
सूत्र x = x0 + µx + \(\frac{1}{2}\) x 0 x ( – 5)2
= – 50 मीटर
अतः t = – 5 सेकण्ड पर, पिण्ड x = – 50 मीटर पर है।
t=25 सेकण्ड पर,
चूँकि t = 0 से t = 30 सेकण्ड तक पिण्ड पर बल आरोपित है। अतः पिण्ड त्वरित गति में होगा।
चूँकि बल की दिशा प्रारम्भिक वेग से विपरीत है अतः यह मंदन, उत्पन्न करेगा।
सूत्र F = ma से,
मंदन, a = \(\frac{F}{M}\) = \(\frac{8}{0.4}\) = 20 मीटर/सेकण्डर2
अतः (x)t = 25 = 0 + 10 x 25 x \(\frac{1}{2}\) (- 20) x (25)
= – 6000 मीटर = – 6 किमी पर है।
अतः t = 2.5 सेकण्ड पर, पिण्ड x = – 6 किमी पर है।
t = 100 सेकण्ड
xt = 30 = 0 + 10 x 30 + \(\frac{1}{2}\) (-20) x 302
= – 8700 मीटर
30 सेकण्ड पश्चात् वेग,
v = u + at = 10 + (-20) x 30
= – 590 मीटर/सेकण्ड
t = 30 सेकण्ड बाद F = 0 है। अतः t = 30 सेकण्ड बाद पिण्ड आगे के 70 सेकण्ड तक नियत चाल से चलेगा।
∴ S = vt = – 590 x 70 = – 41300 मीटर
∴t = 100 सेकण्ड पर,
x = (x)t = 30 + xt = 70
= – 8700 – 41300 = – 50000
= – 50 किमी।
अतः t = 100 सेकण्ड पर पिण्ड x = – 50 किमी पर है।
![]()
प्रश्न 5.11.
कोई ट्रक विरामावस्था से गति आरंभ करके 2.0 ms – 2 के समान त्वरण से गतिशील रहता है। t = 10s पर, मीटर/सेकण्ड ट्रक के ऊपर खड़ा एक व्यक्ति धरती से 6 m की ऊँचाई से कोई पत्थर बाहर गिराता है। t = 11s पर, पत्थर का (a) वेग, तथा (b) त्वरण क्या है? (वायु का प्रतिरोध उपेक्षणीय मानिए।)
उत्तर:
दिया है:
u = 0, a = 2 मीटर/सेकण्ड2
सूत्र v = u + at से,
vt = 10 = 0 + 2 x 10 = 20 मीटर/सेकण्ड (क्षैतिज दिशा में)
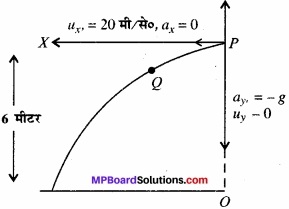
इसी समय व्यक्ति ट्रक पर पत्थर छोड़ता है।
पत्थर छोड़ने के पश्चात् ट्रक का त्वरण पत्थर पर कोई प्रभाव नहीं डालता है। लेकिन इस क्षण तक ट्रक तथा पत्थर का वेग समान होगा। इस दशा में पत्थर गुरुत्वीय त्वरण के अधीन मुक्त गति करेगा।
माना पत्थर बिन्दु P पर छोड़ते हैं। बिन्दु P से जाने वाली क्षैतिज एवम् ऊर्ध्वाधर रेखाओं को क्रमश: x व y – अक्ष माना, जबकि P मूल बिन्दु है।
∴ux = 20 मीटर/सेकण्ड, ax = 0
व uy = 0, ay = – g मीटर/सेकण्ड2
∴x – दिशा में वेग, त्वरण शून्य है। इस प्रकार 1 सेकड़ परचाथ क्ष दिशा मे वेग, ux = 20 मीटर/सेकण्ड
∴पत्थर छोड़ने के 1 सेकण्ड बाद वेग,
v = \(\sqrt { u_{ x }^{ 2 }+u_{ y }^{ 2 } }\)
= \(\sqrt { 20^{ 2 }+10^{ 2 } }\)
= \(\sqrt { 500 }\)
= 22.3 मीटर/सेकण्ड
अत:
(a) गति प्रारम्भ के बाद t = 11 सेकण्ड पर पत्थर का वेग = 22.3 मीटर/सेकण्ड
(b) 11 सेकण्ड पर पत्थर का त्वरण, a = g =10 मीटर/सेकण्ड2
प्रश्न 5.12.
किसी कमरे की छत से 2m लंबी डोरी द्वारा 0.1 kg संहति के गोलक को लटकाकर दोलन आरंभ किए गए। अपनी माध्य स्थिति पर गोलक की चाल 1ms – 1 है। गोलक का प्रक्षेप – पथ क्या होगा यदि डोरी को उस समय काट दिया जाता है जब गोलक अपनी –
- चरम स्थितियों में से किसी एक पर है, तथा –
- माध्य स्थिति पर है?
उत्तर:
- चरम स्थिति पर गोलक की चाल शून्य है। अब डोरी काट दी जाए तब वह ऊर्ध्वाधर अधोमुखी गिरेगा।
- माध्य स्थिति पर गोलक में क्षैतिज वेग होता है। जब डोरी काट दी जाए तब वह किसी परवलयिक पथ के अनुदिश गिरेगा।
प्रश्न 5.13.
किसी व्यक्ति की संहति 70 kg है। वह एक गतिमान लिफ्ट में तुला पर खड़ा है जो:
- 10 ms – 1 की एकसमान चाल से ऊपर जा रही है –
- 5 ms – 2 के एकसमान त्वरण से नीचे जा रही है –
- 5 ms – 2 के एकसमान त्वरण से ऊपर जा रही है तो प्रत्येक प्रकरण में तुला के पैमाने का पाठ्यांक क्या होगा?
- यदि लिफ्ट की मशीन में खराबी आ जाए और वह गुरुत्वीय प्रभाव में मुक्त रूप से नीचे गिरे तो पाठ्यांक क्या होगा?
उत्तर:
दिया है: m=70 किग्रा
1. चूँकि लिफ्ट एकसमान वेग से गतिमान है। अतः त्वरण a=0
तुला के पैमाने का पाठ्यांक,
R = mg = 70 x 9.8 = 686 न्यूटन
2. लिफ्ट का त्वरण, a = 5 मीटर/सेकण्ड2 (नीचे की ओर)
∴तुला के पैमाने का पाठ्यांक,
R = m (g-a)
= 70 x (9.8 – 5) = 336 न्यूटन
3. लिफ्ट का त्वरण, a = 5 मीटर/सेकण्ड (ऊपर की ओर)
∴ तुला के पैमाने का पाठ्यांक,
R = m (g + a)
= 70 ( 9.8 + 5) = 1036 न्यूटन
4. चूँकि लिफ्ट गुरुत्वीय प्रभाव में मुक्त रूप से गिरती है।
∴ a = g
∴ तुला के पैमाने का पाठ्यांक,
R = m (g – a)
= 70 x 0 = 0
![]()
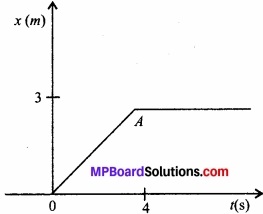
प्रश्न 5.14.
चित्र में 4 kg संहति के किसी पिण्ड का स्थिति – समय ग्राफ दर्शाया गया है।
(a) t < 0; t > 4s; 0
(b) t = 0 तथाt = 4s पर आवेग क्या है?
(केवल एकविमीय गति पर विचार कीजिए)
उत्तर:
(a) t < पर, स्थिति – समय (n – t) ग्राफ समय अक्ष के साथ सम्पाती है। अतः पिण्ड पर आरोपित बल शून्य है। t > 4 सेकण्ड के लिए, x – t ग्राफ समय अक्ष के समान्तर सरल रेखा है। अतः पिण्ड विरामावस्था में है तथा पिण्ड पर कार्यरत बल शून्य है।
0 < t < 4 सेकण्ड के लिए, x – t ग्राफ एक झुकी हुई सरल रेखा है अर्थात् इस काल में पिण्ड की मूल बिन्दु से दूरी नियत दर से लगातार बढ़ रही है अर्थात् इस दौरान नियत है व त्वरण शून्य है। अतः पिण्ड पर आरोपित बल शून्य है।
(b) t=0 से पहले पिण्ड का वेग v 1 = 0
t = 0 के पश्चात् पिण्ड का वेग
V2 = ग्राफ OA का ढाल
= \(\frac{3}{4}\) मीटर/सेकण्ड
अतः t = 0 पर, आवेग = संवेग परिवर्तन की दर
= mv2 – mv1
= 4 x \(\frac{3}{4}\) – 4 x 0
= 3 किग्रा मीटर/सेकण्ड
पुनः t = 4 सेकण्ड के ठीक पहले,
वेग v1, = मीटर/सेकण्ड
t = 4 सेकण्ड के ठीक बाद, वेग v2 = 0
∴t = 4 सेकण्ड दर, आवेग = संवेग परिवर्तन
= mv2 – mv1
= – 3 किग्रा मीटर/सेकण्ड
प्रश्न 5.15.
किसी घर्षणरहित मेज पर रखे 10kg तथा 20kg के दो पिण्ड किसी पतली डोरी द्वारा आपस में जुड़े हैं। 600 N का कोई क्षैतिज बल।
- A पर
- B पर डोरी के अनुदिश लगाया जाता है। प्रत्येक स्थिति में डोरी में तनाव क्या है?
उत्तर:
दिया है: F = 600 न्यूटन
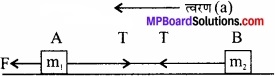
1. माना पिण्ड A पर बल आरोपित करने से दोनों पिण्ड त्वरण a, से चलना प्रारम्भ करते हैं एवम् डोरी में तनाव T है। पिण्ड A पर बल F आगे की ओर एवम् तनाव T पीछे की ओर लगेगा।
अतः इस पिण्ड पर नेट बल,
F = F – T
न्यूटन के गति विषयक द्वितीय नियम से,
F1 = m1a
∴m1a = F – T
या 10a = 600 – T
पिण्ड B पर एकमात्र बल, डोरी का तनाव (T) आगे की ओर लगेगा।
∴ T = m2 = 20a
समी० (2) से T का मान समी0 (1) में रखने पर,
10a = 600 – 20a
या 10a + 20a = 600
∴30a = 600
या a = \(\frac{600}{30}\) = 20 मी/सेकण्डर2
a का यह मान समी० (2) में रखने पर,
T = 20 x 20 = 400 न्यूटन
2. इस स्थिति में, पिण्ड B पर नेट बल F2 = F2 – T होगा।

F – T = m2a
या 600 – T = 20a
पिण्ड A पर नेट बल T आगे की ओर होगा।
∴ T = m, a
= 10a
(4) समी० (4) से T का मान समी० (3) में रखने पर,
600 – 10a = 20a
∴ a = \(\frac{600}{30}\) = 20 मीटर/सेकण्डर2
600 = 20 मीटर/सेकण्ड
a का यह मान समी० (4) में रखने पर
T = 10 x 20
= 200 न्यूटन
प्रश्न 5.16.
8 kg तथा 12 kg के दो पिण्डों को किसी हल्की अवितान्य डोरी, जो घर्षणरहित घिरनी पर चढ़ी है, के दो सिरों से बाँधा गया है। पिण्डों को मुक्त छोड़ने पर उनके त्वरण तथा डोरी में तनाव ज्ञात कीजिए।
उत्तर:
माना घर्षण रहित घिरनी पर हल्की अवितान्य डोरी से द्रव्यमान m1 व m2 लटकाएँ गए हैं।
∴ m1 =8 किग्रा, m2 = 12 किग्रा
माना डोरी में तनाव T व त्वरण a है। यह त्वरण m2 पर नीचे की ओर तथा m1 पर ऊपर की ओर है। m2 की गति की समी० निम्न होगी
F = 12g -T (नीचे की ओर)
गति के नियम से,
F = m2a = 12a
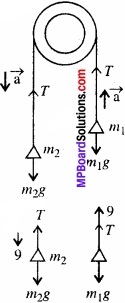
∴ 12g – T = 12a
इसी प्रकार m के लिए,
8g – T = – 8a.
∴ ‘समी० (2) को (1) में से घटाने पर,
4g = 20a
∴ a = \(\frac{4 x 10}{20}\)
= 2 मीटर/सेकण्डर2
∴ समी० (1) से डोरी में तनाव,
T = 12 (g – a) = 12 (10 – 2)
= 12 x 8 = 96 न्यूटन
प्रश्न 5.17.
प्रयोगशाला के निर्देश फ्रेम में कोई नाभिक विराम में है। यदि यह नाभिक दो छोटे नाभिकों में विघटित हो जाता है, तो यह दर्शाइए कि उत्पाद विपरीत दिशाओं में गति करने चाहिए।
उत्तर:
माना विरामावस्था में नाभिक का द्रव्यमान = m विरामावस्था में नाभिक का प्रा० वेग, \(\vec { u } \) = 0
माना विघटित नाभिकों के द्रव्यमान m1 व m2 तथा इनके वेग क्रमश: \(\vec { P_{ i } } \) व \(\vec { P_{ t } } \) है।
माना विघटन से पूर्व तथा बाद में संवेग क्रमशः
\(\vec { P_{ i } } \) व \(\vec { P_{ t } } \)
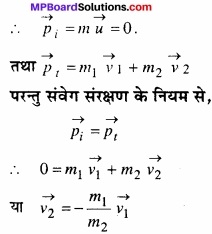
समीकरण (3) से स्पष्ट है कि \(\vec { V_{ 1 } } \) तथा \(\vec { V_{ 2 } } \) विपरीत दिशा में हैं। अतः विघटित नाभिक विपरीत दिशाओं में गति करेंगे।
![]()
प्रश्न 5.18.
दो बिलियर्ड गेंद जिनमें प्रत्येक की संहति 0.05 kg है, 6 ms-1 की चाल से विपरीत दिशाओं में गति करती हुई संघट्ट करती हैं और संघट्ट के पश्चात् उसी चाल से वापस लौटती हैं। प्रत्येक गेंद पर दूसरी गेंद कितना आवेग लगाती है?
उत्तर:
गेंदों का द्रव्यमान m1 = m2 = 0.05 किग्रा
माना पहली गेंद धनात्मक दिशा में चलती है।
∴u1 = 6 मीटर/से
v1 = – 6 मीटर/सेकण्ड
u2 = – 6 मीटर/सेकण्ड
v2 = 6 मीटर/सेकण्ड
सूत्र आवेग = संवेग परिवर्तन से, पहली गेंद का दूसरी गेंद पर आवेग,
= m1v1 – m1u1
= 0.05 x (-6) – 0.05 x 6
= – 0.6 किग्रा मीटर/सेकण्ड
तथा दूसरी गेंद का पहली गेंद पर आवेगा,
= m2v2 – m2u2
= 0.05 x (-6) – 0.05 x – 6
= 0.6 किग्रा मीटर/सेकण्ड
प्रश्न 5.19.
100 kg संहति की किसी तोप द्वारा 0.020 kg का गोला दागा जाता है। यदि गोले की नालमुखी चाल 80 ms – 1 है, तो तोप की प्रतिक्षेप चाल क्या है?
उत्तर:
दिया है: तोप का द्रव्यमान, m1 =100 किग्रा
गोले का द्रव्यमान m2 = 0.02 किग्रा
गोले की नालमुखी चाल, v2 = 80 मीटर/सेकण्ड
तोप की प्रतिक्षेप चाल v1 = ?
प्रश्नानुसार विस्फोट से पूर्व तोप एवम् गोला दोनों विरामावस्था में थे।
संवेग संरक्षण के निकाय से,
विस्फोट से पूर्व संवेग = विस्फोट के बाद संवेग
∴m1v1 + m2v2 = 0
∴v 1 = \(\frac { -m_{ 2 }v_{ 2 } }{ m_{ 1 } }\)
= \(\frac{-0.02 x 80}{100}\) = – 0.016 मीटर/सेकण्ड
प्रश्न 5.20.
कोई बल्लेबाज किसी गेंद को 45° के कोण पर विक्षेपित कर देता है। ऐसा करने में वह गेंद की आरंभिक चाल, जो 54 km/h-1 है, में कोई परिवर्तन नहीं करता। गेंद को कितना आवेग दिया जाता है? (गेंद की संहति 0.15kg है)
उत्तर:
दिया है:
गेंद का द्रव्यमान, m1 = 0.15 किग्रा
प्रा० वेग, u = 54 किमी/घण्टा
= 54 x \(\frac{5}{18}\) = 15 मीटर सेकण्ड
अन्तिम वेग, v = 15 मीटर/सेकण्ड जो कि 4 से 45° के कोण पर है।
माना प्रारम्भिक तथा अन्तिम संवेग क्रमश: \(\vec { P_{ i } } \) व \(\vec { P_{ t } } \)
हैं।
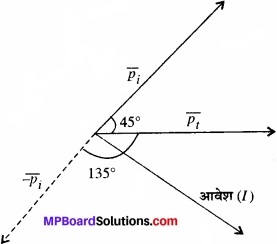
सूत्र आवेग = संवेग परिवर्तन से
\(\vec { I } \) = \(\vec { P_{ t } } \) – \(\vec { P_{ i } } \)
= \(\vec { P_{ t } } \)+ \(\vec { P_{ i } } \)
अतः आवेग दोनों संवेगों का परिणामी है।
∴ \(\vec { I } \) का परिमाण

= 172 न्यूटन सेकण्ड
प्रश्न 5.21.
किसी डोरी के एक सिरे से बँधा 0.25 kg संहति का कोई पत्थर क्षैतिज तल में 1.5 m त्रिज्या के वृत्त पर 40 rev/min की चाल से चक्कर लगाता है? डोरी में तनाव कितना है? यदि डोरी 200N के अधिकतम तनाव को सहन कर सकती है तो अधिकतम चाल ज्ञात कीजिए जिससे पत्थर को घुमाया जा सकता है।
उत्तर:
दिया है: पत्थर का द्रव्यमान, m = 0.25 किग्रा
पत्थर के पथ की त्रिज्या, r = 1.5 मीटर
पर विक्षेपित घूर्णन आवृत्ति, u = 40 चक्कर/मिनट
= \(\frac{40}{60}\)
= \(\frac{2}{3}\) चक्कर/सेकण्ड
माना डोरी में तनाव T है।
जब पत्थर को वृत्ताकार पथ में घुमाते हैं तो आवश्यक अभिकेन्द्र बल डोरी के तनाव T से प्राप्त होता है।
∴ T = mrω2 = mr(2πv)2
डोरी का अधिकतम तनाव, Tmax = 200 न्यूटन
पत्थर की अधिकतम चाल = ?
सूत्र T = \(\frac { mv^{ 2 } }{ 2 } \) से,
v2max = \(\frac { T_{ max\quad }\times \quad R }{ m } \)
= \(\frac{200 x 1.5}{0.25}\)
= 1200
vmax = \(\sqrt { 1200 } \)
= 34.6 = 35 मीटर/सेकण्ड
![]()
प्रश्न 5.22.
यदि अभ्यास 5.21 में पत्थर की चाल को अधिकतम निर्धारित सीमा से भी अधिक कर दिया जाए, तथा डोरी यकायकं टूट जाए, तो डोरी के टूटने के पश्चात् पत्थर के प्रक्षेप का वर्णन निम्नलिखित में से कौन करता है:
- वह पत्थर झटके के साथ त्रिज्यत: बाहर की ओर जाता है।
- डोरी टूटने के क्षण पत्थर स्पर्श रेखीय पथ पर उड़ जाता है।
- पत्थर स्पर्शी से किसी कोण पर, जिसका परिमाण पत्थर की चाल पर निर्भर करता है, उड़ जाता है।
- क्रिकेट का खिलाड़ी गेंद को लपकते समय अपने हाथ गेंद के साथ पीछे को खींचता है।
उत्तर:
1. चूँकि दिक्स्थान से घोड़ा-गाड़ी निकाय पर कोई बाह्य बल कार्यरत नहीं है। घोड़ा तथा गाड़ी के मध्य पारस्परिक बल (क्रिया प्रतिक्रिया के नियम से) निरस्त हो जाता है। अत: फर्श पर, निकाय व फर्श के बीच सम्पर्क बल (घर्षण बल) घोड़े व गाड़ी को विराम से गति में लाने का कारण होते हैं।
2. यात्री के शरीर का जो भाग गद्दी के सीधे सम्पर्क में नहीं है वह जडत्व के कारण गतिमान, बस के यकायक रुकने पर आगे की ओर हो जाता है परिणामस्वरूप यात्री गिर जाते हैं।
3. घास मूवर को किसी कोण पर बल आरोपित करके खींचा या धकेला जाता है। जब हम धक्का देते हैं तब ऊर्ध्वाधर दिशा में सन्तुलन के लिए, अभिलम्ब बल उसके भार से अधिक होना चाहिए जिसके परिणामस्वरूप घर्षण बल बढ़ जाता है। इस प्रकार मूवर को चलाने के लिए अधिक बल आरोपित करना पड़ता है जबकि खींचते समय इसके विपरीत होता है। इसी कारण लॉन मूवर को खींचना आसान होता है।
4. क्रिकेट का खिलाड़ी गेंद को लपकते समय अपने हाथ गेंद के साथ पीछे को ओर इस कारण खींचता है कि ताकि खिलाड़ी संवेग परिवर्तन की दर को घटा दे तथा इस प्रकार गेंद को रोकने के लिए आवश्यक बल को कम करने के लिए हाथ को पीछे की ओर खींचता है।
गति के नियम अतिरिक्त अभ्यास के प्रश्न एवं उनके उत्तर
प्रश्न 5.24.
चित्र में 0.04 kg संहति के किसी पिण्ड का स्थिति-समय ग्राफ दर्शाया गया है। इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिए। पिण्ड द्वारा प्राप्त दो क्रमिक आवेगों के बीच समय – अंतराल क्या है? प्रत्येक आवेग का परिमाण क्या है?
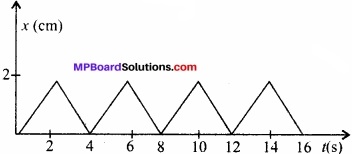
उत्तर:
दिया गया ग्राफ दो समान्तर ऊर्ध्वाधर दीवारों के मध्य एक समान चाल से क्षैतिज गति करती गेंद का ग्राफ हो सकता है जो बार – बार दीवार से टकराकर 2 सेकण्ड बाद दूसरी दीवार से टकराती है। यह प्रक्रिया निरन्तर चलती रहती है अर्थात् प्रत्येक 2 सेकण्ड के पश्चात् पिण्ड का वेग बदलता है।
∴दो क्रमिक आवेगों के बीच समयान्तराल = 2 सेकण्ड
t = 2 सेकण्ड से पहले, वेग v1 = ग्राफ का ढाल
= \(\frac{2}{2}\) = 1 सेमी/सेकण्ड
t = 2 सेकण्ड के बाद वेग V2 = ग्राफ का ढाल
= \(\frac{-2}{-2}\) = -1 सेमी/सेकण्ड
सूत्र आवेग = संवेग परिवर्तन से,
आवेग = Pi = Pt = mv1 – mv2
=m (v1 – v2) = 0.04 [1-(-1)]
= 0.04 x 2 = 0.08 किग्रा सेमी/सेकण्ड
= \(\frac{0.08}{100}\) किग्रा – मीटर/सेकण्ड
= 8 x 10-4 किग्रा – मीटर/सेकण्ड
प्रश्न 5.25,
चित्र में कोई व्यक्ति 1ms-2 त्वरण से गतिशील क्षैतिज संवाहक पट्टे पर स्थित खड़ा है। उस व्यक्ति पर आरोपित नेट बल क्या है? यदि व्यक्ति के जूतों और पट्टे के बीच स्थैतिक घर्षण गुणांक 0.2 है, तो पट्टे के कितने त्वरण तक वह व्यक्ति उस पट्टे के सापेक्ष स्थिर रह सकता है? (व्यक्ति की संहति = 65 kg)

उत्तर:
दिया है: पट्टे का त्वरण, a = 1 मीटर/सेकण्ड2
व्यक्ति का द्रव्यमान, m = 65 किग्रा।
चूँकि व्यक्ति पट्टे पर स्थिर खड़ा है। अत: व्यक्ति का त्वरण a =1 मी/सेकण्ड2
सूत्र F = ma से,
व्यक्ति पर नेट बल, F = 65 x 1
= 65 न्यूटन।
पुनः µs = 0.2
चूँकि पट्टा क्षैतिज अवस्था में है। अत: व्यक्ति पर पट्टे की अभिलम्ब प्रतिक्रिया,
N = mg = 65 x 10 = 650 न्यूटन
माना पट्टे का अधिकतम त्वरण amax है। इस स्थिति में पट्टे के साथ गति करने के लिए व्यक्ति को mammy के बराबर बल की आवश्यकता होगी जो उसे स्थैतिक घर्षण से प्राप्त होगा।
∴mamax ≤ µsN
∴amax = \(\frac { \mu _{ sN } }{ m } \)
= \(\frac{0.2 x 650}{65}\)
= 2 मीटर/सेकण्ड
प्रश्न 5.26.
mसंहति के पत्थर को किसी डोरी के एक सिरे से बाँधकर R त्रिज्या के ऊर्ध्वाधर वृत्त में घुमाया जाता है। वृत्त के निम्नतम तथा उच्चतम बिंदुओं पर ऊर्ध्वाधरतः अधोमुखी दिशा में नेट बल है। (सही विकल्प चुनिए)
निम्नतम बिंदु पर:
- mg – T 1
- mg + T 1
- mg + T 1 – (mv12)/R
- mg – T 1 – (mv12)/R
उच्चतम बिंदु पर:
- mg + T2
- mg – T2
- mg – T 2 + (mv22)/R
- mg + T2 + (mv22)/R
जहाँ T1 तनाव निम्नतम बिन्दु पर ऊपर की ओर तथा भार mg नीचे की ओर है।
तथा नेट अधोमुखी बल = mg + T2
जहाँ’ T2 तनाव उच्चतम बिन्दु पर तथा भार mg दोनों नीचे की ओर हैं।
अतः विकल्प (i) सही है।
![]()
प्रश्न 5.27.
1000 kg संहति का कोई हेलीकॉप्टर 15 ms-2 के ऊर्ध्वाधर त्वरण से ऊपर उठता है। चालक दल तथा यात्रियों की संहति 300 kg है। निम्नलिखित बलों का परिमाण व दिशा लिखिए:
- चालक दल तथा यात्रियों द्वारा फर्श पर आरोपित बल।
- चारों ओर की वायु पर हेलीकॉप्टर के रोटर की क्रिया, तथा।
- चारों ओर की वायु के कारण हेलीकॉप्टर पर आरोपित बल।
उत्तर:
दिया है: हेलीकॉप्टर का द्रव्यमान,
m1 =1000 किग्रा।
चालक दल व यात्रियों का द्रव्यमान m2 = 300 किग्रा।
हेलीकॉप्टर का ऊर्ध्वाधर त्वरण, a =15 मीटर/सेकण्ड2
गुरुत्व के कारण त्वरण, g = 10 मीटर/सेकण्ड 2
1. माना चालक व यात्रियों द्वारा फर्श पर आरोपित बल R1 हैं।
∴R1 = m2 (g + a) = 300 (10 + 15)
= 7500 न्यूटन। जोकि ऊपर की ओर होगा।
2. माना कि रोटर के कारण वायु पर बल R2 है।
∴ R2 = (m1+ m2) (g + a)
= (1000 + 300) (15 + 10)
= 32500 न्यूटन चूँकि हेलीकॉप्टर इस बल के प्रतिक्रिया स्वरूप ऊपर की ओर चलता है अत: यह बल भी ऊपर की ओर दिष्ट होगा।
3. क्रिया प्रतिक्रिया के नियम से, वायु द्वारा हेलीकॉप्टर पर आरोपित बल भी 32500 न्यूटन होगा।
प्रश्न 5.28.
15 ms-1 की चाल से क्षैतिजतः प्रवाहित कोई जलधारा 10-2m अनुप्रस्थ काट की किसी नली से बाहर निकलती है तथा समीप की किसी ऊर्ध्वाधर दीवार से टकराती है। जल की टक्कर द्वारा, यह मानते हुए कि जलधारा टकराने पर वापस नहीं लौटती, दीवार पर आरोपित बल ज्ञात कीजिए।
उत्तर:
दिया है: नली का अनुप्रस्थ क्षेत्रफल, A = 10-2मीटर 2
जल का वेग, µ = 15 मीटर/सेकण्ड
जल का घनत्व, d = 103 किग्रा/मीटर3/सेकण्ड
जल के कारण दीवार पर लगने वाला बल F = ?
नली से प्रतिसेकण्ड निकलने वाले जल का आयतन
= a x v
= 15 x 10-2मीटर3/सेकण्ड
चूँकि दीवार से टकराकर जल वापस नहीं लौटता है।
अतः आरोपित बल = प्रति सेकण्ड निकलने वाले जल के संवेग में परिवर्तन
= 150 x 15
= 2250 न्यूटन
![]()
प्रश्न 5.29.
किसी मेज पर एक – एक रुपये के दस सिक्कों को एक के ऊपर एक करके रखा गया है। प्रत्येक सिक्के की संहतिm है। निम्नलिखित प्रत्येक स्थिति में बल का परिमाण एवं दिशा लिखिए:
- सातवें सिक्के (नीचे से गिनने पर) पर उसके ऊपर रखे सभी सिक्कों के कारण बल,
- सातवें सिक्के पर आठवें सिक्के द्वारा आरोपित बल, तथा
- छठे सिक्के की सातवें सिक्के पर प्रतिक्रिया।
उत्तर:
1. नीचे से सातवें सिक्के के ऊपर तीन सिक्के रखे हैं।
अतः सातवें सिक्के पर तीनों सिक्कों के भार का अनुभव होगा।
∴सातवें सिक्के के ऊपर के सिक्कों के कारण बल = 3mg न्यूटन
2. आठवें सिक्के के ऊपर दो सिक्के रखे हैं। अत: सातवें व आठवें सिक्के के कारण बल, आठवें व इसके ऊपर रखे दो सिक्कों के भारों के योग के समान होगा।
अतः सातवें सिक्के पर आठवें सिक्के के कारण बल
= 3 x mg
= 3mg न्यूटन
3. सातवाँ सिक्का स्वयं व ऊपर के तीन सिक्कों के भारों के योग के समान बल से छठवें सिक्के को दबाएगा।
अतः छठे सिक्के पर सातवें सिक्के के कारण बल = 4mg न्यूटन।
अत: छठे सिक्के की सातवें सिक्के पर प्रतिक्रिया
= 4mg न्यूटन
प्रश्न 5.30.
कोई वायुयान अपने पंखों को क्षैतिज से 15° के झुकाव पर रखते हुए 720 km h-1 की चाल से एक क्षैतिज लूप पूरा करता है। लूप की त्रिज्या क्या है?
उत्तर:
दिया है: वेग = 720 किमी/घण्टा
θ =15° लूप की त्रिज्या, r =?
सूत्र tan θ = \(\frac { v^{ 2 } }{ gr }\) से,܂

प्रश्न 5.31.
कोई रेलगाड़ी बिना ढाल वाले 30 m त्रिज्या के वृत्तीय मोड़ पर 54 kmh-1 चाल से चलती है। रेलगाड़ी की संहति 106 kg है। इस कार्य को करने के लिए आवश्यक अभिकेंद्र बल कौन प्रदान करता है? इंजन अथवा पटरियाँ? पटरियों को क्षतिग्रस्त होने से बचाने के लिए मोड़ का ढाल-कोण कितना होना चाहिए?
उत्तर:
दिया है: v = 54 किमी/घण्टा
= 54 x \(\frac{5}{18}\)
= 15 मीटर/सेकण्ड
r = 30 मीटर
m = 106 किग्रा, g = 10 मीटर/सेकण्ड2
सूत्र tan θ = \(\frac{v}{rg}\) से,
tan θ = \(\frac { (15)^{ 2 } }{ 30\times 10 }\) = \(\frac{3}{4}\)
∴ θ = tan-1(\(\frac{3}{4}\)) = 40°
अर्थात् पटरियों को क्षतिग्रस्त होने से बचाने के लिए पटरियों का झुकाव 40° होना चाहिए।
प्रश्न 5.32.
चित्र में दर्शाए अनुसार 50kg संहति का कोई व्यक्ति 25 kg संहति के किसी गुटके को दो भिन्न ढंग से उठाता है। दोनों स्थितियों में उस व्यक्ति द्वारा फर्श पर आरोपित क्रिया-बल कितना है? यदि 700 N अभिलंब बल से फर्श धंसने लगता है, तो फर्श को धंसने से बचाने के लिए उस व्यक्ति को, गुटके को उठाने के लिए कौन-सा ढंग अपनाना चाहिए?
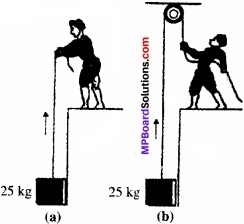
उत्तर:
दिया है: व्यक्ति का द्रव्यमान m1 = 50 किग्रा, गुटके का द्रव्यमान m2 = 25 किग्रा
प्रथम स्थिति (स्थिति-ā) में,
व्यक्ति रस्सी पर 25 g न्यूटन का बल लगाकर ऊपर खींचता है तथा प्रतिक्रिया स्वरूप रस्सी भी व्यक्ति पर नीचे की ओर 25 g N का बल लगाती है।
∴ व्यक्ति पर नेट बल,
F = व्यक्ति का भार + गुटके का भार
= 50g + 25g = 75g = 75 x 10
=750 न्यूटन।
चूँकि व्यक्ति फर्श पर खड़ा है अतः व्यक्ति फर्श पर यही बल आरोपित करेगा।
द्वितीय स्थिति (स्थिति – b) में, व्यक्ति गुटके को उठाने के लिए, रस्सी पर 25 g न्यूटन का बल नीचे की ओर लगाता है। अतः रस्सी भी इतना ही बल व्यक्ति पर ऊपर की ओर लगाएगी।
∴ व्यक्ति पर नेट बल
F = व्यक्ति का भार – रस्सी द्वारा लगाया गया बल
=50 g – 25g
= 25 g = 250 न्यूटन।
यही बल व्यक्ति फर्श पर लगाता है।
उपरोक्त वर्णन से स्पष्ट है कि स्थिति a में फर्श धंस जाएगा। अतः इससे बचाने के लिए यह ढंग अनुप्रयुक्त है।
प्रश्न 5.33.
40 kg संहति का कोई बंदर 600 N का अधिकतम तनाव सह सकने योग्य किसी रस्सी पर चढ़ता है (चित्र)। नीचे दी गई स्थितियों में से किसमें रस्सी टूट जाएगी:
- बंदर 6 ms-2 त्वरण से ऊपर चढ़ता है,
- बंदर 4 ms-2 त्वरण से नीचे उतरता है,
- बंदर5 ms-1 की एकसमान चाल से रस्सी पर चढ़ता है,
- बंदर लगभग मुक्त रूप से गुरुत्व बल के प्रभाव में रस्सी से गिरता है।
(रस्सी की संहति उपेक्षणीय मानिए।)

उत्तर:
माना बन्दर रस्सी पर T बल नीचे की ओर लगाते हुए a त्वरण से ऊपर की ओर चलता है। अतः क्रिया प्रतिक्रिया के नियम से, रस्सी भी बन्दर पर T बल ऊपर की ओर लगाएगी।
∴ बन्दर पर नेट बल,
F = T – mg (ऊपर की ओर)
पुनः सूत्र F = ma से,
ma = T – mg
∴रस्सी पर तनाव, T = mg + ma
1. दिया है: a = 6 मीटर/सेकण्ड2 m = 40 किग्रा, g=10 मीटर/सेकण्डर2
∴ T = 40 x 10 + 40 x 6
= 640 न्यूटन
परन्तु रस्सी पर अधिकतम तनाव 600 न्यूटन है अतः रस्सी टूट जाएगी।
2. दिया है: a = -4 मीटर/सेकण्डर2
∴ तनाव T = 40 x 10 – 40 x 4
= 240 न्यूटन
3. दिया है: a = 0, चूँकि v =5 मीटर/सेकण्ड नियत है।
∴ तनाव, T = 40 x 10 – 40 x 0
= 400 न्यूटन।
4. मुक्त रूप से गिरते हुए, a = – g
∴ तनाव, T = 40 x g – 40 x g
अतः रस्सी केवल प्रथम स्थिति में टूटेगी।
प्रश्न 5.34.
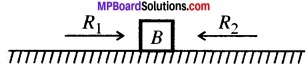
दो पिण्ड A तथा B, जिनकी संहति क्रमशः 5 kg तथा 10 kg है, एक दूसरे के संपर्क में एक मेज पर किसी दृढ़ विभाजक दीवार के सामने विराम में रखे हैं। (चित्र) पिण्डों तथा मेज के बीच घर्षण गुणांक 0.15 है। 200 N का कोई बल क्षैतिजत: A पर आरोपित किया जाता है। (a) विभाजक दीवार की प्रतिक्रिया, तथा (b) A तथा B के बीच क्रिया-प्रतिक्रिया बल क्या हैं? विभाजक दीवार को हटाने पर क्या होता है? यदि पिण्ड गतिशील है तो क्या (b) का उत्तर बदल जाएगा? µs, तथा µk के बीच अंतर की उपेक्षा कीजिए।
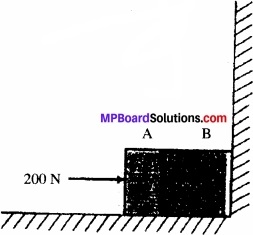
उत्तर:
विभाजक दीवार होने पर, पिण्ड विरामावस्था में होंगे।
∴ पिण्डों का त्वरण, a=0
माना कि पिण्ड A, B पर R1 बल आरोपित करता है जबकि पिण्ड B, A पर विपरीत दिशा में R2, बल आरोपित करता है।
चूँकि पिण्ड A स्थिर अवस्था में है। अतः इस पर नैट बल शून्य होगा।
F = 200 न्यूटन
i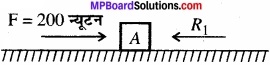
∴ R1 – R2
∴ R2 = R 1 = 200 न्यूटन
विभाजक दीवार हटाने पर पिण्ड गतिशील हो जाते हैं एवम् घर्षण बल कार्यशील हो जाते हैं।
इस दशा में पिण्ड A का बल आरेख चित्र में दिया गया है।
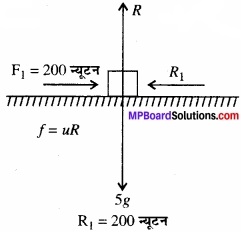
मेज की अभिलम्ब प्रतिक्रिया, R = 5g न्यूटन
माना पिण्ड A, त्वरण a से चलना प्रारम्भ करता है तब पिण्ड का गति समीकरण निम्न होगा –
200 – R1 – µR = 59
∴ R1 – R1 – 5µg = 5a.
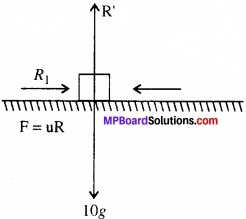
पिण्ड B का बल आरेख चित्र के अनुसार है।
∴अभिलम्ब प्रतिक्रिया, R’ = 10g
तथा गति का समीकरण
R1 – µR’ = 10a.
∴R1 – 10µg = 10a
समी० (i) व (ii) को जोड़ने पर,
200 – 15µg = 15a
∴त्वरण a = \(\frac{200 -15µg}{15}\)
=11.83 ~ 12 मीटर/सेकण्ड2
अर्थात् पिण्डों के गतिशील हो जाएंगे ा का मान समीही (२) मे रकने पर,
R1 – 10 x 0.15 x 10 = 10 x 12
∴R1 = 120 + 15 = 135 न्यूटन।
अर्थात् पिण्डों के गतिशील होने पर बाग़ (बी) का अंतर परिवृत्तिथ हो गए है
प्रश्न 5.35.
15 kg संहति का कोई गुटका किसी लंबी ट्राली पर रखा है। गुटके तथा ट्राली के बीच स्थैतिक घर्षण गुणांक 0.18 है। ट्राली विरामावस्था से 20s तक 0.5 ms-2 के त्वरण से त्वरित होकर एकसमान वेग से गति करने लगती है। (a) धरती पर स्थिर खड़े किसी प्रेक्षक को, तथा (b) ट्राली के साथ गतिमान किसी अन्य प्रेक्षक को, गुटके की गति कैसी प्रतीत होगी, इसकी विवेचना कीजिए।
उत्तर:
दिया है: गुटके का द्रव्यमान, m = 15 किग्रा,
स्थैतिक घर्षण गुणांक, µs = 0.18
t = 20 सेकण्ड के लिए, ट्राली का त्वरण,
a1 = 0.5 मीटर/सेकण्ड 2
t = 20 सेकण्ड के पश्चात् ट्राली का वेग अचर है।
चूँकि प्रारम्भ में ट्राली त्वरित गति करती है। अत: यह एक अजड़त्वीय निर्देश तन्त्र का उदाहरण है।
अतः गुटके पर छद्द बल
F = ma, = 15 x 0.5 = 7.5 न्यूटन बल पीछे की ओर कार्य करेगा।
ट्राली के फर्श द्वारा गुटके पर लगाया गया अग्रगामी घर्षण बल,
F2 = µN = 0.18 x (15 x 10) = 27 न्यूटन
चूँकि घर्षण बल पश्चगामी बल की तुलना में कम है अतः गुटका पीछे की ओर नहीं फिसलेगा व ट्राली के साथ – साथ गतिमान रहेगा।
(a) धरती पर स्थिर खड़े प्रेक्षक को गुटका ट्राली के साथ गति करता प्रतीत होगा।
प्रश्न 5.36. चित्र में दर्शाए अनुसार किसी ट्रक का पिछला भाग खुला है तथा 40 kg संहति का एक संदूक खुले सिरे से 5 m दूरी पर रखा है। ट्रक के फर्श तथा संदूक के बीच घर्षण गुणांक 0.15 है। किसी सीधी सड़क पर ट्रक विरामावस्था से

गति प्रारंभ करके 2 ms-2 से त्वरित होता है। आरंभ बिंदु से कितनी दूर चलने पर वह संदूक ट्रक से नीचे गिर जाएगा? (संदूक के आमाप की उपेक्षा कीजिए।)
उत्तर:
दिया है: घर्षण गुणांक, µ = 0.15
संदूक का द्रव्यमान = 40 किग्रा
खुले सिरे से दूरी, s = 5 मीटर, ट्रक के लिए µ = 0, त्वरण = 2 मीटर/सेकण्ड2 ट्रक द्वारा तय दूरी (जबकि संदूक गिर जाता है) = ?
चूँकि ट्रक की गति त्वरित है अतः यह एक अजड़त्वीय निर्देश तन्त्र होगा।
अतः ट्रक के पीछे रखे संदूक पर पीछे की ओर एक छद्म बल (F =ma) होगा।
∴ F = 40 x 2 = 80 न्यूटन
संदूक पर स्थैतिक घर्षण बल (µs,N) आगे की ओर लगेगा।
संदूक पर नेट बल,
F1 = F – usN
= 80 – 0.15 x 40 x 10
= 20 न्यूटन (पीछे की ओर)
अत: ट्रक के सापेक्ष संदूक का त्वरण a1 = \(\frac { F_{ 1 } }{ m }\) = \(\frac{20}{40}\)
= 0.5 मीटर/सेकण्ड2(पीछे की ओर)
माना संदूक 5 मीटर चलने में। समय लेता है।
∴ सूत्र s = ut + \(\frac{1}{2}\) at2 से,
= 0 + \(\frac{1}{2}\) x 2 x 20 = 20 मीटर
![]()
प्रश्न 5.37.
15 cm त्रिज्या का कोई बड़ा ग्रामोफोन रिकॉर्ड 33 – rev/min की चाल से घूर्णन कर रहा है। रिकॉर्ड पर उसके केंद्र से 4 cm तथा 14 cm की दूरियों पर दो सिक्के रखे गए हैं। यदि सिक्के तथा रिकॉर्ड के बीच घर्षण गुणांक 0.15 है तो कौन-सा सिक्का रिकॉर्ड के साथ परिक्रमा करेगा?
उत्तर:
दिया है: पथों की त्रिज्याएँ
r1 = 0.04 मीटर, r2 = 0.14 मीटर
घर्षण आवृत्ति v = 33 \(\frac{1}{3}\)
= \(\frac{100/3}{60}\)
= \(\frac{5}{9}\) चक्र/सेकण्ड
घर्षण गुणांक, v = 0.15
सिक्कों को रिकायी पर धूमने होथु आवश्यक अभिकेंद्र बाल m1r1ω2 व m2r2ω2 शौथिक दर्शन बाल से प्रप्थ होगा

= 0.12 मीटर = 12 सीमी
पहले सिक्के के लिए, r1 = 0.04 मीटर < r दूसरे सिक्के के लिए,
जबिक r2 = 0.14 मीटर > 0.12
अतः दूसरा सिक्का रिकार्ड से पिसलकर बहार गिर जाएगा
प्रश्न 5.38.
आपने सरकस में ‘मौत के कुएँ’ (एक खोखला जालयुक्त गोलीय चैम्बर ताकि उसके भीतर के क्रियाकलापों को दर्शक देख सकें) में मोटरसाइकिल सवार को ऊर्ध्वाधर लूप में मोटरसाइकिल चलाते हुए देखा होगा। स्पष्ट कीजिए कि वह मोटरसाइकिल सवार नीचे से कोई सहारा न होने पर भी गोले के उच्चतम बिन्दु से नीचे क्यों नहीं गिरता? यदि चैम्बर की त्रिज्या 25 m है, तो ऊर्ध्वाधर लूप को पूरा करने के लिए मोटरसाइकिल की न्यूनतम चाल कितनी होनी चाहिए?
उत्तर:
गोलीय चैम्बर के उच्चतम बिन्दु पर, मोटर साइकिल सवार चैम्बर को अपकेन्द्र बल के कारण बाहर की ओर दबाता है जिसके प्रतिक्रिया स्वरूप चैम्बर भी सवार पर गोले के केन्द्र की ओर प्रतिक्रिया R लगाता है। यहाँ मोटर साइकिल व सवार का भार (mg) भी गोले के केन्द्र की ओर कार्य करते हैं। सवार को वृत्तीय गति के लिए आवश्यक अभिकेन्द्र बल दोनों बल ही प्रदान करते हैं। इसी कारण सवार गिरता नहीं है।
∴इस स्थिति में गति का समीकरण
R+ mg = \(\frac { -m_{ 2 }v_{ 2 } }{ m_{ r } } \)
परन्तु ऊर्ध्वाधर लूप को पूरा करने के लिए उच्चतम बिन्दु पर न्यूनतम चाल होगी।
∴ R = 0 होगा।
⇒mg = \(\frac { -m_{ 2 }v_{ 2 } }{ m_{ r } } \)
∴ v = \(\sqrt { gr }\) = \(\sqrt { 10 x 25 }\) = 15.8 मीटर/सेकण्ड
प्रश्न 5.39.
70 kg संहति का कोई व्यक्ति अपने ऊर्ध्वाधर अक्ष पर 200 rev/min की चाल से घूर्णन करती 3 m त्रिज्या की किसी बेलनाकार दीवार के साथ उसके संपर्क में खड़ा है। दीवार तथा उसके कपड़ों के बीच घर्षण गणांक 0.15 है। दीवार की वह न्यूनतम घूर्णन चाल ज्ञात कीजिए, जिससे फर्श को यकायक हटा लेने पर भी, वह व्यक्ति बिना गिरे दीवार से चिपका रह सके।
उत्तर:
दिया है: m = 70 किग्रा,
घूर्णन आवृत्ति, v = 200 चक्र/मिनट
= \(\frac{200}{60}\)
= \(\frac{10}{3}\) चक्र/सेकण्ड
त्रिज्या, r = 3 मीटर
घर्षण गुणांक, µ = 0.15
घूर्णन करते समय, व्यक्ति दीवार को बाहर की ओर दबाता है तथा दीवार का अभिलम्ब प्रतिक्रिया आवश्यक अभिकेन्द्र बल प्रदान करती है जो कि केन्द्र की ओर दिष्ट होता है।
∴Fc = mrω2
घर्षण बल, जोकि व्यक्ति के भार को सन्तुलित करता है,
F = mg = µFc
∴ ω2 = µ.mrω2
∴ω2 = \(\sqrt { \frac { g }{ \mu r } }[latex]
= [latex]\sqrt { \frac { 10 }{ 0.15\quad } \times \quad 3 }\)
= 4.72 = 5 रेडियन/सेकण्ड
![]()
प्रश्न 5.40.
R त्रिज्या का पतला वृत्तीय तार अपने ऊर्ध्वाधर व्यास के परितः कोणीय आवृत्ति ω से घूर्णन कर रहा है। यह दर्शाइए कि इस तार में डली कोई मणिका ω ≤ \(\sqrt { g/R } \) के लिए अपने निम्नतम बिंदु पर रहती है। ω = 2g/R के लिए, केंद्र से मनके को जोड़ने वाला त्रिज्य सदिश ऊर्ध्वाधर अधोमुखी दिशा से कितना कोण बनाता है। (घर्षण को उपेक्षणीय मानिए।)
उत्तर:
माना कि किसी समय मणिका R त्रिज्या के गोले में A बिन्दु पर है। A बिन्दु पर, वृत्तीय तार की अभिलम्ब प्रतिक्रिया M नीचे की ओर A0 के अनुदिश होगी जिससे ऊर्ध्वाधर तथा क्षैतिज
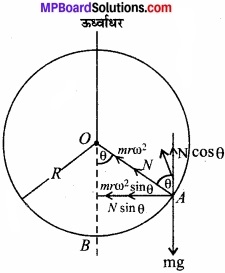
घटकों को वियोजित कर सकते हैं। यहाँ N cos θ भार को सन्तुलित करता है जब N sin θ आवश्यक अभिकेन्द्र बल mrω2 प्रदान करता है।
जहाँ 0 = वृत्त का केन्द्र
θ = त्रिज्या सदिश द्वारा ऊर्ध्व AO से बना कोण
N cos θ = mg
तथा N sin θ = mRω2 sinθ
समी० (1) से (2) से भाग देने पर
cos θ = \(\frac { g }{ R\omega ^{ 2 } } \)
मणिका को निम्नतम बिन्दु B पर रखने के लिए
ω = ≤ \(\sqrt { g/R } \) इस सिद्दिम
∴जब ω = \(\sqrt { \frac { 2g }{ R } } \)
समी० (3) से,
cos θ =\(\frac { g }{ R.2g } \) x R = \(\frac{1}{2}\) = cos 60°
θ = 60°