MP Board Class 11th Physics Solutions Chapter 15 तरंगें
तरंगें अभ्यास के प्रश्न एवं उनके उतर
प्रश्न 15.1.
2.50 kg द्रव्यमान की 20 cm लंबी तानित डोरी पर 200 N बल का तनाव है। यदि इस डोरी के एक सिरे को अनुप्रस्थ झटका दिया जाए तो उत्पन्न विक्षोभ कितने समय में दूसरे सिरे तक पहुँचेगा?
उत्तर:
दिया है: तनाव T = 200 N, डोरी की लम्बाई, l – 20 मी,
∴ डोरी का द्रव्यमान प्रति एकांक लम्बाई
m = \(\frac{M}{l}\) = \(\frac{2.50}{20.0}\) = 0.125 kg m-1
हम जानते हैं कि अनुप्रस्थ तरंगों का वेग,
v = \(\sqrt { \frac { T }{ m } } \) = \(\sqrt { \frac { 200 }{ 0.125 } } \)
= 40 ms-1
माना अनुप्रस्थ तरंगों द्वारा एक सिरे से दूसरे सिरे तक पहुँचने में लिया गया समय t है।
∴ सूत्र t = डोरी की ल०/डोरी का वेग,
∴ t = \(\frac{1}{v}\) = \(\frac{20}{40}\) = 0.5 s
![]()
प्रश्न 15.2.
300 m ऊँची मीनार के शीर्ष से गिराया गया पत्थर मीनार के आधार पर बने तालाब के पानी से टकराता है। यदि वाय में ध्वनि की चाल 340 ms-1 है तो पत्थर के टकराने की ध्वनि मीनार के शीर्ष पर पत्थर गिराने के कितनी देर बाद सुनाई देगी? (g = 9.8 ms-2)
उत्तर:
दिया है: पत्थर का प्रारम्भिक वेग u = 0
त्वरण a = g = 9.8 मीटर/से०2
मीनार की ऊँचाई h = 300 m
वायु में ध्वनि की चाल v = 340 ms-1
माना t1 = पत्थर द्वारा गिरने में लिया गया समय
व t2 = ध्वनि द्वारा मीनार के आधार से शीर्ष तक पहुँचने में लिया गया समय
माना t = शीर्ष पर ध्वनि सुनाई देने का समय है।
अतः t = t1 + t2 ………. (i)
गति के समी० से
s = ut + \(\frac{1}{2}\) at2
दिया है: s = h, u = 0, a = g, t = t1
∴ h = 0 + \(\frac{1}{2}\) gt12
या t1 = \(\sqrt { \frac { 2h }{ g } } \)
या t1 = \(\sqrt { \frac { 2\times 300 }{ 9.8 } } \) = 7.82 s …….. (ii)

या t2 = \(\frac{300}{340}\) = \(\frac{15}{7}\) = 0.88s …….. (iii)
∴ समी० (i), (ii) व (iii) से,
t = 7.82 + 0.88 = 8.7s
प्रश्न 15.3.
12.0 m लंबे स्टील के तार का द्रव्यमान 2.10 kg है। तार में तनाव कितना होना चाहिए ताकि उस तार पर किसी अनुप्रस्थ तरंग की चाल 20°C पर शुष्क वायु में ध्वनि की चाल (343 ms-1) के बराबर हो।
उत्तर:
दिया है: t = 12 मीटर, M = 2.10 किग्रा
माना कि तार में तनाव = T
तथा तार की द्रव्यमान प्रति एकांक लम्बाई m है।
∴ m = \(\frac { M_{ s } }{ l } \) = \(\frac{2.10}{12}\)
= 0.175 किग्रा प्रति मीटर
तार में अनुप्रस्थ तरंग की चाल = 20°C 0
शुष्क वायु में ध्वनि की चाल = 343 मीटर/सेकण्ड
हम जानते हैं कि तार में अनुप्रस्थ तरंग की चाल
v = \(\sqrt { \frac { T }{ m } } \)
या v2 = \(\frac{T}{m}\)
∴ T = mv2 = 0.175 × (343)2
= 20588.6 किग्रा मीटर/सेकण्ड2
= 2.06 × 104 न्यूटन।
![]()
प्रश्न 15.4.
सूत्र v = \(\sqrt { \frac { \gamma P }{ \rho } } \) का उपयोग करके स्पष्ट कीजिए कि वायु में ध्वनि की चाल क्यों
(a) दाब पर निर्भर नहीं करती।
(b) ताप के साथ बढ़ जाती है, तथा।
(c) आर्द्रता के साथ बढ़ जाती है?
उत्तर:
(a) वायु में ध्वनि की चाल पर दाब का प्रभाव:
वायु में ध्वनि की चाल सूत्र v = \(\sqrt { \frac { vP }{ d } } \), से प्रतीत होता है कि दाब P के बदलने पर ध्वनि की चाल (v) का मान भी बदल जाता है। लेकिन वास्तव में ऐसा नहीं होता है। माना कि परमताप T पर किसी गैस के 1 ग्राम – अणु द्रव्यमान का आयतन V व दाब P है। माना कि गैस का अणुभार तथा घनत्व क्रमश: M व d है।
∴ गैस का आयतन, V =  = \(\frac{M}{d}\)
= \(\frac{M}{d}\)
∴ गैस समीकरण PV = RT से,
\(\frac{Pm}{d}\) = RT
या \(\frac{P}{d}\) = \(\frac{RT}{m}\) = (ताप के नियत होने पर)
अतः ताप (T) के नियत रहने पर, यदि दाब P का मान बदलेगा तब उसके साथ घनत्व (d) का मान भी बदलेगा लेकिन P/d का मान नियत रहेगा। इससे ध्वनि की चाल का मान समान रहेगा। अतः वायु या गैस का ताप नियत रहे तो ध्वनि की चाल पर दाब परिवर्तन का कोई प्रभाव नहीं पड़ता है।
(b) वायु में ध्वनि की चाल पर ताप का प्रभाव:
किसी गैस के लिए P/d का मान गैस के ताप पर निर्भर करता है। किसी गैस को गर्म करने पर,
(i) ताप बढ़ने पर यदि गैस फैलने के लिए स्वतन्त्र है, तो उसका घनत्व कम हो जाता है। जिससे P/d का मान बढ़ेगा।
(ii) यदि गैस किसी.बर्तन में बंद है तो उसका घनत्व (d) वही रहेगा लेकिन दाब बढ़ जायेगा जिससे P/d का मान बढ़ेगा।
अर्थात् गैस का ताप बढ़ने पर उसमें ध्वनि की चाल बढ़ती है। जब किसी गैस के एक ग्राम अणु, घनत्व व आयतन क्रमश: M, d व v है तब V = \(\frac{M}{d}\)
यदि गैस का दाब P व परमताप T हो तो गैस समीकरण PV = RT से,
\(\frac{Pm}{d}\) = RT
या \(\frac{P}{m}\) = \(\frac{RT}{m}\)
∴ गैस में ध्वनि की चाल v = \(\sqrt { \frac { vP }{ d } } \)
= \(\sqrt { \frac { \gamma RT }{ M } } \)
अतः किसी गैस में ध्वनि की चाल उसके परमताप के वर्गमूल के समानुपाती होती है।
v ∝\(\sqrt { T } \)
(c) वायु में ध्वनि की चाल पर आवृत्ति का प्रभाव:
आर्द्र वायु का घनत्व शुष्क वायु के घनत्व की तुलना में कम होता है। अतः आर्द्र वायु में ध्वनि की चाल शुष्क वायु की तुलना में बढ़ जाती है।
![]()
प्रश्न 15.5.
आपने यह सीखा है कि एक विमा में कोई प्रगामी तरंग फलन y = f (x,t) द्वारा निरूपित की जाती है जिसमें x तथा t को x – vt अथवा x + vt अर्थात् y = f (x ± vt) संयोजन में प्रकट होना चाहिए। क्या इसका प्रतिलोम भी सत्य है? नीचे दिए गए y के प्रत्येक फलन का परीक्षण करके यह बताइए कि वह किसी प्रगामी तरंग को निरूपित कर सकता है:
- (x – vt)2
- log (x + vt) x0
- 1/(x + vt)
उत्तर:
इसका विलोम असत्य है। चूंकि किसी प्रगामी तरंग के स्वीकार करने योग्य फलन के लिए एक प्रत्यक्ष आवश्यकता यह है कि यह हर समय व हर स्थान पर परिमित होनी चाहिए। दिए गए फलनों में से सिर्फ फलन (3) ही इस प्रतिबन्ध को सन्तुष्ट करता है। शेष फलन सम्भवतया किसी प्रगामी तरंग को व्यक्त नहीं कर सकते हैं।
प्रश्न 15.6.
कोई चमगादड़ वायु में 1000 kHz आवृत्ति की पराश्रव्य ध्वनि उत्सर्जित करता है। यदि यह ध्वनि जल के पृष्ठ से टकराती है, तो (a) परावर्तित ध्वनि तथा (b) पारगमित ध्वनि की तरंगदैर्ध्य ज्ञात कीजिए। वायु तथा जल में ध्वनि की चाल क्रमशः 340 ms-1 तथा 1486 ms-1 है।
उत्तर:
दिया है: v = 1000 kHz = 106 Hz
वायु में ध्वनि की चाल v1 = 340 ms-1
व जल में ध्वनि की चाल V2 = 1486 ms-1
सूत्र, λ = \(\frac{v}{v}\) से
(a) परावर्तित ध्वनि की तरंगदैर्ध्य
λ1 = \(\frac { v_{ 1 } }{ v } \) = \(\frac { 340 }{ 10^{ 6 } } \)
= 0.34 मिमी।
![]()
प्रश्न 15.7.
किसी अस्पताल में ऊतकों में ट्यूमरों का पता लगाने के लिए पराश्रव्य स्कैनर का प्रयोग किया जाता है। उस ऊतक में ध्वनि की तरंगदैर्ध्य कितनी है जिसमें ध्वनि की चाल 1.7 kms-1 है? स्कैनर की प्रचालन आवृत्ति 4.2 MHz है।
उत्तर:
दिया है: आवृत्ति
v = 4.2 MHz = 4.2 × 106 Hz
चाल v = 1.7 kms-1 = 1700 मीटर/सेकण्ड
सूत्र तरंगदैर्ध्य λ = \(\frac{v}{v}\) से
ध्वनि की तरंगदैर्ध्य,
λ = \(\frac { 1700 }{ 4.2\times 10^{ 6 } } \)
= 0.405 मिमी।
प्रश्न 15.8.
किसी डोरी पर कोई अनुप्रस्थ गुणावृत्ति तरंग का वर्णन y (x,t)= 3.0 sin (36t + 0.018x + π/4)
द्वारा किया जाता है। यहाँ x तथा y सेंटीमीटर में तथा t सेकण्ड में है। x की धनात्मक दिशा बाएँ से दाएँ है।
- क्या यह प्रगामी तरंग है अथवा अप्रगामी? यदि यह प्रगामी तरंग है तो इसकी चाल तथा संचरण की दिशा क्या है?
- इसका आयाम तथा आवृत्ति क्या है?
- उद्गम के समय इसकी आरंभिक कला क्या है?
- इस तरंग में दो क्रमागत शिखरों के बीच की न्यूनतम दूरी क्या है?
उत्तर:
दी हुई अनुप्रस्थ गुणावृत्ति तरंग का समीकरण है –
y(x,t) = 3.0 (sin 36 + 0.018x + \(\frac { \pi }{ 4 } \)) …… (i)
संचरित तरंग का सामान्य समीकरण निम्न है –
y (x,t) = A sin [\(\frac { 2\pi }{ \lambda } \) (vt – x) + ϕ0]
A sin [\(\frac { 2\pi }{ T } \) t – \(\frac { 2\pi }{ \lambda } \) + ϕfie0] (∴ \(\frac{1}{T}\) = \(\frac{v}{λ}\)) ….. (ii)
1. समी० () व (ii) की तुलना करने पर स्पष्ट है कि समी० (i) संचरित तरंग को व्यक्त करती है। तथा
\(\frac { 2\pi }{ T } \) = 36, …….. (iii)
\(\frac { -2\pi }{ \lambda } \) = 0.018 ………. (iv)
या λ = – \(\frac { 2\pi }{ 0.018 } \)
समी० (iii) तथा (iv) की गुणा करने पर,
2πvλ = \(\frac { 2\pi \times 26 }{ 0.018 } \)
vλ = -2000
या v = -2000 cms-1 = -20ms-1
जहाँ v = vλ तरंग का वेग है। यहाँ ऋणात्मक चिह्न प्रदर्शित करता है कि तरंग बाएँ से दायीं ओर चलती है।
∴ वेग = 20 sm-1
2. A = 3.0 cm = 3.0 × 10-2 m
\(\frac { 2\pi }{ T } \) = 36
v = \(\frac { 36 }{ 2\pi } \) = \(\frac { 36 }{ 2\times 3.14 } \) = 5.73 Hz
3. प्रारम्भिक कला ϕ = \(\frac { \pi }{ 4 } \) rad
4. तरंग में दो गर्मों के बीच न्यूनतम दूरी = तरंगदैर्ध्य
= λ = \(\frac { 2\pi }{ 0.018 } \)
= \(\frac { 2\times 3.14 }{ 0.018 } \) = 348.9 cm
= 3.489 m
![]()
प्रश्न 15.9.
प्रश्न 15.8 में वर्णित तरंग के लिए x = 0 cm, 2 cm तथा 4 cm के लिए विस्थापन (y) और समय (t) के बीच ग्राफ आलेखित कीजिए। इन ग्राफों की आकृति क्या है? आयाम, आवृत्ति अथवा कला में से किन पहलुओं में प्रगामी तरंग में दोलनी गति एक बिन्दु से दूसरे बिन्दु पर भिन्न है?
उत्तर:
दी हुई तरंग समीकरण है –
y (x,t) = 3.0 sin (36t + 0.018x + \(\frac { \pi }{ 4 } \)) …… (i)
माना x = 0, 2 व 4 सेमी के लिए तरंग के विस्थापन क्रमश: y1, y2 व y3 हैं।
∴ y1 = (0,t) = 3.0 sin (36t + \(\frac { \pi }{ 4 } \)) ……….. (ii)
y2(2,t) = 3.0 sin (36t + 0.036 + \(\frac { \pi }{ 4 } \)) ……….. (iii)
तथा y3(4,t) = 3.0 sin (36t + 0.072 + \(\frac { \pi }{ 4 } \)) ……… (iv)
image 3
समी० (ii), (iii) व (iv) से स्पष्ट है कि ये वक्र ज्यावक्रीय हैं। जैसा कि चित्र में दिखाया गया है। तरंग संचरण में दोलनी गति, एक बिन्दु से दूसरे बिन्दु तक केवल कला में भिन्न है, जैसा कि क्रमश: (i), (iii) व (iv) से दिखाया गया है।
इन तरंगों के आयाम व आवृत्ति क्रमश: 3 सेमी० व \(\frac { 36 }{ 2\pi } \) s-1समान हैं।
प्रश्न 15.10.
प्रगामी गुणावृत्ति तरंग y (x,t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
जिसमें x तथा yको m में तथाt को s में लिया गया है,के लिए उन दो दोलनी बिन्दुओं के बीच कलांतर कितना है जिनके बीच की दूरी है –
(a) 4m
(b) 0.5 m
(c) λ/2
(d) \(\frac { 3\lambda }{ 4 } \)
उत्तर:
दी हुई प्रगामी गुणावृत्ति तरंग का समीकरण निम्न है –
y (x,t) = 2.0 cos 2π (10t – 0.0080x + 0.35) …… (i)
अतः संचरित गुणावृत्ति तरंग की सामान्य समीकरण निम्न है –
y(x,t) = A cos [\(\frac { 2\pi }{ T } \) t – \(\frac { 2\pi }{ \lambda } \) x + ϕ0] …. (ii)
(ii) समी० (i) व (ii) की तुलना से
\(\frac { 2\pi }{ \lambda } \) = 2π × 0.0080 cm-1 ….. (iii)
\(\frac { 2\pi }{ T } \) = 2π × 10
ϕ0 = 0.35
हम जानते हैं कि कलान्तर = \(\frac { 2\pi }{ \lambda } \) × पथान्तर ………… (iv)
(a) पथान्तर = 4m = 400m, (iv) से,
समी० (iv) से, कलान्तर = \(\frac { 2\pi }{ \lambda } \) × 400
= 2π × 0.0080 × 50
= 0.8π rad
(b) पथान्तर = 0.5 m = 50 cm पर
कलान्तर = 2π × 0.0080 × 50
= 0.8π rad
(c) पथान्तर = \(\frac { \pi }{ 2 } \) पर,
कलान्तर = \(\frac { 2\pi }{ \lambda } \) × \(\frac { 3\lambda }{ 4 } \)
= \(\frac { 3\pi }{ 2 } \) rad = (π + \(\frac { \pi }{ 2 } \))
∴ cos (π + θ) = -cos θ
प्रभावी कलान्तर = \(\frac { \pi }{ 2 } \)
![]()
प्रश्न 15.11.
दोनों सिरों पर परिबद्ध किसी तानित डोरी पर अनुप्रस्थ विस्थापन को इस प्रकार व्यक्त किया गया है –
y(x,t) = 0.06 sin( \(\frac { 2\pi }{ 3 } \) x) cos (120 πt) जिसमें x तथा y को m तथा t को s में लिया गया है। इसमें – डोरी की लम्बाई 1.5 m है जिसकी संहति 3.0 × 10-2kg है। निम्नलिखित का उत्तर दीजिए:
(a) यह फलन प्रगामी तरंग अथवा अप्रगामी तरंग में से किसे निरूपित करता है?
(b) इसकी व्याख्या विपरीत दिशाओं में गमन करती दो तरंगों के अध्यारोपण के रूप में करते हुए प्रत्येक तरंग की तरंगदैर्ध्य, आवृत्ति तथा चाल ज्ञात कीजिए।
(c) डोरी में तनाव ज्ञात कीजिए।
उत्तर:
दिया हुआ फलन है –
y (x,t) = 0.06 sin (\(\frac { 2\pi x }{ 3 } \)) cos (120πt) ……… (i)
संचरित तरंग को निम्न रूप में व्यक्त कर सकते हैं –
y (x,t) = A sin \(\frac { 2\pi }{ \lambda } \) (vt – x) …………… (ii)
(a) चूँकि दिया गया फलन प्रगामी तरंग की भाँति है। अतः दिया गया फलन प्रगामी तरंग को व्यक्त करता है।
(b) हम जानते हैं कि यदि तरंग
y1 = A sin \(\frac { 2\pi }{ \lambda } \) (vt + x)
x – अक्ष की धनात्मक दिशा में संचरित होती है,
तो यह तरंग निम्न परावर्तित तरंग द्वारा अध्यारोपित होती है।
अतः y2 = -A sin \(\frac { 2\pi }{ \lambda } \) (vt + x)
अतः अध्यारोपण सिद्धांत से, y = y1 + Y2
= -2A sin (\(\frac { 2\pi }{ \lambda } \) x) cos (\(\frac { 2\pi }{ \lambda } \) vt) …… (iii)
समीकरण (i) तथा (ii) की तुलना करने पर,
\(\frac { 2\pi }{ \lambda } \) = \(\frac { 2\pi }{ 3 } \) or λ = 3m
\(\frac { 2\pi }{ \lambda } \) v = 120π
या v = 60λ = 60 × 3 = 180 ms-1
∴ आवृत्ति v = \(\frac { v }{ \lambda } \) = \(\frac{108}{3}\) = 60 Hz
अनुप्रस्थ तरंग का वेग
v = \(\sqrt { \frac { T }{ m } } \) or v2 = \(\frac{T}{m}\)
∴ T = v2 × m ……….. (iv)
दिया है: द्रव्यमान प्रति एकांक लम्बाई = image 3
= \(\frac { 3\times 10^{ -2 }kg }{ 1.5m } \) = 2 × 10-2 kg m-1 ……… (v)
v = 180 ms-1 प्रति तरंग
(c) माना डोरी में तनाव T है।
∴ समीकरण (iv) व (v) से,
T = (180)2 × (2 × 10-2)
= 32400 × 2 × 10-2 = 648 N
![]()
प्रश्न 15.12.
(i) प्रश्न 15.11 में वर्णित डोरी पर तरंग के (b) कला, (c) आयाम से कंपन करते हैं? अपने उत्तरों को स्पष्ट कीजिए।
(ii) एक सिरे से 0.375 m दूर के बिन्दु का आयाम कितना हैं।
उत्तर:
(a) डोरी के समस्त बिन्दु समान आवृत्ति से कंपन करते हैं।
(b) चूँकि λ = 3 मीटर व डोरी की लम्बाई, l = 1.5 मीटर = \(\frac{1}{2}\)
अर्थात् डोरी को दोनों सिरों पर निस्पंद व मध्य में एक प्रस्पंद बनेगा।
चूँकि अप्रगामी तरंगों में दो क्रमागत निस्पंदों के मध्य के सभी बिन्दु समान कला में कम्पन करते हैं। अतः डोरी के सभी बिन्दु समान कला में कम्पन करेंगे।
(c) दी गई समीकरण निम्न है –
y (x,t) = 0.06 sin (\(\frac { 2\pi }{ 3 } \) x) cos (12πt)
इस समीकरण का आयाम,
A = 0.06 sin (\(\frac { 2\pi }{ 3 } \) x)
x = 0.375 m पर,
A = 0.06 sin (\(\frac { 2\pi }{ 3 } \) × 0.375)
= 0.06 × sin (0.250π)
= 0.06 sin (\(\frac { \pi }{ 4 } \)) = 0.06 × \(\frac { 1 }{ \sqrt { 2 } } \)
= 0.06 \(\sqrt { \frac { 2 }{ 2 } } \) 102 = 0.3 \(\sqrt { 2 } \)
= 0.03 × 1.414
= 0.04242 m = 0.042 m
प्रश्न 15.13.
नीचे किसी प्रत्यास्थ तरंग (अनुप्रस्थ अथवा अनुदैर्ध्य ) के विस्थापन को निरूपित करने वाले x तथा t के फलन दिए गए हैं। यह बताइए कि इनमें से कौन (i) प्रगामी तरंग को, (ii) अप्रगामी तरंग को, (iii) इनमें से किसी भी तरंग को निरूपित नहीं करता है –
- y = 2cos (3x) sin 10t
- y = 2\(\sqrt { x-vt } \)
- y = 3 sin (5x – 0.5t) + 4 cos (5x – 0.5t)
- y = cos x sin t + cos 2x sin 2t
उत्तर:
- महत्व फलन अप्रगामी तरंग को व्यक्त करता है।
- किसी भी तरंग के लिए स्वीकार करने योग्य नहीं है।
- प्रगामी गुणावृत्ति तरंग को प्रदर्शित करता है।
- दो प्रगामी तरंगों के अध्यारोपण प्रदर्शित करता है।
![]()
प्रश्न 15.14.
दो दृढ़ टेकों के बीच तानित तार अपनी मूल विधा में 45 Hz आवृत्ति से कंपन करता है। इस तार का द्रव्यमान 3.5 × 10-2 kg तथा रैखिक द्रव्यमान घनत्व 4.0 × 10-2 kg m-1 है। (a) तार पर अनुप्रस्थ तरंग की चाल क्या है, तथा (b) तार में तनाव कितना है?
उत्तर:
दिया है: m = 3.5 × 10-2 kg
रैखिक द्रव्यमान घनत्व µ = 4 × 10-2 kg m-1
सूत्र µ = \(\frac{m}{l}\) से,
तार की लम्बाई l = \(\frac{m}{µ}\)
= \(\frac { 3.5\times 10^{ -2 } }{ 4\times 10^{ -2 } } \) = \(\frac{7}{8}\) मीटर
माना तार में उत्पन्न तरंग की तरंगदैर्ध्य λ है। चूँकि तार मूल विधा में कम्पन कर रहा है। अतः \(\frac { \lambda }{ 2 } \) = l
∴ λ = 2l = \(\frac{7}{4}\) मीटर
सूत्र v = vλ से, तार में तरंग की चाल
v = 45 × 7 = 79 ms-1
माना कि तार का तनाव t है।
∴ v = \(\sqrt { \frac { T }{ \mu } } \)
∴ T = v2µ = (79)2 × 10-2
= 248 न्यूटन
प्रश्न 15.15.
एक सिरे पर खुली तथा दूसरे सिरे पर चलायमान पिस्टन लगी 1 m लंबी नलिका, किसी नियत आवृत्ति के स्त्रोत (340 Hz आवृत्ति का स्वरित्र द्विभुज) के साथ, जब नलिका में वायु कॉलम 25.5 cm अथवा 79.3 cm होता है तब अनुनाद दर्शाती है। प्रयोगशाला के ताप पर वायु में ध्वनि की चाल का आंकलन कीजिए। कोर-प्रभाव को नगण्य मान सकते हैं।
उत्तर:
नलिका में पिस्टन लगाने से यह बंद आर्गन नलिका की भाँति व्यवहार करेगा।
माना बंद नलिका में nवें तथा (n + 1) वें कम्पन के लिए अनुनादित वायु स्तम्भों की लम्बाइयाँ l1 व l2 हैं।
∴ l1 = 25.5 सेमी
l2 = 79.3 सेमी
माना ध्वनि तरंग का वेग v है। अतः इन कम्पनों के लिए आवृत्ति v1 व’ v2 निम्नवत् होगी।
v1 = (2n -1) \(\frac { v }{ 4l_{ 1 } } \) ………. (i)
तथा v2 = [2(n + 1) -1] \(\frac { v }{ 4l_{ 2 } } \) ………. (ii)
दोनों विधाओं में 340 Hz की आवृत्ति से अनुनाद होगा।
∴ V1 = V2 = 340 …………. (iii)
या (2n – l) – \(\frac { v }{ 4l_{ 1 } } \) = (2n +1) \(\frac { v }{ 4l_{ 2 } } \)
या \(\frac { (2n-1) }{ l_{ 1 } } \) – \(\frac { v }{ 4l_{ 1 } } \) = (2n + 1) \(\frac { v }{ 4l_{ 2 } } \)
या \(\frac { (2n-1) }{ l_{ 1 } } \) = \(\frac { (2n-1) }{ l_{ 2 } } \)
या \(\frac { 2n-1 }{ 2n+1 } \) = \(\frac { l_{ 2 } }{ l_{ 1 } } \) = \(\frac { 22.5 }{ 79.3 } \) ~ \(\frac{1}{3}\)
या 3(2n -1) = 2n +1
या 6n -3 = 2n + 1
या 6n – 2n = 3 + 1
4n = 4
∴ n = 1
समी० (2n -1) \(\frac { v }{ 4l_{ 2 } } \) = 340 में n = 1 रखने पर
(2 × 1 – 1) \(\frac { v }{ 4l_{ 2 } } \) = 340
या (2 – 1) × \(\frac { v }{ 4\times 25.5 } \) = 340
या \(\frac { v }{ 4\times 25.5 } \) = 340
या v = 340 × 4 × 25.5
या v = 340 × 102 = 34680 cms -1
= 346.8 ms -1 = 347 ms-1
![]()
प्रश्न 15.16.
100 cm लंबी स्टील-छड़ अपने मध्य बिन्दु पर परिबद्ध है। इसके अनुदैर्ध्य कंपनों की मूल आवृत्ति 2.53 kHz है। स्टील में ध्वनि की चाल क्या है?
उत्तर:
चूँकि छड़ मध्य बिन्दु पर परिबद्ध है अतः यहाँ एक निस्पंद (A) तथा मूल विधा के लिए सिरों पर दो प्रस्पंद बनेंगे। अतः छड़ की मूल लम्बाई निम्नवत् होगी –
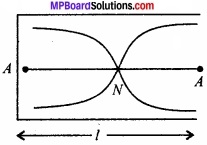
जहाँ l = छड़ की लम्बाई
तथा λ = तरंग की तरंगदैर्ध्य
दिया है =
l = 100 cm, v = 2.53 kHz = 2.53 × 103 Hz
∴ λ = 2 × 100 = 200 cm
माना स्टील में ध्वनि का वेग v है।
अत: v = vλ = 2.53 × 103 × 200
= 506 × 103 cms-1 = 5.06 × 103 ms-1
∴ v = 5.06 kms-1
प्रश्न 15.17.
20 cm लंबाई के पाइप का एक सिरा बंद है। 430 Hz आवृत्ति के स्त्रोत द्वारा इस पाइप की कौन-सी गुणावृत्ति विधा अनुनाद द्वारा उत्तेजित की जाती है? यदि इस पाइप के दोनों सिरे खुले हों, तो भी क्या यह स्त्रोत इस पाइप के साथ अनुनाद करेगा? वायु में ध्वनि की चाल 340 ms-1 है।
उत्तर:
दिया है:
l = 20 cm = 0.2 m, v = 340 ms-1
उत्तेजित स्त्रोत की आवृत्ति vn = 430 Hz
हम जानते हैं कि बंद नली के कम्पनों की आवृत्ति निम्न होती है –
vn = (2n – 1) \(\frac { v }{ 4l } \)
या 430 = (2n -1) \(\frac { 340 }{ 4\times 0.20 } \)
2n -1 = 430 × \(\frac { 0.80 }{ 340 } \) = 1.02
या n = 1.01
अत: आर्गन नली प्रथम सन्नादी या दोलन की मूल आवृत्ति में है।
खुली नली में, कम्पन की nवीं विधा की आवृत्ति v’n = n\(\frac { v }{ 2l } \)
जहाँ मूल विधा में लम्बाई l = \(\frac { \lambda }{ 2 } \) 0r λ = 2l
या 430 = \(\frac { n\times 340 }{ 2\times 0.2 } \)
या n = \(\frac { 430\times 0.4 }{ 340 } \) = \(\frac{172}{340}\) = 0.5
चूँकि n एक पूर्णांक है। अतः n = 0.5 सम्भव नहीं है। अतः समान स्त्रोत खुली नली में अनुनादित नहीं होगा।
प्रश्न 15.18.
सितार की दो डोरियाँ A तथा B एक साथ ‘गा’ स्वर बजा रही हैं तथा थोड़ी-सी बेसुरी होने के कारण 6 Hz आवृत्ति के विस्पंद उत्पन्न कर रही हैं। डोरी A का तनाव कुछ घटाने पर विस्पंद की आवृत्ति घटकर 3 Hz रह जाती है। यदि की मूल आवृत्ति 324 Hz है तो Bकी आवृत्ति क्या है?
उत्तर:
हम जानते हैं कि आवृत्ति ∝ image 4
अत: डोरी में तनाव कम होने से इसकी आवृत्ति भी घटती है। माना A की वास्तविक आवृत्ति VA व B की VB है।
∴ VA – VB = 6 Hz
परन्तु VA = 324 Hz
∴ VB = 324 – 6 =318 Hz
A में तनाव कम करने पर,
∆v = 3 Hz
A की आवृत्ति = 324 – 3 = 321 Hz
∴ B की आवृत्ति = 318 Hz
![]()
प्रश्न 15.19.
स्पष्ट कीजिए क्यों (अथवा कैसे)?
- किसी ध्वनि तरंग में विस्थापन निस्पंद दाब प्रस्पंद होता है और विस्थापन प्रस्पंद दाब निस्पंद होता है।
- आँख न होने पर भी चमगादड़ अवरोधकों की दूरी, दिशा, प्रकृति तथा आकार सुनिश्चित कर लेते हैं।
- वायलिन तथा सितार के स्वरों की आवृत्तियाँ समान होने पर भी हम दोनों से उत्पन्न स्वरों में भेद कर लेते हैं।
- ठोस अनुदैर्ध्य तथा अनुप्रस्थ दोनों प्रकार की तरंगों का पोषण कर सकते हैं जबकि गैसों में केवल अनुदैर्ध्य तरंगें ही संचरित हो सकती हैं, तथा
- परिक्षेपी माध्यम में संचरण के समय स्पंद की आकृति विकृत हो जाती है।
उत्तर:
1. ध्वनि तरंगों में जहाँ माध्यम के कणों का विस्थापन न्यूनतम होता है वहाँ कण अत्यधिक पास-पास होते हैं। अतः वहाँ दाब अधिकतम होता है। (i.e., दाब प्रस्पंद बनता है) एवं जहाँ विस्थापन महत्तम होता है वहाँ कण दूर-दूर होते हैं, । अतः वहाँ दाब न्यूनतम होता है (i.e., दाब निस्पंद बनता है।)
2. चमगादड़ उच्च आवृत्ति की पराश्रव्य तरंगें उत्सर्जित करती है। ये तरंगें अवरोधकों से टकराकर वापस लौटती हैं तो चमगादड़ इन्हें अवशोषित कर लेते हैं। परावर्तित तरंगों की आवृत्ति व तीव्रता की प्रेषित तरंगों से तुलना करके चमगादड़ अवरोधकों की दूरी, प्रकृति, दिशा व आकार सुनिश्चित कर लेते हैं।
3. प्रत्येक स्वर में एक मूल स्वरक के साथ कुछ अधिस्वरक भी उत्पन्न होते हैं। परन्तु वायलिन व सितार से उत्पन्न स्वरों में मूल स्वरकों की आवृत्तियाँ समान रहती हैं लेकिन उनके साथ उत्पन्न होने वाले अधिस्वरकों की संख्या, आवृत्तियों व अपेक्षिक तीव्रताओं में भिन्नता होती है। इसी भिन्नता के आधार पर इन्हें विभेद किया जाता है।
4. ठोसों में आयतन प्रत्यास्थता के साथ-साथ अपरूपण प्रत्यास्थता भी पाई जाती है। अतः ठोसों में दोनों प्रकार की तरंगें संचरित होती हैं। जबकि गैसों में केवल आयतन प्रत्यास्थता ही पाई जाती है। अतः गैसों में केवल अनुदैर्ध्य तरंगें ही संचरित हो पाती हैं।
5. प्रत्येक ध्वनि स्पंद कई विभिन्न तरंगदैर्ध्य की तरंगों का मिश्रण होता है। जब यह स्पंद परिक्षेपी माध्यम में प्रवेश करता है तब ये तरंगें अलग-अलग वेगों से गतिमान रहती हैं। अतः स्पंद की आकृति विकृत हो जाती है।
प्रश्न 15.20.
रेलवे स्टेशन के बाह्य सिग्नल पर खड़ी कोई रेलगाड़ी शांत वायु में 400 Hz आवृत्ति की सीटी बजाती है। (i) प्लेटफॉर्म पर खड़े प्रेक्षक के लिए सीटी की आवृत्ति क्या होगी जबकि रेलगाड़ी (a) 10 ms-1 चाल से प्लेटफॉर्म की ओर गतिशील है, तथा (b) 10 ms-1 चाल से प्लेटफॉर्म से दूर जा रही है? (ii) दोनों ही प्रकरणों में ध्वनि की चाल क्या है? शांत वायु में ध्वनि की चाल 340 ms-1 लीजिए।
उत्तर:
दिया है: v = 400 Hz, Vt = 10 ms-1
शांत वायु में ध्वनि की चाल
v = 340 ms-1
(i) (a) जब रेलगाड़ी (ध्वनि स्त्रोत) स्थिर प्रेक्षक की ओर गतिमान है, तब प्रेक्षक द्वारा सुनी गई ध्वनि की आवृत्ति,
v’ = v(\(\frac { v }{ v-v_{ t } } \))
= 400(\(\frac { 340 }{ 340-10 } \))
= 412 Hz
(b) जब रेलगाड़ी स्थिर प्रेक्षक से दूर जा रही है तब प्रेक्षक द्वारा सुनी गई ध्वनि की आवृत्ति,
v’ = v (\(\frac { v }{ v+v_{ t } } \))
= 400 (\(\frac { 340 }{ 340+10 } \)) = 389 Hz
(ii) दोनों स्थितियों में ध्वनि की चाल (340 ms-1) समान है।
![]()
प्रश्न 15.21.
स्टेशन यार्ड में खड़ी कोई रेलगाड़ी शांत वायु में 400 Hz आवृत्ति की सीटी बजा रही है। तभी 10 ms-1 की चाल से यार्ड से स्टेशन की ओर वायु बहने लगती है। । स्टेशन के प्लेटफॉर्म पर खड़े किसी प्रेक्षक के लिए ध्वनि की आवृत्ति, तरंगदैर्ध्य तथा चाल क्या है? क्या यह स्थिति तथ्यतः उस स्थिति के समरूप है जिसमें वायु शांत हो तथा प्रेक्षक 10 ms-1 चाल से यार्ड की ओर दौड़ रहा हो? शांत वायु में ध्वनि की चाल 340 ms-1 ले सकते हैं।
उत्तर:
दिया है: v = 400 Hz
वायु की प्रेक्षक की ओर चाल vw = 10 ms-1
शांत वायु में ध्वनि की चाल vs = 340 ms-1
चूँकि रेलगाड़ी व प्रेक्षक दोनों स्थिर हैं। अतः V0 = 0 व v’s = 0
अतः प्रेक्षक द्वारा सुनी गई ध्वनि की आवृत्ति

चूँकि वायु प्रेक्षक की ओर चलती है।
अतः प्रेक्षक के लिए वायु की चाल
= vs + vw = 350 ms-1
प्रेक्षक के लिए सीटी की आवृत्ति = 400 Hz
∴ ध्वनि की तरंगदैर्ध्य x = λ’ = \(\frac { v_{ t }+v_{ s } }{ v’ } \)
= \(\frac { 340+10 }{ 400 } \) = \(\frac{7}{8}\) Hz = 0.875 m
प्रश्न 15.22.
किसी डोरी पर कोई प्रगामी गुणावृत्ति तरंग इस प्रकार व्यक्त की गई है y(x,t) = 7.5 sin (0.0050x + 12t + π/4)
(a) x = 1cm तथा t = 1s पर किसी बिन्दु का विस्थापन तथा दोलन की चाल ज्ञात कीजिए। क्या यह चाल तरंग संचरण की चाल के बराबर है?
(b) डोरी के उन बिन्दुओं की अवस्थिति ज्ञात कीजिए जिनका अनुप्रस्थ विस्थापन तथा चाल उतनी ही है जितनी x=1cm पर स्थित बिन्दु की समय t = 25, 5 s तथा 11s पर
उत्तर:
दिया है:

(a) समीकरण (i) की तुलना संचरित तरंग के सामान्य समीकरण से करने पर
y = a sin [\(\frac { 2\pi }{ \lambda } \) (vt +x ) + \(\frac { \pi }{ 4 } \)] we get,
v = velocity of wave
= \(\frac{12}{0.0050}\) = \(\frac { 12\times 10^{ 4 } }{ 50 } \)
= 12 × 200 cm s-1
= 24 ms-1
x = 1 सेमी० पर t = 1 सेकण्ड,
अतः विस्थापन,
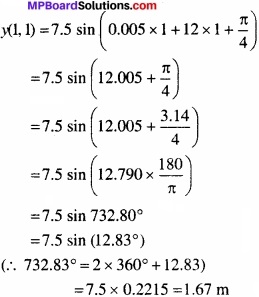
बिन्दु के दोलन का वेग

x = 1 सेमी० पर t = 1 सेकण्ड
v = 90 c0s (0.05 × 1 + 12 × 1 + 0.785)
= 90 cos 732.83° = 90 cos 12.83°
= 90 × 0.9751 cms -1 = 87.76 cms-1
= 88 cms-1
परन्तु तरंग संचरण का वेग 24 मीटर/सेकण्ड है।
स्पष्ट है कि बिन्दु का दोलन वेग तरंग संचरण के वेग के समान नहीं है।
∴नहीं, यह वेग तरंग संचरण के वेग (24 मीटर/से०) के समान नहीं है।
(b) दी हुई समीकरण है,
y (x,t) = 7.5 sin 0.005x + 12 +\(\frac { \pi }{ 4 } \))
इस समीकरण की तुलना समीकरण,
y = A sin (ωt + kx + ϕ) से करने पर,
∴ k = 0.005 रेडियन 1 सेमी०
∴ λ = \(\frac { 2\pi }{ k } \)
= \(\frac { 2\times 3.14 }{ 0.005 } \) = 12.57 मीटर
तरंग में सभी बिन्दुओं का समान अनुप्रस्थ विस्थापन होता है। यह विस्थापन λ, 2λ, 3λ, … इत्यादि होता है। अतः 12.57 मीटर, 25.14 मीटर, 37.71 मीटर इत्यादि दूरी पर स्थित बिन्दु x = 1 सेमी से समान विस्थापन पर होंगे। अतः सभी बिन्दुओं जिनका विस्थापन nλ है। जहाँ n = ± 1, ± 2, ± 3, ± 4, … है, x = 1 सेमी से 12.57 मोटर, 25.14 मीटर … दूरी हैं।
प्रश्न 15.23.
ध्वनि का कोई सीमित स्पंद (उदाहरणार्थ सीटी की पिप) माध्यम में भेजा जाता है। (a) क्या इस स्पंद की कोई निश्चित (i) आवृत्ति, (ii) तरंगदैर्ध्य, (iii) संचरण की चाल है? (b) यदि स्पन्द दर 1 स्पंद प्रति 20 सेकण्ड है अर्थात् सीटी प्रत्येक 20 s के पश्चात् सेकंड के कुछ अंश के लिए बजती है, तो सीटी द्वारा उत्पन्न स्वर की आवृत्ति (1/20) Hz अथवा 0.05 Hz है?
उत्तर:
(a) नहीं, इस स्पंद की कोई निश्चित आवृत्ति या तरंगदैर्ध्य नहीं होती है। स्पन्द के संचरण की चाल निश्चित होती है, जो माध्यम में ध्वनि की चाल के समान है।
(b) नहीं, स्पंद की आवृत्ति (\(\frac{1}{20}\)) Hz
या 0.05 Hz नहीं है।
![]()
प्रश्न 15.24.
8.0 × 10-3 kg m-1 रैखिक द्रव्यमान घनत्व की किसी लंबी डोरी का एक सिरा 256 Hz आवृत्ति के विद्युत चालित स्वरित्र द्विभुज से जुड़ा है। डोरी का दूसरा सिरा किसी स्थिर घिरनी के ऊपर गुजरता हुआ किसी तुला के पलड़े से बँधा है जिस पर 90 kg के बाट लटके हैं। घिरनी वाला सिरा सारी आवक ऊर्जा को अवशोषित कर लेता है जिसके कारण इस सिरे से परावर्तित तरंगों का आयाम नगण्य होता है। t = 0 पर डोरी के बाएँ सिरे (द्विभुज वाले सिरे) y = 0 पर अनुप्रस्थ विस्थापन शून्य है (y = 0) तथा वह y की धनात्मक दिशा के अनुदिश गतिशील है। तरंग का आयाम 5.0 cm है। डोरी पर इस तरंग का वर्णन करने वाले अनुप्रस्थ विस्थापन को तथा के फलन के रूप में लिखिए।
उत्तर:
हम जानते हैं कि तरंग वेग
V = \(\sqrt { \frac { T }{ m } } \) ……… (i)
पलड़े में द्रव्यमान = M = 90 kg
दिया है: T = Mg = 90 × 9.8 = 882.0 N
रेखीय द्रव्यमान घनत्व m = 8 × 10-3 kg m-1
∴ v = \(\sqrt { \frac { 882 }{ 8\times 10^{ -3 } } } \) = 3.32 × 102 ms-1
= 332 ms -1
धनात्मक x – दिशा में y विस्थापन वाली संचारित तरंग का समीकरण
y = A sin (ωt – kx) …………. (ii)
जहाँ ω = 2πv तथा
A = 5.0 cm = 0.05 m, v = 256 Hz
∴ ω = 2π × 256 s-1
= 16.1 × 102 = 1.61 × 103 s-1
=16.1 x 102 =1.61×103 5-1
पुनः
k = \(\frac { \omega }{ v } \) = \(\frac { 2\pi \times 256 }{ 3.32\times 10^{ 2 } } \)
= \(\frac { 1607.7 }{ 3.32\times 10^{ 2 } } \)
= \(\frac { 16.1\times 10^{ 2 }radm^{ -1 } }{ 3.32\times 10^{ 2 } } \)
= 4.84 m-1
समी० (ii) में ω1A तथा k के मान रखने पर,
y = 0.05 sin (1.6 × 103t – 4.84)
प्रश्न 15.25.
किसी पनडुब्बी से आबद्ध कोई ‘सोनार’ निकाय 40.0 KHz आवृत्ति पर प्रचालन करता है। कोई शत्रु-पनडुब्बी 360 kmh-1 चाल से इस सोनार की ओर गति करती है। पनडुब्बी से परावर्तित ध्वनि की आवृत्ति क्या है? जल में ध्वनि की चाल 1450 ms-1 लीजिए।
उत्तर:
दिया है: जल में ध्वनि की चाल v = 1450 ms-1
शत्रु पनडुब्बी की चाल v1 = 1360 kmh-1
= 360 × \(\frac{5}{18}\) = 100 ms-1
सोनार द्वारा प्रेषित तरंग की आवृत्ति
ω = 40 kHz
माना शत्रु पनडुब्बी द्वारा ग्रहण आवृत्ति v1 है।
स्पष्ट है: श्रोता का वेग v0 = v1 = 100 ms-1
∴ आवृत्ति v1 = v(\(\frac { v+v_{ 0 } }{ v } \))
= 40 (\(\frac { 140+100 }{ 1450 } \))
= 42.75 kHz = 43 kHz
शत्रु पगडुब्दी इस आवृत्ति की तरंगों को परावर्तित करती है। माना सोनार द्वारा ग्रहण आवृत्ति n2 है।
इस स्थिति में, स्त्रोत सोनार की ओर vs = 100 ms-1 के वेग से गति करता है।
∴ v2 = v1(\(\frac { v }{ v-v_{ s } } \))
= 42.75 (\(\frac { 1450 }{ 1450-100 } \)) = 46 kHz
![]()
प्रश्न 15.26.
भूकम्प पृथ्वी के भीतर तरंगें उत्पन्न करते हैं। गैसों के विपरीत, पृथ्वी अनुप्रस्थ (S) तथा अनुदैर्ध्य (P) दोनों प्रकार की तरंगों की अनुभूति कर सकती है। S तरंगों की प्रतिरूपी चाल लगभग 4.0 kms-1तथा P तरंगों की प्रतिरूपी चाल लगभग 8.0 kms-1 है। कोई भूकंप-लेखी किसी भकंप की P तथा S तरंगों को रिकॉर्ड करता है। पहली P तरंग पहली S तरंग की तुलना में 4 मिनट पहले पहुँचती है। यह मानते हुए कि तरंगें सरल रेखा में गमन करती हैं यह ज्ञात कीजिए कि भूकंप घटित होने वाले स्थान की दूरी क्या है?
उत्तर:
दिया है: S तरंगों की चाल
v1 = 4 km s-1
= 4 × 60 = 240 km/min
P तरंगों की चाल V2 = 8 kms-1
= 480 km/min
अत: S तरंगों का भूकंप लेखी तक पहुँचने में लगा समय
t1 = \(\frac { x }{ u_{ 1 } } \) = \(\frac{n}{240}\) मिनट व P तरंगों का भूकंप लेखी तक पहुँचने में लगा समय
t2 = \(\frac { x }{ v_{ 2 } } \) = \(\frac{x}{480}\) मिनट
अतः t1 = 2t2
प्रश्नानुसार P तरंगें, Q तरंगों से भूकंप लेखी तक 4 मिनट पहले पहुँचती हैं।
t1 – t2 = 4 मिनट
या 2t2 – t2 = 4
∴ t2 = 4 मिनट
∴ दूरी x = 480 × 4
= 1920 km
![]()
प्रश्न 15.27.
कोई चमगादड़ किसी गुफा में फड़फड़ाते हुए पराश्रव्य ध्वनि उत्पन्न करते हुए उड़ रहा है। मान लीजिए चमगादड़ द्वारा उत्सर्जित पराश्रव्य ध्वनि की आवृत्ति 40 kHz है। किसी दीवार की ओर सीधा तीव्र झपट्टा मारते समय चमगादड़ की चाल ध्वनि की चाल की 0.03 गुनी है। चमगादड़ द्वारा सुनी गई दीवार से परावर्तित ध्वनि की आवृत्ति क्या है?
उत्तर:
दिया है:
उत्सर्जित तरंग की आवृत्ति v = 40 kHz
माना ध्वनि की चाल = v
चमगादड़ की चाल v1 = 0.03v माना दीवार द्वारा ग्रहण की गई तरंग की आगामी आवृत्ति v1 है।
इस स्थिति में श्रोता की ओर गतिमान है तथा श्रोता स्थिर है।
∴ v1 = v (\(\frac { v }{ v-v_{ s } } \))
= 40 (\(\frac { v }{ v-0.03v } \)) kHz
= 41.24 kHz
v1 = 41.24 kHz आवृत्ति की तरंगें दीवारसे टकराकर चमगादड़ की ओर वापस लौटती हैं।
माना चमगादड़ द्वारा ग्रहण की गई तरंगो की आवृत्ति v2 इस स्थिति में, श्रोता, स्थिर स्त्रोत की ओर गतिमान है।
∴ v2 = v1 (\(\frac { v+v_{ 0 } }{ v } \))
= 41.24 (\(\frac { v+0.03v }{ v } \))
= 42.47 kHz
इस प्रकार चमगादड़ द्वारा ग्रहण की गई परावर्तित ध्वनि की आवृत्ति 42.47 kHz है।