MP Board Class 11th Physics Solutions Chapter 13 अणुगति सिद्धांत

MP Board Class 11th Physics Solutions Chapter 13 अणुगति सिद्धांत

अणुगति सिद्धांत अभ्यास के प्रश्न एवं उनके उत्तर

प्रश्न 13.1.
ऑक्सीजन के अणुओं के आयतन और STP पर इनके द्वारा घेरे गए कुल आयतन का अनुपात ज्ञात कीजिए। ऑक्सीजन के एक अणु का व्यास 3Å लीजिए।
उत्तर:
दिया है:
d = 3 Å
∴ r = \(\frac{1}{2}\) × 3 = 1.5 Å
= 1.5 × 10^-10 मीटर
STP पर 1 मोल गैस का आयतन
V₁ = 22.41 = 22.4 × 10^-3 मीटर ³
तथा 1 मोल गैस में अणुओं की संख्या
= N = 6.02 × 10²³
∴ अणुओं का आयतन, V₂ = एक अणु का आयतन × N
= \(\frac{4}{3}\) π³ × N
= \(\frac{4}{3}\) × 3.14 × (1.5 × 10^-10)³ × 6.02 × ²³
= 8.52 × 10^-6 मीटर ²
∴ \(\frac { V_{ 2 } }{ V_{ 1 } } \) = \(\frac { 8.52\times 10^{ -6 } }{ 22.4\times 10^{ -3 } } \) = 3.8 × 10^-4
अतः अणुओं के आयतन तथा STP पर इनके द्वारा घेरे गए आयतन का अनुपात 3.8 × 10^-4 है।\

प्रश्न 13.2.
मोलर आयतन STP पर किसी गैस (आदर्श) के 1 मोल द्वारा घेरा गया आयतन है। (STP : 1 atm) दाब, 0°C। दर्शाइये कि यह 22.4 लीटर है।
उत्तर:
दिया है: STP पर,
P = 1 atm = 7.6 m of Hg column
= 0.76 × 13.6 × 10 ³ × 9.9
= 1.013 × 105 Nm^-2
T = 0°C = 273 K
R = 8.31 J mol^-1K^-1
n = 1 मोल V = 22.41 सिद्ध करने के लिए,
सूत्र PV = nRT से
V = \(\frac { nRT }{ P } \)
= \(\frac { 1\times 8.31\times 273 }{ 1.013\times 10^{ 5 } } \)
= 22.4 × 10 ^-3 m³
= 22.4 लीटर

प्रश्न 13.3.
चित्र में ऑक्सीजन के 100 x 10-3 kg द्रव्यमान के लिए PV/T एवं P में, दो अलग-अलग तापों पर ग्राफ दर्शाये गए हैं।

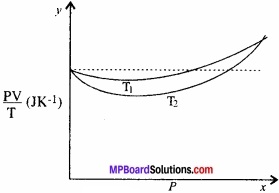
(a) बिंदुकित रेखा क्या दर्शाती है?
(b) क्या सत्य है: T₁ >T₂, अथवा T₁ < T₂ ?
(c) y – अक्ष पर जहाँ वक्र मिलते हैं वहाँ PV/T का मान क्या है?
(d) यदि हम ऐसे ही ग्राफ 100 × 10^-3 kg हाइड्रोजन के लिए बनाएँ तो भी क्या उस बिंदु पर जहाँ वक्र y – अक्ष से मिलते हैं PV/T का मान यही होगा? यदि नहीं तो हाइड्रोजन के कितने द्रव्यमान के लिए PV/T का मान कम दाब और उच्च ताप के क्षेत्र के लिए वही होगा? H₂ का अणु द्रव्यमान = 2.02 u, O₂ का अणु द्रव्यमान = 32.0 u, R = 8.31 Jmol^-1K^-1
उत्तर:
(a) बिन्दुकित रेखा यह व्यक्त करती है कि राशि | PV/T स्थिर है। यह तथ्य केवल आदर्श गैस के लिए सत्य है। अर्थात् बिन्दुकित रेखा आदर्श गैस का ग्राफ है।

(b) ताप T, पर ग्राफ की तुलना में ताप T, पर गैस का ग्राफ आदर्श गैस के ग्राफ के अधिक समीप है। हम जानते हैं कि वास्तविक गैसें निम्न ताप पर आदर्श गैस के व्यवहार से अधिक । विचलित होती हैं। अतः T₁ > T₂

(c) जहाँ ग्राफ y – अक्ष पर मिलते हैं ठीक उसी बिन्दु पर आदर्श गैस का ग्राफ भी गुजरता है। अतः इस बिन्दु पर ऑक्सीजन – गैस, आदर्श गैस का पालन करती है।
अतः गैस समीकरण से,
\(\frac { PV }{ T } \) = nR
हम जानते हैं O₂ का 32 × 10^-3 kg = 1 मोल
∴ O₂ का 1.00 × 10^-3 kg
= \(\frac { 1 }{ 32\times 10^{ -3 } } \) × 1 × 10^-3
i.e; n = \(\frac{1}{32}\)
R = 8.31 JK^-1mol^-1
∴ \(\frac{PV}{T}\) = \(\frac{1}{32}\) × 8.31 = 0.26 JK^-1

(d) नहीं, हाइड्रोजन गैस के लिए PV/T का मान समान नहीं रहता है। चूंकि यह द्रव्यमान पर निर्भर करता है तथा H₂ का द्रव्यमान O₂ से कम है।
माना हाइड्रोजन का अभीष्ट द्रव्यमान m किया है जिसमें PV/T का समान मान प्राप्त होता है।
∴ n = \(\frac { m }{ 2.02\times 10^{ -3 } } \)
\(\frac{PV}{T}\) = nR = 0.26 JK^-1 से,
n = \(\frac { 0.26 }{ R } \) = \(\frac { 0.26JK^{ -1 } }{ 8.31JK^{ -1 }mol^{ -1 } } \)
= 0.0313 mol
∴ समी० (i) व (ii) से,
n₁ = 2.02 × 10^-3 × 0.313
= 0.0632 × 10^-3 kg
= 6.32 × 10^-5 kg

प्रश्न 13.4.
एक ऑक्सीजन सिलिंडर जिसका आयतन 30 लीटर है, में ऑक्सीजन का आरंभिक दाब 15 atm एवं ताप 27°C है। इसमें से कुछ गैस निकाल लेने के बाद प्रमापी (गेज)दाब गिर कर 11 atm एवं ताप गिर कर 17°C हो जाता है। ज्ञात कीजिए कि सिलिंडर से ऑक्सीजन की कितनी मात्रा निकाली गई है। (R = 8.31 Jmol^-1K^-1, ऑक्सीजन का अणु द्रव्यमान 0₂ = 32 u)।
उत्तर:
दिया है: ऑक्सीजन सिलिण्डर में प्रारम्भ में
V₁ = 30 litres = 30 × 10^-3 m³
P₁ = 15 atm = 15 × 1.013 × 10⁵ Pa
T₁ = 27 + 273 = 300K
R = 8.31 JK^-1mol^-1
माना सिलिण्डर में ऑक्सीजन गैस के n₂ मोल हैं।
अतः सूत्र PV = nRT से,
n¹ = \(\frac { P_{ 1 }V_{ 1 } }{ RT_{ 1 } } \)
= \(\frac { 15\times 1.013\times 10^{ 5 } }{ 8.31\times 300 } \) = 18.253
ऑक्सीजन का अणु भार
M = 32 = 32 × 10^-3kg
सिलिंडर में ऑक्सीजन का प्रारम्भिक द्रव्यमान
m₁ = n₁M
= 18.253 × 32 × 10^-3kg
माना अन्त में सिलिंडर में O₂ kg के n² kg मोल बचे हैं।
दिया है: V₂ = 30 × 10^-3 m³, P₂ = 11 atm
= 11 × 1.013 × 10⁵ pa
∴ n₂ = \(\frac { P_{ 2 }V_{ 2 } }{ RT_{ 2 } } \)
= \(\frac { (11\times 1.013\times 10^{ 5 })\times (30\times 10^{ -3 }) }{ 8.31\times 290 } \)
= 13.847
∴ सिलिंडर में O₂ गैस का अन्तिम द्रव्यमान
m₂ = 13.847 × 32 × 10^-3
∴ सिलिंडर से O₂ का लिया गया द्रव्यमान
= m₁ – m₂
= (584.1 – 453.1) × 10^-3 kg
= 141 × 10^-3 kg = 0.141 kg

प्रश्न 13.5.
वायु का एक बुलबुला, जिसका आयतन 1.0 cm³ है, 40 m गहरी झील की तली में जहाँ ताप 12°C है, उठकर ऊपर पृष्ठ पर आता है जहाँ ताप 35°C है। अब इसका आयतन क्या होगा?
उत्तर;
जब वायु का बुलबुला 40 मी० गहराई पर है तब
V₁ = 1.0 cm³ = 1.0 × 10^-6m³
T₁ = 12°C = 12 + 273 = 285 K
= 1 atm + 40 m पानी की गहराई
Pc = 1 atm – h₁ρg
= 1.013 × 10c + 40 × 10³ × 9.8
= 493000 Pa = 4.93 × 10⁵ × Pa
जब वायु का बुलबुला झील की सतह पर पहुँचता है तब
V₂ = ?, T₂ = 35°C = 35 + 273 = 308 K
P₂ = 1 atm = 1.013 × 10⁵ Pa
सूत्र \(\frac { P_{ 1 }V_{ 1 } }{ T_{ 1 } } \) = \(\frac { P_{ 2 }V_{ 2 } }{ T_{ 2 } } \) से,
= \(\frac { P_{ 1 }V_{ 1 } }{ T_{ 1 } } \) × \(\frac { T_{ 2 } }{ P_{ 2 } } \)
= \(\frac { 4.95\times 10^{ 5 }\times 1\times 10^{ -6 }\times 308 }{ 285\times 1.013\times 10^{ 5 } } \)
= 5.275 × 10^-6 m
= 5.3 × 10^-6 m

प्रश्न 13.6.
एक कमरे में, जिसकी धारिता 25.0 m³ है, 27°C ताप और 1 atm दाब पर, वायु के कुल अणुओं (जिनमें नाइट्रोजन, ऑक्सीजन, जलवाष्प और अन्य सभी अवयवों के कण सम्मिलित हैं) की संख्या ज्ञात कीजिए।
उत्तर:
दिया है: V = 25.0 m³
T = 27°C = 27 + 273 = 300 K
K = 1.38 × 10^-23 JK^-1
P =1 atm = 1.013 × 10⁵ Pa
गौस समीकरण से, P = \(\frac { nRT }{ V } \)
= \(\frac{n}{V}\) (Nk) T
= (nN) \(\frac{kT}{V}\) = N’\(\frac{kT}{V}\)
जहाँ N’ =nN = दी गई गैस में ऑक्सीजन अणुओं की संख्या
N’ = \(\frac{PV}{KT}\)
= \(\frac { (1.013\times 10^{ 5 })\times 25 }{ 1.38\times 10^{ -23 }\times 300 } \)
= 6.10 × 10²⁶

प्रश्न 13.7.
हीलियम परमाणु की औसत तापीय ऊर्जा का आंकलन कीजिए

1. कमरे के ताप (27°C) पर
2. सूर्य के पृष्ठीय ताप (6000 K) पर
3. 100 लाख केल्विन ताप (तारे के क्रोड का प्रारूपिक ताप) पर।

उत्तर:
गैस के अणुगति सिद्धान्त के अनुसार, ताप T पर गैस की औसत गतिज ऊर्जा (i. e., औसत ऊष्मीय ऊर्जा) निम्नवत् है –
E = \(\frac{3}{2}\) kT
दिया है: k = 1.38 × 10^-23 JK^-1
1. T = 27°C = 273 + 27 = 300 K पर,
E = \(\frac{3}{2}\) × 1.38 × 10^-23 × 300
= 621 × 10 ^-23 J
= 6.21 × 10 ^-21 J

2. T = 6000 K पर
∴ E = \(\frac{3}{2}\) × 0138 × 10^-23 × 6000
= 1.24 × 10^-19 J

3. T = 10 × 10⁶ K = 10⁷ K पर,
∴ E = 3 × 1.38 × 10^-23 × 10⁷
= 2.07 × 10^-16 J
= 2.1 × 10^-16 J

प्रश्न 13.8.
समान धारिता के तीन बर्तनों में एक ही ताप और दाब पर गैसें भरी हैं। पहले बर्तन में नियॉन (एकपरमाणुक) गैस है, दूसरे में क्लोरीन (द्विपरमाणुक) गैस है और तीसरे में यूरेनियम हेक्साफ्लोराइड (बहुपरमाणुक) गैस है। क्या तीनों बर्तनों में गैसों के संगत अणुओं की संख्या समान है? क्या तीनों प्रकरणों में अणुओं की v_rms (वर्ग माध्य मूल चाल) समान है।
उत्तर:
(a) हाँ, चूँकि आवोगाद्रों परिकल्पना से, समान परिस्थितियों में गैसों के समान आयतन में अणुओं की संख्या समान होती है।
(b) नहीं चूँकि V_rms = \(\sqrt { \frac { 3RT }{ m } } \)
∴ V_rms ∝ \(\frac { 1 }{ \sqrt { m } } \)
अतः तीनों गैसों के ग्राम – अणु भार अलग – अलग हैं। अतः अणुओं की वर्ग माध्य – मूल चाल अलग – अलग होगी।

प्रश्न 13.9.
किस ताप पर आर्गन गैस सिलिंडर में अणुओं की V_rms – 20°C पर हीलियम गैस परमाणुओं की V_rms के बराबर होगी। (Ar का परमाणु द्रव्यमान = 39.9 u एवं हीलियम का परमाणु द्रव्यमान = 4.0 u)।
उत्तर:
माना कि T₁ व T₂ K ताप पर आर्गन व हीलियम गैस की वर्ग माध्य मूल वेग क्रमश: C₁ व C₂ हैं।
दिया है:
M₁ = 39.9 × 10^-3 kg,
M₂ = 4.0 × 10^-3 kg, T₁ = ?
T₂ = – 20 + 273 = 253 K
हम जानते हैं कि वर्ग माध्य मूल वेग
C = \(\sqrt { \frac { 3RT }{ M } } \)
C₁ = \(\sqrt { \frac { 3RT_{ 1 } }{ M_{ 1 } } } \)
तथा C₂ = \(\sqrt { \frac { 3RT_{ 1 } }{ M_{ 2 } } } \)
चूँकि C₁ = C₂ (दिया है)
∴ \(\sqrt { \frac { 3RT_{ 1 } }{ M_{ 1 } } } \) = \(\sqrt { \frac { 3RT_{ 1 } }{ M_{ 2 } } } \)
या \(\frac { T_{ 1 } }{ M_{ 1 } } \) = \(\frac { T_{ 1 } }{ M_{ 2 } } \)
= \(\frac { 39.9\times 10^{ -3 } }{ 4.0\times 10^{ -3 } } \) × 253
या T = 2523.7 K = 2524 K
= 2.524 × 10³ K

प्रश्न 13.10.
नाइट्रोजन गैस के एक सिलिंडर में, 2.0 atm दाब एवं 17°C ताप पर नाइट्रोजन अणुओं के माध्य मुक्त पथ एवं संघट्ट आवृत्ति का आंकलन कीजिए। नाइट्रोजन अणु की त्रिज्या लगभग 1.0 Å लीजिए। संघट्ट काल की तुलना अणुओं द्वारा दो संघट्टों के बीच स्वतंत्रतापूर्वक चलने में लगे समय से कीजिए। ( नाइट्रोजन का आण्विक द्रव्यमान = 28.0 u)।
उत्तर:
मैक्सवेल संशोधन ने गैस अणुओं का मध्य मुक्त पद
λ = \(\frac { 1 }{ \sqrt { 2\pi nd^{ 2 } } } \)
जहाँ d = अणु का व्यास
तथा = N = \(\frac{N}{V}\) = image 1
2 atm दाब पर, m द्रव्यमान गैस का आयतन
V = \(\frac{RT}{P}\), T = 273 + 17 = 290 K
∴ n = \(\frac{N}{V}\) = \(\frac{NP}{RT}\)
दिया है: N = 6.023 × 10²³ mole^-1
P = 2 atm = 2 × 1.013 × 10⁵ Nm^-2
R = 8.3 JK^-1mol^-1

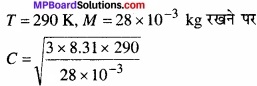
= 5.08 × 10² ms^-1
= 5.10 × 10² ms^-1
∴ संघट्ट आवृत्ति,
v = \(\frac { C }{ \lambda } \) = \(\frac { 5.1\times 10^{ 2 } }{ 1.0\times 10^{ -7 } } \)
= 2.0 × 10^-10 s ….. (i)
पुनः माना संघट्ट के लिया गया समय t है।
∴ t = \(\frac { d }{ C } \) = \(\frac { 2\times 10^{ -10 } }{ 5.10\times 10^{ 2 } } \)
= 4 × 10^-13 s
समी० (i) को (ii) से भाग देने पर,
\(\frac { \tau }{ \tau } \) = \(\frac { 2.0\times 10^{ -10 }s }{ 4\times 10^{ -13 }s } \) = 500
या τ = 500t
अतः दो क्रमागत टक्करों के मध्य समय टक्कर में लिये गए समय का 500 गुना है। इससे यह प्रदर्शित होता है कि गैस के अणु लगभग हर समय मुक्त रूप से चलायमान रहते हैं।

अणुगति सिद्धांत अतिरिक्त अभ्यास के प्रश्न एवं उनके उत्तर

प्रश्न 13.11.
1 मीटर लंबी संकरी (और एक सिरे पर बंद) नली क्षैतिज रखी गई है। इसमें 76 cm लंबाई भरा पारद सूत्र, वायु के 15 cm स्तंभ को नली में रोककर रखता है। क्या होगा यदि खुला सिरा नीचे की ओर रखते हुए नली को ऊर्ध्वाधर कर दिया जाए।
उत्तर:
प्रारम्भ में नली क्षैतिज है तब बंद सिरे पर रोकी गई वायु का दाब वायुमण्डलीय दाब के समान होगा।
∴ P₁ = 76 सेमी पारे स्तम्भ का दाब।
माना कि नली का अनुप्रस्थ क्षेत्रफल A सेमी² है।
वायु का आयतन = 15 × A = 15A सेमी³
जब नली का खुला सिरा नीचे की ओर रखते हैं तथा ऊर्ध्वाधर करते हैं जब खुले’ सिरे पर बाहर की ओर से वायुमण्डलीय दाब कार्य करता है जबकि ऊपर की ओर से 76 सेमी पारद सूत्र का दाब व बंद सिरे पर एकत्र वायु का दाब अधिक है। अतः पारद सूत्र असंचुलित रहेगा व नीचे गिरते हुए वायु को बाहर निकाल देता है।
माना कि पारद सूत्र की λ लम्बाई नीचे नली से बाहर निकलती है।
∴ नली में पारद सूत्र की शेष लम्बाई = (76 – h) सेमी तथा बंद सिरे पर वायु स्तम्भ की लम्बाई
= (15 + 9 + h)
= (24 + h) सेमी³
तथा वायु का आयतन V₂ = (24 + h) A सेमी³
माना कि इस वायु का दाब P₂ है।
∴ सन्तुलन में,
P₂ + (76 – h) सेमी पारद सूत्र का दाब = वायुमण्डलीय दाब
∴ P₂= R सेमी पारद सूत्र का दाब
सूत्र P₁V₁ = P₂V₂ से,
76 × 15A = h × (24 + h) A
या 1140 = 24h + h²
या h² + 24h – 1140 = 0
∴ h = – 24 ± \(\sqrt { 24^{ 2 }-4\times 17-1140 } \)
= 28.23 या – 4784 सेमी
परन्तु h ≠ ऋणात्मक
∴ h = 28.23 सेमी।
अतः पारद सूत्र की 28.23 सेमी लम्बाई नली से बाहर निकल जाएगी।

प्रश्न 13.12.
किसी उपकरण से हाइड्रोजन गैस 28.7 cm³s^-1 की दर से विसरित हो रही है। उन्हीं स्थितियों में कोई दूसरी गैस 7.2 cm³ s^-1 की दर से विसरित होती है। इस दूसरी गैस को पहचानिए। [संकेत : ग्राहम के विसरण नियम R₁/R₂ = (M₂/ M₁)^1/21/2 का उपयोग कीजिए, यहाँ R₁, R₂ क्रमशः गैसों की विसरण दर तथा M₁ एवं M₂ उनके आण्विक द्रव्यमान हैं। यह नियम अणुगति सिद्धांत का एक सरल परिणाम है।
उत्तर:
विसरण के ग्राहम के नियम से,
\(\frac { R_{ 1 } }{ R_{ 2 } } \) = \(\sqrt { \frac { M_{ 2 } }{ M_{ 1 } } } \) … (i)
जहाँ R₁ = गैस – 1 की विसरण दर = 28.7 cm³s^-1
R₂ = गैस – 2 की विसरण दर = 7.2 cm²s^-1 … (ii)
माना इनके संगत अणुभार M₁ व M₂ हैं।
∴H₂ के लिए, M₁ = 2
∴समी० (i) तथा (ii) से
\(\frac { 28.7 }{ 7.2 } \) = \(\sqrt { \frac { M_{ 2 } }{ 2 } } \)
या \(\frac { M_{ 2 } }{ 2 } \) = (\(\frac { 28.7 }{ 7.2 } \))²
या M₂ = 2 × 15.89 = 31.77 = 32 u
हम जानते हैं कि O₂ का अणुभार 32 है। अत: अज्ञात गैस O₂ हैं।

प्रश्न 13.13.
साम्यावस्था में किसी गैस का घनत्व और दाब अपने संपूर्ण आयतन में एकसमान है। यह पूर्णतया सत्य केवल तभी है जब कोई भी बाह्य प्रभाव न हो। उदाहरण के लिए, गुरुत्व से प्रभावित किसी गैस स्तंभ का घनत्व (और दाब) एकसमान नहीं होता है। जैसा कि आप आशा करेंगे इसका घनत्व ऊँचाई के साथ घटता है। परिशुद्ध निर्भरता ‘वातावरण के नियम’ n₂ = n₁ exp [\(\frac { – mg }{ k_{ B }T } \) (h₂ – h₁)] से दी जाती है, यहाँ n₂,n₁ क्रमश: h₂ व h₁ ऊँचाइयों पर संख्यात्मक घनत्व को प्रदर्शित करते हैं। इस संबंध का उपयोग द्रव स्तंभ में निलंबित किसी कण के अवसादन साम्य के लिए समीकरण n₂ = n₁exp \(-\frac { mgN_{ A } }{ \rho RT } \)(ρ – ρ’)( h₂ – h₁)] को व्युत्पन्न करने के लिए कीजिए, यहाँ निलंबित कण का घनत्व तथा ρ’ चारों तरफ के माध्यम का घनत्व है। N_A आवोगाद्रो संख्या, तथा सार्वत्रिक गैस नियतांक है। संकेत: निलंबित कण के आभासी भार को जानने के लिए आर्किमिडीज के सिद्धांत का उपयोग कीजिए।
उत्तर:
माना कि कणों तथा अणुओं का आकार गोलाकार है। कणों का भार निम्नवत् है।
w = mg = \(\frac{4}{3}\) π r²ρg … (i)
जहाँ r = कणों की त्रिज्या
तथा ρ = कणों का घनत्व है।
कणों की गति गुरुत्व के अधीन होने पर, ऊपर की ओर उत्क्षेप लगाती है जिसका मान निम्नवत् है –
B = कण का आयतन × प्रतिवेश का घनत्व × g
= \(\frac{4}{3}\) π r³(ρ – ρ’) g … (ii)
मन कण पर नीचे की और लगाने वाला बा F है।
अतः F = W – B
= \(\frac{4}{3}\) π r³(ρ – ρ’) g … (iii)
पुनः n₂ = n₁ exp [\(\frac { – mg }{ k_{ B }T } \) (h₂ – h₁)] … (iv)
जहाँ k_B = बोल्ट्जमैन नियतांक है।
तथा n₁ व n₂ क्रमश: h₁ व h₂ ऊँचाई पर संख्या घनत्व है। समीकरण (iii) में mg के स्थान पर बल F रखने पर, समीकरण (ii) व (iv) से,

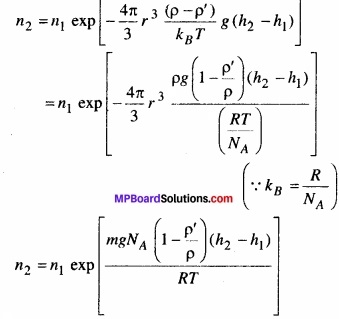
जो कि अभीष्ट समीकरण है।
जहाँ \(\frac{4}{3}\) π r³ ρg
= कण का द्रव्यमान × g = mg

प्रश्न 13.14.
नीचे कुछ ठोसों व द्रवों के घनत्व दिए गए हैं। उनके परमाणुओं की आमापों का आंकलन(लगभग)कीजिए।

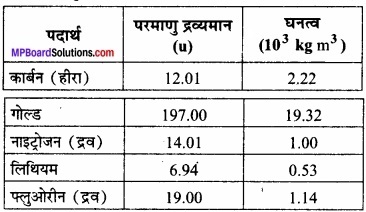
[संकेत: मान लीजिए कि परमाणु ठोस अथवा द्रव प्रावस्था में दृढ़ता से बंधे हैं तथा आवोगाद्रो संख्या के ज्ञात मान का उपयोग कीजिए। फिर भी आपको विभिन्न परमाण्वीय आकारों के लिए अपने द्वारा प्राप्त वास्तविक संख्याओं का बिल्कुल अक्षरशः प्रयोग नहीं करना चाहिए क्योंकि दृढ़ संवेष्टन सन्निकटन की रुक्षता के परमाणवीय आकार कुछA के परास में हैं।
उत्तर:
1. कार्बन का परमाणु भार
M = 12.01 × 10^-3 kg
N = 6.023 × 10²³
∴ एक कार्बन परमाणु का द्रव्यमान
M = \(\frac{M}{N}\) = \(\frac { 12.01\times 10^{ -3 } }{ 6.023\times 10^{ 23 } } \)
या m = 1.99 × 10^-26kg
= 2 × 10^-26 kg
कार्बन का घनत्व ρ_e = 2.2 × 10⁺³ kg m^-3
∴ प्रत्येक कार्बन परमाणु का आयतन
V = \(\frac { m }{ \rho C } \) = \(\frac { 2\times 10^{ -26 } }{ 2.2\times 10^{ 3 } } \)
= 0.9007 × 10^-29m³
माना r_C = कार्बन परमाणु की त्रिज्या
∴ \(\frac{4}{3}\) πr³_C = 0.9007 × 10^-29
या
r_C = [\(\frac { 0.9007\times 10^{ -29 } }{ 4\pi } \) × 3]^1/3
= [2.16 × 10^-30]^1/3
= 1.29 × 10^-10m = 1.29 Å

2.  दिया है: स्वर्ण परमाणु का परमाणु भार
M = 1.97 × 10^-3 kg
∴ प्रत्येक स्वर्ण परमाणु का द्रव्यमान
= \(\frac{M}{N}\) = \(\frac { 197\times 10^{ 3 } }{ 6.023\times 10^{ 23 } } \)
= 3.721 × 10^-25 kg
ρ_g = 19.32 × 10³kg m^-3
माना r_g = गोल्ड परमाणु की त्रिज्या

= (0.04 × 10^-28)^1/3
= 0.159 × 10^-9m
= 1.59 × 10^-10m = 1.59 Å

3. दिया है: नाइट्रोजन परमाणु का परमाणु भार
M = 14.01 × 10^-3 kg
∴ प्रत्येक परमाणु का द्रव्यमान
M = \(\frac{M}{N}\) = \(\frac { 14.01\times 10^{ -3 }kg }{ 6.023\times 10^{ 23 } } \)
= 2.3261 × 10^-26 kg
माना r_n = इसके प्रत्येक परमाणु की त्रिज्या
ρ_n = 1 × 10³ kg m^-3

= (5.55 × 10^-30 m³)^1/3
= 1.77 × 10^-10m = 1.77 Å

4. दिया है: M_Li = 6.94 × 10^-3 kg
ρ_Li = 0.53 × 10³ kg m^-3
∴ M_Li = mass of Li atom
= \(\frac { M_{ Li } }{ \rho _{ Li } } \) = \(\frac { 6.94\times 10^{ -3 } }{ 6.023\times 10^{ 23 } } \)
= 1.152 × 10^-26 kg
माना r_Li = L_i परमाणु की त्रिज्या

5. दिया है: M_F = 19 × 10^-3 kg
ρ_F = 1.14 × 10³ kg m^-3
∴ प्रत्येक फलुओरीन परमाणु का द्रव्यमान
m_F = \(\frac { M_{ F } }{ \rho _{ F } } \) = \(\frac { 19\times 10^{ -3 } }{ 6.023\times 10^{ 23 } } \)
= 3.155 × 10^-26 kg
माना प्रत्येक फलुओरीन परमाणु की त्रिज्या r_F है। अतः

= 1.88 × 10^-10 m = 1.88 Å

MP Board Class 11 Physics Solutions