MP Board Class 11th Physics Important Questions Chapter 9 Mechanical Properties of Solids

Students get through the MP Board Class 11th Physics Important Questions Chapter 9 Mechanical Properties of Solids which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 9 Mechanical Properties of Solids

Mechanical Properties of Solids Class 11 Important Questions Very Short Answer Type

Question 1.
What do you mean by deforming force?
Answer:
External force applied on a body is known as deforming force.

Question 2.
What is deformation?
Answer:
If an application of deforming force, a change in the shape or size of a body takes place, then it is said to be deformed.

Question 3.
What is meant by elasticity?
Answer:
It is the property of a body by virtue of which, it regains its original length, volume and shape when the deforming force is removed.

Question 4.
What is stress and its unit?
Answer:
The internal force of restitution per unit area of a deformed body is called stress.
Stress = \(\frac{\text { Force }}{\text { Area }}\)
Unit: SI unit of stress is Nm^-2.

Question 5.
Define plasticity.
Answer:
Plasticity is the property of remaining deformed even after the removal of deforming forces.

Question 6.
What do you mean by elastic limit?
Answer:
The maximum value of deforming force, by which if the force is applied on a body, the body looses its elastic property, is called elastic limit.

Question 7.
What do you mean by brittleness?
Answer:
Some substances are neither elastic nor plastic but they break easily into pieces, this property of a body is called brittleness and the bodies are called brittle substances.

Question 8.
What is difference between stress and pressure?
Answer:
Stress is internal force while pressure is external force.

Question 9.
How many types of stress are there?
Answer:
There are three types of stress :

1. Tensile stress or longitudinal stress,
2. Normal stress,
3. Tangential or shearing stress

Question 10.
What is strain? Write its unit.
Answer:
The ratio of change in length, volume or shape and its original length, volume or shape is called strain.
As it is the ratio of same quantities, therefore it has no unit.

Question 11.
What is longitudinal stress?
Answer:
It is the restoring force developed per unit cross-sectional area of a body when the length of the body increases in the direction of deforming force.

Question 12.
Define tangential stress.
Answer:
When the deforming force is applied along the plane of the area of cross-section of the body then the stress produced is known as tangential stress.

Question 13.
State the types of strain.
Answer:
There are three types of strain :

1. Longitudinal strain,
2. Shearing strain and
3. Volume strain.

Question 14.
What is longitudinal strain?
Answer:
Within elastic limit, it is the ratio of change in length to original length.
i.e., Longitudinal strain = \(\frac{\text { Change in length }}{\text { Initial length }}\)

Question 15.
Define volume strain.
Answer:
The change in unit volume due to deforming force is called volume strain.
Or
Within elastic limit, the ratio of change in volume to the initial volume is called volume strain, i.e.,
Volume strain = \(\frac{\text { Change in volume }}{\text { Initial volume }}\)

Question 16.
Define shearing strain.
Answer:
When a deforming force is applied on a body along its surface in such a way that the volume of the body remains constant, but the shape changes, then the body is said to be sheared and the strain produced is called shearing strain. Within elastic limit, it is measured by the ratio of the relative displacement of one plane to its distance from fixed plane, i.e.,
Shearing strain, θ = \(\frac{\Delta l}{l}\)
Δ l is relative displacement between two layers and l is the distance between the layers.

Question 17.
State Hooke’s law.
Answer:
Within elastic limit the stress is directly proportional to the strain. i.e.,
Stress ∝ Strain.

Question 18.
What are the types of modulus of elasticity?
Answer:
There are three types of modulus of elasticity :

1. Young’s modulus,
2. Bulk modulus,
3. Modulus of rigidity.

Question 19.
Define Young’s modulus and give its unit.
Answer:
Within elastic limit the ratio of longitudinal stress to the longitudinal strain is called Young’s moduluSIe.,
Young s modulus = \(\frac{\text { Longitudinal stress }}{\text { Longitudinal strain }}\)
Unit: Its SI unit is Nm^-2.

Question 20.
What is compressibility?
Answer:
‘The reciprocal of bulk modulus is called compressibility.

Question 21.
Define coefficient of rigidity.
Answer:
Within elastic limit, the ratio of tangential stress to the shearing strain is called coefficient of regidity.

Question 22.
Write the following in form of increasing elasticity of copper, iron, glass and rubber.
Answer:
Rubber < Glass < Copper < Iron.

Question 23.
If an ivory ball and an iron ball are dropped from the same height on a hard floor. Which one will rebounce higher?
Answer:
The ivory ball will rebounce higher because its elasticity is greater than that of iron ball.

Question 24.
Springs are made of steel and not of copper. Why?
Answer:
The Young modulus of steel is more than that of copper. If the same deforming force is applied on the spring of steel and spring of copper then the steel regain its initial position faster than that of copper spring. So the spring are made of steel.

Question 25.
What do you mean by restoring force?
Answer:
The force due to which the body regain its original shape and size is called restoring force.

Question 26.
State the condition for deforming force and restoring force to be equal and opposite.
Answer:
When the strain produced in the body is within the elastic limit then the deform¬ing force and restoring force are equal and opposite to each other.

Question 27.
On increasing temperature, Young modulus of elasticity increases or de¬creases.
Answer:
Decreases.

Question 28.
Why the work is done in stretching a wire?
Answer:
When a wire is stretched, the inter reaction force is developed within the wire and hence work is done against this force.

Question 29.
What happens with work to stretch a wire?
Answer:
The work done to stretch a wire is stored as elastic potential energy within wire.

Question 30.
If the length of the wire is halved, then what will be the effect in its Young modulus of elasticity?
Answer:
No effect on Young modulus of elasticity as it depends on the mass of the mate¬rial of the body not in its length.

Question 31.
If the length of wire is cut to its half then :
(i) What will be the effect on increase in length?
Answer:
Increase in length will get halved with respect to initial length.

(ii) Effect on maximum weight it can resist?
Answer:
No effect.

Question 32.
If a wire is replaced by another wire of same length and material but of double diameter, then :
(i) What will be increase in length for same given weight?
Answer:
Increase in length will remain one-fourth.

(ii) Effect on maximum weight that it can resist?
Answer:
Maximum weight it can resist will become four times.

Question 33.
Why the suspension wires are made up of quartz or phospher bronze?
Answer:
This is because the elastic after effect is negligible in quartz and phospher bronze.

Question 34.
In Searl’s apparatus, two similar wires of same material are taken, why?
Answer:
The temperature of room changes, hence the effect of temperature will be same on both the wires. Thus, the change in temperature does not cause any error.

Question 35.
In Searl’s experiment the readings are taken both by loading and unload¬ing the weights, why?
Answer:
There are two reasons :

1. It ensures that the experiment is performed within elastic limit.
2. The errors produced due to elastic fatigue, torsion and backlash ‘are removed.

Question 36.
Why the readings are taken after some time in the experiments of elasticity?
Answer:
To remove the error caused by elastic after effect.

Question 37.
What is elastic hysteresis?
Answer:
On applying deforming force on a body the strain is produced in it on removal of deforming force some time body do not regain its original position completely. Some strain remains left in that body. It is called elastic hysteresis.

Question 38.
Write down the effect of impurities on elasticity.
Answer:
In the presence of impurities the elasticity of the bodies is increased.

Question 39.
What is the effect of temperature on elasticity?
Answer:
With increase in temperature, usually the elasticity of the bodies decreases and with decrease in temperature, the elasticity increases. But the effect of temperature is negligible in the elasticity of’Invar steel’.

Mechanical Properties of Solids Class 11 Important Questions Short Answer Type

Question 1.
State the difference between elastic and plastic bodies.
Answer:
Difference between Elastic and Plastic bodies :

Elastic bodies	Plastic bodies
1. The bodies which regain their original position after the withdrawn of deforming force, are called elastic bodies.	1. The bodies which get permanently deformed by the deforming force, are called plastic bodies.
2. The change is temporary.	2. The change is permanent.
3. Examples : Gold, iron etc.	3. Examples : Melting wax, wet clay, plasticine.

Question 2.
Steel is more elastic than rubber. Explain with reason.
or
Why steel is more elastic than rubber?
Answer:
Let two wires of steel and rubber of equal length L and equal area of cross-section A are taken. Both are subjected by a force F, so that the elongation produced in steel is l_s and in rubber l_r.
∴ Modulus of elasticity of steel, Y_s = \(\frac{F \cdot L}{A \cdot l_{s}}\) …(1)
and Modulus of elasticity of rubber, Y_r = \(\frac{F \cdot L}{A \cdot l_{r}}\) …(2)
Now, dividing eqn. (1) by eqn. (2),
\(\frac{Y_{s}}{Y_{r}}=\frac{l_{r}}{l_{s}}\)
∵ l_r > l_s
∴ Y_s > Y_r
Hence, it is clear that steel is more elastic than rubber.

Question 3.
What do you mean by Young’s modulus of elasticity. Write its unit and dimensional formula. Derive the formula for Young’s modulus and hence define it.
Answer:
Within elastic limit, the ratio of longitudinal stress to the longitudinal strain is called Young’s modulus.
i.e., Y = \(\frac{\text { Longitudinal stress }}{\text { Longitudinal strain }}\)

SI unit is Nm^-2 and dimensional formula is [ML^-1T^-2].
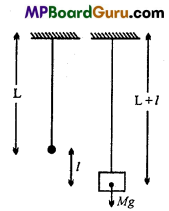
Formula: Let a mass M is suspended by a wire of length L and hence the elongation produced is l. If the radius of the wire is r, then
Stress = \(\frac{\text { Force }}{\text { Area }}=\frac{M g}{\pi r^{2}}\)
and strain = \(\frac{l}{L}\)
But Y = \(\frac{\text { Longitudinal stress }}{\text { Longitudinal strain }}\)
∴ Y = \(\frac{M g / \pi r^{2}}{l / L}\)
Or
Y = \(=\frac{M g L}{\pi r^{2} l}\)
Within elastic limit, Young’s modulus of elasticity is numerically equal to that force, which extends the length of wire of unit cross-sectional area by the original length i.e., the final length becomes double the initial length.

Question 4.
What do you mean by bulk modulus? Establish the formula for bulk modulus.
Answer:

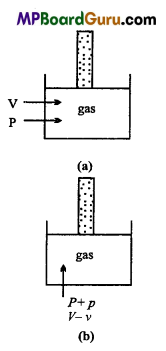
Bulk modulus : Within elastic limit, the normal stress is directly proportional to the volume strain.
∴ K = \(\frac{\text { Normal stress }}{\text { Volume strain }}\)
Formula : Let initial volume of a gas is V and pressure P. If the pressure is increased to P + p, so that its volume becomes V- v, hence the decrease in volume is v.
Since, force acting per unit area is called pressure. Hence,
Normal stress = Increase in pressure = (P + p)- P = p
Volume strain = – \(\frac{v}{V}\)
By Hooke’s law, within elastic limit,
Bulk modulus of elasticity = \(\frac{\text { Normal stress }}{\text { Volume strain }}\)
K = \(\frac{p}{-\frac{v}{V}}=\frac{-p V}{v}\)
-ve sign shows that, with increase in pressure, volume decreases.

Question 5.
What do you mean by coefficient of rigidity? Derive formula for it.
Answer:
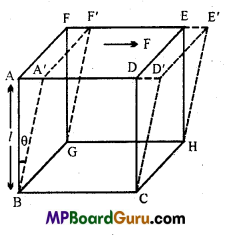
Coefficient of rigidity : Within elastic limit the ratio of tangential stress and shearing strain is called modulus of rigidity.
i.e., η = \(\frac{\text { Tangential stress }}{\text { Shearing strain }}\)

Formula derivation : Let ABCDEFGH be a cuboid (of side l). A tangential force F is applied on the surface ADEF, If the area of surface is A and angular displacement due to force F is θ, then
Tangential stress = \(\frac{F}{A}\)
If the relative displacement between the layers is
AA’ = X, then
Shearingstrain, θ = \(\frac{A A^{\prime}}{A B}=\frac{x}{l}\)
Modulus of rigidity = \(\frac{\text { Tangential stress }}{\text { Shearing strain }}\)
∴ η = \(\frac{F / A}{x / l}=\frac{F l}{x A}\)

Question 6.
Why are girders I shaped?
Answer:

Girders of iron are made of I shapped.
Let l be the length of a rod, b be the breadth and d be its thickness. If weight W be suspended at its middle point the bending (δ) is given by
δ = \(\frac{\mathrm{W} l^{3}}{b d^{3} \mathrm{Y}}\) …(1)
For the strength of girder, should be smaller, δ will be smaller if
(a) Y is large.
(b) From eqn. (1) it is clear that δ∝\(\frac{1}{b}\) and δ∝\(\frac{1}{d^{3}}\) Therefore depth d should be greater than breadth b.
Therefore, girders of made of I shape.

Question 7.
Define Poisson’s ratio. What is its unit? What is its value?
Answer:
When a deforming force F is applied to a wire, then its length increases, but its radius or breadth decreases. This strain which occurs along the width of the body is called lateral strain. Within elastic limit, the lateral strain is proportional to longitudinal strain.
i.e., Lateral strain ∝ Longitudinal strain
or
Lateral strain = σ × Longitudinal strain
or
Poisson’s ratio,
Where D = Initial diameter of wire, d = Change in diameter, L = Original length of wire, l = Change in length.
It has no unit. Theoretical values lies from – 1 to 0.5.

Question 8.
Derive an equation for the force acting on the clamps, when the wire gets cooled. f’
Answer:

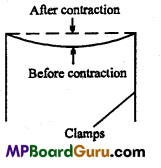
Let a wire of length L and area of cross-section A be clamped between the two ends. If it is being cooled, then its temperature decreases by Δ t°C, as a result it gets strinked and so it tries to contract the clamps. This force has to be found out. If Y is the Young’s moduliis of elasticity and a is the coefficient of linear expansion, then
α = \(\frac{\text { Change in length }(l)}{\text { Original length }(L) \times \text { Change in temp. }(\Delta t)}\)
Hence, αLΔt = l or \(\frac{l}{L}\) = αΔt
∴ Strain = αΔt …(1)
But, Young s modulus, Y = \(\frac{\text { Stress }}{\text { Strain }}\)
∴ Stress = Y × Strain= YαΔt …(2)
Moreover, Stress = \(\frac{\text { Force }}{\text { Area }}\)
or
Force = Stress × Area = YαΔt × A
∴ F =YAαΔt
This is the required relation.

Question 9.
Figure shows the strain-stress curve for a given material. What are:
(a) Young’s modulus and
(b) Approximate yield strength for his material?

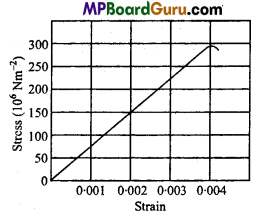
Answer:
From the given graph for a stress of 150 × 10⁶ Nm^-2, the strain is 0.002.
(a) Young’s modulus of the material (Y) is given by
∴ Y = \(\frac{\text { Stress }}{\text { Strain }}=\frac{150 \times 10^{6}}{0.002}=\frac{150 \times 10^{6}}{2 \times 10^{-3}}\)
= 75 ×10⁹ Nm^-2
= 7.5 × 10¹⁰Nm^-2.

(b) Yield strength of a material is defined as the maximum stress it can sustain.
∴ From graph, the approximate yield strength of the given material = 300 × 10⁶ Nm2 = 3 × 10⁸ Nm^-2. Actually, it is slightly less than 3 × 10⁹ Nm^-2.

Question 10.
The stress-strain graphs for materials A and if are shown in figure (a) and (b):

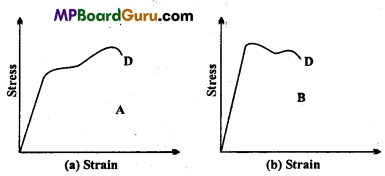
The graphs are drawn to the same scale :
(a) Which of the materials has greater Young’s modulus?
(b) Which of the two is the stronger material?
Answer:
(a) From the two graphs we note that for a given strain, stress for A is more than that of B. Hence Young’s modulus = \(\left(\frac{\text { Stress }}{\text { Strain }}\right)\) is greater forA than that of B.

(b) Strength of a material is determined by the amount of stress (load) required to cause breaking or fracture of material corresponding the breaking point.
∴ Material A is stronger than B as it can withstand more load without breaking than the material B corresponding to point D.

Question 11.
Prove that energy stored per unit volume in a stretched string is, given by:
U = \(\frac{1}{2}\) × Stress × Strain
= \(\frac{1}{2}\) × Young’s modulus × (Strain )²
Derive the formula for the potential energy of a stretched string.
Answer:
Consider a wire of length L and it is extended by a force F due to which its extension takes place by l.
If A is the area of cross-section of the wire and Fis the Young’s modulus of elasticity,
then
Y = \(\frac{\text { Longitudinal stress }}{\text { Longitudinal strain }}\) = \(\frac{F / A}{l / L}\) = \(\frac{F L}{A l} .\)
Or
YAl = Fl or F = \(\frac{Y A l}{L}\) …(1)

When, the wire is stretched by a force F, then work is done by the deforming force
which is stored in the wire in the form of potential energy.
Small amount of work done to stretch by dl i.e.,
dW = Fdl= \(\frac{Y A l}{L}\)dl
∴ The total amount of work done will be

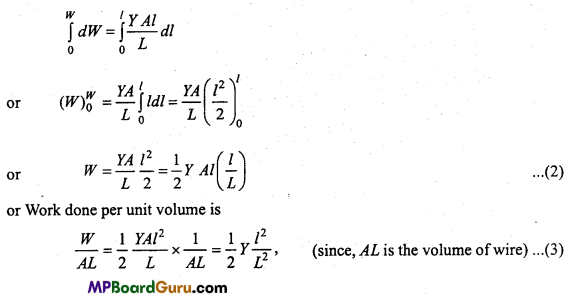
Where, \(\frac{l}{L}\)is the longitudinal strain
Work done per unit volume is called elastic potential energy per unit volume (U).
∴ U= \(\frac{1}{2}\) × Y × (Strain)², [from eqn. (3)]
But, Y = \(\frac{\text { Stress }}{\text { Strain }}\)
∴ U= \(\frac{1}{2}\) × \(\frac{\text { Stress }}{\text { Strain }}\) × (Strain)²
or
U= \(\frac{1}{2}\) × Stress × Strain. Proved.

Mechanical Properties of Solids Class 11 Important Numerical Questions

Question 1.
A steel wire of length 4.7 m and cross-sectional area 3.0 × 10^-5 m²stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area 4.0 × 10^-5
m² under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
Solution:
Here, for steel wire,
Length of wire, l₁ = 4.7 m
Area of cross-section, a₁ = 3.0 × 10^-5 m²
Stretching, Δl₁, = Δl(say)
Stretching force on steel, F₁ = F
For copper wire,
Length of wire,l₂ = 3.5 m
Area of cross-section, a₂ = 4.0 × 10^-5 m²
Stretching, Δl₂ = Δl(given);
Stretching force on copper, F₂ = F
Let Y₁ and Y₂ be the Young’s modulus of steel and copper wire respectively.

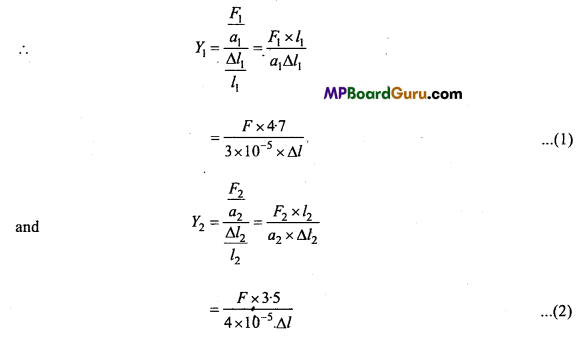
Dividing eqn. (1) by eqn. (2), we get

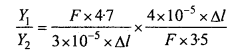
= \(\frac{18 \cdot 8}{10 \cdot 5}\) = 1.79 = 1.8:1

Question 2.
Two wires of diameter 0.25 cm. One made of steel and the other made of brass are loaded as shown in fig. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. If Young’s modulus of steel and brass are 2.0 × 10¹¹ Pa and 0.91 × 10¹¹ Pa, then compare the elongation of the steel and the brass wires.
Solution:

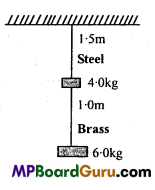
Using, Y = \(\frac{M g L}{\pi r^{2} l}\)
l = \(\frac{M g L}{\pi r^{2} Y}\)
For brass wire,
M= 6 kg, L = 1.0 m, Y = 0.91 × 10¹¹N/m²
and 2r = 0.25 cm = 0.25 × 10^-2m
r = 0.125 × 10^-2m
Putting the values in formula,
l = \(\frac{6 \times 9 \cdot 8 \times 1 \cdot 0}{3 \cdot 14 \times\left(0 \cdot 125 \times 10^{-2}\right)^{2} \times 0 \cdot 91 \times 10^{1}}\)
= 1.3 × 10^-4 m.
For steel wire,
M = 6 + 4 = 10 kg,L = 1.5 m, Y = 2.0 × 10¹¹ N/m²and 2r = 0.25cm
∴ r = 0.125 × 10^-2m
Putting the values in formula,
l = \(\frac{10 \times 9 \cdot 8 \times 1 \cdot 5}{3 \cdot 14 \times\left(0 \cdot 125 \times 10^{-2}\right)^{2} \times 2 \cdot 0 \times 10^{1}}\)
= 1.5 × 10^-4m

Question 3.
A piece of copper having a rectangular cross-section of 15.2 mm × 19.1 mm is pulled in tension with 44500 N. force, producing only elastic deformation. Calculate the resulting strain. Y for copper = 1.1 × 10¹¹ Nm^-2.
Solution:
Here, Y = 1.1 × 10¹¹Nm^-2
A = Area of cross-section
= 15.2 mm × 19.1 mm
= 15.2 × 10^-3m × 19.1 × 10^-3 m
Force, F = 44500 N
Resulting Strain = Longitudinal Strain = ?
∴ Y = \(\frac{\text { Stress }}{\text { Strain }}\)
or
Strain \(=\frac{\text { Stress }}{Y}=\frac{F}{A Y}\)
or
Longitudinal Strain = \(\frac{44500}{15 \cdot 2 \times 19 \cdot 1 \times 10^{-6} \times 1 \cdot 1 \times 10^{1}}\)
= 139.34 × 10^-3 m = 0.139.

Question 4.
A steel cable with a radius of 1.5 cm supports a chair lift at a ski area. If the maximum stress is not to exceed 10⁸ Nm^-2, what is the maximum load the cable can support?
Solution:
Here, radius of steel cable r = 1.5cm = 1.5 × 10^-2 m
Max. Stress = 10⁸ Nm^-2
∴ Area of cross-section of cable A = πr^-2 = π(1.5 × 10^-2)²
Maximum load the cable can withstand = Maximum force ? We know that,
Maximum stress = \(\frac{\text { Maximum force }}{\text { Area of cross-section }}\)
or
Maximum force = Maximum stress × Area of cross-section
= 10⁸ × π × (1.5 × 10^-2)²
= 3.142 × 2.25 × 10⁸ × 10^-4 N
or
Maximum load the cable can withstand = 7.1 × 10⁴N.

Question 5.
A 4.0 metre long copper wire of area of cross-section 1.2 cm² is stretched by a force of 4.8 × 10³N. If the Young’s modulus of copper is Y = 1.2 × 10¹¹ N/m², then calculate:
(i) Stress,
(ii) Strain,
(iii) Increase in length of wire.
Solution:
Given : L=4.0 metre, A = 1.2 cm² = 1.2 × 10^-4m², F = 4.8 × 10³ N, Y= 1.2 × 10¹¹ N/m²

(i) Stress : The stress on wire will be = \(\frac{F}{A}=\frac{4 \cdot 8 \times 10^{3}}{1 \cdot 2 \times 10^{-4}}\)
∴ Stress = 4 × 10⁷ N/m².

(ii) Strain: The Young’s modulus of wire is Y = \(\frac{\text { Stress }}{\text { Strain }}\)
∴ Strain = \(\frac{\text { Stress }}{\mathrm{Y}}=\frac{4 \times 10^{7}}{1 \cdot 2 \times 10^{11}}\)
∴ Strain = 3.3 × 10^-4

(iii) Increase in Length of wire : From the formula of Young’s modulus
Y = \(\frac{\mathrm{FL}}{\mathrm{A} . l}\)
∴ l = \(\frac{\mathrm{FL}}{\mathrm{AY}}\)
\(=\frac{4 \cdot 8 \times 10^{3} \times 4}{1 \cdot 2 \times 10^{11} \times 1 \cdot 2 \times 10^{-4}}\)
= 13.2 × 10^-4 = 1.32 mm.

Question 6.
Two wires made of same material, length of first wire is half the length of second wire and its diameter is double the diameter of second wire. If same weight is suspended in both wires then find the ratio of increase in length.
Solution:

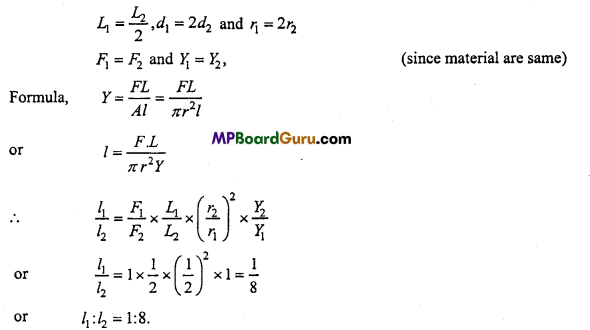
Question 7.
On stretching a gold wire, Its length Increases by 1%. Find out linear strain of it, if its coefficient of Young modulus is 8 × 10¹⁰ N/m². Find out the stress produced.
Solution:
According to question,
l = 1%, Y = 8 × 10¹⁰ N/m²
∴ Linear strain = \(\frac{\text { Increase in length }}{\text { Original length }}\)
= \(\frac{1}{100}\)
= 0.01
Stress = Y × Strain = (8 × 10¹⁰) × (0.01)
=8 ×10⁸N/m².

Question 8.
2 kg weight elongates a wire of 3 m length by 1 mm. The diameter of wire is 1 mm. Determine Young’s modulus of the material of the wire.
Solution:
Given : M = 2 kg, L = 3 m, l = 1 mm = 10^-3 m, r= \(\frac{1}{2}\)mm= 0.5 x 10^-3m, g = 9.8 ms^-2. ,
We have, Y = \(\frac{M g L}{\pi r^{2} l}\)
or
Y = \(\frac{2 \times 9 \cdot 8 \times 3}{3 \cdot 14 \times\left(0 \cdot 5 \times 10^{-3}\right)^{2} \times 10^{-3}}\)
=  \(\frac{58 \cdot 8 \times 10^{6} \times 10^{3}}{3 \cdot 14 \times 0 \cdot 25}\)
∴ Y = \(\frac{588 \times 10^{12}}{314 \times 25}\)
= 7.49 × 10¹⁰Nm^-2

Question 9.
The diameter of a wire is \(\frac{2}{\sqrt{\pi}}\) cm. The force required to double the length is 2 × 10¹²dyne. Calculate Young’s modulus of the material of the wire.
Solution:
Given: r = \(\frac{1}{2}\) × \(\frac{2}{\sqrt{\pi}}\)cm = \(\frac{1}{\sqrt{\pi}}\) 10^-2 m, L = l
and Mg = 2 × 10¹²dyne = 2 × 10¹² × 10^-5N = 2 × 10⁷N
Now, we have Y = \(\frac{M g L}{\pi r^{2} l}\)

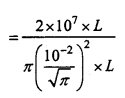
∴ Y = \(\frac{2 \times 10^{7}}{10^{-4}}\) = 2 × 10¹¹ Nm^-2

Question 10.
Calculate the force required to elongate 1 m long the 2 mm thick wire by 1 mm. (Y = 2 x 10¹¹ Nm^-2)
Solution:
Given: L = 1m,r = \(\frac{2}{2}\) = 1mm =10^-3m = 10^-3m, l = 1mm 10^-3m Y = 2 × 10¹¹Nm^-2
Frmula, Y = \(\frac{M g L}{\pi r^{2} l}\)
or
Mg = \(\frac{Y \pi r^{2} l}{L}\)
\(=\frac{2 \times 10^{11} \times 3 \cdot 14 \times\left(10^{-3}\right)^{2} \times 10^{-3}}{1}\)
= 6.28 × 10¹¹ × 10^-9
= 6.28 × 10² = 628 N.

Question 11.
Calculate the work done in extending a wire of length lm and of cross-section 1mm2 through 2mm. (Given y = 2 × 10¹¹Nm^-2)
Solution:
Given: L= 1m, A = nr² = 1mm² = (1 × 10^-3m)²= 10^-6m²
l = 2mm = 2 × 10^-3m and Y = 2 × 10^-11 Nm^-2
Strain = \(\frac{l}{L}=\frac{2 \times 10^{-3}}{1}\) = 2 × 10^-3
∴ Volume of wire = A.L = 10^-6 × 1 = 10^-6m³
Work done = \(\frac{1}{2}\) × Y × (Strain)² × Volume
= \(\frac{1}{2}\) × 2 × 10¹¹ × (2 ×10^-3)¹¹× 10^-6
= 0.4 J.

Question12.
A rubber ball while taking to the bottom of a lake 200 m deep its volume de-creases by 0.1%. Calculate the Bulk modulus of rubber. Density of water is 10³ kg/ m³ and g = 10 m/sec².
Solution:
Given : Depth h = 200m, Density of water = 10³ kg/m³ Acceleration due to gravity g = 10 m/sec²,
Volume strain = 0.1% = –\(\frac{0 \cdot 1}{100}\)
∴ Bulk modulus K = \(\frac{\frac{-p}{\Delta v}}{\frac{V}{V}}\)
or
K = \(\frac{-200 \times 10^{3} \times 10}{\frac{-0 \cdot 1}{100}}\)
= 2 × 10⁹N/m²

Question 13.
A weight of 20 kg is suspended in a wire. Area of cross-section of it is 1mm². The length of the wire in extended state is 6 m. On withdrawing the weight its length become 5.995 m. Find out Young modulus of elasticity.
Solution:
Given : M = 20 kg, A = 1mm² = 10^-6m², L = 6m,
Change in length = 6 – 5.995 = 0.005 m
∴ Y = \(\frac{M g L}{A l}\)
or
Y \(=\frac{20 \times 9 \cdot 8 \times 6}{10^{-6} \times 0-005}\)
= 2.35 × 10¹¹N/m².

Question 14.
On iron wire of radius 0.5 mm is heated up to 300°C and then it is fixed between two clamp. When the temperature reduces to 30°. What will be the force acting upon the clamp. (α = 1.2 × 10^-5/°C and Y= 1.4 × 10¹² dyne/cm²)
Solution:
Given : r = 0.5mm = 0.05 cm, α = 1.2 × 10×^-5/°C, Y = 1.4 × 10¹²dyne/cm²
ΔT = 300 – 30 = 270° C
From F = YΔ α. AT, we get
F = Y πr² α ΔT
∴ F = 1.4 × 10¹² × 314 × (0.05)² × 1.2 × 10^-5 × 270
F = 3.56 × 10⁷ dyne.

Mechanical Properties of Solids Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
A wire of radius r and length L on which a mass M is suspended so that its increase in length is T. Young modulus will be:
(a) \(\frac{\mathrm{MgL}}{\pi r^{2} l}\)
(b) \(\frac{\mathrm{Mgl}}{\pi r^{2} \mathrm{~L}}\)
(c) \(\frac{\pi r^{2} L}{M g l}\)
(d) \(\frac{\pi r^{2} l}{\mathrm{MgL}}\)
Answer:
(a) \(\frac{\mathrm{MgL}}{\pi r^{2} l}\)

Question 2.
Which substance is more elastic:
(a) Glass
(b) Steel
(c) Plastic
(d) Rubber.
Answer:
(b) Steel

Question 3.
Magnitude of Poisson’s ratio is in between :
(a) – 1 and \(\frac{1}{2}\)
(b) –\(\frac{3}{4}\) and –\(\frac{1}{2}\)
(c) \(\frac{1}{2}\) and 1
(d) 1 and 2
Answer:
(a) – 1 and \(\frac{1}{2}\)

Question 4.
Work done per unit volume for a wire is :
(a) Stress × Strain
(b) \(\frac{1}{2}\)× Stress × Strain
(e) 2(Stress × Strain)
(d) Stress/Strain.
Answer:
(b) \(\frac{1}{2}\)× Stress × Strain

Question 5.
Four wire made of same material, equal weight is suspended on them, increase in length will be maximum for wire :
(a) Length 50 cm and diameter 0.5 mm
(b) Length 100 cm and diameter 1 mm
(c) Length 200 cm and diameter 2 mm
(d) Length 300 cm and diameter 3 mm.
Answer:
(a) Length 50 cm and diameter 0.5 mm

Question 6.
10 newton force is needed to break a wire of radius one millimetre. What is force needed to break a wire of radius 3 mm :
(a) 90N
(b) \(\frac{10}{3}\)N
(c) \(\frac{10}{9}\)N
(d) 30N
Answer:
(a) 90N

Question 7.
In general modulus of rigidity is than modulus of elasticity:
(a) Less
(b) More
(c) Equal
(d) None of these.
Answer:
(a) Less

Question 8.
A wire of length L, Area of cross-section A, Young modulus of elasticity Y and coefficient of linear expansion a is heated up to t°C. Force experience on wire will be :
(a) γAαt
(b) γAαLt
(c) tALα
(d) \(\frac{t \alpha \mathrm{L}}{\mathrm{A}}\)
Answer:
(a) γAαt

2. Fill in the blanks:

1. SI unit of stress is …………………
Answer:
Newton/metre²

2. On increasing temperature, coefficient of elasticity ………………….
Answer:
decreases

3. Within elastic limit ……………….. is directly proportional to strain.
Answer:
stress

4. Rubber is ………………. elastic than steel.
Answer:
less

5. For an ideal rigid body Young modulus is ………………..
Answer:
infinity

3. Match the following:

Column ‘A’	Column ‘B’
1. Hooke’s law	(a) Proportional to area of cross-section
2. Normal stress	(b) Zero
3. Breaking stress	(c) Shearing strain
4. Young modulus of elastic body	(d) Applicable within elastic limit
5. Tangential strain	(e) Volume strain.

Answer:
1. (d) Applicable within elastic limit
2. (e) Volume strain
3. (a) Proportional to area of cross-section
4. (b) Zero
5. (c) Shearing strain

4. Write true or false:

1. Hooke’s law is applicable within elastic limit.
Answer:
True

2. Diamond can be considered as rigid body.
Answer:
True

3. Product of strain and stress is equal to stored energy.
Answer:
False

4. Young modulus of elasticity is dimensionless.
Answer:
False

5. Breaking stress depends on body of material.
Answer:
True

6. Young modulus of elasticity is valid for solid only.
Answer:
True

7. Rubber is more elastic than steel.
Answer:
False

8. Hookes law is defined within elastic limit.
Answer:
False

9. Quartz does not exhibit elastic after effect practically.
Answer:
True

10. It is difficult to twist a small rod in comparison to long rod.
Answer:
True

11. A hollow rod of same length and mass is more strong than a solid rod.
Answer:
True