MP Board Class 11th Physics Important Questions Chapter 6 Work, Energy and Power

Students get through the MP Board Class 11th Physics Important Questions Chapter 6 Work, Energy and Power which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 6 Work, Energy and Power

Work, Energy and Power Class 11 Important Questions Very Short Answer Type

Question 1.
What is work? Is it scalar or vector quantity?
Answer:
Work is said to be done by a force when the force produces a displacement of the body on which it acts in any direction except perpendicular to the direction of force, i.e.,
W = Fs cosθ
It is a scalar quantity.

Question 2.
Write the unit and dimensional formula of work.
Answer:
Unit: SI unit of work is joule.
Dimensional formula : Work = Force × Displacement
= [MLT^-2][L]
= [ML²T^-2].

Question 3.
Define 1 joule and 1 erg.
Answer:
1 joule : When a force of 1 N is applied on a body and is displaced 1 m in the direction of force, then 1 joule work is done.
1 erg : When a force of 1 dyne is applied on a body and is displaced 1 cm in the direction of force, then 1 erg work is done.

Question 4.
What is zero work? Give one example.
Answer:
If force applied on an object is perpendicular to its displacement then the work is zero.
∴ W = Fs cos90° = 0
Example: A coolie carrying suitcase on his head. The work done against gravity is zero.

Question 5.
When does the work done become maximum by a force?
Answer:
When the direction of force and displacement are same.

Question 6.
Can a satellite do any work against gravitational force, while revolving around the earth? Why?
Answer:
No, because the direction of motion of satellite is always perpendicular to the gravitational force.

Question 7.
What is energy? Give examples. Write its unit and dimensional formula.
Answer:
The efficiency of work done of a body is called energy.
Examples: Mechanical energy, heat energy, light energy etc.
SI unit: joule.
Dimensional formula: [ML²T^-2].

Question 8.
Write the statement of laws of conservation of energy.
Answer:
According to this law energy is neither created nor destroyed but transformed from one form to another.

Question 9.
A man walk 10 metre with a luggage in his head. How much work will be done by him against gravitational force.
Answer:
Zero, because displacement of the man is perpendicular to the direction of gravitational force.

Question 10.
What do you mean by variable force? Explain with example.
Answer:
When the magnitude and direction of a force are changing with time then such force is called variable force.
Example :
The gravitational force acting between two bodies depends upon the distance between the bodies, hence it is variable force.

Question 11.
What do you mean by mechanical energy? What are the types of it?
Answer:
The energy due to mechanical work is called mechanical energy. The mechanical energy are of two types :

• Kinetic energy,
• Potential energy.

Question 12.
If velocity of an object is doubled then what will be the increase in its kinetic energy?
Answer:
Kinetic energy will become four time as
K = \(\frac{1}{2}\) mν²

Question 13.
Write the formula for gravitational potential energy at height ‘h’.
Answer:
Gravitational potential energy at height ‘h’ of a body of mass ‘m’ is mgh.

Question 14.
When a bullet strike a target and get stopped, then in which form its kinetic energy get changes?
Answer:
Kinetic energy of the bullet get changes into sound energy and heat energy.

Question 15.
What is power? Write its S.I. unit.
Answer:
Rate of doing work is defined as power. Its S.I. unit is watt. It is a scalar quantity.
power = \(\frac{\text { Work }}{\text { Time }}\)

Question 16.
Define watt.
Answer:
If the rate of work done is 1 joule per second, then the power is called watt.

Question 17.
Write the magnitude of one horse power.
Answer:
1 H.P. = 746 watt.

Question 18.
What do you mean by collision? Which quantities are transferred during the collision?
Answer:
The interaction between two bodies due to impact, is called collision. During the collision momentum and kinetic energy are transferred.

Question 19.
Do the bodies touch each other compulsorily in collision? Give example.
Answer:
Not necessary. When alpha particles (₂He⁴), which are positively charged particles are made to strike the nucleus, then they get deviated from their path without contact with each other.

Question 20.
How many types of collisions are there? Describe them.
Answer:
Collisions are of two types :
(i) Elastic collision: The collisions in which the momentum and kinetic energy of the system conserved are called elastic collision.
Example : The collisions between the molecules and atoms. In daily life collision of glass or ivory balls are considered as elastic collision.

(ii) Inelastic collision : The collisions in which the momentum of the system is conserved but not kinetic energy.
Example : Spreading of mud and stick to wall. A bullet embedded with a wooden block.

Question 21.
Write the magnitude of one kilowatt and one megawatt.
Answer:
1 kilowatt = 1000 watt = 10³ watt.
1 megawatt = 10⁶ watt.

Question 22.
How kinetic energy is measured?
Answer:
Kinetic energy is measured by formula \(\frac{1}{2}\) mν²

Question 23.
What do you mean by variable force? write the formula for work done by variable force.
Answer:
When the magnitude and direction of a force are changing with time, then such force is called variable force.
Work done by variable force W = F. d cosθ.

Question 24.
Power is a scalar quantity or vector quantity. Write its dimensional formula.
Answer:
Power is a scalar quantity. Its dimensional formula is [ML² T^-3 ].

Question 25.
An object is displaced by applying force on it. When will be the work done maximum?
Answer:
When the displacement of an object is in direction of applied force, then work done is maximum.

Question 26.
In which direction force must be applied on a body so that work done is zero?
Answer:
When the force is applied perpendicular to the displacement work done is zero.
Since, W = F.d cosθ
If θ = 90°, cos 90° = 0.
∴ W = 0.

Question 27.
A car is moving on the plane road with uniform velocity, does the car work, why?
Answer:
Yes, the car does work against frictional force.

Question 28.
What type of energy is stored in the spring of a watch?
Answer:
Elastic potential energy.

Question 29.
What is spring constant? What is its S.I. unit?
Answer:
The spring constant of a spring is defined by the force, which changes its length by unity. Its S.I. unit is Nm^-1.

Question 30.
Write the formula for potential energy of a compressed spring.
Answer:
Elastic potential energy of a compressed spring is =\(\frac{1}{2}\) kx² where k is spring constant and x is displacement from normal state.

Question 31.
When a bulb glow, does electric energy get transformed into any energy?
Answer:
Yes, electrical energy get transformed into light energy and thermal energy.

Question 32.
Write the different forms of energy.
Answer:
Different form of energy are Mechanical energy, Thermal energy, Light energy, Magnetic energy, Electrical energy, Sound energy, Chemical energy, Nuclear energy etc.

Question 33.
What is kilowatt hour ? Write its magnitude.
Answer:
kilowatt hour is a unit of energy.
1 kilowatt hour = 1000 watt × 1 hour
= 1000 joule/second × (3600 second) = 3.6 × 10⁶ joule.

Question 34.
Write the relation between momentum (p) and kinetic energy (E). The K.E. of a body is increased 4 times. What will be the change in momentum?
Answer:
p = \(\sqrt{2 m E}\)
∴ p ∝√E
or
\(\frac{p_{1}}{p_{2}}=\sqrt{\frac{E_{1}}{E_{2}}}=\sqrt{\frac{E}{4 E}}=\frac{1}{2}\)
∴p₂ = 2p₁
Hence, momentum will be doubled.

Question 35.
if the momentum of a body becomes 4 times. How many time its K.E. will be ?
Answer:
We have, \(\frac{p_{1}}{p_{2}}=\sqrt{\frac{E_{1}}{E_{2}}}\)
or \(\frac{E_{1}}{E_{2}}=\frac{p_{1}^{2}}{p_{2}^{2}}=\left(\frac{p_{1}}{4 p_{1}}\right)^{2}=\frac{1}{16}\)
or E₂= 16E₁
Hence, K.E. will be 16 times.

Question 36.
The quantity whose unit is kWh?
Answer:
Energy.

Question 37.
What do you mean by mass-energy equivalence?
Answer:
It means that mass can be converted into energy and energy can be converted into mass.
i.e., E = mc²
Where, c is velocity of light.
This relation is called mass-energy equivalence equation.

Question 38.
What is the equivalent energy of 1 gm mass?
Answer:
1 gm = 9 × 10¹³ joule.

Question 39.
How much energy is produced by the absorption of an electron and a positron?
Answer:
1.02 MeV.

Question 40.
Which mechanical energy increases or decreases when a body is thrown vertically upwards?
Answer:
Potential energy and kinetic energy.

Question 41.
Two bodies of same mass are moving with a velocity of u₁ and u₂ collide with each other, what will be the velocity after collision?
Answer:
Let the velocity after collision be ν₁ and ν₂.
According to conservation of momentum,
mu₁ + mu₂ = mν₁ + mν₂
or
u₁+u₂ = ν₁+ν₂ …(1)
and for elastic collision ν₁ – ν₂ = – (u₁– u₂) …(2)
Solving eqns. (1) and (2), we get
ν₁ = u₂ and ν₂ = u₁.

Question 42.
Write the forms of energy we get from the following :

• Dynamo,
• Electric motor,
• Photoelectric cell,
• Loudspeaker,
• Glow of electric bulb,
• Free falling stone.

Answer:

• Dynamo : Mechanical energy into electrical energy.
• Electric motor: Electrical energy into mechanical energy.
• Photoelectric cell: Light energy into electrical energy.
• Loudspeaker: Electrical energy into sound energy.
• Glow of electric bulb : Electrical energy into light energy.
• Free falling stone : Potential energy into kinetic energy.

Question 43.
Does a satellite do any work against gravitation while it revolve in its orbit? Why?
Answer:
No, because motion of a satellite is always perpendicular to the direction of gravitation. ‘
Since, W = F.d cosθ
and θ= 90°,
∴ cosθ= cos 90° = 0
∴ W = 0.

Question 44.
When a body is thrown upward and when it fall downward, what type of mechanical energy is increased?
Answer:
When a body is thrown upward potential energy increases and when body fall downward its kinetic energy increases.

Question 45.
Force of repulsion acts between two similar charge, when they bought closer does their potential energy increases?
Answer:
Yes, there potential energy increases as work is done against force of repulsion.

Work, Energy and Power Class 11 Important Questions Short Answer Type

Question 1.
Explain geometrical meaning of scalar product of two vectors and write its three properties.
Answer:
Geometrical meaning of the scalar product of two vectors : If \(\vec{a} \text { and } \vec{b}\) are the two given vectors and θ is the angle between them, then
\(\vec{a} \cdot \vec{b}\) = abcosθ = a(bcosθ) -b(acosθ)

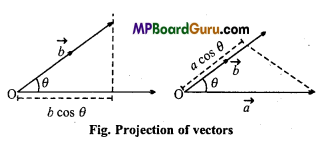
Now, b cos θ is the components or projection of the vector \(\vec{b}\) in the direction of the vector \(\vec{a}\) and a cos θ is the component of the vector \(\vec{a}\) in the direction of the vector \(\vec{b}\)

Thus, the scalar product of two vectors is equal to the multiplication of the magnitude of one vector and the magnitude of the component or projection of the other vector in the direction of the first vector.

Scalar product of two equal vectors :
\(\vec{a} \cdot \vec{b}\) = a.acos0° = a²
\(\vec{a} \cdot \vec{a}\) is also called \(\overrightarrow{a^{2}}\)

\(\vec{a} \cdot \vec{a}\) = \(\overrightarrow{a^{2}}\) = a ²
i.e., the dot product of a vector itself is equal to the square of its magnitude.

Properties of the scalar product of two vectors :
(i) The scalar product of two vectors is commutative i.e., the order of the vectors can be interchanged i.e.,
\(\vec{b} \cdot \vec{a}=\vec{a} \cdot \vec{b}\)
Proof:
\(\vec{a} \cdot \vec{b}\) = ab cosθ
Now, \(\vec{b} \cdot \vec{a}\) = ba cosθ
⇒ ab cosθ = \(\vec{a} \cdot \vec{b}\)

(ii) The scalar product of vectors follows the distributive law in relation to the addition. Thus,
\(\vec{a} \cdot(\vec{b}+\vec{c})=\vec{a} \cdot \vec{b}+\vec{a} \cdot \vec{c}\)

(iii) The scalar product of two vectors follows the multiplicative law in relation to scalar. Thus,
\((m \vec{a}) \cdot \vec{b}=m(\vec{a} \cdot \vec{b})=\vec{a} \cdot(m \vec{b})\)

Question 2.
Explain the geometrical meaning of cross product of two vectors and write its properties.
Answer:
Geometrical meaning of vector product of two

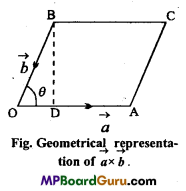
vectors : Let two vectors \(\vec{a} \text { and } \vec{b}\) are represented by the adjacent sides of parallelogram OACB, i.e.,
\(\overrightarrow{O A}=\vec{a} \text { and } \overrightarrow{O B}=\vec{b}\)
Now, draw perpendicular BD from point B, on OA.
Area of parallelogram OACB = OA × BD
= OA × OB sinθ [∵ sinθ = \(\frac{B D}{O B}\)
or
absinθ =\(|\vec{a} \times \vec{b}|\)
Hence, modulus of \(\vec{a} \times \vec{b}\) represents the area of parallelogram whose adjacent sides are \(\vec{a} \text { and } \vec{b}\).

Properties of vector or cross product of two vectors :
(i) The vector multiplication of two vectors is non-commutative i.e.,
\(\vec{a} \times \vec{b} \neq \vec{b} \times \vec{a}\)
As
\(\vec{a} \times \vec{b}=a b \sin \theta \hat{n}\)
and \(\vec{b} \times \vec{a}=a b \sin \theta(-\hat{n})\)
\(=-a b \sin \theta \hat{n}\)
\(=-\vec{a} \times \vec{b}\)

(ii) The vector multiplication of two vectors does not follow the law of association Le.,
\(\vec{a} \times(\vec{b} \times \vec{c}) \neq(\vec{a} \times \vec{b}) \times \vec{c}\)

(iii) The vector multiplication of two vectors follows the law of association in relation to scalar i.e.,
\(m \times(\vec{a} \times \vec{b})=(m \vec{a}) \times \vec{b}=\vec{a} \times(m \vec{b})\)

(iv) The vector multiplication of two vectors follows the law of distribution in relation to addition i.e.,
\(\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}\)

(v) If \(\vec{a} \text { and } \vec{b}\) are two non-zero vectors and are parallel also i.e., θ = 0 or π, then ,
sinθ =0
∴ \(\vec{a} \times \vec{b}=a b \sin \theta \hat{n}\)
\(=0 \times \hat{n}=\overrightarrow{0}\)
Therefore, the vector product of two parallel vectors is a zero or null vector.

Question 3.
Explain with example work done upon a body and work done by a body.
Answer:
When the displacement of the body is in the direction of external force applied the work is done upon the body and when the displacement is opposite to the direction of force then work is done by the body.
Example: When a stone is thrown vertically upward a force equivalent to its weight is applied upon it in the vertically upward direction, the work is done upon the stone while it fall downward work is done by the stone.

Question 4.
What do you mean by kinetic energy? Derive the expression for it.
Answer:
The efficiency of work done by the motion of a body is called its kinetic energy. Let m = Mass of a body at rest (i.e., u = 0)
F = Force applied on the body.
a = Acceleration produced in the body in the direction of applied force,
ν = Velocity acquired by the body in moving thrown a distance s.
From ν² -u² = 2as
ν²– 0 = 2as
or a = \(\frac{v^{2}}{2 s}\)
As F = m.a
∴ F = m\(\left(\frac{v^{2}}{2 s}\right)\)

Work done on the body,
W= Force × Displacement
or W = m\(\left(\frac{v^{2}}{2 s}\right)\) ×s
or W = \(\frac{m \cdot v^{2}}{2}\) = \(\frac{1}{2}\) mν²
This work done on the body is measure of kinetic energy (K.E.) of the body.
∴ K.E. = \(\frac{1}{2}\) mν²

Question 5.
What is work-energy theorem? Prove it.
Or
Write work-energy theorem and prove it for constant force.
Answer:
According to this theorem, the work done by a force is equal to the. change in kinetic energy of a body.
Let a force F is applied on a body of mass m so that its velocity becomes v.
If the body is displaced to distance d, then work done,
W = F.d
But, F = ma
∴ W = mad …(1)
Now, by the equation of motion ν² = u² + 2as, we get
2ad=ν² – u², ∴ (s =d)
or ad = \(\frac{1}{2}\)(ν² – u²)
Putting this value in eqn. (1), we get
W = m.\(\frac{1}{2}\)(ν² – u²)
or W = \(\frac{1}{2}\)mν² – \(\frac{1}{2}\)mu²
Work done = Change in K.E.

Question 6.
Momentum of a lighter body and heavier body is same, whose kinetic energy will be more?
Answer:
Let a body of mass m moves with a velocity of ν.
∴ Momentum of the body pm = m.ν …(1)
and Kinetic energy of the body K = \(\frac{1}{2}\)mν² …(2)
From eqn(1), ν = \(\frac{p}{m}\)
∴ K = \(\frac{1}{2}\)m.\(\frac{p^{2}}{m^{2}}\)
or
K = \(\frac{1}{2}\)\(\frac{p^{2}}{m}\)
or
P² = 2Km
or
p = \(\sqrt{2 m K}\) …(3)
Since, momentum of both bodies are same.
∴ From eqn. (3),
mK = Constant
or
K = \(\frac{\text { Constant }}{m}\)
K = \(\frac{1}{m}\)
∴ Kinetic energy of lighter body will be more.

Question 7.
What do you mean by variable force? Derive the expression for the work done by variable force.
Answer:
Variable force : When the magnitude and direction of a force are changing with time then such force is called variable force.
Example :
The gravitational force acting between two bodies depends upon the distance between the bodies, hence it is variable force.

Work done by variable force :
Case 1. Only magnitude of force changes not direction :

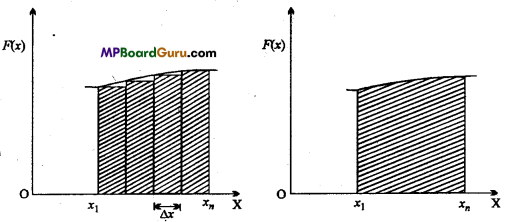
Let a variable force F(x) is applied along the direction of X-axis and body is displaced from x₁, to x_n in the direction of X-axis.
Graph (a) and (b) show the relation between force F (x) and displacement x.
Now the total displacement can be divided into so many small parts of Δx. As Δx is very small, the force during this displacement may be considered constant.
∴ Work done for the displacement Δx:
ΔW=F.Δx
Now, the work done for the displacement from x₁, to x_n will be the sum of work done of all displacements such as Δx.
∴ Total work done W = \(\sum_{x_{1}}^{x_{n}}\) F(x)Δx …(1)
If the displacement Δx is very small then the eqn. (1) can be written in the form of integration as
W = \(\int_{x_{1}}^{x_{n}}\)F{x)dx
or W = Area enclosed between the curve and displacement axis.

Case 2. When the magnitude and direction both are changing :
Let a particle is moving in irregular path and the coordinates of initial point are (x₁ , y₁, z₁,) and that of final point are (x₂ ,y₂ ,z₂).
∴ W\(\int_{x_{1}}^{x_{2}}\) F_xdx + \(\int_{y_{1}}^{y_{2}}\)F_ydy + \(\int_{z_{1}}^{z_{2}}\)F_zdz
Where \(\vec{F}=F_{x} \hat{i}+F_{y} \hat{j}+F_{z} \hat{k}\)

Question 8.
Kinetic energy of a lighter and heavier body are same, whose momentum will be more ?
Answer:
From the formula,
p = \(\sqrt{2 m K}\)
When the kinetic energy of both bodies are same, then
p ∝√ m
or
p²∝m
∴ \(\frac{p_{1}^{2}}{p_{2}^{2}}=\frac{m_{1}}{m_{2}}\)
Since, m₁>m₂
∴ p₁²> p₂²
∴ Momentum of heavier body will be more than lighter body.

Question 9.
Derive the expression for gravitational potential energy.
Answer:
Let, m = Mass of the body, g = Acceleration due to gravity on the surface of earth, h = Height through which the body is raised.
If we assume that height h is not too large and the value of g is practically constant, then the force applied just to overcome gravitational attraction is
F= mg …(1)

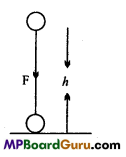
As the distance moved in the direction of the force applied, therefore F h Work done = Force x Distance
or
W = F × h
or
W= mg × h = mgh
Hence, gravitational potential energy = mgh.

Question 10.
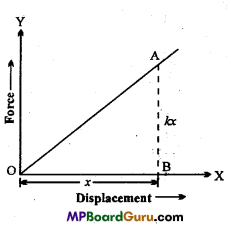
Derive the formula for the work done in stretching a spring.
Or
What will be the work done in compressing a spring of force constant k by an amount x?
Answer:
For an ideal spring the force is proportional to the displacement. Hence, the graph between force and displacement is a straight line.
Consider a point A on the force-displacement curve.
∴ The corresponding force of point
A = F = kx
∴ Work done in stretching the spring,
W = Area of Δ ABO
or
W = \(\frac{1}{2}\) OB × AB
= \(\frac{1}{2}\) × kx
= \(\frac{1}{2}\)kx²
∴P.E. of stretched spring = \(\frac{1}{2}\)kx².

Question 11.
What is meant by collision ? Differentiate elastic and inelastic collision.
Answer:
Collision : The striking of one particle with another or an interaction between them is called collision.

For example: Hitting a ball by a bat, striking carrom-coin by a striker, etc.
Difference between Elastic collision and Inelastic collision:

Elastic collision	Inelastic collision
1. In this collision, the kinetic energy and the momentum of the system are conserved.	1. In this collision, momentum of the system is conserved but not kinetic energy.
2. Collisions between the atoms, molecules and nuclear particles are the examples of elastic collision.	2. Sticking of the splashed mud, embedding of a bullet in a target are the examples of inelastic collision.

Question 12.
If the momentum of a body is increased by four times, what will be in
crease in its kinetic energy?
Answer:
We know,

ie., kinetic energy will increase by 16 times.

Question 13.
If the kinetic energy of a body is increased by four times, then what will be
increase in Its momentum?
Answer:
We know,

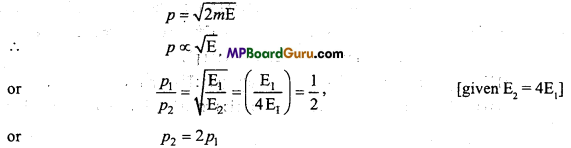
i.e., momentum will increase by 2 times.

Question 14.
The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:
(a) Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket
(b) Work done by gravitational force in the above case.
(c) Work done by friction on a body sliding down an inclined plane.
(d) Work done by an applied force on a body moving on a rough horizontal plane with uniform velocity.
(e) Work done by the resistive force of air on a vibrating pendulum in bringing it to rest.
Answer:
We know that the work done is given by W = F.s = Fs cos θ, where θ = smaller angle between force F and displacement s.
(a) To lift the bucket, force equal to the weight of the bucket has to be applied vertically upwards and the bucket moves along the same direction, thus 0 – 0, so W= FscosO = Fs i.e., positive.

(b) Here as the bucket moves in a direction opposite to the gravitational force which always acts vertically downwards.
∴ θ = 180°, so W= Fs cos 180° = Fs (- 1) = -Fs
i.e., W = negative.

(c) Work done by friction on a body sliding down an inclined plane is negative as friction opposes the relative motion,
Thus, θ = 180° ∴ W = Fs cos 180° = – Fs.

(d) As the body moves in the same direction in which the force is applied, so e = 0, thus W=Fs cos 0° = Fs i.e., it is positive.

(e) Work done is negative as the direction of the resistive force of air on the vibrating pendulum is opposite to the direction of displacement {i.e., motion) of the bob.

Question 15.
What do you mean by positive, negative and zero work? Give one example of each.
Answer:
Positive work:
When the angle between force and displacement is zero or acute angle then the work is positive.
Examples :

• When a bucket of .water from a well is pulled, the directions of force and displacement are same and hence positive work is done.
• A body falling freely under gravity. Then work done by gravity force is positive.

Negative work :
When the angle between force and displacement is 180° or obtuse angle then the work done is negative.
∴ Fs cos 180° = -Fs
Examples :

• When a bucket full of water is pulled from the well, the work done by the gravity force is negative, because the directions of force of gravity and displacement are opposite, (gravity acts downwards and displacement up).
• The work done by the friction force on an inclined plane is negative.

Zero work:
If the force applied is perpendicular to its displacement, then the work is
zero.
W = Fs cosθ = Fs cos 90° = 0
Examples :

• A coolie carrying suitcase on his head. The work done against gravity is zero.
• A body moving in circular motion. The centripetal force is perpendicular to its velocity. Hence, the work done by the centripetal force is zero.

Question 16.
A lighter body moving with velocity u. Collide with a heavy body at rest. What will be its velocity after collision?
Answer:
Let the velocity of lighter body (mass m) be ν₁ and the velocity of heavy body (mass M) be ν₂ after collision.
∴ From laws of conservation of momentum,
m u = m ν₁+ Mν₂ and For elastic collision
ν₁ – ν₂, = -(u – 0)
or
ν₂ – ν₁
On solving,
ν₁ = \(-\left(\frac{M-m}{M+m}\right)\) u
and ν₂ = \(\frac{2 m u}{(M+m)}\)
If m<< M, then
ν₁ = -u and ν₂ = 0.

Question 17.
(a) An artificial satellite orbiting the earth in very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth?

(b) In fig.-given below
(i) the man walks 2m carrying a mass of 15 kg on his hands. In fig.
(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley and a mass of 15 kg hangs at its other end. In which case is the work done greater?

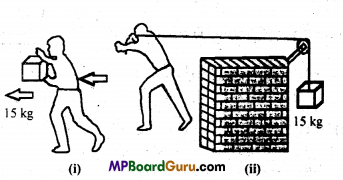
Answer:
(a) When an artificial satellite comes closer to earth, its gravitational P.E. decreases (as its height from the earth surface decreases). By law of conservation of energy, the sum of kinetic and potential energy should remain constant. To keep the total energy constant, kinetic energy should increase and so, velocity of satellite should increase. But, total energy of satellite continuously decreases at a very small rate due to atmospheric resistance.

(b) In case (a) : No work is done against gravity as the displacement of 2m (horizontal)
and the weight of 15 kg (acting vertically downwards) are perpendicular to each other
(θ=90°),
W = Fs cos 90° = 0.
In case (b): Work is done against gravity
W = mgh ,
= 15 × 9.8 × 2=294 J.
Apart from the work to be done against. Friction while moving through a distance of 2m.
So, the work done in case (b) is more than that of case (a).

Work, Energy and Power Class 11 Important Questions Long Answer Type

Question 1.
Two bodies of masses m₁and m₂ are moving in straight line with velocities
u₁ and u₂ respectively, collide each other. After collision calculate the velocities of the bodies. What will happen ¡f:
(i) The masses of the bodies are equal.
(ii) One of the body is at rest.
(iii) Lighter body is at rest.
(iv) Heavier body is at rest.
Answer:
Consider two bodies A and B of masses m₁and m₂ moving with velocities u₁ and u₂ (u₁> u₂) in the same direction.
After collision the bodies move in the same direction with velocities ν₁ and ν₂ respectively.
The collision is perfectly elastic, hence the momentum and K.E. of the system will be
conserved.

As the momentum is conserved:
Momentum before collision = Momentum after collision
m₁u₁ + m₂u₂ = m₁ν₁ + m₂ν₂
or
m₁u₁ – m₁ν₁ = m₂ν₂ – m₂u₂
or
m₁(u₁ – ν₁)=m₂(ν₂ – u₂) …(1)

As the K.E. is conserved :
K.E. before collision K.E. after collision


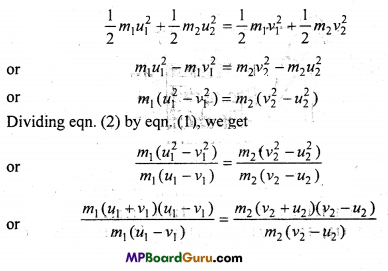
or
u₁+ ν₁ = ν₂ + u₂
or
u₁ – u₂ = ν₂ – ν₁, =-(ν₁ – ν₂) … (3)
So, relative velocity before collision = – (Relative velocity after collision) i.e., The direction of relative velocity is reversed after collision.

Calculation of velocities after collision :
(i) Velocity of A: From eqn. (3), we have
ν₂ = u₁ – u₂ + ν₁
Putting the value of ν₂ in eqn. (1), we get

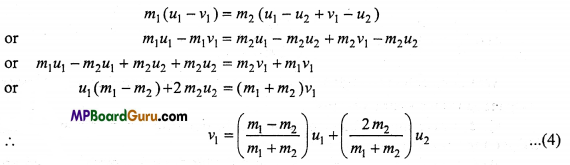
(ii) Velocity of B : From eqn. (3), we have
ν₁ = ν₂ + u₂ – u₁
Putting the value of ν₁ in eqn. (1), we get

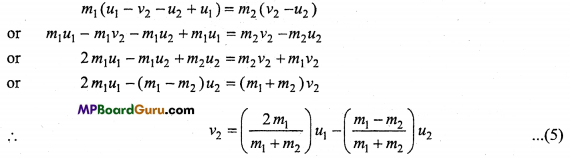
Case (i) : When m₁ = m₂
Then, from eqn. (4), ν₁ = u₂
and from eqn. (5), ν₂ = u₁
Hence, when the mass of the bodies are equal then they interchange their velocities after collision.

Case (ii) : m₂ is rest i.e., u₂ = 0
Then, from eqn. (4), ν₁ = \(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right)\)u₁ …(6)
and From eqn. (5), ν₂ = \(\left(\frac{2 m_{1}}{m_{1}+m_{2}}\right)\)u₁ …(7)
If m₁=m₂=m, then
From eqn. (6), we get ν₁ = 0
and From eqn. (7), ν₂ = u₁
Thus, when the masses are equal and one body is at rest, then after collision second body comes to rest and first body gains the velocity of second.

Case (iii): If m₂ << m₁], then from eqn. (6), we get
ν₁ = u₁
and From eqn. (7), we get ν₂ =2u₁
Thus, when heavier body collide with lighter body then heavier body moves with same velocity by lighter gains the velocity double of heavier body.

Case (iv): If m₁ << m₂], then
From eqn. (6), ν₁ = u₁
and From eqn. (7), ν₂ = \(\frac{2 m_{1}}{2 m_{2}}\)u₁ = 0
When lighter body collide with heavy body then heavy body remains at rest and lighter body rebounds with same velocity.

Question 2.
Prove that in inelastic collision in one dimension, always energy is lost. Derive the expression for the loss of energy.
Answer:
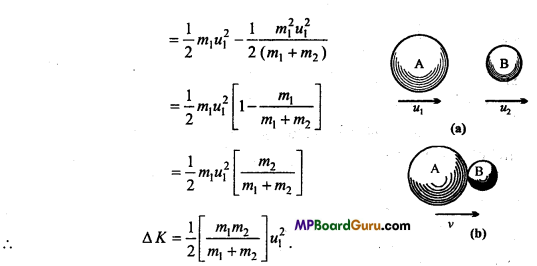
Consider a body A of mass m₁, and another body B of mass m₂ which are moving in the same direction with velocities u₁ and u₂ (u₁ > u₂). Both collide and stick together and move with common velocity ν.

Now, in inelastic collision, the momentum is conserved, i.e.,
Momentum before collision = Momentum after collision
m₁u₁ + m₂u₂ = (m₁ + m₂)ν
∴ ν = \(\frac{m_{1} u_{1}+m_{2} u_{2}}{m_{1}+m_{2}}\) …(1)
Now, K.E. before collision is
K₁ = \(\frac{1}{2}\) m₁u₁² … (2)
and K.E. after collision will be
K₂ = \(\frac{1}{2}\) (m₁ + ₂)ν² …(3)
Putting the value of ν from eqn. (1), we get
K₂ = \(\frac{1}{2}\) (m₁ + ₂)\(\left(\frac{m_{1}}{m_{1}+m_{2}}\right)^{2}\)
u₁² [∵ u₁ >u₂
or
K₂ = \(\frac{1}{2\left(m_{1}+m_{2}\right)}\) …(4)
From eqns. (2) and (4), we.get
\(\frac{K_{1}}{K_{2}}=\frac{m_{1}+m_{2}}{m_{1}}\)
∵ m₁ < (m₁ + m₂
∴ K₁ > K₂
Hence, after collision the K.E. of the system decreases.
Now, loss of energy, Δ K =K₁ – K₂

Question 3.
A truck and a car are moving with same kinetic energy, which will stop first
(i) Both are stopped by applying same retardation force.
(ii) Brake is applied at same time on both.
Answer:
(i) K.E. = \(\frac{1}{2}\)mν² =F. s
or
s = \(\frac{\text { Kinetic energy }}{\text { Retarding force }}\)
Since, kinetic energy of both are equal therefore distance travelled by both before stopping will also be equal i.e., both will get stopped at same time.

(ii) After applying brake both will stop due to friction force.
Then \(\frac{1}{2}\)mν² = F.s = (µR)s = µ.mg.s
or
s∝ν²
Since kinetic energy of both are same.
∴ ν² ∝ \(\frac{1}{m}\)
∴ s ∝ \(\frac{1}{m}\)
i.e.; Whose mass is more, less distance will be travelled before stopping. Therefore truck will stop first than car.

Question 4.
Two Identical spring A and B of which spring B is harder than spring A if
(i) Both are extended to same distance then upon which spring more work has to be done?
(ii) Both are extended by applying same force then upon which more work has to be done?
Answer:
Since spring constant k of hard spring is more
∴ Work = \(\frac{1}{2}\) kx² = \(\frac{F^{2}}{2 k}\)
(i) For same displacement,
W_A = \(\frac{1}{2}\)k_Ax²
and W_B =\(\frac{1}{2}\)k_Bx²
Since k_A > k_B
∴ W_A > W_B
∴ More work has to be done on first spring A.

(ii) For same force,
W_A = \(\frac{F_{A}}{2 k_{A}}\)
and W_B = \(\frac{F_{B}}{2 k_{B}}\)
Since k_A >k _B
∴ W_B > W_A
Therefore more work has to be done on spring B.

Question 5.
A truck and a car are moving with the same kinetic energy are stopped by applying brakes of same retarding force. Which one will stop at a lesser distance?
Answer:
Let the mass of car and truck be m₁ and m₂and velocity be u₁ and u₂.
∴ \(\frac{1}{2}\)m₁u₁² = \(\frac{1}{2}\)m₂u₂²
or
\(\frac{m_{1}}{m_{2}}=\frac{u_{2}^{2}}{u_{1}^{2}}\) …(1)
If retardation ¡s a₁ and a₂ on applying brakes, then
m₁ a₁ = m₂ a₂
or
\(\frac{m_{1}}{m_{2}}=\frac{a_{2}}{a_{1}}\) …(2)
From eqns. (1) and(2),
\(\frac{a_{2}}{a_{1}}=\frac{u_{2}^{2}}{u_{1}^{2}}\)
or
\(\frac{u_{1}^{2}}{a_{1}}=\frac{u_{2}^{2}}{a_{2}}\) …(3)
Ifs₁ and s₂ be the distance travelled before stopping, then 0 = u₁² – 2a₁s₁
s₁ = \(\frac{u_{1}^{2}}{2 a_{1}}\) and s₂ = \(\frac{u_{2}^{2}}{2 a_{2}}\)
From eqn. (3),
s₁ = s₂
i.e, Both will stop arc travelling same distance.

Question 6.
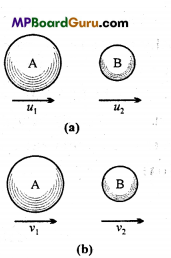
What is elastic collision in two dimensions? After collision, what will be the velocities of the bodies?
Answer:
When the collision takes place on a plane and momentum and K.E. of the system is conserved, then the collision is called elastic collision in two dimensions.
Let A and B are two bodies of masses m₁ and m₂, moving along X-axis with the velocities u₁ and u₂ (u₁ > u₂) respectively and they collide elastically.

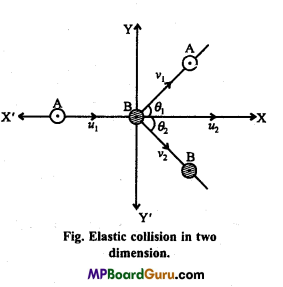
After collision, let A and B make angles θ₁ and θ₂ with the X-axis and move with velocities ν₁ and ν₂ respectively as shown in the figure.
As the collision is elastic, the K.E. of the system will be conserved.
∴ \(\frac{1}{2}\)m₁u₁² +
\(\frac{1}{2}\)m₂u₂² = \(\frac{1}{2}\)m₁ν₁² + \(\frac{1}{2}\)m₂ν₂² …(1)

Now, before collision, the momentum of A and B along X-axis
= m₁u₁+m₂u₂
and After collision, momentum along X-axis
= m₁ν₁ cosθ₁ + m₂ν₂ cosθ₂
Again, momentum along Y-axis before collision = 0
and Momentum along Y-axis after collision = m₁ν₁ cos?₁ + m₂ν₂ cosθ₂
As the momentum is conserved. Therefore along X-axis,
m₁u₁ +m₂u₂ = m₁ν₁ cosθ₁ + m₂ν₂ cosθ₂ …(2)
and Along Y-axis,
0 = m₁ν₁ sinθ₁ + m₂ν₂ sinθ₂
∴ m₁ν₁ sinθ₁ = – m₂ν₂ sinθ₂  …(3)
Solving eqns. (1), (2) and (3), we can determined the values of ν₁ ν₂, θ₁ (or θ₂).

Work, Energy and Power Class 11 Important Numerical Questions

Question 1.
If \(\vec{A}=2 \hat{i}+2 \hat{j}+p \hat{k} \text { and } \vec{B}=2 \hat{i}-\hat{j}+\hat{k}\) are perpendicular, then find the value of p
Solution:
Given : \(\vec{A} \text { and } \vec{B}\) are perpendicular
∴ \(\vec{A} \cdot \vec{B}\) = 0
or
\((2 \hat{i}+2 \hat{j}+p \hat{k}) \cdot(2 \hat{i}-\hat{j}+\hat{k})\) = 0
∴ 2.2 + 2.(-1)+p.(1) = 0
or
4 – 2 +p = 0
or
p = – 2.

Question 2.
If vector \(\vec{A}=5 \hat{i}-\hat{j}+k \text { and } \vec{B}=2 \hat{i}-3 \hat{j}-4 \hat{k}\) then find the vector product
\(\vec{A} \times \vec{B}\)
Solution:
Given :\(\vec{A}=5 \hat{i}-\hat{j}+\hat{k}, \vec{B}=2 \hat{i}-3 \hat{j}-4 \hat{k}\)
∴ \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}=\left|\begin{array}{rrr}
\hat{i} & \hat{j} & \hat{k} \\
5 & -1 & 1 \\
2 & -3 & -4
\end{array}\right|\)
= \(\hat{i}\)[(-1 × -4) – (1 × -3)] –\(\hat{j}\) [(5 × -4)-2 × 1] + \(\hat{k}\) [(5 × -3) – (2 × -1)]
= \(\hat{i}\)[4 + 3] – \(\hat{j}\)[-20-2] + \(\hat{k}\)[-15 +2]
= \(7 \hat{i}+22 \hat{j}-13 \hat{k}\)

Question 3.
When a force \(\vec{F}=3 \hat{i}-4 \hat{j}+9 \hat{k}\) newton is applied on a body so that if get displace by \(\vec{s}=3 \hat{i}+4 \hat{j}+8 \hat{k}\) metre. Find out work done by force ? •
Solution:
Work done
W = \(\vec{F} \cdot \vec{s}\)
= \((3 \hat{i}-4 \hat{j}+9 \hat{k}) \cdot(3 \hat{i}+4 \hat{j}+8 \hat{k})\) = 3.3 + (-4.4) + 9.8
= 9-16 + 72
or
W = 65 joule.

Question 4.
The bob of a pendulum is released from a horizontal position .4 as shown in the figure. If the length of the pendulum is 1-5 m, what is the speed with which the bob arrives at the lower most point B, given that it dissipated 5% of its initial energy against air resistance?
Solution:
At point A, the energy of the pendulum is entirely P.E. At point B, the energy of the pendulum is entirely K.E. It means that as the bob of the pendulum lowers from A to B, P.E. is converted into K.E. Thus, at B, K.E = P.E. But 5% of the P.E. is dissipated against air resistance.
K.E.atB = 95% of P.E.at A
m = Mass of bob
ν = It speed at B,
h = Height of point A w.r.t. B
= 1.5m.

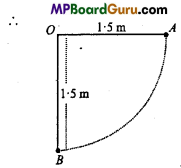
∴ From eqn(1),\(\frac{1}{2}\)mν² = \(\frac{95}{100}\)mgh
or
ν² = 2 × \(\frac{95}{100}\)gh = 2 × \(\frac{95}{100}\) × 9.8 × 1.5
or
ν = \(\sqrt{\frac{19 \times 9 \cdot 8 \times 1 \cdot 5}{10}}=\sqrt{27 \cdot 93}\)
= 5.285ms^-1
ν = 5.3ms^-1

Question 5.
A pump on the ground floor of a building can pump up water to fill a tank
of value 30 m in 15 min. If the tank is 40 m above the ground and the efficiency of the pump is 30% how much electric power is consumed by the pump?
Solution:
Mass of water to be pumped up,
m = Volume × Density of water ‘
= 30 × 10³ = 3 × 10⁴kg
Height of the tank, h =40 m
∴ Work done by the pump to fill the tank,
W= mgh = 3 × 10⁴ × 9.8 × 40 J
= 1.176 × 10⁷ J
Time t =15 minutes = 15 × 60 s = 900 s
∴ Required power, P = \(\frac{W}{t}=\frac{1 \cdot 176 \times 10^{7}}{900}\) = 13.07kW
Efficiency of pump = 30%
Now η% = \(\frac{\text { Output power }}{\text { Input power }}\) × 100
or
Input power = Power consumed by the pump
= \(\frac{\text { Output power }}{\eta \%}\) × 100
= \(\frac{13 \cdot 07}{30}\) × 100 = 43.55kW
= 43.6kW.

Question 6.
A body constrained to move along Z -axis of a coordinate system is subjected to a constant force \(\vec{F}\) given by
\(\vec{F}=-\hat{i}+2 \hat{j}+3 \hat{k} \mathbf{N}\)
where \(\hat{i}\), \(\hat{j}\) and \(\hat{k}\) are the unit vector along the X, Y and Z -axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the Z -axis?
Solution:
Since, the body is displaced 4 m along Z -axis only
∴ S = \(4 \hat{k}=(0 \hat{i}+0 \hat{j}+4 \hat{k})\)m
Also F = \(-\hat{i}+2 \hat{j}+3 \hat{k}\)
∴ Work done (W) is given by,
W = F.S .
= \((-\hat{i}+2 \hat{j}+3 \hat{k}) \cdot(0 \hat{i}+0 \hat{j}+4 \hat{k})\)
= (-1)× 0 + 2 × 0 + 3 × 4
= 12 J.

Question 7.
A body of mass 0.5 kg travels in a straight line with velocity ν = ax^3/2 where
a = 5m^-1/2 s^-1What is the work done by the net force during its displacement from x = 0 to x= 2 m ?
Solution:
Here, m = 0.5 kg, ν = ax^3/2, a = 5m^-1/2 s^-1
Let F = net force acting on the body and producing an acceleration a’ in it
∴ F =ma = m\(\frac{d v}{d t}\)
If dW be the work done by F in displacing the body by dx,
Then dW = Fdx = m\(\frac{d v}{d t}\)dx
= mdν.\(\frac{d x}{d t}\) = mdν(ν)
= mνdν …(1)
If W be the total work done in displacing the body from x = 0 to x = 2m, then integrating eqn. (1), we get
W = ∫dW = m∫νdν = m\(\frac{v^{2}}{2}\)
= \(\frac{1}{2} m\left(a x^{\frac{3}{2}}\right)^{2}\) = \(\frac{1}{2}\)m × a²x³
Putting x = 2-0 = 2m,a = 5,m = 0.5, we get
W = \(\frac{1}{2}\) × 0.5 ×(5)² × (2)³
= \(\frac{1}{2}\) × \(\frac{1}{2}\) × 25 × 8 = 50J

Question 8.
Power of a machine is 2 kilowatt. What will be the work done by it in 5 minute?
Solution:
Given : P = 2 kilowatt = 2000 watt, t = 5 min = 5 × 60 = 300 sec.
Therefore work done, W = Power × t
or W= P × t
or W = 2000 × 300 = 6 × 10⁵ joule.

Question 9.
What will be the work done to raised a body of mass 10 kg through a height of 10 metre?
Solution:
Given : m = 10 kg, h = 10 metre, g = 9.8 m/s²
Therefore work done W = Potential energy
or W= mgh
or W=10 × 9.8 × 10
or W= 980joule

Question 10.
The power of pump is 7.5 kilo watt. How much water, per minute will be raised to a height of 25 m ?
Solution:
Given: P= 7.5 kilo watt = 7.5 × 10³watt,g = 10 ms^-2
h = 25 m, t = 1 min = 60s.
Now P = \(\frac{\mathrm{W}}{t}=\frac{m g h}{t}\)
m = \(\frac{P \times t}{g h}\)
or
m = \(\frac{7 \cdot 5 \times 10^{3} \times 60}{10 \times 25}\)
= 1.8 × 10³ =1800 kg.

Question 11.
A body of mass 60 kg is pulled with 20 Newton force to a distance of 8m in 10 second.Calculate the work and power.
Solution:
Given : Mass m = 60 kg, Force F = 20 N, Distance s = 8m
Time t = 10 sec.
∴ Work = Force × Displacement
= 20 × 8
= 160 joule.
and Power = \(\frac{\text { Work }}{\text { Time }}=\frac{160}{10}\)
= 16 watt

Question 12.
The force constant of a spring is loo Nm. It stretched by a force through
0.5 cm. Calculate the work done by the force.
Solution:
Given: k = 100 Nm^-1 x = 0.5 cm =0.5 × 10^-2m.
Now \(\frac{1}{2}\)kx²
= \(\frac{1}{2}\) ×100 ×(0.5 × 10^-2)²
= \(\frac{1}{2}\) × 100 × 0.25 ×10^-4
= 1.25 × 10^-3joule

Question 13.
Energy of an object moving with velocity 10 m/s is 10 joule. Determine the
velocity of the object if the energy becomes 90 joule.
Solution:
Given: ν₁ 10 m/s, k₁ 10 joule, k₂ 90 joule, ν₂ = ?
We know

Question 14.
14. What will be the work donc to bring a bullet to rest of mass 200 gram moving with velocity of 400 m/s?
Solution:
Given :m=200gms.=0.2kg, ν = 400m/s
∴ Work done = Change in kinetic energy
= 0 – \(\frac{1}{2}\)mν² = – \(\frac{1}{2}\)mν²
= \(\frac{1}{2}\) × 0.2 ×(400)²
= -1.6 × 10⁴joule

Question 15.
An athlete jumps 4.9 m high. What is its velocity?
(Given h = 4.9 m, g = 9.8 m/s²)
Solution:
K.E = P. E
or
\(\frac{1}{2}\)mv2 = mgh
or
ν² = 2gh
or
ν = \(\sqrt{2 g h}\)
Putting the value, we get
ν = \(\sqrt{2 \times 9 \cdot 8 \times 4 \cdot 9}\)
or
ν = 9.8 m/s.

Question 16.
Find out force constant of a spring to stretched by a force through 0*1 metre. The change in potential energy to do it is 0.5 joule.
Solution:
Given : ΔU = \(\frac{1}{2}\) kx²
or
k = \(\frac{2 \Delta U}{x^{2}}\)
or
k = \(\frac{2 \times 0.5}{(0-1)^{2}}=\frac{2 \times 5 \times 10 \times 10}{1 \times 1 \times 10}\)
or
k = 100 newton/metre.

Question 17.
The weight of a man is 80 kg weight and he. lift a weight of 20 kg -weight, and move to roof of house of height 30 metre. Find out the work done to do it?
Solution:
Given: Weight of the man = 80 kg – wt
Weight of luggage = 2Okg – wt
∴ ForcerequiredF = 80 + 20 = 100kg-wt 100 × 9.8 = 980N.
Displacement d = 30 m
∴ Work done W = F.d
= 980 × 30
= 29400 joule.

Question 18.
Momentum of 1kg and 4kg masses are equal. Find out ratio of their kinetic energy?
Solution:
Given m₁ = 1 kg, m₂= 4 kg
We know k = \(\frac{p^{2}}{2 m}\)
or

∴ [ p₁ = p₂]
or
\(\frac{k_{1}}{k_{1}}=\frac{4}{1}\) = 4:1

Question 19.
A ball is dropped from a height of 10m. What is the height up to which the ball will rebound if the loss of energy on striking the surface is 40%.
Solution:
Initial Potential energy of ball = mgh
On striking ground surface its energy get loss by 40% i.e., 60% energy remains.
∴ Kinetic energy after striking surface = \(\frac{60}{100}\)mgh₁
If the ball rebound to height h₂, then
\(\frac{60}{100}\) × mgh₁ = mgh₂
or
h₂ = \(\frac{60}{100}\) h₁
or
h₂ = \(\frac{60}{100}\) × 10 = 6 metre

Question 20.
An engine of power 25 horse power moves with uniform speed of 9 km/hr. Find out the resistance force acting on it?
Solution:
Given : P = 25 H.P. = 25 × 746 watt
ν = 9km/hr = \(\frac{9 \times 1000}{3600}\) = 2.5 m/s
3600
Let the resistance force be F .
∴ From P = F.v, we get
25 × 746 =F× 2.5
or
F = \(\frac{25 \times 746}{2 \cdot 5}\) = 7460 joule

Work, Energy and Power Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
Which statement is not true :
(a) Power = Work / Time
(b) Work = Force × Displacement
(c) Work = Energy
(d) Work = Power × Displacement.
Answer:
(d) Work = Power × Displacement.

Question 2.
A wound spring has stored :
(a) Mechanical kinetic energy
(b) Mechanical potential energy
(c) Electrostatic electrical energy
(d) No energy.
Answer:
(b) Mechanical potential energy

Question 3.
The unit of energy is :
(a) joule/second
(b) kilowatt
(c) kilowatt hour
(d) joule × second.
Answer:
(c) kilowatt hour

Question 4.
The formula for kinetic energy is:
(a) mν
(b) mν²
(c) \(\frac{1}{2}\) mν²
(d) \(\frac{1}{2}\)m²ν
Answer:
(c) \(\frac{1}{2}\) mν²

Question 5.
One horse power is equal to :
(a) 74.6 watt
(b) 746 watt
(c) 7460 watt
(d) 550 watt.
Answer:
(b) 746 watt

Question 6.
If a force F acts produce a velocity v on a body then the power will be :
(a) F × ν
(b) F/ν
(c) F/ν²
(d) Fν² .
Answer:
(a) F × ν

Question 7.
When kinetic energy of a lighter and heavier body is same then :
(a) Momentum of heavy body is more
(b) Momentum of heavy body is less
(c) Momentum of both bodies is equal
(d) None of these.
Answer:
(a) Momentum of heavy body is more

Question 8.
A ball is dropped from 8 cm height, if the collision between ball and surface is perfectly elastic then how much the ball will rebounce :
(a) 8 cm
(b) 1 cm
(c) 5 cm
(d) Zero.
Answer:
(a) 8 cm

Question 9.
In elastic collision, the following remain conserved :
(a) Linear momentum of each particle
(b) Speed of each particle
(c) Kinetic energy of each particle
(d) Kinetic energy of both particles.
Answer:
(d) Kinetic energy of both particles.

Question 10.
A buUet get embedded inside a block, kept at a frictionless surface, which remain conserved:
(a) Only momentum
(b) Only kinetic energy
(c) Both momentum and kinetic energy
(d) None of these.
Answer:
(a) Only momentum

Question 11.
If the velocity of a particle is doubled, then its kinetic energy will be :
(a) Doubled
(b) Four times
(C) Equal
(d) One fourth.
Answer:
(b) Four times

Question 12.
In inelastic collision, which remain conserved :
(a) Kinetic energy
(b) Momentum
(c) Mass
(d) Impulse.
Answer:
(b) Momentum

Question 13.
Ratio of kinetic energy of two bodies is 4:1, they are moving with same momentum. The ratio of their mass will be :
(a) 1 : 2
(b) 2 : 1
(c) 4 : 1
(d) 1 : 4
Answer:
(d) 1 : 4

Question 14.
If momentum of an object is ^increased by 50%, then the percentage increase in kinetic energy will be :
(a) 50%
(b) 100%
(c) 125%
(d) 150%.
Answer:
(c) 125%

Question 15.
Two bodies of same momentum are of masses m and 2m respectively. The ratio of their kinetic energies kx and k2 is.
(a) 1 : 2
(b) 4 : 1
(c) 1 : 4
(d) 2 : 1.
Answer:
(c) 1 : 4

2. Fill in the blanks:

1. In elastic collision ………………….. remain conserved.
Answer:
Linear momentum and kinetic energy

2. In inelastic collision ………………….. remain conserved.
Answer:
Linear momentum

3. S.I. unit of energy is …………………….
Answer:
joule

4. Dimensional formula of energy and work is ……………………
Answer:
[ML²T^-2]

5. S.I. unit of power is …………………….
Answer:
watt

6. Dimensional formula of power is ………………….
Answer:
[ML²T^-3]

7. The work done by a force is equal to the change in its …………………….
Answer:
Kinetic energy

8. Work is a ……………… quantity.
Answer:
Scalar

9. Water stored in dam have ………………. energy.
Answer:
Potential

10. Capacity of doing work is called ………………………
Answer:
Energy

11. The energy stored in a body due to mechanical work done on it is called …………………
Answer:
Mechanical energy

12. If velocity of an aeroplane is doubled, then its kinetic energy will become …………………..
Answer:
Four times

13. According to work energy theorem the work done on a body is equal to change in
its ………………….
Answer:
Kinetic energy

14. Work done in extending a spring to x length is equal to …………………..
Answer:
\(\frac{1}{2}\) kx²

15. If vectors \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\) are perpendicular to each other, then their scalar product will be …………………….
Answer:
Zero

16. If vectors \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\) are parallel to each other then their vector product will be …………………………
Zero vector.

3. Match the following:
I.

Column ‘A’	Column ‘B’
1. Magnitude of gravitational potential energy at surface of earth is	(a) Mechanical energy
2. Water stored in dam posses	(b) Negative
3. Energy of a free falling body have	(c) Zero
4. When the direction of force and displacement are same, then work done by the force will be	(d) Potential Energy
5. When a ball is thrown upward then .work done by gravitational force will be	(e) Positive.

Answer:
1. (c) Zero
2. (d) Potential Energy
3. (a) Mechanical energy
4. (e) Positive
5. (b) Negative

II.

Column ‘A’	Column ‘B’
1. Unit of spring constant	(a) p2 = 2mK
2. Formula for gravitational potential energy is	(b) E = mc2
3. Einstein mass-energy equivalence is	(c) newton/metre
4. Relation between momentum and kinetic energy of a body	(d) 746 watt
5. Magnitude of one horse power is	(e) mgh.

Answer:
1. (c) newton/metre
2. (e) mgh
3. (b) E = mc²
4. (a) p² = 2mK
5. (d) 746 watt

III.

Column ‘A’	Column ‘B’
1. Dynamo	(a) Electrical energy into sound energy
2. Electric motor	(b) Electrical energy into thermal energy
3. Photoelectric sell	(c) Mechanical energy into electrical energy
4. Loudspeaker	(d) Electrical energy into mechanical energy
5. Electric heater	(e) Light energy into electrical energy.

Answer:
1. (c) Mechanical energy in to electrical energy
2. (d) Electrical energy into mechanical energy
3. (e) Light energy into electrical energy.
4. (a) Electrical energy into sound energy
5. (b) Electrical energy into thermal energy

IV.

Column ‘A’	Column ‘B’
1. Glow of electric bulb	(a) Transformation of chemical energy into electrical energy.
2. Rubbing palm of hands	(b) \(\frac{1}{2}\) mν2
3. Free falling stone	(c) Transformation of mechanical energy into thermal energy.
4. Kinetic energy	(d) Transformation of potential energy into kinetic energy
5. Cell	(e) Trans formation of electrical energy into light energy

Answer:
1. (e) Trans formation of electrical energy into light energy
2. (c) Transformation of mechanical energy into thermal energy
3. (d) Transformation of potential energy into kinetic energy
4. (b) \(\frac{1}{2}\) mν²
5. (a) Transformation of chemical energy into electrical energy

4. Write true or false:

1. Potential energy of a bubble increases when it raise upward inside a water.
Answer:
False

2. If the momentum of a lighter body and heavier body are same, then kinetic energy of lighter body will be more.
Answer:
True

3. The work done in winding the spring of watch is stored in it in the form of potential energy.
Answer:
True

4. Work done by resisting force of air on an oscillating bob is negative.
Answer:
True

5. In nuclear reaction masses get converted into energy.
Answer:
True

6. Principle of hydrogen bomb is based on nuclear fission.
Answer:
False

7. In elastic collision between two bodies, their momentum and kinetic energy re-mains conserved.
Answer:
False

8. The sum of kinetic energy and potential energy of all the particles of a body is called its internal energy.
Answer:
True

9. One kilowatt hour = 3.6 × 10⁸ joule.
Answer:
False

10. If the displacement of a body is zero on applying a force on it, then work done on it is positive.
Answer:
False

11. Work done to extend a spring is stored in it as elastic potential energy.
Answer:
True

12. A bullet on striking on a wooden plank get embedded in it the collision will be
elastic collision.
Answer:
False

13. Kinetic energy is always positive.
Answer:
True

14. In inelastic collision loss in kinetic energy is in the form of heat, light energy and sound.
Answer:
True

15. When a force of 1 newton is applied on a body so that it get displace by 1 metre in direction of force, then the work done will be 1 joule.
Answer:
True