MP Board Class 11th Physics Important Questions Chapter 12 Thermodynamics

Students get through the MP Board Class 11th Physics Important Questions Chapter 12 Thermodynamics which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 12 Thermodynamics

Thermodynamics Class 11 Important Questions Very Short Answer Type

Question 1.
What do you mean by thermodynamical system?
Answer:
A thermodynamical system is an assembly of the large number of particles (atoms or molecules).

Question 2.
Explain the meaning of thermodynamical variables.
Answer:
It is the parameter which describe equilibrium state of the system.

Question 3.
What do you mean by equation of state?
Answer:
Relation between thermodynamical variables which describe the thermodynamical state of a system is known as equation of state.

Question 4.
What do you understand by positive and negative work?
Answer:
Work done by the system is said to be positive work and work done upon the system is said to be negative work.

Question 5.
Among internal energy and work, which depends on path and which doesn’t depend upon the path?
Answer:
Work depends upon the path and internal energy does not depend upon the path.

Question 6.
State first law of thermodynamics.
Answer:
First law of thermodynamics: If a system is capable of doing an external work, the net amount of heat energy given to the system is equal to the sum of the energy spent in doing work (by the system) and the increase in internal energy of the system.

If the amount of heat absorbed by a thermodynamic system is ΔQ and due to it the work done by the system is ΔW and increase in the internal energy is ΔU, then
ΔQ = ΔW +ΔU.

Question 7.
What do you understand by reversible process? Give examples.
Answer:
The process which can be retraced in a reverse path so that the system under consideration passes through the same states as in the direct process with reversed effect is known as a reversible process.

Examples:

•  When a certain amount of heat is given to ice, it changes to water. If the same amount of heat is taken from the water thus formed, the water changes to ice. This is a reversible.
  process:
• Peltier effect is a reversible process because on passing the electric current in the thermocouple, the heat produced at any junction is the same as heat absorbed at that junction on reversing the direction of current.
• Slow compression and expansion of a gas are reversible process.

Question 8.
Give difference between reversible and irreversible processes.
Answer:
Difference between Reversible and Irreversible process :

Reversible process	Irreversible process
1. This process can be retraced in reverse direction. 2. The system returns to its initial state after passing through various states.	1. This process cannot be retraced in reverse direction. 2. The system does not return to its initial state.

Question 9.
What is cyclic process?
Answer:
If a system undergoes changes of state through a number of stages and finally acquires the original state, the process is known as cyclic process. In a cyclic process, the internal energy of the system remains unchanged, i.e., ΔU = 0.

Question 10.
What is isothermal process?
Answer:
The process in which the temperature remains constant and pressure and volume changes, then the process is called isothermal process i.e., ΔT = 0.
Example: The boiling water at the boiling point and melting solid at melting point.

Question 11.
What is adiabatic process?
Answer:
The process in which temperature, volume and pressure may change but amount of heat of the system remains constant is called adiabatic processes., ΔQ = 0.
Example: A bottle filled with CO₂ at high pressure opened suddenly, bursting of cycle tube.

Question 12.
What do you mean by internal energy? On what factors does the internal energy of a gas depend?
Answer:
Internal energy: The total kinetic energy and potential energy of the molecules of a gas is called internal energy of a substance.
The internal energy of a gas depends upon the temperature and the force of attraction between the molecules.

Question 13.
Define mechanical equivalent of heat and write its C.G.S. and M.K.S. units.
Answer:
Work done to obtain one calorie heat is known as mechanical equivalent of heat. Its C.G.S. unit is erg./calorie and M.K.S. unit is joule/calorie.

Question 14.
State first law of thermodynamics.
Answer:
First law of thermodynamics: If a system is capable of doing an external work, the net amount of heat energy given to the system is equal to the sum of the energy spent in doing work (by the system) and the increase in internal energy of the system.

Question 15.
Will the temperature of a room decrease, if fan works in a closed room?
Answer:
No, the temperature of the room will increase, because the kinetic energy and hence the internal energy Of gas molecules increases.

Question 16.
Distinguish Between isothermal and adiabatic process.
Answer:
Difference between Isothermal and Adiabatic process:

Isothermal process	Adiabatic process
1. In this process the temperature remains constant.	1. In this process the amount of heat of a system remains constant.
2. The internal energy of a gas remain constant.	2. The internal energy does not remain constant.
3. It is a slow process.	3. It is a fast process.
4. The heat is exchanged with atmosphere.	4. The heat is not exchanged with atmosphere.

Question 17.
Cooling is possible in adiabatic expansion. Why?
Or
When a gas suddenly expands at high pressure it becomes cold. Why?
Answer:
When in adiabatic expansion work is done then internal energy of the system reduces. Hence, its temperature decreases which gives cooling effect.

Question 18.
When the valve of cycle tube is removed, the air coming out becomes cold. Why?
Answer:
The pressure inside the cycle tube is greater than the atmospheric pressure. When the valve is removed the air rushes out and expand suddenly. Therefore work is done by the gas hence its temperature decreases.

Question 19.
When a bullet strikes a target, the temperature of the target increases, why?
Answer:
The kinetic energy of the bullet changes into heat and hence the temperature of the target increases.

Question 20.
A thermos flask is filled with water. It is shaken for some time. Does the temperature of water increase? Give reason.
Answer:
The work done in shaking the water, will change into heat thus its temperature will increase.

Question 21.
In a cycle pump when the piston is rapidly brought down the pump get heated. Why?
Answer:
This is because, some amount of work done in pumping get converted into heat. If the piston is rapidly brought down, there is no time to exchange the heat from piston to surrounding, so the pump get heated.

Question 22.
A hot piece of iron is dipped in a bucket filled with cold water. Will its internal energy be increased? Would there be some work by iron piece?
Answer:
The internal energy of water will be increased, because of transfer of heat from iron to water. There will be no work done by the iron piece.

Question 23.
When we rub our hands, then the temperature increases to a certain value. Why?
Answer:
While rubbing out the hands together, the work is converted to heat, as a result temperature increases a certain value. But after that, the increase in heat goes in the atmosphere and hence the temperature remains constant.

Question 24.
What is isobaric process?
Answer:
The thermodynamical process in which pressure of the system remains constant is called isobaric process. For isobaric process \(\frac{V}{T} \) = constant or V∝T.

Question 25.
What is isochoric process? What will be the work done in the process?
Answer:
The thermodynamical process in which the volume of the system remains constant is called isochoric process. In this process work done will be zero because there is no change in the volume of gaseous system.

Question 26.
Does any change occur in the internal energy of an ideal gas during the isothermal change? Give reason.
Answer:
During isothermal process there is no change in the internal energy of ideal gas. Because the total kinetic energy of ideal gas is due to its kinetic energy which depends on the temperature of gas. In the isothermal process the temperature remains constant. So, there is no change in internal energy of gas.

Question 27.
Is there any change in the internal energy of a gas in adiabatic process? Why? ‘
Answer:
Yes, in adiabatic process the internal energy of gas is changed. For adiabatic process dQ = 0 hence by first law of thermodynamics
dQ = dU + dW
or 0 = dU+dW
or dU =-dW
Thus, the amount of work done by the gas be equal to decrease in its internal energy.

Question 28.
Can two isothermal curves intersect each other?
Answer:
No, if they intersect each other, then at the point of intersection for a value of pressure P and volume F, there will be two temperature value. But it is not possible.

Question 29.
The air in atmosphere gets cooled on rising up. Why?
Answer:
At higher altitudes, the atmospheric pressure is less. Hence, the air expands adiabatically on rising up. So, it get cooled due to decrease in its internal energy.

Question 30.
What is irreversible process? Give examples.
Answer:
Processes which are not reversible are called irreversible process. In the other words, an irreversible process cannot be retraced in reverse direction so as to pass through the same states as in the direct process.
Examples :

• Work done against the friction is an irreversible because on changing the direction of motion work has to be done again, against the friction.
• Rusting of iron is an irreversible process.
• On passing the electric current through a resistance wire, heat is produced. This is also an irreversible process because on reversing the direction of current, heat is again produced.

Question 31.
When the efficiency of Carnot engine is 100%? Is it possible?
Answer:
Efficiency of Carnot cycle is η = 1 – \(\frac{T_{2}}{T_{1}} \)
If T₂ = 0, then η= 1.
Hence, the temperature of sink should be 0K, which is not possible. Hence, the efficiency cannot be 100 %.

Question 32.
What do you mean by heat engine?
Answer:
A cyclic device which can convert heat energy into mechanical work is called a heat engine.
There are three main parts of a heat engine :

1. Heat source,
2. Sink,
3. Working substance.

Question 33.
Define the efficiency of heat engine.
Answer:
In each cycle the ratio of useful work done and the amount heat absorbed by the working substance in a complete cycle is called efficiency of heat engine, i.e.,
η=\(\frac{\text { Useful work done }}{\text{ Heat absorbed }}\)
or
η = \(\frac{W}{Q_{1}} \)
Where, W is the net work done and Q₁ is the heat absorbed from source.

Question 34.
Carnot engine is not practical. Why?
Answer:
The Carnot engine is an ideal engine which is not possible in practice, because :

• The walls of cylinder and piston cannot be perfectly insulator.
• It is supposed that thermal capacity of source and sink are infinite which is not possible.
• Compression and expansion in isothermal condition for reversible process in Carnot cycle is not ideal conditions.

Question 35.
Write the name of working substance in internal combustion engine and external combustion engine.
Answer:
Air is the working substance in internal combustion engine and vapour in external combustion engine.

Question 36.
Write the name of working substance used in Carnot engine.
Answer:
The working substance used in Carnot engine is ideal gas.

Question 37.
What is critical temperature?
Answer:
The critical temperature of a gas is the maximum temperature up to which the gas can be liquefied by the pressure-volume variation.

Question 38.
Write the critical temperature of water.
Answer:
The critical temperature of water is 374.1°C.

Question 39.
What is critical temperature of carbon dioxide?
Answer:
The critical temperature of carbon dioxide 31.4°C.

Question 40.
Explain why air pressure in a car tyre increases during driving? (NCERT)
Answer:
The temperature of tyre and hence of the air inside it increases during driving, due to friction between the tyres and road. Now the volume of the tyre remains unchanged practically. So according of Charle’s law
(P∝T), due to increases in temperature, the air pressure inside the tyre increases.

Question 41.
The coolant in a chemical on a nuclear plant (i.e., liquid used to prevent the different parts of a plant from getting too hot) should have high specific heat. Explain. (NCERT)
Answer:
The functions of the coolant in a chemical or nuclear plant is to absorb the heat produced and hence to prevent its different parts from getting too hot. It has high specific heat. The heat absorbed by a substance is directly proportional to the specific heat of the substance. Thus higher the value of specific heat, more will be the heat absorbed by the coolant for the same rise of temperature and hence the plant is protected from overheating.

Question 42.
Two bodies at different temperature T₁ and T₂ if brought in thermal contact don’t necessarily settle to the mean temperature (T₁+ T₂)/2. Explain. (NCERT)
Answer:
This is because the two bodies may have different masses and different specific heats. In thermal contacts, heat flows form the body at higher temperature to the body at lower temperature till temperature of the two become equal. The final temperature can be the mean temperature i.e.,\(\frac{T_{1}+T_{2}}{2}\)
only when the thermal capacities of two bodies are equal.

Thermodynamics Class 11 Important Questions Short Answer Type 

Question 1.
Calculate work done by the gas in the expansion against the external pressure.
Answer:
As shown in fig. a gas-filled in a cylinder fitted with a piston, at pressure P. The area of cross section of cylinder is A. The force exerted by piston on the gas is

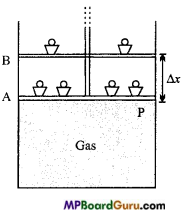
F = P×A
If the gas is expanded by reducing the weight, then displacement of piston is Δx.
Hence, the work done by gas on the small displacement Δ x be:
ΔW = Force x Displacement
=F. Δx
ΔW = PA.Δx = P.ΔV
If at pressure P the volume of gas changes from V₁ to V₂, then work done by
W = \(\sum_{V_{1}}^{V_{2}}\)P. ΔV = \(\int_{1}^{V_{2}}\) PdV
This is expression of work done.

Question 2.
What is first law of thermodynamics? Explain the following on the basis of this law : (i) Isothermal process, (ii) Adiabatic process.
Answer:
First law of thermodynamics: First law of thermodynamics: If a system is capable of doing an external work, the net amount of heat energy given to the system is equal to the sum of the energy spent in doing work (by the system) and the increase in internal energy of the system.

(i) Isothermal process: In the isothermal process the temperature of the system remains constant, hence the internal energy of the system will not change.
∴ ΔU = 0
But,
ΔQ = ΔW + ΔU, (first law of thermodynamics)
∴ΔQ = ΔW
Hence, the amount of heat given to system, in isothermal process, is equal to the total work done,

(ii) Adiabatic process: In this process the amount of heat of a system does not change.
∴ΔQ = 0
But,
ΔQ = ΔW + ΔU
or
0 = ΔW+ ΔU
or
ΔW = ΔU
Hence, work done by the system is equal to the decrease of internal energy.

Question 3.
What is the first law of thermodynamics? Explain the cyclic process.
Answer:
First law of thermodynamics: If a system is capable of doing an external work, the net amount of heat energy given to the system is equal to the sum of the energy spent in doing work (by the system) and the increase in internal energy of the system.

Let ΔQ heat is given to a system so that ΔW work is done by the system and its internal energy increases by ΔU.
∴ ΔQ = ΔW + ΔU
Now, in cyclic process, there will be no change in internal energy.
∴ ΔU = 0
From first law of thermodynamics,
ΔQ = ΔW + ΔU
or
ΔQ = ΔW
Thus, the heat given to a system in cyclic process is equal to the work done by the system.

Question 4.
Two cylinders A and B of equal capacity are connected to each other via a stopcock. A contains a gas at standard temperature and pressure. B is completely evacuated. The entire system is thermally insulated. The stopcock is suddenly opened. Answer the following:
(a) What is finally pressure of the gas in A and B?
(b) What is the change in internal energy of the gas?
(c) What is the change in temperature of the gas?
(d) Do the intermediate states of the system (before settling to the final equilibrium state) lie on its P- V-T Surface? (NCERT)
Answer:
(a) As the initial and final temperature remain the same. When the stopcock is suddenly opened, the volume available to the gas at 1-atmosphere pressure will become two times. Thus pressure will decrease t.o one-half i.e., 0.5 atmospheres. i.e., ” P₂V₂=P₁V₂
Here P₂ = 1 atm
∴ V₁= V
V₂ = 2V
P₂ = ?
P₂ = \(\frac{P_{1} V_{1}}{V_{2}} \) = \(\frac{1 \times V}{2 V}\)
= 0.5 atm

(b) Zero. This is because no work is done on/by the gas, thus there will be no change in the internal energy of the gas under constant temperature conditions.

(c) If the gas is assumed to be ideal, then there is no change in the temperature of the gas it does not work in expansion i.e., ΔT = 0.

(d) No, since the process (called free expansion) is rapid and cannot be controlled. The intermediate states of the system (gas here) are non-equilibrium states and don’t satisfy the gas equation so it does not lie on the P-V-T surface. In due course, the gas does return to an equilibrium state which lies on its P-V-T surface.

Question 5.
Determine the expression for the work done by the gas in isothermal process.
Answer:
Consider a fixed mass of a gas which is pressurized from above by a piston. The gas exerts a pressure P and occupies a volume V.
Now, the work done against the pressure for small change in volume dV is
dW=P.dV …(1)
If the volume of gas becomes V₂ from V₁ under isothermal changes, then
W=\(\int_{v_{1}}^{v_{2}} \) P.dV …… (2)
Now, we have by gas equation PV = RT, (for 1 mole)
or
P= \(\frac{R T}{V} \)

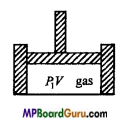
Putting the value of P in eqn. (2), we get
W = \(\int_{v_{1}}^{v_{2}} \) \(\frac{R T}{V} \).dV = RT \(\int_{v_{1}}^{v_{2}} \frac{d V}{V} \)
or
W = RT log_e\(\frac{V_{2}}{V_{1}} \)
= RT 2.3026 log10 \(\frac{V_{2}}{V_{1}} \)
= 2.3026 RT . log10 \(\frac{V_{2}}{V_{1}} \) …….. (3)
But,
P₁V₁ = P2V2
or
\(\frac{P_{1}}{P_{2}}\) =\(\frac{V_{2}}{V_{1}} \)
Putting the value of \(\frac{V_{2}}{V_{1}} \) in eqn. (3), we get
W =2.30267RT.log10\(\frac{P_{1}}{P_{2}}\)
If the number of moles is n, then
W = 2.3026nRT. log10 \(\frac{P_{1}}{P_{2}}\).

Question 6.
Derive the expression for the work done by a gas in adiabatic process.
Answer: Let 1 mole of an ideal gas undergoes an adiabatic change. Its initial volume is V₁ and final volume is V₂.
∴ Work done, W = \(\int_{V_{1}}^{v_{2}}\) P.dV
Equation for adiabatic process is
PV^γ  = a constant = K.
or
P = \(\frac{K}{V^{\gamma}}\)

Question 7.
What do you mean by isobaric process and isochoric process? Write equation of states.
Answer:
The thermodynamical process in which pressure of the system remains constant is called isobaric process. For isobaric process \(\frac{V}{T} \) = constant or V∝T.
The thermodynamical process in which the volume of the system remains constant is called isochoric process. In this process work done will be zero because there is no change in the volume of gaseous system.
Equation of state : (i) Isobaric process = \(\frac{\mathrm{V}}{\mathrm{T}} \) = constant (V ∝ T).

Question 8.
What Is a heat engine? Describe its main parts, explain Its principle and obtain the formula of its efficiency.
Answer:
Heat engine: It is a cyclic device which convert heat energy into mechanical work continuously. Theoretically, there are three main parts of a heat engine which are given below:

1. Heat source: It is a reservoir at high temperature and of infinite thermal capacity i.e., any amount of heat can be taken from it without changing its temperature.
2. Sink: It is also a reservoir of infinite heat capacity at low temperature. There is no change in its temperature if heat is continuously given to it.
3. Working substance: It is a system which absorb some heat is coverted into mechanical work and remaining heat is given to sink. After that is comes in its initial state and thus a cycle is completed.

Efficiency of heat engine: The working of heat engine for a complete cycle is shown in fig.

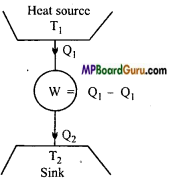
Let in a cycle the working substance absorb Q₁ amount of heat from the source and it gives Q₂ amount of heat to sink. Obviously, the heat (Q₁ – Q₂) is used to do mechanical work by the working substance. If there is no loss of heat, then by the law of conservation of energy.
w = Q₁– Q₂
The efficiency of a heat engine is defined as the ratio of amount of external mechanical work done by the engine, to the amount of heat absorbed in each cycle. It is denoted by η i.e.,
η = \(\frac{\text { External mechanical work }}{\text { Heat absorbed }} \) = \(\frac{W}{Q_{1}} \)
or
η = \(\frac{Q_{1}-Q_{2}}{Q_{2}} \) = 1 = \(\frac{Q_{2}}{Q_{1}}\)
This is formula of efficiency of heat engine.

Question 9.
Write down differences between isothermal and adiabatic process.
Answer:
Differences between Isothermal and Adiabatic Expansion

Isothermal process	Adiabatic process
1. In this process, the temperature of the system remains constant.	In this process the heat of the system remains constant.
2. Internal energy of gaseous system re-main constant hence ΔU = 0.	In this process Δθ = 0 hence ΔU = – Δ W.
3. In this process the system obeys Boyle’s law PV=K.	In this process, the system obeys Adiabatic PVγ = K.
4. This process is a slow process.	This process is a fast process.

Question 10.
What is isochoric process? Explain it by first law of thermodynamics. Draw its indicator diagram.
Answer:
A thermodynamic process, in which during the process, the volume of system remains constant is called isochoric process.
The work done in this process is
dW=PdV = P x 0 = 0
By the first law of thermodynamics:
dQ = dU + dW
or dQ = dU + 0 = dU
Thus, in isochoric process the net amount of heat given to a system is utilized to increase the internal energy of the system. The indicator diagram of isochoric process of shown in fig.

Question 11.
What is isobaric process? Draw its P-V indicator diagram and explain it on the basis of first law of thermodynamics.
Answer:
A thermodynamic process in which during the process, the pressure of the system remains constant is called isobaric process.
The evaporization of water in the boiler of steam engine is its example.
The work done in this process be
dW = P(V₂ – V₁,)
By the first law of thermodynamics,
dQ = dU+dW
or
dQ = dU + P(V₂ – V₁)
or
dU = dQ- P(V₂ -V₁)
With the help of this formula, the change in internal energy of a system in isobaric process can be calculated. Its P-V indicator diagram is shown in fig.

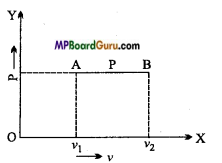
Question 12.
What is Carnot’s engine? Describe its different parts.
Or
What is heat engine? Describe its different parts with diagram and working.
Answer:

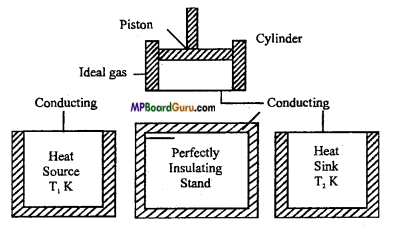
Sadi Carnot in 1824, conceived an ideal heat engine which is not possible to realize in practice but its efficiency in maximum. This engine is called Carnot reversible engine. The plan of Carnot reversible engine is shown in figure.

Carnot engine consists of following main parts :
(i) Source of heat: It is a hot body maintained at a constant high temperature T₁K. It has infinite heat capacity. Whatsoever be the amount of heat taken from it, its temperature T₁ remains constant..

(ii) Sink: It is a body maintained at a constant low temperature T₂K where T₂ < T₁. It also has infinite heat capacity. Whatsoever be the amount of heat given to it, its temperature T₂ remains constant.

(iii) Cylinder and piston: There is a cylinder with perfectly non-conducting walls but with a perfectly conducting base. This cylinder is fitted with perfectly non-conducting piston which has a frictionless movement.

(iv) Perfectly insulating platform: It is a perfectly non-conducting platform. It serves as a stand for the cylinder.

(v) Working substance: The ideal gas acts as a working substance. It is enclosed in the cylinder.

Question 13.
Carnot engine is not practical. Why?
Answer:
The Carnot engine is an ideal engine which is not possible in practice, because :

• The walls of cylinder and piston cannot be perfectly insulator.
• It is supposed that thermal capacity of source and sink are infinite which is not possible.
• Compression and expansion in isothermal condition for reversible process in Carnot cycle is not ideal conditions.

Question 14.
What do you mean by internal energy ?
Answer:
Internal energy: The total kinetic energy and potential energy of the molecules of a gas is called internal energy of a substance.
The internal energy of a gas depends upon the temperature and the force of attraction between the molecules.

Question 15.
Can the efficiency of Carnot engine be 100%. Explain with reason.
Answer:
Efficiency of Carnot cycle is η = 1 – \(\frac{T_{2}}{T_{1}} \)
If T₂ = 0, then η= 1.
Hence, the temperature of sink should be 0K, which is not possible. Hence, the efficiency cannot be 100 %.

Question 16.
What is principle of an ideal Carnot’s engine? Describe the working of the different parts of this engine.
Answer:
The efficiency of a Carnot engine is equal to the ratio of the useful work done by the engine to the heat energy absorbed by it. Thus, the efficiency of a Carnot engine, i.e.,
η = \(\frac{\text { Useful work done }}{\text { Heat energy absorbed }} \)
If the working substance (ideal gas) takes in heat energy Q₁ at T₁ from the source and gives up heat energy Q₂ at T₂ to the sink, then Useful work done by the engine = Q₁ – Q₂
∴ The efficiency of Carnot engine,
η = \(\frac{Q_{1}-Q_{2}}{Q_{1}}\)
or
η = 1 – \(\frac{Q_{2}}{Q_{1}} \) ……… (1)

On the basis of mathematical treatment, it can be proved that the ratio of heat rejected to the heat absorbed is equal to the ratio of the temperatures of the sink and the source, i.e.,
\(\frac{Q_{2}}{Q_{1}} \) = \(\frac{T_{2}}{T_{1}}\)
Putting this value in eqn. (1), we get
η = 1 – \(\frac{T_{2}}{T_{1}}\)
Working:

Sadi Carnot in 1824, conceived an ideal heat engine which is not possible to realize in practice but its efficiency in maximum. This engine is called Carnot reversible engine. The plan of Carnot reversible engine is shown in figure.

Carnot engine consists of following main parts :
(i) Source of heat: It is a hot body maintained at a constant high-temperature T₁K. It has infinite heat capacity. Whatsoever be the amount of heat taken from it, its temperature T₁ remains constant..

(ii) Sink: It is a body maintained at a constant low temperature T₂K where T₂ < T₁. It also has infinite heat capacity. Whatsoever be the amount of heat given to it, its temperature T₂ remains constant.

(iii) Cylinder and piston: There is a cylinder with perfectly non-conducting walls but with a perfectly conducting base. This cylinder is fitted with perfectly non-conducting piston which has a frictionless movement.

(iv) Perfectly insulating platform: It is a perfectly non-conducting platform. It serves as a stand for the cylinder.

(v) Working substance: The ideal gas acts as a working substance. It is enclosed in the cylinder.

Question 17.
State second law of thermodynamics and explain its importance.
Answer:
Second law of thermodynamics: The first law of thermodynamics shows an equivalence between heat and mechanical energy but it does not say anything about the direction in which the energy change takes place.

We know that heat always flows from a body at higher temperature to a body at lower temperature but heat does not flow from a body at lower temperature to a body at higher temperature. Why? Why is the efficiency of a heat engine less than 1? When the water in a beaker is stirred with a chum, it gets heated. But on putting a chum in the hot water placed in a beaker, no mechanical work is obtained. Why ? These questions can be replied with the help of second law of thermodynamics.

The following are the important statements of second law of thermodynamics :
(i) Clausius statement: It is impossible for a self-acting machine, unaided by any external source, to transfer heat from a body at lower temperature to a body at higher temperature, It is clear from this statement that heat can never flow from a body at lower temperature to a body at higher temperature until the work is done on it by external source.

This statement agrees with the experiences in other branches of physics, e.g., the electric current does never flow from a conductor at lower potential to a conductor at higher potential until the external work is done on it. Similarly a body cannot reach from the lower surface to the higher surface until the work is done on it by external source.

(ii) Kelvin statement: It is impossible to derive a continuous supply of work by cooling a body to a temperature lower than of the coldest of the surroundings. In Carnot engine, if the temperatures of the source and sink are same then engine will not operate because if the engine operates, work will be done and the source will cool down below the temperature of the surroundings.

(iii) Kelvin-Planck statement: It is impossible to construct a machine, operating in a cycle, which converts all the heat taken from the source into work completely. It is clear from this statement that in heat engine, the working substance can never convert all of the heat absorbed from the source into work.

It is essential to reject some of the heat to the sink. The present of both, the source and the sink, is a must for the conversion of heat into work. Since all of the heat does not convert into work, the efficiency of the engine is always less than one.

Question 18.
Explain the principle of refrigeration.
Or
What is refrigerator? Explain the principle of an ideal refrigerator and define its coefficient of performance. Write its formula related to efficiency.
Answer:
Principle of refrigeration: We know that in heat engine, the working substance absorbs some heat from the source, converts a part of it into work and rejects the remaining part of it to the sink. In practice, its reverse is also possible i.e., such a device can be used in which the working substance absorbs some heat from the sink at low temperature, has some work done on it and rejects a large amount of heat to the source at high temperature. This device is called a ‘refrigerator’ and the working substance is called a ‘refrigerant’.

The device which transfers the heat from the body at low temperature to the body at high temperature, is called refrigerator.

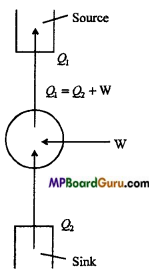
A refrigerator consists of following main parts :

• Source: It is a body of infinite heat capacity which has a large and fixed temperature.
• Sink: Its temperature is less than the temperature of the source.
• Working substance: Ordinarily, the liquid (ammonia or freon) is used as working substance which undergoes the cyclic change. The working substance is called coolant.

Let the working substance absorbs an amount of heat Q₂ from the sink, work W is done on it and rejects the heat Q₁ to the source.
Since the working substance comes back to its initial state after each cycle, there is no change in its internal energy. From first law of thermodynamics, Q₂ – Q₁= – W
Minus sign indicates that the work is done on the substance.
∴ Q₁= Q₂ + W .
It is clear from the above equation, to transfer the heat from the source to the sink, work must be done on the working substance.

Thermodynamics Class 11 Important Questions Long Answer Type

Question 1.
State first law of thermodynamics and on the basis of this law proves C_p – C_v =R.
Or
Prove Mayer’s relation C_p– C_v = R.
Or
Establish a relationship between the specific heat of a gas at constant pressure and at constant volume.
Answer:
First law of thermodynamics: If a system is capable of doing an external work, the net amount of heat energy given to the system is equal to the sum of the energy spent in doing work (by the system) and the increase in internal energy of the system.

Relation between C_p and C_v: Let one mole of an ideal gas be given an amount of heat ΔQ at constant volume so that its temperature increases by ΔT.
∴ Δ Q = 1. C_v.ΔT, (∵ ΔQ = mSΔT)
ΔQ = C_v.ΔT …(1)
Since, the volume of the gas remains constant therefore no external work is done by the gas.
∴ ΔW=0

From first law of thermodynamics, we have
ΔQ=ΔW+ΔU
or
ΔQ = 0 + ΔU
or
ΔQ = ΔU …(2)
From eqns. (1) and (2), we get
ΔU = C_v.ΔT …(3)

Let one mole of an ideal gas be given an amount of heat AQ at constant pressure so that its temperature increases by Δ T.
ΔQ = 1.C_p.ΔT …(4)
If ΔV be the increase in volume of the gas at constant pressure P, then the work done by the gas
ΔW = P.ΔT,
[∵ Work = Force × Distance =\(\frac{\text { Force }}{\text { Area }} \) × Volume = Pressure × Volume]

Now, from first law of thermodynamics,
ΔQ=ΔW+ΔU
or
ΔQ = PΔV + ΔU …(5)
From eqns. (4) and (5), we get
PΔV + ΔU = C_pΔT
Putting the value of A U from eqn. (3),
we get PΔV+C_vΔT=C_pΔT
or
(C_p– C_v)ΔT=PΔV …(6)
The ideal gas equation is given by
PV = RT
or
PΔV=RΔT, (∵ P is constant)

Putting the value of PΔV Fin eqn. (6),
we get (C_p– C_v)ΔT=RΔT
or
C_p– C_v= R
Which is the required relation.

Question 2.
Draw the graph of Carnot cycle and explain each process.
Answer:
The graph of Carnot cycle is shown in the figure. The change are as follows :
(i) Isothermal expansion: Let 1 gm mol of working ideal gas is filled in cylinder at temperature (T₁K). Its pressure is P₁ and volume is V₁. This position is shown by point A in the graph.
Now, suppose the cylinder is kept on source (at T₁K) and allowed a slow expansion. Since, the base of the cylinder is perfectly conducting, therefore its temperature will remain constant during the expansion.

Thus, the expansion will be isothermal. The change is shown by AB curve in the figure. Now, the pressure and volume of gas become P₂ and V₂ respectively at point B. In this process, work done by the gas W₁ is equal to the amount of heat absorbed Q₁.

(ii) Adiabatic expansion: Now, the cylinder is removed from the source and kept on a perfectly non-conducting platform and gas is allowed for adiabatic expansion slowly, shown by BC curve. Now, the temperature falls to T₂K. The corresponding pres¬sure and volume are P₃ and V₃ respectively of the point C.

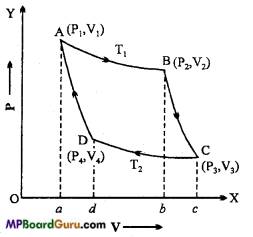
(iii) Isothermal compression: Now, the cylinder is kept on sink (at T₂K) and the gas is compressed slowly so that the pressure and volume become P4 and VA respectively under constant temperature. The CD portion of the curve shows the change. In this process, the heat produced is given to sink. In this process, the work done W₃ on gas, is equal to the amount of heat Q₂, given to sink.

(iv) Adiabatic compression: At the end, the cylinder is again kept on the non-con-ducting base and piston is compressed slowly so that the gas reached to its initial position A, at the temperature T₁K, the pressure is P₁ and the volume V₁. Thus, the working gas is ready to work again.

Question 3.
Describe the different parts of Carnot’s engine and draw the graph of Carnot’s cycle and calculate its efficiency. Can it be achieved in practice, if not then why?
Or
Prove that the efficiency of Carnot’s engine is given by the expression η =1 – \(\frac{T_{2}}{T_{1}}\)
where symbols have their usual meanings.
Or
Describe Carnot’s engine under the following heads :
(i) Main parts, (ii) Carnot’s cycle, (iii) Formula of efficiency, (iv) Non- practicability.
Answer:
Description of different parts of Carnot’s engine:

Sadi Carnot in 1824, conceived an ideal heat engine which is not possible to realize in practice but its efficiency in maximum. This engine is called Carnot reversible engine. The plan of Carnot reversible engine is shown in figure.

Carnot engine consists of following main parts :
(i) Source of heat: It is a hot body maintained at a constant high-temperature T₁K. It has infinite heat capacity. Whatsoever be the amount of heat taken from it, its temperature T₁ remains constant..

(ii) Sink: It is a body maintained at a constant low temperature T₂K where T₂ < T₁. It also has infinite heat capacity. Whatsoever be the amount of heat given to it, its temperature T₂ remains constant.

(iii) Cylinder and piston: There is a cylinder with perfectly non-conducting walls but with a perfectly conducting base. This cylinder is fitted with perfectly non-conducting piston which has a frictionless movement.

(iv) Perfectly insulating platform: It is a perfectly non-conducting platform. It serves as a stand for the cylinder.

(v) Working substance: The ideal gas acts as a working substance. It is enclosed in the cylinder.

Graph:

Efficiency of Carnot’s engine : It is defined by the ratio of useful work and the heat absorbed. ,
∴ η = \(\frac{\text { Useful work }}{\text { Heat absorbed }} \)
(i) In isothermal expansion the work done is equal to the amount of heat absorbed by source
∴ w₁=Q₁ = RT₁ log_e \(\frac{V_{2}}{V_{1}}\) = Area ABba A
(ii) In adiabatic expansion, the work done is given by
W₂ = \(\frac{R}{\gamma-1} \) (T₁– T₂) = AreaBCcbB
(iii) In isothermal compression the work done is equal to the heat ejected into the sink
W₃ = Q₂
= RT₂ log_e\(\frac{V_{3}}{V_{4}} \) = AreaDCdcC
(iv) in adiabatic compression the work done by ideal gas,

Now, efficiency of Carnot’s engine,

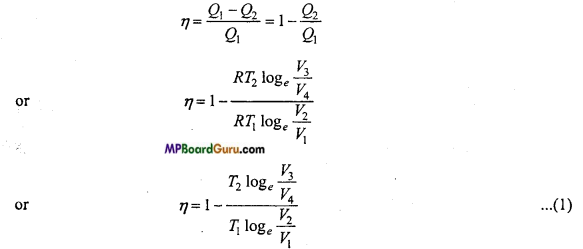
∵ B and C are on the same adiabatic curve.
∴T₁ V₂^γ-1 = T₂ V₄^γ-1
or
\(\frac{T_{1}}{T_{2}}\) = \(\left(\frac{V_{3}}{V_{2}}\right)^{\gamma-1}\)
Similarly, A and D are on same adiabatic curve.

or
\(\frac{\log _{e} \frac{V_{3}}{V_{4}}}{\log _{e} \frac{V_{2}}{V_{1}}} \) = 1
From eqn. (1), we get
η = 1- \(\frac{T_{2}}{T_{1}}\) ……… (2)

Impracticability of Carnot engine: Carnot engine is an ideal engine which is not practicable. The reasons for this are following:

• In Camot engine, it is assumed that the walls of the cylinder are perfectly non conducting and movement of piston is frictionless. This is only an ideal imagination.
• It is assumed that the thermal capacity of source and sink is infinite which is impracticable.
• The process of compression and expansion takes place very slowly so that Carnot cycle remains reversible. In practice, it is not possible to achieve this ideal state.

Thermodynamics Class 11 Important Numerical Questions

Question 1.
What amount of heat must be supplied to 20× 10^-2 kg of nitrogen (at room temperature) to raise its temperature by 45°C at constant pressure ? (Molecular mass of N₂ = 28; R = 8.3 J mor^-1 K^-1.) (NCERT)
Solution:
Given: Mass of gas M = 2.0 × 10^-2 kg
= 2.0×10^-2x10³g=20g
Increase in temperature ΔT = 45°C
Molecular weight of N₂, m = 28g
Number of moles n = \(\frac{M}{m}\) = \(\frac{20}{28} \) = 0.714
N₂ is diatomic gas therefore specific heat at constant press
C_p = \(\frac{7}{2} \) R= \(\frac{7}{2} \) × 8.31 mol^-1 k ^-1 = 934 J.

Question 2.
In changing the state of a gas adiabatically from an equilibrium state A to another equilibrium state B. An amount of work equal to 22.3 J Is done on the system.
If the gas is taken from state A to B ‘via a process in which the net heat absorbed by the system is 9.35 cal, how much Is the net work done by the system in the latter case? (Take 1 caI=4.19J) (NCERT)
Solution:
Given: In first adiabatic process dQ = O and dW = -223 J, (-ve sign indicates here that work is done on the system)
By the first law of thermodynamics,
dQ = dU +dW
∴ 0 = dU – 22.3
or
dU = 22.3J

In second process
dQ = 9.35 cal = 9.35 × 4.19 J = 39.18 J
in second process , By the first law of thermodynamics ,
dQ = dU+ dW
39.18 = 22.3+ dW
or
dW = 39.18 – 22.3 = 16.88J
≈ 16.9J.

Question 3.
A steam engine delivers 5.4 x 10⁸ J of work per minute and services 3.6 x 10⁹J of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute? (NCERT)
Solution:
Given : Q₁ =Heat absorbed by boiler per minute = 3.6 × 10⁹ J
W = Work done per minute by heat engine = 5.4 × 10⁸ J
∴ Efficiency of engine
η = \(\frac{W}{Q_{1}}\) = \(\frac{5 \cdot 4 \times 10^{8}}{36 \times 10^{9}}\) = 0.15 = 15%
Now, Q₁ = Q₂ + W
or
Q₂ = Q₁ – W
= 3.6 × 10⁹ – 5.4 ×10⁸
=( 36 -5.4) ×10⁸ = 30.6 × 10⁸ J
= 3.06 × 10⁹J ≈ 3.1 × 10⁹ J

Question 4.
A refrigerator is to maintain eatables kept inside at 9°C. If room temperature is 36°C. Calculate the coefficient of performance. (NCERT)
Solution:
Given : T₂ = 273 + 9 = 282K
T₁ =273 + 36 = 309K
The coefficient of performance of refrigerator be .
α = \(\frac{T_{2}}{T_{1}-T_{2}}\)
= \(\frac{282}{309-282} \) = 10.44
≈ 10.4

Question 5.
A thermodynamic system is taken from an original state D to an intermediate state E by the linear process shown in Fig.(NCERT)

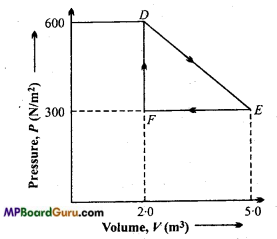
Its volume is then reduced to the original value from E to F by an isobaric process. Calculate the total work done by the gas from D to E to F.
Solution:
Work done by the gas in the process from D to E and then from E to F is
W = Area of Δ DEF
W = ΔDEF
= \(\frac{1}{2} \) EF × DF
= \(\frac{1}{2} \) ( 5- 2) × (600 – 300)
= \(\frac{1}{2} \) × 3× 300 = 450J.

Question 6.
In a thermodynamic process, 400 J of heat is given to a gas and 100 J of work is done on the gas. Find the change in the internal energy of the gas. (NCERT)
Solution:
Given : ΔQ = 400J and ΔW = -100 J (since, the work done on the gas is taken negative).
From first law of thermodynamics,
we have ΔQ = ΔW+ ΔU
ΔU = ΔQ-AW = 400-(-100)
= 400+100 = 500 J.

Question 7.
Calculate the efficiency of Carnot’s engine if the temperature of source and sink are 300°C and 15°C respectively. If the engine absorbs 100 calories at high temperature, calculate the work done by it.
Solution:
T₁ = 273 + 300 = 573 K,
T₂ = 273 + 15 = 288 K and Q₁ = 100 cal.

Now, Efficiency,
η = 1 – \(\frac{T_{2}}{T_{1}}\) = 1 – \(\frac{288}{573}\)
Again, η = 1- \(\frac{Q_{2}}{Q_{1}} \)
or
0.50 = 1 – \(\frac{Q_{2}}{100} \)
or
\(\frac{Q_{2}}{100} \) = 0.50
or
Q₂ = 50 cal
∴ W = Q₁ – Q₂ = 100 – 50 = 50 cal .

Question 8.
If the work done, by giving 40 joule to a system is -8 joule, then find the change in the internal energy of the system.
Solution:
Given : ΔQ = 40 joule,ΔW= -8 joule
Now, we have ΔQ = ΔW+ΔU
or
40 = – 8 + ΔU
or
Δ U = 48 joule.

Question 9.
A Carnot engine, obtain 300 calorie heat at 500 K and give 150 calorie heat to the sink. What will be the temperature of sink?
Solution:
Given Q₁ = 300 Calorie, T₁ = 500 K, Q₂ = 150 Calorie, T₂ = ?
from \(\frac{Q_{1}}{Q_{2}} \) = \(\frac{T_{1}}{T_{2}}\)
\(\frac{300}{150} \) = \(\frac{500}{T_{2}} \)
or
T₂ = \(\frac{500 \times 150}{300} \) = 250K

Question 10.
A refrigerator takes heat from 250 K body and gives to the atmosphere which is at 310 K. Find out working performance of refrigerator.
Solution:
Given : T₁ = 310 K, T₂= 250 K,
β = \(\frac{\mathrm{T}_{2}}{\mathrm{~T}_{1}-\mathrm{T}_{2}}\)
β = \(\frac{250}{310-250} \) = \(\frac{250}{60}\)
or
β = \(\frac{25}{6} \) = 4.16

Question 11.
In Carnot engine, the temperature of the source and the sink are 500 K and 375 K respectively. If the engine absorbs 600-kilo calories of heat per cycle from the source, compute the following :
(i) The efficiency of engine,
(ii) Work done per cycle,
(iii) Heat given to the sink per cycle.
Solution:
Given : T₁ = 500 K,T₂ = 375 K
Q₁ = 600 kilo calories = 600 × 10³ calories
= 600 × 10³ × 4.2 × 10⁷ergs, [∴ W = JH]
(i) Efficiency,
η = 1 – \(\frac{T_{2}}{T_{1}}\)

Question 12.
At atmospheric pressure, air is suddenly compressed so that its volume become one-fourth of initial. Find out its pressure. [γ = 1.5]
Solution:
Given : V₂=\(\frac{V_{1}}{\gamma} \), P₁ = 1 [Atmospheric pressure] γ =1.5 = \(\frac{3}{2}\)
We know
P₁V₁^γ = P₂V₂^γ
or
\(\frac{P_{1}}{P_{2}}\) = \(\left(\frac{V_{2}}{V_{1}}\right)^{\gamma}\)

Question 13.
A reversible engine absorbs 746 joule from the source and eject 546 joule into the sink. The difference of temperature of source and sink is 100°C. Find (i) Work from the engine, (ii) Efficiency of engine, (iii) Temperatures of source and sink.
Solution:
Given : Q₁ = 746 joule, Q₂ = 546 joule,
T₁-T₂ =100°C = 100K.
Now, (i) Work done by engine = Q₂ – Q₁ = 746 – 546 = 200 joule,

(ii) Efficiency of engine, .
η = 1 – \(\frac{Q_{2}}{Q_{1}} \)
= 1 – \(\frac{546}{746} \) = \(\frac{200}{746}\) = 0.268 = 26.8%

(iii) ∵η = 1 – \(\frac{T_{2}}{T_{1}}\) = \(\frac{T_{1}-T_{2}}{T_{1}}\)
or
0.268 = \(\frac{100}{T_{1}} \)
Temperature of source, T₁ =\(\frac{100}{0 \cdot 268}\) = 373.13 K
Again, T₁ – T₂ = 100
∴ 373.13 – T₂ = 100
∴ Temperature of sink, T₂ = 273.13K.

Thermodynamics Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
In isothermal process, the internal energy of an ideal gas depends only on :
(a) Pressure
(b) Volume
(c) Temperature
(d) Volume of molecules.
Answer:
(c) Temperature

Question 2.
Which statement is true for adiabatic process:
(a) ΔQ = ΔU + ΔW
(b) ΔQ = θ + ΔW
(c) ΔQ= ΔU+θ
(d) Q=ΔU+ΔW.
Answer:
(d) Q=ΔU+ΔW.

Question 3.
Internal energy of ideal gas in isothermal process ¡s:
(a) Increases
(b) Decreases
(c) No change
(d) None of these.
Answer:
(c) No change

Question 4.
In adiabatic process, which remain constant:
(a) Temperature
(b) Pressure
(c) Volume
(d) Amount of heat.
Answer:
(d) Amount of heat.

Question 5.
in isothermal process amount of heat given to ideal gas is used to:
(a) Increase temperature
(b) Perform external work
(c) increase temperature and perform external work
(d) Increase internal energy.
Answer:
(b) Perform external work

Question 6.
300 calorie heat is given to a system such that it perform work of 64)0 joule. Increase in its internal energy will be:
(a) 654 J
(b) 156.5 J
(c) – 300 J
(d) 528.2 J.
Answer:
(a) 654 J

Question 7.
Formula for efficiency of Carnot Engine is:
(a) η=\(1-\frac{\mathrm{Q}_{1}}{\mathrm{Q}_{2}}\)
(b) η = 1- \(\frac{\mathrm{Q}_{2}}{\mathrm{Q}_{1}} \)
(c) η = 1- \(\frac{\mathrm{T}_{1}}{\mathrm{~T}_{2}}\)
(d) η=\(\frac{\mathrm{T}_{1}}{\mathrm{~T}_{2}}\)-1.
Answer:
(b) η = 1- \(\frac{\mathrm{Q}_{2}}{\mathrm{Q}_{1}} \)

Question 8.
Which gas is used in refrigerator generally used in home:
(a) Ammonia
(b) Freon
(c) Chlorine
(d) None of these.
Answer:
(b) Freon

Question 9.
The coefficient of performance of refrigerator working between 30°C and 0°C is:
(a) 0
(b) 0.1
(c) 9
(d) 10.
Answer:
(c) 9

Question 10.
An ideal engine absorbs heat a 127°C and reject at 77°C. Its efficiency will be:
(a) 39 %
(b) 13 %
(c) 61 %
(d) 88%.
Answer:
(b) 13 %

Question 11.
The coefficient of performance of ideal engine working between 0°C and 27°C ¡s:
(a) \(\frac{273}{27} \)
(b) \(\frac{300}{273}\)
(c) \(\frac{273}{300} \)
(d) 1- \(\frac{273}{300} \)
Answer:
(a) \(\frac{273}{27} \)

Question 12.
On reducing temperature of sink, efficiency of Carnot Engine will be:
(a) First increases then decreases
(b) Increases
(c) Decreases
(d) No change.
Answer:
(b) Increases

Question 13.
If all the doors and windows of a room are closed then the fan Is switched on temperature of room will:
(a) Decrease
(b) Increase
(c) Zero
(d) Remain constant.
Answer:
(b) Increase

2. Fill in the blanks:

1. Work done in isothermal process is ………………….. .
Answer:
RT log\(\left(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\right) \)

2. First law of thermodynamics ΔQ =…………………..+ ………………….. .
Answer:
ΔU + ΔW

3. In isothermal process ………………….. remain constant.
Answer:
Temperature

4. In adiabatic process ………………….. remain constant.
Answer:
Amount of heat

5. Work done in adiabatic process is ………………….. .
Answer:
w =\(\frac{\mathrm{R}\left(\mathrm{T}_{2}-\mathrm{T}_{1}\right)}{\gamma-1} \)

6. Efficiency of Carnot engine is ………………….. .
Answer:
η =1-\(\frac{\mathrm{T}_{2}}{\mathrm{~T}_{1}} \)

7. Value of joule’s constant in M.K.S. unit is ………………….. .
Answer:
4.18 joule/calorie

8. Adiabatic equation for ideal gas is ………………….. .
Answer:
PV^γ=constant

9. Process which are not reversible is called ………………….. process.
Answer:
Irreversible

10. In isothermal process ΔP = ………………….. .
Answer:
0.

3. Match the following:

Column ‘A’	Column ‘B’
1. Work done in isothermal process	(a) \( \frac{1-\eta}{\eta}\)
2. Work done in adiabatic process	(b) ΔQ =ΔU+ΔW
3. Efficiency of Carnot engine	(c) \( \frac{\mathrm{R}\left(\mathrm{T}_{1}-\mathrm{T}_{2}\right)}{\gamma-1}\)
4. Coefficient of working performance of refrigerator	(d)1-\(\frac{\mathrm{T}_{2}}{\mathrm{~T}_{\mathrm{l}}} \)
5.First law of thermodyanamics	(e) RTlog\(\left(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\right) \)

Answer:
1.  (e) RTlog\(\left(\frac{\mathrm{V}_{2}}{\mathrm{~V}_{1}}\right) \)
2. (c) \( \frac{\mathrm{R}\left(\mathrm{T}_{1}-\mathrm{T}_{2}\right)}{\gamma-1}\),
3. (d)1-\(\frac{\mathrm{T}_{2}}{\mathrm{~T}_{\mathrm{l}}} \)
4. (a) \( \frac{1-\eta}{\eta}\),
5. (b) ΔQ =ΔU+ΔW.

4. state true or Flase:

1. Work done by thermodynamical system does not depend upon path of working process.
Answer:
False

2. Internal energy of ideal gas depends upon its temperature.
Answer:
True

3. Average kinetic energy of single-molecule Df any gas depends upon pressure of the gas-only.
Answer:
False

4. For isothermal process PV = constant.
Answer:
True

5. In isothermal process change in internal energy is equal to work done.
Answer:
False

6. Work done in adiabatic process is equal to amount of heat given.
Answer:
False

7. Heat engine fully convert the amount of heat taken into work.
Answer:
False

8. First law of thermodynamics is in actual the laws of conservation of energy.
Answer:
True

9. Work done by ideal engine depends upon only on the temperature at which it accept heat.
Answer:
False

10. Carnot engine is an irreversible engine.
Answer:
False

11. Efficiency of Carnot engine depends oh nature of working substance.
Answer:
False

12. Internal energy of ideal gas depends on size of the molecules.
Answer:
False.