MP Board Class 11th Physics Important Questions Chapter 11 Thermal Properties of Matter

Students get through the MP Board Class 11th Physics Important Questions Chapter 11 Thermal Properties of Matter which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 11 Thermal Properties of Matter

Thermal Properties of Matter Class 11 Important Questions Very Short Answer Type

Question 1.
Ice is cold, why?
Answer:
When the ice is touched by hand, the ice takes heat from the hand. Thus, heat is lost from the hand and the temperature of hand decreases and therefore we feel cold.

Question 2.
What is temperature?
Answer:
It is that physical quantity which determines the direction of flow of heat when two objects are placed in contact with each other.

Question 3.
Define calorie.
Answer:
Amount of heat required to raise the temperature of one gram pure water from 14.5°C to 15.5°C is known as one calorie.

Question 4.
What are the different scale to measure temperature? Write relation be¬tween them.
Answer:

• Centigrade or celcius scale.
• Farenheit scale.
• Kelvin scale.
• Reumar scale.

Relation between them is
\(\frac{C}{5}\) = \(\frac{F-32}{9}\) = \(\frac{R}{4}\) = \(\frac{K-273}{5}\).

Question 5.
What is ideal gas thermometer?
Answer:
Ideal gas thermometer is that thermometer whose zero is that temperature at which pressure remain zero and 1 degree is equal to 1°C.

Question 6.
What is absolute zero ? Write its value.
Answer:
It is that temperature at which pressure and volume of a gas becomes zero, known as absolute zero. Its value is 273.15°C.

Question 7.
In absolute temperature scale, what is the melting point and boiling point of pure water?
Answer:
In absolute temperature scale melting point of pure water is 273K and boiling point is 373K.

Question 8.
Can the temperature of an object have a negative value on Kelvin’s scale?
Answer:
No.

Question 9.
Why H₂ – thermometer is called standard thermometer? What is its range?
Answer:
The H₂– thermometer is called standard thermometer because it is used for the calibration of other thermometers. It can measure the temperature from – 200°C to 500°C.

Question 10.
Define coefficient of linear expansion and write its unit.
Answer:
It is defined by the change in length per unit original length per degree rise of temperature.
Let the initial length of a rod be l and the length increases by Δl for Δt change in temperature, then
Coefficient of linear expansion, α = \(\frac{\Delta l}{l \Delta t}\)
Unit: Its unit is °C ^-1 or K ^-1.

Question 11.
What are the two types of specific heat? Why C_p is greater than C_v?
Answer:
The two specific heats of gases are specific heat at constant pressure (C_p) and specific heat at constant volume (C_v).
C_p is greater than C_v because same part of heat given at constant pressure is utilized to increase the volume, (hence work done) against the applied pressure.

Question 12.
Define coefficient of superficial expansion and give its unit.
Answer:
It is defined by the change in area per unit original area per degree rise in temperature.
Let initial area of a body be A and the area change by ΔA, with the rise of temperature Δt.

∴ Coefficient of superficial expansion, β = \(\frac{\Delta A}{A \Delta t}\)
Unit: Its unit is °C^-1 or K ^-1.

Question 13.
Define coefficient of volume expansion and give its unit.
Answer:
It is defined by the change in volume per unit original volume per degree rise in temperature.
Let initial volume of a substance is V and change in volume with change in temperature ΔT is ΔV.
∴ Coefficient of volume expansion, γ = \(\frac{\Delta V}{V \Delta T}\)
Unit: Its unit is °C ^-1 or K ^-1.

Question 14.
Write the relations between α,β and γ.
Answer:
β = 2α and γ = 3α
∴ α : β : γ = 1:2:3.

Question 15.
Define specific heat and give the unit of specific heat.
Answer:
We know that,
Q = ms Δt
or
s = \(\frac{Q}{m \Delta t}\)
If m = 1 gm, Δt = 1°C
Then, s = Q
The amount of heat required to raise the temperature of 1 gm substance through 1°C is called specific heat of the substance.
Unit: Unit of specific heat is calorie × gm^-1 × °C^-1.

Question 16.
Define latent heat of fusion.
Answer:
Latent heat of fusion: The amount of heat required to change unit mass of a solid into liquid at its melting point is called latent heat of fusion.
If the latent heat of fusion is L, then Q = mL
Latent heat of ice is 80 cal × gm^-1.

Question 17.
Define latent heat of vaporization.
Answer:
Latent heat of vaporization: The amount of heat required to change a liquid of unit mass into vapour at its boiling point, is called latent heat of evaporation.
Latent heat of steam is 536 cal × gm^-1.
Unit: The practical unit of latent heat is cal × gm^-1.

Question 18.
Write the principle of thermometry.
Answer:
The properties of any object which depends on temperature and can be used to measure temperature.

Question 19.
Which is more sensitive, liquid thermometer or gas thermometer?
Answer:
Gas thermometer is more sensitive than liquid thermometer because expansion of gas is more than liquid for a given temperature difference.

Question 20.
Among metal and alloy, whose coefficient of thermal expansions is more?
Answer:
Thermal expansion of metal is more than that of alloy.

Question 21.
Can the value of coefficient of thermal expansion be always positive?
Answer:
No.

Question 22.
There is a hole in a metal plate. What will happen on heating it?
Answer:
The size of hole will increase on heating the metal plate.

Question 23.
A gap is left between two rails, why?
Answer:
The temperature of the atmosphere is always changing. With the rise of temperature the rails expands, therefore the gaps are left between them. If gap is not kept, then with the rise in temperature the rails will bend and will cause serious accidents.

Question 24.
What do you mean by the anomalous expansion of water?
Answer:
Generally, the volume of liquids increases with the rise of temperature. But, the volume of water decreases when it is heated from 0°C to 4°C and then after 4°C the volume increases. Similarly, when the water is cooled its volume decreases up to 4°C and then increases from 4°C to 0°C. Such expansion of water is called anomalous expansion.

Question 25.
The bulb of one thermometer is spherical while that of the other is cylindrical. Both have equal amounts of mercury. Which one will response quickly to temperature change?
Answer:
For a given volume,the surface area of the cylinder is large than that of sphere. Therefore heat will be quickly conducted through the cylindrical bulb. Thus, the response of cylindrical bulb thermometer will be quicker.

Question 26.
Pendulum invar of a pendulum clock is made of alloy. Why?
Answer:
Coefficient of thermal expansion of alloy is very less, thus when temperature changes there is no effect on pendulum invar, so it is made of alloy.

Question 27.
During change of state, heat given to a body is lost in which form?
Answer:
During change of state, heat given to the body is lost to increase internal molecu¬lar potential energy of the body.

Question 28.
Hot water is used for formentation. Why?
Answer:
Due to high specific heat of water, it gives more heat in comparison to other liquids. Therefore, hot water is used for formentation.

Question 29.
Ice at 0°C appear to be more cold than water at 0°C. Why?
Answer:
When the ice melt, amount of heat required for melting is absorbed from our body, therefore ice appear more cold than water at 0°C.

Question 30.
Burning due to steam is more severe than that of boiling water, why?
Answer:
When steam vapour gets contact with the skin, then first it gets converted to water of 100°C. In this process, it liberates 536 calories of heat. This extra heat is not present in boiling water. Since steam has more latent heat, hence, it produces severe bums.

Question 31.
The sand near the bank of river becomes colder than water, why?
Answer:
The specific heat of sand is very low, therefore it gains heat soon and radiate heat soon. While the specific heat of water is very high. Hence, the sand becomes colder than water.

Question 32.
Atmospheric temperature reduces after icefall. Why?
Answer:
Due to high value of latent heat, when the ice start melting it takes heat from the atmosphere, hence atmospheric temperature reduces after icefall.

Question 33.
Why the specific heat of the coolent used in nuclear reactor is high?
Answer:
Due to high specific heats coolent is able to absorb more heat in nuclear reactor.

Question 34.
At boiling point of a liquid, how much is the specific heat ?
Answer:
We know,
ΔQ = m.sΔT
or
s = \(\frac{\Delta Q}{m \cdot \Delta T}\)
At boling point, change in temperature
ΔT = o
s = \(\frac{\Delta Q}{m .0}\) = \( \frac{\Delta Q}{0}\) = ∞
∴ At boiling point, specific heat of a liquid is infinity.

Question 35.
Name the methods of transmission of heat.
Answer:
There are three methods of transmission of heat:

1. Conduction,
2. Convection and
3. Radiation.

Question 36.
What do you understand by conduction?
Answer:
In this process the particle which is heated first gives a part of its energy to its adjacent particles. The particles undergo simple harmonic motion about their mean position and the heat is transmitted from one particle to the next. Solids are heated by this process only.

Question 37.
What do you mean by convection?
Answer:
In this mode of flow the particles of substance absorb heat and leave their place or get displaced. Liquids and gases are heated by this method.

Question 38.
What is radiation?
Answer:
In this method heat is transmitted from one body to another body without any medium or without affecting the medium. Heat from sun reaches to earth by radiation.

Question 39.
What is meant by variable state in conduction?
Answer:
When one end of a rod of a conductor is heated then temperature of the different parts of the rod go on increasing slowly. This state is called variable state of temperature.

Question 40.
What is meant by steady-state?
Answer:
When one end of a conductor is heated then initially the temperature of its different parts go on increasing slowly but a stage comes when the temperature of each part of the conductor becomes constant, though the temperature of different parts are different. This state of temperature is called steady state.

Question 41.
What is temperature gradient? What type of quantity is it? Write the unit.
Answer:
Temperature gradient: Fall of temperature per unit length is called temperature gradient.
Let temperature of two surfaces of a conductor at distances x and x + Δx are θ and θ- Δ θ.
∴ Temperature gradient = \( \frac{(\theta-\Delta \theta)-\theta}{(x+\Delta x)-x}\)
Negative sign shows that as the distance increases the temperature decreases. Temperature gradient is a vector quantity and its unit is °C × m ^-1.

Question 42.
Define coefficient of thermal conductivity. Write its unit and find out its dimensional formula.
Or
Define the coefficient of thermal conductivity and obtain expression for it.
Answer:
The coefficient of thermal conductivity is defined by the amount of heat, flowing per second in steady state through the rod of length 1 long and area of cross-section 1 m², with a unit temperature difference between the opposite faces.

The quantity of heat, flowing per second through a unit cube having unit temperature difference between opposite faces, during steady-state.
i.e., Q = \(\frac{K A\left(\theta_{1}-\theta_{2}\right) t}{d}\)
K = \(\frac{Q d}{A\left(\theta_{1}-\theta_{2}\right) t}\)
Unit: Its SI unit is \(\frac{\text { joule } \times \mathrm{m}}{\mathrm{m}^{2} \mathrm{~K} \mathrm{sec}}\) = J m^-1K ^-1sec ^-1
But, joule /sec is watt.
Other unit is watt × m^-1 × K^-1.

Dimensional formula :\( \frac{\left[\mathrm{M} \mathrm{L}^{2} \mathrm{~T}^{-2}\right][\mathrm{L}]}{\left[\mathrm{L}^{2}\right][\theta][\mathrm{T}]} \) = \( \left[\mathrm{MLT}^{-3} \theta^{-1}\right] \).

Question 43.
What do you mean by thermal resistance? Write its unit and find out its dimensional formula.
Answer:
The resistance offered by the body in the flow of heat is called thermal resistance,
Thermal resistance = \( \frac{d}{\mathrm{~K} A} \) = \( \frac{\left(\theta_{1}-\theta_{2}\right) t}{Q}\)
Unit: Its SI unit is \( \frac{\mathrm{K} \mathrm{sec}}{\mathrm{J}}\) = K sec J^-1 = K watt^-1

Dimensional Formula: [Thermal resistance] = \(\frac{[\theta][\mathrm{T}]}{\left[\mathrm{ML}^{2} \mathrm{~T}^{-2}\right]}\) = \(\left[\mathrm{M}^{-1} \mathrm{~L}^{-2} \mathrm{~T}^{3} \theta\right] \) .

Question 44.
What is meant by thermal diffusivity?
Answer:
Thermal diffusivity: The ratio of thermal conductivity and thermal capacity of unit volume of a substance is called thermal diffusivity of the substance.
Thermal diffusivity = \( \frac{K}{\rho S} \).

Question 45.
The ice blocks are covered with saw dust. Why?
Answer:
Sawdust is bad conductor of heat. Hence, the heat of atmosphere does not conduct through sawdust and thus ice does not melt soon.

Question 46.
Woollen clothes are used in winter. Why?
Answer:
Woollen clothes have fine pores which are filled with air. Air and woollen clothes are bad conductor of heat. There it does not allow the heat to escape from the body to atmosphere. Thus, it keeps body warm.

Question 47.
A woollen blanket keeps the body warm and also prevent the ice from melting. Why?
Answer:
Air is insulator which is filled between the fibres of blanket. Therefore, blanket does not allow the heat of body to radiate into the atmosphere as well as the heat of atmosphere could not reach to ice. Thus, it keeps the body warm and protect the ice from melting.

Question 48.
State two properties of thermal radiation.
Answer:

1. Thermal radiations are electromagnetic waves.
2. They do not affect the medium through they pass.

Question 49.
Differentiate between light and heat radiations.
Answer:
Difference between Light and Heat radiations :

Light radiation	Heat radiation
1. The wavelength of light rays is very small i. e., between 4 × 10-5 cm to 8 × 10-5cm.	The wavelength of heat radiation is long i.e., between 8 × 10-5cm to 0.04 cm.
2. It falls in the visible region of electromagnetic spectrum.	It falls in the invisible region of electromagnetic spectrum.
3. Heating effect is negligible.	Heating effect is greater.

Question 50.
What is emissive power? Write its SI unit.
Answer:
Emissive power: The amount of heat radiated per unit area per unit time, is called emissive power of the surface.
If int sec, through area A, amount of heat radiated is Q, then
Emissive power, e = \(\frac{Q}{A \times t}\)
SI unit: joule × m^-2 × s^-1 or watt × m^-2.

Question 51.
What is absorptive power of surface?
Answer:
The ratio of amount of heat radiation absorbed by a surface in a given time and total amount of heat incident is called absorptive power of that surface.
i.e., a = \(\frac{q}{Q}\)
Where, q = Amount of heat radiation absorbed and Q = Amount of heat radiation incident.

Question 52.
Define perfectly black body.
Or
What do you mean by perfectly black body?
Answer:
A perfectly black body is one which absorbs completely all the thermal radiation incident on it and does not reflect or transmit any fraction of it. Emissivity for this body is 1.
No such body exists in nature, but in practice we consider lamp black and platinum black as perfectly black body.

Question 53.
State Stefan’s law of black body radiation.
Answer:
Stefan’s law : The total radiant energy emitted per second per unit surface area of a black body is proportional to the fourth power of the absolute temperature.
If the radiant energy per second per unit area is E and absolute temperature of the surface is T, then
E∝T⁴
or E = σT⁴
Where σ is called Stefan’s constant.
If the area of a black body is A and its temperature is T, then the radiant energy per second will be
E= σ AT⁴.

Question 54.
State Newton’s law of cooling.
Answer:
The rate of cooling of a body is proportional to the temperature difference of the average temperature of the body and surroundings provided the temperature difference between the source and surrounding is very less.

Question 55.
State Kirchhoff’s law of radiation.
Answer:
According to Kirchhoff’s law, at a given temperature the ratio of emi¬ssive power and absorptive power for a given wavelength is equal to the emissive power of black body for the same wavelength.
If the emissive power of a surface for wavelength λ is e_λ and absorptive power is a_λ, then
\(\frac{e_{\lambda}}{a_{\lambda}}\) = E_λ
Where, E_λ is emissive power of black body.

Question 56.
If a red glass is heated up to high temperature and placed in a dark room, then it appears green. Why?
Answer:
A body appears red because the body absorbs all the colours but red. It reflects red only thus it appears red. The emissive power of a red body is maximum for the green colour. Thus, it appears green, when heated up to a high temperature.

Question 57.
The cloudy nights are warmer than the day. Why?
Answer:
The clouds reflect the heat radiation waves, which are radiated from the earth. Thus, the temperature of earth does not fall. Hence, the nights become hot.

Question 58.
Deserts are very hot during the day and very cold during the night Why?
Answer:
We know that good absorber are good radiators. Sand is good absorber, during the day time the sand absorbs heat and becomes very hot. But, during the nights it radiates heat soon and becomes cold.

Question 59.
State three uses of heat radiation.
Answer:

• In the cold country, the hot water is flown through the metallic pipes to warm the rooms.
• The walls and roof of greenhouse are made up of glass.
• To decrease the temperature of hot substance, it is spread over, thus it becomes cold soon.

Question 60.
In a chilled weather, animals curl themselves. Why?
Answer:
The rate of radiation of heat is directly proportional to the area of the surface. The sphere has the minimum surface area for a given volume. Thus, by curling, the animals reduce the area through which the heat is radiated and they keep the body warmer.

Question 61.
State two applications of Newton’s law of cooling.
Answer:

1. The hot water cools soon than the warm water.
2. When milk is added to tea, the rate of cooling decreases.

Question 62.
Hot water cools soon than the warm water. Why?
Answer:
The rate of cooling is directly proportional to the difference of mean temperature of the body and the temperature of the surrounding. The difference of temperature of hot water and surrounding is greater than that of warm water, therefore hot water cools soon.

Question 63.
On what factors does the loss of heat energy per second depend?
Answer:

• Nature of the surface,
• Area of the surface,
• Temperature difference between the temperature of the surface and surrounding.

Question 64.
The walls and roofs of greenhouse are made of glass, why?
Answer:
Glass has the property, that it transmits the heat radiation of high temperature but absorbs the heat radiations of low temperature. Hence, the glass allows the radiations coming from the sun, but it does not allow the radiations waves coming from the plants. Thus, the room remains warm.

Question 65.
In summer the hills remains cold, why?
Answer:
The reasons are :

• On the hill the air is thin and dust particles are less, thus radiations are absorbed less.
• The sun rays are reflected due to inclined surface.

Question 66.
The outer surface of cooking utensils are made black and inner bright Why?
Answer:
The black surfaces are good absorber of heat. Thus, more heat is absorbed and bright surface reflects the heat into the cooking pot. Thus, more heat is given to the food, which cooks the food soon.

Question 67.
The stars X and Y are radiating yellow and blue rays respectively. Which has greater temperature?
Answer:
By Wien’s displacement law, λ_m ∝\(\frac{1}{T}\). As the wavelength of blue rays is lesser
than that of yellow rays, hence, the temperature of the Y-star will be greater than X-star.

Question 68.
Whenever an object is heated, why does it appear red first?
Ans. According to Wien’s law, that λ_m T = constant, the maximum wavelength is for the red light in the visible spectrum. Hence, for ordinary temperatures i.e., for less T, λ_m must be more. Hence, an object appears red. As temperature increases, wavelength decreases and the emitted colour will shift towards violet.

Question 69.
A teacup has shining surface whereas the bottom of cooking pot is blackened, why?
Answer:
The shining surface is a good reflector of heat radiation, whereas the blackened surface is good absorber. The shining surface reflects the heat into the cup and maintains the tea hot. for long time, outer surface of cup does not radiate heat. Black surface of cooking pot absorbs more heat and makes the cooking fast.

Question 70.
The steady-state is necessary for the different substances to compare their conductivity. Why?
Answer:
In the steady-state the heat is not absorbed by any part of the body. Hence, the amount of heat given to one end transmit through the body completely. Therefore, the substance are brought in the steady-state.

Question 71.
In Searl’s apparatus to find the conductivity of a rod, the holes are filled with some mercury then thermometer are fixed. Why?
Answer:
The mercury is good conductor of heat therefore, it gives good contact between the bulb of thermometer and the surface of rod.

Question 72.
Eskimos built double-walled houses of snow. Why?
Answer:
The air is filled between the walls, which is bad conductor of heat. Ice itself is bad conductor of heat. Hence, the heat of the room does not transmit to the atmosphere.

Question 73.
In summer, in the evening when the temperature of outside the room decreases, the temperature of the inner surface of room remains at higher temperature. Why?
Answer:
After sunset, the temperature of the atmosphere decreases fast. The wall is bad conductor of heat, hence the heat of room conduct slowly and the room temperature remains higher than the atmosphere.

Question 74.
When a tumbler of thick glass is filled with hot tea it breaks down. Why?
Answer:
Glass is a bad conductor of heat. When hot tea is poured into the tumbler, the temperature of inner surface increases and the surface expands. While the outer surface remains at same position. Hence, the tumbler breaks down.

Thermal Properties of Matter Class 11 Important Questions Short Answer Type 

Question 1.
Establish the relation between coefficient of linear expansion and coefficient of superficial expansion.
Or
Prove that coefficient of superficial expansion is double of coefficient of linear expansion.
Answer:
Let one side of a square lamina be l.Its temperature is increased through Δt so that each side increases by Δl.
∴ Initial area = l²
and Final area = (l + Δl)²
∴ Change in area, ΔA = (l + Δl)² -l²
or =l² +2l.Δl + Δl² -l²
or = 2lΔl+ Δl²

Since Δl is a small quantity, hence Δl² can be neglected.
∴ ΔA=2l.Δl.
Now, coefficient of superficial expansion,
β = \(\frac{\Delta A}{A \times \Delta t}\)
or
β = \(\frac{2 l \Delta l}{l^{2} \Delta t}\) = 2. \(\frac{\Delta l}{l \Delta t}\)
or
β = 2α (∵ α = \(\frac{\Delta l}{l \Delta t}\) )

Question 2.
Establish the relation between coefficient of linear expansion and coefficient of volume expansion.
Or
Prove that coefficient of volume expansion is three times of coefficient of linear expansion.
Answer:
Consider a cube of side of length l. The temperature of cube is increased by, Δt so that the length of the cube becomes (l + Δl).

Now, Initial volume = l³
and Final volume = (l + Δl)³
∴ Change in volume, ΔV = (l + Δl)³ — l³
= l³ +3l²Δl + 3l.Δl² + Δl³ -l³ = 3l²Δl + 3l Δl2 + Δl3
Since, Δl is a small quantity, therefore powers of Δl can be neglected.
∴ ΔV = 3l²Δl .

Now, coefficient of volume expansion,
γ = \(\frac{\Delta V}{V \times \Delta t}\)
= \(\frac{3 l^{2} \Delta l}{l^{3} \Delta t}\)
γ = 3. \(\frac{\Delta l}{l \Delta t}\) = 3α,
( ∵ α = \(\frac{\Delta l}{l \Delta t}\)).

Question 3.
Distinguish between specific heat and thermal capacity.
Answer:
Difference between Specific heat and Thermal capacity :

Specific heat	Thermal capacity
1. The amount of heat required to raise the temperature of 1 gm sub- temperature of a substance through 1°C called specific heat of the substance.	The amount of heat required to raise the is stance through 1°C is called thermal capacity.
2. Its SI unit is joule x kg-1 x K-1.	Its SI unit is joule x K-1.
3. Its dimensional formula is [M°L2T-2θ-1].	Its dimensional formula is [ML2T-2θ-1].

Question 4.
Give an application of anomalous expansion of water.
Answer:
The volume of water decreases when it is heated from 0°C,to 4°C and then the volume increases, above 4°C. Hence, the density of water at 4°C is maximum. In the cold countries when the temperature of the atmosphere decreases, the temperature of the water of the lake also decreases.

Now, weigh the calorimeter with stirrer. Fill it with water about 2/3 and weigh it again. Find the initial temperature of water.

When the temperature reaches to 4°C, the density of the water becomes maximum. Then the ice begins to float on the surface, preventing the heat of water to go out into the atmosphere. Hence, water remains at 4°C at bottom. Thus, the animals survive in this water of 4°C.

Question 5.
Describe the method to find out the specific heat of a solid.
Answer:
(i) Method: Take the solid and measure its mass by physical balance and place it inside the steam chamber with the help of a thread. Fix a thermometer so that the bulb of thermometer touches the solid. Then start flowing the steam through the steam chamber.

Now, weigh the calorimeter with stirrer. Fill it with water about 2/3 and weigh it again. Find the initial temperature of water. When the temperature of the solid becomes constant for sometimes, then remove the wooden screen and move the calorimeter below the steam chamber. Then drop the solid into calorimeter carefully. Close the lid and stirr it slowly. Measure the temperature of the mixture when it becomes constant.

(ii) Observation:

•  Mass of solid = m gm
• Mass of calorimeter + stirrer = m₁ gm
• Mass of calorimeter + stirrer + water = m₂ gm
• Initial temperature of water = t₁°C
• Temperature of solid = t₂°C
• Temperature of mixture = t₃°C
• Specific heat of calorimeter = S₁ (known).

(iii) Calculation : Let the Specific heat of solid = s
Mass of water = (m₂ – m₁) gm
∴ Heat given by the solid = Mass × Specific heat × Temperature difference = m.s.(t2-t3)
Heat taken by calorimeter =m₁s₁ (t₃ – t₁)
and Heat taken by water = (m₂ – m₁ ).(t₃– t₁)

Now, by the principle of calorimetry, we have
Heat given = Heat taken
∴ ms(t₂ -t₃) = m₁s₁(t₃ -t₁)+(m₂ – m₁ ) (t₃-t₁)
∴ S = \(\frac{m_{1} s_{1}\left(t_{3}-t_{1}\right)+\left(m_{2}-m_{1}\right)\left(t_{3}-t_{1}\right)}{m\left(t_{2}-t_{3}\right)} \)
Thus, specific heat can be calculated.

Question 6.
Write difference between heat and temperature.
Answer:
Difference between Heat and Temperature :

Heat	Temperature
1. Heat is a form of energy which is due to motion of molecules of the substance.	Temperature is a physical quantity tells the direction of flow of heat when two bodies are in contact with each other.
2. Heat measurement is based on the principle of calorimetry.	Temperature measurement is based on the principle of thermometry.
3. Two bodies having same heat, might have different temperatures.	Two bodies having same temperature, might have different heat.
4. Practically it is measured in terms of calorie. Its SI unit is joule.	Practically it is measured in terms of degree centigrade. Its SI unit is kelvin.
5. Quantity of heat of a body depends on its mass, temperature and nature.	Temperature of a body depends on its quantity of heat.

Question 7.
On what factors does the amount of heat-conducting through a rod in steady state depend?
Or
In steady stae, find the expression for the amount of heat flowing through a rod.
Answer:
In steady-state the amount of heat Q flowing through one face to another is :
(i) Directly proportional to the area of cross-section A i.e.,
Q ∝ A
(ii) Directly proportional to the temperature difference ( θ₁ – θ₂) of the faces i.e.,
Q ∝ θ₁ -θ₂
(iii) Directly proportional to the time t of flowing heat i.e.,
Q ∝ t
(iv) Inversely proportional to the distance between the faces i.e.,
Q ∝ \(\frac{1}{d} \)
Combining all these, we get
Q ∝\(\frac{A\left(\theta_{1}-\theta_{2}\right) t}{d}\)
∴ Q = K \(\frac{A\left(\theta_{1}-\theta_{2}\right) t}{d}\)

Where, K is a constant called thermal conductivity or coefficient of thermal conductivity of the substance.

Question 8.
Differentiate between steady-state and variable state.
Answer:
Difference between Steady state and Variable state :

Steady state	Variable state
1. Whenever a conducting rod is heated, then the temperature of various parts goes on increasing and after sometime, its temperature becames constant, although the temperature of various parts may be different.	This is called steady state. Whenever a conducting rod is heated at one end, then the temp, of various parts goes on increasing. This is called variable state.
2. In this state, no part of the conducting rod absorbs heat.	In this state each part of the rod absorbs heat.
3. The rate of flow of heat depends on thermal conductivity and not on thermal capacity.	The rate of flow of heat depends on thermal conductivity and capacity.

Question 9.
State the properties of heat radiation.
Answer:
Properties :

• Heat radiations are electromagnetic waves.
• Heat radiations travel in straight line and can travel through vacuum also.
• Thermal radiations travel with the speed of light i.e., 3 × 10¹⁰ cm × s^-1 and transmit in the form of radiant energy.
• Like light, they follow the inverse-square law.
• They follow the laws of reflection, refraction, polarization etc.
• They do not affect the mediums through they pass,but the medium which stops the radiation, are heated up.

Question 10.
State Newton’s law of cooling? What are the limitations of this law? Establish the relation between the temperature difference and rate of cooling. What is cooling curve.
Or
Describe the Newton’s law of cooling, deduce the formula and write its limitations.
Answer:
Newton’s law of cooling: According to this law, the rate of cooling is directly proportional to the difference of mean temperature of the body and the temperature of surroundings.

Limitations:

• The temperature difference between the body and surrounding should not be more than 30°C.
• The loss of heat should be only by radiation.
• The temperature of the surrounding and nature of body should not be changed. Let a substance be cooled from θ₁ °C to θ₂ °C in t sec and temperature of surrounding is θ .

∴ Rate of cooling = \(\frac{\theta_{1}-\theta_{2}}{t}\)
And Mean temperature of the substance = \(\frac{\theta_{1}+\theta_{2}}{2}\)
∴ Temperature difference = \(\frac{\theta_{1}+\theta_{2}}{2} \) – θ
Hence by Newtons law \(\frac{\theta_{1}-\theta_{2}}{t}\) ∝( \(\frac{\theta_{1}+\theta_{2}}{2} \) – θ)
∴ \(\frac{\theta_{1}-\theta_{2}}{t}\) = K ( \(\frac{\theta_{1}+\theta_{2}}{2} \) – θ)
Where, K is constant.
Cooling curve: The graph plotted between rate of cooling and temperature difference is called cooling curve. It is a straight line.

Question 11.
Derive the Newton’s law of cooling by Stefan’s-Boltzmann law.
Answer:
Let the temperature of a black body is T and temperature of surrounding is T₀. Now by Stefan’s-Boltzmann law, we have
Radiant energy per second per unit area,
E =σ (T₄ – T₀⁴)
If the temperature difference is ΔT, then

T₀ and σ are constant.
E ∝ ΔT
Hence, the rate of radiation of heat energy is directly proportional to the temperature difference.

Question 12.
Define coefficient of thermal conductivity. Write its unit and find out its dimensional formula.
Or
Define the coefficient of thermal conductivity and obtain expression for it.
Answer:
The coefficient of thermal conductivity is defined by the amount of heat, flowing per second in steady-state through the rod of length 1 m long and area of cross-section lm2, with a unit temperature difference between the opposite faces.

The quantity of heat, flowing per second through a unit cube having unit temperature difference between opposite faces, during steady state.
i.e., Q = \(\frac{K A\left(\theta_{1}-\theta_{2}\right) t}{d}\)
∴ K = \(\frac{Q d}{A\left(\theta_{1}-\theta_{2}\right) t}\)
Unit: Its SI unit is \(\frac{\text { joule } \times \mathrm{m}}{\mathrm{m}^{2} \mathrm{~K} \mathrm{sec}}\) = Jm^-1K^-1sec^-1
But, joule/sec is Watt
∴ Other unit is Watt × m^-1×K^-1

Dimensional Formula :[K] = \(\frac{\left[\mathrm{M} \mathrm{L}^{2} \mathrm{~T}^{-2}\right][\mathrm{L}]}{\left[\mathrm{L}^{2}\right][\theta][\mathrm{T}]} \) = [MLT³θ^-1].

Question 13.
What do you mean by thermal resistance? Write its unit and find out its dimensional formula.
Answer:
The resistance offered by the body in the flow of heat is called thermal resistance,
Thermal resistance = \(\frac{d}{K A}\) = \(\frac{\left(\theta_{1}-\theta_{2}\right) t}{Q}\)
Unit: Its SI unit is =\(\frac{\mathrm{K} \mathrm{sec} .}{\mathrm{J}}\) = K sec^-1 = K watt^-1

Dimensional formula:
[Thermal resistance] = \(\frac{[\theta][T]}{\left[\mathrm{M} \mathrm{L}^{2} \mathrm{~T}^{-2}\right]}\) = [M^-1L^-2T³θ].

Thermal Properties of Matter Class 11 Important Questions Long Answer Type

Question 1.
Prove that for thermal expansion in solid :
α : β : γ= 1 : 2 : 3.
Answer:
Let one side of a square lamina be l.Its temperature is increased through Δt so that each side increases by Δl.
∴ Initial area = l²
and Final area = (l + Δl)²
∴ Change in area, ΔA = (l + Δl)² -l²
or =l² +2l.Δl + Δl² -l²
or = 2lΔl+ Δl²

Since Δl is a small quantity, hence Δl² can be neglected.
∴ ΔA=2l.Δl.
Now, coefficient of superficial expansion,
β = \(\frac{\Delta A}{A \times \Delta t}\)
or
β = \(\frac{2 l \Delta l}{l^{2} \Delta t}\) = 2. \(\frac{\Delta l}{l \Delta t}\)
or
β = 2α (∵ α = \(\frac{\Delta l}{l \Delta t}\) )

Consider a cube of side of length l. The temperature of cube is increased by, Δt so that the length of the cube becomes (l + Δl).

Now, weigh the calorimeter with stirrer. Fill it with water about 2/3 and weigh it again. Find the initial temperature of water. When the temperature of the solid becomes constant for some times, then remove the wooden screen and move the calorimeter below the steam chamber. Then drop the solid into calorimeter carefully. Close the lid and stirred it slowly. Measure the temperature of the mixture when it becomes constant.

(ii) Observation :

• Mass of solid =m gm
• Mass of calorimeter + stirrer = m₁ gm
• Mass of calorimeter + stirrer + water = m₂ gm
• Initial temperature of water = t₁°C
• Temperature of solid = t₂°C
• Temperature of mixture = t₃°C
• Specific heat of calorimeter = S₁ (known).

(iii) Calculation : Let the Specific heat of solid = s
Mass of water = (m₂ – m₁) gm
∴ Heat given by the solid = Mass × Specific heat × Temperature difference
= m.s.(t₂-t₃)
Heat taken by calorimeter = m₁S₁(t₃ – t₁)
and Heat taken by water = (m₂ – m₁).(t₃– t₁)
Now, by the principle of calorimetry, we have
Heat given = Heat taken
∴ ms(t₂ – t₃) =m₁s₁(t₃ – t₁) +(m₂ – m₃) (t₃ – t₁)
∴ S = \(\frac{m_{1} s_{1}\left(t_{3}-t_{1}\right)+\left(m_{2}-m_{1}\right)\left(t_{3}-t_{1}\right)}{m\left(t_{2}-t_{3}\right)} \)
Thus, specific heat can be calculated.

Question 2.
Describe Newton’s experiment to prove the law of cooling on following points:
(i) Labelled diagram of apparatus, (ii) Method and (iii) Cooling curve.
Answer:
(i) Apparatus : C = Calorimeter, S = Stirrer, T= Thermometer, V= Vessel.
(ii) Method: Take some water in a beaker and heat it. Then put hot water into calorimeter about 2/3 of it. When the temperature difference is nearly 30°C, then stir the water slowly and after every half minute record the temperature of the water, with the help of stop watch.

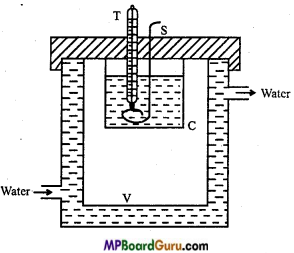
Then, draw graph between temperature and time. This curve is called cooling curve.
On the cooling curve take some points A, B, C, D,… Now, for each pair of points find the rate of cooling and temperature difference. For example, let the temperature of A and B points are θ1 and θ2°C.
∴ Rate of cooling = \(\frac{\theta_{1}-\theta_{2}}{t}\)
and Temp. difference = \(\frac{\theta_{1}-\theta_{2}}{2}\) – θ
Where, θ is the temperature of surroundings.

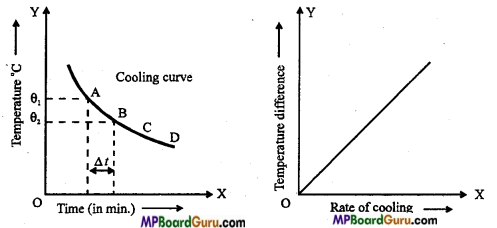
Hence, the graph between rate of cooling and temperature difference is a straight line. Thus, rate of cooling is directly proportional to temperature difference.

Question 3.
Describe the experiment to find conductivity of a rod by Searl’s apparatus on following points:
(i) Labelled diagram of apparatus, (ii) Procedure, (iii) Observation, (iv) Calculation and (v) Precautions.
Answer:
(i) Searl’s apparatus :

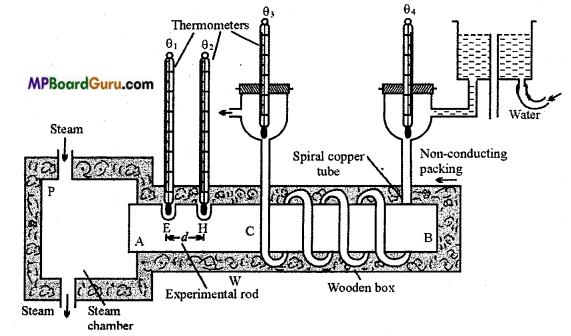
(ii) Procedure: First of all water is regulated through the copper tube, slow and continuous. Then steam is passed through the steam chamber. When the temperature of all the four thermometers become constant, steady state is achieved. Note the reading of ther mometer and with the help of stop watch collect the water in a weighed beaker for a particular time.

(iii) Observation :

• Area of cross-section of rod = A cm²
• Distance between the holes on rod = d cm
• Temperature of first thermometer = θ₁ °C
• Temperature of second thermometer = θ₂ °C
• Initial temperature of water = θ₃ °C
• Final temperature of water = θ₄°C
• Mass of water collected in t sec = m gm

(iv) Calculation: We know that,
Q = \(\frac{K A\left(\theta_{1}-\theta_{2}\right) t}{d}\)
or
K = \(\frac{Q \cdot d}{A\left(\theta_{1}-\theta_{2}\right) t}\)
Now, Q = Heat taken by water
= m × 1 × (θ₄ – θ₃) = m(θ₄ – θ₃)
∴ K = \(\frac{m\left(\theta_{4}-\theta_{3}\right) d}{A\left(\theta_{1}-\theta_{2}\right) t}\)
Hence, K can be calculated.

(v) Precautions :

• The steam should be passed after regulating the flow of water.
• The flow of water should be slow and continuous.
• When the temperature of all the four thermometers becomes constant, then only the readings should be taken.

Question 4.
Write the differences between conduction, convection and radiation.
Answer:
Difference between Conduction, Convection and Radiation :

Conduction	Convection	Radiation
1. In this mode, heat flows from one particle to another particles. The particles do not leave their places.	1. The particles receive the heat and move away.	1. In this mode, heat travels in a straight line.
2. Medium is necessary for conduction.	2. Medium is necessary for convection.	2. Medium is not required.
3. Solids are heated by conduction.	3. Liquids and gases are heated by convection.	3. Heat is given to the bodies directly without affecting the medium.
4. The flow is in zig-zag manner.	4. The path may be zig-zag or curved.	4. The path is always straight line.

Thermal Properties of Matter  Class 11 Important Numerical Questions

Question 1.
The triple point of neon and carbon dioxide are 24.57 K and 216.55 K respectively. Express these temperature on the Celsius and Fahrenheit scales. (NCERT)
Solution:
Here, Triple point of neon,
C = K-273
For neon,
C = 24-57 – 273 = -248-43°C
For C02,
C = 216-55-273=-56-45°C Relation between Kelvin scale and Fahrenheit scale:
\(\frac{\mathrm{K}-273}{5}\) = \(\frac{\mathrm{F}-32}{9}\)
or
F =\(\frac{9}{5}\) (K – 273) + 32
For neon,
F =\(\frac{9}{5}\) (24-57-273)+ 32
⇒ F = \(\frac{9}{5}\) × (-248.43) + 32
⇒ F =-447-2+32 = -415-2°
For CO₂,
F = \(\frac{9}{5}\) (K-273) + 32
⇒ F = \(\frac{9}{5}\) (216.55-273)+ 32
⇒ F = \(\frac{9}{5}\) × (-56.45) + 32
∴ F = -101.61 + 32 = -69.61° .

Question 2.
Two absolute scales A and B have triple points of water defined to be 200 A and 350 B. What is the relation between T_A and T_B ? (NCERT)
Solution:
Here, triple point of water on absolute scale A = 200 A and triple point of water on obsolute scale B = 350 B
Triple point of water T = 273.16 K
According to question 200 A = 350 B = 273.16 K
or
1A = \(\frac{273 \cdot 16}{200}\) K and 1B = \(\frac{273 \cdot 16}{350}\) K
As T_A and T_B are at the same temperature,
\(\frac{273 \cdot 16}{200}\) T_A = \(\frac{273 \cdot 16}{350}\) T_B
or T_B = \(=\frac{350}{200} \) T_A
⇒ T_B = \(\frac{7}{5}\) T_A.

Question 3.
A steel tape 1 m long is correctly calibrated for a temperature of 27°C. The length of steel rod measured by this tape is found to be 63’0 cm on a hot day when the temperature is 45°C. What is the actual length of the steel rod on that day? What is the length of the same steel rod on a day when temperature is 27°C? Coefficient of linear expansion of steel a= 1.2 × 10^-5 K-1. (NCERT)
Solution:
The steel tape is calibrated at 27°C is correct. That is the length of 100 cm steel tape has correct magnitude 100 cm.
When the temperature raises from 27°C to 45°C then length of steel tape.
l_t =l₀+ l₀ αt
l_t = 100 + 100× 1.2× 10^-5 (45-27)
l_t =100 + 100 × 1.2 × 10^-5 × 18
l_t =100 + 0.0216 = 100.0216 cm.

At 45°C the measure of 63 cm. steel tape.
= \(\frac{100 \cdot 0216}{100}\) × 63
= 63.0136 cm.
If the tape is measured at 27°C then its measure is 63 cm.

Question 4.
A brass boiler has a base area of 0.15 m² and thickness 1.0 cm. It boils water at the rate of 6.0 kg/min, when placed on a gas stove. Estimate the temperature of the part of the flame in contact with the boiler. Thermal conductivity of brass 109 Js^-11m^-1°C^-1 . (Heat of vaporization of water = 2256 × 10³ J/kg.) (NCERT)
Solution:
Let the temperature of flame of source be T°C .
Given: K = 109 J/s.m°C = 109 × 10^-2 J/s.cm°C
A = 0.15 m²; d= 1 cm = 10^-2m
T₁-T₂ =(T-100)° C ,
t= 1 minute = 60 sec
m = 6 kg, L = 2256 J/gm
Q = \(\frac{109 \times 0 \cdot 15 \times(T-100) \times 60}{1 \times 10^{-2}} \)
= 98100(T -100)
Now, Q = mL = 6 ×2256 × 10³
∴ 98100(T – 100) = 6 × 2256 × 10³
or
T = \(\frac{6 \times 10^{3} \times 2256}{98100} \) + 100
= 138+ 100 = 238° C.

Question 5.
A body cools from 80°C to 50°C in 5 minutes. Calculate the time it takes to cool from 60°C to 30°C. The temperature of the surrounding is 20°C. (NCERT)
Solution:
According to Newton’s law,
\(\frac{\theta_{1}-\theta_{2}}{t}\) = K (\(\frac{\theta_{1}+\theta_{2}}{2}\) – θ

Question 6.
At what temperature °C and F are equal to each other.
Solution:
Let at x degree temperature of both °C and °F are equal.
∴ \(\frac{\mathrm{C}}{5} \) = \(\frac{\mathrm{F}-32}{9}\)
\(\frac{x}{5}\) = \(\frac{x-32}{9}\)
∴9x = 5x – 160
or 9x – 5x = -160
4x = -160
∴ x =\(\frac{-160}{4}\) = -40
i.e., -40°C = -40°F.

Question 7.
Volume of a brass ball at 0°C is 50 cm³ and at 100°C is 50.25 cm³. Find out coefficient of linear expansion.
Solution:
Given, V₀ = 50 cm3, V₁₀₀ = 50.25 cm³
ΔV = 50.25-50, =0.25 cm³ and Change in temperature ΔT = 100° C – 0° C = 100° C
∴ γ = \(\frac{\Delta V}{V \cdot \Delta T}\)
or
γ = \(\frac{0 \cdot 25}{50 \times 100}\) = 5 × 10^-5
Also, γ = 3α
∴ α = \(\frac{\gamma}{3}\) = \(\frac{5 \times 10^{-5}}{3}\)
or = 1.7 × 10^-5/°C.

f

Question 8.
Ratio of density of two metal A and B is 1 : 3. On giving equal amount of heat on equal volume of A and B, ratio of change in temperature is 2 :1. Find out ratio of specific heats.
Solution:
Given, d₁ : d₂ = 1 : 3, V₁ = V₂, Q₁ = Q₂, θ₁ : θ₂ = 2:1
Heat given to metal A, Q₁ = Mass × Specific heat × Change in temperature.
Q₁ =V₁d₁s₁θ₁
Heat given to metal B,Q₂ =Mass × Specific heat × Change in temperature.
Q₂ = V₂d₂s₂θ₂
Since Q₁ = Q₂
∴ V₁d₁s₁θ₁ = V₂d₂s₂θ₂
or
\(\frac{s_{1}}{s_{2}}\) = \(\frac{V_{2}}{\mathrm{~V}_{1}} \times \frac{d_{2}}{d_{1}} \times \frac{\theta_{2}}{\theta_{1}} \)
= 1 ×\(\frac{3}{1} \times \frac{1}{2}\) = \(\frac{3}{2} \)
i.e., s₁:s₂ = 3:2

Question 9.
Temperature of 1 kg of water is 60°C. It is mixed in a water of 1 kg at 40°C. What will be the temperature of mixture ? Specific heat of water = 1 calorie/gram °C.
Solution:
Let the temperature of the mixture be t°C.
Heat given by hot water =ms Δt = 1000× 1 × (60-t)calorie.
Heat taken by cold water = ms Δt = 1000 × 1 × (t – 40) calorie.
According to principle of mixture.
1000 × 1 × (60-t)= 1000 × 1 × (t-40)
∴ 60-t = t-40
or
2t = 100
or
t= 50°C.

Question 10.
What will be the resultant temperature when 5-gram ice at 0°C is mixed in 50 gram water at 30°C. Letent heat of ice = 80 calorie/gm.
Solution:
Let the resultant temperature be t°C.
Heat given by ice = Heat taken by water 5 × 80 + 5 × 1×(t-0) = 50× 1 ×(30-t)
or
400 + 5t = 1500-50t
or
55t = 1500-400= 1100
t =\(\frac{1100}{55}\) = 20°C.

Question 11.
How much heat is required to change 0°C of 10 gm ice into 100°C steam? The latent heat of ice and steam are 80 and 540 cal/gm respectively.
Solution:
Heat required to change 0°C ice to 0°C water = mL = 10×80 = 800 cal
Heat required to change 0°C water to 100°C water = ms ΔT
= 10× 1 × (100-0) = 1000 cal
and Heat required to change 100°C water to 100°C steam = mL = 10 × 540 = 5400cal
Total amount of heat = 800+1000 + 5400 = 7200cal.

Question 12.
Calculate the heat required to convert 15 gm ice at -15°C into steam of 100°C. Given, specific heat of ice is 0.5 cal × gm^-1 × °C^-1. Latent heat of ice is 80 cal × gm^-1 and latent heat of steam is 536 cal × gm^-1.
Solution:
Heat required to convert 15 gm ice at -15°C into 0°C
= mst = 15 × 0.5 × (0+15) = 112.5cal
Heat required to convert 0°C ice into 0°C water
= mL =15 × 80= 1200cal
Heat required to convert 0°C water into 100°C water
= mst = 15 × 1 × (100 – 0) = 1500 cal
Heat required to convert 100°C water into 100°C steam = mL = 15 × 536 = 8040 cal
∴ Total heat = 112.5 + 1200 + 1500 + 8040 = 10852.5 cal.

Question 13.
A piece of metal of mass 50 gm is heated up to 200°C and then put into 400 gm water kept into a beaker. The initial and final temperatures of water are 20°C and 22.4°C respectively. Calculate the specific heat of metal.
Solution:
Heat given by metal = Heat taken by water
or ( 50 × s × (200 – 22.4) = 400 × 1 × (22.4 – 20)
or
8880s = 960
or
s = \(\frac{960}{8880}\) = 0.108
∴ s = 0.108 cal ×gm^-1 × °C^-1

Question 14.
An iron piece of 100 gm is heated up to 10°C. How much water will be riased through 1°C, by the same amount of heat? specific heat of iron is 01 unit.
Solution:
Heat required to raise the temperature of iron piece
= 100× 0.1 × 10 = 100 cal.
Let the temperature of m gm water is raised through 1°C.
∴ Q = msΔT
or 100 = m × 1×1
or m = 100gm.

Question 15.
A wall has two faces of thickness 3 cm and 6 cm respectively and conductivities are K and 3K. Temperature of their outer faces are 20°C and -5°C respectively. Evaluate their common temperature instead state.
Solution:
Given, d₁ = 3cm, d₂= 6cm, K₁ = K,K₂ = 3K, θ₁ = 20°C,θ₂ = -5°C
From formula, θ = \(\frac{K_{1} d_{2} \theta_{1}+K_{2} d_{1} \theta_{2}}{K_{2} d_{1}+K_{1} d_{2}} \)
∴ θ = \(\frac{K \times 6 \times 20+3 K \times 3 \times(-5)}{3 K \times 3+K \times 6} \)
= \(\frac{120 K-45 K}{15 K} \) = \(\frac{75 K}{15 K}\) = 5°C

Question 16.
Two vessels of same shape, length, breadth and height are made of to different metals. They are filled with same amount of ice at 0°C. They talc 25 and 20 minutes respectively for melting the ice completely. Compare the thermal conductivities of two metals.
Solution:
Given:t₁ =25 minutes, t₂ = 20 minutes
Since, equal quantity of ice is filled in two vcssels, hence same quantity of heat is required for melting the ice.
θ = \(\frac{K_{1} A\left(\theta_{1}-\theta_{2}\right) t_{1}}{d}\) = \(\frac{K_{2} A\left(\theta_{1}-\theta_{2}\right) t_{2}}{d} \)
A θ₁ – θ₂ and d are some for both.
∴ K₁t₁ = K₂t₂
or
\(\frac{K_{1}}{K_{2}} \) = \(\frac{t_{2}}{t_{1}}\)
= \(\frac{20}{25} \) = \(\frac{4}{5}\)
∴ K₁ :K₂ = 4:5

Question 17.
The surface area of a box is 5000 cm2 and its thickness is 6 mm. It is filled with the ice at 0°C and kept in a room of temperature 20°C. If 1 kg ice ¡s melted in 20 min. then calculate the conductivity of box. (Latent heat of ice = 80 cal/gm)
Solution:
Given m = 1kg = 1000 gm, L = 80 cal/gm, d = 6 mm = 0.6 cm,
A= 5000 cm2, θ1 – θ2=20 – 0=20°C t=20min = 20 × 60s

Thermal Properties of Matter  Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
Magnitude of absolute zero in Fahrenheit scale is :
(a) 273° F
(b) 459° F
(c) 182° F
(d) 0° F.
Answer:
(b) 459° F

Question 2.
Two system whose temperature is T_A and T_B are in thermal equilibrium, the relation between T_A and T_A is :
(a) T_A > T_B
(b)T_A < T_B
(C) T_A =T_B
(d) None of these.
Answer:
(C) T_A =T_B

Question 3.
A hole is done in a rectangular copper plate, when the plate is heated, then the size of hole will be :
(a) Not change
(b) Increase
(c) Decrease
(d) Nothing can be said.
Answer:
(b) Increase

Question 4.
There is a spherical cavity inside a solid sphere of metal, when the sphere is heated the volume of spherical cavity will:
(a) Increase
(b) Decrease
(c) No change
(d) Shape will change.
Answer:
(a) Increase

Question 5.
If it is coefficient of superficial expansion of a metal then its coefficient of volume expansion will be :
(a) \(\frac{\beta}{2}\)
(b) 3β
(c) \(\frac{3 \beta}{2}\)
(d) \(\frac{2 \beta}{3} \)
Answer:
(c) \(\frac{3 \beta}{2}\)

Question 6.
If the temperature of a diseased person is 40°C, then his temperature in Farenheit will be:
(a) 72°F
(b) 96°F
(c) 100°F
(d) 104°F.
Answer:
(d) 104°F.

Question 7.
Temperature of sun is measured by:
(a) Gas thermometer
(b) Pyrometer
(c) Platinium thermometer
(d) Constant pressure thermometer.
Answer:
(b) Pyrometer

Question 8.
For whom medium is not required for transmission of heat:
(a) Conduction
(b) Convection
(c) Radiation
(d) All.
Answer:
(c) Radiation

Question 9.
Coefficient of thermal conductivity for ideal conductor is:
(a) 0
(b) 1
(c) -1
(d) ∞ .
Answer:
(d) ∞

Question 10.
Unit of coefficient of thermal conductivity is :
(a) joule metre/ second ×°C
(b) joule × metre × second / °C
(c) joule / metre × second × °C
(d) joule × second / metre × °C.
Answer:
(c) joule / metre × second × °C

Question 11.
In steady state, heat stored in metai does not depends on :
(a) Temperature gradient
(b) Area of cross-section
(c) Length
(d) Thermal capacity.
Answer:
(d) Thermal capacity.

Question 12.
An equivalent rod is made by joining two rod of same length. If their coefficient of thermal conductivity are K₁ and K₂, then thermal conductivity of equivalent rod is:
(a) K₁+K₂
(b) K₁– K₂
(c) 2K₁ K₂/ (k₁+ K₂)
(d) (K₁ – K₂)/(k₁+ K₂).
Answer:
(c) 2K₁ K₂/ (k₁+K₂)

Question 13.
Monsoon is due to:
(a) Conduction
(b) Convection
(c) Radiation
(d) All the above.
Answer:
(b) Convection

Question 14.
PolIshed body are for thermal radiation:
(a) Good absorber and bad reflector
(b) Good absorber and good reflector
(c) Bad absorber and good reflector
(d) Bad absorber and bad reflector.
Answer:
(c) Bad absorber and good reflector

Question 15.
Whose specific heat is more :
(a) Iron
(b) Water
(c) Copper
(d) Glass.
Answer:
(b) Water

2. Fill in the blanks:

1. Coefficient of linear expansion of solid depend upon ……………. .
Answer:
Nature of matter

2. SI Unit of temperature gradient is……………. .
Answer:
joule / metre

3. Density of water is maximum at …………… temperature.
Answer:
4°C

4. α: β: γ = ……………
Answer:
1:2 : 3

5. The point where all three phases in solid, liquid and gas co-exist is called …………… .
Answer:
Triple point

6. Wavelength of light radiation is …………… than heat radiation.
Answer:
Less

7. Conversion of matter from solid-state to vapour state directly is called ……………
Answer:
Sub-limation.

3. Match the following:

Column ‘A’	Column ‘B’
1. Coefficient of linear expansion	(a) kilogram
2. Coefficient of volume expansion	(b) Rate of cooling ∝ difference temperature
3. Specific heat	(c) Only for solid
4. Newton’s laws of cooling	(d) Raise of temperature by 1°C
5. Water equivalent	(e) Solid, liquid and gas.

Answer:
1.  (c) Only for solid
2. (e) Solid, liquid and gas.
3. (d) Raise of temperature by 1°C
4. (b) Rate of cooling ∝ difference temperature
5. (a) kilogram.

4. state true or False:

1. Volume of water at 4°C is maximum.
Answer:
False

2. At triple point of water, temperature is 273.16K.
Answer:
True

3. On increasing temperature the volume of mercury increases uniformly.
Answer:
True

4. Gases has two type of specific heat.
Answer:
True

5. Cp is always less than Cv.
Answer:
False

6. For monoatomic gas the value of Y is 1.67.
Answer:
True

7. In convection molecules changes their position for transfer of heat.
Answer:
True

8. Absorbtive power of ideal black body is one.
Answer:
True.