MP Board Class 11th Physics Important Questions Chapter 10 Mechanical Properties of Fluids

Students get through the MP Board Class 11th Physics Important Questions Chapter 10 Mechanical Properties of Fluids which are most likely to be asked in the exam.

MP Board Class 11th Physics Important Questions Chapter 10 Mechanical Properties of Fluids

Mechanical Properties of Fluids Class 11 Important Questions Very Short Answer Type

Question 1.
What do you mean by pressure? Is it scalar or vector? Write its SI unit.
Answer:
The force acting normally on unit area of the surface is known as pressure. It is a scalar quantity. The SI unit of pressure is N/m².

Question 2.
What is thrust? Write its SI unit.
Answer:
The total force acting normally on a surface, by the liquid pressure is called thrust.
Unit: Its SI unit is N.

Question 3.
What is Pascal’s law? State its two applications.
Answer:
The pressure in a fluid in equilibrium is the same everywhere if the effect of gravity can be neglected.
Or
Pressure applied to any part of an enclosed fluid at rest is transmitted equally to every portion of the fluid and the walls of the containing vessel.
Applications :

• Hydraulic lift,
• Hydraulic brakes.

Question 4.
Why is the dam of water reservoir thick at the bottom?
Answer:
It is so because the pressure of water in the reservoir increases with depth.

Question 5.
What do you understand by atmospheric pressure? What are its various units?
Answer:
The force exerted by the air of atmosphere, per unit area on the surface of earth is called atmospheric pressure.
latm = 1.013 × 10⁵Nm^-2 = 1 Pascal.

Question 6.
Explain 1 bar and 1 tor.
Answer:
1 bar: It is the unit of pressure.
1 bar = 1.0 × 10⁵Nm^-2 =10⁵Pa.
1 tor: It is also unit of pressure named after Torricelli’s.

Question 7.
What is the value of atmospheric pressure?
Answer:
1.013 ×10⁵ Newton/metre².

Question 8.
“Atmospheric pressure is 760 mm of Hg”. What it means?
Answer:
It means that it equilibrium the 760 mm height of mercury column pressure.

Question 9.
What is known as Torricellian vacuum?
Answer:
The vacuum is the simple barometer above the mercury column is known as Torricellian vacuum.

Question 10.
What will be the effect on mercury level of barometer if a small hole is made in the upper portion?
Answer:
The level of mercury will come down.

Question 11.
What will be the effect on the level of mercury in a barometer if a water droplet is inserted inside it.
Answer:
The level of mercury will fall due to the water vapour formation when a water droplet is inserted inside the barometer.

Question 12.
What will be the effect on level of mercury of the barometer is baught to hill?
Answer:
The level of mercury will fall as atmospheric pressure at hill is less.

Question 13.
How atmospheric pressure is change with altitude?
Answer:
Atmospheric pressure will decrease with altitude.

Question 14.
Which liquid is used in barometer?
Answer:
Mercury is used in barometer.

Question 15.
The surface tension of a liquid does not depend upon the area of the surface. Why?
Answer:
Because the surface tension is defined as the force acting on unit length of the line drawn on the liquid surface.

Question 16.
What is difference between cohesive force and adhesive force?
Or
What do you mean by cohesive force and adhesive force?
Answer:
Cohesive force: The force of attraction between the molecules of same sub-stance is called cohesive force.
Adhesive force: The force of attraction between the molecules of different sub-stances is called adhesive force.

Question 17.
What is surface tension? Give its SI unit.
Answer:
In equilibrium, the force acting per unit length on an imaginary line drawn on the liquid surface, perpendicular to the line and tangential to the surface is called surface tension.
Its SI unit is Nm^-1.

Question 18.
How can be the surface tension of a liquid be reduced?
Answer:
Surface tension of a liquid can be reduced by increasing temperature.

Question 19.
Soaps and detergents are helpful in cleaning the clothes. Why?
Answer:
The soap or detergent reduces the surface tension of water. Therefore, the soap solution can penetrate deep into the pores, where water cannot normally reach and thus dirt and dust are removed.

Question 20.
Why hot soup tastes better than cold soup?
Answer:
Soup is a liquid. Whenever a liquid is heated, its surface tension decreases and it gets more spread up in the tongue and it reaches to the sensitive layers rather than cold soup. Hence, hot soup tastes better than cold soup.

Question 21.
At which surface the pressure is excess, on what factors it depends?
Answer:
The excess of pressure is at concave surface. This is because of surface tension. The excess pressure depends upon :

• Surface tension of liquid and
• Radius of curvature of liquid surface.

Question 22.
What is angle of contact? How do the angles of contact differ for the liquids which (i) wet the solid surface and (ii) does not wet the solid surface?
Answer:
The angle that the tangent to the liquid surface at the point of contact makes with the solid surface inside the liquid is called the angle of contact. The angle of contact is acute for the liquids which wet the solid surface and is obtuse which do not wet.

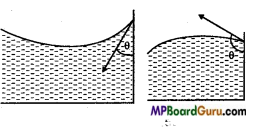
Question 23.
What is capillarity? Give example.
Answer:
The phenomenon of ascending and descending of liquid in a capillary is called capillarity. In kerosene lamp oil rises in the wick due to capillarity.

Question 24.
Towels are used to wipe and dry the body after bathe. Why?
Answer:
A towel has number of pores, which act as capillary, hence it soaks the water of the body.

Question 25.
If wax is polished on clothes, they become water proof. Why?
Answer:
When wax is polished, then the pores of the threads, which act as capillaries get closed and it cannot suck water. Hence it becomes water proof.

Question 26.
Why the blood pressure in humans is greater at the feet than at the brain? (NCERT)
Answer:
The height of the blood column is quite large at the feet than at the brain. There fore the blood pressure in humans is greater at the feet than at the brain.

Question 27.
What are the factor that effect air pressure at a place?
Answer:

1. Height of atmosphere
2. Density of atmosphere
3. Acceleration due to gravity.

Question 28.
On which principle hydraulic lift work?
Answer:
Hydraulic lift work on Pascal’s law.

Question 29.
Why the droplets of liquid are spherical?
Answer:
The free surface of liquid has tendency to achieve to least surface area, because of its potential energy. The sphere has the least surface area therefore droplets are spherical.

Question 30.
The oil spreads over the water surface but when the water is put into oil it becomes spherical droplets. Why?
Answer:
This is because the adhesive force between the molecules of water and oil is greater than the cohesive force of oil.

Question 31.
When a glass rod is heated at one end, that end becomes spherical, why?
Answer:
When the end of a glass rod is heated, it melts and changes into liquid, hence due to the surface tension the liquid tries to achieve the least surface area, thus it becomes spherical.

Question 32.
In which material of capillary the water will descent not ascent? What will happen if a capillary made up of silver is dipped into water?
Answer:
The water will descent in the capillary made up of paraffin wax. The water will neither rise nor descent in silver capillary.

Question 33.
When two lead pieces are pressured against each other they stick together, why?
Answer:
When two pieces of lead are pressured against each other, then the molecules come into contact and the cohesive force acts between the molecules and hence they stick together.

Question 34.
The small needle of steel floats in the water but it sinks into water with little soap solution. Why?
Answer:
The needle floats in the water because the surface tension force balance the weight of the needle. When the soap solution is added into water its surface tension decrease and hence the force which balances the needle decreases and needle sinks.

Question 35.
Why the farmers plough the fields after rain?
Answer:
When the fields are ploughed the capillaries of earth broken and the under- ground water remains there which is used by the plants.

Question 36.
What is molecular range?
Answer:
The maximum distance, within which the molecules of a liquid experience cohesive force.
Unit: It is of the order 10^-9 m.

Question 37.
What is meant by surface film of a liquid?
Answer:
Surface film is a thin film of liquid near its surface and having thickness equal to the molecular range for that liquid.

Question 38.
What is viscosity ?
Answer:
The inherent property of the fluids (liquids or gases) by virtue of which they oppose the relative motion between their layers is called viscosity.

Question 39.
What do you mean by ideal liquid?
Answer:
The liquid whose viscosity and compressibility both are zero called an ideal liquid.

Question 40.
What do you understand by streamline flow?
Answer:
When a fluid flows in such a way, that at any point the velocity of all the particles of fluid remain constant, then its flow is called streamline flow.

Question 41.
What do you mean by turbulent flow?
Answer:
The flow of the fluid in which the motion of the particles are irregular and zig-zag is called turbulent flow.
Fast-flowing rivers during the flood, storms are the examples of turbulent flow.

Question 42.
Two streamline flow do not intersect each other, why?
Answer:
If two streamline flow intersects at a point, then at that point, there will be two directions of velocity of the particles of fluid, which is not possible, hence they do not intersect.

Question 43.
State Stoke’s law.
Answer:
Stoke’s law states that, if a sphere of radius r moving with uniform velocity v, through a homogeneous incompressible fluid of viscosity p, the retarding force Fis given by
F = 6 πηrν.

Question 44.
What is terminal velocity?
Answer:
When a ball falls through a liquid then initially the ball is accelerated due to gravity but soon it achieves a constant velocity called terminal velocity.

Question 45.
Define coefficient of viscosity.
Answer:
The coefficient of viscosity of a liquid is the viscous force acting tangentially per unit area of a liquid layer having unit velocity gradient in a direction perpendicular to the direction of flow of liquid.

Question 46.
What is critical velocity?
Answer:
The maximum velocity of a fluid, below which the flow remains streamline flow, is called critical velocity.

Question 47.
State the principle of continuity.
Answer:
When a non-viscous and incompressible liquid flows through a tube of non-uniform bore and its flow is streamlined, then the product of velocity of flow and the area of cross-section of the tube at every transverse cross-section remains constant.
i.e., A.v = a constant
or A₁v₁=A₂v₂.

Question 48.
How many types of energy does a flowing liquid possess?
Answer:
The flowing liquid possesses three types of energies :

1. Potential energy,
2. Kinetic energy and
3. Pressure energy.

Question 49.
Two small light balls are hanging near to each other by two threads. If air is blown between them, they come near to each other, why?
Answer:
When air is blown the speed of air increases, hence the pressure between the balls decreases. Thus due to outer pressures, the balls come closer.

Question 50.
Air is blown below the pan of a balance in equilibrium, what will happen?
Answer:
When the air is blown below the pan, the velocity of air is increased and hence the pressure below the pan will decrease. Hence the air above the pan, presses the pan downward, thus that pan will be lowered down.

Question 51.
When a fast-moving train passes through a platform, all the dust particle and others attract toward train, why?
Answer:
When a fast-moving train passes through a platform according, Bernoulli’s theorem pressure of that place get dropped at once, so the dust particle and other’s get attracted toward the train.

Mechanical Properties of Fluids Class 11 Important Questions Short Answer Type 

Question 1.
Explain why :
(a) Atmospheric pressure at a height of about 6 km decreases to nearly half of its value at the sea level, though the height of the atmosphere is more than 100 km.
(b) Hydrostatic pressure is a scalar quantity even though pressure is force divided by area. (NCERT)
Answer:
(a) Atmospheric pressure at height of 6km
h = 6km = 6× 10₃m, d = 1.30kg m^-3, g = 9.8 ms^-2
∴ P = hdg = 6 × 10³ × 1.30 × 9.8 = 0.7644 × 10⁵Pa
Atmospheric pressure at sea level = 1.013 × 10⁵Pa
Thus, it is clear that the atmospheric pressure at height of 6 km is nearly half the atmospheric pressure. But the atmosphere is extended nearly up to 100km from the surface of earth. It is so because the density of air decreases as we go up from the surface of earth.

(b) When the force is exerted at a point on the liquid, then the pressure is equally transmitted in all directions. Thus, the pressure is not concerned with direction. Hence, the hydrostatic pressure is a scalar quantity.

Question 2.
Explain why :
(a) The angle of contact of mercury with glass is obtuse, while that of water with glass is acute.
(b) Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.) (NCERT)
Answer:
(a) When a drop of liquid is put on the solid surface then three interfaces are formed:

1. Solid-liquid interface,
2. Solid-vapour interface,
3. Liquid-vapour interface.

Let the surface tension in these interfaces are T_SLT_SV and T_LV respectively. Then at point 0 for the equilibrium of liquid
T_SV = T_SL+T_LV cos θ,
where θ is angle of contact.
∴ cos θ = \(\frac{T_{S V}-T_{S L}}{T_{L V}}\)
For mercury – glass pair Tsv < TSL ∴ cos θ is negative i.e., θ is obtuse angle.
For water-glass Tsv >T_SL
cos θ is positive i.e., θ is acute angle.

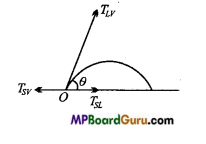
(b) The angle of contact for water glass pair is acute angle. Hence, the water spreads over the surface of glass. The angle of contact for mercury-glass pair the angle of contact is obtuse angle. Hence, the mercury tries to contract and acquire the shape of drop so that the angle of contact becomes obtuse angle.

In the other words, the adhesive force between molecules of water and glass is greater than the cohesive forces between the molecules of water. Hence, water wets the glass. While the adhesive force between the molecules of mercury and glass is less than cohesive forces between the molecules of mercury, hence the mercury does not wet the glass.

Question 3.
Explain why :
(a) Surface tension of a liquid is independent of the area of the surface.
(b) A drop of liquid under no external forces is always spherical in shape. (NCERT)
Answer:
(a) The force acting per unit length on either side of an imaginary line at right angles on the surface of liquid is called surface tension. This force does not depend on the area of surface.

(b) In the absence of external force, only surface tension acts on the liquid surface. The surface tension tries to minimize the surface area of liquid. For the given volume the surface area of sphere is least. Hence, in the absence of external forces the liquid drop acquires the spherical shape.

Question 4.
Explain why :
(a) To keep a piece of paper horizontal, you should blow over, not under it.
(b) When we try to close a water tap with our Angers, fast jets of water gush through the openings between our Angers. (NCERT)
Answer:
(a) When a piece of paper (paper strip) is blown over, then the velocity of air in that region increases, hence the kinetic energy of air increases, then according to Bernoulli’s theorem the pressure in that region decreases than the pressure in below region. Hence, due to decrease in pressure in upper region, the paper strip becomes horizontal.

(b) When we try to close the water tap with our fingers. The area for the flow of liquid decreases.
According to principle of continuity Av = constant.

Obviously if A decreases then v increases. Thus, the velocity of flow of liquid increases and fast jets of water gush through the opening between our finger.

Question 5.
Explain the construction and working of hydraulic lift.
Answer:
Construction: The construction of a hydraulic lift is shown in the Fig. In it there are two cylinders C₁ and C₂ of different area of cross-sections. These are interconnected by means of a narrow tube. Two frictionless and watertight pistons A and B are fitted in the cylinders C₁ and C₂ respectively. The area of cross-section of the piston A is small while that of the piston B is quite large. The body to be lifted up is placed on the platform attached to the piston B. The force is applied on the piston A. The two cylinders are filled with water.

Principle: The hydraulic lift consists of two cylinders C₁ and C₂ and they are connected by a horizontal tube T. There are two air resistance pistons P₁ and P₂ and their area of cross-section is A₁ and A₂ respectively. Such that A₁ solid A₂ i. e., area of container C₁ is less than that of C₂ On piston P₁ if F, is the force applied, then applied pressure will be
P = \(\frac{F_{1}}{A_{1}}\) …….. (1)
This pressure now gets transmitted to the container C₂ and so the liquid gives an upward force to the piston P₂. By Pascal’s law,
Pressure on piston P₂ = Pressure on piston P1 = \(\frac{F_{1}}{A_{1}}\)
Force F₂ on piston P₂ = Pressure × Area
or F₂ = \(\frac{F_{1}}{A_{1}} \) × A₂ ……….. (2)
As A₁ < A₂, hence F₂>F₁ So by applying lesser force on small area, we get large force on larger areas. This is the principle of hydraulic lift.

Question 6.
Show that a body when immersed in a liquid looses its weight equal to the weight of the liquid displaced by the body.
Answer:
According to this principle, when a body is immersed wholly or partially in a liquid at rest, it loses some of its weight which is equal to the weight of liquid displaced by immersed part of the body.

Consider a rectangular body of mass M and height h is completely immersed in a liquid of density p. Let A be the area of the lower and upper face of the body and l is the depth of the upper face of the body from the free surface of liquid.

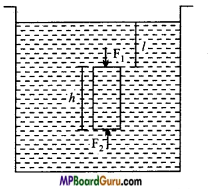
Volume of liquid displaced = Volume of the body ( V) = Ah.
Mass of the liquid displaced, m = Vρ= Ahρ ………… (1)
Pressure acting on the upper face of the body due to
liquid, P₁ = lρg ……………… (2)
and Pressure acting on the lower face of body, P₂ = (l+ h)ρg ………….. (3)
Downward force on the upper face of the body is Fx = P1A = IρgA …………… (4)
Upward force on the lower face of the body is F₂ = P₂A = A(l + h)ρg …………… (5)
Net upward thrust on the body
F = F₂-F₁ =(l + h)ρgA – lρgA
or
F = Ahρg …………….. (6)
From eqns. (1) and (6), we get
F = mg = Weight of liquid displaced Actual weight of the body W = Mg
Upward thrust F = mg
Hence, the apparent weight of the body in liquid = W-F= Mg – mg.

Question 7.
What is Pascal’s law? State and prove it.
Answer:
In a closed liquid the pressure applied at any part is equally transmitted in all direction and in the same amount.
Or
If a liquid is in equilibrium, then the pressure in every part of it is equal.
Deduction of Pascal’s law: Consider two points O₁ and O₂ inside a liquid. Now, imagine a right circular cylinder with O₁, O₂ as the axis. Its end faces will be circular with O₁ and O₂ as centres.

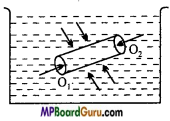
The liquid inside the cylinder is in equilibrium, therefore the forces exerted by the outside liquid on the inner liquid will be perpendicular to the surface.
In accordance with it the forces acting on the end faces of the cylinder with O₁ and O₂ as centre will be perpendicular to them.

If the force acting on the face with O₁ as centre is F₁ then
Pressure at O₁ P = \(\frac{F_{1}}{A}\)
Where A is the area of the end face.
∴ F₁ = P₁A
Similarly, if F₂ is the force acting on the end face with O₂ as centre, then
Pressure at O₂ is P₂ = \(\frac{F_{2}}{A}\)
or F₂ = P₂ A
As the liquid is in equilibrium.
∴ F₁=F₂
P₁ A = P₂A
or P₁ = P₂
Therefore, the pressure on O₁ and O₂ are equal.

Question 8.
State Pascal’s law. Explain the effect of gravity on Pascal’s law.
Answer:
Pascal’s law:

In a closed liquid the pressure applied at any part is equally transmitted in all direction and in the same amount.
Or
If a liquid is in equilibrium, then the pressure in every part of it is equal.
Deduction of Pascal’s law: Consider two points O₁ and O₂ inside a liquid. Now, imagine a right circular cylinder with O₁, O₂ as the axis. Its end faces will be circular with O₁ and O₂ as centres.

The liquid inside the cylinder is in equilibrium, therefore the forces exerted by the outside liquid on the inner liquid will be perpendicular to the surface.
In accordance with it the forces acting on the end faces of the cylinder with O₁ and O₂ as centre will be perpendicular to them.

If the force acting on the face with O₁ as centre is F₁ then
Pressure at O₁ P = \(\frac{F_{1}}{A}\)
Where A is the area of the end face.
∴ F₁ = P₁A
Similarly, if F₂ is the force acting on the end face with O₂ as centre, then
Pressure at O₂ is P₂ = \(\frac{F_{2}}{A}\)
or F₂ = P₂ A
As the liquid is in equilibrium.
∴ F₁=F₂
P₁ A = P₂A
or P₁ = P₂
Therefore, the pressure on O₁ and O₂ are equal.

Suppose a trough is filled with a liquid of density ρ. A and B are two points on the same vertical line and separated by a distance of h. A is above the point B shown in Fig.
Imagine a right cylinder of height h and area of cross-section A with the vertical line AB as axis, Weight of the cylinder = Mass × g
= Volume × Density × g
= Ahpg, (∵ Volume=Area × Height)

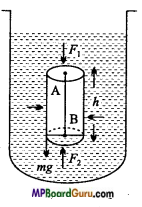
This weight will be acting vertically downwards. If the pressures at the points A and B are P₁ and P₂ respectively, then the force acting on the upper face of the cylinder in the downward direction is
F₁ = Pressure x Area
or
F₁ = P₁A
Similarly, the force acting on the lower face of the cylinder in the upward direction is F₂ = P₂A
But, the liquid is in equilibrium, therefore F₁ + Ahρg – F₂ = 0
∴ P₁A + Ahρg- P₂A = 0
or (P₂ – P₁ )A = Ahρg
or P₂ – P₁ = hρg …………… (1)
From eqn. (1), it is clear that there is a difference of pressure between any two points in the same vertical line in a liquid.

Question 9.
Explain why: The size of the needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection. (NCERT)
Answer:
The area of needle of a syringe is very small. According to principle of continuity Aν = constant. Since area is small therefore ν will be large. The doctor exerts pressure P with his thumb. According to Bernoulli’s theorem.
P + \(\frac{1}{2}\) dv²+ dgh = Constant

In this expression, the power of P is 1 and that of ν is 2. Obviously, ν is more effective than P. This is reason due to which the size of needle of syringe controls flow rate better than the thumb pressure exerted by doctor while administering an injection.

Question 10.
The farmer plough their field after rain. Why?
Answer:
In a dry clay, number of pores are there, which acts as capillaries. After rain if farmers plough their field, then the capillaries of earth broken and the underground water remain there, which is used by the plant.

Question 11.
Explain why: A fluid flowing out of a small hole in a vessel results in a backward thrust on the vessel. (NCERT)
Answer:
The velocity of liquid emerging out of a small hole is high (∵ Aν = constant). Hence, its linear momentum will be large. Since no external force is acting on the system, so the linear momentum of the system remains conserved. Thus, it is clear that a reaction will act on the vessel and it will experience a thrust.

Question 12.
Explain why: A spinning cricket ball in air does not follow a parabolic trajectory. (NCERT)
Answer:
When a spinning cricket ball is thrown in air then at one side of ball the resultant velocity of air increases and at other side, the velocity decreases. According to Bernoulli’s theorem, a pressure difference is created between the two sides and a resultant force acts on the ball. Hence, the ball follows a curved path, it is called Magnus effect. Due to this effect, the ball does not follow a parabolic trajectory.

Question 13.
Describe Torrecelli’s experiment of atmospheric pressure. How does it measure the pressure?
Answer:
Torricelli’s Experiment: Torricelli performed an experiment to measure the atmospheric pressure. This experiment is called the
Torricelli’s experiment. The device used for the mea¬surement of atmospheric pressure is called a Barometer.
A barometer consists of a one-metre long glass tube of nearly 1.5 cm internal diameter.

One end of this tube is closed. This tube is completely filled with mercury. Now, closing the open end with thumb, we invert the tube and place the open end in a trough containing mercury such that the tube is vertical and the open end is well inside the mercury. Care is taken that no air bubble enters the tube. On removing the thumb the level of mercury in the tube starts falling and at a certain definite height the fall in level stops.

In this state the height of the level of mercury in the tube above the (fee surface of mercury in the trough i. e., the height of the mercury column is nearly 76 cm.
In the space inside the tube above the mercury, column is fully vacuumed, this empty space is called the Torricellian vacuum.

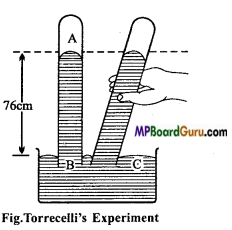
Explanation: Torricelli explained the above phenomenon as follows: The column of mercury in the tube tries to fall due to its own weight while the atmospheric pressure tries to push it upwards. When the pressure of the mercury column equals the atmospheric pressure an equilibrium is achieved and the fall of mercury level stops. In this way by measuring the height of mercury column in the tube the atmospheric pressure can be measured.

Question 14.
What are the factors which effect surface tension? How they effect surface tension?
Answer:
Factor affecting surface tension are :

• Substance dissolved in the liquid: The substance which are highly soluble in the liquid increases the surface tension, while the insoluble substance decreases surface tension.
• Contamination of the surface: Dust particles, oil, grease etc. decrease the surface tension of liquid.
• Temperature of the liquid: Generally on increasing the temperature, the surface tension decreases. According to the formula,
  T = T₀ (1 – αt)
  Where, T= S.T. at t°C, TQ = S.T. at 0°C and α = Temperature coefficient of surface tension.

Question 15.
Explain the phenomenon of capillary rise.
Answer:
Capillary rise: Let a capillary be dipped vertically in a liquid which wets the glass surface. The me¬niscus of the liquid in the capillary will be concave. Suppose the liquid does not rise in the capillary [figure (a)]. Imagine two points A and B at the same horizontal level below the surface of the liquid. Another point C is above the meniscus of the liquid

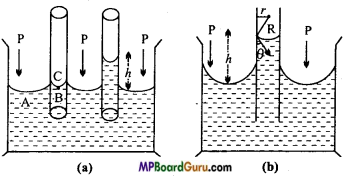
The pressure on the concave side of the meniscus is more than that on the convex side. This excess of pressure on the concave side is 2T/R, where, T is the surface tension of the liquid and R is the radius of the meniscus. The pressure on the point C is equal to the atmospheric pressure P. Therefore, the net pressure at the point
B = P – \(\frac{2 T}{R}\)

At point A the pressure is equal to the atmospheric pressure P. Points A and B are in the same horizontal level. Therefore, the pressure on both these points must be equal. Clearly, the liquid will rise in the capillary to a height such that the pressure of the liquid column at the point B equals 2 T/R. Thus, the total pressure at the point
B = P – \(\frac{2 T}{R}+\frac{2 T}{R}\) = P.

Question 16.
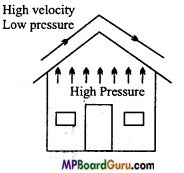
In strong storm, the roofs of houses fly away, High-velocity Low pressure why?
Answer: At the time of strong wind or storms the air above the roof moves with very high velocity, creating low pressure above the roof. Hence P₂ becomes greater than P₁. Due to the pressure difference P₁ -P₂, a large upthrust acts on the roof and therefore it fly away.

Question 17.
What is critical velocity? What is its relationship with Reynold’s number?
Answer:
The maximum velocity of a fluid, till the flow is streamline is called critical velocity. If the critical velocity is V_c, coefficient of viscosity is η, density of liquid is ρ and diameter of tube is D, then
V_c = \(\frac{K \eta}{\rho D}\)
Where, K is called Reynold’s number.
K is a dimensionless quantity.

Question 18.
Differentiate between the streamlined flow and turbulent flow of liquids.
Answer:
Difference between Streamlined flow and Ttirbulent flow :

Streamlined flow	Turbulent flow
1. In this flow each particle follows the path of its preceding particle passing through a given point.	In this flow the particles do not follow the path and velocity of preceding particle.
2. The velocity is less than critical velocity.	The velocity of flow is greater than critical velocity.
3. The path of flow may be straight line or curve.	The path is irregular and zig-zag.

Question 19.
State Newton’s law of viscosity. Define coefficient of viscosity and write its unit and dimensional formula.
Answer:
Newton’s law of viscosity: According to this law, the friction force F between the two layers is :
(i) Directly proportional to the area A of the layers, i.e.,
F ∝ A

(ii) Directly proportional to the velocity gradient between the layers, i.e.,
F ∝\(\frac{d v}{d x}\)
Combining both the laws, we get
F ∝ A .\(\frac{d v}{d x} \)
F = – η A. \(\frac{d v}{d x}\)

Where, η is a constant, called coefficient of viscosity.
Negative sign shows that viscous force acts in the opposite direction of flow.
Now, if A = 1 and \(\frac{d v}{d x}\) = 1, then F = – η
Thus, the coefficient of viscosity of a liquid is the tangential force required to maintain a unit velocity gradient between two layers of unit area separated by unit distance. Unit: MKS unit of η is N-s/m².

Question 20.
Find out dimensional formula of coefficient of viscosity.
Answer:
We know that fricition force
F = – ηA \(\frac{d v}{d x}\)
∴ Coefficient of viscosity η = – \(\frac{F}{A \frac{d v}{d x}}\)
or [η] = \(\frac{\left[\mathrm{MLT}^{-2}\right]}{\left[\mathrm{L}^{2}\right]\left[\frac{\mathrm{LT}^{-1}}{\mathrm{~L}}\right]}\) = [ML^-1T^-1].

Question 21.
What is terminal velocity? Calculate the terminal velocity of a sphere falling through a viscous liquid.
Answer:
Terminal velocity: When a ball falls through a liquid then initially the ball is accelerated due to gravity but soon it achieves a constant velocity called terminal velocity.
Formula for terminal velocity: Let a sphere of radius r, density d is falling through a liquid of density ρ and coefficient of viscosity η.
Now, the forces acting on falling body are:

• Weight of the sphere acting vertically downwards.
• Force of buoyancy liquid, acting vertically upward.
• Viscous force acting vertically upwards.

Now, Weight of sphere = Volume × Density × g
= \(\frac{4}{3}\) πr³dg,
Where, r is the radius of ball.
Force of buoyancy = Weight of liquid displaced
= \(\frac{4}{3}\) πr³ρg
∴ Resultant weight of body =\(\frac{4}{3}\) πr³ dg – \(\frac{4}{3}\) πr³ρg
= \(\frac{4}{3}\) πr³ (d – ρ) g

Again, Viscous force = 6 πηrν
When the body is falling with terminal velocity, then Viscous force = Resultant weight
∴ 6 πηrν = \(\frac{4}{3}\) πr³(d – ρ) g
or ν = \(\frac{2}{9} \frac{r^{2}(d-\rho) g}{\eta}\).

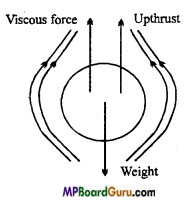
Question 22.
What is terminal velocity? On what factors does it depend?
Answer:
Terminal velocity:

Terminal velocity: When a ball falls through a liquid then initially the ball is accelerated due to gravity but soon it achieves a constant velocity called terminal velocity.
Formula for terminal velocity: Let a sphere of radius r, density d is falling through a liquid of density ρ and coefficient of viscosity η.
Now, the forces acting on falling body are:

• Weight of the sphere acting vertically downwards.
• Force of buoyancy liquid, acting vertically upward.
• Viscous force acting vertically upwards.

Now, Weight of sphere = Volume × Density × g
= \(\frac{4}{3}\) πr³dg,
Where, r is the radius of ball.
Force of buoyancy = Weight of liquid displaced
= \(\frac{4}{3}\) πr³ρg
∴ Resultant weight of body =\(\frac{4}{3}\) πr³ dg – \(\frac{4}{3}\) πr³ρg
= \(\frac{4}{3}\) πr³ (d – ρ) g

Again, Viscous force = 6 πηrν
When the body is falling with terminal velocity, then Viscous force = Resultant weight
∴ 6 πηrν = \(\frac{4}{3}\) πr³(d – ρ) g
or ν = \(\frac{2}{9} \frac{r^{2}(d-\rho) g}{\eta}\).

Factors on which it depends :

• It is directly proportional to the square of the radius of the body.
• Directly proportional to the difference of the densities of the liquid and body.
• Inversely proportional to the coefficient of viscosity of the liquid.
• Directly proportional to acceleration due.to gravity.

Question 23.
State and prove principle of continuity.
Answer:
Principle of continuity: When a non-viscous and incompressible liquid flows through a tube of non-uniform bore and its flow is streamline, then the product of velocity of flow and the area of cross-section of the tube at every transverse cross-section remains constant.
i. e., A.ν = a constant
or A₁ν₁ = A₂V₂ .
Proof: Let an incompressible and non-viscous liquid be flowing through a tube XY of non-uniform bore.
A and B are two transverse sections of the tube having areas A₁ and A₂ respectively. Also let the velocity of flow of the liquid at these transverse sections be V₁, and v₂ respectively. Let the density of the liquid bed.
The liquid flowing through the transverse section of A travels a distance v₁ in 1 second, therefore the volume of the liquid flowing per second through section at A is A₁v₁. Hence, the mass of the liquid flowing per second through this section is A₁V₁d.

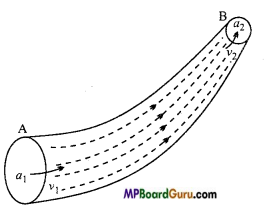
Similarly, the mass of the liquid flowing through the transverse section at B is A₂v₂d. Since the liquid is incompressible, it cannot accumulate in any portion of the tube. Therefore, whatever amount of liquid enters the segment AB of the tube at section A, the same amount of liquid will flow out of the section at B.
A₁V₁d = A₂v₂d
or A₁v₁ = A₂V₂
or A.v = Constant
This is the principle of continuity.

Question 24.
How many types of energy are there in a flowing liquid? Write the expressions for them.
Answer:
A non-compressible flowing liquid possesses three types of energies :
1. Kinetic energy: If the mass of liquid flowing is m, then its kinetic energy,
K.E = \(\frac{1}{2}\) mv²
If the volume of liquid be V, then K.E. of unit volume of liquid = \(\frac{1}{2}\) \(\frac{m v^{2}}{V}\)
But, \(\frac{m}{V}\) = d. (density)
∴ K.E. of unit volume of liquid =\(\frac{1}{2}\) dv².

2. Potential energy : If a liquid of mass m is at a height h, then its
P.E.= mgh
Where, g is acceleration due to gravity.
∴ P.E of unit volume of liquid = \(\frac{m g h}{V}\) = dgh, (∵ \(\frac{m}{V}\) = d)

3. Pressure energy: For the flow of liquid pressure is applied, with result in pressure energy.
Let the pressure P is applied on a liquid of area of cross-section A, so that liquid flows through a distance of x.
∴ Pressure energy = Work done
= Force × Distance
= Pressure × Area × Distance
= P × A × x =PV, (∵ Ax = V)
∴ Pressure energy per unit volume =\(\frac{P V}{V}\) = P
and pressure energy per unit mass = \(\frac{P V}{V}\) = \(\frac{P}{\frac{m}{V}}\) = \(\frac{P}{d}\).

Question 25.
What is Stoke’s law? What are the conditions of Stoke’s law?
Answer:
According to Stoke, if a spherical body moves through a homogeneous viscous liquid, the viscous force F is :
(i) Directly proportional to the coefficient of viscosity
i.e., F ∝η
(ii) Directly proportional to the radius of body
i.e., F ∝ r
(iii) Directly proportional to the velocity of the body
i.e., F ∝ v
Combining all the laws, we get
F ∝ ηrv
or
F = Kηrv
Where K is constant of proportionality. For spherical ball, K is equal to 6π.
∴ F=6πηrv

Conditions of Stoke’s law :

• The sphere should be very small.
• The sphere should be rigid and smooth.
• The liquid should be extended infinitely.
• The liquid should be viscous and homogeneous.

Mechanical Properties of Fluids Class 11 Important Questions Long Answer Type

Question 1.
State-Bernoulli’s theorem and prove it.
Or
State Bernoulli’s theorem and prove that:
P +\(\frac{1}{2}\) ρv₂ + ρgh = A constant.
Answer:
Bernoulli’s theorem: When a non-viscous and incompressible liquid flows in streamlined condition through a tube then the total energy of its unit mass or unit volume remains constant, i.e.,
For unit volume,
P +\(\frac{1}{2}\) ρv + ρgh = a constant
and For unit mass,
\(\frac{P}{\rho}+\frac{1}{2}\)v₂ +gh = a constant
Where, P – Pressure, p = Density, v = Velocity of liquid flow, g = Acceleration due to gravity, h – Height of liquid above ground level.

Proof: Suppose an incompressible and non-viscous liquid is flowing through a tube XY of non-uniform bore. Its flow is streamlined [See fig.].
A and B are two transverse sections of the tube. The areas of these sections are A₁ and A₂ respectively. At the section A let the velocity of flow of the liquid be v, and its pressure P₁. At the section B let the corresponding quantities be v₂ and P₂ respectively.

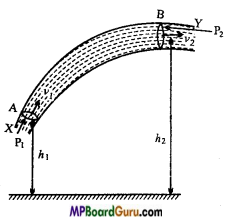
Also let the heights of A and B above the ground be h₁ and h₂ respectively and p the density of the liquid.
The force, acting on the liquid at the section A is
F₁=P₁A₁
Therefore, the work done on the liquid entering the cross-section at A in each second
W₁ = F₁ × V₁ = P₁A₁v₁
Similarly, the amount of work done by the liquid coming out of the section at B in each second
W₂ = P₂A₂V₂
∴ Net amount of work done on the liquid
W = W₁ – W₂
= P × A × v₁ – P₂A₂V₂ ……………… (1)
But, from the principle of continuity,
A₁ V₁ = A₂V₂

Where, A₁v₁, or A₂V₂ is the volume of the liquid flowing in each second through any cross-section.
∴ Mass of the liquid flowing any cross-section in one-second
m = A₁v₁ρ= A₂v₂ρ
or
A₁v₁ = \(\frac{m}{\rho}\)
Putting this value in eqn. (1), we get
W = P₁ \(\frac{m}{\rho}\) – P₂\(\frac{m}{\rho}\)
= (P₁ – P₂)\(\frac{m}{\rho}\)
The potential energies of the liquid flowing per second at A and B are mgh₁ and mgh₂ respectively.
∴ Increases in the potential energy of the liquid
= mgh₂ – mgh₁ = mg(h₂-h₁)

The K.E. of the liquid flowing per second at A is \(\frac{1}{2}\)mv₁ ² and at B is \(\frac{1}{2}\) mv₂ ².
∴ Increase in the kinetic energy of the liquid
= \(\frac{1}{2}\) mv₂ ² – \(\frac{1}{2}\)mv₁ ²
= \(\frac{1}{2}\) m(v₂ ² – v₁ ²)

From the principle of conservation of energy,
Work done on the liquid = Increase in potential energy of the liquid + Increase in the kinetic energy of the liquid
∴ (P₁ – P₂)\(\frac{m}{\rho}\) = mg (h₂ – h₁) + \(\frac{1}{2}\)m (v₂² – v₁²)
or
P₁ – P₂ = ρg (h₂ – h₁) + \(\frac{1}{2}\)ρ(v₂² – v₁²)
or
P₁ – P₂ = ρgh₂ – ρgh₁ + \(\frac{1}{2}\)ρ(v₂² – \(\frac{1}{2}\)ρ(v₁²
or
P₁ + ρgh₁+\(\frac{1}{2}\)ρ(v₁² = P₂ + ρgh₂ + \(\frac{1}{2}\)ρ(v₂² ………… (2)
or
P + ρgh + \(\frac{1}{2}\)ρv² ……………… (3)

∴ Therefore, the total energy of unit volume of the liquid remains constant at every point during flow.
From eqn. (3),
\(\frac{P}{\rho}\) + \(\frac{1}{2}\)v² + gh = constant
The total energy of unit mass of the liquid remains constant. From eqn. (2),
P₁ + \(\frac{1}{2}\)ρv₁²+ dgh₁ = P₂ + \(\frac{1}{2}\)ρv₂² + dgh₂
For horizontal tubes : h1 = h2.
∴ P₁ + \(\frac{1}{2}\)ρv₁² = P₂ + \(\frac{1}{2}\)ρv₂²
P + \(\frac{1}{2}\)ρv² = Constant.

Question 2.
In venturi meter the area of cross-sections at two points are A₁ and A₂ and pressure difference is h. Derive an expression for the volume of liquid flowing per second.
Or
Establish the formula for the flow of liquid by venturi meter.
Or
Explain an application of Bernoulli’s theorem.
Answer:
Venturimeter: It is a device based upon the Bernoulli’s theorem. It is used to measure the rate of flow of a liquid through a given pipe.
The construction of a venturi meter is shown in the fig., AB is a horizontal pipe, the middle portion R of it, is constricted. Two vertical tubes M and N are attached to it as shown in the figure. They constitute the manometer arrangement.

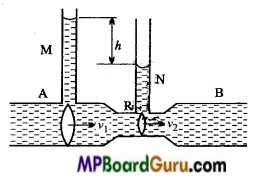
When the liquid (say, water) flows through the pipe AB, then in accordance with the principle of continuity, the velocity of flow at the points is smaller and that at/? it is larger. Therefore, according to the Bernoulli’s theorem, the pressure at A will be larger than the pressure at R. This causes the liquid to rise more in-tube Ethan in the tube N. By measuring the difference in the heights of liquid column M and N we can calculate the rate of flow of liquid through pipe.

Let at A the area of cross-section of the pipe be A₁, the velocity of flow V₁ and pressure P₁. At R the area of cross-section of the tube is A₂, the velocity of flow v₂ and the pressure is P₂.
As the pipe is horizontal, according to Bernoulli’s theorem,
P₁ + \(\frac{1}{2}\)ρv₁² = P₂\(\frac{1}{2}\)ρv₂²
or
P₁ – P₂ = \(\frac{1}{2}\) ρ (v₂² – v₁²) ……………… (1)
But, from the principle of continuity,
A₁v₁=A₂V₂ =Q

Where, Q is the volume of the liquid flowing per second i.e., the rate of flow of the liquid.
Therefore,
v₁ = \(\frac{Q}{A_{1}}\) and V₂ =\(\frac{Q}{A_{2}}\)
Putting these values in the eqn. (1), we have
or
P₁ – P₂ = \(\frac{1}{2}\)ρ (\(\frac{Q^{2}}{A_{2}^{2}}-\frac{Q^{2}}{A_{1}^{2}}\) )
or
P₁ – P₂ = \(\frac{1}{2}\) \(\frac{\rho Q^{2}}{A_{1}^{2} A_{2}^{2}}\) (A₁² – A ₂²)

If the difference in levels of the liquid in tubes M and N is h, then
P₁ -P₂ = hpg
Therefore, from eqn. (2),
hpg = \(\frac{1}{2}\) [/latex] \(\frac{\rho Q^{2}}{A_{1}^{2} A_{2}^{2}}\) (A₁² – A ₂²).

Question 3.
State and prove Torricelli’s theorem.
Answer:
Torricelli’s theorem: The velocity of efflux is equal to the velocity that a body acquires when allowed to fall freely from rest through a height equal to the depth of the hole below the free surface of liquid.
Let liquid is filled in a jar, up to height H and from the free surface there is a hole below depth h.
The velocity by the liquid emerges from the hole is called the velocity of efflux.

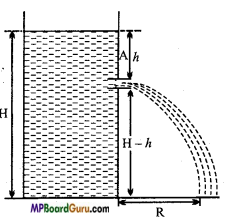
Now, the K.E. of free surface is zero and P.E. is maximum.
∴ Energy of free surface, per unit volume is
= P+0+ ρgH = P+ ρgH
Where, P is atmospheric pressure and ρ is the density of liquid.

Similarly, the energy per unit volume of liquid at the hole
= P + \(\frac{1}{2}\)ρv²+ ρg (H -h)
Again, by the Bernoulli’s theorem,
P +ρgH=P +\(\frac{1}{2}\)ρv² +pg(H-h)
or
pgH = \(\frac{1}{2}\)ρv² +pgH-pgh
or
\(\frac{1}{2}\)v² =gh
or
v² = 2 gh,
or
v = \(\sqrt{2 g h}\)

Again, if a body is allowed to fall from a height h freely, then u = 0.
∴ v² = u² + 2 gs
or
v² = 0+2gh = 2gh
or v = \(\sqrt{2 g h}\).

Question 4.
What is meant by surface energy of a liquid? Prove that surface energy per unit area is equal to the surface tension.
Or
What is surface energy? Derive an expression for it.
Answer:
Surface energy: The potential energy stored in unit area of free surface of liquid is called its surface energy.
Let PQRS be a rectangular frame of wire. AB is another straight wire which can slide over the arms PQ and RS of the frame as shown in the Fig.

Let the frame be dipped in soap solution and taken out so that a soap film ABRQ is formed. Due to the force of surface tension, the wire AB starts sliding towards QR. If the wire is to be prevented from sliding, a force F must be applied on the wire AB. In equilibrium this force will be equal and opposite to the force of surface tension on the wire AB.
If the length of the wire AB is l and the surface tension of the soap film is T, then F = 2Tl

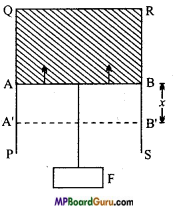
The factor of 2 appears because soap film has two surfaces.
If the wire AB is displaced through a distance x against the force of surface tension to the position A ‘B’, this will increase the area of the film.
Work done in increasing the area of the film,
W=Fx = 2Tlx ,
or W=T2lx
But, 2lx= A, the total increase in the area of the two surfaces of the film.
∴ W=TA
or
T = \(\frac{W}{A}\)

In the above expression if A = 1, then T= W
Hence, the surface tension of a liquid is numerically equal to the amount of work done in increasing the surface area of the film by unity under isothermal conditions. Thus, surface tension is equal to the surface energy per unit area.

Question 5.
Derive an expression for the excess of pressure inside a drop.
Answer:
Excess of pressure inside a drop: A liquid drop is spherical in shape and its outer surface is convex. Therefore, due to surface tension a net inward force acts on every molecule situated on the surface of the drop. As a result the pressure inside the drop is more than that outside. Let the radius of the drop be R and the excess of pressure inside it be P. Due to this excess of pressure an outward force acts on the surface of the drop.

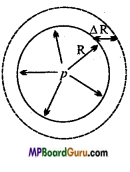
Suppose due to this excess of pressure, the radius of the drop increases from R to R + ΔR.

Therefore, the work done by the excess of pressure in expansion of the drop,
W = Force × Displacement
= Pressure × Area × Displacement
= P × 4πR² × A R
Increase in the surface area of the drop = Final surface area – Initial surface area
= 4π(R + ΔR)² – 4πR² =8 πRΔR
∵ 4π( ΔR)² will be very small and can be neglected.
∴ Increase in the surface energy
= Surface tension x Increase in the surface area = T ×8 πRΔR
This increase in surface energy is due to the excess of pressure.
∴ P × 4πR² × ΔR = T × 8 πR.ΔR
or P = \(\frac{2 T}{R}\).

Question 6.
Derive an expression for excess pressure inside a bubble.
Answer:
Excess of pressure inside a bubble: Due to air inside it, the bubble has two free surface. One inside and another outside. Let the radius of the bubble be R. Due to excess of pressure P in it, an outward force acts on the surface of the bubble. This is balanced by the force due to the surface tension.
Suppose due to excess of pressure P, let the radius of the bubble increase from R to R +ΔR.
∴ Work done by the excess of pressure
= Force × Distance = Pressure × Area × Distance
= P × 4πR² × ΔR
Since, there are two surfaces in a bubble, the increase in the surface area of the bubble
= 2[4π(R + ΔR)² – 4 πR² ]
= 16πR.ΔR
∴ Increase in surface energy = T×16πR.ΔR
The increase in surface energy is due to the excess of pressure.
∴ P × 4πR² × ΔR = T × 16 πR.ΔR
or P =\(\frac{2 T}{R}\).

Question 7.
What is meant by capillarity? Give two examples of capillarity in daily life. Establish the formula to determine surface tension of water by capillary rise.
Or
Derive the formula to determine the surface tension in the laboratory.
Answer:
Capillarity: The phenomenon of ascenting and descenting of liquid in a capillary is called capillarity. In kerosene lamp oil rises in the wick due to capillarity.
Formula derivation: Let a uniform capillary tube of radius r be immersed into water and water rises up to height h. The meniscus is concave in the tube and its ra¬dius is nearly equal to the radius of capillary. The surface tension of liquid acts at the point of contact of meniscus along the direction of tangent, making an angle θ with the wall of tube.

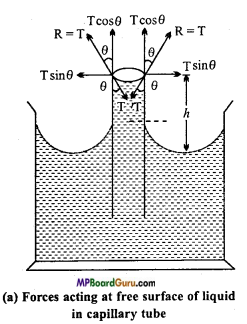
Now, according to Newton’s third law, reaction force R is equal to T.
Resolving R we get horizontal components R sin θ = T sin θ acting diametrically opposite, around the meniscus, hence their resultant will be zeros.
And vertical component R cos θ= T cos θ acting upwards around the circumference of meniscus, due to which the water rises.
The total force which rises the water
= Tcosθ × 2 πr …………. (1)
(2 πr has been multiplied because it is the total circumference on which T cosθ acts)

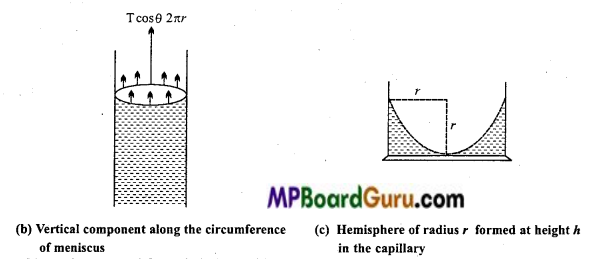
Now, the upward force is balanced by the weight of the water.
Now, volume of water raised = Volume of water to height h + Volume of water in meniscus.
Where, volume of water in meniscus = Volume of cylinder of radius and height r -Volume of hemisphere filled with air
= πr²r – \(\frac{2}{3}\) πr³
∴ Volume of water raised = πr² h + (πr² r – \(\frac{2}{3}\) πr³)
= πr²h + \(\frac{1}{3}\)πr³

If the density of water is ρ then weight of water acting vertically downwards.
W = mg – Volume × Density × g
=( πr²h + \(\frac{1}{3}\)πr³)ρg
= πr²(h +\(\frac{1}{3}\)r) ρg

Now, in equilibrium position,
Total force upwards = Total force downwards
T cosθ.2πr = πr²(h+ \(\frac{1}{3}\)r)ρg
or T = \(\frac{r\left(h+\frac{1}{3} r\right) \rho g}{2 \cos \theta}\)
Since,\(\frac{r}{3}\) is negligible in comparison to h.
∴T = \(\frac{r h \rho g}{2 \cos \theta}\)

But, for pure water and clean glass θ = 0°
∴ cos θ = cos 0° = 1
∴ T = \(\frac{r h \rho g}{2}\)
This is the required formula.

Mechanical Properties of Fluids Class 11 Important Numerical Questions

Question 1.
A 50 kg girl wearing high heel shoes balances on a single heel. The heel is circular with a diameter 1.0 cm. What is the pressure exerted by the heel on the horizontal floor? (NCERT)
Solution:
Given, m = 50kg; 2r = 1.0cm ⇒ r = 0.5 cm = 0.5 × 10^-2 m
F = mg = 50 × 9.8 = 490N.
Now pressure,
P =\(\frac{F}{A}\) = \(\frac{F}{\pi r^{2}}\) = \(\frac{490}{3 \cdot 14\left(0 \cdot 5 \times 10^{-2}\right)^{2}} \)
= \(\frac{490 \times 10^{4}}{0 \cdot 785}\)
= 624.20 × 10⁴
= 6.24 × 10⁶ N/m².

Question 2.
Torricelli’s barometer used mercury. Pascal duplicated it using French wine of density 984 kgm^-3. Determine the height of the wine column for normal atmospheric pressure.(NCERT)
Solution:
Given, d = 984kg/m³; g = 9.8ms ^-2, P = 1.013 × 10⁵Pa
Formula, P = hdg
∴ h = \(\frac{P}{d g}\) = \(\frac{1 \cdot 013 \times 10^{5}}{984 \times 9 \cdot 8}\) =10.5m.

Question 3.
In a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70 ms^-1 and 63 ms^-1 respectively. What is the lift on the wing if its area is 2.5 m²? Take the density of air to be 1.3 kg m^-3. (NCERT)
Solution:
Given, ν₁ = 70ms^-1 ;ν₂ = 63ms^-1;A = 2.5m² , d = 1.3 kgm^-3
According to Bernoulli’s theorem,
\(\frac{1}{2} d v_{1}^{2}\) + P₁ = \(\frac{1}{2} d v_{2}^{2}\) +P₂
or
P₁ – P₂ = \(\frac{1}{2} \)d (ν₂² – ν₁²)A
∴ Applied thrust force will be
F = (P₁ – P₂)A
= \(\frac{1}{2}\)d (ν₂² – ν₁²)A
= \(\frac{1}{2}\) ×1.3 [ (63)² – (70)²] × 2.5
= 0.5 × 1.3 [3969 – 4900] × 2.5
= -1.5 × 10³N.

Question 4.
What is the pressure inside the drop of mercury of radius 3-00 mm at room temperature? Surface tension of mercury at that temperature (20°C) is 4.65 × 10^-1 Nm^-1. The atmospheric pressure is 1.01 × 10⁵ Pa. Also give the excess pressure inside the drop. (NCERT)
Solution:
Given, R = 3.00mm = 3 × 10³m, T = 4.65 × 10^-1Nm –¹
Atmospheric pressure = 1.01 × 10⁵Pa
Formula: ρ = \(\frac{2 T}{R}\)
Or ρ = \(\frac{2 \times 4 \cdot 65 \times 10^{-1}}{3 \times 10^{-3}}\) = 310Pa.

Total pressure inside the drop = Atmospheric pressure + Excess pressure
= 1.01 × 10⁵ +310
= 1.01 × 10⁵ +0.00310 × 10⁵
= 1.01310 × 10⁵Pa
= 1.01 × 10⁵ Pa (UP to three significant digits).

Question 5.
At what depth in the water the pressure will be double the atmospheric pressure ?
Solution:
Let the depth = hm
∴ Pressure of Am depth water + Atmospheric pressure
= 2 × Atmospheric pressure
or Pressure of water at h m depth = Atmospheric pressure
or h × 1 × 10³ × 9.8 = 1 × 10⁵(∵ P = hρg)
or h = \(\frac{10^{5}}{10^{3} \times 9 \cdot 8}\) = 10.20m.

Question 6.
The weight of a piece of lead in water is 100 g. Find out its weight in air if relative density of lead is 11.3.
Solution:
Let die weight of lead in air be x
The weight of lead in air = 100 g.
The loss in its weight in water = x – 100

Relative density of lead = \(\frac{\text { The weight of lead in air }}{\text { The loss in its weight in water }} \)
∴ \(\frac{11 \cdot 3}{1}\) = \(\frac{x}{x-100}\)
or 11.3x – 11.30 = x
or 10.3x = 1130
x = 109.7 gm.

Question 7.
The surface tension of a liquid is 70 × 10.3 Nm^-1. A needle of 5 cm is floating on it. Calculate the lateral force acting on the pin.
Solution:
Given : T = 70 × 10³Nm^-1, l = 5 cm = 5 x 10^-2m.
Now we have T = \(\frac{F}{l}\)
F=T.l
= 70 × 10^-3 × 5 × 10 ^-2
= 3.5 × 10^-3N.

Question 8.
The radius of a soap bubble is 0.5 cm. If the surface tension of soap solution is 0.2 Nm^-1, then find the surface energy of the bubble.
Solution:
Given : R = 0.5cm = 0.5 × 10^-2m, T = 0.2Nm ^-1.
A = 4πR² = 4 × 3.14 × (0.5 × 10^-2)²
= 12.56 × 0.25 × 10^-4m²
Now, Surface energy,
W=2TA,
= 2 × 0.2 × 12.56 × 0.25 × 10^-4 = 1.256 × 10^-4 joule.

Question 9.
Calculate the work done in blowing a bubble of soap solution of radius 5cm. Surface tension of soap solution is = 3 × 10 ^-2Nm^-1
Solution:
Given : r = 5 cm =\(\frac{5}{100}\) = \(\frac{1}{20}\)m,
T = 3 × 10^-2 Nm^-1
Since, the bubble has two surfaces.
∴ A = 2 × 4πr²
or
A = 8π\(\left(\frac{1}{20}\right)^{2}\) = 628 × 10^-4m²
Now,
W = T.A
= 3 ×10^-2 × 628 x 10^-4
= 1884 x 10^-6 = 0.001884 joule.

Question 10.
Radius of a soap bubble is r and its surface tension is T. At constant temperature the radius of bubble is blown doubled, calculate the required force.
Solution:
ΔA = 2 [4πr²₂ – 4πr²₂ ]
= 8π (r²₂ – r²₂ )
Given:
r₁=r and r₂ = 2r.
ΔA = 8π (4r² -r²)
= 24πr²
∵ W=T.ΔA
∴ W=T.24 πr² = 24 πr². T.

Question 11.
A drop of diameter 2.8 mm is broken into 125 droplets of equal radii. If the surface tension of liquid is 75 dyne × cm^-1, then calculate the change in energy.
Solution:
Given :
2R = 2.8 mm
or
R = 1.4 mm
= 1.4 × 10^-3m
and, T = 75 dyne × cm^-1
= 75 × 10^-5 N × (10^-2 m)^-1
∴ T = 75 × 10^-3 Nm-1

Now, Volume of big drop = Volume of 125 droplets.
∴ \(\frac{4}{3} \pi R^{3}\) = 125 × \(\frac{4}{3} \) πr³
or R3 = 125r³
or
R = 5r
or
r = \(\frac{R}{5}\)
∴ Surface area of bigger drop = 4πR²
and Surface area of 125 droplets = 125 × 4πr²
= 125 × 4π × \(\left(\frac{R}{5}\right)^{2}\)
∴ Δ A = 20πR² – 4πR² = 16 πR²
∴ Change in energy,
ΔW = T.Δ A
= 75 × 10^-3 × 16 × πR²
= 75 × 10^-3 × 16 × \(\frac{22}{7}\) × (1.4 × 10 ^-3)²
= 7392 × 10^-9
= 7.392 × 10^-9 joule.

Question 12.
The surface tension of soap solution is l-9xl0-2 Nm”1. Calculate the excess of pressure inside the bubble of diameter 2 cm.
Solution:
Given : T = 1.9 × 10^-2 Nm^-1
R = \(\frac{2}{2}\) cm = 1cm = 1 × 10^-2m.
Now, ρ = \(\frac{4 T}{R}\)
or
ρ = \(\frac{4 \times 1 \cdot 9 \times 10^{-2}}{10^{-2}}\) = 7.6 Nm^-2.

Question 13.
Water is flowing through a tube of non-uniform cross-section. The velocity at a point A is 4 times that of another point B. Compare the diameters of tube at A and B.
Solution:
Given: ν₁ = 4v₂
We have, by the principle of continuity,

Question 14.
The diameter of a spherical ball A is half of that of B. What will be the ratio of their terminal velocities in water?
Solution:
Given: a1 = \(\frac{a_{2}}{2}\)
We have,
ν ∝ a²
or
\(\frac{v_{1}}{v_{2}}\) = \(\frac{a_{1}^{2}}{a_{2}^{2}}\)
∴ \(\frac{v_{1}}{v_{2}}\) = \(\frac{\left(a_{2} / 2\right)^{2}}{a_{2}^{2}}\) = \(\frac{1}{4}\)
∴ ν₁ :ν₂ = 1:4

Question 15.
Water is flowing through a horizontal tube of non-uniform area of cross-section. At a place where the pressure is 20 cm (of water) the velocity of flow of water is 60 cm/s. Find the velocity of flow at a place where the pressure is 15 cm (of water).
Solution:
Given, P₁ = 20 cm(of water) =20 × 1 × 980 dyne /cm², v, = 60 cm/s,
P₂ = 15 × 1 × 980 dyne/cm² and ρ= 1 gm/cm3.

By the Bernoulli’s theorem,
\(\frac{1}{2}\) ρ (ν₂² – ν₁²) = P₁ – P₂
⇒ \(\frac{1}{2}\) × 1 × (ν₂² – 60²) = 20 × 1 × 1980 – 15 × 1 × 1980
⇒ \(\frac{1}{2}\) (ν₂² – 60²) = 5 × 980
⇒ ν₂² = 9800 + 3600 = 13400
∴ ν₂ = 115.76 cm/s.

Question 16.
Calculate the terminal velocity of a spherical ball of diameter 2mm, in a viscous liquid. The density of liquid 1.0 × 10³ kg m^-3 and density of ball is 8.0 × 10³kg m³ and coefficient of viscosity of liquid is 1.0 kg m^-1s^-1.
Solution:
Given : 2a = 2mm or a = 1mm = 1 x 10^-3m,
ρ = 1.0 × 10 ³kg m^-3 ,d = 8.0 × 10³ kg m^-3, η = 1.0 kg m^-1s^-1

Now, ν = \(\frac{2}{9} \cdot \frac{a^{2}(d-\rho) g}{\eta}\)
= \(\frac{2}{9}\) . \(\frac{\left(1 \times 10^{-3}\right)^{2}\left(8 \cdot 0 \times 10^{3}-1 \cdot 0 \times 10^{3}\right) 9 \cdot 8}{1 \cdot 0}\)
= \(\frac{2}{9}\) × 10^-6 × 7 × 10³ × 9.8
= 15.2 ×10^-3 ms^-1

Question 17.
A drop of water radius 0.0015 mm is falling in the air. If the coefficient of viscosity of air is 1.8 × 10 ^-6 kgm^-1s^-1 then calculate the terminal velocity of drop. The density of air is negligible.
Solution:
Given : a = 0.0015 mm = 0.0015 × 10^-3m = 1.5 × 10⁶m,
d = 1 × 10³ kgm^-3, ρ = 1.0 × 10³ kg m^-3, η = 8.0 × 10^-6 kg m^-1 s^-1

Formula,
ν = \(\frac{2}{9} \cdot \frac{a^{2}(d-\rho) g}{\eta}\)
= \(\frac{2}{9}\) .\(\frac{\left(1 \cdot 5 \times 10^{-6}\right)^{2} \times 1 \times 10^{3} \times 9 \cdot 8}{1 \cdot 8 \times 10^{-6}}\)
= \(\frac{2}{9}\) \(\frac{2 \cdot 25 \times 10^{-12} \times 9 \cdot 8 \times 10^{3}}{1 \cdot 8 \times 10^{-6}}\)
= 2.72 × 10^-3ms^-1.

Question 18.
Two horizontal pipes of different diameters are joined together, water is flowing through them. The velocity and pressure through one pipe are 4 ms^-1 and 2.0 × 10^-3Nm^-2 respectively. The diameters of pipes are 3 cm and 6 cm. Calculate the velocity and pressure in second pipe.
Solution:
Given :
v₁ = 4 ms^-1 , P ¹ = 2.0 × 10⁴ Nm^-1
r₁cm = 1.5 × 10^-2m, r² = \(\frac{6}{2}\) = 3cm = 3 × 10^-2
Now we have
A₁ v₁ = A₂v₂
or πr₁ ²v₁ = πr₁ ²v₂
or
r₁ ²v₁ = r₁ ²v₂

∴ ν₂ = \(\frac{r_{1}^{2} \cdot v_{1}}{r_{2}^{2}} \)
= \(\frac{\left(1 \cdot 5 \times 10^{-2}\right)^{2} \times 4}{\left(3 \times 10^{-2}\right)^{2}}\)
= 1 ms^-1
Again, P₂ – P₁ = \(\frac{1}{2}\) ρ (ν₁² – ν₂²)
or P₂ – 2 × 10⁴ = \(\frac{1}{2}\) × 10³ (4² – 1²)
or
P₂ = \(\frac{1}{15}\) × 10³ + 2 × 10⁴
= 2.75 × 10 ⁴ Nm^-2

Question 19.
What will be the maximum velocity of water for streamline flow through a tube of diameter 2 cm? (η= 10³ kgm^-1s^-1).
Solution:
Given: D = 2cm = 2 × 10²m. η= 10³ kgm^-1s^-1
K=2000,
ρ= 10 kgm^-3
Now, ν_c = \(\frac{K \eta}{\rho D}\)
or ν_c = \(\frac{2000 \times 10^{-3}}{10^{3} \times 2 \times 10^{-2}}\) = 0.1ms^-1.

Mechanical Properties of Fluids Class 11 Important Questions Objective Type

1. Multiple- choice questions:

Question 1.
The sudden fall of atmospheric pressure indicates :
(a) Storm
(b) Rainfall
(c) Clear weather
(d) Coldwave.
Answer:
(a) Storm

Question 2.
On which principle the Hydraulic lift work :
(a) Pascal’s law
(b) Archimedis principle
(c) Boyle’s law
(d) Bernoulli’s theorem.
Answer:
(a) Pascal’s law

Question 3.
Systolic and diastolic blood pressure of a healthy human being is :
(a) 140 mm/80 mm of Hg
(b) 120 mm/80 mm of Hg
(c) 160 mm/90 mm of Hg
(d) 80 mm/ 120 mm of Hg.
Answer:
(b) 120 mm/80 mm of Hg

Question 4.
On which condition liquid flowing through a tube :
(a) When high density and more viscous liquid flows through less radius tube
(b) When low density and more viscous liquid flows through less radius tube
(c) When high density and less viscous liquid flows through more radius tube
(d) When less density and less viscous liquid flows through more radius tube.
Answer:
(b) When low density and more viscous liquid flows through less radius tube

Question 5.
On increasing temperature viscosity of liquid :
(a) Increases
(b) Becomes zero
(c) Decreases
(d) No effect.
Answer:
(c) Decreases

Question 6.
Bernoulli’s equation is based on which law :
(a) Conservation of momentum
(b) Conservation of energy
(c) Conservation of mass
(d) No law.
Answer:
(b) Conservation of energy

Question 7.
Rain droplet is spherical in shape, its reason is :
(a) Gravitational force
(b) Viscosity
(c) Atmospheric pressure
(d) Surface tension.
Answer:
(d) Surface tension.

Question 8.
On increasing temperature, surface tension of liquid :
(a) Increases
(b) Becomes zero
(c) Decreases
(d) No effect.
Answer:
(c) Decreases

Question 9.
At critical temperature, the surface tension of the liquid is :
(a) Zero
(b) Infinity
(c) Same as that any other temperature
(d) Cannot be determined.
Answer:
(a) Zero

Question 10.
The shape of meniscus of mercury in capillary tube is :
(a) Convex
(b) Cancave
(c) Flat
(d) Not definite.
Answer:
(a) Convex

Question 11.
Magnitude of angle of contact due to which surface of glass become wet is :
(a) 0°
(b) 90°
(c) More than 90°
(d) Less than 90°.
Answer:
(d) Less than 90°

Question 12.
On dipping glass capillary inside a mercury :
(a) Level of mercury in capillary tube increases
(b) Level of mercury in capillary tube increases and overflow
(c) Level of mercury in capillary tube falls
(d) Level of mercury in capillary tube falls and does not rise.
Answer:
(c) Level of mercury in capillary tube falls

Question 13.
Which phenomenon is not related to surface tension :
(a) Dancing of piece of camphor in water surface
(b) Spherical shape of small mercury drop
(c) The liquid become stable after jerking in a vessel
(d) None of these.
Answer:
(c) The liquid become stable after jerking in a vessel

2. Fill in the blanks:

1. Pressure exerted by one-millimeter column of mercury is called ……………………. .
Answer:
one tor

2. Blood pressure at leg of a human is ……………………. in comparison to his brain.
Answer:
more

3. In generally surface tension of a liquid ……………………. on increasing temperature.
Answer:
decreases

4. Viscosity of gas ……………………. and viscosity of liquid ……………………. on increasing temperature.
Answer:
increases, decreases

5. On mixing detergent in water, its ……………………. decreases.
Answer:
surface tension

6. When the magnitude of Reynold’s number is between 0 to 2000, the flow of liquid is ……………………. .
Answer:
streamline

7. ……………………. type of energy is associated with flowing liquid.
Answer:
three

8. Poisson’s is C.G. S. unit of ……………………. .
Answer:
coefficient of viscosity

9. The liquid which is incompressible is known as ……………………. liquid.
Answer:
ideal

10. Mercury does not wet glass because cohesive force is ……………………. than adhesive force.
Answer:
less.

3. Match the following:

I.

Column ‘A’	Column ‘B’
1. Ploughing of field after rain by farmer	(a) Use of detergent
2. Surface tension	(b) Pressure is less
3. Below concave surface	(c) Capillarity
4. Below conox surface	(d) Cohesive force
5. Spreading of oil drop over surface of water	(e) Pressure is more.

Answer:
1.  (c) Capillarity
2. (a) Use of detergent,
3 (b) Pressure is less
4. (e) Pressure is more
5. (d) Cohesive force.

II.

Column ‘A’	Column ‘B’
1. Viscous force F	(a) \( \frac{K \cdot \eta}{\rho \cdot D} \)
2. Critical velocity	(b) A.v = constant
3. Terminal velocity	(c) P+ \( \frac{1}{2} d v^{2} \)+ dgh = constant
4. Principle of continuity	(d) \( \eta A \frac{d v}{d x} \)
5. Bernoulli’s theorem	(e) \( \frac{2}{9} \cdot \frac{r^{2}(d-\sigma) g}{\eta} \)

Answer:
1. (d) \( \eta A \frac{d v}{d x} \)
2. (a) \( \frac{K \cdot \eta}{\rho \cdot D} \),
3. (e) \( \frac{2}{9} \cdot \frac{r^{2}(d-\sigma) g}{\eta} \)
4. (b) A.v = constant
5. (c) P+ \( \frac{1}{2} d v^{2} \)+ dgh = constant.

4. state true or False:

1. Hydrostatic pressure is vector quantity.
Answer:
False

2. Surface tension of a liquid does not depend upon area of cross-section of the surface.
Answer:
True

3. Angle of contact of mercury with glass is more.
Answer:
True

4. The man who jump with parachute, its velocity increases initially and then become constant.
Answer:
True

5. Viscosity of gas decreases on increasing temperature.
Answer:
False

6. Surface tension is numerically equal to surface energy.
Answer:
True

7. Greece is more viscous than honey.
Answer:
False

8. In flowing liquid, streamline of layer cannot intersect each other.
Answer:
False.