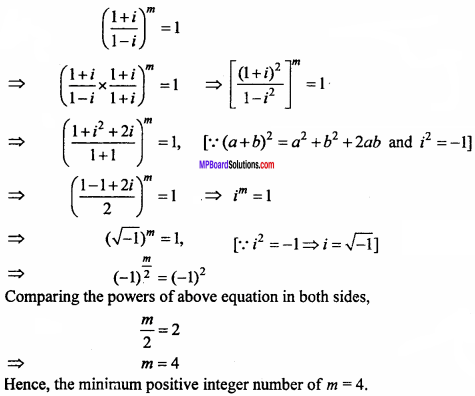MP Board Class 11th Maths Important Questions Chapter 5 Complex Numbers and Quadratic Equations
Relations and Functions Important Questions
Relations and Functions Objective Type Questions
(A) Choose the correct option :
Question 1.
If x + iy = 2 + 3i, then (x, y) will be :
(a) (3, 2)
(b) (2, 3)
(c) (- 2,- 3)
(d) (3, 3)
Answer:
(b) (2, 3)
Question 2.
The simplest form of \(\frac { 1 + i }{ 1 – i }\) :
(a) – i
(b) i
(c) ± i
(d) None of these.
Answer:
(b) i
Question 3.
If z is a complex number, then z + z is :
(a) Real number
(b) Imaginary number
(c) Nothing can be said
(d) None of these.
Answer:
(a) Real number
Question 4.
The value of \(\sqrt {i}\) = ……………..
(a) ± \(\frac { 1 – i }{ \sqrt { 2 } }\)
(b) ± \(\frac { 1 + i }{ \sqrt { 2 } }\)
(c) ± (1 + i)
(d) ± (1 – i)
Answer:
(b) ± \(\frac { 1 + i }{ \sqrt { 2 } }\)
![]()
Question 5.
Number of solution of the equation z + z = 0 is :
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4
Question 6.
Argument of complex number 0 is :
(a) 0
(b) π
(c) 2π
(d) Not defined
Answer:
(d) Not defined
Question 7.
Conjugate of \(\frac { 1 – i }{ 1 + i }\) is :
(a) \(\frac { 1 – i }{ 1 + i }\)
(b) \(\frac { 1 – i }{ 1 – i }\)
(c) i
(d) – i
Answer:
(c) i
Question 8.
Argument (z1.z2) = ………………
(a) arg (z1) – arg (z2)
(b) arg (z1) + arg (z2)
(c) arg (z1). arg (z2)
(d) None of these
Answer:
(b) arg (z1) + arg (z2)
![]()
Question 9.
The least positive integer n for which \(\frac { 1 – i }{ 1 + i }\)n = 1 is :
(a) 2
(b) 4
(c) 8
(d) 12
Answer:
(b) 4
Question 10.
If |z – \(\frac { 4}{ z}\)| = 2, then |z| has maximum value:
(a) \(\sqrt {3}\) + 1
(b) \(\sqrt {5}\) + 1
(c) 2
(d) 2 + \(\sqrt {2}\)
Answer:
(b) \(\sqrt {5}\) + 1
(B) Match the following :

Answer:
- (d)
- (a)
- (f)
- (b)
- (c)
- (e)
(c) Fill in the blanks :
- The value of (1 + i)4 (1 + \(\frac {1}{i}\))4 is ……………….
- The value of \(\frac {1}{i}\) is ……………….
- The value of z – \(\bar { z }\) is ……………….
- Argument of – 1 – i is ……………….
- polar form of i3 is ……………….
- Argument of complex number is \(\frac { 1+\sqrt { 3i } }{ \sqrt { 3 } +i }\) is ……………….
- If |\(\frac { z – i }{ z + i }\)| = 1, then locus of z will be ……………….
- If x + \(\frac {1}{x}\) = 2cosθ, then the value of xn = \(\frac { 1 }{ { x }^{ n } }\) will be ……………….
- If z = 2 – 3i, then the value of z. \(\bar { z }\) is ……………….
- If 2 + (x + yi) = 3 – i, the x = ……………… and y = ……………….
Answer:
- 16
- – i
- Imaginary number
- \(\frac {5π}{4}\)
- cos\(\frac {π}{2}\) – i sin\(\frac {π}{2}\)
- \(\frac {π}{6}\)
- X – axis
- 2cos nθ
- 13
- 1, – 1
(D) Write true / false :
- Additive inverse of complex number – 2 + 5i is 2 – 5 i.
- If | z2 – 1 |= z2 + 1, then z lies on a circle.
- If | z1 | = 12 and | z2 – 3 – 4i | = 5, then the least value of | z1 – z2 | is 7.
- If arg(z) < 0, then arg(- z) – arg(z) = π.
- Polar form of 1 + \(\sqrt {- 1}\) is \(\sqrt {2}\)(cos\(\frac {π}{4}\) + isin\(\frac {π}{4}\)).
- If z is a complex number such that | z | ≥ 2, then the minimum value of |z + \(\frac { 1 }{ 2 }\) | equal \(\frac { 5 }{ 2 }\)
Answer:
- True
- False
- False
- True
- True
- False.
(E) Write answer in one word / sentence :
- If Z1 = 2 – i, z2 = 1 + i, them find the value \(\frac { { { z }_{ 1 }+{ z }_{ 2 }+1 } }{ { z }_{ 1 }-{ z }_{ 2 }+1 }\)
- Modulus of \(\frac {1 – i }{ 1 + i }\) – \(\frac { 1 – i }{ 1 + i }\) will be.
- Polar form of complex number \(\sqrt {3}\) + i will be.
- If Z1 = 2 – i and z2 = – 2 + i, then Re(\(\frac { { { z }_{ 1 }{ z }_{ 2 } } }{ { z }_{ 1 } }\)) will be
- If the number \(\frac { z – 1 }{ z + 1 }\) is purly imaginary, then the value of |z| will be.
Answer:
- \(\sqrt {2}\)
- 2
- 2(cos\(\frac {π}{6}\) + isin\(\frac {π}{6}\))
- \(\frac { – 2 }{ 5 }\)
- 1
Complex Numbers and Quadratic Equations Very Short Answer Type Questions
Question 1.
If 1, ω, ω2 are the cube root of unity then find the value of ω3n.
Solution:
Since ω3 = 1
ω3n = (ω3)n = (1)n = 1.
Question 2.
Find the value of i4n.
Solution:
i4n = (i4)n = (i2.i2)n = [(- 1)(- 1)]n = (1)n = 1.
Question 3.
Find the condition of two complex numbers x + iy and a + ib are compaired.
Solution:
If x + iy = a + ib
Then, x = a, y = b.
Question 4.
Write conjugate of a complex number z = a – ib.
Solution:
z = conjugate of a – ib = a – (- ib)
= a + ib.
![]()
Question 5.
Write the complex number – 63 in ordered form.
Solution:
Ordered form of z = a + ib is (a, b).
Given: z = 0 – 6i
Ordered pair (0, – 6).
Question 6.
Write the complex number 3 – \(\sqrt { 7i }\) in ordered form.
Solution:
Ordered pair of z = a + ib is (a, b).
∴Ordered pair of 3 – \(\sqrt { 7i }\) = (3, – \(\sqrt { 7i }\))
Question 7.
Find the value of i + \(\frac { 1 }{ i }\).
Solution:
i + \(\frac { 1 }{ i }\) = \(\frac { { i }^{ 2 }+1 }{ i }\) = \(\frac { – 1 + i }{ i }\) = 0.
Question 8.
Find the value of i-19.
Solution:
i-19 = \(\frac { 1 }{ { i }^{ 19 } }\) = \(\frac { 1 }{ { i }^{ 18 }i } \) = \(\frac { 1 }{ (i^{ 2 })^{ 9 }.i }\)
= \(\frac { 1 }{ -1.i }\) = \(\frac { – 1 }{ i }\)
= \(\frac { – 1.i }{ { i }^{ 2 } }\) = i.
Question 9.
Write (1 – i)4 in form of a + ib.
Solution:
(1 – i)4 = [ (1 – i)2 ]2 (NCERT)
= [1 + i2 – 2i]2 = [1 – 1 – 2i]2, [∵ i2 = – 1]
= (- 2i)2 = 4i2 = 4(- 1) = – 4
= – 4 + 0i.
Question 10.
Find the modulus of complex number z = – 1 – i \(\sqrt {3}\) .
Solution:
Z = – 1 – i\(\sqrt {3}\)
a = – 1, b = \(\sqrt {3}\)
Modulus = \(\sqrt { { a }^{ 2 }+{ b }^{ 2 } }\) = \(\sqrt {1 + 3}\) = \(\sqrt {2}\)
Question 11.
Find the modulus of complex number 1 – i.
Solution:
z = 1 – i
a = 1, b = – 1
Modulus = \(\sqrt { { a }^{ 2 }+{ b }^{ 2 } }\) = \(\sqrt {1 + 1}\) = \(\sqrt {2}\)
Question 12.
Find the sum of 2 – 3i and its conjugate.
Solution:
z = 2 – 3i and \(\bar { z }\) = 2 + 3i
z + \(\bar { z }\) = 2 – 3i + 2 + 3i = 4.
Question 13.
Solve the quadratic equation x2 + 2 = 0. (NCERT)
Solution:
x2 + 2 = 0
⇒ x2 = – 2
⇒ x2 = – 1 x 2
= 2i2 [∵ i2 = – 1]
x = ± \(\sqrt {2i}\) or + \(\sqrt {2}\)i, – \(\sqrt {2}\)i
Question 14.
Solve the quadratic equation x2 + 3 = 0. (NCERT)
Solution:
x2 + 3 = 0
⇒ x2 = – 3 = – 1 x 3
⇒ x2 = 3i2, [∵ i2 = – 1]
x2 = ± \(\sqrt {3i}\) or + \(\sqrt {3}\)i, – \(\sqrt {3}\)i
Question 15.
Write the triangle inequality for the two complex number Z1 and z2.
Solution:
| Z1| and | z2| are the two sides of any triangle
Then, | z0 + z2| ≤ | z1| +| z2|
![]()
Question 16.
If T and 9 are the modulus and argument of the complex number a + ib, then write its polar form.
Solution:
Polar form of a + ib is r(cosθ + i sinθ).
Question 17.
If z = cosθ + i sinθ where |z| = 1, then find \(\frac { 1 }{ z }\).
Solution:
\(\frac { 1 }{ z }\) = cosθ – isinθ.
Question 18.
Write the statement of De – moivre’s theorem.
Solution:
If polar form of z = a + ib is r(cosθ + isinθ), then De – moivre’s theorem is
(cosθ + isinθ)n = cos nθ + i sin nθ.
Question 19.
Write polar form of i.
Solution:
a + ib = 0 + i. 1
r = \(\sqrt { { a }^{ 2 }+{ b }^{ 2 } }\) =1, θ = tan-1\(\frac { b }{ a}\) = tan-1∞ = \(\frac { π }{ 2}\)
Polar form of i = (cos\(\frac { π }{ 2}\) + i sin \(\frac { π }{ 2}\)).
Question 20.
Find the polar form of (- 2 + 2i).
Solution:
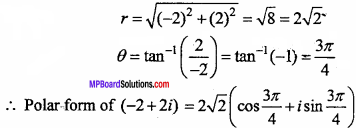
Complex Numbers and Quadratic Equations Long Answer Type Questions
Question 1.
Convert (\(\frac { 1 }{ 3}\) + 3i)3 in form of a + ib. (NCERT)
Solution:
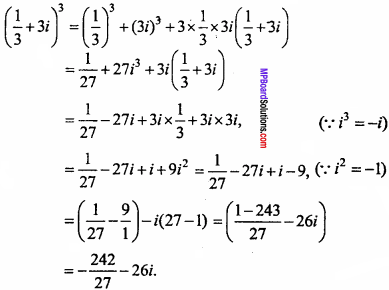
Question 2.
Write ( – 2 – \(\frac { 1 }{ 3}\)i)3 in form of a + ib. (NCERT)
Solution:
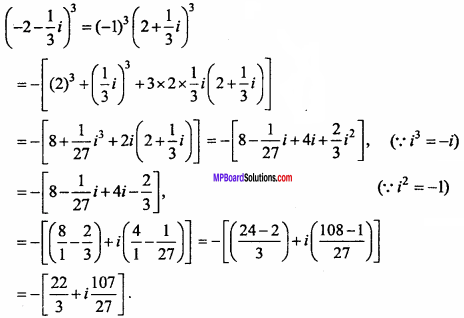
Question 3.
Write (5 – 3i)3 in the form of a + ib.
Solution:
(5 – 3i)3 = (5)3 – (3i)3 – 3(52.3i) + 3.5(3i)2
= 125 – 27.i3 – 75.3i + 15.9i2
= 125 – 27i.i2 – 225i + 15(- 9)
= 125 + 27i – 225i – 135
= – 10 – 198i.
Find the multiplicative inverse of following complex number :
Question 4.
4 – 3i
Solution:
Let the multiplicative inverse of 4 – 3i is a + ib.
Then, (4 – 3i) x (a + ib) = 1
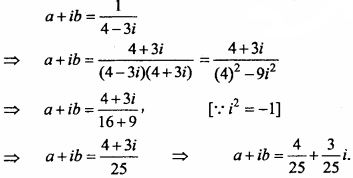
Question 5.
\(\sqrt {5}\) + 3i
Solution:
Let z = \(\sqrt {5}\) + 3i
Be multiplicative inverse

Question 6.
Find the polar form of the following :
(i) \(\frac { 1 + 7i }{ { 2 – i }^{ 2 } }\), (ii) \(\frac { 1 + 3i }{ 1 – 2i }\)
Solution:
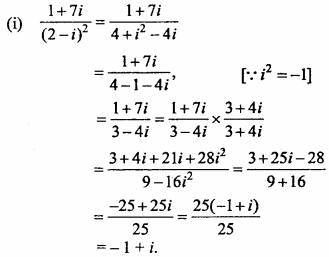
Now, let – 1 + i = r(cosθ + i sinθ),
Then, r cosθ = – 1 …. (1)
and r sinθ = 1 …. (2)
Squaring and adding equation (1) and (2),
r2 = 1 + 1 = 2
⇒ r = \(\sqrt {2}\)
Put value of r in equation (1) and (2),
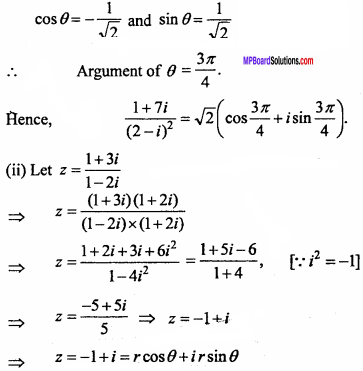
Comparing the real and imaginary parts,
r cosθ = – 1
r sinθ = 1
Squaring and adding equation (1) and (2),
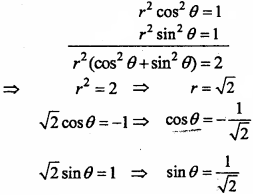
∵ Real part is negative and imaginary part is positive of z, hence θ will lie in 4th quadrant
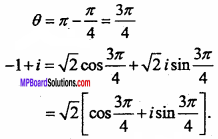
Question 7.
Find modulus and argument of complex number z = – 1 – i\(\sqrt {3}\) (NCERT)
Solution:
Let z = – 1 – i\(\sqrt {3}\) = rcosθ + ir sinθ
Comparing the real and imaginary parts,
rcosθ = – 1 …. (1)
rsinθ = – \(\sqrt {3}\) …. (2)
Squaring and adding equation (1) and (2),

Since both the real and imaginary part of z are negative.
∴ θ lies in third quadrant
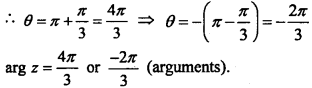
Question 8.
Find the modulus and argument of z = – \(\sqrt {3}\)+ i.
Solution:
Let z = – \(\sqrt {3}\)+ i = rcosθ + ir sinθ
Comparing the real and imaginary parts,
r cosθ = – \(\sqrt {3}\)
rsinθ = 1
Squaring and adding eqns. (1) and (2),
rcosθ = – \(\sqrt {3}\) …. (1)
rsinθ = 1 …. (2)
Squaring and adding equation (1) and (2),
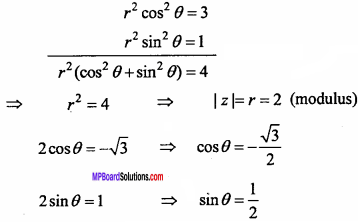
Since both the real and imaginary part of z are negative and positive respectively.
∴ θ lies in 22nd quadrant
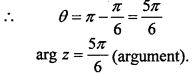
Question 9.
Find the modulus and argument of 1 – i.
Solution:
Let z = 1 – i = rcosθ + ir smθ
Comparing the real and imaginary parts,
1 = r cosθ
and – 1 = rsinθ
Squaring and adding equation (1) and (2),
(1)2 + (- 1)2 = r2 cos20 + r2 sin20
⇒ r2(cos20 + sin20) = 1 + 1,
⇒ r2= 2 ⇒ r = \(\sqrt {2}\) (modulus)
Dividing equation (2) by equation (1),

Question 10.
Find square root of complex number 3 + 4i.
Solution:
Let \(\sqrt {3 + 4i}\) = x + iy
On squaring,
3 + 4 i = (x + iy)2
⇒ 3 + 4i = x2 + 2ixy + i2y2
⇒ 3 + 4i = x2 + 2ixy – y2
⇒ 3 + 4i = (x2 – y2) + i(2xy)
x2 – y2 = 3 …. (1)
2xy = 4 …. (2)
(x2 + y2)2 = (x2 – y2)2 + 4x2y2
= (3)2 + (4)2
= 25
∴ x2 + y2 = 5 …. (3)
Now adding eqns. (1) and (3),
2x2 = 8
⇒ x2 = 4
⇒ x = ± 2
From equation (2), 2(± 2)y = 4
∴ y = ± 1
\(\sqrt { x + iy }\) = ± 2 ± i.
Question 11.
Find square root of complex number 8 – 6i.
Solution:
Let \(\sqrt { 8 – 6i }\) = x + iy
On squaring,
8 – 6i = (x + iy)2
⇒ 8 – 6i = x2 + 2ixy + i2y2 .
⇒ 8 – 6i = (x2 – y2) + 2ixy
∴ 8 = x2 – y2 …. (1)
and – 6 = 2 xy …. (2)
(x2 + y2)2 = (x2 – y2)2 + 4x2y2
(x2+y2)2 = (8)2 + (- 6)2
= 64 + 36 = 100
∴ x2 + y2 = 10 …. (3)
Now adding equation (1) and (3),
2x2 = 18
⇒ x2 = 9
⇒ x = ±3
From equation (3), y2 = 10 – 9 = 1
∴ y = ± 1
\(\sqrt { 8 – 6i}\) = ± 3 ± i.
Question 12.
x2 + 3x + 9 = 0.
Solution:
Given : x2 + 3x + 9 = 0
Comparing the above equation by ax2 + bx + c = 0,
a = 1, b = 3, c = 9
Now, D = b2 – 4ac
= 32 – 4 x 1 x 9 = 9 – 36 = – 27 < 0

Question 13.
– x2 + x – 2 = 0.
Solution:
Given : – x2 + x – 2 = 0
Comparing the above equation by ax2 + bx + c = 0,
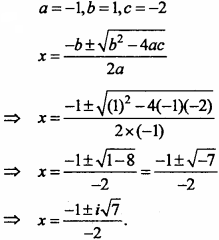
Question 14.
x2 + 3x + 5 = 0.
Solution:
Given : x2 + 3x + 5 = 0
Comparing the above equation by ax2 + bx+c = 0,
a = 1, b = 3, c = 5
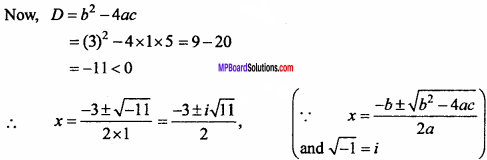
Question 15.
x2 – x + 2 = 0
Solution:
Given : x2 – x + 2 = 0
Comparing the above equation by ax2 + bx + c = 0,
a = 1, b = – 1, c = 2
Now, D = b2 – 4ac
= (- 1)2 – 4 x 1 x 2 = 1 – 8 = – 7 < 0
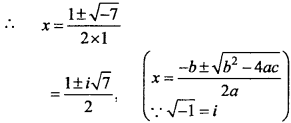
Question 16.
If (\(\frac { 1 + i }{ 1 – i }\)) = 1, then And the minimum positive integer number of m. (NCERT)
Solution: