MP Board Class 11th Maths Important Questions Chapter 11 Conic Sections

MP Board Class 11th Maths Important Questions Chapter 11 Conic Sections

Conic Sections Important Questions

Conic Sections Objective Type Questions

(A) Choose the correct option :

Question 1.
Coordinates of the focus of the parabola y = 2x² + x are:
(a) (0, 0)
(b) (\(\frac { 1 }{ 2 }\), \(\frac { 1 }{ 4 }\))
(c) (- \(\frac { 1 }{ 4 }\), 0)
(d) ( – \(\frac { 1 }{ 4 }\), \(\frac { 1 }{ 8 }\))
Answer:
(c) (- \(\frac { 1 }{ 4 }\), 0)

Question 2.
In a ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 a > b, the relation between a, b an eccentricity e is:
(a) b² = a²(1 – e²)
(b) b² = a²(e² – 1)
(c) a² = b²(1 – e²)
(d) a² = b²(e² – 1)
Answer:
(a) b² = a²(1 – e²)

Question 3.
The length of latus rectum of ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, represent a circle then its eccentricity will be:
(a) \(\frac { { 2a }^{ 2 } }{ b }\)
(b) \(\frac { { 2b }^{ 2 } }{ a }\)
(c) \(\frac { { a }^{ 2 } }{ b }\)
(d) \(\frac { { b }^{ 2 } }{ a }\)
Answer:
(b) \(\frac { { 2b }^{ 2 } }{ a }\)

Question 4.
The eccentricity of the parabola is:
(a) Less than 1
(b) Greater than 1
(c) 0
(d) 1
Answer:
(d) 1

Question 5.
The eccentricity of the ellipse is:
(a) Less than 1
(b) Greater than 1
(c) 0
(d) 1
Answer:
(a) Less than 1

Question 6.
The eccentricity of the hyperbola is:
(a) Less than 1
(b) Greater than 1
(c) 0
(d) 1
Answer:
(b) Greater than 1

Question 7.
In a ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, represent a circle then its eccentricity will be:
(a) Less than 1
(b) Greater than 1
(c) 0
(d) 1
Answer:
(c) 0

Question 8.
The sum of focal distances from any point on the ellipse is:
(a) Equal to major axis
(b) Equal to minor axis
(c) The distance between two foci
(d) Equal to latus rectum.
Answer:
(a) Equal to major axis

Question 9.
The differecne of the focal distances from any point on the hyperbola is:
(a) Equal to its conjugate axis
(b) Equal to its transverse axis
(c) The distance between two foci
(d) Equal to its latus rectum.
Answer:
(b) Equal to its transverse axis

Question 10.
The value of the eccentricity of ellipse 25x² + 16y² = 400 is:
(a) \(\frac { 3 }{ 5 }\)
(b) \(\frac { 1 }{ 3 }\)
(c) \(\frac { 2 }{ 5 }\)
(d) \(\frac { 1 }{ 5}\)
Answer:
(a) \(\frac { 3 }{ 5 }\)

Question 11.
Equation ax² + 2hxy + by² + 2gx + 2fy + c = 0 represent a circle if:
(a) a = b, c = 0
(b) f = g, h = 0
(c) a = b, h = 0
(d) f = g, c = 0
Answer:
(a) a = b, c = 0

Question 12.
Area of triangle whose centre (1,2) and which is passes through the point (4,6) will be:
(a) 5π
(b) 10π
(c) 25π
(d) 25π²
Answer:
(c) 25π

Question 13.
The circle passing through (1, – 2) and touching the X – axis at (3,0), also passes through the point:
(a) (2, – 5)
(b) (5, – 2)
(c) (- 2, 5)
(d) (- 5, 2)
Answer:
(a) (2, – 5)

Question 14.
The length of the diameter of the circle which touches the X – axis at the point (1,0) and passes through the point (2,3) is:
(a) \(\frac { 10 }{ 3 }\)
(b) \(\frac { 3 }{ 5 }\)
(c) \(\frac { 6 }{ 5 }\)
(d) \(\frac { 5 }{ 3 }\)
Answer:
(a) \(\frac { 10 }{ 3 }\)

Question 15.
Eccentricity of the hyperbola 3x² – y² = 4 :
(a) 1
(b) 2
(c) – 2
(d) \(\sqrt {2}\)
Answer:
(b) 2

(B) Match the following :

Answer:

1. (c)
2. (e)
3. (b)
4. (a)
5. (d)
6. (i)
7. (h)
8. (f)
9. (j)
10. (g)

(C) Fill in the blanks :

1. The length of the latus rectum of the parabola y² = 4ax is ……………
2. The centre of the ellipse \(\frac { { (x-1) }^{ 2 } }{ 9 } +\frac { { (y-2) }^{ 2 } }{ 4 }\) = 1 will be ……………
3. The vertex of the parabola (y – 2)² = 4a(x -1) is ……………
4. The lines \(\frac { x }{ a }\) – \(\frac { y }{ b }\) = m and \(\frac { x }{ a }\) + \(\frac { y }{ b }\) = \(\frac { 1 }{ m }\) meets always at ……………
5. If an ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1, a > b and its eccentricity is e, then the foci will be
6. Standard form of equation of parabola is ……………
7. Parametric equation of a circle x² + y² = 4 is ……………
8. A line y = x + a\(\sqrt {2}\) touches the circle x² + y² = a² point ……………
9. A line y = mx + c touches the circle x² + y² = a² if c = ……………
10. Vertex of the parabola 3y² + 6y – 4x + 11 = 0 is ……………
11. Equation 2x² + 2y² – 12x – 16y + 4 = 0 represent a point circle if k = ……………
12. Radius of circle 3x² + 3y² – 5x – 6y + 4 = 0 is ……………

Answer:

1. 4a
2. (1, 2)
3. (1, 2)
4. Hyperbola
5. (± ae, 0)
6. y² = 4ax
7. x = 2cosθ
8. (- \(\frac { a }{ \sqrt { 2 } }\), \(\frac { a }{ \sqrt { 2 } }\) )
9. ±a\(\sqrt { 1+{ m }^{ 2 } }\)
10. (5, 1)
11. 50, 12
12. \(\sqrt {61}\)

(D) Write true / false :

1. Conic section is a locus of the point whose the ratio between the distance from the fixed point and distance from the fixed line, this ratio is called eccentricity of the conic section.
2. The ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 has two directrics, the equation of directrics are x = ± \(\frac { a }{ e }\); Where a > b and y = ± \(\frac { b }{ e }\) ; where b > a.
3. The foci of the ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 are (0, ± be) where a < b.
4. A circle drawn by taking major axis of the ellipse as diameter is called auxiliary circle of the ellipse.
5. The locus of intersection point of the lines bx + ay = abt and bx – ay = \(\frac { ab}{ t }\) will be a ellipse.
6. The focus of a parabola x² = – 16y will be (0, – 4).
7. Equation x² + y² – 6x + 8y + 50 = 0 represent a circle.
8. Circle x² + y² = 9 and x² + y² + 8y + c = 0 touches externally if c = 15 .
9. Eccentricity of hyperbola is 1.
10. Minimum distance between line y – x = 1 and curve x = y² is \(\frac { 3\sqrt { 2 } }{ 8 }\)

Answer:

1. True
2. True
3. True
4. True
5. False
6. True
7. False
8. True
9. False
10. True

(E) Write answer in one word / sentence :

1. If the circle x² + y² + 2ax + 8y +16 = 0, touches X – axis, then the value of α will be.
2. Coordinate of focus of parabola x² = – 10y will be.
3. Write the equation of a circle whose centre is (2,2) and passes through the point (4, 5).
4. The centre of a circle is (5, 7) and touches Y – axis, then its radius will be.
5. If the radius of a circle x² + y² – 6x + ky – 25 = 0 is \(\sqrt {38}\) the value of k will be.
6. Vertex of the parabola y = x² – 2x + 3 will be.
7. Equation of a parabola whose vertex (0, 0) and focus (0, 3) will be.
8. Length of major axis of ellipse 9x² + 16y² = 144 will be.
9. Eccentricity of an ellipse whose latus rectum in half of its minor axis will be.
10. Equation of hyperbola whose one focus in (4, 0 ) and corresponding equation of directrix x = 1 will be.

Answer:

1. ± 4
2. (0, \(\frac { – 5 }{ 2 }\))
3. x² + y² – 4x – 4y – 5 = 0
4. 7, 5
5. ± 4
6. (1, 2)
7. x² = 12y
8. 6
9. \(\frac { \sqrt { 3 } }{ 2 }\)
10. \(\frac { x^{ 2 } }{ 4 } -\frac { y^{ 2 } }{ 12 } \) = 1

Conic Sections Long Answer Type Questions

Question 1.
Find the equation of circle which touches the X – axis at a distance of 4 units in the negative direction and makes intercept of 6 units on positive direction of Y – axis.
Solution:
Here OA = CM = 4, BD = 6.
Length of perpendicular drawn from centre C on BD.
Then, BM = MD = 3
In right angled ∆ CMB,
CB² = CM² + BM²
= 4² + 3²
= 16 + 9 =25
⇒ CB = 5

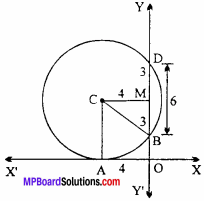
∴ CA = Radius of circle = CB = 5
∴ Centre of circle (- 4, 5) and radius = 5
Hence, equation of circle :
(x + 4)² + (y – 5)² = 5²
⇒ x² + 8x + 16 + y² – 10y + 25 = 25
⇒ x² + y² + 8x – 10y + 16 = 0

Question 2.
Find the equation of circle which touches Y – axis at a distance of 4 units and makes intercept of 6 units on Y – axis?
Solution:
Given : OP = 4, AB = 6, PC = AC = radius.
CM ⊥ AB ∴ AM = BM = \(\frac { 6 }{ 2 }\) = 3
OP = CM = 4
In right angled ∆ AMC,

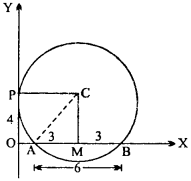
AC² = AM² + CM²
= (3)² + (4)² = 9 + 16 = 25
∴ AC = 5
From figure PC – OM= 5 = radius
Centre of circle is (5, 4) and radius = 5.
Hence, required equation of circle :
(x – 5)² + (y – 4)² = (5)²
x² – 10x + 25 + y² – 8y + 16 = 25
x² + y² – 10x – 8y + 16 = 0.

Question 3.
ABCD is a square. Supposing AB and AD as the coordinate axes. Find the equation of the circle circumscribing the square if each side of square is of length l.
Solution:
Taking AB and AD as X – axis and Y – axis respectively
Given : AB = BC = CD = DA = 1
M is mid point of AB.
N is mid point of AD.
AM = \(\frac { l }{ 2 }\), AN = \(\frac { l }{ 2 }\) = OM
In ∆OAM,
OA² = AM² + OM²
= \(\frac { l }{ 2 }\)² + \(\frac { l }{ 2 }\)²
= \(\frac{l^{2}}{4}+\frac{l^{2}}{4} = \frac{l^{2}}{2}\)
∴ Radius = OA = \(\frac{l}{\sqrt{2}}\)
Centre of circle (AM, OM) = ( \(\frac { l }{ 2 }\), \(\frac { l }{ 2 }\) )

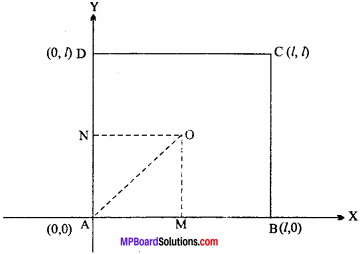
Required equation of circle is :
(x – \(\frac { l }{ 2 }\) )² + (y – \(\frac { l }{ 2 }\) )² = \(\frac{l^{2}}{2}\)
Centre of circle (AM, OM) = (\(\frac { l }{ 2 }\), \(\frac { l }{ 2 }\))
Required equation of circle is :
(x – \(\frac { l }{ 2 }\))² + (y – \(\frac { l }{ 2 }\))² = \(\frac{l^{2}}{2}\)
⇒ x² – lx + \(\frac{l^{2}}{4}\) + y² – ly + \(\frac{l^{2}}{4}\) = \(\frac{l^{2}}{2}\)
⇒ x² + y² – l(x + y) = 0
⇒ x² + y² = l(x + y)

Question 4.
Find the equation of the circle passing through the points (4, 1) and (6, 5). Whose centre lies on line 4x + y = 16. (NCERT)
Solution:
Let the equation of circle be
x² + y² + 2gx + 2 fy + c = 0 …. (1)
It passes through points (4, 1) and (6, 5).
∴ 8g + 2f + c + 17 = 0 …. (2)
and 12g + 10f + c + 61 = 0 …. (3)
Centre of circle (1) is (- g, – f) which lies on line 4x + y = 16.
∴ – 4g – f – 16 = 0
⇒ 4g + f + 16 – 0 …. (4)
Subtracting equation (2) from equation (3), we get
4g + 8f + 44 = 0
⇒ g + 2f + 11 = 0 …. (5)
On solving equation (4) and (5), g = – 3, f = – 4
Put g = – 3 and f = – 4 in equation (2),
– 24 – 8 + C + 17 = 0
⇒ c = 15
Put values of g, f and c in equation (1), then required equation of circle is :
x² + y² – 6x – 8y + 15 = 0.

Question 5.
Find the equation of the circle which passes through the points (2, 3) and (- 1, 1) whose centre lies on line x – 3y – 11 = 0. (NCERT)
Solution:
Let the equation of circle is :
x² + y² + 2gx + 2fy + c = 0 …. (1)
∵Points (2, 3) and (- 1, 1) lies on equation (1),
∴ (2)² + (3)² + 2g(2) + 2f(3) + c = 0
⇒ 4 + 9 + 4g + 6f + c + 13 = 0
4g + 6f + c + 13 = 0 …. (2)
and (-1)² + (l)² – 2g + 2f + c = 0
⇒ 1 + 1 – 2g + 2f + c = 0
⇒ – 2g + 2f + c + 2 = 0 …. (3)

Putting the value of g, f and c in equation (1), then required equation of circle will be :
x² + y² + 2(\(\frac { -7 }{ 2 }\))x + 2(\(\frac { 5 }{ 2 }\))y + c = 0 …. (1)
x² + y² – 7x + 5y -14 = 0.

Question 6.
Find the equation of circle whose radius is 5, centre is on Y – axis and which passes through point (2, 3).
Solution:
Centre of circle is on X – axis, so k = 0.
Let the equation of circle be :
(x – h)² + (y – k)² = a²
Here a = 5
(x – h)² + (y – 0)² = (5)²
(x – h)² + y² = 25
Circle (1) passes through point (2, 3),
∴ (2 – h)² + (3)² = 25
⇒ (2 – h)² = 25 – 9 = 16 = (4)²
⇒ 2 – h = ± 4

Question 7.
y = mx is a chord of the circle whose radius is ‘a’ and its diameter is X – axis. Origin is one of the limiting points of the chord. Show that the equation to a circle whose diameter is the given chord is given by the equation (1 + m²) (x² + y² ) – 2a (x + my) = 0. Solution:
Equation of circle whose radius is a and centre is (a, 0) will be
(x – a)² + y² = a²
⇒ x² – 2ax + y² + a² = a²
⇒ x² – 2ax + y² = 0 …. (1)
Equation of given line is :
y = mx …. (2)
Now, equation of circle passing through the intersection of eqns. (1) and (2) will be :
x² + y² – 2ax + λ(y – mx) = 0 … (3)
Centre of co – ordinate of circle (3) are (\(\frac { λm + 2a }{ 2 }\), \(\frac { λ }{ 2 }\))
∵ Centre lies on line y = mx.
∴ – \(\frac { λ }{ 2 }\) = m\(\frac { λm + 2a }{ 2 }\)
⇒ λ = \(\frac{-2 a m}{1+m^{2}}\)

Put the value of λ in Equation (3),
x² + y² – 2ax + \(\frac{-2 a m}{1+m^{2}}\) (y – mx) = 0
⇒ (l + m²)(x² + y²) = 2ax + 2am²x + 2amy – 2am²x
⇒ (l + m²)(x² + y²) = 2a(x + my)
⇒ (l + m²)(x² + y²) – 2a(x + my) = 0
Which is required equation of circle.

Question 8.
If the straight line x cos α + y sin α = p cuts a circle x² + y² = a² in two points M and N, then show that the equation of the circle whose diameter is MN will be x² + y² – a² = 2p(x cos α + y sin α – p).
Solution:
Given : Equation of line is :
x cos α + y sin α = p …. (1)
and Equation of circle is
x² + y² = a² …. (2)
Now, equation of circle passing through the intersection of line (1) and circle (2) at points M and N is :
x² + y² – a² + λ(x cos α + y sin α – p) = 0 …. (3)
If MN is diameter of above circle then centre is :
(- \(\frac { λ }{ 2 }\)cos α, – \(\frac { λ }{ 2 }\)sin α)
Which is lies on line x cos α + y sin α = p.
– ( \(\frac { λ }{ 2 }\)cos α )cos α + (- \(\frac { λ }{ 2 }\)sin α)sin α = p
⇒ – \(\frac { λ }{ 2 }\)[cos² α + sin² α] = p
⇒ λ = – 2p
Put the value of λ in equation (3), then required equation of circle is
x² + y² – a² – 2p(x cos α + y sin α – p) = 0
⇒ x² + y² – a² = 2p(x cos α + y sin α – p)

Question 9.
Find the following equation of parabola : (i) co – ordinates of focus, (ii) axis, (iii) equation of directrix, (iv) length of Iatus rectum. (NCERT)
(A) y² = 12x
Solution:
Equation of parabola : y² = 12x
Comparing with y² = 4 ax,
4a = 12 ⇒ a = 3
∴Co – ordinates of focus (a, 0) = (3, 0).
Axis of parabola = X – axis.
Equation of directrix is x = – a ⇒ x = – 3.
Length of latus rectum = 4a = 4 x 3 = 12.

(B) x² = 6y.
Solution:
Equation of parabola: x² = 6y
Comparing with x² = 4ay
4a = 6 a ⇒ 3/2
∴ Co – ordinate of focus (0, a) = (0, 3/2).
Axis of parabola = Y – axis.
Equation of directrix is y = – a ⇒ y = – 3/2.

(C) y² = – 8x
Solution:
Equation of parabola : y² = – 8x
Comparing with y² = – 4ax
– 4a – = – 8 ⇒ a = 2
∴ Co – ordinates of focus (- a, 0) = (- 2, 0).
Axis of parabola = X – axis.
Equation of directrix is x = a ⇒ x = 2.
Length of latus rectum 4a = 4 x 2 = 8.

(D) x² = – 16y
Solution:
Equation of parabola : x² = – 16y
Comparing with x² = – 4ay
– 4a = – 16 ⇒ a = 4
∴ Co – ordinate of focus (0, – a) = (0, – 4)
Axis of parabola = Y – axis
Equation of directrix is y = a ⇒ y = 4
Length of latus rectum = 4a = 16.

Question 10.
An equilateral triangle inscribed in the parabola y² = 4ax, where one vertex is at the vertex of parabola. Find the length of the side of triangle. (NCERT)
Solution:
Let the equation of parabola is y² = 4ax.
Let APQ be the equilateral triangle whose vertex A(0, 0), P(h, k) and Q(h, – k).
AP² = (h – 0)² + (k – 0)²
= h² + k²
⇒ AP = \(\sqrt{h^{2}+k^{2}}\)
Similarly, AQ = \(\sqrt{h^{2}+k^{2}}\)

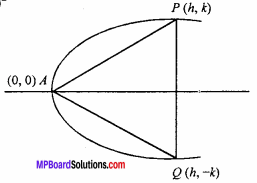
Again, PQ = \(\sqrt{(h-k)^{2}+(k+h)^{2}}\)
= \(\sqrt{(2k)^{2}}\) = 2k
∴ AP = PQ
⇒ \(\sqrt{h^{2}+k^{2}}\) = 2k
⇒ h² + k² = 4k²
⇒ h² = 3k²
⇒ h = \(\sqrt {3}\).k
∵ Point P(h, k) lies on parabola y² = 4ax.
k² = 4ah = 4a.\(\sqrt {3}\)k
⇒ k = 4a\(\sqrt {3}\), [∵ k ≠ 0]
Hence, length of side PQ = 2k = 2.(4a\(\sqrt {3}\)) = 8a\(\sqrt {3}\).

Question 11.
If a parabola reflector is 20 cm in diameter and 5 cm deep. Find the focus. (NCERT)
Solution:
Taking vertex of parabola reflector at origin and X – axis along the axis of parabola.

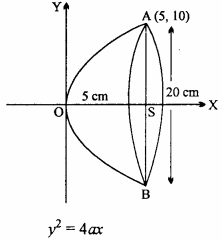
Equation of parabola y² = 4ax …. (1)
Given : OS = 5 cm, AB = 20 cm, AS = 10 cm
∴ Co – ordinate of A will be (5, 10).
∴ (10)² = 4a x 5
⇒ 100 = 20a
⇒ a = 5
∴ OS = 5 cm
Co – ordinates of focus S will be (5, 0).

Question 12.
An arch is in the form of a parabola with its vertical axis. The arch is 10 m high and 5 m wide at the base. How wide it is 2 m vertex of the parabola. (NCERT)
Solution:
Let the equation of parabola is :
x² = 4 ay …. (1)
Given : AB = 5 metre
AF = BF = \(\frac { 5 }{ 2 }\) metre
OE = 2 metre
OF = 10 metre
Co – ordinate of A will be (\(\frac { 5 }{ 2 }\), 10)
This point lies on parabola, hence it will be satisfy equation (1),
∴ \(\frac { 5 }{ 2 }\)² = 4a x 10
⇒ \(\frac { 25 }{ 4 }\) = 4 x a x 10
⇒ a = \(\frac { 25 }{ 4 × 4 × 10 }\)
⇒ a = \(\frac { 5 }{ 32 }\)

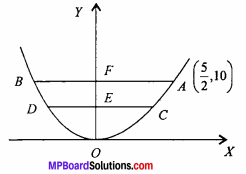
Put the value of a in Equation (1),
∴ x² = 4 x \(\frac { 5 }{ 32 }\)y
⇒ x² = \(\frac { 5 }{ 8 }\)y
Let EC = k
OE = 2
Co – ordinate of C will be (k, 2) and it will satisfy equation of parabola.
We get k² =\(\frac { 5 }{ 8 }\) x 2
⇒ k² = \(\frac { 5 }{ 4 }\)
⇒ k = \(\frac{\sqrt{5}}{2}\)
DE = 2EC
2 x \(\frac{\sqrt{5}}{2}\) = \(\sqrt {5}\)
= 2.23 metre (approx.)

Question 13.
In each of the following ellipse. Find the co – ordinates of the foci and vertices, the length of major axis and minor axis, the eccentricity and the length of latus rectum of the ellipse. (NCERT)
(A) = \(\frac{x^{2}}{36}+\frac{y^{2}}{16}\) = 1.
Solution:
Comparing with standard form of ellipse, \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
We get, a² = 36 ⇒ a = 6, b² = 16 ⇒ b = 4
Here a > b.
∴ b² = a²(1 – e²)
⇒ 16 = 36(1 – e²)
⇒ 1 – e² = \(\frac { 16 }{ 36 }\) = \(\frac { 4 }{ 9 }\)
⇒ e² = 1 – \(\frac { 4}{9 }\) = \(\frac { 5 }{ 9 }\)
∴ Eccentricity e = \(\frac{\sqrt{5}}{3}\)
Foci (± ae, o) = (± 6 × \(\frac{\sqrt{5}}{3}\), o)
= (± 2\(\sqrt {5}\), 0)
Vertices (± a, 0) = (± 6, 0)
Length of major axis = 2a = 2 x 6 = 12.
Length of minor axis = 2b = 2 x 4 = 8.
Length of latus rectum = \(\frac{2 b^{2}}{a}\) = \(\frac { 2 × 16 }{ 6 }\) = \(\frac { 16 }{ 3 }\).

(B) \(\frac{x^{2}}{4}+\frac{y^{2}}{25}\) = 1.
Solution:
Comparing with standard form of ellipse, \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1
We get, a² = 36 ⇒ a = 6, b² = 16 ⇒ b = 4
Here a < b.
∴ a² = b²(1 – e²)
⇒ 4 = 25(1 – e²)
⇒ 1 – e² = \(\frac { 4 }{ 25 }\)
⇒ e² = 1 – \(\frac { 4}{25 }\) = \(\frac { 21 }{ 25 }\)
∴ Eccentricity e = \(\frac{\sqrt{21}}{5}\)
Foci (0, ± b) = (0, ± 5 × \(\frac{\sqrt{21}}{5}\))
= (0, ± \(\sqrt {21}\))
Vertices (0, ± b) = (0, ± 5)
Length of major axis = 2b = 2 x 5 = 12.
Length of minor axis = 2a = 2 x 2 = 8.
Length of latus rectum = \(\frac{2 a^{2}}{b}\) = \(\frac{2 \times 2^{2}}{5}\) = \(\frac { 2 × 4 }{ 5 }\) = \(\frac { 8 }{ 5 }\).

Question 14.
Find the equation of hyperbola whose foci is (± 4, 0) and length of latus rectum is 12. (NCERT)
Solution:
Foci of hyperbola (± 4, 0).
Hence equation of hyperbola will be :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1
Foci (±ae, 0) = (± 4, 0)
∴ ae = 4
Length of latus rectum = \(\frac{2 b^{2}}{a}\) = 12
⇒ b² = 6a
We know, b² = a²(e² – 1)
⇒ 6a = a²e² – a²
⇒ 6a = 4² – a²
⇒ 6a = 16 – a²
⇒ 6a = 16 – a²
⇒ a² + 6a – 16 = 0
⇒ a² + 8a – 2a – 16 = 0
⇒ a(a – 2)(a + 8) = 0
⇒ a = 2, a = – 8, (∵ a cannot be negative)
∴ a = 2
b² = 6a = 6 x 2 = 12
⇒ b = \(\sqrt {12}\)
Putting values of a and b in equation (1), then required equation of hyperbola will be :
\(\frac{x^{2}}{2^{2}}-\frac{y^{2}}{(\sqrt{12})^{2}}\) = 1
⇒ \(\frac{x^{2}}{4}+\frac{y^{2}}{12}\) = 1
⇒ 3x² – y² = 12.

Question 15.
Find the axis, foci, directrix, eccentricity and the latus rectum of the ellipse 9x² + 4y² = 36.
Solution:
Given equation of ellipse
9x² + 4y² = 36
⇒ \(\frac{x^{2}}{4}+\frac{y^{2}}{9}\) = 1
Here, b² > a² or b > a
∴ Major axis = 2.3 = 6
Minor axis = 2.2 = 4
Now,
a² = b²(1 – e²)
(2)² = (3)²(1 – e²)
⇒ 4 = 9(1 – e²)
⇒ \(\frac { 4 }{ 9 }\) = 1 – e²
⇒ e² = 1 – \(\frac { 4 }{ 9 }\) = \(\frac { 9 – 4 }{ 9 }\) = \(\frac { 5 }{ 9 }\)
∴ e = \(\frac{\sqrt{5}}{3}\)
Co – ordinate of foci = (0, ± be )
= (0, ± 3. \(\frac{\sqrt{5}}{3}\))
= (0, ± \(\sqrt {5}\)).
Co – ordinate of vertex = (0, ± b )
= (0 ± 3 ).
Length of latus rectum = \(\frac{2 a^{2}}{b}\)
= \(\frac { 2.4 }{ 3 }\) = \(\frac { 8 }{ 3 }\).

Question 16.
(A) Find the equation of ellipse whose vertices are (± 5, 0) and foci (± 4, 0).
Solution:
Given : Vertices are (± 5, 0) and foci are (± 4, 0)
∴ a = 5
and ae = 4
⇒ 5e = 4
⇒ e = \(\frac { 4 }{ 5 }\)
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1, where a > b …. (1)
∴ From b² = a²(1 – e²),
b² = 5²(1 – (\(\frac { 4 }{ 5 }\))²)
b² = 25(1 – \(\frac { 16 }{ 25 }\))
b² = 25 x \(\frac { 9 }{ 25 }\) = 9
Putting values of a and b in equation (1), the required equation of ellipse will be :
\(\frac{x^{2}}{25}+\frac{y^{2}}{9}\) = 1
⇒ 9x² + 25y² = 225

(B) Find the equation of ellipse whose vertices are (0, ± 13) and foci is (0, ± 5).
Solution:
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1, where a < b …. (1)
Vertices of ellipse = (0, ± b) = (0, ± be)
∴ b = 13
Foci = (0, ± 5) = (0, ± be)
∴ be = 15
⇒ 13 x 3 = 5
⇒ e = \(\frac { 5 }{ 13 }\)
Now, a² = b²(1 – e²)
⇒ a² = 13²[1 – ( \(\frac { 5 }{ 13 }\))² ]
⇒ a² = 169[1 – \(\frac { 25 }{ 169 }\) ]
⇒ a² = 169\(\frac { 169 – 25 }{ 169 }\)
⇒ a² = 144
⇒ a = 12.
Putting values of a and b in equation (1), then required equation of ellipse will be :
\(\frac{x^{2}}{(12)^{2}}-\frac{y^{2}}{(13)^{2}}\) = 1
⇒ \(\frac{x^{2}}{144}+\frac{y^{2}}{169}\) = 1

Question 17.
Find the equation of ellipse whose centre is at (0, 0), major axis on the Y – axis passing through the points (3, 2) and (1, 6).
Solution:
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1, where a < b …. (1)
∵ Equation (1) passes through points(3, 2) and (1, 6)
∴ \(\frac{9}{a^{2}}+\frac{4}{b^{2}}\) = 1 …. (2)
and \(\frac{1}{a^{2}}+\frac{36}{b^{2}}\) = 1 …. (3)
Multiply equation (2) by 9, we get

Putting value of a² in equation (2), we get
\(\frac { 9 }{ 10 }\) + \(\frac{4}{b^{2}}\) = 1
⇒ \(\frac{4}{b^{2}}\) 1 – \(\frac { 9 }{ 10 }\)
⇒ \(\frac{4}{b^{2}}\) = \(\frac { 1}{ 10 }\)
⇒ b² = 40
Putting values of a² and b² in equation (1), then required equation of ellipse will be :
\(\frac{x^{2}}{10}+\frac{y^{2}}{40}\) = 1

Question 18.
Find the equation of ellipse whose major axis on the X – axis which passes through the points (4, 3) and (6, 2).
Solution:
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 …. (1)
∵ It passes through points(4, 3) and (6, 2)
∴\(\frac{36}{a^{2}}+\frac{4}{b^{2}}\) = 1 …. (2)
and \(\frac{16}{a^{2}}+\frac{9}{b^{2}}\) = 1 …. (3)
Subtracting equation (3) from equation (2), we get
\(\frac{20}{a^{2}}-\frac{5}{b^{2}}\) = 1
⇒ \(\frac{4}{a^{2}}-\frac{1}{b^{2}}\) = 1
⇒ \(\frac{4}{a^{2}} = \frac{1}{b^{2}}\)
⇒ a² = 4b²
Putting value of a² in equation (2), we get
\(\frac{36}{4b^{2}}+\frac{4}{b^{2}}\) = 1
⇒ \(\frac{9}{b^{2}}+\frac{4}{b^{2}}\) = 1
⇒ 9 + 4 = b²
⇒ b² = 13
Putting values of a² and b² in equation (1), hence
Required equation of ellipse \(\frac{x^{2}}{52}+\frac{y^{2}}{13}\) = 1

Question 19.
An arch is the form of a semi ellipse. It is 8 m wide and 2 m high of the centre. Find the height of the arch at a point 1-5 m from one end. (NCERT)
Solution:
Let the equation of ellipse is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 …. (1)
Here 2a = 8 ⇒ a = 4, b = 2
Putting the values of a and b, we get

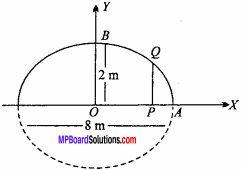
\(\frac{x^{2}}{4^{2}}-\frac{y^{2}}{2^{2}}\) = 1 …. (1)
\(\frac{x^{2}}{16}+\frac{y^{2}}{4}\) = 1
Given :
AP = 1.5m, OA = \(\frac { 8 }{ 2 }\) = 4m,
OP = OA – AP = 4 – 1.5 = 2.5m.
Let PQ = k
∴ Co – ordinate of Q will be (2.5, k), which will satisfy ellipse’s equation.
Hence,
\(\frac{(2.5)^{2}}{16}+\frac{k^{2}}{4}\) = 1
⇒ \(\frac { 6.25}{ 16 }\) + \(\frac{k^{2}}{4}\) = 1
⇒ \(\frac{k^{2}}{4}\) = 1 – \(\frac { 6.25 }{ 16 }\)
⇒ \(\frac{k^{2}}{4}\) = \(\frac { 16 – 6.25 }{ 16 }\)
⇒ k² = \(\frac { 9.75 }{ 4 }\)
⇒ k² = 2.437
⇒ k = 1.56metre (approx).

Question 20.
A rod of length 12 cm moves with its ends always touching the co – ordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the X – axis. (NCERT)
Solution:
Let AB be the rod of length 12 cm which make an angle θ with X – axis.
∴ ∠BAO = θ
AB = 12 cm
AP = 3 cm, then PB = 9 cm

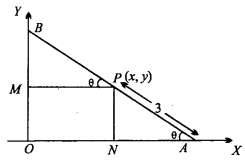
In ∆PNA,
sin θ = \(\frac {PN }{ PA }\) = \(\frac { y }{ 3 }\)
In ∆PMB,
cos θ = \(\frac { PM }{ PB }\) = \(\frac { x }{ 9 }\)
sin²θ + cos²θ = \(\frac { y }{ 3 }\)² + \(\frac { x }{ 9 }\)²
⇒ 1 = \(\frac{y^{2}}{9}+\frac{x^{2}}{81}\)
Hence required equation is :
\(\frac{x^{2}}{81}+\frac{y^{2}}{9}\) = 1

Question 21.
Find the eccentricity, co – ordinate of foci, equation of directrix and length of Iatus rectum of ellipse 4x² + y² – 8x + 2y + 1 = 0.
Solution:
4x² + y² – 8x + 2y + 1 = 0
⇒ 4x² – 8x + y² + 2y +1 = 0
⇒ 4x² – 8x + (y + 1)² = 0
⇒ 4(x² – 2x) + (y + 1)² = 0
⇒ 4(x² – 2x + 1) + (y + 1)² = 4
⇒ 4(x² – 2x + 1) + (y + 1)² = 4
⇒ \(\frac{(x-1)^{2}}{1}+\frac{(y+1)^{2}}{4}\) or \(\frac{X^{2}}{1}+\frac{Y^{2}}{4}\) = 1
Here, b > a
a² = b²(1 – e²)
⇒ 1 = (1 – e²)
⇒ \(\frac { 1 }{ 4}\) = 1 – e²
⇒ e² = 1 – \(\frac { 1 }{ 4}\) = \(\frac { 3 }{ 4}\)
⇒ Eccentricity e = \(\frac{\sqrt{3}}{2}\)
Co – ordinate of foci (0, ± be)
= (0, ±2. \(\frac{\sqrt{3}}{2}\)
= (0, ± \(\sqrt {3}\) )
Here X = 0, Y = ± \(\sqrt {3}\)
∴ x – 1 = 0, y + 1 = ± \(\sqrt {3}\)
⇒ x = 1, y = – 1 ± \(\sqrt {3}\)
foci = (1 ± \(\sqrt {3}\) – 1)
Equation of directrix Y = ± \(\frac { b }{ e}\)
⇒ Y = ± \(\frac{2}{\sqrt{3}}\).2
⇒ Y = ± \(\frac{4}{\sqrt{3}}\)
Y + 1 = \(\frac{4}{\sqrt{3}}\), (∵ Y = y+1)
⇒ y = ± \(\frac{4}{\sqrt{3}}\) – 1
Length of latus rectum = \(\frac{2 a^{2}}{b}\)
= 2. \(\frac { 1 }{ 2 }\) = 1.

Question 22.
Find the vertices, co-ordinate of foci, eccentricity and length of latus rectum of hyperbola :
(A) 9y² – 4x² = 36.
Solution:
Given : 9y² – 4x² = 36
⇒ \(\frac{9 y^{2}}{36}-\frac{4 x^{2}}{36}\) = 1
⇒ \(\frac{y^{2}}{4}-\frac{x^{2}}{9}\) = 1
Comparing the above equation with the standard form of hyperbola
\(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1 …. (1)
b² = 4 ⇒ b = 2, a² = 9 ⇒ a = 3
Let e is the eccentricity of hyperbola.
Then, a² = b²(e² – 1)
⇒ 9 = (e² – 1)
⇒ \(\frac { 9 }{ 4 }\) = e² – 1
⇒ e² = \(\frac { 9 }{ 4 }\) + 1 = \(\frac { 13 }{ 4 }\)
∴ Eccentricity e = \(\frac{\sqrt{3}}{2}\)
Vertices = (0, ± b) = (0, ± 2)
Foci = (0, ± be) = (0, ± 2 x \(\frac{\sqrt{3}}{2}\)) = (0, ±\(\sqrt {3}\))
Length of latus rectum = \(\frac{2 a^{2}}{b}\) = \(\frac { 2 x 9 }{ 2 }\) = 9

(B) 16x² – 9y² = 576.
Solution:
Given : 16x² – 9y² = 576
⇒ \(\frac{16 x^{2}}{576}-\frac{9 y^{2}}{576}\) = 1
⇒ \(\frac{x^{2}}{36}-\frac{y^{2}}{64}\) = 1
Comparing the above equation with the standard form of hyperbola
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 …. (1)
Here, a² = 36 ⇒ a = 6, b² = 64 ⇒ b = 3
We Know that, b² = a²(e² – 1)
64 = 36(e² – 1)
⇒ \(\frac { 64 }{ 36 }\) = e² – 1
⇒ \(\frac { 16 }{ 9 }\) = e² – 1
⇒ e² = \(\frac { 16 }{ 9 }\) + 1 = \(\frac { 25 }{ 9 }\)
∴ Eccentricity e = \(\frac{5}{3}\)
Vertices = (± a, 0) = (± 6, 0)
Foci = (± ae, 0) = (± 6 x \(\frac { 5 }{ 3 }\)) = (± 10, 0)
Length of latus rectum = \(\frac{2 b^{2}}{a}\) = \(\frac { 2 x 64 }{ 6 }\) = \(\frac { 64 }{ 3 }\).

(c) 5y² – 9x² = 36.
Solution:
Given : 5y² – 9x² = 36
⇒ \(\frac{5 y^{2}}{36}-\frac{9 x^{2}}{36}\) = 1
\(\frac{y^{2}}{\frac{36}{5}}-\frac{x^{2}}{4}\) = 1
Comparing the above equation with the standard form of hyperbola
\(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1 …. (1)
Here b² = \(\frac { 36 }{ 5 }\) ⇒ b = \(\frac{\sqrt{6}}{5}\), a² = 4 ⇒ a = 2
We know that, a² = b²(e² – 1)
⇒ 4 = \(\frac{\sqrt{36}}{5}\)(e² – 1)
⇒ e² – 1 = \(\frac { 20 }{ 36 }\) = \(\frac { 5 }{ 9 }\)
⇒ e² = 1 + \(\frac { 5 }{ 9 }\) = \(\frac { 14 }{ 9 }\)

Question 23.
Find the equation of hyperbola whose foci are (0, ± \(\sqrt {10}\)) and which passes through point (2,3).
Solution:
Foci of hyperbola are (0, ±\(\sqrt {10}\)).
∴Form of hyperbola is :
\(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1 …. (1)
Foci (0, ± be) = (0, ± \(\sqrt {10}\))
be = \(\sqrt {10}\)
Equation (1) passes through point (2, 3).
∴ \(\frac{9}{b^{2}}-\frac{4}{a^{2}}\)
⇒ 9a² – 4b² = a²b²
We know that, a² = b² (e² – 1)
⇒ a² = b²e² – b²
a² = ( \(\sqrt {10}\))² – b²
⇒ a² = 10 – b²
⇒ b² = 10 – a²
Putting value of b² in equation (2),
9a² – 4(10 – a²) = a² (10 – a²)
⇒ 9a² – 40 + 4a² = 10a² – a⁴
⇒ 13a² – 40 = 10a² – a⁴
⇒ a⁴ + 13a² – 10a² – 40 = 0
⇒ a⁴ + 3a² – 40 = 0
⇒ a⁴ + 8a² – 5a² – 40 = 0
⇒ a²(a² + 8) – 5(a² + 8) = 0
⇒ (a² – 5)(a² + 8) = 0
a² = 5, a² = – 8
∵ The value of a cannot be negative.
∴ a² = 5
b² = 10 – a²
⇒ b²  = 10 – 5
⇒  b² = 5
Putting values of a² and b² in equation (1), then required equation of hyperbola will be :
\(\frac{y^{2}}{5}-\frac{x^{2}}{5}\) = 1
⇒ y² – x² = 5.

Question 24.
Find the equation of hyperbola in which the distance between foci is 8 and distance between directrix is 6.
Solution:
Let the equation of hyperbola is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) … (1)
and Eccentricity of hyperbola is e and foci are (ae, 0) and (- ae, 0) and latus rectum
are x = \(\frac { a }{ e }\) and x = – \(\frac { a }{ e }\)
Distance between foci = 2ae
Distance between latus rectum = \(\frac { 2a }{ e }\)
According to question, 2ae = 8
and \(\frac { 2a }{ e }\) = 6
Multiplying equation (2) and (3),
4a² = 48 ⇒ a² = 12
⇒ a = 2\(\sqrt {3}\)
Putting value of a in equation (2),
2.2\(\sqrt {3}\)e = 8 ⇒ e = \(\frac{2}{\sqrt{3}}\)
b² = a²(e² – 1)
= 12( \(\frac { 4 }{ 3 }\) – 1) = 4
Putting values of a² and b² in equation (1), the required equation of hyperbola is :
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\)
⇒ x² – 3y² = 12.

Question 25.
Find the centre, eccentricity, foci and length of latus rectum of hyperbola 9x² – 16y² + 18x + 32y – 151 = 0.
Solution:
Equation of hyperbola is :
9x² – 16y² + 18x + 32y – 151 = 0
⇒ 9x² + 18x – 16y² + 32y = 151
⇒ 9(x² + 2x) – 16(y² – 2y) = 151
⇒ 9(x + 1)² – 16(y – 1)² = 151 – 16 + 9
⇒ 9(x + 1)² – 16(y – 1)² = 144
⇒ \(\frac{9(x+1)^{2}}{144}-\frac{16(y-1)^{2}}{144}\)
⇒ \(\frac{(x+1)^{2}}{16}-\frac{(y-1)^{2}}{9}\) = 1
Let x + 1 = X and y – 1 = Y, then equation of hyperbola is
\(\frac{X^{2}}{16} – \frac{Y^{2}}{9}\) = 1
∴ a² = 16 ⇒ a = 4 and b² = 9 ⇒ b = 3.
∴ Centre is (- 1, 1).
For eccentricity = e
b² = a²(e² – 1)
⇒ 9 = 16(e² – 1)
⇒ \(\frac { 9 }{ 16 }\) = e² – 1
⇒ e² = 1 + \(\frac { 9 }{ 16 }\) = \(\frac { 25 }{ 16 }\)
⇒ e = \(\frac { 5 }{ 4 }\)
For foci, X = ± ae, Y = 0
⇒ x +1 = ± 4 x \(\frac { 5 }{ 4 }\), y – 1 = 0
⇒ x + 1 = ± 5, y = 1
⇒ x = 4, – 6, y = 1
∴ Foci are (4, 1) and (6, 1).
Equation of directrix is X = ± \(\frac { a }{ e }\)
⇒ x +1 = ± \(\frac { 4 }{ 5/4 }\)
⇒ x = ± \(\frac { 16 }{ 5 }\) – 1
⇒ x = ± \(\frac { 11 }{ 5 }\) and x = – \(\frac { 21 }{ 5 }\)
⇒ 5x = 11 and 5x + 21 = 0.

Question 26.
If e and ex are the eccentricity of hyperbola \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) and \(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1, then prove that: \(\frac{1}{e^{2}}+\frac{1}{e_{1}^{2}}\) = 1.
Solution:
Equation of hyperbola is
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1
and
\(\frac{y^{2}}{b^{2}}-\frac{x^{2}}{a^{2}}\) = 1
For eccentricity e of equation (1),
b² = a²(e² – 1)
⇒ \(\frac{b^{2}}{a^{2}}\) = (e² – 1)
⇒ e ² = 1 + \(\frac{b^{2}}{a^{2}}\) = \(\frac{a^{2}+b^{2}}{b^{2}}\)
⇒ \(\frac{1}{e_{1}^{2}}\) = \(\frac{a^{2}}{a^{2}+b^{2}}\)
Again for eccentricity e of equation (2),

Question 27.
On a level plain the crack of the rifle and the thud of the ball striking the target are heard at the same instant, prove that the locus of the hearer is a hyperbola.
Solution:
Let P be the situation of hearer and T be the situation of the rifle and S is target. Let the velocity of the ball be v₁ and the velocity of sound be v₂.

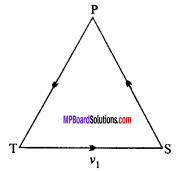
Then,
Time to reach the ball from T to S = \(\frac{T S}{v_{1}}\)
Time to reach the sound from S to P = \(\frac{S P}{v_{2}}\)
and Time to reach the sound from T to P = \(\frac{T P}{v_{2}}\)
∴ The crack of the rifle and the thud of the ball are heard at the same instant.
∴ \(\frac{T S}{v_{1}}\) + \(\frac{S P}{v_{2}}\) = \(\frac{T P}{v_{2}}\)
⇒ \(\frac{T P}{v_{2}}\) – \(\frac{S P}{v_{2}}\) = \(\frac{T S}{v_{1}}\)
⇒ TP – SP = \(\frac{v_{2}}{v_{1}}\)
⇒ PT – PS = A constant (∵ v₂, v₂, TS are constant)
Hence locus of point P is hyperbola whose foci is T and S.

MP Board Class 11th Maths Important Questions