MP Board Class 11th Chemistry Important Questions Chapter 5 States of Matter

Students get through the MP Board Class 11th Chemistry Important Questions Chapter 5 States of Matter which are most likely to be asked in the exam.

MP Board Class 11th Chapter 5 States of Matter

States of Matter Class 11 Important Questions Very Short Answer Type

Question 1.
What is meant by pressure of a gas?
Answer:
Pressure is produced by the collisions of gas molecules on the walls of the container. Force acting per unit area is called pressure.
Pressure =\(\frac{\text { Force }}{\text { Area }}\) = P = \(\frac{\mathrm{F}}{\mathrm{A}}\)
S.l. unit of pressure is Newton/meter². It is also known as pascal.

Question 2.
What is meant by atmospheric pressure?
Answer:
Earth is surrounded by a 800 km thick blanket around it. This air is pulled to wards the earth’s surface due to gravitational force by which a pressure is produced on the earth which is called atmospheric pressure. One atmospheric pressure is equal to the pres¬sure that will support a column of mercury of 76 cm height at 0°C and at standard gravity.

Question 3.
According to one of the postulate of kinetic molecular theory. “There is no intermolecular υ, attractive force in between the gas molecules”.
Up to what extent is this statement correct? Is liquefaction of Ideal gas possible? Explain.
Answer:
This statement is correct only for ideal gas. It is not possible to liquefy an ideal gas because there is no intermolecular force of attraction between the molecules of ideal gas.

Question 4.
Write the definition of absolute zero temperature and state its value in centigrade scale.
Answer:
That imaginative temperature at which volume of a gas becomes zero, is called absolute zero temperature. In centigrade scale its value is -273°C. The temperature measured by this zero is called absolute temperature. It is also expressed by Kelvin.
0°C = 273 K
To convert 0°C temperature to absolute temperature 273 is added to it.

Question 5.
How does the volume of balloons released for the study the weather changes?
Answer:
As the balloon rises up, atmospheric pressure decreases. Due to decrease in pressure, pressure inside the balloon increases and its volume increases.

Question 6.
In winter season a layer of ice is formed on the lake but fish and other organisms present inside remain alive. Why?
Answer:
Maximum density of water is at 4°C temperature but at temperature below 4°C density is less. When the temperature of the lake falls then the water of the surface above becomes more dense and goes down. This order goes on till the temperature does not reach 4°C.

If the tempefature of the surface is less than 4°C, then water remains on the surface above and slowly gets converted to ice where as the water below due to high density remains below and stays in liquid state only. Therefore, organism and fish remain alive in it.

Question 7.
Write name of two intermolecular forces present in HF molecules in liquid state.
Answer:
HF is a polar covalent molecule. In liquid state, it possess intermolecular dipole-dipole force and H-bond.

Question 8.
What is meant by completely elastic collision?
Answer:
Gas molecules move in zig-zag motion in all directions. During this motion, these molecules collide with each other and with the wall of the container. During these collisions, there is a change only in their direction but their kinetic energy remain unchanged. Therefore, these collisions are said to be completely elastic.

Question 9.
Why is the density of hot gas less than cold gas?
Answer:
According to charle’s law, volume of a definite mass of a gas is directly proportional to its absolute temperature. Thus, increase in temperature leads to an increase in volume, but due to an increase in volume density decreases. Therefore, density of hot gas is less than cold gas.

Question 10.
On climbing high mountains, we feel nausea and difficulty in breathing. Why?
Answer:
At high mountains, atmospheric pressure decreases, by which air becomes rarer due to which oxygen in the atmosphere decreases. Therefore, we feel nausea and difficulty in breathing.

Question 11.
What is critical temperature?
Answer:
Critical temperature is that temperature, at which a gas can be liquefied but above this temperature, the gas cannot be liquefied even at high pressure. It is represented by Tc.
Example: Critical temperature of CO₂ is 31.1°C.

Question 12.
What is critical pressure and critical volume?
Answer:
Critical pressure is the minimum pressure required to liquefy the gas at the critical temperature. It is represented by Pe.
The volume occupied by one mole of the gas at critical temperature and pressure is called critical volume. It is represented by Vc.

Question 13.
In automobile vehicles, less air is filled in summer than in winter. Why?
Answer:
When automobile vehicles are in motion then due to friction between the tyre and road, temperature of tyre increases, due to which volume of air inside the tyre increase, as a result of which pressure applied on the tyre also increases. In summer temperature is high which leads to increase in pressure. As a result there is more possibility of the tyre to burst.

Question 14.
What is the S.I. unit for PV²T²/n?
Answer:
\(\frac{\mathrm{PV}^{2} \mathrm{~T}^{2}}{n}\) = \(\frac{\left(\mathrm{Nm}^{-2}\right)\left(\mathrm{m}^{3}\right)^{2}(\mathrm{~K})^{2}}{\mathrm{~mol}}\)
= Nm⁴K²mol^-1.

Question 15.
On the basis of Charles law explain that the minimum possible temperature is -273°C.
Answer:
According to Charles law:
V_t = V₀\([1+\frac{t}{273}]\)
At t = -273°C
V_t= V₀ \([1-\frac{273}{273}] \) = 0
Thus, at -273°C,
volume of gas will become zero and at temperature lower than this, volume will be negative which has no meaning.

Question 16.
Gases which obey Boyle’s, Charles and Avogadro’s law are called Ideal gas? Under which conditions real gas behaves like ideal gas?
Answer:
At low temperature and high pressure, real gases behave like ideal gas.

Question 17.
What is the reason that soda water bottles are stored in cold water in summer?
Answer:
In soda water bottles CO₂ gas is soluble at high pressure. With the increase in temperature solubility decrease due to which high pressure is produced at the walls of the bottle and there are chances of breaking of bottles. Thus, to prevent the bottles from breaking. It is stored in water in hot summer days.

Question 18.
Ammonia bottles are cooled before opening the seal. Why?
Answer:
Bottles of liquid ammonia are cooled before opening because at normal temperature and high pressure it is in liquid state but due to decrease in pressure, it changes to gasesous state.

If NH₃ bottle is opened without cooling, then NH₃ easily changes to vapour and moves out. NH₃ is a harmful gas, its harmful effect can be produced on the person opening it. To prevent from this effect NH₃ bottle is cooled.

Question 19.
Why are liquid drops spherical?
Answer:
Small drops are spherical in shape: Surface tension tries to decrease the surface area of a given liquid for a given volume. Therefore, drops of liquid are spherical because for a given volume sphere has minimum volume.

Question 20.
What is Root Mean Square Velocity and Average velocity?
Answer:
1. Root Mean Square Velocity: It is the square root of the mean of the squares of different velocities of the molecules of gas. It is represented by V.
V = \(\sqrt{\frac{n_{1} v_{1}^{2}+n_{2} v_{2}^{2}+\ldots \ldots}{n}}\)

2.Average velocity: It is the average of the different velocities of all the molecules present in a gas. It is represented by V_n.
V_n = \(\frac{n_{1} v_{1}+n_{2} v_{2}+\ldots \ldots \ldots}{n}\)

Question 21.
Explain the difference between Evaporation and Boiling.
Answer:
Differences between Evaporation and Boiling

Evaporation	Boiling
1. Evaporation decreases spontaneously and occur at all temperatures.	1.Boiling takes place only when the vapour pressure of the liquid becomes equal to atmospheric pressure.
2. Evaporation is a process of the surface of liquid.	2. Boiling is a process of the entire liquid and occurs in the form of bubbles inside the liquid.
3. Evaporation is a slow process.	3. Boiling is a fast process.

Question 22.
What do you mean by compressibility factor of gases?
Answer:
The ratio of observed volume and calculated volume of a gas at a given temperature and pressure is known as Compressibility factor. It is denoted by Z.
Thus, Z = \(\frac{\text { Observed volume }}{\text { Calculated volume }}\) = \(\frac{\text { Real volume }}{\text { Ideal volume }}\)
or Z = \(\frac{\mathrm{PV}}{n \mathrm{RT}}\)
For ideal gases, PV = RT
∴ For ideal gas, Z = 1.

Question 23.
What is the change in melting point of ice with the increase of pressure?
Answer:
Increase in pressure leads to extreme increase in kinetic energy of molecules, as a result of which at low temperature due to kinetic energy of molecules they move independently. Thus on increasing the pressure, ice melts into a liquid at a temperature below its melting point.

Question 24.
Mountaineers carry oxygen cylinders with them on climbing high mountains. Why?
Answer:
At high altitudes, atmospheric pressure decreases, due to which gases become rarer as a result of which amount of oxygen decreases. Thus, mountaineers get less oxygen for breathing due to which they feel uneasy. Therefore, they carry oxygen cylinder with them.

Question 25.
Define viscosity and write the effect of temperature on viscosity.
Answer:
Resistance in flow of any liquid is called viscosity. Such resistance is produced due to internal friction of different layers of liquid.

When temperature is increased, the cohesive force, which opposes liquid flow, decreases and molecular velocity increases. Due to this, viscosity decreases.

Question 26.
Magnitude of surface tension of a liquid depends on the inter attractive force between its molecules. Write the surface tension of the following in their increasing order :
Water, Alcohol (C₂H₅OH) and Hexane [CH₃(CH₂)₄CH₃].
Answer:
In hexane, only london force acts between the molecules. These forces are very weak. H-bond in water molecules is stronger than is alcohol (C₂H₅OH) Thus, increasing order of surface tension is as follows :
Hexane < Alcohol < Water.

Question 27.
At the same temperature if ether and water are poured in different hands, then ether feels more cold. Why? Answer:
In ether, intermolecular forces between its molecules in less as compared to water. Therefore, ether evaporates faster than water and it absorbs the energy required for evaporation from hand, therefore, ether feels cold.

Question 28.
What is surface tension? Write its S.I. unit.
Answer:
It is an important property of a liquid, which is related with interatomic attraction force. Due to compactness, the surface of liquid behaves as a stretched membrane. This effect is called surface tension. “Surface tension is a measure of work which is necessary to increase the unit cross-section of liquid.” Its S.I. unit is Joule/metre² or Newton metre.

Question 29.
Rate of diffusion is slow in liquid. Why?
Answer: Intermolecular force of attraction in liquids is more than in gas, therefore their molecules are held strongly as compared to gas. Therefore, the molecules of liquid cannot move indepnedly like gas molecules and therefore, rate of diffusion in gas is slower than in gas.

Question 30.
Expansion in gases is unlimited. Why?
Answer:
In gases, intermolecular attractive force is negligible, therefore gas molecules moves independently in indefinite order. It does not have a definite shape or volume due to which its molecules expands and acquires the shape and volume of the container.

States of Matter Class 11 Important Questions Short Answer Type

Question 1.
What is meant by S.T.P. and N.T.P.?
Answer:
Volume of a definite amount of gas, changes with temperature and pressure i.e, properties of gas depend on temperature and pressure, therefore, properties of various gases can be compared at a definite temperature and pressure. For this 0°C (273 K) temperature and 1 atmospheric pressure (760 mm) is selected, which is known as Normal temperature, pressure or N.T.P. At N.T.P.

volume of one mole gas is 22.4 litre and 25°C (298K) temperature and 1 atmospheric pressure (760 mm) or 1 bar is known as standard temperature and pressure. At S.T.P. Volume of 1 mole gas is 24.8 litre.

Question 2.
Value of compressibility factor Z of a gas is : Z = \(\frac{\text { PV }}{\text { nRT }}\) (i) What is the value of Z for an ideal gas ? (ii) For real gas, what will be the effect on the value of Z above Boyle’s temperature?
Answer:
(i) For ideal gas, compressibility factor Z = 1.
(ii) Above Boyle’s temperature, real gases show positive deviation. Thus, Z > 1.

Question 3.
For ideal gas, van der Waals’ equation in relation for P, V and is as follows :
\([\mathrm{P}+\frac{a n^{2}}{\mathrm{~V}^{2}}]\) (V – b) = nRT
Where, a and ft are van der Waals’ constant, nb is equal to about total volume of gas molecules a is the measure of resultant of intermolecular attractive forces.
(i) Write the following gases in the increasing order of b. Give reason also. O₂, CO₂, H₂,
(ii) Write the following gases in the magnitude of decreasing order of a CH₄, O₂, H₂
Answer:
(i) Molar volume of gas molecules represents size of a-molecules and van der Waals’ constant ‘b’ represent molar volume of gas molecules. Thus, increasing order of ‘b’ is a follows:
H₂ < He < O₂ < CO₂

(ii) van der Waals’ constant is a measure of magnitude of intermolecular force. In a molecular, with the increase in size of electron cloud, magnitude of intermolecular force of attraction also increases. Thus, for the following gases in order of decreasing value of a is.
CH₄ > O₂ > H₂
Higher the size of electron cloud, higher will be the polarising capacity of the molecules as a result of which london force will be high.

Question 4.
What is Boyle’s law? Write its mathematical expression.
Answer:
Boyle’s law: At constant pressure the volume (V) of a given mass of a gas is inversely proportional to the pressure applied.
Mathematically V ∝ \(\frac{1}{P} \) (At constant temperature for a definite amount of gas)
⇒ P = Constant × \(\frac{1}{\mathrm{~V}}\)
⇒ PV = constant
Thus, at constant temperature, product of volume and pressure of a definite amount of a gas is constant.
In initial state: P₁V₁ = K ………. (i)
In Final state: P₂V₂ = K ……….. (ii)
By equations (i) and (ii)
P₁V₁ = P₂V₂

Question 5.
What is the nature of gas constant (R)?
Answer:
Formula: By, PV = nRT
R = \(\frac{\mathrm{PV}}{\mathrm{nT}}\)

Question 6.
Write Charles law with the derivation of = \(\frac{\mathbf{V}_{1}}{\mathbf{T}_{1}}\) = \(\frac{\mathbf{V}_{2}}{\mathbf{T}_{2}} \)
Answer:
Charles law may also be stated as; The volume of a given mass of gas is directly proportional to the absolute or Kelvin temperature at constant pressure.

Thus, V∝T
or V = constant × T
(By keeping pressure and amount of gas constant)
or \(\frac{\mathrm{V}}{\mathrm{T}}\) = constant

If in initial state, at constant pressure volume of definite amount of gas is V₁ and temperature is T₁ then
\(\frac{\mathrm{V}_{1}}{\mathrm{~T}_{1}}\) = K …………….. (i)
If in final state volume is V₂ and temperature T₂, then
\(\frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}}\) = K ………………. (ii)
By equation, (i) and (ii)
\(\frac{\mathrm{V}_{1}}{\mathrm{~T}_{1}}\) = \(\frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}}\).

Question 7.
On the basis of Charles law, justify the concept of absolute zero.
Answer:
Charles law: According to this law, “At constant pressure, volume of a definite amount of a gas increases or decreases by\(\frac{1}{273}\) of its volume at 0°C with every 1° rise or fall
in temperature”.

If volume of gas at 0°C temperature = V₀ cm³
Volume of gas at 1 °C temperature = V₀\([1+\frac{1}{273}]\)
MLume of gas at t°C temperature = V₀\([1+\frac{t}{273}]\)
Volume of gas at -1°C temperature = V₀\([1-\frac{t}{273}]\)
Volume of gas at -t°C = V₀\([1-\frac{t}{273}]\)
Volume of gas at -273°C = V₀\([1-\frac{273}{273}]\)

By Charles law, it becomes clear that with the decrease in temperature, there is de-crease in volume and at -273°C temperature volume of gas becomes zero. The minimum temperature at which volume of a gas becomes zero is called absolute temperature and the scale based on absolute zero temperature is called kelvin scale and is represented by T.

Question 8.
What is Gay Lussac law?
Answer:
Gay Lussac law: According to this law “At constant volume, pressure of a definite amount of gas is directly proportional to absolute temperature.”

P∝T
⇒ P = K × T
Similarly, in final state pressure is P₂ and temperature is T₂, then
\(\frac{\mathrm{P}_{1}}{\mathrm{~T}_{\mathrm{l}}}\) = K …………. (i)
Similarly, in final state pressure is P₂ and temperature is T₂, then
\(\frac{\mathrm{P}_{2}}{\mathrm{~T}_{2}}\) = K …………. (ii)
By eqns. (i) and (ii) .
\(\frac{\mathrm{P}_{1}}{\mathrm{~T}_{\mathrm{l}}}\) = \(\frac{\mathrm{P}_{2}}{\mathrm{~T}_{2}}\)

Question 9.
What is Avogadro’s law?
Answer:
“Equal volume of all gases, under similar conditions of temperature and pressure contain equal number of molecules”.
If volume of a gas at constant pressure is V, Number of molecules is represented by N .
V ∝ N ……….. (i)
At constant temperature and pressure number of moles n of a gas is directly propor-tional to N.
N ∝n
By equation (i)
V ∝ n
⇒ \(\frac{\mathrm{V}}{n}\) = Constant
If in initial state volume is V₁ and no. of moles is n₁ then
\(\frac{\mathrm{V}_{1}}{n_{1}}\) = constant …(ii)
If in initial state volume is V₂ and no. of moles is n₂, then
\(\frac{\mathrm{V}_{2}}{n_{2}}\) = constant ………… (iii)
By eqns. (ii) and (iii)
\(\frac{\mathrm{V}_{1}}{n_{1}}\) = \(\frac{\mathrm{V}_{2}}{n_{2}}\)

Question 10.
Derive gas equation PV = nRT and write the value of R in two different units.
Or, What is Ideal gas equation ? Derive it.
Answer:
If on adding Boyle’s, Charles and Avogadro’s law for a definite amount of gas, a relation is established between them, then it is known as gas equation.
According to Boyle’s law :
V ∝ C \(\frac{1}{\mathrm{P}}\) (At constant temperature) ……………. (i)
According to Charles law :
V∝T (At constant pressure) ……………… (ii)
According to Avogadro’s law :
V∝n (At constant temperature and pressure) …………………. (iii)
By equations (i), (ii) and (iii)

V ∝ \(\frac{n \mathrm{~T}}{\mathrm{P}}\)
⇒ V = \(\frac{n \mathrm{RT}}{\mathrm{P}}\)
⇒ PV = nRT
Where R is gas constant.

If n = 1, then PV = RT
⇒ \(\frac{\mathrm{PV}}{\mathrm{T}}\) = R
If in initial state pressure is P₁ volume V₁ and temperature T₁ then
\(\frac{P_{1} V_{1}}{T_{1}}\) = R ……………… (iv)
If in final state pressure is P₂, Volume V₂ and temperature T₂ then \(\frac{\mathrm{P}_{2} \mathrm{~V}_{2}}{\mathrm{~T}_{2}}\) = R
By eqns. (iv) and (v)

Volume of R in different units :
1. 0.0821 Litre atm K^-1 mol^-1,
2. 8.314 joule K^-1 mol^-1.

Question 11.
What is Avogadro’s hypothesis? With the help of this prove that volume of one gram of a gas at N.T.P. is 22.4 litre.
Answer:
Avogadro’s law: “At equal temperature and equal pressure, equal volumes of gases have same number of molecules.”
V ∝ n
Volume of one gram mole of a gas at N.T.P.:
Mass of 1 litre gas at N .T. P. Vapour density = \(\frac{\text { Mass of 1 litre gas at } N . T . P .}{\text { Mass of } 1 \text { litre of } H_{2} \text { at N.T.P. }}\)
= \(\frac{\text { Massof 1litre gas at N.T.P. }}{1000 \times 0.00009}\)
( Mass of 1ml of H₂ at N.T.P. = 0.00009 gm)

or Vapour density = \(\frac{\text { Mass of } 1 \text { litre of gas at } \mathrm{N} \text { . T.P. }}{0.09}\) …………… (i)
But, Vapour density = \(\frac{\text { Molecular mass of gas }}{\text { Molecular mass of } \mathrm{H}_{2}}\)
or Vapour denisity = \(\frac{\mathrm{M}}{2 \cdot 016}\) …………….. (ii)

From eqns. (i) and (ii),
\(\frac{\text { Mass of 1 litre of gas at N. T.P. }}{0.09}\) = \(\frac{\mathrm{M}}{2 \cdot 016}\)
∴ Mass of 1 litre of gas at N.T.P. = \(\frac{\mathrm{M}}{2 \cdot 016}\) × 0.09 gm
∵ M ,, ,, ,, = \(\frac{2 \cdot 016 \times \mathrm{M}}{\mathrm{M} \times 0 \cdot 09}\) = 22.4 litre
So, Volume of one gm mole of gas at N.T.P. = 22.4 litre.

Question 12.
What is he effect of increase In temperature on the intermolecular force between the molecules ola liquid ? What is the effect of increase in temperature of the liquid on its viscosity?
Answer:
With the increase in temperature of a liquid, the kinetic energy of its molecules increase due to winch intermolecular force decreases. Thus, liquid can flow easily due to which its viscosity decreases.

Question 13.
How is molar mass of a gas determined by the help of ideal gas equation?
Answer:
By ideal gas equation,
PV = nRT [where, n = no.of moles = \(\frac{\text { Mass }}{\text { Molar mass }}\) \(\frac{\mathrm{W}}{\mathrm{M}}\)]

⇒ PV = \(\frac{\mathrm{W}}{\mathrm{M}}\) × RT
⇒ P = \(\frac{\mathrm{W}}{\mathrm{V}}\) × [Latex]\frac{\mathrm{RT}}{\mathrm{M}}[/latex] [Density = \( \frac{\text { Mass }}{\text { Volume }}\) or ρ =\(\frac{\mathrm{W}}{\mathrm{V}}\)]
⇒ P = ρ × \(\frac{\mathrm{RT}}{\mathrm{M}}\)
⇒ M= ρ × \(\frac{\mathrm{RT}}{\mathrm{P}}\).

Question 14.
By the help of Avogadro’s law, develop a relation between molecular mass and vapour density.
Answer:
Vapour density = \(\frac{\text { Mass of definite volume of a gas }}{\text { Mass of same volume of hydrogen }}\)
Suppose, no. of molecules in definite volume of a gas = n
In the same volume no. of molecules of hydrogen = n

Vapour density = \(\frac{\text { Mass of } n \text { molecules of gas }}{\text { Mass of } n \text { molecules of hydrogen }}\)
= \(\frac{\text { Mass of 1,molecules of gas }}{\text { Mass of } 1 \text { molecules of hydrogen }}\)
= \(\frac{\text { Mass of } 1 \text { molecules of gas }}{2 \times \text { Mass of } 1 \text { atom of hydrogen }}\)
Vapour density = \(\frac{1}{2}\) × Molecular mass of gas
Thus, molecular mass = 2 × Vapour density.

Question 15.
Write numerical value of R in different units.
Answer:
Numerical value of R in different units is as follows :

1. 0.0821 litre atm K^-1 mol^-1
2. 8.31 ×10⁷ erg K^-1 mol^-1 .
3. 82.05 atm cm³ K^-1 mol^-1
4. 8.31 joule K^-1 mol^-1
5. 62.3 litre mm K^-1 mol-1
6. 1.99 cal K^-1 mol^-1 .
7. 8.31 pa dm³ K^-1 mol^-1.

Question 16.
Derive gas equation by the help of kinetic equation.
Answer:
According to the postulate of kinetic theory, average kinetic energy of molecules is directly proportional to absolute temperature.

Average kinetic eneigy = \( \frac{1}{2}\)mnv²
\( \frac{1}{2}\)mnv² ∝ T
⇒\( \frac{1}{2}\)mnv² = KT
⇒ \( \frac{3}{2}\) × \( \frac{1}{3}\)mnv² = KT
⇒ \( \frac{1}{3}\)mnv² = \( \frac{2}{3}\)KT
⇒ PV = \( \frac{2}{3}\)KT [∵ \( \frac{1}{3}\)mnv² = PV]
⇒ \(\frac{\mathrm{PV}}{\mathrm{T}}\) = \( \frac{2}{3}\)K
⇒ \(\frac{\mathrm{PV}}{\mathrm{T}}\) = R [ ∵ \( \frac{2}{3}\)K = constant (R)] PV = RT .

Question 17.
What is Dalton’s law of partial pressure?
Answer:
Dalton’s law of partial pressure: Dalton observed that if two or more gases which do not react chemically are enclosed in a space the total pressure P, exerted by the gaseous mixture is the sum of partial pressures P₁, P₂, P₃, etc., which each one will exert if present alone in that space.

This law states, “The total pressure of mixture of gases (or vapour) which does not react chemically is equal to the sum of the partial pressure of the component gases.”
Mathematically, it is expressed as,
P = P₁+P₂+P₃+………………………+P_n.

Question 18.
Write Graham’s law of diffusion. What types of calculations can be performed by the help of it?
Answer:
Graham’s law of diffusion: For any specified temperature and pressure the relative rates of diffusion of gases through a porous partition are inversely proportional to the square roots of their densities.
Thus, Rate of diffusion ∝ \(\sqrt{\frac{1}{\text { Density }}}\)

Let r₁ and r₂ be the rate of diffusion of two gases A and B, d₁ and d₂ are their densities respectively.
According to Graham’s law of diffusion,
r₁ ∝ \(\sqrt{\frac{1}{d_{1}}}\) and r₂∝ \(\sqrt{\frac{1}{d_{2}}}\)
Thus, \(\frac{r_{1}}{r_{2}}\) = \(\sqrt{\frac{d_{2}}{d_{1}}}\) (At the same temperature and pressure)

where M₁ and M₂ are the molecular masses of two gases.
But, Density = \(\frac{\text { Molecular mass }}{2}\)
∴ \(\frac{r_{1}}{r_{2}} \) = \(\sqrt{\frac{\mathrm{M}_{2}}{2} / \frac{\mathrm{M}_{1}}{2}}\)
or \(\frac{r_{1}}{r_{2}} \) = \(\frac{\mathrm{M}_{2}}{\mathrm{M}_{1}}\) = \(\frac{\sqrt{d_{2}}}{\sqrt{d_{1}}}\)

Question 19.
The relation between (P_Ideal) observed by an ideal gas and observed pressure (P_Real) is as follows :
P_Ideal = P_Real + \(\frac{a n^{2}}{V^{2}}\)
(i) If pressure is taken in Nm², no. of moles in mol and volume in m³, then deter mine the unit of ‘a’.
(ii) If pressure is taken in atm and volume in dm3, then determine the unit of ’a’.
Answer:
(i) a = \(\frac{\mathrm{PV}^{2}}{n^{2}}\)
Given, Unit of P = Nm^-2, V = m³ and n mole
∴ Unit of a = \(\frac{\mathrm{Nm}^{-2}\left(\mathrm{~m}^{3}\right)^{2}}{(\mathrm{~mol})^{2}}\) = Nm₄mol^-2

(ii) Given, Unit of P = atm, V = dm³, n = mol
∴Unit of a = \(\frac{\mathrm{PV}^{2}}{n^{2}}\) = \(\frac{a t m \cdot\left(d m^{3}\right)^{2}}{m o l^{2}}\) =atm dm⁶mol^-2.

Question 20.
Write the applications of Graham’s law of diffusion.
Answer:

• In (he determination of density and molecular mass of gas: If time of diffusion and density of a gas is known and time of diffusion of the other gas is known, then by its help density and molecular mass of the other gas can be determined.
• Marsh gas indicator: People working in coal mines can become alert from the leakage of poisonous gases by the help of this indicator.
• In the Separation of gases: Due to difference in the rate of diffusion of gases, they can be easily separated from their mixture.
• Bad odour: Bad odour and poisonous gas due to diffusion in air goes on separating.

Question 21.
On heating fine corners of glass in a flame to its melting point, why does it becomes smooth ? Write the name of the property responsible for it.
Answer:
Glass of fine corners are made smooth by heating in a flame because on heating glass melts and corner of the liquid tries to achieve a round shape, whose surface tension is minimum. This is known as of glass.

Question 22.
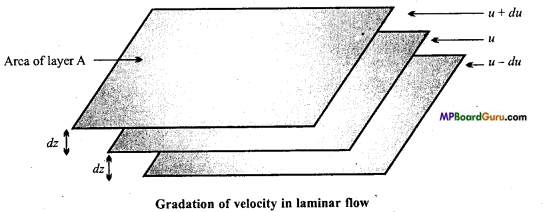
Discuss the step of‘Laminar flow’. Is velocity of every particle of laminar flow same? Discuss your answer.
Answer:
When flow of liquid is on fixed surface then the larger of liquid which is in contact with the surface become stationary as the distance of the upper layers from the fixed surface increases, velocity of layer goes on increasing.

This type of flow, in which velocity of one layer increases by the other layer is called laminar flow. In laminar flow, speed of particles in all the layers is not same because a layer applies friction or resistance flow on the layer below:

Question 23.
Derive Dalton’s law of partial pressure on the basis of kinetic theory.
Answer:
Suppose n₁ molecules of mass m₁ gram of a gas A are closed in a container of volume V, then
P_AV = \(\frac{1}{3}\)m₁n₁v₁²
P_A = \(\frac{1}{3}\) \(\frac{m_{1} n_{1} v_{1}^{2}}{\mathrm{~V}}\)

Similarly, P_B = \(\frac{1}{3}\)\(\frac{m_{1} n_{1} v_{2}^{2}}{\mathrm{~V}}\)
If both the gases are closed in the container at the same temperature, then pressure of the mixture
P = \(\frac{m_{1} n_{1} v_{1}^{2}}{\mathrm{~V}}\) + \(\frac{m_{1} n_{1} v_{2}^{2}}{\mathrm{~V}}\)
P = P_A + P_B
This is Dalton’s law of partial pressure.

Question 24.
Derive Avogadro’s law by the help of kinetic equation.
Answer:
According to Avogadro’s law “Equal volume of all gases under the same temperature and pressure contain equal number of molecules”.
If there are two gases :
For first gas PV = \(\frac{1}{3}\)m₁n₁v₁² ……………. (i)
For second gas PV = \(\frac{1}{3}\) m₁n₁v₂² ……………. (ii)
By eqns. (i) and (ii)
\(\frac{1}{3}\)m₁n₁v₁² = \(\frac{1}{3}\) m₁n₁v₂²
⇒ m₁n₁v₁² = m₁n₁v₂²

If temperature of both the gases are same, then their kinetic energy will also be same.
Thus,
\(\frac{1}{2}\)m₁v₁¹ = \(\frac{1}{2}\) m₂v₂²
⇒ m₁v₁¹ = m₂v₂² ……………. (iv)
Dividing eqns. (iii) by eqns. (iv)
\(\frac{m_{1} n_{1} v_{1}^{2}}{m_{1} v_{1}^{2}}\) = \(\frac{m_{2} n_{2} v_{2}^{2}}{m_{2} v_{2}^{2}}\)
∴ n₁ = n₂

Question 25.
How is rate of diffusion of gases compared?
Answer:
Suppose, two gases A and B of same volume V require time t₁, and t₂ for diffusion.
r₁ = \(\frac{\mathrm{V}}{t_{1}}\)
and r₂ = \(\frac{\mathrm{V}}{t_{2}}\)
∴ \(\frac{r_{1}}{r_{2}}\) = \(\frac{\mathrm{V}}{t_{1}}\) × \(\frac{t_{2}}{V}\) = \(\frac{t_{2}}{t_{1}}\)

Thus, \(\frac{r_{1}}{r_{2}}\) = \(\frac{t_{2}}{t_{1}}\) = \(\frac{\sqrt{d_{2}}}{\sqrt{d_{1}}}\)
[∵ \(\frac{r_{1}}{r_{2}}\) = \(\left.\sqrt{\frac{d_{2}}{d_{1}}}\right]\)

Question 26.
Using gas equation, justify that at a given temperature, density of a gas is directly proportional to pressure of the gas.
Answer:
PV = nRT
PV =\(\frac{m}{M} \)RT [ n = \(\frac{m}{M}\) = \(\frac{\text { Mass of gas (g) }}{\text { Molar mass of gas }}\)

or P = \(\frac{m \mathbf{R} \mathrm{T}}{\mathrm{VM}}\) [ ∵ Density ,d =\(\frac{m}{V}\) ]
or P = \(\frac{d \mathrm{RT}}{\mathrm{M}}\)
or P = \(\frac{\mathrm{PM}}{\mathrm{RT}}\)
If T = Constant
d ∝ P.

Question 27.
Derive Charles law on the basis of kinetic theory.
Answer:
By kinetic theory, kinetic energy of gas molecules is directly proportional to absolute temperature.
Thus, kinetic energy ∝T
\(\frac{1}{2}\)mnv²
⇒ \(\frac{1}{2}\) mnv² = KT
⇒ \(\frac{3}{2}\) × \(\frac{1}{3}\)mnv² = KT

⇒ \(\frac{1}{3}\) mnv² = \(\frac{2}{3}\)KT
⇒ PV = \(\frac{2}{3}\)KT , [∵ \(\frac{1}{3}\)mnv² = PV]
⇒ V = \(\frac{2}{3}\) \(\frac{\mathrm{K}}{\mathrm{P}}\).T
At constant pressure \(\frac{2}{3}\) \(\frac{\mathrm{K}}{\mathrm{P}}\) = Constant
∴ V = Constant × T
⇒ V ∝ T.

Question 28.
What is Ideal gas? Write its characteristics.
Answer:
Ideal gas: Gas which obey gas laws and gas equation at all pressure and temperature is called Ideal gas.

Characteristics :

• At constant temperature, product of pressure and volume of a gas should always be constant and at constant temperature graph between PV and P should be a horizontal line.
• If ideal gas is cooled at constant pressure, then its volume should decrease gradually and at -273°C temperature it should be zero.
• Without external work, there should be no thermal effect on its expansion or contraction.
  PV
• Value of compressibility factor of ideal gas z =\(\frac{\mathrm{PV}}{n \mathrm{RT}}\) is 1.

Question 29.
What is Real gas? What are its characteristics?
Answer:
Gas which does not obey Boyle’s law, Charles law and ideal gas equation strictly is called Real gas.

Characteristics:

• Force of attraction between gas molecules is negligible.
• Volume of a molecule is not considered to be negligible as compared to the total volume of gas.
• At -273°C their volume does not become zero because maximum gases get converted into liquid before cooling.
• At low temperature and high-pressure gases do not obey Boyle and Charles law.

Question 30.
Write difference between Real and Ideal gas under four points.
Answer:
Differences between Ideal gas and Real gas

Ideal gas	Real gas
1. Ideal gas obeys the equation, PV = RT at all temperatures and pressure.	1. Real gas obeys PV = RT only at low pressure and high temperature.
2. There is no ideal gas, they are hypothetical.	2. All existing gases are real gases and show deviation from ideal gas behaviour, positive or negative.
3. Total volume of gas molecules is supposed to be negligible in comparison to total volume.	3. Volume of gas molecules are not negligible in comparison to total volume.
4. There is no attraction force between gas molecules.	4. Gas molecules attract each other. Therefore, total pressure is less than ideal gas.
5. Value of compressibility factor for ideal gas is 1.	5. Value of compressibility factor for ideal gas is not zero.

Question 31.
Explain Boyle’s law on the basis of kinetic theory.
Answer:
Pressure of gas is produced by the collisions of its molecules on the walls of the container. Thus magnitude of pressure depends on the frequency of collisions, which in turn depend on number of molecules and their velocity. If volume of gas is reduced, then number of molecules in unit volume increase, as a result of which number of molecules colliding on unit area in unit time increases.

Alternatively if volume is increased, number of molecules present in unit area will decrease, due to which number of collisions on unit area in unit time will decrease by which there will be decrease in pressure. Thus, it is justified that at constant temperature volume of definite amount of gas is inversely proportional to pressure.

Question 32.
Explain Charles law by the help of kinetic equation of gases.
Answer:
With the increase in temperature of gas, its kinetic energy also increase as a result of which velocity of molecules increases and due to increase in velocity possibility of collisions between the molecules increase. The force with which they collide increase as result of which pressure increase.

If pressure is to be kept constant, then it is necessary that possibility of collisions between the molecules should not increase. It may be possible, only when distance between the gas molecules may increase thus volume may increase. Thus, it is clear that at constant pressure volume of a definite amount of gas is directly proportional to absolute temperature.

States of Matter Class 11 Important Questions Long Answer Type

Question 1.
Write the main postulates of kinetic theory of gases.
Answer:
Following are the main postulates of kinetic theory of gases :

• Every gas consists of extremely small particles called molecules, which are assumed to be pointed masses dispersed in a lot of vacant space. The molecules of any given gas are identical and have same mass (m).
• The molecules of a gas are in a state of constant random motion in all possible directions colliding with one another and the walls of the container. .
• Molecules travel in straight lines with uniform velocity till they collide with other molecules or with the walls of the vessel.
• The molecules have no force of attraction between them. The force of gravity on them is negligible.
• The pressure on the gas is due to the hits, recorded by the molecules on the walls of the vessel.
• The molecules are perfectly elastic, i.e., there is no loss of energy as a result of such collisions.
• The average kinetic energy of the molecules is directly proportional to the absolute temperature (T) of the gaseous system. With the increase of temperature, the average kinetic energy of the gas molecules increases.

Question 2.
Derive an expression for pressure of gas on the basis of kinetic gas theory. Or, Prove the kinetic gas equation PV = \(\frac{1}{3} \)Mv².
Answer:
Suppose in a cubic vessel some gas is present for which :
Length of core of cube = l cm,
Number of moles of gas = n,
Mass of one molecule of gas = m,
Root Mean Square velocity = v.

Though gas molecules move in all possible directions but for a particular time the movement of any molecule can be resolved in X, Y and Z-directions. Let n/3 molecules move in a particular direction and these particles colloid one face and after collision they return back to opposite direction. If locity is – v, because molecules are elastic in nature.
∴ Momentum before collision = mv and
Momentum after collision = -mv

Change in momentum in each collision = mv – (- mv) = 2 mv
This molecule will colloid with face A after 2l distance,
∵ Molecule travel v cm in one second.
∵ Time required to travel 21 distance = \(\frac{2 l}{v}\) seconds.
Number of collisions in each second = \(\frac{v}{2 l}\)
∴ Change in momentum in face A per second = 2mv× \(\frac{v}{2 l}\) = \(\frac{m v^{2}}{l}\)

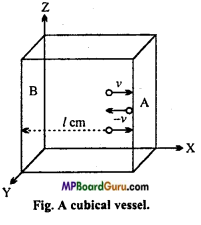
This change in momentum is for one molecule but there is \(\frac{n}{3}\) molecules behaving same, therefore the change in momentum for \(\frac{n}{3}\) molecules = \(\frac{m v^{2}}{l}\) × \(\frac{n}{3}\) = \(\frac{1}{3}\). \(\frac{m n v^{2}}{l}\)
But, rate of change of momentum = Force

F = \(\frac{1}{3}\).\(\frac{m n v^{2}}{l}\)
Force per unit area is called pressure, suppose area of face A is ‘a’.
∴ P = \(\frac{1}{3}\) .\(\frac{m n v^{2}}{a \times l}\)
or P = \(\frac{1}{3}\).\(\frac{m n v^{2}}{\mathrm{~V}}\)
[∵ a × l = V(volume)]
or PV = \(\frac{1}{3}\)mnv²
This is called kinetic gas equation.
∵ m ×n = M, (where,M = molecular mass)
So, PV = \(\frac{1}{3}\)Mv².

Question 3.
To justify the ideal behaviour of gases. What modification did van der Waals do in gas equation?
Answer:
According to van der Waals, the reason for deviation of real gases from ideal behaviour is some errotic concepts in postulates of kinetic theory of gases. Two postulates which are supposed doubtful are following:

1. Actual volume of gas molecules is negligible in comparision to total volume which gas occupies.
2. There is no attractive force between gas molecules.

Actually these concepts are not true in all conditions. At high pressure and very low-temperature volume of gas becomes very less. At this condition, the volume of gas molecules are not negligible because molecules are not compressible.

At high pressure and low temperature when volume of gas becomes very less, gas molecules come very close to each other and attractive force between molecules is produced which cannot be supposed negligible.

Volume correction : Since at normal temperature and low pressure the volume of a molecule cannot be considered to be negligible as compared to the total volume of the gas and this effective volume is represented by constant b. Thus in gas equation in place of volume V, (V – b) must be used, which is available for independent motion of molecules.

Pressure correction: It exerts less pressure. In other words, observed pressure is less than the ideal pressure (P).
Hence, corrected pressure P + p
Where,p is the correction term and it is proportional to the density of the gas near the wall and the density of the gas inside i.e.,
p ∝ (Density)²
But, Density ∝ \(\frac{1}{\mathrm{~V}}\) (For one mole)
and Density ∝ \(\frac{n}{V}\), (For one moles)
Hence, p ∝ \(\frac{1}{\mathrm{~V}^{2}} \), (For one mole)
or p = \(\frac{a}{V^{2}}\)

Where, a is a constant depending upon the nature of gas.
∴ p = \(\frac{a n^{2}}{V^{2}}\) (For n moles)
Hence, corrected pressure = \(\left(\mathrm{P}+\frac{a}{\mathrm{~V}^{2}}\right) \) (For 1 mole)
= \(\left(\mathrm{P}+\frac{a n^{2}}{\mathrm{~V}^{2}}\right)\) (For n moles)
Substituting the corrected values of volume and pressure in the ideal gas equation, we get
\(\left(\mathrm{P}+\frac{a n^{2}}{\mathrm{~V}^{2}}\right)\) (V – nb) = nRT
This is known as van der Waals’ equation.

Question 4.
What do you understand by viscosity? Which factors affect viscosity?
Answer:
Every liquid possess a tendency to flow because intermolecular attractive force in liquids is less and they are incompressible. Some liquids like honey, castor oil etc. flow rapidly. Difference in rate of flow is due to viscosity. Viscosity is internal resistance to flow in liquids, which arises due to internal friction between the layers of liquids.

Liquid is made up of various layers. When a liquid flows on any surface then these layers flow with various velocities. Molecules present in various layers of liquid attract each other and this intermolecular attractive force produce resistance.

Factors which affect viscosity :

1. Intermolecular attractive force: Intermolecular attractive force resist the flow of molecules in liquids. Thus viscosity depend on inter-molecular attractive force. Higher the intermolecular attractive force, higher is the viscosity.
2. Molecular mass: Viscosity increases with the increase in molecular mass.
3. Pressure: Increase in pressure leads to a decrease in volume as a result intermolecular attractive force increases therefore, due to increase in pressure viscosity increases.
4. Temperature: By increase in temperature cohesive force which reduces the flow of liquid decreases by which molecular motion increase. Thus, viscosity decreases.

Question 5.
What is Surface tension? Discuss the factors affecting it.
Answer:
It is an important property of a liquid, which is related with interatomic attraction force. The molecules present inside the liquid is attracted equally by molecules present in all direction. But molecule present on the surface of liquid is attracted by molecules at bottom and insides, as a result the molecules at surface are pulled downward and nature of surface is to lessen the area.

Due to compactness, the surface of liquid behaves as a stretched membrane. This effect is called Surface tension.

“Surface tension is a measure of work, which is necessary to increase the unit cross-section of liquid.”
Its S.I. unit is Joule / metre² or Newton metre.

Factors affecting Surface tension :
1. Temperature: On increasing the temperature, intermolecular attractive force decreases due to which surface tension decreases.
2. Solute: On mixing solute in liquids surface tension is affected.

• If surface tension of solute is equal to the surface tension of solute then surface tension is directly proportional to the amount of solute. Higher the amount of solute mixed, higher is the surface tension.
• If surface tension of solute is less than the surface tension of liquid then, surface tension of liquid decreases.
• Surface tension of liquids decreases on adding substances activating the surface.
  Like – Soap, detergents etc.

Question 6.
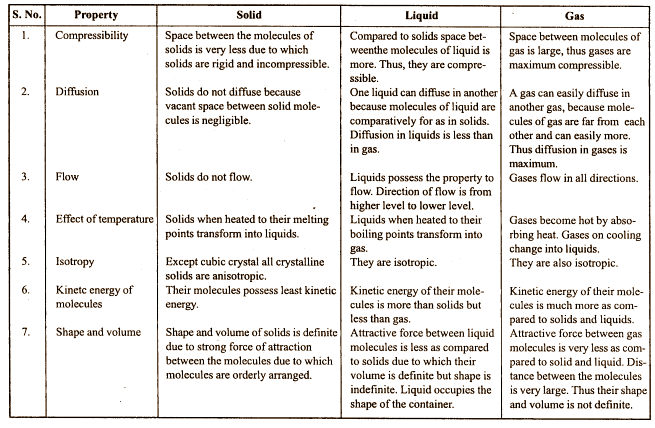
Solid, liduid and gas differ in structure .write
Answer:
Structural difference between solid, liquid and gas.

States of Matter Class 11 Important Numerical Questions

Question 1.
How many moles of hydrogen are present in 1000 cm3 of hydrogen at 760mm pressure of mercury and 300K temperature?
Solution:
P = 760 mm Hg, V = 1000 cm₃ or 1 liter, T = 300 K, n = ?, R = 62.35 mm KT^-1mol^-1 ∵ PV =RT
∴ n = \(\frac{P V}{R T}\) = \(\frac{760 \times 1}{62 \cdot 35 \times 300}\)
= 4.06 × 10^-2mol.

Question 2.
Volume of a gas at 27°C is 30 ml. If at constant pressure, temperature of this gas is made 37°C, then what will be the new volume of the gas?
Solution:
V₁ = 30 ml, V₂ = ?, T₁ = 273 + 27 = 300 K, T₂ = 273 + 37 = 310 K.
∴ \(\frac{\mathrm{V}_{1}}{\mathrm{~T}_{1}}\) = \(\frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}}\)
or V₂ = \(\frac{\mathrm{V}_{1} \times \mathrm{T}_{2}^{\circ}}{\mathrm{T}_{1}}\)
⇒ V₂ = \(\frac{30 \times 310}{300}\) = 31ml.

Question 3.
A container is filled with air at atmospheric pressure and it is closed with cork at 35 °C temperature. Calculate that how much heating is required to be thrown out of cork? It is known that three times of pressure is required for throwing out of cork.
Solution:
Given, P₁ = 1 (atmospheric pressure), P₂ = 3 (three times of P₁),
T₁ =273 + 35 = 308K, T₂ =?

From temperature, pressure law of constant volume,
\(\frac{P_{1}}{T_{1}}\) = \(\frac{\mathrm{P}_{2}}{\mathrm{~T}_{2}}\)
or T₂ = \(\frac{P_{2} T_{1}}{P_{1}}\) = \(\frac{3 \times 308}{1}\) = 924K.
∴ Required temperature = 924 – 273 =651° C.

Question 4.
A gas mixture contains 2.8 gm N₂ and 4.0 gm Ne, volume of this mixture is 5 litre at 25 °C. Calculate partial pressure of each gas.
Solution:
Moles of N₂= \(\frac{2 \cdot 8}{28} \) = 0.1
Moles of Ne = \(\frac{4}{20 \cdot 18}\)
Let partial pressure of N₂ and Ne are P₁ and P₂ respectively.

For N₂, P₁ = \(\frac{n_{1}}{\mathrm{~V}} \mathrm{RT} \)
= \(\frac{0 \cdot 1}{5}\) × 0.0821 × 298 = 0.4893 atm
For Ne, P₂ = \(\frac{n_{2}}{V} R T\)
= \(\frac{4 \times 0 \cdot 0821 \times 298}{20 \cdot 18 \times 5}\) = 0.9699 atm.
Thus, Partial pressure of N₂ = 0.4893 atm. ≈ 0.49 atm.
Partial pressure of Ne = 0.9699 atm. ≈ 0.97 atm.

Question 5.
If ratio of rate of diffusion of an unknown gas and CO₂ is 40 :45. Determine the molecular mass of the unknown gas.
Answer:
r₁ : r₂ = 40 : 45, M₂ = 44, M₁ = ?
∴ \(\frac{r_{1}}{r_{2}}\) = \(\sqrt{\frac{\mathrm{M}_{2}}{\mathrm{M}_{1}}}\)
⇒ \(\frac{40}{45}\) = \(\sqrt{\frac{44}{\mathrm{M}_{1}}}\) or \(\frac{40^{2}}{45^{2}}\)= \( \frac{44}{\mathrm{M}_{1}}\) or M₁ = \(\frac{44 \times 45 \times 45}{40 \times 40}\) = 55.6875

Question 6.
If relative density of chlorine is 36 and for the diffusion Of 15 volume of hydrogen from a porous pot 40 seconds is required, then in the same state 30 volume of chlorine will diffuse in how much time ?
solution:
d₁ =1,
d₂ = 36,
r₁ = \(\frac{25}{40}\)
r₂ = \(\frac{30}{t}\)
∴\( \frac{r_{1}}{r_{2}}\) = \(\sqrt{\frac{d_{2}}{d_{1}}}\)
⇒ \(\frac{\frac{25}{40}}{\frac{30}{t}}\) = \(\sqrt{\frac{36}{1}}\)
⇒ \(\frac{25 \times t}{40 \times 30}\) = 6
⇒ t = \(\frac{6 \times 40 \times 30}{25}\) = 288 second.

Question 7.
Volume of a gas at 27°C is 500 ml. What will be its volume at 0°C?
Solution:
V₁ = 500 ml, V₂ = ?, T₁ = 27°C = 27 + 273 = 300 K,
T₂ =0° C= 0 + 273 = 273 K.
According to Charles law
\(\frac{\mathrm{V}_{1}}{\mathrm{~T}_{1}}\) = \(\frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}}\)
or \(\frac{500}{300}\) = \(\frac{\mathrm{V}_{2}}{273}\)
or V₂ = \(\frac{500 \times 273}{300}\) = 455 ml.

Question 8.
Volume of a gas at 27°C temperature and 760 mm. pressure is 1000 ml. What will be the volume of the gas at 327°C temperature and 380 mm. pressure?
Solution:
Given, V₁ = 1000 ml, V₂ = ?
T₁ = 27° C or 273 + 27 = 300K, T₂ = 327° C or 273 + 327 = 600K,
P₁ = 760mm, P₂ = 380mm
∴ \(\frac{P_{1} V_{1}}{T_{1}}\) = \(\frac{\mathrm{P}_{2} \mathrm{~V}_{2}}{\mathrm{~T}_{2}}\)
⇒ \(\frac{760 \times 1000}{300}\) = \(\frac{380 \times \mathrm{V}_{2}}{600}\)
∴ V₂ = \(\frac{760 \times 1000 \times 600}{300 \times 380}\) = 4000ml.

Question 9.
What will be the minimum pressure rquired to compress 500 dm³ of air at 1 bar to 200 dm³ at 30°C? (NCERT)
Solution:
P₁ = 1bar, P₂ = ?, V₁ = 500 dm³, V₂ = 200 dm³
By Boyle’s law P₁V₁ = P₂V₂
P₂ = \(\frac{\mathrm{P}_{1} \mathrm{~V}_{1}}{\mathrm{~V}_{2}}\) = \(\frac{1.2 \mathrm{bar} \times 120 \mathrm{ml}}{180 \mathrm{ml}} \) = 0.8 bar
P₂ = 0.8 bar

Question 11.
What will be the pressure exerted by a mixture of 3.2g of methane and 4.4g of carbondioxide contained in a 9 dm³ flask at 27° C ? (NCERT)
Solution:
Number of moles in CH₄

Question 12.
34.05 ml if phosphorus vapour weighs 0.0625g at 546°C and 0.1 bar pressure. What is the molar mass of phosphorus ? (NCERT)
Solution:
∵ Ideal gas equation PV = nRT
∴ PV = \(\frac{m \mathrm{RT}}{\mathrm{M}}\)
( m = Mass of phosphorus (g) and M = Molar mass of phosphorus)
M = \(\frac{m \mathrm{RT}}{\mathrm{PV}}\)
M = \(\frac{0.0625 \mathrm{~g} \times 0.0821 \mathrm{Latm} \mathrm{K}^{-1} \mathrm{~mol}^{-1} \times 819 \mathrm{~K}}{0 \cdot 1 \times 0 \cdot 987 \mathrm{~atm} \times 0 \cdot 03405 \mathrm{~L}}\)
M = 1250.4gmol^-1.

Question 13.
A student forget to add the reaction mixture to the round-bottomed flask at 27°C but instead he/she placed the flask on the flame. After a lapse of time, he realized his mistake and using a pyrometer he found the temperature of the flask was 477°C. What fraction of air would have been expelled out? (NCERT)
Solution:
At 27°C (= 300K) volume of air in the flask = Vcm³
Given, V₁ = V cm³, V₂ = ?, T₁ = 300K, T₂ = 750K
∵ \(\frac{\mathrm{V}_{\mathrm{1}}}{\mathrm{T}_{1}}\) = \(\frac{\mathrm{V}_{2}}{\mathrm{~T}_{2}}\)
∵ \(\frac{\mathrm{V}}{300} \) = \(\frac{\mathrm{V}_{2}}{750}\)
⇒ 300 V₂ = \(\frac{\mathrm{V}_{2}}{750 \mathrm{~V}}\)
V₂ = 2.5 V

Volume expelled out = 2.5 V – V = 1.5 V
Fraction of air expelled out = \(\frac{1.5 \mathrm{~V}}{2 \cdot 5 \mathrm{~V}}\) = 0.6
Second method, PV =nRT
n ∝ \(\frac{1}{\mathrm{~T}}\)
\(\frac{n_{2}}{n_{1}}\) = \(\frac{\mathrm{T}_{1}}{\mathrm{~T}_{2}}\) = \(\frac{300}{750}\)
\(\frac{n_{2}}{n_{1}}\) = 0.4
∴ Fraction of air expelled out = 0.6

Question 14.
Calculate the temperature of 4.0 mol of a gas occupying 5 dm³ at 3.32 bar. (R = 0.083 bar dm³ K^-1mol^-1) (NCERT)
Solution:
Given, P = 3.32 bar
Volume V = 5 dm³
No. of moles n = 4 mol
Gas constant R = 0.083 bar dm³ K^-1mol^-1
Temperature T = ?

Ideal gas equation PV = nRT
T = \(\frac{P V}{R n}\) = \(\frac{3 \cdot 32 \mathrm{bar} \times 5 \mathrm{dm}^{3}}{0 \cdot 083 \text { bar } \mathrm{dm}^{3} \mathrm{~K}^{-1} \mathrm{~mol}^{-1} \times 4 \mathrm{~mol}}\)
T = 50 K.

Question 15.
How much time would it take to distribute one Avogadro number of wheat grains if 10¹⁰ grains are distributed each second? (NCERT)
Solution:
Time required = \(\frac{\text { Total number of grains }}{\text { Number of grains distributed }}\)
= \(\frac{6.022 \times 10^{23}}{10^{10}}\) = 6.022 × 10¹³ second
= \(\frac{6 \cdot 022 \times 10^{13}}{365 \times 24 \times 60 \times 60}\)
= 1.909 × 10⁶ Years

Question 16.
Calculate the total pressure in a mixture of 8 gm of dioxygen and 4 gm of dihydrogen confined in a vessel of 1 dm³ at 27°C R = 0.083 bar dm³ K^-1 mol^-1. (NCERT)
Solution:
No.of moles of O₂, nO₂ = \(\frac{\text { Mass of } \mathrm{O}_{2}}{\text { Molecular mass }} \) = \(\frac{8}{32}\) = 0.25n
[molecular mass of O₂ = 16+ 16 = 32]
[molecular mass of H₂ = 1+1 = 2]

No.of moles of H₂, nH₂= \(\frac{4}{2}\) = 2.0 ml
Total no.of moles = 0.25 + 2.0 = 2.25 ml
Given, n = 2.25 mol, V = 1 dm₃, R = 0.083 bar dm³K^-1 mol^-1 T = 27°C = 300K, P = ?
Thus, PV =nRT
Pressure P = \(\frac{n \mathrm{RT}}{\mathrm{V}}\)
= \(\frac{2 \cdot 25 \mathrm{~mol} \times 0 \cdot 083 \mathrm{bar} \mathrm{dm}^{3} \mathrm{~K}^{-1} \mathrm{~mol}^{-1} \times 300 \mathrm{~K}}{1 \mathrm{dm}^{3}}\)
P = 56.025 bar.

Question 17.
Calculate the volume occupied by 8.8g of CO₂ at 31.1°C and 1 bar pressure. (R = 0.083 bar LK^-1 mol^-1) (NCERT)
Solution:
By the formula : PV = nRT
PV = \(\frac{m}{M}\)RT
Given, P = 1bar, V = ? , m = 8.8g
M = 44g mol^-1 (CO₂)
R = 0.083 bar LK ^-1 mol ^-1 and T = 304.1K

Volume occupid by 8.8 g CO₂, V = \(\frac{m \mathrm{RT}}{\mathrm{PM}}\) = \(\frac{8 \cdot 8 \mathrm{~g} \times 0 \cdot 083 \mathrm{bar} \mathrm{LK}^{-1} \mathrm{~mol}^{-1} \times 304 \cdot \mathrm{K}}{1 \mathrm{bar} \times 44 \mathrm{~g} \mathrm{~mol}^{-1}} \)
V = 5.048 L

Question 18.
Payload is defined as the difference between the mass of displaced air and the mass of the balloon. Calculate the payload when a balloon of radius 10m, mass 100 kg is filled with helium at 1.66 bar at 27°C (Density of air = 1.2 kg m³ and R = 0.083 bar dm³ K^-1 mol^-1). (NCERT)
Solution :
Radius of balloon R = 10 m

Question 19.
At 27C pressure of 1 gm of Ideal gas is 2 bar When at the same temperature and pressure 2 gm of Ideal gas is mixed In it Then the pressure becomes 3 bar. Develop a relation between their molecuLar mass. (NCERT)
Solution:
PV = nRT
For gas A, P_AV = n_ART ……………..(i)
Similarly for gas B, P_BV n_BRT ………………..(ii)
No. of moles of gas A n_A = \(\frac{1}{M_{A}}\) [M_A= molar mass of A]
No. of moles of gas B n_B = \(\frac{1}{M_{B}}\) [M_B = molar mass of B]
Precsure of gas A P_A=2 Bar
Totai pressure, P_total = P_A + P_B = 3 bar
Pressure of gas B = P01 PA =3—2= 1 bar

V, R and Taresame for both
Thus, from eqns. (i) and (ii)
\(\frac{P_{A}}{P_{B}}\) = \(\frac{n_{\mathrm{A}}}{n_{\mathrm{B}}}\) = \(\frac{1 \times M_{\mathrm{B}}}{\mathrm{M}_{\mathrm{A}} \times 2} \)
\(\frac{\mathrm{M}_{\mathrm{B}}}{\mathrm{M}_{\mathrm{A}}}\) = \(\frac{2 P_{A}}{P_{B}}\)
\(\frac{\mathrm{M}_{\mathrm{A}}}{\mathrm{M}_{\mathrm{B}}}\) = \(\frac{2 \times 2_{\mathrm{A}}}{1} \)
M_B = 4M_A.

Question 20.
A mixture of dihydrogen and dioxygen at one bar pressure contains 20% by weight of dihydrogen. Calculate the partial pressure of dihydrgen 20% by weight
Solution:
H₂ = 20 g and O₂ = 80 g
No.of moles in H₂ nH₂ = \(\frac{20}{2}\) = 10 mol
No.of moles in O₂, nO₂ = \(\frac{80}{32}\) = 2.5 mol

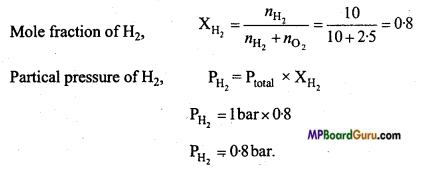
Question 21.
2.9 g of a gas at 95°C occupied the same volume as 0.184 g of dihydrogen at 17°C at the same pressure. What is the molar mass of the gas? (NCERT)
Solution:
Formula : PV = nRT
PV = \(\frac{m R \cdot T}{M}\)
Unknown gas P₁V₁ = \(\frac{m_{1} \mathrm{RT}_{1}}{\mathrm{M}_{1}}\)
H₂ gas P₂ V₂ = \(\frac{m_{2} \mathrm{RT}_{2}}{\mathrm{M}_{2}}\)
Again, Formula P₁V₁ = P₁V₁
\(\frac{m_{1} \mathrm{RT}_{1}}{\mathrm{M}_{1}}\) = \(\frac{m_{2} \mathrm{RT}_{2}}{\mathrm{M}_{2}} \)

Chemical Bonding and Molecular Structure Class 11 Important Questions Objective Type

1. Choose the correct answer:

Question 1.
At the time of opening the bottle of ammonia, it can be recognized from a distance because:
(a) It is very reactive
(b) it diffuses very fast
(c) It possesses a pungent smell
(d) It is lighter than air.
Answer:
(b) it diffuses very fast

Question 2.
Who established the relationship between density and rate of diffusion of a gas:
(a) Boyle
(b) Charles
(c) Graham
(d) Avogadro.
Answer:
(c) Graham

Question 3.
The value of R in calorie (approx):
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(d) 4

Question 4.
Value of gas constant R is :
(a) 83.14 × 10⁷ergs/degree/mol
(b) 83.14 × 10⁶ ergs/degreelmol
(c) 83.14 × 10⁵ eigs/degree/mol
(d) 83.14 × 10⁷ ergs/degree/mol.
Answer:
(c) 83.14 × 10⁵ eigs/degree/mol

Question 5.
Absolute temperature is:
(a) 0°C
(b) -100°C
(c) -273°C
(d) -373°C.
Answer:
(c) -273°C

Question 6.
To get general gas equation, which two laws are combined:
(a) Charles law and Dalton’s law
(b) Graham’s law and Dalton’s law
(c) Boyle’s law and Charles law
(d) Avogadro’s law and Dalton’s law.
Answer:
(c) Boyle’s law and Charles law

Question 7.
WhIch is correct in the following:
(a) r.ms. velocity = 0.9212 × Average velocity
(b) Average velocity= 0.9212 × r.ms. velocity
(c) r.rn.s. velocity = 0.9013 × Average velocity
(d) Average velocity = 0.9013 × r.m.s. velocity.
Answer:
(b) Average velocity= 0.9212 × r.ms. velocity

Question 8.
At constant volume the pressure of monoatomic gas depends on:
(a) Thickness of the wall of the vessel
(b) Absolute temperature
(c) Atomic number of the element
(d) Number of valence electrons.
Answer:
(b) Absolute temperature

Question 9.
Behaviour of real gases is near to that of ideal gases, if:
(a) Temperature is low
(b) Pressure is high
(c) Low pressure and high temperature
(d) Gas is monoatomic.
Answer:
(c) Low pressure and high temperature

Question 10.
At mountains or high attitude, water boils at lower temperature because of:
(a) Low atmospheric pressure
(b) High atmospheric pressure
(e) Hydrogen bonding in water is more strong at heights
(d) Water vapour is lighter than liquid.
Answer:
(a) Low atmospheric pressure

Question 11.
If molecular masses of two gases A and B are 16 and 64 respectively, ratio of rates of diffusion A and B will be:
(a) 1:4
(b) 4: 1
(c) 2: 1
(d) 1:2.
Answer:
(c) 2: 1

Question 12.
Gases deviate from ideal behaviour at high pressure because:
(a) At pressure number of collisions of molecules increases
(b) Attraction between molecules increases at high pressure
(c) Size of molecules decreases at high pressure
(d) Molecules become steady at high pressure.
Answer:
(b) Attraction between molecules increases at high pressure

Question 13.
Distance on which magnitude of energy is minimum is called:
(a) Atomic radius
(b) Lattice radius
(c) Critical distance
(d) Molecular distance.
Answer:
(a) Atomic radius

Question 14.
Diffusion rate of methane is twice than that of gas x, molecular mass of gas ‘x’ will be:
(a) 64
(b) 32.0
(c) 4.0
(d) 8.0.
Answer:
(a) 64

Question 15.
Part of van der Waals’ equation, which illustrate the intermolecular forces of real gases :
(a) (V-b)
(b) RT
(c) \(\mathrm{P}+\frac{a}{\sqrt{2}} \)
(d) (RT)-1
Answer:
(c) \(\mathrm{P}+\frac{a}{\sqrt{2}} \)

Question 16.
Temperature which is same in both Celsius scale and Fahrenheit scale :
(a) 0°C
(b) 32°F
(c) -40°C
(d) 40°C.
Answer:
(c) -40°C

Question 17.
A gas diffuses \(\frac{1}{5} \mathrm{th}\) part as compared to hydrogen, molecular mass of the gas will be:
(a) 25
(b) 50
(c) 25\(\sqrt{2}\)
(d) 50\(\sqrt{2}\)
Answer:
(b) 50

Question 18.
0.5 mole of H₂, SO₂ and CH₄ are kept in a container, which has a hole. After three hours, partial pressure will be :
(a) P_SO2 > P_CH4 > P_H2
(b) P_H2 > P_SO2 > P_CH4
(c) P_CH4 > P_SO2 > P_H2
(d) P_H2 > P_CH4 > P_SO2
Answer:
(a) P_SO2 > P_CH4 > P_H2

Question 19.
Density ratio of O₂ and H₂ is 16:11 r.m.s. velocity of molecules will be :
(a) 4:1
(b) 1:16
(c) 1:4
(d) 16:1.
Answer:
(c) 1:4

Question 20.
A gas of volume 300ml is cooled from 27°C to 7°C at constant pressure. Volume of gas will be :
(a) 135ml
(b) 540ml
(c) 350ml
(d) 280ml.
Answer:
(d) 280ml.

2. Fill in the blanks:

1. According to kinetic theory, the average kinetic energy of a gas is directly proportional to its ……………… temperature.
Answer:
Absolute

2. The kinetic energy of one mole of a gas is equal to ……………… .
Answer:
\(\frac{3}{2}\) RT

3. Root Mean Square velocity is ……………… .
Answer:
\(\sqrt{\frac{P V}{m}}\) or \(\sqrt{\frac{3 \mathrm{RT}}{m}}\)

4. Average velocity = ………………×……………… .
Answer:
0.92× Root mean Squre velocity

5. Formula of kinetic molecular equation is ……………… .
Answer:
PV = \(\frac{1}{3}\)

6. Formula of ideal gas equation is ……………… .
Answer:
PV =nRT

3. Match the following:

‘A’	‘B’
1. CaF2	(a) Molecular crystal
2. Solid CO2	(b) Covalent crystal
3. Diamond	(c) Metallic crystal
4. Glass	(d) Molecular crystal
5. Ice	(e) Non-crystalline crystal
6. Sodium	(f) Ionic crystal.

Answer:
1. (f) Ionic crystal.
2. (a) Molecular crystal
3. (b) Covalent crystal
4. (e) Non-crystalline crystal
5. (d) Molecular crystal
6. (c) Metallic crystal.

4. Answer in one word/sentence:

1. The resistance produced in the flow of a liquid is called.
Answer:
Viscosity

2. Unit of surface tension is.
Answer:
Dynepercm

3. Write S.l. unit of pressure.
Answer:
Pascal

4. Scientist who proposed the law of partial pressure is.
Answer:
Dalton

5. Name the scientist who developed relation between density and rate of diffusion of gas.
Answer:
Graham

6. Value of gas constant in S.l. unit.
Answer:
8.314 JK^-1 mol^-1

7. 1 Pascal is equal to.
Answer:
1Nm².