MP Board Class 11th Chemistry Important Questions Chapter 2 Structure of Atom

Students get through the MP Board Class 11th Chemistry Important Questions Chapter 2 Structure of Atom which are most likely to be asked in the exam.

MP Board Class 11th Chemistry Important Questions Chapter 2 Structure of Atom

Structure of Atom Class 11 Important Questions Very Short Answer Type

Question 1.
Write the complete symbol of the atoms with the following atomic number (Z) and atomic mass (A):
(i) Z = 17,A = 35
(ii) Z = 92, A = 233
(iii) Z = 4,A = 9
Solution:
(i) \({ }_{17}^{35} \mathrm{Cl}\)
(ii) \({ }_{92}^{233} \mathrm{U}\)
(iii) \({ }_{4}^{9} \mathrm{Be}\)

Question 2.
Which of the following are Iso-electronic species ue., which have same number of electrons :
Na⁺, K⁺, Mg²⁺, Ca²⁺, S^2-, Ar
Solution:

Thus, iso-electronic species are as follows :
(i) Na⁺ and Mg²⁺
(ii) K⁺,Ca²⁺,S^2- and Ar

Question 3.
What is Threshold frequency?
Answer:
For every metal there is a specific minimum frequency υ₀ which is called Threshold frequency. On frequency less than this, photoelectric effect is not observed.

Question 4.
What is work function?
Answer:
For ejecting an electron, the minimum energy required is hυ₀. This is also known as work function (w₀).

Question 5.
Arrange the following types of radiations in increasing order of their fre-quencies :
(a) Radiations by microwave oven.
(b) Amber light by traffic signal.
(c) Radiations obtained by F.M. Radio.
(d) Cosmic rays by outer dip.
(e) X-rays.
Answer:
Increasing order of frequency of radiations is as follows :
c < a < b < e < d

Question 6.
Write two characteristics of X-rays.
Answer:
Characteristics :

1. Cathode rays travel in a straight line. If an opaque solid object is placed in their path then its shadow is formed on the other side of the glass tube.
2. These rays strike on metals and produce X-rays.

Question 7.
How was neutron discovered? Write its two characteristics.
Answer:
James Chadwick discovered Neutron in the year 1932, by the bombardment of a-particles on Be, a neutral particle was obtained whose mass is nearly equal to the mass of proton and it was called neutron.
Characteristics of Neutron:
Neutron is a neutral particle present in the nucleus of an atom whose mass is nearly equal to the mass of proton i.e., 1.00893 a.m.u or 1.6749 × 10^-27 kg. Its symbol is \({ }_{0}^{1} n[/latex

Question 8.
Write the difference between Atomic number and Mass number.
Answer:
Differences between Atomic number and Mass number

Atomic number	Mass number
1. Atomic number is the number of neutrons present in the nucleus.	Mass number is the sum of the number of protons and neutrons.
2. It is represented by Z.	It is represented by A.

Question 9.
What is Atomic orbital?
Answer:
The three dimensional region in space around the nucleus in which the probability of presence of electron is maximum is called atomic orbital.

Question 10.
What are α-particles?
Answer:
α-particles are nuclei of helium atom which contains 2 unit positive charge. Mass of these particles are 4 unit. These are represented by [latex]\left({ }_{2}^{4} \mathrm{He}\right)^{2+}\)

Question 11.
What conclusions are drawn for Rutherford’s Atomic model by α-particle scattering?
Answer:
Conclusions of Rutherford’s experiment:

1. Most of the α-particles passed through the gold foil undeflected which concludes that there is a lot of empty space in an atom.
2. Few α-particles were deflected through small angles. Thus, the central part of an atom consists of positive charge.
3. Out of the 20,000 particles bombarding only one particle gets deflected and returns back. Thus, the size of nucleus is very small and rigid as compared to the size of the atom.

Question 12.
Write defects of Rutherford’s atomic model.
Answer:
In 1913 Niel Bohr pointed out some defects in proposed Rutherford’s atomic model:
(i) According to electromagnetic theory whenever an electric charge is subjected to acceleration, it emits radiation and loses energy. Bohr argued that due to rotation around positively charged nucleus, electron should continuously emit radiation and lose energy. As a result of this its orbit should become smaller and finally it should drop into the nucleus.
This however does not happen.
(ii) According to this model the atomic spectrum should be continuous but it is line spectrum.
(iii) This model does not determine the number of electrons rotating in different orbits.

Question 13.
In 3p orbital of AI and Si unpaired electrons are present. Which electron experience higher effective nuclear charge by the nucleus?
Solution:
₁₃Al = 1s²,2s²2p⁶,3s²3p¹
₁₄Si = 1s²,2s²2p⁶,3s²3p²
In both, number of orbitals are same i.e., Si (+ 4) and Al (+ 3). Nuclear charge is higher in Si due to which nuclear charge is more effective.

Question 14.
(a) How many subshells are in n = 4?
(b) How many electrons will be present in that subshell for which m_s = –\(\frac{1}{2}\) and n = 4.
Solution:
(a) For n =4 l_max= (n -1)
= (4 – 1) = 3
l = 0,1,2,3
Four subshells which are 4s,4p, Ad, 4f

(b) n = 4 Number of orbitals = n² = 4² =16
Maximum number of electrons in an orbital will be = 2
In every orbital m_s = –\(\frac{1}{2}\) No. of spinning electron = 1
Thus, in 16 orbitals m_s = –\(\frac{1}{2}\)  No. of spinning electrons = 16.

Question 15.
Quantum number of six electrons are given below. Arrange them in in-creasing order of their energy. Is the energy of any of them same :
(a) n = 4,l = 2,m_t= -2,m_s = –\(\frac{1}{2}\)
(b) n = 3,l = 2,m_l, = 1,m_s = +\(\frac{1}{2}\)
(c) n = 4,l = 1,m₁ = 0,m_s = +\(\frac{1}{2}\)
(d) n = 3,l = 2,m_l, = -2,m_s = –\(\frac{1}{2}\)
(e) n = 3,l = 1,m_l = -1,m_s = +\(\frac{1}{2}\)
(f) n = 4,l= 1,m = 0,m_s = +\(\frac{1}{2}\)
Solution:
Energy of Polyelectron atom is equal to the sum of (n + l).
(a) Subshell of set 4d = (n + l) = 4 + 2 = 6
(b) Subshell of set 3d = (n + l) = 3 + 2 = 5
(c) Subshell of set 4p = (n + l) = 4 + 1 = 5
(d) Subshell of set 3d = (n + l) – 3 + 2 = 5
(e) Subshell of set 3p = (n + l) = 3 +1 = 4
(f) Subshell of set 4p = (n + l) = 4 +1 = 5
Thus, (e) < (b) = (d) < (c) = (f) < (a) ‘
3P < 3d = 3d < 4p = 4p < Ad (Increasing order of energy of orbitals).

Question 16.
What are Electromagnetic waves?
Answer:
Radiant energy propagatic through space in the form of waves which travel with the velocity of light and are produced due to oscillations of electric and magnetic field. Therefore, they are known as Electromagnetic waves.

Question 17.
Nucleus of an atom repels α-particles. Why?
Answer:
Each α-particle carry a charge of+2 unit. Every atom contains a positively charged nucleus at its centre. We know that similar charge repel each other. Therefore, nucleus of atom repels α-particle.

Question 18.
Write the difference between Anode rays and Cathode rays.
Answer:
Differences between Anode rays and Cathode rays

Anode Rays	Cathode Rays
1. These are made up of positively charged particles.	These are made up of negatively charged particles.
2. Nature of Anode rays depend on the nature of gas taken in the discharge tube.	Nature of Anode rays do not depend on the nature of gas taken in the discharge tube.
3. Mass of particles present in Anode rays is equal to the mass of gas taken  in the discharge tube.	Mass of particles present in Cathode rays is negligible.

Question 19.
Which of the following orbital will experience high effective nuclear charge:
(a) 2s and 3s,
(b) 4d and 4f
(c) 3d and 3p.
Answer:
(a) 2s orbital is more closer to nucleus, thus it will experience higher effective nuclear charge.
(b) 4d orbital will experience higher effective nuclear charge.
(c) 3p orbital will experience higher effective nuclear charge.

Question 20.
Determine the total number of angular node and radial nodes present in 3p orbital.
Answer:
For 3p orbital: Principal Quantum number n = 3
and Azimuthal Quantum number l = 1
Number of angular nodes = l = 1
Number of Radial nodes = n – l – 1 = 3 – 1 – 1 = 1.

Question 21.
What is the difference between Atom and Ion?
Answer:
Differences between Atom and Ion

Atom	Ion
1. Atoms are completely neutral.	Ions are positively or negatively charged.
2. It contains same number of protons and Electrons.	In it number of protons and neutrons are not same.
3. Atoms are unstable and take part in chemical reaction.	Ion is stable in solution state.

Question 22.
What is Electromagnetic Spectrum?
Answer:
The graph obtained by the arrangement of different types of electromagnetic radiations in the increasing or decreasing order of their frequency or wavelength is called Electromagnetic spectrum.

Question 23.
Matter waves are different from Electromagnetic waves. Explain.
Answer:
Matter waves differ from Electromagnetic waves as follows :

• Value of their wavelength is less than Electromagnetic waves.
• Their velocity is less than that of Electromagnetic waves.
• Matter waves do not emit by particles but are related to particles.

Question 24.
Electrons move around the nucleus in a definite energy orbit. Why?
Answer:
Jumping from one energy level to another energy level by any moving charged particle like electron, will cause absorption or emission of energy radiation which will make it unstable. To provide stability to atom, electron rotates in specific energy orbits.

Question 25.
A moving electron represents both particle and wave nature. Explain the cause.
Answer:
Due to its particle nature an electron has a definite momentum and due to its motion it represents wave character. In this way, electron represents both the characters.

Question 26.
Tell the number of Neutrons and Protons present in the following nuclei:

Answer:

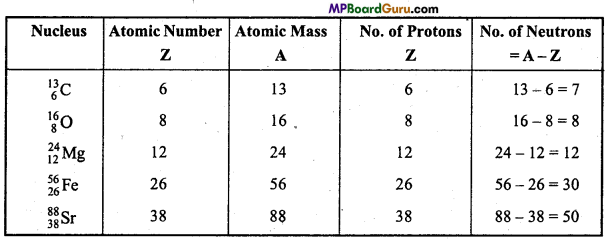
Question 27.
Show that the circumfereiice of the Bohr orbit for the hydrogen atom is an integral multiple of the de-Broglie wavelength associated with the electron revolving around the orbit.
Solution:
According to Bohr model of H atom, in the given state, angular momentum of electron:
mνr = \(\frac{n h}{2 \pi}\)
2πr = \(\frac{n h}{m v}\)
according to de-Broglie
Wavelength λ = \(\frac{h}{m v}\)
2πr = nλ
Thus, circumference (2πr) of Bohr’s orbit of H atom is whole number multiple of deBroglie wavelength.

Question 28.
It is impossible to determine the position and velocity of a fast moving electron simultaneously. Why?
Answer:
Electron is an extremely minute particle. Thus, it can only be seen by smaller wavelength light like y-rays or x-rays. For seeing an electron, it is necessary that photon should return back after striking the electron. But after striking the photon, velocity of electron changes. Therefore, it is not possible to determine the position and velocity of electron simultaneously.

Question 29.
Electronic configuration of Chromium is written as 4s¹3d⁵ instead of 4s²3d⁴. Why?
Answer:
Electronic configuration of Chromium in ground state should be [Ar] 4s²3d⁴ but due to presence of 4 electrons in 3d orbital it is incomplete and unstable. If 1 electron of 4s gets excited and goes to 3d orbital then both 4s and 3d orbitals become half filled and achieve stability. Therefore, electronic configuration of Chromium is written as 4s¹ 3d⁵ instead of 4s² 3d⁴.

Question 30.
Electronic configuration of Copper is written as 4s¹3d¹⁰ instead of 4s¹3d⁵.
Answer:
Electronic configuration of Copper in ground state is [Ar] 4s²3d⁹ in d orbital, there are 9 electrons which is an incomplete orbital and unstable. If an electron of 4s get excited and goes to 3d orbital such that 4s is half filled and 3d orbital is a completely filled orbital which is more stable. Therefore, electronic configuration of Copper is written as 4s¹3d¹⁰ in place of 4s²3d⁹.

Question 31.
Write Max Planck’s Quantum Theory.
Answer:
Max Planck’s Quantum Theory:

• Energy emitted or absorbed by an atom or molecule is not continuous but discontinuous in the form of bundles or packets which are called quantam.
• Energy related to each quanta is directly proportional to the frequency of radiation.
  E ∝ υ
  E = hυ, where h = Planck’s constant.
• Any molecule or atom absorbs or emits energy in simple multiples of quantum.

Question 32.
What are the basic particles of an atom. Write their name, mass and charge.
Answer:
Atom is made up of three particles which are known as fundamental particles or
basic particles.

Question 33.
What are Photons?
Answer:
Energy particles radiated are called photons i.e. for light, quantum ho of radiation is called one photon. These are packets or bundles of negligible mass.

Question 34.
Write main characteristics of Sommerfield atomic model.
Answer:
Main characteristics of Sommerfield atomic model are :

• Electron revolve in spherical orbits along with bigger spherical orbits where there are two radii.
• Orbits are made up of orbitals.
• Number of subshells in a shell is equal to quantum number n.

Question 35.
What is Quantum?
Answer:
According to Max Planck’s Quantum theory, emission or absorption of energy by an atom or molecule is not continuous but is discontinuous in the form of minute packets or quanta and unit of this energy emitted or absorbed is quantum.

Question 36.
Write ‘Aufbau’s principle’.
Answer:
Aufbau’s principle: Aufbau is German word meaning ‘building up’. The building up orbitals means the filling up of orbitals with electrons. Thus, this rule gives us a sequence in which various orbitals are filled up depending upon the relative-order of their energies.
According to this principle, the electrons in various or¬bitals are added progressively in the order of increasing energies starting with the orbital of lowest energy. The increasing order of energies of various orbitals is :

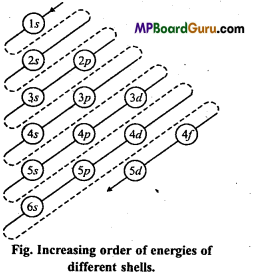
1s, 2s, 2p, 3s, 3p, 4s, 3d,4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f ……………

Question 37.
What is Zeeman Effect?
Answer:
According to Zeeman: “The splitting up of spectral lines under the influence of a magnetic field in fine lines is called Zeeman effect.”

Question 38.
Write the values of all the four quantum numbers for the last electron and unpaired electron of Chlorine.
Answer:

Cl₁₇ = 1s² 2s² 2p⁶ 3s² 3p⁵
For last electron,
n = 3,l=1,m = 0, s = –\(\frac{1}{2}\)
For unpaired electron,
n = 3,l=1,m = +1, s = +\(\frac{1}{2}\)

Question 39.
Why is Emission spectrum known as Line Spectrum?
Answer:
On passing electric current of high voltage through hydrogen gas in a discharge tube, radiations are emitted. If this radiation is allowed to pass through a prism, it splits into various thin lines. If the spectrum of these fine lines are observed then series of coloured lines are obtained, and each line has a definite wavelength, therefore, it is known as line spectrum.

Question 40.
What information is obtained by Azimuthal Quantum number?
Answer:
Azimuthal Quantum number helps to determine the angular momentum. It repre¬sents the shape of the subshells.

Question 41.
What are the symbols of orbitals of p, d and f subshells?
Answer:

• Three orbitals ofp subshell are represented as p_x, p_y and p_z.
• d subshell has five orbitals which are represented as d_xy, d_yz, d_zx, d _{x² – y²} , d_z²
• f subshell has seven orbital? which are represented as f_x³ f_y³ f_z³,f_{x(z²– y²)}’ f_{y,(x²– z²)}’f_{z(y² – x²})’f_xyz.

Question 42.
Determine the mass of one mole electron.
Solution:
Mass of Electron =9.1 × 10^-28 gm
1 mole Electron = 6.023 × 10²³ Electron
Mass of 1 mole Electron =9.1 × 10^-28 × 6.023 × 10²³
= 5.48 × 10^-4gm.

Question 43.
Determine the charge of 1 mole electron.
Solution:
Charge of Electron = 1.6 × 10^-19 coulomb
1 mole Electron = 6.023 × 10²³
Charge of 1 mole Electron .= 1.6 × 10^-19 × 6.023 × 10²³
= 9.63 × 10⁴coulomb.

Question 44.
Which subshell is represented by each group of quantum number in the following:
(a) n = 1 l = 0
(b) n = 2 l= 1
(c) n = 3 l = 2
(d) n = 4 l = 3.
Answer:
On the basis of the given quantum numbers subshells are as follows :
(a) 1s,
(b) 2p,
(c) 3d,
(d) 4f.

Question 45.
On the basis of Bohr’s atomic model what are stable orbits?
Answer:
According to Bohr’s principle, electrons revolve around the nucleus in certain specific orbits where it does not lose any energy. In these orbits, momentum of electrons is \(\frac{h}{2 \pi}\).
These orbits are known as stable orbits.

Question 46.
What are Isotopes and Isobars? Explain with example.
Answer:
Isotopes : Atoms of the same element which have same atomic number but different mass number are called Isotopes.
Example : Hydrogen has three isotopes : \({ }_{1}^{1} \mathrm{H},{ }_{1}^{2} \mathrm{H},{ }_{1}^{3} \mathrm{H}\)
Isobars : Atoms of different elements with same mass number but different atomic number are called Isobars. Example : \({ }_{20}^{40} \mathrm{Ca},{ }_{18}^{40} \mathrm{Ar}\) and \({ }_{19}^{40} \mathrm{~K}\)
are isobars as they have same mass number but different atomic numbers.

Question 47.
Write the values of n and l according to their orbital:
(i) 3s
(ii) 4d
(iii) 5p
(iv) 6f.
Answer:
(i) n = 3, l = 0,
(ii) n = 4, l = 2,
(iii) n = 5, l = 1,
(iv) n = 6, l = 3.

Question 48.
What will be the maximum number of lines emitted obtained when an excited electron n = 6 jumps to ground state in hydrogen atom?
Solution:
Number of lines emitted on moving from n shell to ground state = \(\frac{n(n-1)}{2}\)
∴ n = 6, number of lines obtained = \(\frac{6(6-1)}{2}=\frac{6 \times 5}{2}\) = 15

Question 49.
Write down the electronic configuration of elements with following atomic numbers:
(i) 17
(ii) 24
(iii) 29
(iv) 35.
Answer:
(i) 1s²,2s²,2p⁶,3s²,3p⁵
(ii) 1s²,2s²,2p⁶,3s²,3p⁶,3d⁵,4s¹
(iii) 1s²,2s²,2p⁶,3s²,3p⁶,3d¹⁰,4s¹
(iv) 1s²,2s²,2p⁶,3s²,3 p⁶,3d¹⁰,4s²,4p⁵.

Structure of Atom Class 11 Important Questions Short Answer Type 

Question 1.
Write Pauli’s Exclusion Principle with example. Write its importance.
Answer:
Pauli’s Exclusion principle : No two electrons of an atom can have the same values of all the four quantum numbers.
Example:

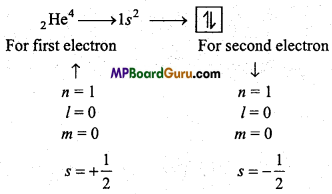
The three quantum numbers are same for these two electrons but one quantum number is different, i.e., spin quantum number. Which proves the Pauli’s exclusion principle.

Importance:
From this principle, number of electrons in a shell or main energy level can be known because the number of electrons in an orbit is equal to the number of groups of four quantum numbers in different combinations.

Question 2.
Explain Hund’s rule of maximum multiplicity with example.
Answer:
Hund’s rule :
This rule deals with degenerate orbitals (orbitals having similar energy). It states as, “pairing of electron in the orbitals of a particular subshell (p, d,f) does not take place until all the orbitals of the subshell are singly occupied.”

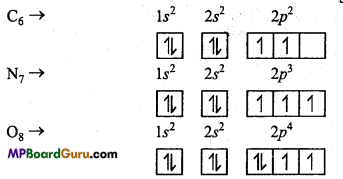
Question 3.
How de-Broglie explained dual nature of particle?
Answer:
de-Broglie describes the wave nature of electron. According to him, ‘all moving small particles show wave nature’. Behaviour of electron is governed by following funda-mental equations. According to Planck’s wave theory,
E = hυ …(1)
From Einstein’s energy mass relation,
E = mc² …(2)
Where, m is mass of particle and c is velocity of light.
From both eqns. (1) and (2),
mc² = hυ
or
mc² = h\(\frac{c}{\lambda}\), (∵ υ = \(\frac{c}{\lambda}\))
or
λ = \(\frac{h}{m c}\)
Where, λ = wavelength and me = momentum.
This is de Broglie’s equation.
Thus, it is clear that wavelength of any moving particles depends upon its momentum.

Question 4.
Write the main characteristics of Cathode Rays.
Answer:
Characteristics of Cathode Rays :

• Cathode rays travel in straight line with the velocity of light.
• If an electric field is applied in the path of Cathode rays, then these deflect towards positive region.
• A light paddle wheel when kept in the path of Cathode rays start moving which is due to high kinetic energy particles present in the rays.
• These rays ionize the gases.
• These rays strike metals like tungsten and produce X-rays.
• These rays affect the photographic plate.

Question 5.
Write main properties of Electrons.
Answer:
Properties of Electrons :
(i) All gases consist of negatively charged particles which are produced from the Cathode on passing a high voltage current at 10^-4 atmospheric pressure through a gas in the discharge tube.
(ii) Electrons are represented as _-1e⁰
(iii) Mass of electron is \(\frac{1}{1837}\) parts the* mass of hydrogen atom and mass of every electron is 9.1 × 10^-28 gm
or
9.1 × 10^-31kg .
(iv) Charge on an electron is 1.60 × 10^-19 coulomb.

Question 6.
How are anode rays produced? Write characteristics of anode rays.
Answer:
In 1886, Goldstein used perforated and found that some rays liberates from anode and passes through perforated cathode if electric arc is produced in the discharge tube at low pressure and high voltage. These rays deflects in electrical field and magnetic field in opposite direction than electrons. These rays are called anode rays or positive rays.
Four properties of anode rays :

• Anode rays travel in straight line.
• Anode rays consist of positive residues of the gas left when electrons are knocked out from the atoms of the gas.
• Anode rays are positively charged and deflect in electrical field towards negative plate.
• The charge and mass ratio (e/m) are different from electron. These particles are called protons.

Question 7.
Write the characteristics of Protons.
Answer:
Characteristics of protons :
1. Proton is the fundamental particle of proton by passing an electric discharge through a gas in a discharge tube H⁺ ions obtained are called protons or bombarding electron on H atom electrons is released and H⁺ is obtained.
H+ e^– → H⁺+ 2e^–
1. By taking different gases in the discharge tube positive particles of different masses are obtained. Positive particle (proton) obtained from hydrogen is the least. Thus, proton is the fundamental particle of an atom.
2. Mass of proton is 1.00753 a.m.u. or 1.67 x 10^-27 kg.
3. Proton is represented by \({ }^{1} \mathrm{H}\) or \({ }^{1} \mathrm{P}\).
4. Charge on the proton is 1.6 x 10 ^-19 coulomb of positive charge. Magnitude of charge on proton is equal to that of the charge on an electron. Thus, this charge is called unit positive charge.

Question 8.
Write Bohr Bury Scheme of filling of electrons in various shells of atoms.
Answer:
Scientist Bohr Bury proposed the arrangement of filling of electrons in various shells:

• Maximum number of electrons in orbit n is 2n².
• Last shell contains 8 electrons and next inner shell will contain not more than 18 electrons.
• Last shell will contain more than 2 and next to the last will contain more than 9 electrons only when inner shells are filled up.
• Electrons are filled up in the next shell only when there are 8 electrons in the last shell.
• It is not necessary that electrons will be filled in the next shell till the electrons are not filled up according to 2n² rule.

Question 9.
What do you understand by Stability of orbitals?
Answer:
Distribution of half filled and fully filled electrons is symmetrical and this symmetry provides extra stability to electrons. Exchange of electrons in orbitals of similar energy takes place in an atom and during this process energy is released as a result the orbital achieves stability. In half filled and fully filled orbitals possibilities of exchange of electrons is maximum. Therefore, these orbitals are more stable.

Question 10.
Write the difference between Isotopes and Isobars.
Answer:
Differences between Isotopes and Isobars

Isotopes	Isobars
1. Atoms of the same element which have same atomic number but different mass number are called Isotopes.	Atoms of different elements which have same atomic mass but different atomic numbers are called Isobars.
2. Number of protons in the nucleus is same but number of neutrons are different.	Number of protons and neutrons present in the nucleus are different.
3. Chemical properties are same.	Chemical properties are different.
4. Number of electrons present in the outermost shell is same.	Number of electrons present in the outermost shell is different.

Question 11.
Write any four postulates of Bohr’s Atomic model.
Answer:
Bohr’s model of the atom is based on the following postulates :
(i) The electron in the atom moves around the nucleus in a fixed circular path called orbits. These orbits are associated with definite energies and are called energy shells or
energy levels. These are numbered as 1,2, 3, 4, , etc., (from the nucleus) or these are
designated as K, L, M, N, ……….. etc. shells.

(ii) The electron can move only in those orbits for which its angular momentum is an integral multiple of the quantity h/2π.
i. e., Angular momentum = mνr = \(\frac{n h}{2 \pi}\)
Where, mass of electron = m, speed = ν, orbit or radius = r, Planck’s constant = h, an integer (1, 2, 3, 4, ) = n.

(iii) As long as the electron moves in a given orbit, it does not radiate energy. Hence, the energy of the electron is constant as long as it does not change its orbit. Because of this the orbits are also known as stationary states or states of fixed energy.

(iv) The electron absorbs energy when it jumps from an orbit of lower energy to an orbit of higher energy. The energy is emitted when the electron returns to lower energy state. The change of energy Δ E, i.e., energy absorbed or emitted, when the electron moves from one orbit to another, is given by Bohr frequency equation,
ΔE = E₂ -E₁ = hυ.

Question 12.
Show the difference between Orbit and Orbital.
Answer:
Differences between Orbit and Orbital

Orbit	Orbital
1. Spherical path outside the nucleus in which electron revolves is called as orbit.	The three-dimensional area in space around nucleus in which probability of presence of electron is maximum.
2. The position of mobile electron in shell and momentum is decided more accurately in case of orbit.	In orbital the position and momentum of electron is decided by Heisenberg uncertainty principle.
3. Shows planar motion of electron.	Shows three-dimensional motion of electron.
4. All orbits are circular.	Shapes of orbitals are different e.g., s = spherical.
5. Orbits are of scalar nature.	Except s orbital all shows directional property.
6. In any orbit the maximum No. of electron is 2n2 where n is No. of orbit.	In any orbital there are maximum two electrons.

Question 13.
What is (n + l) rule?
Answer:
1.(n + l) rule : Subshell in which sum of ‘n’ and ‘l’ quantum numbers is less, energy of that subshell is also less and electrons will be filled first in that subshell.
Example: For 3d → n = 3, l = 2
∴ (n + l) = 3 + 2 = 5
and 4s → n = 4, l = 0
∴ (n + l) = 4 + 0 = 4
So, the energy of 4s subshell will be less than 3d and electrons will be filled in 4s subshell and after this 3d will be filled.

2. (n + l) value is equal for 2 or more subshells, the electrons will be filled in the subshell having minimum principal quantum number (n) value.
Example: For2p → n = 2,p = 1
∴ (n +l) = 2+1 = 3
and 3s —> n = 3, l = 0
∴ (n +l) = 3 + 0 = 3
But the value of n for 2p subshell is 2 which is less than that of 3s (n = 3), so energy of 2p will be less and electrons will be filled in 2p.

Question 14.
What are the main defects of Bohr’s theory?
Answer:
Main defects of Bohr’s theory are as follows :

• Bohr’s theory could not explain the spectrum of polyelectron atoms.
• According to Bohr’s theory orbits of electrons are considered to be spherical but they are bigger spheres also.
• It does not explain Heisenberg’s uncertainty principle.
• It does not explain dual nature of electron.

Question 15.
What is Heisenberg’s uncertainty principle? Write its mathematical form.
Answer:
Heisenberg’s uncertainty principle : Heisenberg pointed out uncertainty in determination of two conjugate properties simultaneously. According to this principle, it is impossible to determine charge momentum and charge position of electron simultaneously. Mathematical form of uncertainty principle,
Δx × Δp ≥ \(\frac{h}{4 \pi}\)
or
Δx × mΔν ≥ \(\frac{h}{4 \pi}\)
Where, Δx = Uncertainty in position, Δp = Uncertainty in momentum, h = Planck’s constant.
On the basis of wave nature and uncertainty principle of an electron structure of atom can be explained.

Question 16.
Write the ground state electronic configuration of the following on the basis of Aufbau’s principle.
(i) Neon (Z = 10)
(ii) Phosphorus (Z = 15)
(iii) Chlorine (Z = 17)
(iv) Potassium (Z = 19).
Answer:
(i) Neon (Z= 10) : 1s² 2s² 2p_x²,2p_y² 2p_z²:
(ii) Phosphorus (Z = 15) : 1s² 2s² 2p⁶ 3s² 3p_x¹ 3p_y¹ 3p_z¹:
(iii) Chlorine (Z = 17) : 1s² 2s² 2p⁶ 3s². 3p_x²3p_y² 3 p_z¹.
(iv) Potassium (Z = 19) : 1s² 2s² 2p⁶ 3s² 3p⁶4s¹.

Question 17.
Represent Hund’s rule for the following electronic configuration.
(i) \({ }_{8} \mathrm{O}^{+2}\),
(ii) \({ }_{7} \mathbf{N}^{-3}\),
(iii) \({ }_{6} \mathrm{C}^{-1}\)
Answer:
(i) \({ }_{8} \mathrm{O}^{+2}\),
Electronic configuration of 8^O = 1s² 2s² 2p⁴
Electronic configuration of \({ }_{8} \mathrm{O}^{+2}\)

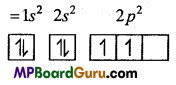
(ii) \({ }_{7} \mathbf{N}^{-3}\),
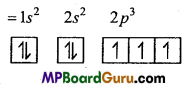
Electronic configuration of 7^N = 1s² 2s² 2p³
Electronic configuration of \({ }_{7} \mathbf{N}^{-3}\)

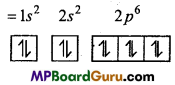
(iii) \({ }_{6} \mathrm{C}^{-1}\)
Electronic configuration of 6^C = 1s² 2s² 2p²
Electronic configuration of \({ }_{6} \mathrm{C}^{-1}\)

Question 18.
If one-one electrons are present in 3p_x, 4p_y,and 5P_z then determine value of
four quantum numbers for them.
Answer:
3p_x n = 3, l = 1,m = -1,s = +\(\frac{1}{2}\)
4p_y n = 4, l = 1, m = 0,s = +\(\frac{1}{2}\)
5P_z n = 5, l = 1, m = +1,s = +\(\frac{1}{2}\)

Question 19.
Write the values of the four quantum numbers for 17 ^thelectron of chlorine atom and 26^th electron of Fe.
Answer:
Cl₁₇ : 1s² 2s² 2p⁶ 3s² 3p⁵

Last electron is in 3p subshell n = 3, l = 1, m = 0, s = –\(\frac{1}{2}\)
Fe₂₆ : 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d⁶

Last electron is in 3d subshell. Thus,
n = 3, l = 2, m = -2,s = –\(\frac{1}{2}\)

Question 20.
Who determine the e/m value of an electron and how?
Answer:
Sir J.J. Thomson determined the charge to mass ratio of electron by measuring the deflection under the simultaneous application of electric and magnetic field, applied perpendicular to each other. The apparatus is shown in figure. It is possible to adjust the two fields in such a way that the cathode rays strike the fluorescent screen at the same position as they do when no magnetic field is applied. From the magnitudes of electric and magnetic field thus applied, charge to mass (e/m) ratio of electron can be calculated. The value of elm was found to be 1 .76 × 10⁸ coulomb per gram for electron.

Question 21.
What is natural Radioactivity? Explain.
Answer:
Professor Henry Becquerel observed in the year 1898 that Uranium and its com-pounds possess a unique property. Invisible rays are emitted by these compounds, which produce glow on striking the zinc sulphide screen, affect the photographic plate like X-rays and ionize the gases and these rays also possess the ability to penetrate thin metal sheets. These rays are known as Becquerel rays. Madam Curie called these rays as radioactive rays and this property as Radioactivity.

Thus, “Substances which possess the property of emitting active invisible rays are called radio-active substance and this property is known as Radioactivity.”

Question 22.
Explain the difference between shell, subshell and orbital.
Answer:
Shell:
Shell are circular path around the nucleus in which the electron revolve. Electrons can stay only in those shells in which the value of their angular momentum (mνr)
is \(\frac{h}{2 \pi}\) or its simple integral multiple.

According to Bohr’s principle shells are spherical. Principal Quantum number of shell is represented by (n). Maximum number of electrons in a shell is 2n².

Sub shell or Sub-orbit:
Each shell is made up of various sub-orbits. Sub-orbits are designated by s,p,d,f Sub orbits are determined by values of l.
For s sub-orbit l = 0, No. of electrons = 2
For p sub-orbit l = 1,No. of electrons = 6
For d sub-orbit l = 2,No. of electrons = 10
For/sub-orbit l = 3, No. of electrons = 14
Maximum number of electrons in various sub-orbits are as follows 2 in s, 6 in p, 10 in d and 14 in f.

Orbital :
Every sub-orbit is made up of orbitals. The three-dimensional region in ‘ space around the nucleus where the probability of the presence of electron is maximum is called orbital. There is 1 orbital ins sub-orbit, 3 inp sub-orbit, 5 in d sub-orbit and 7 orbitals in/sub-orbit. Each orbital can have 2 electrons.
Shape of s-orbital is spherical,p orbital is dumb-bell, d orbital is double dumb-bell and/orbitals are complex.

Question 23.
Explain why?
(i) Particles present in cathode rays are negatively charged.
(ii) Cathode rays rotate the wheel placed in its path.
Answer:
(i) If cathode rays are allowed to pass through an electric field then they deflect towards the positive plates, which proves that cathode rays are made up of negatively charged particles.
(ii) If a light paddle wheel is placed in the path of cathode rays, it starts rotating which represents that cathode rays are made up of particles of high kinetic energy. Thus, cathode rays are made up of material particles.

Question 24.
Explain the principle of filling of electrons in various Energy levels.
Answer:
Aufbau’s principle:
Aufbau is German word meaning ‘building up’. The building up orbitals means the filling up of orbitals with electrons. Thus, this rule gives us a sequence in which various orbitals are filled up depending upon the relative-order of their energies.
According to this principle, the electrons in various or¬bitals are added progressively in the order of increasing energies starting with the orbital of lowest energy. The increasing order of energies of various orbitals is :

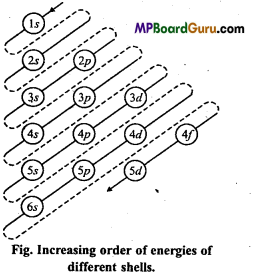
1s, 2s, 2p, 3s, 3p, 4s, 3d,4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f ……………

1.(n + l) rule : Subshell in which sum of ‘n’ and ‘l’ quantum numbers is less, energy of that subshell is also less and electrons will be filled first in that subshell.
Example: For 3d → n = 3, l = 2
∴ (n + l) = 3 + 2 = 5
and 4s → n = 4, l = 0
∴ (n + l) = 4 + 0 = 4
So, the energy of 4s subshell will be less than 3d and electrons will be filled in 4s subshell and after this 3d will be filled.

2. (n + l) value is equal for 2 or more subshells, the electrons will be filled in the subshell having minimum principal quantum number (n) value.
Example: For2p → n = 2,p = 1
∴ (n +l) = 2+1 = 3
and 3s → n = 3, l = 0
∴ (n +l) = 3 + 0 = 3
But the value of n for 2p subshell is 2 which is less than that of 3s (n = 3), so energy of 2p will be less and electrons will be filled in 2p.

Question 25.
What do you mean by dual nature of electron?
Answer:
Momentum and wave are generally not associated with some object or energy medium. Particles have momentum due to mass while energy produces waves. Electron is a microscopic particle in motion. Being a particle it has momentum and due to motion it behaves like waves also. Thus, particle and wave character of electron are its dual nature. Other particles like proton and neutron also exhibits dual nature when they are accelerated.

Wavelength of waves associated with microscopic particles can be determined by de Broglie’s equation
λ = \(\frac{h}{m v}=\frac{h}{p}\)
or
λ ∝ \(\frac{1}{p}\) (mν = p)
Where λ is the wavelength of microscopic particles, h = Planck constant, m = mass of particle, ν = velocity of particle and p is momentum of particle.

Question 26.
What is Balmer formula? How does it explain hydrogen spectrum?
Answer:
In 1885 J.J. Balmer studied emission spectrum of hydrogen. He provided a for- v mula for the frequencies ofhydrogen spectrum in visible region.
\(\bar{v}=\frac{1}{\lambda}=\mathrm{R}_{\mathrm{H}}\left(\frac{1}{2^{2}}-\frac{1}{n^{2}}\right)\)
Where, value of n is higher than 2, R_H = Rydberg constant.
Putting the value of n as 3,4,5, 6, lines of Balmer series are obtained which are in
visible region. After this in UV region Lyman series, while Paschen series, Brackett series and Pfund series in IR region, are obtained. To explain these lines, Balmer formula is modified as,
\(\overline{\mathrm{v}}=\frac{1}{\lambda}=\mathrm{R}_{\mathrm{H}}\left(\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right)\)
Where, n₂ > n₁.
For Lyman series, n₁ = 1, n₂ = 2, 3,4,…
∴ \(\bar{v}=R_{H}\left(\frac{1}{1^{2}}-\frac{1}{n_{2}^{2}}\right)\) (In ultraviolet region)
In the near and far infrared region following series of spectral lines are obtained :
Paschen series \(\bar{v}=\mathrm{R}_{\mathrm{H}}\left(\frac{1}{3^{2}}-\frac{1}{n_{2}^{2}}\right)\), n₂ = 4,5,6,…
Brackett series \(\bar{v}=R_{H}\left(\frac{1}{4^{2}}-\frac{1}{n_{2}^{2}}\right)\),
n₂ = 5,6,7,…
Pfund series
\(\bar{v}=R_{H}\left(\frac{1}{5^{2}}-\frac{1}{n_{2}^{2}}\right)\),
n₂ = 6,7,8,…

Question 27.
Atomic spectrum is known as line spectrum. Why?
Answer:
This type of spectrum is given by atoms of all elements. These consist of various series of thin bright lines of every colour which are separated by black rays. Every element gives a special type of line spectrum and these spectrum gives a specific identity to those elements.
Example : In spectrum of sodium two clear yellow lines of wavelength 5890A and 5896A are observed.If electric current is passed at low pressure through hydrogen gas filled in a discharge tube then a red light is observed. If light emitted in this way is analysed by the help of spectr6scope then a continuous spectrum containing four main lines is observed which are known as H_α,H_β,H_γ, and H_δ. Such type of spectrum in which only lines are present is called line spectrum.

Question 28.
Write the main conclusions of Rutherford’s scattering experiment.
Answer:
Conclusions of Rutherford’s experiment:
1. Most of the α-particles passed through the gold foil undeflected which concludes that there is a lot of empty space in an atom.
2. Few α-particles were deflected through small angles. Thus the central part of an atom consist of positive charge which is called nucleus.
3. Out of the 20,000 particles bombarding only one particle gets deflected and returns back. Thus the volume of nucleus is a minute part of the atom. Rutherford determined that the radius of the atom is 10^-8 cm (1 Å) and radius of nucleus is 10^-13cm.
4. Electrons revolve in great speed around the nucleus. Due to this speed the centrifugal force produced balanced the electrostatic force of attraction between the positively charged nucleus and the electrons. Due to this balance electron do not fall into the nucleus.

Question 29.
What are Iso-electronic ions? Give examples.
Answer:
Such ions of different elements which differ in charge but the number of electrons are same in ionic state are Called Iso-electronic Ions.
Example 1.

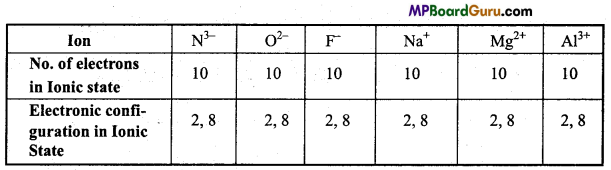
Example 2.
K⁺ and Ca²⁺ are iso-electronic ions.
No. of electrons in K⁺ = 18 Electronic configuration = 2, 8, 8
No. of electrons in Ca²⁺ = 18 Electronic configuration = 2, 8, 8.

Structure of Atom Class 11 Important Questions Long Answer Type

Question 1.
Derive an expression for radius of an orbit on the basis of Bohr’s principle.
Answer:
Bohr’s Radius :
In a hydrogen atom an electron revolves around the centre of spherical orbit. If the radius of this orbit is r and atomic number of hydrogen is Z, then total charge on nucleus is Ze. If a particle moves with constant velocity in the spherical orbit then the centripetal force (force towards the centre) and centrifugal force (force away from the centre) are equal.
Centripetal Force = Electrostatic attractive force between nucleus and electron.
\(=\frac{Z e \times e}{r^{2}}=\frac{Z e^{2}}{r^{2}}\)
and centrifugal force = \(\frac{m v^{2}}{r}\)
Thus \(\frac{Z e^{2}}{r^{2}}=\frac{m v^{2}}{r}\)
∴ r = \(\frac{Z e^{2}}{m v^{2}}\) …(1)
According to Quantum theory, Angular momentum is equal to n\(\left(\frac{h}{2 \pi}\right)\)
Thus, mνr = n\(\frac{h}{2 \pi}\)
or
ν = \(\frac{n h}{2 \pi m r}\) …(2)
From eqns. (1) and (2),
r = \(\frac{n^{2} h^{2}}{4 \pi^{2} m Z e^{2}}\)
Here h, n, m, Z and e are constant.
On substituting the values
r = n² × 0.529 × 10^-8cm
This way radius (r) of First Bohr orbit (n = 1) of hydrogen is 0.529 × 10^-8 cm.

Question 2.
How is a light ray separates into constituent components by pris? Explain with figure.
Answer:

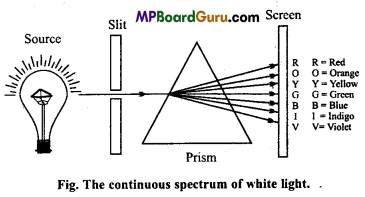
When a white light is allowed to pass through a prism, then its components gets separated into bands of different colours and wavelength. If a photographic plate is placed on the side of the prism, then the seven colours of light form seven bands which is known as continuous spectrum. In this band, one colour band partially overlaps the other colour band. In it, wavelength of violet colour is minimum but refraction is maximum due to which it bends more and gets refracted and its frequency is maximum. Wavelength of red colour is maximum and its frequency is minimum.

Question 3.
What is Heisenberg’s uncertainty principle? Write its mathematical ex-pression.
Answer:
Heisenberg pointed out uncertainty in determination of two conjugate properties simultaneously. According to this principle, it is impossible to determine charge momentum and charge position of electron simultaneously.
Mathematical form of uncertainty principle,
Δx × Ap≥\(\frac{h}{4 \pi}\)
Where, Δx = Uncertainty in position, Δp = Uncertainty in momentum, h = Planck constant.
This equation shows that uncertainty in position (Δx) and uncertainty in momentum (Δp) are inversely proportional to each other i.e.,
Δx ∝ \(\frac{1}{\Delta p}\)
If the uncertainty in position is reduced any way, its uncertainty in velocity or momentum will increase definitely.

Physical concept of uncertainty principle :
It can be understood by the study of effect of light on micro objects like electrons.
Effect of light on position and momentum of micro objects :

In order to observe an object, the wavelength of the incident light should be shorter than its size. If we use light radiations of higher wavelengths, the light reflected does not fall in the visible region. Hence, these are not visible and exact position cannot be determined. But, if we use radiations of high frequency or wavelength shorter than size of object, the electrons will be visible but the photons of high frequency change the momentum. This is because, the photons transfer their energy to the electrons during collision, as a result the electrons change their path.

Question 4.
What do you mean by quantum numbers? Explain the informations obtained by each quantum number. [Most Imp.]
Answer:
There are four types of quantum numbers :
1. Principal quantum number :
It is represented by n. This number informs about the main shell of the atom. It expresses the energy level and its distance from the nucleus in which electron revolves i.e., it determines the size of atom. The value of n are 1, 2, 3, 4, , means electron exist in K, L, M, N,…. energy levels.

2. Azimuthal quantum number :
It is represented by l. It expresses the angular momentum of electron in an elliptical state around the nucleus i.e., the shape of subshell is indicated.
Value of l may be from 0 to (n – 1) i.e.,
For n = 1 value of l = 0 subshell is one s
For n = 2 value of l = 0, 1, subshells are two s and p.

3. Magnetic quantum number :
According to this under magnetic influence the fundamental line for a quantum number m is oriented in various directions. This orientation means an electron of a subshell due to change in energy revolve in different directions. These orientations are called orbitals and are represented by number m. The possible values of m depend upon value of l i.e., for any value of l the value of m may be – l to + l passing through zero.
For 5 electron, l = 0, then m = 0
For/? electron, l = 1, then m = -1, 0, +1
For d electron, l =2, then m = – 2, -1, 0, +1, +2.

4. Spin quantum number :
It is represented by s. From the observation of various spectral evidences it has become clear that each electron in addition to its motion around the nucleus spins like a top about its own axis. As a result of it, angular momentum of electron is increased hence its energy changes. This spinning energy is represented by spin quantum number.
When there is a single electron in the orbital it spins clockwise and its magnetic field
is expressed as +\(\frac{1}{2}\) or [↑] but when another electron enters the same orbital it spins anticlockwise and its magnetic field is expressed as – \(\frac{1}{2}\) or [↑]

Question 5.
Describe Bohr model by different spectral lines present in hydrogen spectrum.
Or,
How is Bohr’s atomic theory helpful to explain line spectrum of hydrogen atom? Describe.
Answer:
Bohr’s model of hydrogen spectrum: In line spectrum of hydrogen atom five series of many lines are obtained. In ultraviolet region Lyman series, in visible region Balmer series and in infrared region Paschen, Brackett and Pfund series are found.

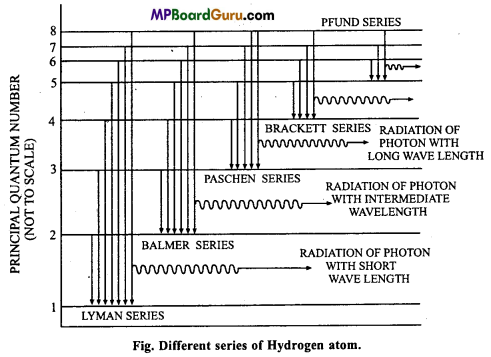
In hydrogen atom only one electron is present. Neil Bohr in 1913 explain the pres-ence of different series. According to Bohr, different energy levels of definite energy are found in atom in which various electrons rotate around the nucleus. Many hydrogen atoms are present in hydrogen gas. When same energy is supplied various electrons jumps to higher energy orbitals by absorbing different amount of energy but these are unstable there. These electrons return back to lower energy levels by emitting photons of different frequencies. Due to these emissions, various lines are obtained in spectrum.

When electrons return to n = 1 energy level from higher energy levels like 2, 3, 4; first, second or third lines of Lyman series are obtained and Balmer series obtained when electron return to n = 2 energy orbit from the higher orbits 3, 4, 5 etc. In such a way Paschen, Brackett and Pfund series are also obtained.
Suppose an electron of energy level n,, having energy Ej, jumps to energy level n2 having energy E2. If the frequency of spectral lines is u then the energy difference will be
ΔE = E₂ – E₁

This is Rydberg’ eqation.
Where R_H = \(\frac{2 \pi^{2} Z^{2} e^{4} m}{c h^{3}}\) = Rydberg constant = 109677.8cm^-1
The value of Rydberg constant is equal to its experimental value.
If the value of n1 is being put 1, 2, 3, 4 or 5, Lyman, Balmer, Paschen, Brackett,
Pfund series of spectral lines are obtained which are accordingly with Bohr’s model.

Question 6.
What is the shape of s,p and d orbital?
Answer:
s-orbital:
Azimuthal quantum number determines the shape of an orbital. If l = 0 then value of angular momentum of the orbital is zero. Thus, s orbital is non-directional and spherically symmetrical. Thus, the probability of the presence of electron up to a definite distance is same in all directions. With the increase in principaL quantum number, size of s-orbital also increases. If value of principal quantum number is n, then in s-orbital n is symmetrically spherical and with the increase in the value of n, energy of s-orbital alsoincreases and number of nodal planes for principal quantum number n is n -1.

Shape of p – orbital : If n = 2 then l=0, 1. For l = 1, value of m are three-1,0,+ 1. It
means p-subshell has three orbitais represented as p_x‚p_y and p_z whose energies are same.
But their orientation is different. p_x‚p_y, p_z are symmetrical in the directions of X, Y and Z axis, p-orbital is dumb-bell in shape. Both the lobes of every orbitai is separated by a plane where electron density is zero and it is called nodal plane.

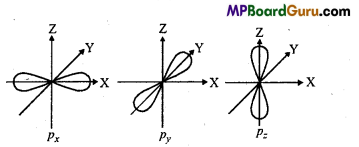
Shape of d – orbital : For d-orbital l=2, thus five various values of magnetic quan
tum numbers are -2,-1, 0, +1, +2 which are represented as ,d_xy d_yz ,d_zx,d_{x² – y²},d_z² . Their sizes are different but energy is same, Size of three orbitals d_xy,d_xz, d_yz are same but their four lobes represent high electron density. They are of double dumb-bell shape. d_{x² – y²}
orbital is like d_xy, but the lobes are on X-and Y-axis. Lobes of d_z² orbital are on Z-axis. It has a ring representing high electron density which lies at XY-plane.

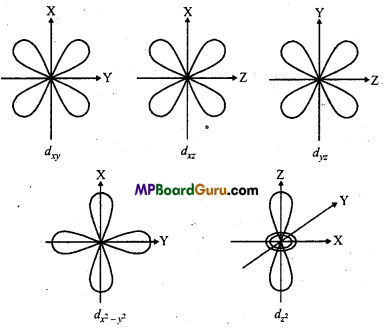
Question 7.
Explain Quantum Mechanical model of an atom.
Answer:
Concept of Quantum Mechanical Model of Atom :
Louis de Broglie’s hypothesis and Heisenberg’s uncertainty principle led to the development of new model of atom called quantum mechanical model.
de-Broglie, on the basis of similarity expressed the behavior of an electron like light i. e., wave and particle nature. He gave a mathematical expression for the wave obtained by minute particles like electrons and protons according to which
λ = \(\frac{h}{p}\)
or
λ = \(\frac{h}{m v}\)
Where λ = wavelength of wave obtained from particle, p = momentum of particle,
m mass of particle, ν = velocity of particle.

Heisenberg’s uncertainty principle :
Heisenberg pointed out uncertainty in deter-mination of two conjugate properties simultaneously. According to this principle, it is im-possible to determine charge momentum and charge position of electron simultaneously.
Mathematical form of uncertainty principle,
Δx × Δp ≥\(\frac{h}{4 \pi}\)
Where, Δx = Uncertainty in position, Δp = Uncertainty in momentmh, h = Planck’s constant.
On the basis of wave nature and uncertainty principle of an electron structure of atom can be explained.

Probability picture of an Electron:
The concept of well-defined orbits suggested by Bohr is ruled out because according to the uncertainty principle the simultaneous determination of position and momentum of electron is not possible. The quantum mechanical model, on the other hand, considers the probability of presence of an electron with a particular energy in certain region of space. The probability of finding electron at a particular part in an atom is given by square of wave function i.e., Ψ² corresponding to that location.

The probability of finding electron may differ from one location to the other and even at a large distance from the nucleus it does not become zero, though it may become negligible. Due to this it is not possible to draw boundary enclosing the region of 100% probability. However, for simplicity we draw arbitrary boundary enclosing the region of maximum probability of 90-95% called orbital. Thus, orbital may be defined as “Region of space around the nucleus where the probability of finding on electron is maximum. ”

Schrodinger Equation :
In this model behaviour of the electron in an atom is de-scribed by an equation called Schrodinger wave equation.

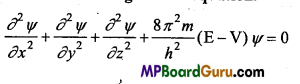
Where, m is mass of the electron,
h is the Planck’s constant,
E is the total energy,
V is the potential energy of the electron,
x, y and z are the three space coordinate.
Ψ (Greek letter psi) is amplitude of the electron wave called wave function.
By the solution of Schrodinger’s equation three quantum numbers n, l and m are obtained which determine the size and shape of electrons.
Value of l may be from 0 to (n-1) i.e.
For n = 1 value of l = 0 subshell is one s
For n = 2 value of l = 0,1, subshell are two s and p.

Question 8.
How does Schrodinger Equation represent the possibility of the presence of electron near the nucleus ? What do you understand by orbital?
Answer:
Possibility of Presence of Electron : Schrodinger Equation keeps into account the particle and wave nature of de-Broglie. Both the principles were given a mathematical form known as Schrodinger equation.

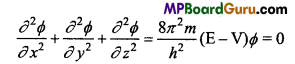
Where x,y, z axis, m= mass of electron, h = Planck’s constant, E = Energy, V = Potential energy, Φ = wave function.
Solution of equation, gives the knowledge of various energy levels, radiated frequency for hydrogen atom which is represented by the symbol θ.

Utility of Wave-function :
In an atom, orbitals of electron, wave function or rihas no physical significance on itself. Square of wave function in a point represents the probability of density of electron at that point. In Schrodinger equation energy level is represented by the square of wave function. Higher the value of square of wave function higher is the possibility of the presence of electron. If the value of square of wave function (θ²) of a point is zero, then the probability of finding the electron at that place is also zero.
θ² is also known as probability density and it is positive. In an atom at various points by the value of θ² can predict the maximum probability of the presence of electron at a place.

By this equation energy of electrons in an atom is quantized i. e., it has certain specific values. Corresponding wave functions related to every energy level is also found. Corresponding wave functions are characterized by a group of three quantum numbers. These are Principal, Azimuthal and Magnetic Quantum numbers. These quantum numbers are obtained by the solution of Schrodinger wave equation. According to Heisenberg’s uncertainty principle actual position and actual momentum of an electron cannot be determined simultaneously.

Path of electron is not accurate but only possible.. This led to the concept of atomic orbital. Atomic orbit is denoted by Φ. For every electron, such types of various wave functions are possible. Thus, their corresponding atomic orbital are also possible. Energy of electron in every orbit is definite. These orbitals cannot have more than 2 electrons. Region around the nucleus where the probability of presence of an electron is maximum 90-95% is called orbital.

In the stage of H- atom, there is le^– with charge -e and nuclear charge +e, its potential energy can be given as follows :
V = \(\frac{-e^{2}}{r}\)
∴ On the basis of above facts Schrodinger wave equation can be written as follows :

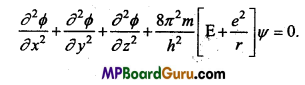
Structure of Atom Class 11 Important Numerical Questions

Question 1.
(i) Calculate the number of electrons which will together weigh one gram,
(ii) Calculate the mass and charge of one mole of electrons.
Solution:
(i) ∵ Mass of 1 electron = 9.11 × 10^-28 g (or 9.11 × 10^-31 kg )
No. of electrons in mass of 1 gm = \(\frac{1}{9 \cdot 11 \times 10^{-28}}\) = 1.0976 × 10²⁷ electrons

(ii) ∵ Mass of 1 electron = 9.11 × 10^-31 kg
Mass of 1 mole electron = 9.11 × 10^-31 × 6.022 × 10²³
= 54.86 × 10<sup-8kg = 5.486 × 10^-7kg
Charge on 1 electron = 1.602 × 10^-19 C
Charge on 1 mole electron = 1.602 × 10^-19 × 6.022 × 10²³
= 9.647 × 10⁴C

Question 2.
(i) Calculate the total number of electrons present in one mole of methane.
(ii) Find (a) the total number and (b) the total mass of neutrons in 7 mg of ¹⁴C.
[Assume that mass of a neutron = 1.675 × 10^-27 kg ]
(iii) Find (a) the total number and (b) the total mass of protons in 34 mg of NH₃ at S.T.P.
Will the answer change if the temperature and pressure are changed?
Solution:
(i) No. of electrons in one molecule of methane (CH₄)
= 6 + 4= 10
(6 from carbon and 1 from each hydrogen)
∴ No. of electrons present in 1 mole methane
= 6.022 × 10²³ × 10
= 6.022 × 10²⁴

(ii)
(a) 1 mole ¹⁴C = 14g = 6.022 × 10²³carbonatom.
∵ No. of neutrons in 1 carbon atom = Mass number – Atomic number
= 14-6 = 8 neutrons.
∵ No. of neutrons in 6.022 × 10²³ carbon atoms
= 6.022 x10²³ × 8
Or, No. of neutrons in 14 g of Carbon-14 = 6.022 × 10²³ × 8

∴ No of neutrons in 7 mg (or 7 × 10^-3 g) = \(\frac{7 \times 10^{-3} \times 6 \cdot 022 \times 10^{23} \times 8}{14}\)
= 24.088 × 10²⁰
= 2.4088 × 10²¹ Neutrons.

(b) ∵ Mass of 1 neutron = 1.675 × 10²⁷ kg
∴ Massof 2.4088 × 10²¹ neutrons = 2.4088 × 10²¹ × 1.675 × 10^-27kg
= 4.0347 × 10^-6 kg.

(iii) No. of protons in 1 mole NH₃ = 7 + 3 = 10 mole proton,
(7 in N and 1 in each H)
No. of 10 mole protons = 6.022 × 10²³ × 10
= 6.022 × 10²⁴ protons.

(a) ∵ No. of protons in 17 g NH₃ = 6.022 × 10²⁴ protons
∴ No. of protons in 34 mg (or 34 × 10^-3g) NH₃
\(=\frac{34 \times 10^{-3} \times 6 \cdot 022 \times 10^{24}}{17}\)
= 12.044 × 10²¹ protons.
= 1.2044 × 10²² protons.

(b) ∵ Mass of 1 proton = 1.6726 × 10^-27kg
∴ Mass of 1.2044 × 10²²protons = 1.2044 × 10²² × 1.6726 × 10^-27kg
= 2.01447 × 10^-5 kg
There is no effect of pressure and temperature on the number of basic particles. Thus, answer will be same.

Question 3.
Yellow light emitted from a sodium lamp has a wavelength (λ) of 580 nm. Calculate the frequency (υ) and wave number (\(\text { (\overline{U) } }\)) of the yellow light.
Solution:
Frequency (υ) = \(\frac{c}{\lambda}\) ,(1nm = 10m^-9m)
= 580 nm = 580 × 10^-9m = 580 × 10^-7cm
υ = \(\frac{c}{\lambda}=\frac{3 \cdot 0 \times 10^{8} \mathrm{~ms}^{-1}}{580 \times 10^{-9} \mathrm{~m}}\) = 5.17 × 10¹⁴s^-1 (∵ Velocity of light, c = 3 × 10⁸ms^-1)
Wave number, \(\bar{v}=\frac{1}{\lambda}=\frac{1}{580 \times 10^{-7} \mathrm{~cm}}\) = 1.724 10⁴cm^-1

Question 4.
Calculate the frequency of a light wave whose time period is 2.0 × 10^-10s.
Solution:
Frequency υ = \(\frac{1}{\text { Time period }}\) = \(\frac{1}{2 \cdot 0 \times 10^{-10} \mathrm{~s}}\) = 5 × 10^-9 s^-1.

Question 5.
What is the number of photons of light with a wavelength of 4000 pm that provide 1 J of energy?
Solution:
Energy of 1 photon E = \(\frac{h c}{\lambda}\) = \(\frac{6 \cdot 626 \times 10^{-34} \mathrm{Js} \times 3 \cdot 0 \times 10^{8} \mathrm{~ms}^{-1}}{4000 \times 10^{-12} \mathrm{~m}}\)
(∵ 1pm = 10^-12m
= 4.9695 × 10^-17J
No. of photons N = \(\frac{1 \mathrm{~J}}{4 \cdot 9695 \times 10^{-17} \mathrm{~J}}\) = 2.0122 × 10¹⁶.

Question 6.
A photon of wavelength 4 × 10^-7 m strikes on metal surface, the work function of the metal being 2-13eV. Calculate
(i) The energy of photon (eV)
(ii) The kinetic energy of emission and
(iii) The velocity of the photoelectron. (leV = 1.6020 × 10^-19J)
Solution:
(i) Energy of a photon E = \(\frac{h c}{\lambda}\) = \(\frac{6 \cdot 626 \times 10^{-34} \mathrm{Js} \times 3 \cdot 0 \times 10^{8} \mathrm{~ms}^{-1}}{4 \times 10^{-7} \mathrm{~m}}\)
E = 4.969 × 10^-19.J (1.602 × 10^-19J = 1eV)
or
E = \(\frac{4 \cdot 969 \times 10^{-19}}{1 \cdot 602 \times 10^{-19}}\) = 3.10eV

(ii) Kinetic Energy of emitted electron, K.E. = hυ – hυ₀
hυ = 3.10e V (Energy of striking photon)
hυ₀ = W₀ =2.13eV (Work function of metal)
K.E. = 3.10 – 2.13 = 0.97eV

(iii) K.E. = \(\frac{1}{2}\)mν² = 0.97eV (∵ 1eV = 1.602 × 10^-19J)
or
\(\frac{1}{2}\)mν² = 0.97 × 1.602 × 10^-19 J
or
= \(\frac{1}{2}\) × 9.1 1 × 10^-31kg × v² = 0.97 × 1.602 × 10^-19 J
∵(Mass of1e = 9.11 × 10^-31kg)
or
ν² = \(\frac{0.97 \times 1.602 \times 10^{-19} \mathrm{~J} \times 2}{9.11 \times 10^{-31} \mathrm{~kg}}\) = 0.341 × 10¹²
or
ν = \(\sqrt{0 \cdot 341 \times 10^{12}}\)
or
ν = 5.84 10⁵ms^-1

Question 7.
Electromagnetic radiation of wavelength 242 nm is just sufficient to ionise the sodium atom. Calculate the ionisation energy of sodium in kJ mol^-1.
Solution:
Wavelength λ = 242 × 10^-9 m, (∵ 1 nm = 10^-9 m)
Energy E = hυ = \(\frac{h c}{\lambda}\) = \(\frac{6 \cdot 626 \times 10^{-34} \mathrm{Js} \times 3 \cdot 0 \times 10^{8} \mathrm{~ms}^{-1}}{242 \times 10^{-9} \mathrm{~m}}\)
E = 0.0821 × 10^-17 J/atom
Above energy is sufficient for the ionisation of 1 Na atom. Energy for 1 mole Na is the ionisation energy of Na.
Energy for 1 mole Na (Ionisation energy)
E = 6.02 × 10²³ × 0.0821 × 10^-17 J/mol
= 4.945 × 10⁵ J/mol
\(=\frac{4 \cdot 945 \times 10^{5}}{1000}\)KJ/mol ( ∵1KJ = 1000J)
= 4.945 × 10² kJ/mol

Question 8.
A 25 watt bulb emits monochromatic yellow light of wavelength 0.57µm. Calculate the rate of emission of quanta per second.
Solution:
Wavelength λ = 0.57 µpm = 0.57 × 10^-6m (∵ 1µm = 10^-6 m)
Energy of photon E hυ = \(\frac{h c}{\lambda}\) = \(\frac{6 \cdot 626 \times 10^{-34} \mathrm{Js} \times 3 \cdot 0 \times 10^{8} \mathrm{~ms}^{-1}}{0.57 \times 10^{-6} \mathrm{~m}}\)
or
E = 34.84 × 10^-20J
25 watt = 25Js^-1 ( ∵1watt = 1Js^-1)
Number of photons emitted per second = \(\frac{\text { Total Energy per second }}{\text { Energy of } 1 \text { photon }}\)
\(=\frac{25 \mathrm{Js}^{-1}}{34 \cdot 87 \times 10^{-20} \mathrm{~J}}\)
= 0.7169 × 10²⁰ photon/second
= 7.169 × 10¹⁹ photon/second.

Question 9.
Electrons are emitted with zero velocity from a metal surface when it is exposed to radiation of wavelength 6800 Å. Calculate threshold frequency (υ₀) and work function (W₀) of the metal.
Solution:
Threshold wavelength, λ₀ =6800Å = 6800 × 10^-10m (∵ 1Å= 10^-10m)
Threshold Frequency υ₀ = \(\frac{c}{\lambda_{0}}\) = \(\frac{3 \cdot 0 \times 10^{8} \mathrm{~ms}^{-1}}{6800 \times 10^{-10} \mathrm{~m}}\) = 4.41 × 10¹⁴ s^-1
Work function W₀ = hυ₀
= 6.626 × 10^-34Js × 4.41 × 10¹⁴s^-1
= 29.22 × 10^-20J=2.922 × 10^-19J.

Question 10.
What is the wavelength of Light emitted when the electron in a hydrogen
atom undergoes transition from an energý level with n = 4 to an energy level with
n = 2?
Solution:
Wavenumber, \(\vec{v}=\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right]\)
(Where R Rydberg constant = 109677cm^-1)

= 486 × 10^-9m = 486nm
Colour of this wavelength of light is blue.

Question 11.
How much energy is required to ionise a H-atom if the electron occupies n = 5 orbit. Compare your answer with the ionisation enthalpy of H-atom (energy required to remove an electron from n = 1 orbit is ionisation Enthalpy)
Solution:
Energy change ΔE = E_f – E_i
ΔE = 2.18 ×10^-18\(\left(\frac{1}{n_{i}^{2}}-\frac{1}{n_{f}^{2}}\right)\) J
When n_i, = 5 and n_f = ∝Change in Energy
ΔE = 2.18 ×10^-18 \(\left(\frac{1}{c^{2}}-\frac{1}{\infty}\right)\) J=0.0872 × 10^-18J
When n_i = 1 and n_f = ∝, Energy change
ΔE1 = 2.18 × 10^-18\(\left(\frac{1}{1^{2}}-\frac{1}{\infty}\right)\)J = 2.18 10^-18J
∴ \(\frac{\Delta \mathrm{E}^{1}}{\Delta \mathrm{E}}\) = \(\frac{2 \cdot 18 \times 10^{-18}}{0 \cdot 0872 \times 10^{-18}}\) = 25
Thus, energy required to emit an electron from the first orbit is 25 times the energy required to emit an electron from the fifth orbit.

Question 12.
Dual behaviour of matter proposed by de-Broglie led to the discovery of electron microscope often used for the highly magnified images of biological molecules and other type of material. If the velocity of the electron in this microscope is
1.6 × 10⁶ms Calculate de-Broglie wavelength associated with this electron.
Solution:
de-Broglie wavelength, λ = \(\frac{h}{m v}\)
λ = \(\frac{6 \cdot 626 \times 10^{-34} \mathrm{Js}}{9 \cdot 11 \times 10^{-31} \mathrm{~kg} \times 1 \cdot 6 \times 10^{6} \mathrm{~ms}^{-1}}\) (1J = 1kgm²s^-2)
= 0.455 × 10^-9m = 4.55 × 10^-10m
= 455 × 10^-12m = 455pm.

Question 13.
Similar to electron diffraction, neutron diffraction microscope often used for the highly magnified images of biological molecules and other type of material. If the wavelength used here is 800pm, calculate the characteristic velocity associated
with the neutron. (Mass of Neutron = 1.675 × 10^-27kg)
Solution:
λ = \(\frac{h}{m v}\)
λ = 800pm = 800 × 10<sup-12m, m = 1.675 × 10^-27kg
∴ ν = \(\frac{6 \cdot 626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-2}}{1 \cdot 675 \times 10^{-27} \mathrm{~kg} \times 800 \times 10^{-12} \mathrm{~m}}\)
= 0.494 × 10³ ms^-1
= 4.94 × 10²ms^-1

Question 14.
Calculate the wavelength for the emission transition if it starts from the orbit having radius 1.3225nm and ends at 211.6pm. Name the series to which this transition belongs and the region of the spectrum.
Solution:
Radius of n^th orbit of H like species :

If n₁ = 5 and n₂ = 2, then emission transition occurs from fifth orbit to second orbit. Thus, it represents Balmer series :

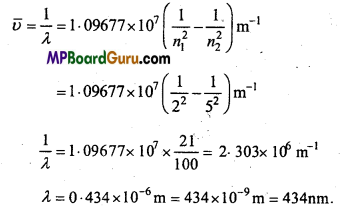
Question 15.
Emission transitions in the Paschen series end at orbit n = 3 and start from orbit n and can be represented as υ = 3.29 x 10¹⁵ \(\left(\frac{1}{3^{2}}-\frac{1}{n^{2}}\right)\) Hz. Calculate the value of
n if the transition is observed at 1285 nm. Find the region of spectrum.
Solution:


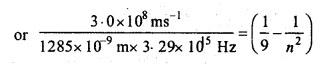
0.0709 = 0.1111 – \(\frac{1}{n^{2}}\)
or
\(\frac{1}{n^{2}}\) = 0.1111-0.0709 = 0.0402 = 0.04 = \(\frac{1}{25}\)
or
n² = 25 or n = 5
∴ Electron jumps from n = 5 to n = 3. i.e., transition occurs in Paschen series and is present in infrared region.

Question 16.
An ion with mass number 56 contains 3 units of positive charge and 30*4% more neutrons than electrons. Assign the symbol to this ion.
Solution:
Let, No. of electrons in ion = x .
∴ No. of neutrons = x + \(\frac{30 \cdot 4}{100}\)x = 1.304x
(∵ No. of neutrons is 30.4% more than No. of electrons)
No. of electrons in neutral atom = x + 3 (∵ + 3 charge is on the ion)
Thus, No. of protons = x + 3
We know that, Mass no. = n + p = 1.304x + x + 3 = 56
2.304x = 53
or
x = \(\frac{53}{2 \cdot 304}\) = 23.003 ≈ 23
No. of protons = 23 + 3 = 26 = Atomic No.
Thus, symbol of ion is \({ }_{26}^{56} \mathrm{Fe}^{+3}\).

Question 17.
An ion with mass number 37 possesses one unit of negative charge. If the ion contains 11.1% more neutrons than the electrons. Find the symbol of the ion.
Solution:
Mass no. of ion = 37
Thus, p + n = 37
Unit negative charge is one on the ion.
Let no. of Protons = x ?
No. of Electrons = x + 1
No. of Neutrons = 37- x
According to the equation,
x + 1 + x + 1 ×\(\frac{11 \cdot 1}{100}\) = 37 – x
or
(x + 1) \(\left[1+\frac{1 \cdot 1}{100}\right]\) = 37 – x
111.1(x+1) = 3700 – 100x
or
211.1x = 3700 -111.1 = 3588 .9
x = \(\frac{3588 \cdot 9}{211 \cdot 1}\) =17
No. of Protons = 17
No. of Electrons = 17+1 18
No. ofNeutrons =37 – 17=20
Thus, symbol of the ion will be \({ }_{17}^{37} \mathrm{Cl}^{-1}\)

Question 18.
Neon gas is generally used in sign boards. If it emits strongly at 616 nm.
Calculate
(a) The frequency of emission,
(b) Distance travelled by this radiation in 30s,
(c) Energy of quanta,
(d) No. of quanta present ¡fit produces 2J of energy.
Solution:
(a) Frequency u = \(\frac{c}{\lambda}\)
λ = 616nm = 616 × 10^-9 m
υ = \(\frac{3 \cdot 0 \times 10^{8} \mathrm{~ms}^{-1}}{616 \times 10^{-9} \mathrm{~m}}\)
= 4.870 × 10¹⁴s^-1

(b) Distance travelled Speed × Time
= 3.0 × 10⁸ms^-1× 30s=9.0 × 10 ⁹m.

(c) Energy of quanta (or photon)
E = hυ = 6.626 × 10^-34Js × 4.870 × 10¹⁴s^-1
= 32.268 × 10^-20J= 3.2268 × 10^-19J.

(d) No. of quanta present = \(\frac{\text { Total energy produced }}{\text { Energy of one photon }}\)
= \(\frac{2 \mathrm{~J}}{3 \cdot 232 \times 10^{-19} \mathrm{~J}}\)
= 6.691 × 10¹⁸

Question 19.
The work function of sodium atom is 1.9 eV. Calculate
(a) The threshold wavelength of emitted radiation.
(b) Threshold frequency.
(c) If sodium element is irradiated with a wavelength of 500 nm, then calculate the kinetic energy of photoelectrons.
(d) Velocity of photoelectrons.
Solution:
(a) Work function W₀ = hυ₀
W₀ = 1.9eV = 1.9 × 1.602 × 10J
υ₀ = \(\frac{\mathrm{W}_{\mathrm{o}}}{h}\) = \(\frac{1 \cdot 9 \times 1 \cdot 602 \times 10^{-19} \mathrm{~J}}{6 \cdot 626 \times 10^{-34} \mathrm{Js}}\)
υ₀ = 4.59 × 10¹⁴S^-1

(b) Threshold wavelength λ₀ = \(\frac{c}{v_{0}}\) = \(\frac{3 \cdot 0 \times 10^{8} \mathrm{~ms}^{-1}}{4 \cdot 59 \times 10^{14} \mathrm{~s}^{-1}}\) = 6.536 × 10^-7 m
= 653.6 × 10^-9m = 653.6nm.

(c) Kinetic energy of emitted photoelectrons, K.E. = h(υ – υ₀)
Wavelength of particle after striking λ = 500nm = 500 × 10^-9m
υ = \(\frac{c}{\lambda}\) = \(\frac{3 \cdot 0 \times 10^{8} \mathrm{~ms}^{-1}}{500 \times 10^{-9} \mathrm{~m}}\) = 6.0 × 10¹⁴s^-1
∴ K.E. = 6.626 × 10^-34Js(6.0 × 10¹⁴s^-1-4.59 × 10¹⁴s^-1)
or
K.E. = 9.34 × 10^-20 J.

(d) Calculation of velocity :
Kinetic energy = \(\frac { 1 }{ 2 }\)mν²
9.34 × 10^-20 J = \(\frac { 1 }{ 2 }\) × 9.1 1 × 10^-31 kg × ν²
(Mass of electron =9.11 × 10^-31kg)
or
ν² = 2.050 × 10¹¹m²s^-2 (1J = 1kgm²s^-2
ν = \(\sqrt{20 \cdot 50 \times 10^{10} \mathrm{~m}^{2} \mathrm{~s}^{-2}}\)
ν = 4.527 × 10⁵ms^-1

Question 20.
Following results are observed when sodium metal is irradiated with different wavelengths. Calculate (a) Threshold wavelength and (b) Planck’s constant.

Solution:
Kinetic Energy (K.E.) = h(υ – υ₀) = \(\frac { 1 }{ 2 }\) mν²
Substituting the values obtained from the three experiments in the equation,

(i) 1^st Experiment:
λ = 500nm = 500 × 10^-9m



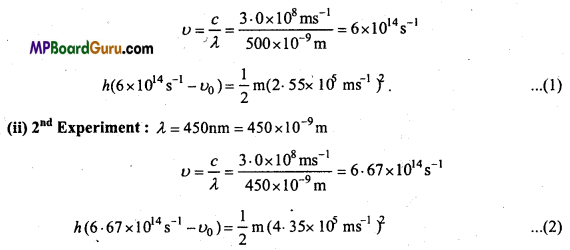
∴ h = 7.043 × 10^-34JS. (∵ 1J = 1 kg m²s^-2)

Question 21.
The ejection of photoelectrons from the silver metal in the photoelectric effect experiment can be stopped by applying the voltage of 0.35V when the radiation of 256.7 nm is used. Calculate the work function for silver metal.
Solution:
Energy of radiation used hυ = hυ₀ + K.E.
E = hυ = \(\frac{h c}{\lambda}\) = \(\frac{6 \cdot 626 \times 10^{-34} \mathrm{Js} \times 3 \cdot 0 \times 10^{8} \mathrm{~ms}^{-1}}{256 \cdot 7 \times 10^{-9} \mathrm{~m}}\)
= 7.74 × 10^-19J = \(\frac{7.74 \times 10^{-19} \mathrm{~J}}{1.602 \times 10^{-19}}\) = 4.8eV
Kinetic energy is obtained by the potential applied
K.E. = eV₀
= 1.6 × 10^-19× 0.35 = \(\frac{0.56 \times 10^{19} \mathrm{~J}}{1 \cdot 6 \times 10^{-19}}\) = eV = 0.35eV
K.E. = 0.35eV
Work function, W₀ = hυ₀ = hυ – K.E.
= 4.83eV-0.35eV = 4.48eV

Question 22.
If the photon of wavelength 150 pm strikes an atom and one of this inner bound electrons is ejected out with a velocity of 1.5 × 10⁷ ms^-1. Calculate the energy with which it is bound to the nucleus.
Solution:
Energy of reflected radiation hυ = hυ₀ + \(\frac { 1 }{ 2 }\) mν²
E = hυ =\(\frac{h c}{\lambda}\) = \(\frac{6 \cdot 626 \times 10^{-34} \mathrm{Js} \times 3 \cdot 0 \times 10^{8} \mathrm{~ms}^{-1}}{150 \times 10^{-12} \mathrm{~m}}\)
(∵ 1pm = 10^-12m)
E = 13.25 × 10^-16J

Kinetic Energy of ejected electron K.E. = \(\frac { 1 }{ 2 }\) mν²
= \(\frac { 1 }{ 2 }\) × 9.11 × 10^-31kg × (1.5 × 10⁷ms^-1)²
K.E. = 1.025 × 10^-16J
W₀ = hυ₀ = hυ -K.E.
= 13.25 × 10^-16 J-1.025 × 10^-16 J= 12.225 × ^-16 J
= \(\frac{12 \cdot 225 \times 10^{-16}}{1 \cdot 602 \times 10^{-19}}\)eV =
7.63 × 10³eV

Question 23.
The velocity related to a proton moving with a potential difference of 1000V is 4.37 × 10⁵ ms^-1. If a hockey bail of mass 0.1 kg is moving with this velocity, then calculate the wavelength related to this.
Solution:
Wavelength related to hockey ball,
λ = \(\frac{h}{m v}\) = \(\frac{6 \cdot 626 \times 10^{-34} \mathrm{~kg} \mathrm{~m}^{2} \mathrm{~s}^{-2}}{0 \cdot 1 \mathrm{~kg} \times 4 \cdot 37 \times 10^{5} \mathrm{~ms}^{-1}}\)
= 15.16 × 10^-39m = 1.516 × 10^-38m.

Question 24.
Nitrogen laser produces a radiation at wavelength of 337.1 nm. If the number of photons emitted is 5.6 × 10²⁴. Calculate the power of this laser.
Solution:
If n photons are emitted from the laser, then total energy of the ejected photons will be equal to the capacity of the laser.
Energy of L photon, = \(\frac{h c}{\lambda}\) =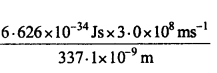
(∵ 1nm = 10^-9m

= 0-.05896 × 10^-17uJ
-Energy of 5.6 × 10<sup24photons = 0.05896 × 10^-17 × 5.6 × 10²⁴J
= 0.3302 × 10⁷J
= 3.302 × 10⁶J.

Question 25.
What transition in the hydrogen spectrum would have the same wave-length as Balmer transition n = 4 to n = 2 of He⁺ spectrum?

On solving, n₁ = 1 and n₂ = 2
Thus, wavelength of transition from n = 2 to n₁ = 1 in H spectrum will be equal to transition of n = 3 to n = 2 in Balmer series in He⁺.

Question 26.
Calculate the energy required for the process
He_(g)⁺ → He_(g)²⁺ + e^–
The ionisation energy for the H atom in the ground state is 2.18 10^-18 J atom^-1.
Solution:
Energy of electron in atomic orbital

E_n = \(\frac{-2 \pi^{2} m Z^{2} e^{4}}{n^{2} h^{2}}\)
For H-atom, ionisation energy (IE) =E_∝ – E₁
IE = 0 – \(\left(-\frac{2 \pi^{2} 1^{2} e^{4}}{1^{2} h^{2}}\right)\)
(∵ For H-atom Z = 1 and n = 1)
IE = 2.18 × 10^-18J atom^-1

For He⁺, IE = E_∝ – E₁, E₁ = 0 \(\left(\frac{-2 \pi^{2} 2^{2} e^{4}}{1^{2} h^{2}}\right)=4 \times \frac{2 \pi^{2} m e^{4}}{h^{2}}\)
=4 × 2.18 × 10^-18J atom^-1
= 8.72 × 10^-18J atom^-1
Thus, Energy required for He⁺ → He²⁺ +e^–
= 8.72 × 10^-18J atom^-1.

Question 27.
In Milikan’s experiment, statk electric charge on the oil drops has been
obtained by shining X-rays. If the static electric charge on the oil drop ¡s-1.282 × 10^-18C. Calculate the number of electrons present on it.
Solution:
No. of electrons = \(\frac{\text { Total charge on oil drop }}{\text { Charge on } 1 \text { electron }}\)

= \(\frac{-1 \cdot 282 \times 10^{-18} \mathrm{C}}{-1 \cdot 6022 \times 10^{-19} \mathrm{C}}\) = 0.800 × 10=8.0.

Question 28.
A certain particle carries 25 × 10^-16C of static electric charge. Calculate
the number of electrons present in it.
Solution:
Charge on 1 electron = 1.6022 × 10^-19C
Total charge = 2.5 × 10^-16 C
Number of electrons present in particles
\(=\frac{2 \cdot 5 \times 10^{-16} \mathrm{C}}{1 \cdot 6022 \times 10^{-19} \mathrm{C}}\) = 1.5603 × 10³
= 1560.

Question 29.
29.2 × 10⁸ atoms of carbon are arranged side by side. Calculate the radius of carbon atom if the length of this arrangement is 2.4 cm.
Solution:
Total length = 2.4 cm.
No. of carbon atoms arranged in line = 2 × 10⁸
∴ Diameter of 1 carbon atom = \(\frac{2 \cdot 4 \mathrm{~cm}}{2 \times 10^{8}}\) = 1.2 × 10^-8 cm
Radius of 1 carbon atom \(=\frac{\text { Diameter }}{2}=\frac{1 \cdot 2 \times 10^{-8}}{2}\)
= 0.60 × 10^-8cm
= 0.060 × 10^-7cm = 0.060 × 10^-9m = 0.060nm.

Question 30.
The diameter of Zinc atom is 2.6 Å. Calculate (a) Radius of Zinc atom in pm and (b) Number of atoms present in a length of 1.6 cm if the Zinc atoms are ar-ranged side by side lengthwise.
Solution:
(a) Diameter of Zn atom = 2.6Å = 2.6 × 10^-10 m
Radius of Zn atom = \(\frac{2 \cdot 6 \times 10^{-10} \mathrm{~m}}{2}\) = 1.3 × 10^-10m
= 130 × 10^-12m = 130pm

(b) Given, Length = 1.6 cm = 1.6 × 10^-2 m
Number of Zn atoms in 1.6 × 10^-2 m long line
\(=\frac{1 \cdot 6 \times 10^{-2} \mathrm{~m}}{2 \cdot 6 \times 10^{-10} \mathrm{~m}}\) = 0.6154 × 10⁸ = 6.154 × 10⁷

Structure of Atom Class 11 Important Questions Objective Type

1. Choose the correct answer:

Question 1.
Atomic number of an element is 27, and number of neutrons in its atom are 14, number of electrons will be :
(a) 14
(b) 27
(c) 13
(d) 41.
Answer:
(c) 13

Question 2.
Protons and Neutrons are collectively known as :
(a) Deutron
(b) Positron
(c) Meson
(d) Nucleon.
Answer:
(d) Nucleon.

Question 3.
Similarity found in Na⁺ ion and Ne element is :
(a) In number of protons
(b) In number of Neutrons
(c) In number of Electrons
(d) In Atomic mass.
Answer:
(c) In number of Electrons

Question 4.
According to Hund’s Rule Electronic configuration (1s²,2s²,2p^x1, 2p^y1 2p^z1,) is of which element:
(a) Of Oxygen
(b) Of Nitrogen
(c) Of Fluorine
(d) Of Boron.
Answer:
(b) Of Nitrogen

Question 5.
Value of all four quantum numbers of seventh electron of nitrogen is :
(a) n = 2,l = 1, m = +1, s = –\(\frac{1}{2}\)
(b) n = 2,l = 2, m = -1, s = +\(\frac{1}{2}\)
(c) n = 2, l =1, m = +1, s = +\(\frac{1}{2}\)
(d) n = 2,l = 2, m = +2,s = +\(\frac{1}{2}\)
Answer:
(c) n = 2, l =1, m = +1, s = +\(\frac{1}{2}\)

Question 6.
Total number of orbitals in Azimuthal quantum number of l subshell are :
(a) 2l + 1
(b) 3l + 1
(c) 4l + 1
(d)2(l+l).
Answer:
(a) 2l + 1

Question 7.
In Isotopes number of this is same:
(a) Proton
(b) Neutron
(c) Proton and Neutron
(d) Nucleon.
Answer:
(a) Proton

Question 8.
Which of the following expression represents de-Broglie relation:
(a) \(\frac{h}{m v}\) = p
(b) λ = \(\frac{h}{m v}\)
(c) λ = \(\frac{h}{m p}\)
(d) λm = \(\frac{h}{p}\)
Answer:
(b) λ = \(\frac{h}{m v}\)

Question 9.
In Rutherford’s experiment a-particles are bombarded on which metal:
(a) Aluminium
(b) Silver
(c) Iron
(d) Gold.
Answer:
(d) Gold.

Question 10.
What will be the number of electrons in a molecule of CO₂
(a) 22
(b) 44
(c) 11
(d) 38.
Answer:
(a) 22

Question 11.
A neutral atom of an element contain two K, nine M and two N electrons, then
total number of d electrons will be:
(a) 2
(b) 3
(c) 1
(d) 4.
Answer:
(c) 1

Question 12.
According to Heisenberg’s uncertainty principle :
(a) Δx.Δp ≥ \(\frac{h}{4 \pi}\)
(b) Δx.Δυ≥ \(\frac{h}{4 \pi}\)
(c) Δx\(\frac{c}{\lambda} \geq \frac{h}{4 \pi}\)
(d) Δx.Δm≥\(\frac{h}{4 p}\)
Answer:
(a) Δx.Δp ≥ \(\frac{h}{4 \pi}\)

Question 13
For an atom n = 3, / = 2 then value of m will be :
(a) -2, – 1,0, + 1, + 2
(b) -1, 0, +1
(c) -3, -1, 0, + 1, + 3
(d) -2, 0+1.
Answer:
(a) -2, – 1,0, + 1, + 2

Question 14.
By the removal of a neutron from the nucleus of an atom :
(a) Positive charge of atom increases
(b) Atomic mass decreases
(c) α and β-particles are ejected
(d) None of these.
Answer:
(b) Atomic mass decreases

Question 15.
Number of Electrons in Cl^– ion will be :
(a) 17
(b) 18
(c) 35
(d) 37.
Answer:
(b) 18

Question 16.
Which of the following configuration is not according to Aufbau’s Principle :
(a) 1s²,2s²p¹
(b) [Kr]4d¹⁰,5s²
(c) [Ar]3d¹⁰,4s¹
(d) [Ar]3d⁴,4s².
Answer:
(c) [Ar]3d¹⁰,4s¹

Question 17.
Number of orbitals in f sub-shell is :
(a) 3
(b) 4
(c) 5
(d) 7.
Answer:
(d) 7.

Question 18.
Lightest particle of an atom is :
(a) Proton
(b) Electron
(c) Neutron
(d) α -particle.
Answer:
(b) Electron

Question 19.
In Rutherford’s Experiment on which metal are α particles bombarded :
(a) Al
(b) Ag
(c) Fe
(d) Au.
Answer:
(d) Au.

Question 20.
For n = 3 values of l will be :
(a) 1, 2, 3
(b) 0, 1, 2
(c) 0 , 1, 3
(d) None of these.
Answer:
(b) 0, 1, 2

Question 21.
Which shell is nearest to the nucleus :
(a) M
(b) N
(c) K
(d) L.
Answer:
(c) K

Question 22.
Bohr’s Atomic model can explain :
(a) Spectrum of only hydrogen atom
(b) Spectrum of an atom or ion containing only one electron
(c) Spectrum of hydrogen molecule
(d) Spectrum of sun.
Answer:
(b) Spectrum of an atom or ion containing only one electron

Question 23.
Rutherford’s a-particle scattering experiment reaches the conclusion :
(a) Mass and energy are interrelated
(b) Electron resides in the region around the nucleus
(c) Neutron is deeply inserted in the nucleus
(d) Position of a point in a substance can be determined accurately.
Answer:
(b) Electron resides in the region around the nucleus

Question 24.
Order of mass of Neutron is :
(a) 10^-23 kg
(b) 10^-24 kg
(c) 10^-26 kg
(d) 10^-27 kg.
Answer:
(d) 10^-27 kg.

Question 25.
Two electrons of K shell will differ:
(a) In principle quantum number
(b) In azimuthal quantum number
(c) In magnetic quantum number
(d) In spin quantum number.
Answer:
(d) In spin quantum number.

Question 26.
Magnetic quantum number is related to :
(a) Size
(b) Shape
(c) Orientation
(d) Spin.
Answer:
(c) Orientation

Question 27.
Number of unpaired electrons in Ni2+ ion (For Ni, Z = 28):
(a) 0
(b) 2
(c) 4
(d) 8.
Answer:
(b) 2

Question 28.
In hydrogen spectrum lines of Lyman series are present in :
(a) UV
(b) IR
(c) Visible
(d) Remote.
Answer:
(a) UV

Question 29.
Electronic configuration (outermost) of Mn²⁺ ion Atomic no. of manganese = 25 in minimum energy state is :
(a) 3d⁵
(b) 2d⁴ 4s²
(c) 3d<sup3 4s²
(d) 3d²4s²4p².
Answer:
(a) 3d⁵

Question 30.
If nucleus of Electron, Hydrogen, Helium and Neon are moving with velocity of light, then order of wavelength connected to these particles will be :
(a) Electron > Hydrogen > Helium > Neon
(b) Electron > Helium > Hydrogen > Neon
(c) Electron < Hydrogen < Helium < Neon (d) Neon > Hydrogen > Helium > Electron.
Answer:
(a) Electron > Hydrogen > Helium > Neon

Question 31.
Atomic number of Ca is 20 and atomic mass is 40, which of the following statement is incorrect for Ca atom :
(a) Number of electrons is equal to number of neutrons
(b) Number of nucleons is twice the number of electrons
(c) Number of protons are half the number of neutrons
(d) Number of nucleons is twice the atomic number.
Answer:
(c) Number of protons are half the number of neutrons

Question 32.
Four quantum numbers of outermost electrons of K (Atomic No. = 19) :
(a) n = 2,l = 0,m = 0,s = +\(\frac{1}{2}\)
(b) n = 4,l = 0,m 0,s = +\(\frac{1}{2}\)
(c) n = 3,l = 1 ,m = 1,s = +\(\frac{1}{2}\)
(d) n = 4,l = 2, m = -1, s = +\(\frac{1}{2}\)
Answer:
(b) n = 4,l = 0,m 0,s = +\(\frac{1}{2}\)

Question 33.
How many mole electrons are in one kilogram :
(a) 6.023 × 10²⁵
(b) \(\frac{1}{9 \cdot 108}\) × 10³¹
(c) \(\frac{6 \cdot 02}{9 \cdot 108}\) × 10⁵⁴
(d) \(\frac{1}{9 \cdot 108 \times 6 \cdot 02}\) × 10⁸
Answer:
(d) \(\frac{1}{9 \cdot 108 \times 6 \cdot 02}\) × 10⁸

Question 34.
Total number of orbitals for principal quantum number n =:
(a) 2n
(b) n²
(c) 2n²
(d) n + l.
Answer:
(b) n²

Question 35.
An outermost electron represents the following quantum numbers n = 3, l= 2, m = + 2 and s = +1/2. Atomic number will be :
(a) 13
(b) 21
(c) 29
(d) 39.
Answer:
(c) 29

Question 36.
An ion isoelectronic with carbon monoxide is represented as :
(a) O₂^–
(b) N₂⁺
(c) CN^–
(d) O₂⁺
Answer:
(c) CN^–

2. Fill in the blanks:

1. Atomic -number of an atom is 20 and atomic mass is 40. Number of neutrons in its
nucleus will be ………………….
Answer:
20

2. Atomic number of chlorine gas is 17. Number of electrons in its outermost shell will
be ………………………
Answer:
7

3. If the sum of total magnetic quantum numbers is 7, then value of azimuthal quantum
number will be …………………….
Answer:
3

4. Nucleus of an atom contain ………………….. and ………………….
Answer:
Proton, Neutron

5. Neutron was discovered by ………………..
Answer:
Chadwick

6. Magnitude of mass of neutron is ………………….
Answer:
10^-27 kg

7. Lines of Lymann series in hydrogen spectrum are present in ………………….
Answer:
Ultraviolet rays

8. Radiations of highest wavelength are …………………
Answer:
Radiowaves

9. If value of azimuthal quantum number is one, then shape of orbital will be ………………..
Answer:
Dumb-bell

10. Region in space around the nucleus where there is maximum probability of presence
of electron is called ……………………..
Answer:
Orbital

11. Atomic number of an element is 30 and its mass number is 66. In its atom number of
protons is ………………… and number of neutrons is ………………….
Answer:
30, 36

12. Magnetic quantum number is related to …………………
Answer:
Orientation

13. In Isotopes number of ……………….. is same.
Answer:
Proton

3. Match the following:

‘A’	‘B’
1. Goldstein	(a) Atomic number
2. J.J. Thomson	(b) Molarity
3. Moseley	(c) Anode rays
4. Rutherford	(d) Structure of atom
5. Rydberg	(e) Cathode rays
6. Soddy	(f) Uncertainty principle
7. Heisenberg	(g) Large elliptical orbit
8. Sommer Field	(h) Isotopes.

Answer:
1. (c) Anode rays
2. (e) Cathode rays
3. (a) Atomic number
4. (d) Structure of atom
5. (b) Molarity
6. (h) Isotopes.
7. (f) Uncertainty principle
8. (g) Large elliptical orbit

4. Answer in one word/sentence:

1. Who discovered electron?
Answer:
J. J. Thomson

2. What is de-Broglie equation?
Answer:
λ = \(\frac{h}{m v}=\frac{h}{p}\)

3. Azimuthal quantum number is represented by.
Answer:
l

4. Formula of Heisenberg’s uncertainty principle is.
Answer:
Δx.Δp ≥ \(\frac{h}{4 \pi}\)

5. Who discovered neutron?
Answer:
Chadwick

6. Maximum number of electrons in first and second shell is.
Answer:
2, 8