In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 8 त्रिकोणमिति का परिचय Additional Questions Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Additional Questions
MP Board Class 10th Maths Chapter 8 अतिरिक्त परीक्षोपयोगी प्रश्न
MP Board Class 10th Maths Chapter 8 दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
यदि cosec θ + cot θ = p, तो सिद्ध कीजिए कि \(\cos \theta=\frac{p^{2}-1}{p^{2}+1}\)
हल :
\(\frac{p^{2}-1}{p^{2}+1}\)

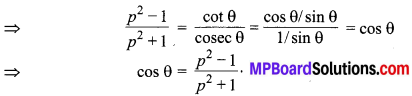
इति सिद्धम
प्रश्न 2.
सिद्ध कीजिए कि \(\sqrt{\sec ^{2} \theta+\csc ^{2} \theta}=\tan \theta+\cot \theta\)
हल :
LHS =

= tan θ + cot θ
= RHS
LHS = RHS
इति सिद्धम
प्रश्न 3.
सिद्ध कीजिए कि \(\frac{1+\sec \theta-\tan \theta}{1+\sec \theta+\tan \theta}=\frac{1-\sin \theta}{\cos \theta}\)
हल :
LHS =

LHS = RHS
इति सिद्धम
प्रश्न 4.
सिद्ध कीजिए कि \(\frac{\sec \theta+\tan \theta-1}{\tan \theta-\sec \theta+1}=\frac{1+\sin \theta}{\cos \theta}\)
हल :
LHS =

LHS = \(\frac{1+\sin \theta}{\cos \theta}\) = RHS
LHS = RHS
इति सिद्धम
![]()
प्रश्न 5.
सिद्ध कीजिए कि \(\sqrt{\frac{1-\sin \theta}{1+\sin \theta}}=\sec \theta-\tan \theta\)
हल :
LHS =

= secθ – tanθ
= RHS
LHS = RHS
इति सिद्धम
प्रश्न 6.
सिद्ध कीजिए कि \(\sqrt{\frac{1-\cos \theta}{1+\cos \theta}}=\csc \theta-\cot \theta\)
हल :
LHS =

= cosecθ – cotθ
= RHS
LHS = RHS
इति सिद्धम
प्रश्न 7.
सिद्ध कीजिए कि \(\sqrt{\frac{1+\cos \theta}{1-\cos \theta}}=\csc \theta+\cot \theta\)
हल :
LHS =

= cosecθ + cotθ
= RHS
LHS = RHS
इति सिद्धम
MP Board Class 10th Maths Chapter 8 लघु उत्तरीय प्रश्न
प्रश्न 1.
सिद्ध कीजिए कि : \(\frac{1+\cos A}{\sin A}+\frac{\sin A}{1+\cos A}=\frac{2}{\sin A}=2 \csc A\)
हल:
L.H.S. =

LHS = RHS
इति सिद्धम
प्रश्न 2.
सिद्ध कीजिए कि : \(\frac{\tan A}{1+\sec A}-\frac{\tan A}{1-\sec A}=2 \csc A\)
हल:
L.H.S. =

LHS = RHS
इति सिद्धम
प्रश्न 3.
यदि tanA = 3/4 तो सिद्ध कीजिए कि sin A cos A = \(\frac { 12 }{ 25 }\)
हल :
चूँकि tan A = 3/4 = p/b
p = 3 एवं b = 4
⇒ \(h=\sqrt{p^{2}+b^{2}}=\sqrt{(3)^{2}+(4)^{2}}=\sqrt{9+16}=\sqrt{25}=5\)
L.H.S. = sin A. cos A = \(\frac{3}{5} \times \frac{4}{5}=\frac{12}{25}\)
= R.H.S.
L.H.S. = R.H.S.
इति सिद्धम्
प्रश्न 4.
सिद्ध कीजिए कि:
(sin α + cos α) (tan α + cot α) = sec α + cosec α.
हल:
L.H.S. = (sin α + cos α) (tan α + cot α)
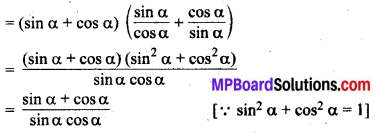
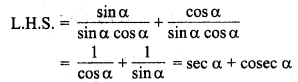
LHS = RHS
इति सिद्धम
![]()
प्रश्न 5.
सिद्ध कीजिए कि : (√3 + 1) (3 – cot 30°) = tan³ 60° – 2 sin 60°.
हल:
L.H.S. = (√3 +1) (3 – cot 30°)
= (√3 + 1) (3 – √3)
= 3 √3 – 3 + 3 – √3
= 2√3
R.H.S. = tan³ 60° – 2 sin 60°
= (√3) – 2 (√3/2)
= 3 √3 – √3
= 2√3
L.H.S. = R.H.S.
इति सिद्धम्
प्रश्न 6.
सिद्ध कीजिए कि :
\(1+\frac{\cot ^{2} \alpha}{1+\csc \alpha}=\csc \alpha\)
हल :
L.H.S. =

L.H.S. = R.H.S.
इति सिद्धम्
प्रश्न 7.
सिद्ध कीजिए कि : tanθ + tan (90° – θ) = sec θ. sec (90° – θ).
हल :
L.H.S. = tanθ + tan (90° – 0)
= tan θ + cot θ
= sin θ/cos θ + cos θ/sin θ
= \(\frac{\sin ^{2} \theta+\cos ^{2} \theta}{\cos \theta \sin \theta}\)
= \(\frac{1}{\cos \theta \sin \theta}\)
= sec θ cosec θ
= sec θ. sec (90° – θ)[ ∵ sec (90° – θ) = cosec θ]
= R.H.S.
L.H.S. = R.H.S.
इति सिद्धम्
प्रश्न 8.
यदि √3 tanθ = 1 हो तो sin²θ – cos²θ का मान ज्ञात कीजिए।
हल :
∵ √3 tanθ = 1 ⇒ tan θ = \(\frac{1}{\sqrt{3}}\) = tan 30°
θ = 30°
तब sin²θ – cos²θ = sin² 30° – cos² 30
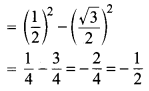
अतः sin²θ – cos²θ का अभीष्ट मान = \(-\frac { 1 }{ 2 }\) है।
![]()
प्रश्न 9.
सरल कीजिए :
(1 + tan²θ) (1 – sin θ) (1 + sin θ).
हल :
(1 + tan²θ) (1 – sin θ) (1 + sin θ).
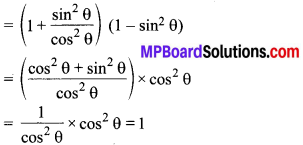
अतः अभीष्ट सरल मान = 1 है।
प्रश्न 10.
दर्शाइए कि : \(\frac{\cos ^{2}\left(45^{\circ}+\theta\right)+\cos ^{2}\left(45^{\circ}-\theta\right)}{\tan \left(60^{\circ}+\theta\right) \cdot \tan \left(30^{\circ}-\theta\right)}=1\)
हल:
L.H.S. =

= R.H.S.
L.H.S. = R.H.S.
इति सिद्धम्
प्रश्न 11.
दर्शाइए कि : tan4 + θ + tan2 θ = sec4 θ – sec2 θ.
हल :
L.H.S. = tan4 + θ + tan2 θ = sec4 θ – sec2 θ
= (sec² θ – 1) (sec² θ) [∴ 1 + tan² θ = sec² θ]
= sec4 θ – sec² θ
= R.H.S.
L.H.S. = R.H.S.
इति सिद्धम्
प्रश्न 12.
सिद्ध कीजिए :
sin6θ + cos6θ + 3 sin2θ cos2θ = 1.
हल :
हम जानते हैं कि
sin2θ + cos2θ = 1
⇒ (sin2θ + cos2θ)3 = (1)3 = 1
⇒ sin6θ + cos6θ + 3 sin2θ cos2θ (sin2θ + cos2θ) = 1
⇒ sin6θ + cos6θ + 3 sin2θ cos2θ = 1. [∴ sin2 θ + cos2 θ = 1]
इति सिद्धम्
![]()
प्रश्न 13.
सिद्ध कीजिए कि :
(sin4θ – cos4θ + 1) x cosec2θ = 2
हल:
L.H.S. = (sin4θ – cos4θ + 1) x cosec2θ
= [(sin2θ + cos2θ) (sin2θ – cos2θ) + 1] x cosec2θ
= (sin2θ – cos2θ + 1) x cosec2θ
= sin2θ cosec2θ – cos2θ cosec2θ + cosec2θ)
= (1 – cot2θ + cosec2θ)
= (1 – cot2θ + 1 + cot2θ)
= 2 (∵ sin2θ cosec2θ = 1, cos2θ cosec2θ = cot2θ)
= R.H.S.
L.H.S. = R.H.S.
इति सिद्धम्
प्रश्न 14.
(secθ + tanθ) (1 – sinθ) को सरल कीजिए।
हल:
(secθ + tanθ) (1 – sinθ)
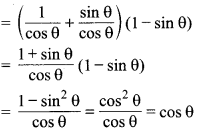
अत: अभीष्ट मान = cosθ है।
प्रश्न 15.
निम्न सर्वसमिका सिद्ध कीजिए :
\(\frac{\csc A}{\csc A-1}+\frac{\csc A}{\csc A+1}=2 \sec ^{2} A\)
हल:
L.H.S. =

L.H.S. = R.H.S.
इति सिद्धम्
MP Board Class 10th Maths Chapter 8 अति लघु उत्तरीय प्रश्न
प्रश्न 1.
निम्नांकित कथनों में सत्य/असत्य लिखिए तथा अपने उत्तर की पुष्टि कीजिए :
(i) \(\frac{\tan 47^{\circ}}{\cot 43^{\circ}}=1\)
(ii) (cos² 23° – sin² 67°) का मान धनात्मक है।
(iii) \(\sqrt{\left(1-\cos ^{2} \theta\right) \sec ^{2} \theta}=\tan \theta\)
(iv) (tanθ + 2) (2 tanθ + 1) = 5 tanθ + sec²θ
(v) sinθ + cosθ का मान सदैव 1 से बड़ा होता है।
(vi) tan θ (θ < 90°) का मान θ के बढ़ने के साथ बढ़ता है।
(vii) θ का मान बढ़ने पर sinθ की अपेक्षा tanθ का मान तेजी से बढ़ता है।
हल :
(i) कथन सत्य है,
क्योंकि
![]()
(ii) कथन असत्य है,
क्योंकि
(cos² 23° – sin² 67°) = cos² 23° – cos² 23° = 0.
![]()
(iii) कथन सत्य है,
क्योंकि
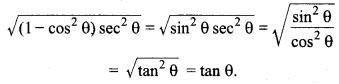
(iv) कथन असत्य है,
क्योंकि (tan θ + 2) (2 tan θ + 1) = 2 tan²θ + 4 tan θ + tan θ + 2
= 5 tan θ + 2 (1 + tan²θ)
= 5 tan θ + 2 sec²θ
≠ 5 tan θ + sec²θ.
(v) कथन असत्य है, क्योंकि θ = 0° के लिए sin θ + cos θ = sin 0 + cos 0 = 0 + 1 = 1.
(vi) कथन सत्य है, क्योंकि tan 0 = 0, tan 30° = \(\frac{1}{\sqrt{3}}\) , tan 45° = 1, tan 60° = √3.
(vii) कथन सत्य है,
क्योंकि
\(\tan \theta=\frac{\sin \theta}{\cos \theta}\)
जब θ का मान बढ़ता है तो sin θ का मान बढ़ता है लेकिन cos θ का मान घटता है, इसलिए tan θ का मान तेजी से बढ़ता है।
MP Board Class 10th Maths Chapter 8 वस्तुनिष्ठ प्रश्न
MP Board Class 10th Maths Chapter 8 बहु-विकल्पीय प्रश्न
प्रश्न 1.
यदि cos A = \(\frac { 4 }{ 5 }\), तो tan A का मान है :
(a) 3/5
(b) 3/4
(c) 4/3
(d) 5/3.
उत्तर:
(b) 3/4
प्रश्न 2.
यदि sin A = \(\frac { 1 }{ 2 }\), तब cot A का मान होगा :
(a) √3
(b) \(\frac{1}{\sqrt{3}}\)
(c) \(\frac{\sqrt{3}}{2}\)
(d) 1.
उत्तर:
(a) √3
प्रश्न 3.
cosec (75° + θ) – sec (15° – θ)]- tan (55° + θ) + cot (35° – θ) का मान है :
(a) -1
(b) 0
(c) 1
(d) 3/2.
उत्तर:
(b) 0
प्रश्न 4.
यदि sin θ = \(\frac { a }{ b }\) हो तो cosθ का मान होगा :
(a) \(\frac{b}{\sqrt{b^{2}-a^{2}}}\)
(b) \(\frac { b }{ a }\)
(c) \(\frac{\sqrt{b^{2}-a^{2}}}{b}\)
(d) \(\frac{a}{\sqrt{b^{2}-a^{2}}}\)
उत्तर:
(c) \(\frac{\sqrt{b^{2}-a^{2}}}{b}\)
प्रश्न 5.
यदि cos 9α = sin α एवं 9α. < 90°, तब tan 5α का मान होगा :
(a) \(\frac{1}{\sqrt{3}}\)
(b) √3
(c) 1
(d) 0.
उत्तर:
(c) 1
![]()
प्रश्न 6.
\(\left(\frac{\sin ^{2} 22^{\circ}+\sin ^{2} 68^{\circ}}{\cos ^{2} 22^{\circ}+\cos ^{2} 68^{\circ}}+\sin ^{2} 63^{\circ}+\cos 63^{\circ} \cdot \sin 27^{\circ}\right)\) का मान होगा :
(a) 3
(b) 2
(c) 1
(d) 0.
उत्तर:
(b) 2
प्रश्न 7.
यदि 4 tanθ = 3 तब \(\left[\frac{4 \sin \theta-\cos \theta}{4 \sin \theta+\cos \theta}\right]\) का मान है :
(a) 2/3
(b) 1/3
(c) 1/2
(d) 3/4.
उत्तर:
(c) 1/2
प्रश्न 8.
यदि sinθ – cosθ = 0, तब (sin4 θ + cos4 θ) का मान है :
(a) 1
(b) 3/4
(c) 1/2
(d) 1/4.
उत्तर:
(c) 1/2
प्रश्न 9.
sin (45° + θ) – cos (45° – θ) का मान है :
(a) 2 cosθ.
(b) 0
(c) 2 sinθ
(d) 1.
उत्तर:
(b) 0
प्रश्न 10.
(sin 30° + cos 30°)-(sin 60° + cos 60°) का मान है:
(a) -1.
(b) 0
(c) 1
(d) 2.
उत्तर:
(b) 0
![]()
प्रश्न 11.
tan 30°/ cot 60° का मान है:
(a) \(\frac{1}{\sqrt{2}}\)
(b) \(\frac{1}{\sqrt{3}}\)
(c) √3
(d) 1.
उत्तर:
(d) 1.
प्रश्न 12.
(sin 45° + cos 45°) का मान है :
(a) \(\frac{1}{\sqrt{2}}\)
(b) √2
(c) \(\frac{\sqrt{3}}{2}\)
(d) 1.
उत्तर:
(b) √2
प्रश्न 13.
sin²20° + cos²20° का मान होगा :
(a) 0
(b) 1
(c) tan² 20°
(d) cot² 20°.
उत्तर:
(b) 1
प्रश्न 14.
\(\frac{1}{\csc ^{2} \theta}+\frac{1}{\sec ^{2} \theta}\) का मान होगा:
(a) 1
(b) 0
(c) sin²θ
(d) cos²θ.
उत्तर:
(a) 1
![]()
प्रश्न 15.
sin² 40° + cos² 40° का मान है :
(a) 40
(b) 0
(c) 1
(d) 2.
उत्तर:
(c) 1
प्रश्न 16.
\(\sqrt{1-\cos ^{2} \theta}\) का मान है :
(a) sin θ
(b) cos θ
(c) tan θ
(d) – cos θ.
उत्तर:
(a) sin θ
प्रश्न 17.
tan 45° का मान होगा:
(a) 0
(b) 45
(c) 1
(d) -1.
उत्तर:
(c) 1
प्रश्न 18.
sin (90° – θ) का मान है :
(a) sinθ
(b) cosθ
(c) – cosθ
(d) – sinθ.
उत्तर:
(b) cosθ
![]()
रिक्त स्थानों की पूर्ति
1. \(\sqrt{1-\cos ^{2} \theta}\) का मान ……. होगा।
2. \(\frac{\cot 59^{\circ}}{\tan 31^{\circ}}\) का मान ………….. होगा।
3. (cosec 90° – θ) का मान ………… होगा।
4. \(\sqrt{\sec ^{2} \theta-1}\) का मान …………. होगा।
5. 1 + tan²θ = …………
6. sec (90° – θ) का मान ………… होता है।
उत्तर-
1. sinθ,
2. 1,
3. sec θ,
4. tan θ,
5. sec²θ,
6. cosec²θ.
जोड़ी मिलाइए
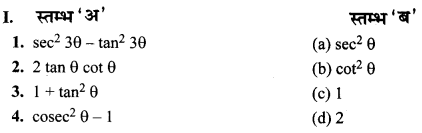
उत्तर-
1. →(c),
2. →(d),
3. →(a),
4. →(b).
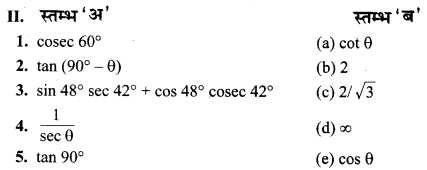
उत्तर-
1.→(c),
2.→(a),
3.→(b),
4.→(e),
5.→(d).

उत्तर-
1.→(c),
2.→(d),
3.→(a),
4.→(b).
![]()
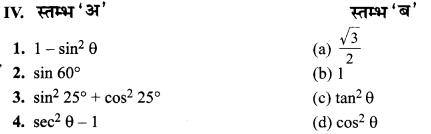
उत्तर-
1.→(d),
2.→(a),
3.→(b),
4.→(c).

उत्तर-
1.→(c),
2.→(d),
3.→(a),
4.→(b)
5.→(f),
6.→(e).
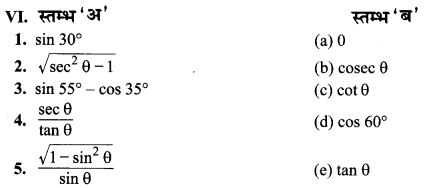
उत्तर-
1.→(d),
2.→(e),
3.→(a),
4.→(b)
5.→(c).
![]()

उत्तर-
1.→(c),
2.→(d),
3.→(e),
4.→(a)
5. →(b).
सत्य/असत्य कथन
1. tan (90° – θ) = cotθ
2. sin² θ + cos² θ = – 1
3. \(\sqrt{1-\sin ^{2} \theta}=\sec \theta\)
4. sec²θ – 1 = tan²θ
5. sin 60° + cos 60° = \(\frac{\sqrt{3}+1}{2}\)
6. cosec θ = \(\sqrt{1+\cot ^{2} \theta}\)
7. sin 12° cos 78° + cos 12° sin 78° = 2
उत्तर-
1. सत्य,
2. असत्य
3. असत्य,
4. सत्य,
5. सत्य
6. सत्य,
7. असत्य
एक शब्द/वाक्य में उत्तर
1. 1 + tan²θ का मान लिखिए।
2. 1 + cot²θ का मान लिखिए।
3. sin²θ + cos²θ का मान लिखिए।
4. cos 0° का मान लिखिए।
5. sin (90° – θ) का मान लिखिए।
6. cos (90° – θ) का मान लिखिए।
7. tan (90° – θ) का मान लिखिए।
8. sin θ / cosθ का मान क्या होगा ?
उत्तर-
1. sec²θ,
2. cosec²θ,
3. 1 (एक),
4. 1 (एक),
5. cos θ,
6. sin θ,
7. cote θ
8. tan θ.