In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 6 त्रिभुज Additional Questions Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 6 त्रिभुज Additional Questions
MP Board Class 10th Maths Chapter 6 अतिरिक्त परीक्षोपयोगी प्रश्न
MP Board Class 10th Maths Chapter 6 दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
संलग्न आकृति 6.72 में यदि ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm और CP = 4 cm, तो PD और CD की लम्बाई ज्ञात कीजिए।
हल :
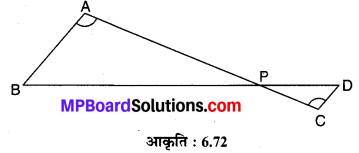
∆ABP एवं ∆CDP में,
∠A = ∠C (दिया है)
∠APB = ∠CPD (शीर्षभिमुख कोण हैं)
∆ABP ~ ∆CDP [AA समरूपता]

![]()
अतः PD की अभीष्ट लम्बाई = 5 cm एवं CD की अभीष्ट लम्बाई = 2 cm है।
प्रश्न 2.
∆ABC ~ ∆EDF दिए हैं जिनमें AB = 5 cm, AC = 7 cm, DF = 15 cm एवं DE = 12 cm. त्रिभुजों की शेष बची भुजाएँ ज्ञात कीजिए।
हल :
∵ ∆ABC ~ ∆EDF (दिया है)
\(\frac{A B}{E D}=\frac{B C}{D F}=\frac{A C}{E F}\) ….(1) (समरूप त्रिभुजों के प्रगुण)
AB = 5 cm, AC = 7 cm, DF = 15 cm एवं ED = DE = 12 cm के दिए हुए मान समीकरण (1) में रखने पर,

अतः शेष बची भुजाओं BC एवं EF की अभीष्ट लम्बाइयाँ क्रमशः 6.25 cm एवं 16.8 cm है।
प्रश्न 3.
एक त्रिभुज की एक भुजा के समानान्तर खींची गई रेखा अन्य दो भुजाओं को जिन दो बिन्दुओं पर प्रतिच्छेद करती है, वे बिन्दु उन भुजाओं को समान अनुपात में विभाजित करते हैं।
अथवा
यदि किसी त्रिभुज में एक भुजा के समानान्तर एक सरल रेखा खींची जाए तो वह अन्य दो भुजाओं को समान अनुपात में विभक्त करती है।
हल :
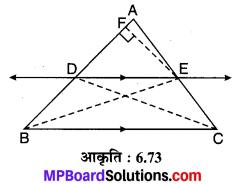
ज्ञात है : ∆ABC जिसमें रेखा DE || BC और रेखा DE, AB को D पर तथा AC को E पर प्रतिच्छेद करती है।
सिद्ध करना है: \(\frac{A D}{D B}=\frac{A E}{E C}\)
रचना : D को C से तथा B को E से मिलाइए एवं EF ⊥ AB खींचिए (देखिए आकृति 6.73)।


प्रश्न 4.
एक 5 m लम्बी सीढ़ी एक ऊर्ध्वाधर के सहारे इस प्रकार रखी है कि उसका शीर्ष दीवार की 4 m ऊँचाई तक पहुँचता है। यदि सीढ़ी के पाद को दीवार की तरफ 1.6 m विस्थापित कर दिया जाए तो वह दूरी ज्ञात कीजिए जिससे सीढ़ी का शीर्ष दीवार पर ऊपर की ओर खिसकता है।
हल :

AB = 5 m लम्बी एक सीढ़ी एक ऊर्ध्वाधर दीवार CA के सहारे खड़ी है जहाँ AC = 4 m है। अब सीढ़ी को दीवार की ओर BB’ = 1.6 m खिसकाने पर नई
स्थिति A’B’ हो जाती है।
अब समकोण ∆ACB में पाइथागोरस प्रमेय से,
BC² = AB² – AC²
BC² = (5)² – (4)²
= 25 – 16
= 9
BC = √9 = 3 m
एवं समकोण ∆A’CB’ में पाइथागोरस प्रमेय से,
A’C = A’B’² – B’C
लेकिन A’B’ = AB = 5 m
B’C = BC – BB’
= 3 m – 1.6 m
= 1.4 m
A’C² = (5)² – (1.4)²
= 25 – 1.96
= 23.04
A’C = √23.04
= 4.8 m
A’A = A’C – AC = 4.8 – 4 = 0.8 m
अतः दीवार के सहारे सीढ़ी का शीर्ष 0.8 m ऊपर की ओर खिसकेगा।
![]()
प्रश्न 5.
किसी शहर A से दूसरे शहर B तक जाने का रास्ता शहर C से होकर जाता है, इस प्रकार कि AC ⊥ CB एवं AC = 2x km तथा CB = 2 (x + 7) km. एक 26 km लम्बा राजमार्ग (हाईवे) बनाना प्रस्तवित है जो शहर A एवं B को सीधा जोड़ेगा। बताइए शहर A से शहर B तक जाने में राजमार्ग बनने पर कितनी दूरी की बचत होगी?
हल :
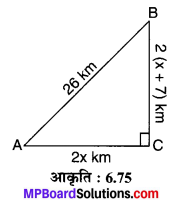
तीनों सड़कें समकोण त्रिभुज ACB की संरचना करती हैं, जहाँ AB = 26 km, AC = 2x km एवं CB = 2 (x + 7) km है।
अब समकोण ∆ACB में पाइथागोरस प्रमेय से,
AC² + BC² = AB²
(2x)² + [2 (x + 7)]² = (26)²
4x² + 4 (x² + 14x + 49) = 676
4x² + 4x² + 56x + 196 = 676
8x² + 56x – 480 = 0
x² + 7x – 60 = 0
x² + 12x – 5x – 60 = 0
x (x + 12) – 5 (x + 12) = 0
(x + 12) (x – 5) = 0
या तो x + 12 = 0 ⇒ x = – 12 km [जो असम्भव है]
अथवा
x – 5 = 0 ⇒ x = 5 km
राजमार्ग बनने से पहले तय की जाने वाली दूरी
= AC + CB = 2x + 2x + 14
= 4x + 14
= 4 × 5 + 14
= 20 + 14
= 34 km
दूरी में अन्तर = 34 km – 26 km = 8 km
अतः तय की गई दूरी में अभीष्ट बचत = 8 km.
प्रश्न 6.
संलग्न आकृति 6.76 में ABC एक समकोण त्रिभुज है जो B पर समकोण है एवं BD ⊥ AC. यदि AD = 4 cm एवं CD = 5 cm तो BD एवं AB के मान ज्ञात कीजिए।
हल :
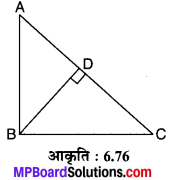
समकोण त्रिभुज के समकोण वाले शीर्ष से कर्ण AC पर डाला गया लम्ब BD त्रिभुज को दो समरूप त्रिभुजों में विभाजित करता है जो मूल त्रिभुज के भी समरूप होते हैं (हम जानते हैं)।
⇒∆ADB ~ ∆BDC ~ ∆ABC [प्रमेय : 6.7 से]
⇒\(\frac{A D}{B D}=\frac{B D}{C D}\)
[समरूप त्रिभुजों के प्रगुण]
⇒\(\frac{4 \mathrm{cm}}{B D}=\frac{B D}{5 \mathrm{cm}}\)
⇒[∵ AD = 4 cm एवं CD = 5 cm दिया है।]
⇒BD² = 4 x 5 = 20
⇒BD = √20 = 2√5 cm
अब समकोण ∆ADB में पाइथागोरस प्रमेय से,
⇒AB² = AD² + BD² = (4)² + (2√5)²
= 16 + 20
= 36
⇒AB = √36 = 6 cm
अंत: BD एवं AB की अभीष्ट लम्बाइयाँ क्रमशः 2√5 cm एवं 6 cm हैं।
प्रश्न 7.
संलग्न आकृति 6.77 में ∆POR एक समकोण त्रिभुज है, जो बिन्दु Q पर समकोण है एवं QS ⊥ PR तथा PQ = 6 cm एवं PS = 4 cm तो QS, RS एवं QR के मान ज्ञात कीजिए।
हल :
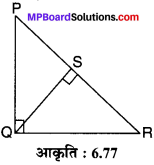
∵ समकोण ∆PSQ में पाइथागोरस प्रमेय से,
QS² = PQ² – PS² = (6)² – (4)²
[∵ PQ = 6 cm एवं PS = 4 cm दिया है]
QS² = 36 – 16 = 20
QS = √20 = 2√5 cm
∵ समकोण ∆ में समकोण वाले शीर्ष पर डाला गया लम्ब त्रिभुज को दो समरूप त्रिभुजों में विभक्त करता है तथा प्रत्येक त्रिभुज मूल त्रिभुज के भी समरूप होता है। (हम जानते हैं)
∆PQS ~ ∆QRS ~ ∆PRQ

[समीकरण (1) में PQ = 6 cm, QS = 2√5 cm एवं RS = 5 cm मान रखने पर]
\(Q R=\frac{6 \times 5}{2 \sqrt{5}}=3 \sqrt{5} \mathrm{cm}\)
अत: QS, RS एवं QR के अभीष्ट मान क्रमश: 2√5 cm, 5 cm एवं 3√5 cm हैं।
प्रश्न 8.
एक चतुर्भुज ABCD में ∠A + ∠D = 90°, तो सिद्ध कीजिए कि : AC² + BD² = AD² + BC²
हल :
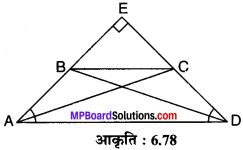
ज्ञात है : चतुर्भुज ABCD जिसमें ∠A + ∠D = 90°
तथा AC एवं BD को मिलाया गया है।
सिद्ध करना है : AC² + BD² = AD² + BC²
रचना : AB एवं DC को बढ़ाइए जो बिन्दु E पर मिलते हैं।
उपपत्ति : चूँकि ∆EAD में ∠A + ∠D = 90° (दिया है)
⇒∆AED, ∆AEC, ∆BEC एवं ∆DEB समकोण ∆ हैं, जिसमें ∠E = 90°
∵ समकोण ∆AEC में पाइथागोरस प्रमेय से,
AC² = AE² + CE² …(1)
∵ समकोण ∆DEB में पाइथागोरस प्रमेय से,
BD² = DE² + BE² …(2)
⇒AC² + BD² = AE² + DE² + BE² + CE² …(3)
[समीकरण (1) + (2) से]
∵ समकोण ∆AED में पाइथागोरस प्रमेय से,
AD² = AE² + DE² …(4)
∵ समकोण ∆BEC में पाइथागोरस प्रमेय से,
BC² = BE² + CE² ….(5)
⇒AD² + BC² = AE² + DE² + BE² + CE² …(6)
[समीकरण (4) + (5) से]
⇒AC² + BD² = AD² + BC². [समीकरण (3) एवं (6) से]
इति सिद्धम्
![]()
प्रश्न 9.
समलम्ब चतुर्भुज ABCD जिसमें AB || DC है के विकर्ण AC एवं BD का प्रतिच्छेद बिन्दु O है। O से होकर AB के समान्तर एक रेखाखण्ड PQ खींचा गया है जो AD को P पर तथा BC को Q पर मिलता है। सिद्ध कीजिए : PO = QO
हल :
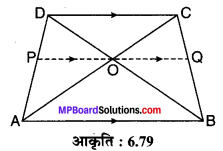
∵ AB || DC एवं AB || PQ
PQ || DC अर्थात् OQ|| DC || AB
तथा PO || AB || DC
∵ ∆BDC में, OQ || DC


PO = QO.
इति सिद्धम्
प्रश्न 10.
संलग्न आकृति 6.80 में रेखाखण्ड DF, ∆ABC की भुजा AC को बिन्दु E पर इस प्रकार विभाजित करता है कि E बिन्दु भुजा CA का मध्य-बिन्दु है एवं ∠AEF = ∠AFE है तो सिद्ध कीजिए कि:
\(\frac{B D}{C D}=\frac{B F}{C E}\)
हल :
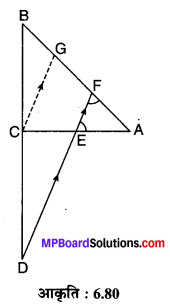
दिया है : रेखाखण्ड DE, ∆ABC की भुजा AC को बिन्दु E पर इस प्रकार प्रतिच्छेद करते हुए कि E, CA का मध्य-बिन्दु AB पर बिन्दु F पर मिलता है तथा ∠AEF = ∠AFE है। रचना : GC || DF खींचिए जो ∆ABC की भुजा AB के बिन्दु G पर मिलती है। चूँकि E, भुजा AC का मध्य-बिन्दु,
CE = AE (दिया है)
चूँकि ∠AEF = ∠AFE (दिया है)
AE = AF
AE = CE = AF
CG || DF खींचिए जो AB को बिन्दु G पर मिलती है।
∆ACG में, DF || CG

MP Board Class 10th Maths Chapter 6 लघु उत्तरीय प्रश्न
प्रश्न 1.
सिद्ध कीजिए कि किसी समकोण ∆ के कर्ण पर बने समाबाहु त्रिभुज का क्षेत्रफल शेष भुजाओं पर बने समबाहु त्रिभुजों के क्षेत्रफल के योग के बराबर होता है।
हल :
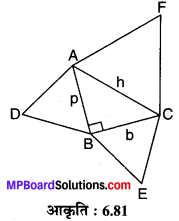
मान लीजिए ∆ABC एक समकोण त्रिभुज है जिसका ∠B समकोण है तथा कर्ण AC पर समबाहु ∆FAC, AB पर बना समबाहु ∆DAB एवं BC पर बना समबाहु त्रिभुज EBC है।
AB = p, BC = b एवं AC = h.
समकोण ∆ABC में पाइथागोरस प्रमेय से,
AB² + BC² = AC²
⇒ p² + b² = h² …(1)
ar (DAB) + ar (EBC)

अतः किसी समकोण त्रिभुज के कर्ण पर बने समबाहु त्रिभुज का क्षेत्रफल अन्य भुजाओं पर बने समबाहु त्रिभुजों के क्षेत्रफल के योग के बराबर होता है।
इति सिद्धम्
प्रश्न 2.
∆PQR में, PD ⊥ QR इस प्रकार है कि D बिन्दु QR पर स्थित है। यदि PQ = a, PR = b, QD = c तथा DR = d तो सिद्ध कीजिए कि : (a + b) (a – b) = (c + d) (c – d)
हल :
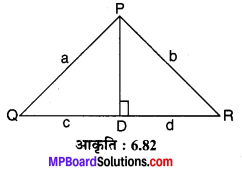
ज्ञात है : ∆PQR जिसमें PD ⊥ QR जहाँ D बिन्दु रेखा QR पर स्थित होगा। PQ = a, PR = b, QD = c एवं DR = d है।
सिद्ध करना है: (a + b)(a – b) = (c + d) (c – d)
अब समकोण ∆PDQ में पाइथागोरस प्रमेय से,
⇒ PD² = PQ² – QD² = a² – c² …(1)
एवं समकोण ∆PDR में पाइथागोरस प्रमेय से,
⇒ PD² = PR² – DR² = b² – d² ….(2)
⇒ a² – c² = b² – d² [समीकरण (1) एवं (2) से]
⇒ a² – b² = c² – d²
⇒ (a + b) (a – b) = (c + d) (c – d).
इति सिद्धम्
![]()
प्रश्न 3.
एक बल्ब एक खम्भे पर सड़क के तल से 6 m की ऊँचाई पर लगा है। एक 1.5 m ऊँचाई की स्त्री की छाया 3 m लम्बी पड़ती है। बताइए कि स्त्री खम्भे के आधार से कितनी दूरी पर खड़ी है?
हल :
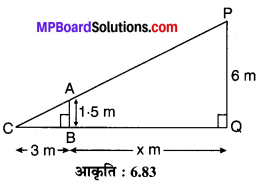
मान लीजिए एक खम्भा PQ = 6 m ऊँचा है। एक स्त्री AB = 1.5 m ऊँचे खम्भे के आधार Q से QB = x m की दूरी पर खड़ी है जिसकी छाया CB = 3 m लम्बी पड़ती है।
चूँकि AB || PQ (ऊधर्वाधर है)
⇒ ∆ABC ~ ∆PQC [∠C उभयनिष्ठ ∠B = ∠Q = 90°]
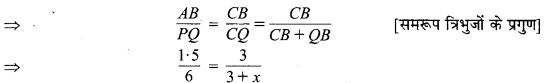
⇒ 4.5 + 1.5x = 18
⇒ 1.5x = 18 – 4.5 = 13.5
⇒ x = \(\frac { 13.5 }{ 1.5 }\) = 9m
अतः स्त्री खम्भे के आधार से 9 m की दूरी पर खड़ी है।
प्रश्न 4.
18 m ऊँचे झण्डे के स्तम्भ की छाया 9.6 m लम्बी है। स्तम्भ के शीर्ष की छाया के दूर अन्त्यः बिन्दु से दूरी ज्ञात कीजिए।
हल :
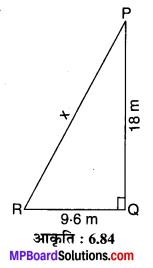
मान लीजिए कि PQ = 18 m ऊँचे झण्डे के स्तम्भ की छाया QR = 9.6 m लम्बी पड़ती है।
बिन्दु R से खम्भे के शीर्ष P की दूरी PR = x m है।
समकोण ∆PQR में पाइथागोरस प्रमेय से,
PR² = PQ² + QR²
= (18)² + (9.6)²
= 324 + 92.16
= 416.16
PR = √416.16
= 20.4 m
अतः बिन्दु R से स्तम्भ के शीर्ष की अभीष्ट दूरी = 20.4m है।
प्रश्न 5.
संलग्न आकृति 6.85 में DE || AB तो x का मान ज्ञात कीजिए।
हल :
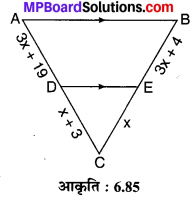
∆CAB में,
चूँकि DE || AB
⇒ \(\frac{C D}{D A}=\frac{C E}{E B}\) (प्रमेय : 6.1 से)
⇒ \(\frac{x+3}{3 x+19}=\frac{x}{3 x+4}\) (चित्रानुसार)
⇒ 3x² + 19x = 3x² + 4x + 9x + 12
⇒ 19x = 13x + 12
⇒ 6x = 12
⇒ x = \(\frac { 12 }{ 2 }\) = 2
अतः x का अभीष्ट मान = 2 है।
प्रश्न 6.
समलम्ब चतुर्भुज PQRS के विकर्ण परस्पर O बिन्दु पर प्रतिच्छेद करते हैं, जहाँ PQ || RS तथा PQ = 3RS, तो त्रिभुज POQ एवं ROS के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
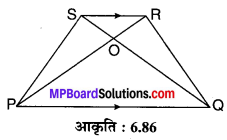
ज्ञात है PQRS एक समचतुर्भुज जिसमें PQ || RS एवं PQ = 3RS. इसके विकर्ण PR एवं QS परस्पर O बिन्दु पर प्रतिच्छेद करते हैं।
अब ∆POQ एवं ∆ROS में,
∵ ∠POQ = ∠ROS [शीर्षाभिमुख कोण हैं।]
⇒ ∠RPQ = ∠PRS
[एकान्तर कोण हैं जहाँ PQ || RS एवं RP तिर्यक रेखा है]
⇒ ∆POQ ~ ∆ROS [AA समरूपता]
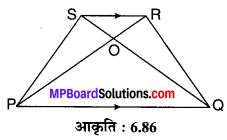
अतः ∆POQ एवं ∆ROS के क्षेत्रफलों का अभीष्ट अनुपात 9:1 है।
![]()
प्रश्न 7.
∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm एवं FD = 12 cm. ∆ABC का परिमाप ज्ञात कीजिए।
हल :
चूंकि
∆ABC ~ ∆DEF

∆ABC की परिमाप = AB + BC + CA
= 4 cm + 6 cm + 8 cm
= 18 cm
अत: ∆ABC की अभीष्ट परिमाप = 18 cm है।
प्रश्न 8.
संलग्न आकृति 6.87 में, यदि DE || BC तो ∆ADE एवं ∆ABC के क्षेत्रफलों में अनुपात ज्ञात कीजिए।
हल :
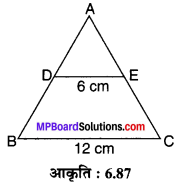
⇒ ∆ADE एवं ∆ABC में
⇒ ∠A = ∠A [उभयनिष्ठ हैं।]
⇒ ∠D = ∠B [संगत कोण हैं]
चूँकि DE || BC एवं AB तिर्यक रेखा है।
⇒ ∆ADE ~ ∆ABC [AA समरूपता]

अत: ∆ADE एवं ∆ABC के क्षेत्रफलों में अभीष्ट अनुपात 1 : 4 है।
प्रश्न 9.
दो समरूप त्रिभुजों के क्षेत्रफल क्रमश: 36 cm² एवं 100 cm² हैं। यदि बड़े त्रिभुज की कोई भुजा की लम्बाई = 20 cm हो तो छोटे त्रिभुज की संगत भुजा की लम्बाई ज्ञात कीजिए।
हल :
मान लीजिए छोटी त्रिभुज की संगत भुजा की लम्बाई x cm है और हम जानते हैं कि समरूप त्रिभुजों में,

अतः छोटे त्रिभुज की संगत भुजा की अभीष्ट लम्बाई = 12 cm है।
प्रश्न 10.
एक 10 m लम्बी सीढ़ी एक ऊर्ध्वाधर दीवार के आधार से 6 m दूरी पर रखी हुई दीवार के साथ टिकी है। दीवार के उस बिन्दु की ऊँचाई ज्ञात कीजिए, जहाँ पर सीढ़ी का शीर्ष टिका है।
हल :
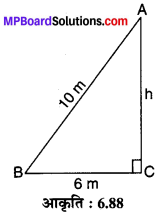
मान लीजिए एक सीढ़ी AB = 10 m लम्बी है और दीवार AC के आधार C से BC = 6 m की दूरी पर रखी हुई है तथा दीवार के साथ बिन्दु A पर टिकी है। A की ऊँचाई आधार से AC = h है तो समकोण ∆ACB में पाइथागोरस प्रमेय से,
⇒ AC² = AB² – BC²
⇒ h² = (10)² – (6)²
= 100 – 36
= 64
⇒ h = √64
= 8 m
अतः दीवार के अभीष्ट बिन्दु की ऊँचाई = 8 m
![]()
प्रश्न 11.
आकृति 6.89 में ∠P ज्ञात कीजिए।
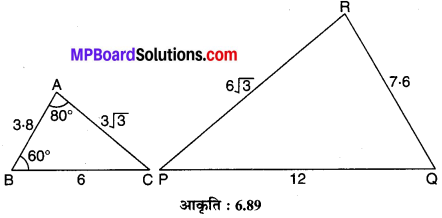
हल :
∆ABC एवं ∆PQR में,
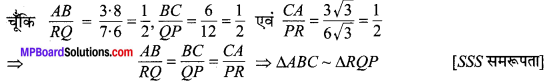
⇒ ∠A = ∠R, ∠A = ∠Q एवं ∠C = ∠P
लेकिन ∠C + 60° + 80° = 180° [त्रिभुज के अन्त:कोण हैं।]
⇒ ∠C = 180° + 140° = 40°
⇒ ∠P = ∠C = 40°
अतः ∠P का अभीष्ट मान = 40° है।
MP Board Class 10th Maths Chapter 6 अति लघु उत्तरीय प्रश्न
प्रश्न 1.
क्या त्रिभुज जिसकी भुजाएँ 25 cm, 5 cm और 24 cm हैं, समकोण त्रिभुज है? अपने उत्तर का कारण दीजिए।
हल :
नहीं, क्योंकि (24)² + (5)² = 576 + 25 = 601 ≠ (25)²
प्रश्न 2.
∆DEF ~ ∆RPQ दिया है। क्या यह कहना सत्य है कि ∠D = ∠R = एवं ∠F = ∠P.
हल :
कथन सत्य नहीं है, क्योंकि ∠F ≠ ∠P बल्कि ∠F = ∠Q.
प्रश्न 3.
किसी ∆POR की भुजाओं PQ एवं PR पर बिन्दु क्रमश: A एवं B इस प्रकार हैं कि PQ= 12.5 cm, PA = 5 cm, BR = 6 cm एवं PB = 4 cm. क्या AB || QR ? अपने उत्तर का कारण दीजिए।
हल :
हाँ AB || OR. क्योंकि
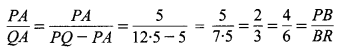
प्रश्न 4.
संलग्न आकृति 6.90 में BD एवं CF परस्पर बिन्द P पर प्रतिच्छेद करती हैं। क्या ∆PBC ~ ∆PDE और क्यों?
हल :
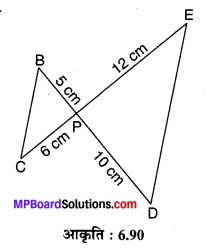
हाँ, ∆PBC ~ ∆PDE,
क्योकि \(\frac{P B}{P D}=\frac{5}{10}=\frac{1}{2}, \frac{P C}{P E}=\frac{6}{12}=\frac{1}{2}\)
एवं ∠BPC = ∠DPE [शीर्षाभिमुख कोण]
अर्थात् SAS समरूपता है।
प्रश्न 5.
∆PQR एवं ∆MST में ∠P = 55°, ∠Q = 25°, ∠M = 100° एवं ∠S = 25°, क्या ∆QPR ~ ∆TSM ? क्यों?
हल :
नहीं, क्योंकि ∆QPR ~ ∆STM.
![]()
प्रश्न 6.
क्या निम्न कथन सत्य है? और क्यों? “दो चतुर्भुज समरूप हैं अगर उनके संगत कोण बराबर हैं।”
हल :
नहीं, क्योंकि संगत भुजाएँ भी समानुपाती होनी चाहिए।
प्रश्न 7.
एक त्रिभुज की दो भुजाएँ एवं परिमाप क्रमशः दूसरे त्रिभुज की संगत भुजाओं और परिमाप का तीन गुना है। क्या दोनों त्रिभुज समरूप हैं? और क्यों?
हल :
हाँ, वे त्रिभुज समरूप हैं, क्योंकि दो संगत भुजाएँ एवं परिमाप समानुपाती हैं तो तीसरी भुजा भी समानुपाती होगी। (SSS समरूपता)
प्रश्न 8.
एक समकोण त्रिभुज का एक न्यूनकोण दूसरे समकोण त्रिभुज के एक न्यूनकोण के बराबर हो तो क्या दोनों त्रिभुज समरूप होंगे? और क्यों?
हल :
हाँ, समरूप होंगे। (AAA समरूपता)
प्रश्न 9.
दो समरूप त्रिभुजों के संगत शीर्ष लम्बों का अनुपात \(\frac { 3 }{ 5 }\) है तो क्या यह कहना सत्य है कि उनके क्षेत्रफलों का अनुपात \(\frac { 6 }{ 5 }\) होगा? और क्यों?
हल :
नहीं, यह कहना असत्य है क्योंकि क्षेत्रफलों का अनुपात \(\frac { 9 }{ 25 }\) होगा।
प्रश्न 10.
∆POR की भुजा QR पर बिन्दु D इस प्रकार है कि PD ⊥ QR, क्या यह कहना सत्य होगा कि ∆PQD ~ ∆RPD ? और क्यों?
हल :
नहीं, यह कहना असत्य है, क्योंकि यह तभी सम्भव है जब ∠P = 90° हो।
![]()
प्रश्न 11.
संलग्न आकृति 6.91 में ∠D = ∠C तो क्या यह कहना सत्य होगा कि ∆ADE ~ ∆ACB ? और क्यों?
हल :
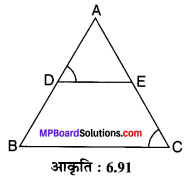
हाँ, कथन सत्य है क्योंकि AA समरूपता है।
प्रश्न 12.
क्या यह कहना सत्य है कि यदि दो त्रिभुजों में एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो एवं एक त्रिभुज की दो भुजाएँ दूसरे त्रिभुज की दो भुजाओं के समानुपाती हों तो त्रिभुज समरूप होंगे? अपने उत्तर का कारण दीजिए।
हल :
नहीं, कथन असत्य है क्योंकि दो जोड़े समानुपाती भुजाओं के मध्य कोण बराबर होने चाहिए।
प्रश्न 13.
∆ABC में, AB = 24 cm, BC = 10 cm एवं AC = 26 cm. क्या यह त्रिभुज एक समकोण त्रिभुज है? अपने उत्तर का कारण दीजिए।
हल :
हाँ, त्रिभुज समकोण त्रिभुज है क्योंकि
AB² + BC² = (24)² + (10)²
= 576 + 100
= 676
= (26)²
= AC²
प्रश्न 14.
एक त्रिभुज DEF की भुजाओं DE एवं DF पर क्रमशः बिन्दु P एवं Q इस प्रकार स्थित हैं कि DP = 5 cm, DE = 15 cm, DQ = 6 cm एवं DF = 18 cm. क्या PQ || EF ? अपने उत्तर का कारण दीजिए।
हल :
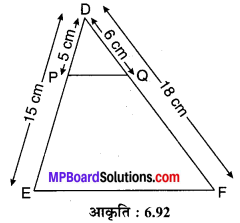
हाँ, क्योंकि
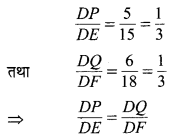
अत: PQ || EF है।
प्रश्न 15.
∆FED ~ ∆STU दिया है क्या \(\frac{D E}{S T}=\frac{E F}{T U}\) और क्यों?
हल :
नहीं, \(\frac{D E}{S T} \neq \frac{E F}{T U}\) क्योंकि \(\frac{D E}{T U}=\frac{E F}{S T}\) संगत भुजाओं का अनुपात समान होना चाहिए।
![]()
MP Board Class 10th Maths Chapter 6 वस्तुनिष्ठ प्रश्न
MP Board Class 10th Maths Chapter 6 बहु-विकल्पीय प्रश्न
प्रश्न 1.
दो त्रिभुज समरूप होंगे, यदि :
(a) त्रिभुजों के संगत कोण बराबर हैं,
(b) त्रिभुजों की संगत भुजाएँ आनुपातिक हों,
(c) त्रिभुजों के संगत क्षेत्रफल बराबर हों,
(d) त्रिभुजों के संगत कोण बराबर हों तथा संगत भुजाएँ आनुपातिक हों।
उत्तर:
(d) त्रिभुजों के संगत कोण बराबर हों तथा संगत भुजाएँ आनुपातिक हों।
प्रश्न 2.
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। इनमें से समकोण त्रिभुज नहीं है :
(a) 7 सेमी, 24 सेमी, 25 सेमी,
(b) 5 सेमी, 8 सेमी, 11 सेमी,
(c) 5 सेमी, 12 सेमी, 13 सेमी,
(d) 3 सेमी, 4 सेमी, 5 सेमी।
उत्तर:
(b) 5 सेमी, 8 सेमी, 11 सेमी,
प्रश्न 3.
“एक त्रिभुज की एक भुजा के समान्तर खींची गई रेखा अन्य दो भुजाओं को जिन दो बिन्दुओं पर प्रतिच्छेद करती है, वे बिन्दु भुजाओं को समान अनुपात में विभाजित करते हैं।” यह कथन है : (a) थेल्स प्रमेय का,
(b) पाइथागोरस प्रमेय का,
(c) थेल्स प्रमेय के विलोम का,
(d) पाइथागोरस प्रमेय के विलोम का।
उत्तर:
(a) थेल्स प्रमेय का,
प्रश्न 4.
“यदि कोई रेखा किसी त्रिभुज की दो भुजाओं को समान अनुपात में विभाजित करती है, तो यह रेखा तीसरी भुजा के समान्तर होती है।” यह कथन है :
(a) थेल्स प्रमेय का,
(b) पाइथागोरस प्रमेय का,
(c) थेल्स प्रमेय के विलोम का,
(d) पाइथागोरस प्रमेय के विलोम का।
उत्तर:
(c) थेल्स प्रमेय के विलोम का,
प्रश्न 5.
“एक समकोण त्रिभुज में कर्ण का वर्ग अन्य दो भुजाओं के वर्गों के योगफल के बराबर होता है।” यह कथन है:
(a) थेल्स प्रमेय का,
(b) पाइथागोरस प्रमेय का,
(c) थेल्स प्रमेय के विलोम का,
(d) पाइथागोरस प्रमेय के विलोम का।
उत्तर:
(b) पाइथागोरस प्रमेय का,
![]()
प्रश्न 6.
“एक त्रिभुज में यदि एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योगफल के बराबर हो, तो पहली भुजा के सामने का कोण समकोण होता है।” यह कथन है :
(a) थेल्स प्रमेय का,
(b) पाइथागोरस प्रमेय का,
(c) थेल्स प्रमेय का विलोम का,
(d) पाइथागोरस प्रमेय के विलोम का।
उत्तर:
(d) पाइथागोरस प्रमेय के विलोम का।
प्रश्न 7.
एक आदमी पूर्व की ओर 150 मीटर जाता है और फिर उत्तर की ओर 200 मीटर जाता है। आदमी की प्रारिम्भक बिन्दु से दूरी होगी :
(a) 150 मीटर,
(b) 25 मीटर,
(c) 15 मीटर,
(d) 250 मीटर।
उत्तर:
(d) 250 मीटर।
प्रश्न 8.
एक व्यक्ति पूर्व की ओर 15 मीटर जाता है और फिर उत्तर की ओर 8 मीटर जाता है। व्यक्ति की प्रारम्भिक बिन्दु से दूरी होगी :
(a) 23 मीटर,
(b) 17 मीटर,
(c) 7 मीटर,
(d) 25 मीटर।
उत्तर:
(b) 17 मीटर,
प्रश्न 9.
एक 25 मीटर लम्बी सीढ़ी एक भवन की जमीन से 20 मीटर ऊँची खिड़की तक जाती है। भवन से सीढ़ी के निचले सिरे की दूरी होगी :
(a) 45 मीटर,
(b) 5 मीटर,
(c) 15 मीटर,
(d) 25 मीटर।
उत्तर:
(c) 15 मीटर,
प्रश्न 10.
एक सीढ़ी इस तरह रखी गई है कि उसका निचला सिरा दीवार से 5 मीटर की दूरी पर है और उसका ऊपरी सिरा जमीन से 12 मीटर ऊँची खिड़की तक जाता है। सीढ़ी की लम्बाई होगी :
(a) 7 मीटर,
(b) 17 मीटर,
(c) 25 मीटर,
(d) 13 मीटर।
उत्तर:
(d) 13 मीटर।
![]()
प्रश्न 11.
दो समरूप त्रिभुजों के क्षेत्रफलों में 9 : 16 का अनुपात है, तो उनके शीर्ष लम्बों का अनुपात होगा :
(a) 3 : 4,
(b) 4 : 3,
(c) 9 : 1,
(d) 16 : 9.
उत्तर:
(a) 3 : 4,
प्रश्न 12.
समरूपता के लिए आवश्यक प्रतिबन्ध है :
(a), कोण-कोण-कोण समरूपता,
(b) कोण-कोण समरूपता,
(c) भुजा-कोण-भुजा समरूपता,
(d) ये सभी।
उत्तर:
(d) ये सभी।
प्रश्न 13.
एक ∆ABC की भुजाओं AB और AC पर क्रमश: दो बिन्दु एवं E इस प्रकार हैं कि: AD = 2 cm, BD = 3 cm, BC = 7.5 cm एवं DE || BC, तब DE की लम्बाई (cm में) होगी :
(a) 2.5,
(b) 3,
(c) 5,
(d) 6.
उत्तर:
(b) 3,
प्रश्न 14.
किसी समचतुर्भुज के विकर्णों की लम्बाई 16 cm एवं 12 cm है तो उसकी भुजा की लम्बाई है:
(a) 9 cm,
(b) 10 cm,
(c) 8 cm,
(d) 20 cm.
उत्तर:
(b) 10 cm,
प्रश्न 15.
यदि ∆ABC ~ ∆EDF एवं ∆ABC एवं ∆DEF समरूप नहीं हैं तब निम्न में से कौन सत्य नहीं है?
(a) BC.EF = AC.FD,
(b) AB.EF = AC.DE,
(c) BC.DE = AB. EF
(d) BC.DE = AB.FD.
उत्तर:
(c) BC.DE = AB. EF
![]()
प्रश्न 16.
यदि दो त्रिभुजों ABC एवं PQR में
(a) ∆PQR ~ ∆CAB,
(b) ∆PQR ~ ∆ABC,
(c) ∆CBA ~ ∆POR,
(d) ∆BCA ~ ∆POR.
उत्तर:
(a) ∆PQR ~ ∆CAB,
प्रश्न 17.
दो त्रिभुज DEF एवं PQR में ∠D = ∠Q एवं ∠R = ∠E तब निम्न में कौन सही नहीं है?

उत्तर:
(b) \(\frac{D E}{P Q}=\frac{E F}{R P}\)
प्रश्न 18.
∆ABC ~ ∆PQR दिया है एवं \(\frac{B C}{Q R}=\frac{1}{3}\) तब \(\frac{a r(P R Q)}{a r(B C A)}\) बराबर होगा :
(a) 9,
(b) 3,
(c) \(\frac { 1 }{ 3 }\).
(d) \(\frac { 1 }{ 9 }\).
उत्तर:
(a) 9,
प्रश्न 19.
∆ABC एवं ∆DEF में \(\frac{A B}{D E}=\frac{B C}{F D}\) तब ये दोनों त्रिभज समरूप होंगे जब :
(a) ∠B = ∠E,
(b) ∠A = ∠D,
(c) ∠B = ∠D,
(d) ∠A = ∠E
उत्तर:
(c) ∠B = ∠D,
प्रश्न 20.
यदि ∆ABC ~ ∆QRD एवं \(\frac{a r(A B C)}{a r(P Q R)}=\frac{9}{4}\), AB = 18 cm, BC = 15 cm तब PR बराबर
होगा :
(a) 10 cm,
(b) 12 cm,
(c) \(\frac { 20 }{ 3 }\) cm
(d) 8 cm.
उत्तर:
(a) 10 cm
![]()
रिक्त स्थानों की पूर्ति
1. यदि दो त्रिभुजों की संगत भुजाएँ आनुपातिक हों, तो वे त्रिभुज ……… होते हैं।
2. ………. त्रिभुज सदैव समरूप होते हैं।
3. सभी वर्ग ……….. होते हैं।
4. दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात किन्हीं दो संगत भुजाओं के ……….. के अनुपात के बराबर होता है।
5. किसी त्रिभुज के शीर्ष कोण का ………….. सम्मुख भुजा को शेष भुजाओं के अनुपात में विभाजित करता है।
6. यदि दो त्रिभुजों के संगत कोण बराबर हों, तो वे त्रिभुज ………… कहलाते हैं।
7. दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 9 : 16 के अनुपात में है, तो उन त्रिभुजों की संगत भुजाओं का अनुपात ………… होगा।
उत्तर-
1. समरूप,
2. समबाहु,
3. समरूप,
4. वर्गों,
5. समद्विभाजक,
6. समरूप त्रिभुज
7. 3 : 4
जोड़ी मिलाइए

उत्तर-
1.→(c),
2. →(d),
3.→(e),
4.→(a),
5. →(f),
6.→(b).
![]()
सत्य/असत्य कथन
1. समकोण त्रिभुज में कर्ण सबसे बड़ी भुजा होती है।
2. यदि त्रिभुज की संगत भुजाएँ आनुपातिक हों, तो वे त्रिभुज समरूप नहीं होते हैं।
3. समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के बराबर होता है।
4. यदि दो त्रिभुज समकोणिक हों तो त्रिभुज समरूप होंगे।
5. यदि किसी त्रिभुज में एक भुजा के समानान्तर एक सरल रेखा खींची जाए, तो वह अन्य दोनों भुजाओं को ___ समान अनुपात में विभक्त करती है।
6. थेल्स प्रमेय का कथन है-“यदि किसी त्रिभुज में कोई सरल रेखा उसकी दो भुजाओं को समान अनुपात __ में विभक्त करे, तो वह तीसरी भुजा के समानान्तर होती है।”
7. सभी वर्ग समरूप होते हैं। (2019)
8. समकोण त्रिभुज का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x आधार x शीर्ष लम्ब होता है। (2019)
उत्तर-
1. सत्य,
2. असत्य,
3. सत्य,
4. सत्य,
5. सत्य,
6. असत्य,
7. सत्य,
8. सत्य।
एक शब्द/वाक्य में उत्तर
1. एक त्रिभुज की एक भुजा के समानान्तर खींची गई रेखा अन्य दो भुजाओं को जिन दो बिन्दुओं पर प्रतिच्छेद करती है, वे बिन्दु उन भुजाओं को समान अनुपात में विभाजित करते हैं। यह प्रमेय किस नाम से जानी जाती है?
2. समकोण त्रिभुज प्रमेय का नाम लिखिए।
3. यदि किसी ∆ABC में AD ⊥ BC एवं AC² = AB² + BC² + 2BC.BD हो, तो यह प्रमेय किस नाम से जानी जाती है?
4. यदि किसी ∆ABC में AD ⊥BC एवं AC² = AB² + BC² – 2BC.BD हो, तो यह प्रमेय किस नाम से जानी जाती है?
5. यदि किसी ∆ABC की माध्यिका AD हो, तब AB² + AC² = 2 (AD² + BD²), तो यह प्रमेय किस नाम से जानी जाती है?
6. आकृतियों का वह गुण जिसमें उनका आकार समान हो तथा विस्तार भिन्न-भिन्न हो, क्या कहलाता है?
7. समरूप त्रिभुज, ∆ABC एवं ∆PQR के क्षेत्रफल एवं भुजाओं में सम्बन्ध लिखिए।
8. दो समरूप त्रिभुजों के शीर्षलम्बों की माप में 2 : 3 का अनुपात हो, तो उनके क्षेत्रफलों में क्या अनुपात होगा?
9. पाइथागोरस प्रमेय का कथन लिखिए।
उत्तर-
1. थेल्स प्रमेय,
2. पाइथागोरस प्रमेय,
3. अधिककोण त्रिभुज प्रमेय,
4. न्यूनकोण त्रिभुज प्रमेय,
5. अपोलोनियसपमेय
6. समरूपता
7.
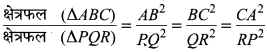
8. 4 : 9
9.”समकोण त्रिभुज में कर्ण पर बना वर्ग शेष भुजाओं पर बने वर्गों के योग के बराबर होता है।”