MP Board Class 10th Maths Solutions Chapter 14 सांख्यिकी Additional Questions

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 14 सांख्यिकी Additional Questions Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 14 सांख्यिकी Additional Questions

MP Board Class 10th Maths Chapter 14 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 10th Maths Chapter 14 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
निम्न वितरण से विद्यार्थियों के अंकों का माध्य ज्ञात कीजिए

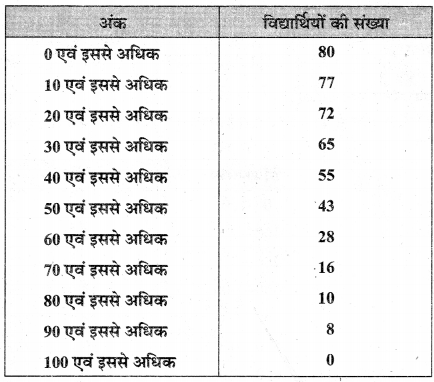
हल :
वर्ग अन्तराल एवं बारम्बारता सारणी प्राप्त करने पर

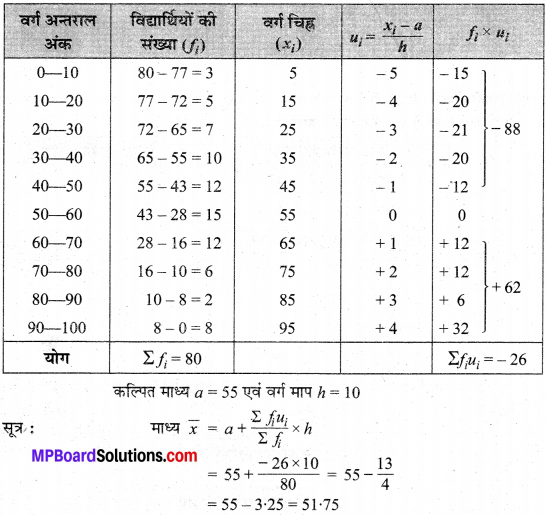
अतः, अभीष्ट माध्य अंक = 51.75 है।

प्रश्न 2.
निम्न वितरण का माध्य ज्ञात कीजिए

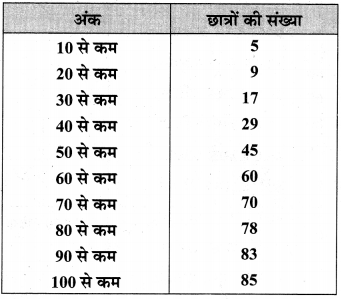
हल :
वर्ग अन्तराल एवं बारम्बारता सारणी प्राप्त करने पर

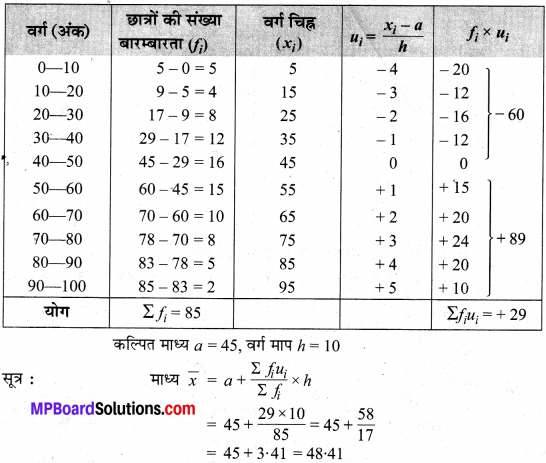
अतः, अभीष्ट माध्य अंक = 48.41.

प्रश्न 3.
निम्न बारम्बारता बंटन का माध्य 50 है। लेकिन वर्ग (20-40) एवं (60-80) की बारम्बारताएँ क्रमशः f1 एवं f2 अज्ञात हैं। इन बारम्बारताओं को ज्ञात कीजिए यदि सभी बारम्बारताओं का योग 120 है।

हल :

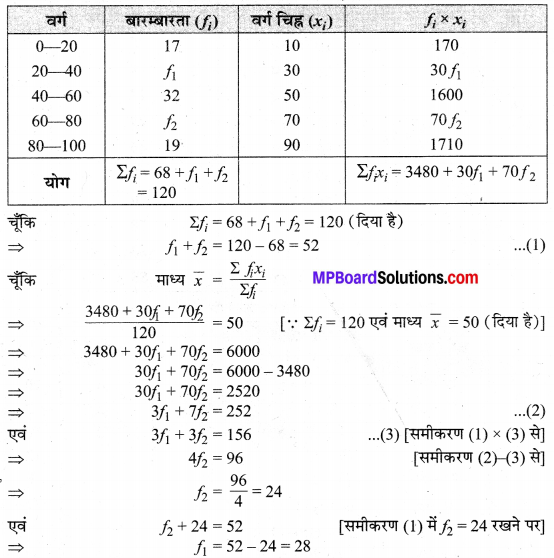
अतः, एवं के अभीष्ट मान हैं क्रमशः 28 एवं 24 हैं।

प्रश्न 4.
निम्न आँकड़ों का माध्यक 50 है। p एवं q के मान ज्ञात कीजिए यदि सभी बारम्बारताओं का योग 90 है।

हल :
संचयी बारम्बारता सारणी बनाने पर

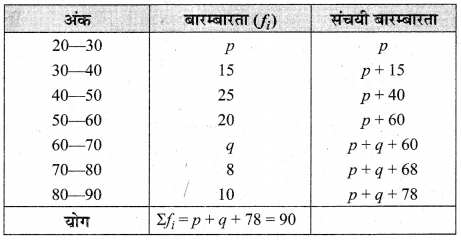
चूँकि बारम्बारताओं का योग n = 90 दिया है।

30 – p = 25 ⇒ p= 30 – 25 = 5 …(1)
⇒ ∑f_i = p + q + 78 = n = 90 (दिया है)
⇒ p + q = 90 – 78 = 12 ….(2)
समीकरण (1) से p = 5 का मान समीकरण (2) में रखने पर,
⇒ 5 + q = 12
⇒ q = 12 – 5 = 7
अतः, p एवं q के अभीष्ट मान क्रमशः 5 एवं 7 हैं।

प्रश्न 5.
96 बच्चों की ऊँचाई (cm में) का वितरण निम्न प्रकार दिया है:

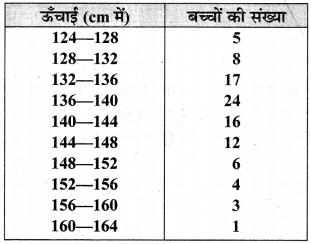
इन आँकड़ों के लिए से कम प्रकार का संचयी बारम्बारता वक्र खींचिए और इसका प्रयोग बच्चों के माध्यक ऊँचाई ज्ञात करने में कीजिए।
हल :
‘से कम प्रकार’ का संचयी बारम्बारता वक्र खींचने के लिए हम सर्वप्रथम से कम प्रकार की संचयी बारम्बारता सारणी तैयार करते हैं

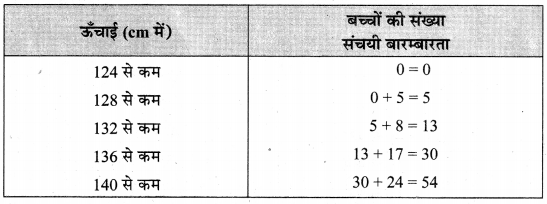
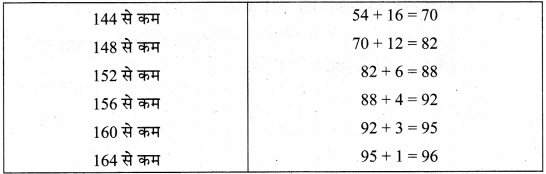
से कम से कम प्रकार का संचयी बारम्बारता वक्र :

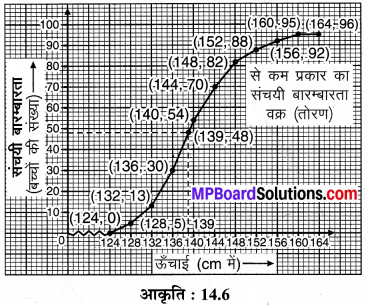
अतः उपर्युक्त वक्र अभीष्ट से कम प्रकार का संचयी बारम्बारता वक्र’ है तथा इसके प्रयोग से ज्ञात की गयी माध्यम ऊँचाई = 139 cm है।

प्रश्न 6.
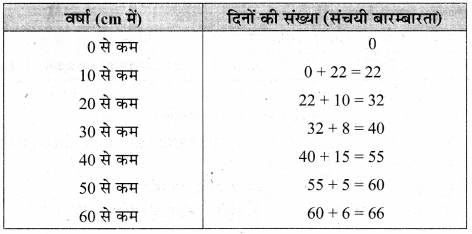
एक शहर का 66 दिन के लिए हुई वार्षिक वर्षा के आँकड़े निम्न तालिका (सारणी) में दिए गए हैं:

दिए आँकड़ों से ‘से कम प्रकार’ का एवं से अधिक प्रकार’ का तोरण खींचकर माध्यक वर्षा का परिकलन कीजिए।
हल :
‘से कम’ प्रकार की संचयी बारम्बारता सारणी तैयार करने पर

‘के बराबर या से अधिक प्रकार की संचयी बारम्बारता सारणी बनाने पर,

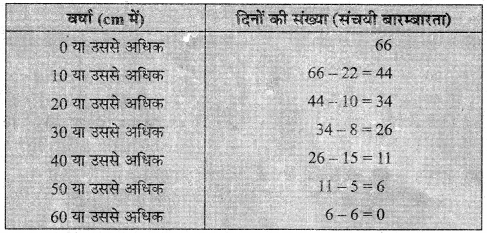
से कम प्रकार का तोरण एवं से अधिक प्रकार का तोरण :

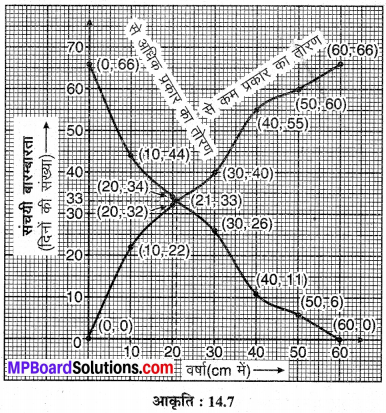
दोनों तोरणों का प्रतिच्छेद बिन्दु (21,33) है।
अतः, अभीष्ट माध्य 21 (लगभग) है।

प्रश्न 7.
भाला फेंक (Javelin throw) स्पर्धा में 50 छात्रों ने भाग लिया। उनके द्वारा फेंके गए भाले द्वारा तय की गयी दूरी (m में) निम्न प्रकार प्रेक्षित की गयी

(i) एक संचयी बारम्बारता सारणी का निर्माण कीजिए।
(ii) ‘से कम’ प्रकार का संचयी बारम्बारता वक्र (तोरण) खींचिए एवं फेंकी गयी माध्यक दूरी का परिकल्पना कीजिए।
(iii) सूत्र का प्रयोग करके माध्यक दूरी का परिकलन कीजिए।
(iv) क्या चरण (ii) एंव (iii) में ज्ञात की गयी माध्यक दूरियाँ समान हैं।
हल :
(i) संचयी बारम्बारता सारणी :

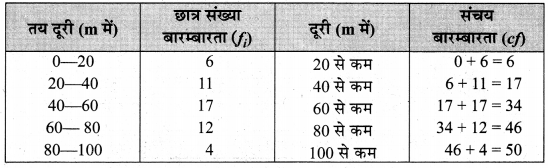
(ii) से कम’ प्रकार का संचयी बारम्बारता वक्र (तोरण) :

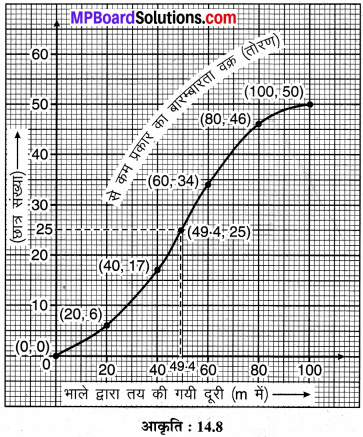
अभीष्ट माध्यक दूरी = 49.4 m (लगभग) (तोरण द्वारा) है।

(iii) सूत्र के प्रयोग द्वारा माध्यक दूरी का परिकलन :

अतः, सूत्र के प्रयोग द्वारा ज्ञात की गयी अभीष्ट माध्यक दूरी = 49.41 m है।

(iv) चरण (ii) एवं (iii) में ज्ञात की गयी माध्यक दूरियाँ मापन की सीमा के अन्तर्गत लगभग समान हैं।

MP Board Class 10th Maths Chapter 14 लघु उत्तरीय प्रश्न

प्रश्न 1.
निम्न बंटन (वितरण) का माध्य ज्ञात कीजिए :

हल:

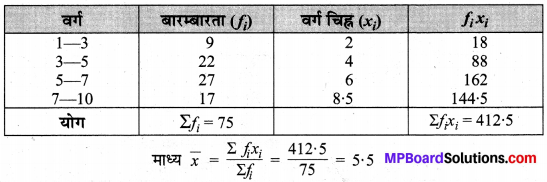
अतः, बंटन (वितरण) का अभीष्ट माध्य = 5.5.

प्रश्न 2.
20 छात्रों के गणित परीक्षा में प्राप्त अंकों का माध्य ज्ञात कीजिए :

हल:

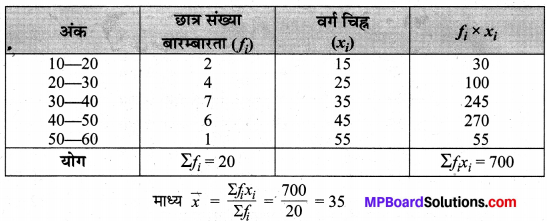
अतः, अभीष्ट माध्य अंक = 35.

प्रश्न 3.
दिए गए आँकड़ों में समान्तर माध्य ज्ञात कीजिए : (2019)

हल :
[निर्देशः उपर्युक्त प्रश्न की तरह हल करें।]
उत्तर : अभीष्ट माध्य = 62.47]

प्रश्न 4.
निम्नलिखित तालिका (सारणी) में अपनी पुस्तक को 30 दिन में पूरा करने के लिखे गए पृष्ठों की संख्या दी गयी है:

प्रतिदिन लिखे गए पृष्ठों की माध्य संख्या ज्ञात कीजिए।
हल:

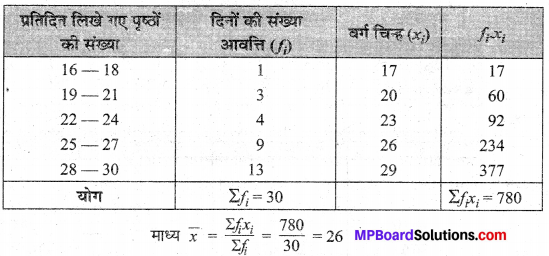
अतः प्रतिदिन लिखे गए पृष्ठों की अभीष्ट माध्य संख्या 26 है।

प्रश्न 5.
निम्न वितरण 40 व्यक्तियों के भारों (kg में) की स्थिति है :

‘से कम’ प्रकार की संचयी बारम्बारता सारणी बनाइए।
हल :
से कम प्रकार की संचयी बारम्बारता सारणी:

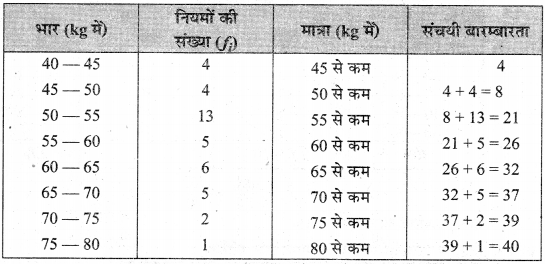
अतः उपरोक्त सारणी अभीष्ट सारणी है।

प्रश्न 6.
निम्न सारणी संचयी बारम्बारता बंटन है, जो 800 छात्रों द्वारा एक परीक्षा में अर्जित अंकों को दर्शाती है:

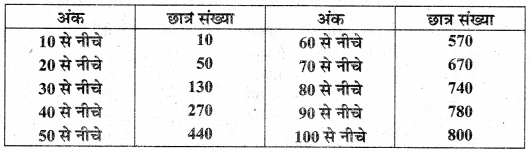
उपरोक्त आँकड़ों के लिए बारम्बारता वितरण सारणी बनाइए।
हल:
बारम्बारता सारणी वितरण :

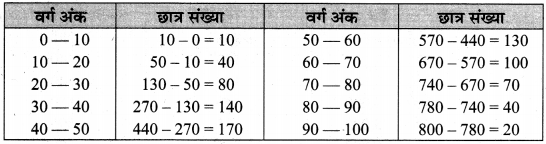
अतः उपरोक्त सारणी अभीष्ट बारम्बारता वितरण सारणी है।

प्रश्न 7.
निम्न आँकड़ों से बारम्बारता वितरण सारणी का निर्माण कीजिए :

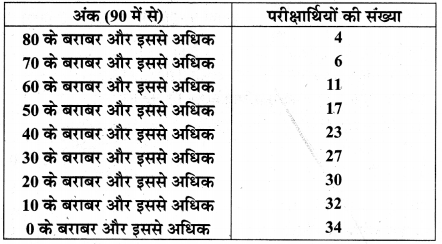
हल :
बारम्बारता वितरण सारणी :

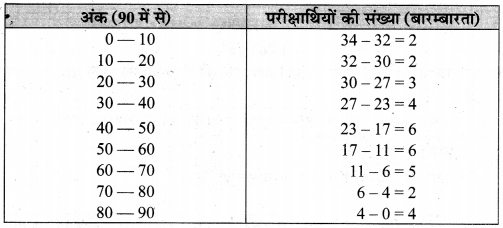
अतः उपरोक्त सारणी अभीष्ट बारम्बारता वितरण सारणी है।

प्रश्न 8.
600 परिवारों की साप्ताहिक आय निम्न सारणी में दी गयी है:

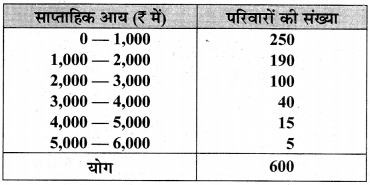
माध्यक आय का परिकलन कीजिए।
हल:

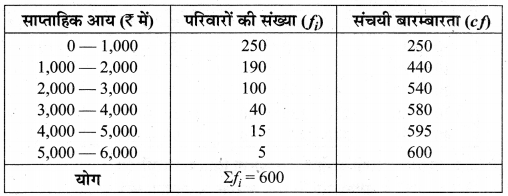
माध्यक = \(\frac { n }{ 2 }\) वाँ पद = \(\frac { 600 }{ 2 }\) = 300वाँ पद जो वर्ग (1,000 – 2,000) में आता है जिसमें
l = 1,000, cf = 250, f = 190, h = 1,000

= 1,000 + 263.16
= Rs 1,263.16
अत: अभीष्ट माध्यक आय = Rs 1,263.16 है।

प्रश्न 9.
एक क्रिकेट कोचिंग केन्द्र के 33 खिलाड़यों की गेंदबाजी की चाल (km/h) निम्न सारणी में दी है:

गेंदबाजी की माध्यक चाल का परिकलन कीजिए।
हल:

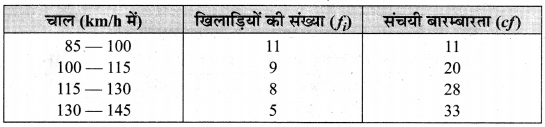
माध्यक चाल = \(\frac { 33 }{ 2 }\) = 16.5वाँ पद जो वर्ग (100 – 115) में है।
जहाँ l = 100, cf = 11, f = 9, h = 115 – 100 = 15 .
सूत्र : माध्यक चाल = \(l+\left(\frac{\frac{n}{2}-c f}{f}\right) \times h\)

अतः अभीष्ट माध्यक चाल = 109.17 (km/h) है।

प्रश्न 10.
100 परिवारों की मासिक आय निम्न तालिका (सारणी) में दी गयी है :

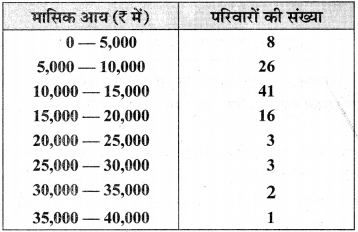
बहुलक आय ज्ञात कीजिए।
हल :
बहुलक वर्ग सर्वाधिक बारम्बारता 41 वाला वर्ग (10,000 – 15,000) है जहाँ l = 10,000,
f₁ = 41, f₀ = 26, f₂ = 16 एवं h = 15,000 – 10,000 = 5,000 है।

अतः अभीष्ट बहुलक आय = Rs 11,875 है।

प्रश्न 11.
70 पैकिटों में रखी कॉफी का भार निम्न सारणी में दिया गया है:

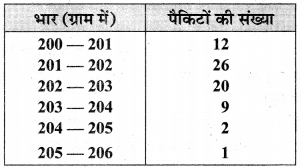
बहुलक भार की गणना कीजिए।
हल :
अधिकतम बारम्बारता 26 वाला वर्ग (201 – 202) बहुलक वर्ग है, जहाँ l = 201, f₁ = 26, f₀ = 12, f₂ = 20 एवं h = 202 – 201 = 1

अतः अभीष्ट बहुलक भार = 201.7g है।

MP Board Class 10th Maths Chapter 14 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
अवर्गीकृत आँकड़ों से निकाले गए माध्यक एवं उन आँकड़ों को वर्गीकृत करके निकाले गए माध्यक का मान सदैव समान रहता है। क्या आप भी यह सोचते हैं कि उक्त कथन सत्य है? कारण दीजिए।
हल :
उक्त कथन सदैव सत्य नहीं होता, क्योंकि वर्गीकृत आँकड़ों से माध्यक ज्ञात करने में प्रयुक्त सूत्र इस धारणा पर आधारित है कि वर्ग में प्रेक्षण समान रूप में बराबर-बराबर वितरित हैं।

प्रश्न 2.
एक वर्गीकृत आँकड़े समान माप के वर्गों में वर्गीकृत किए गए हों, तो माध्य के परिकलन के लिए निम्न सूत्र का प्रयोग कर सकते हैं।
\(\overline{x}=a+\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}\)
जहाँ a एक कल्पित माध्य है। a किसी वर्ग का मध्य-बिन्दु होना चाहिए। क्या अन्तिम कथन सत्य है? अपने उत्तर का औचित्य दीजिए।
हल :
आवश्यक नहीं, क्योंकि किन्हीं आँकड़ों का माध्य कल्पित माध्य के चयन पर निर्भर नहीं करता है।

प्रश्न 3.
क्या यह कहना सत्य है कि वर्गीकृत आँकड़ों के माध्य, माध्यक व बहुलक सदैव भिन्न-भिन्न होंगे? अपने उत्तर का औचित्य दीजिए।
हल :
यह सदैव सत्य नहीं है, क्योंकि ये तीनों मान किसी विशेष आँकड़ों के लिए बराबर भी हो सकते हैं क्योंकि यह उन आँकड़ों पर निर्भर करता है।

प्रश्न 4.
क्या वर्गीकृत आँकड़ों के लिए माध्यक वर्ग एवं बहुलक वर्ग सदैव भिन्न-भिन्न होंगे? अपने उत्तर का औचित्य दीजिए।
हल :
यह सदैव सत्य नहीं है, क्योंकि यह बात आँकड़ों पर निर्भर करती है।

प्रश्न 5.
क्या अवर्गीकृत आँकड़ों का माध्य और उन आँकड़ों को वर्गीकृत करके निकाले गए माध्य सदैव समान होते हैं? अपने उत्तर का औचित्य दीजिए।
हल :
यह कथन सदैव सत्य नहीं है, क्योंकि जब हम वर्गीकृत आँकड़ों से माध्य ज्ञात करते हैं, तो यह मानकर चलते हैं कि बारम्बारता सम्पूर्ण वर्ग में समान रूप से वितरित होता है।

प्रश्न 6.
क्या यह कहना सत्य है कि तोरण बारम्बारता बंटन का ग्राफीय निरूपण है। अपने उत्तर का कारण दीजिए।
हल :
नहीं, क्योंकि बारम्बारता बंटन का ग्राफीय निरूपण तोरण नहीं, बल्कि आयत चित्र, बारम्बारता बहुभुज एवं बारम्बारता वक्र हो सकता है और तोरण संचयी बारम्बारता बंटन का ग्राफीय निरूपण होता है।

MP Board Class 10th Maths Chapter 14 वस्तुनिष्ठ प्रश्न

MP Board Class 10th Maths Chapter 14 बहु-विकल्पीय प्रश्न

प्रश्न 1.
संचयी बारम्बारता सारणी बनाना निम्न के परिकलन में उपयोगी है
(a) माध्य
(b) माध्यक
(c) बहुलक
(d) ये सभी।
उत्तर:
(b) माध्यक

प्रश्न 2.
निम्न वितरण में :

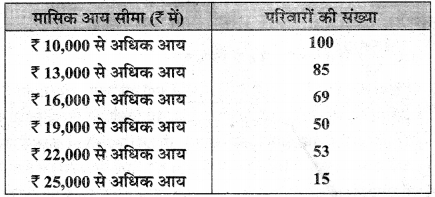
आय सीमा Rs 16,000 – 19,000 रखने वाले परिवारों की संख्या होगी :
(a) 15
(b) 16
(c) 17
(d) 19.
उत्तर:
(d) 19.

प्रश्न 3.
एक कक्षा के 60 विद्यार्थियों की ऊँचाईयों के निम्न बारम्बारता बंटन का अवलोकन कीजिए :

बहुलक वर्ग की निम्न सीमा एवं माध्यक वर्ग की उच्च सीमा का योग होगा :
(a) 310
(b) 315
(c) 320
(d) 330.
उत्तर:
(b) 315

प्रश्न 4.
\(\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}\) सूत्र है:
(a) माध्य का
(b) माध्यक का
(c) बहुलक का
(d) सूचकांक का।
उत्तर:
(a) माध्य का

प्रश्न 5.
\(a+\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}\) सूत्र है.
(a) माध्य का
(b) माध्यक का
(c) बहुलक का
(d) सूचकांक का।
उत्तर:
(a) माध्य का

प्रश्न 6.
\(a+\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}} \times h\) सूत्र है :
(a) माध्य का
(b) माध्यक का
(c) बहुलक का
(d) सूचकांक का।
उत्तर:
(a) माध्य का

प्रश्न 7.
\(l_{1}+\left(\frac{\frac{n}{2}-c f}{f}\right) \times h\) सूत्र है:
(a) माध्य का
(b) माध्यक का
(c) बहुलक का
(d) सूचकांक का।
उत्तर:
(b) माध्यक का

प्रश्न 8.
\(l_{1}+\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right) \times h\) सूत्र है:
(a) माध्य का
(b) माध्यक का
(c) बहुलक का
(d) सूचकांक का।
उत्तर:
(c) बहुलक का

प्रश्न 9.
सूत्र \(\overline{x}=a+\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}\) में d विचलन है a से निम्न वर्ग :
(a) वर्गों की निम्न सीमाओं का
(b) वर्गों की उच्च सीमाओं का
(c) वर्गों के.मध्य-बिन्दुओं का
(d) वर्ग चिन्हों की बारम्बारताओं का।
उत्तर:
(c) वर्गों के.मध्य-बिन्दुओं का

प्रश्न 10.
जब वर्गीकृत आँकड़ों का माध्य ज्ञात किया जाता है, तो हम यह कल्पना करते हैं कि बारम्बारताएँ
(a) सम्पूर्ण वर्गों में समान रूप से वितरित होती हैं
(b) वर्ग चिह्नों पर केन्द्रीकृत होती हैं
(c) उच्च वर्ग सीमाओं पर केन्द्रित होती हैं
(d) निम्न वर्ग सीमाओं पर केन्द्रित होती हैं
उत्तर:
(b) वर्ग चिह्नों पर केन्द्रीकृत होती हैं

प्रश्न 11.
यदि x_i वर्ग अन्तरालों के मध्य-बिन्दु हों, f_i संगत बारम्बारताएँ एवं \(\overline{x}\) माध्य हो, तब \(\frac{\Sigma f_{i} x_{i}}{n}-\overline{x}\) बराबर होगा:
(a) 0
(b) -1
(c) 1
(d) 2.
उत्तर:
(a) 0

प्रश्न 12.
वर्गीकृत बारम्बारता बटन में प्रयुक्त सूत्र \(\overline{x}=a+h\left(\frac{\Sigma f_{i} u_{i}}{\Sigma f_{i}}\right)\) में u; बराबर होगा :

उत्तर:
(c) \(\frac{x_{i}-a}{h}\)

प्रश्न 13.
‘से कम’ प्रकार के एवं ‘से अधिक’ प्रकार के संचयी बारम्बारता वक्रों के प्रतिच्छेद बिन्दु का गुण होगा:
(a) माध्य
(b) माध्यक
(c) बहुलक
(d) ये सभी।
उत्तर:
(b) माध्यक

प्रश्न 14.
निम्न वितरण :

में माध्यक वर्ग एवं बहुलक वर्ग की निम्न सीमाओं का योग होगा :
(a) 15
(b) 25
(c) 30
(d) 35.
उत्तर:
(c) 30

प्रश्न 15.
निम्न बारम्बारता बंटन (वितरण) का अवलोकन कीजिए :

माध्यक वर्ग की उच्च सीमा है:
(a) 17
(b) 17.5
(c) 18
(d) 18.5.
उत्तर:
(b) 17.5

प्रश्न 16.
निम्न वितरण के लिए:

बहुलक का वर्ग है:
(a) 10-20
(b) 20-30
(c) 30-40
(d) 50-60.
उत्तर:
(c) 30-40

प्रश्न 17.
निम्न प्रेक्षणों का अवलोकन कीजिए :

माध्यक वर्ग की उच्च सीमा एवं बहलक वर्ग की निम्न सीमा का अन्तर है
(a) 0
(b) 19
(c) 20
(d) 38.
उत्तर:
(c) 20

प्रश्न 18.
150 धावकों द्वारा 110 m हर्डल दौड़ में लिए गए सेकण्ड में समयों को निम्न प्रकार सारणीकृत किया गया है:

14.6 सेकण्ड से कम समय में अपनी दौड़ सम्पन्न करने वाले धावकों की संख्या है
(a) 11
(b) 71
(c) 82
(d) 130.
उत्तर:
(c) 82

प्रश्न 19.
निम्न वितरण का अवलोकन कीजिए :

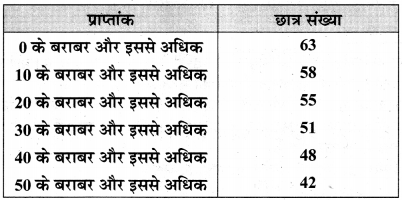
वर्ग 30-40 की बारम्बारता है:
(a) 3
(b) 4
(c) 48
(d) 57
उत्तर:
(a) 3

रिक्त स्थानों की पूर्ति

1. …………….. = 3 x माध्यक – 2 x माध्य।
2. सूत्र \(\overline{x}=a+\frac{\Sigma f_{i} d_{i}}{\Sigma f_{i}}\) में a ………………… कहलाता है।
3. माध्यक = \(l+\left(\frac{\frac{n}{2}-c f_{i}}{f}\right) h\) में l ……. होती है।
4. बहुलक = \(l+\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right) \times h\) में h …………… होता है।
5. सूत्र \(\overline{x}=a+\left(\frac{\sum f_{i} u_{i}}{\Sigma f_{i}}\right) \times h\) में u_i = ………. होगा।
उत्तर-
1. बहुलक,
2. कल्पित माध्य,
3. माध्यक वर्ग की निम्न सीमा,
4. बहुलक वर्ग की वर्ग माप,
5. \(\frac{x_{i}-a}{h}\)

जोड़ी मिलाना

उत्तर-
1.→(c),
2.→(d),
3.→(e),
4.→(a),
5. →(b).

सत्य/असत्य कथन

1. समान प्रेक्षणों के वर्गीकृत एवं अवर्गीकृत आँकड़ों से निकाले गए माध्यमों का मान सदैव समान होता है।
2. सूत्रों द्वारा केन्द्रीय मापों के परिकलन में वर्गों का सतत होना आवश्यक है।
3. समान प्रेक्षणों के वर्गीकृत एवं अवर्गीकृत आँकड़ों से निकाले गए बहलकों का मान सदैव समान होता है।
4. संचयी बारम्बारता सारणी की आवश्यकता माध्यक का परिकलन करने में होती है।
5. बारम्बारता वक्र तोरण कहलाता है।
उत्तर-
1. असत्य,
2. सत्य
3. असत्य,
4. सत्य,
5. असत्य।

एक शब्द/वाक्य में उत्तर

1. केन्द्रीय प्रवृत्ति की मापों माध्य, माध्यक एवं बहुलक में से कोई भी दो मापें दी हैं, तो तीसरी माप कैसे , ज्ञात करेंगे?
2. संचयी बारम्बारता वक्र को क्या कहते हैं?
3. सर्वाधिक बारम्बारता वाला वर्ग क्या कहलाता है?
4. सम्पूर्ण वितरण को दो बराबर भागों में बाँटने वाला अंक जिस वर्ग अन्तराल में होता है उस वर्ग को क्या कहते हैं?
5. तोरण कितने प्रकार के होते हैं?
6. 1, 2, 3, 4, 5 समान्तर माध्य क्या होगा? (2019)
7. माध्यिका का सूत्र लिखिए। (2019)
उत्तर-
1. बहुलक = 3 x माध्यक – 2 x माध्य सूत्र का प्रयोग करके,
2. तोरण,
3. बहुलक वर्ग,
4. माध्यक वर्ग.
5. दो प्रकार के,
6. 3 (तीन).
7. माध्यिका = \(l+\left(\frac{n / 2-c f}{f}\right) \times h\)