MP Board Class 10th Maths Solutions Chapter 1 वास्तविक संख्याएँ Additional Questions

In this article, we share MP Board Class 10th Maths Book Solutions Chapter 1 वास्तविक संख्याएँ Additional Questions Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 10th Maths Solutions Chapter 1 वास्तविक संख्याएँ Additional Questions

MP Board Class 10th Maths Chapter 1 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 10th Maths Chapter 1 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
दर्शाइए कि धनात्मक पूर्णांक 6q + r, जहाँ q एक पूर्णांक है और r = 0, 1, 2, 3, 4, 5 के रूप का घन भी 6m + r के रूप का होगा।
हल:
(6q)³ = 216q³ = 6 (36q³) = 6m, जहाँ m एक पूर्णांक है।
(6q+ 1)³ = 216q³ + 108q² + 18q + 1
= 6 (36q³ + 18q² +3q) + 1 = 6m + 1, जहाँ m एक पूर्णांक है।
(6q + 2)³ = 216q³ + 216q² + 72q + 8
= 6 (36q³ + 36q² + 12q + 1)+ 2 = 6m + 2, जहाँ m एक पूर्णांक है।
(6q + 3)³ = 216q³ + 324q² + 162 q + 27
= 6 (36q³ + 54q² + 27q + 4)+ 3 = 6m + 3
(6q + 4)³ = 216q³ + 432q² + 288q + 64
= 6 (36q³ + 72q² + 48q + 10) + 4 = 6m + 4
एवं (6q + 5)³ = 216q³ + 540q² + 450q + 125
= 6 (36q³ + 90q² + 75q + 20) + 5 = 6m + 5
अतः, पूर्णांक 6q+r का घन 6m +r के रूप का होगा, जहाँ m एक पूर्णांक है तथा r = 0, 1, 2,3,4,5. इति सिद्धम्

प्रश्न 2.
दर्शाइए कि किसी विषम धनात्मक पूर्णांक का वर्ग 6q + 1 या 6q + 3 के रूप का हो सकता है, जहाँ एक पूर्णांक है।
हल:
हम जानते हैं कि कोई भी धन पूर्णांक 6m, 6m + 1, 6m + 2, 6m + 3, 6m + 4 एवं 6m +5 के रूप का हो सकता है, जहाँ m कोई धन पूर्णांक है लेकिन इन धन पूर्णांकों में विषम धन पूर्णांक केवल 6m + 1,6m + 3 एवं 6m + 5 के रूप के हो सकते हैं।
अब (6m + 1)² = 36m² + 12m + 1 = 6 (6m² + 2m) + 1
= 6q + 1, जहाँ q= 6m² + 2m एक पूर्णांक है।
(6m + 3)² = 36m² + 36m + 9 = 6 (6m² + 6m + 1) + 3
= 6q + 3, जहाँ q = 6m² + 6m + 1 एक पूर्णांक है।
एवं (6m + 5)² = 36m² + 60m + 25 = 6(6m² + 10m + 4) + 1
= 6q + 1, जहाँ q = 6m² + 10m + 4 एक पूर्णांक है।
अतः, हम देखते हैं कि विषम धनात्मक पूर्णांक का वर्ग 6q + 1 या 6q + 3 के रूप का हो सकता है, जहाँ q एक पूर्णांक है।

प्रश्न 3.
यूक्लिड की विभाजन एल्गोरिथ्म का प्रयोग करके वह बड़ी-से-बड़ी संख्या ज्ञात कीजिए जिससे 1251, 9377 एवं 15628 को विभाजित करने पर क्रमशः 1,2,3 शेषफल बचते हैं।
हल:
चूंकि 1251 – 1 = 1250
9377 – 2 = 9375
15628 – 3 = 15625
अब H. C. F. (1250, 9375) के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग करने पर,
9375 = 1250 × 7 + 625
1250 = 625 × 2 + 0 =
⇒ H. C. F (1250, 9375) = 625
अब HCF (625, 15625) के लिए यूक्लिड विभाजन एल्गोरिथ्म का प्रयोग करने पर,
15625 = 625 × 25 + 0
⇒ HCF (625, 15625) = 625
⇒ HCF (1250, 9375, 15625) = 625
अतः, 625 वह अभीष्ट बड़ी से बड़ी संख्या होगी जिससे 1251, 9377 एवं 15628 को विभाजित करने पर क्रमशः 1, 2, एवं 3 शेषफल बचते हैं।

प्रश्न 4.
दर्शाइए कि किसी धनात्मक पूर्णांक का घन 4m, 4m +1 या 4m + 3 के रूप का हो सकता है, जहाँ m एक पूर्णांक है।
हल:
∵ कोई धनात्मक पूर्णांक 4q, 4q + 1, 4q + 2 एवं 4q + 3 के रूप का हो सकता है, जहाँ व एक धनात्मक पूर्णांक है।
(4q)³ = 64q³ = 4 (16q³)= 4m एक धनात्मक पूर्णांक है।
∴ (4q + 1)³ = 64q³ + 48q² + 12q + 1
⇒ (4q + 1)³ = 4 (16q3 + 12q² + 3q) + 1 = 4m + 1
जहाँ m = 16q³ + 12q² + 3q एक पूर्णांक है।
चूँकि (4q + 2)³ = 64q³ + 96q² + 48q + 8
⇒ (4q+ 2) = 4(16q³ + 24q² + 12q + 2) = 4m
जहाँ m = 16q3 + 24q2 + 12q + 2 एक पूर्णांक है।
चूँकि (4q + 3)³ = 64q³ + 144q² + 108q + 27
⇒ (4q + 3)³ = 4 (16q³ + 36q² + 27q + 6) + 3 = 4m + 3
जहाँ m = 16q³ + 36q² + 27q + 6 एक पूर्णांक है।
अतः, किसी धनात्मक पूर्णांक का घन 4m, 4m + 1 या 4m + 3 के रूप का हो सकता है, जहाँ m कोई पूर्णांक है। इति सिद्धम्

प्रश्न 5.
दशाईए कि किसी धनात्मक पूर्णांक का वर्ग 5q + 2 अथवा 5q + 3 के रूप का नहीं हो सकता, जहाँ q एक पूर्णांक है।
हल:
कोई धनात्मक पूर्णांक 5m, 5m + 1, 5m + 2, 5m +3 अथवा 5m + 4 के रूप का हो सकता है, जहाँ m एक धनात्मक पूर्णांक है।
चूँकि (5m)² = 25m² = 5 (5m²) = 5q
जहाँ q = 5m² एक धन पूर्णांक है।
चूँकि (5m + 1)² = 25m² + 10m + 1 = 5(5m² + 2m) + 1 = 5q + 1
जहाँ q = 5m² + 2m एक पूर्णांक है।
चूँकि (5m + 2)² = 25m² + 20m + 4 = 5 (5m² + 4m) + 4 = 5q + 4
जहाँ q = 5m + 4m एक पूर्णांक है।
चूँकि (5m + 3)² = 25m² + 30m + 9 = 5 (5m² + 6m + 1) + 4
= 5q + 4, जहाँ q = 5m² + 6m + 1 एक पूर्णांक है।
चूँकि (5m + 4)² = 25m² + 40m + 16 = 5(5m² + 8m + 3) + 1
= 5q + 1, जहाँ q = 5m² + 8m + 3 एक पूर्णांक है।
इस प्रकार हम देखते हैं कि किसी धनात्मक पूर्णांक का वर्ग 5q, 5q + 1, 5q + 4 के रूप का हो सकता है। लेकिन 5q + 2 एवं 5q + 3 के रूप का नहीं हो सकता। अतः किसी धनात्मक पूर्णांक का वर्ग कभी 5q + 2 एवं 5q + 3 के रूप का नहीं हो सकता, जहाँ व एक पूर्णांक है। इति सिद्धम्

MP Board Class 10th Maths Chapter 1 लघु उत्तरीय प्रश्न

प्रश्न 1.
दर्शाइए कि किसी विषम पूर्णांक का वर्ग 4q + 1 के रूप का होता है, जहाँ q कोई पूर्णांक है।
हल:
चूँकि विषम पूर्णांक (2m + 1) के रूप का होता है, जहाँ m कोई पूर्णांक है।
⇒ (2m + 1)² = 4m² + 4m + 1 = 4(m² + m) + 1 = 4q + 1
जहाँ q = m2 + m एक पूर्णांक है क्योंकि m पूर्णांक है।
अतः, विषम पूर्णांक का वर्ग 4q + 1 के रूप का होता है, जहाँ q कोई एक पूर्णांक है। इति सिद्धम्

प्रश्न 2.
यदि n एक विषम पूर्णांक है, तो दर्शाइए कि n² – 1,8 से विभाज्य है।
हल:
चूँकि n कोई विषम पूर्णांक है, तो n = (2m + 1) के रूप का होगा।
अब, n² – 1 = (2m + 1)² – 1
= 4m² + 4m + 1 – 1 = 4m² + 4m
= 4m(m + 1)
लेकिन m(m + 1) एक सम पूर्णांक है, क्योंकि m एवं (m + 1) में से एक विषम तथा दूसरा सम होगा। इस प्रकार गुणन सम होगा।
अब मान लीजिए m(m + 1) = 2q
⇒ n² – 1 = 4m(m + 1)= 4 × 2q = 8q, जो कि 8 से विभाज्य है।
अतः, यदिn एक विषम पूर्णांक है, तो (n² – 1), 8 से विभाज्य है। इति सिद्धम्

प्रश्न 3.
यदि x एवं y दोनों विषम पूर्णांक हों, तो दर्शाइए कि x² + y² एक समपूर्णांक है लेकिन 4 से विभाज्य नहीं है।
हल:
चूँकि x एवं y दोनों विषम पूर्णांक हैं, तो मान लीजिए कि x = (2p + 1) एवं y = (2q + 1), जहाँ p एवं कोई पूर्णांक हैं।
अब x² + y² = (2p + 1)² + (2q + 1)²
= 4p² + 4p + 1 + 4q² + 4q + 1
= 4p(p + 1)+ 4q(q + 1) + 2
लेकिन p(p + 1) एवं q(q + 1) दोनों समपूर्णांक हैं। मान लीजिए इनके क्रमशः मान 2m एवं 2n हैं
x² + y² = 4p(p + 1) + 4q(q + 1) + 2
= 4(2m) + 4(2n) + 2
= 8m + 8n + 2 = 2(4m + 4n + 1)
जो एक समपूर्णांक संख्या है लेकिन 4 से विभाज्य नहीं है।
अतः, यदि एवं दोनों विषम पूर्णांक हों, तो x² + y² समपूर्णांक होंगे, लेकिन 4 से विभाज्य नहीं। इति सिद्धम् ‘

प्रश्न 4.
यूक्लिड के विभाजन एल्गोरिथ्म का प्रयोग करके HCF (441,567,693) ज्ञात कीजिए।
हल:
यूक्लिड के विभाजन एल्गोरिथ्म प्रयोग द्वारा HCF (441,567) ज्ञात करने पर,
567 = 441 × 1 + 126
441 = 126 × 3 + 63
126 = 63 × 2 + 0
⇒ HCF (441,567) = 63
अब यूक्लिड के विभाजन एल्गोरिथ्म की सहायता से HCF (63, 693) ज्ञात करने पर,
693 = 63 × 11 + 0
⇒ HCF (63, 693) = 63
अतः, HCF (441,567,693) का अभीष्ट मान 63 है।

प्रश्न 5.
सिद्ध कीजिए कि \(\sqrt { 3 }\) + \(\sqrt { 5 }\) एक अपरिमेय संख्या है।
हल:
मान लीजिए \(\sqrt { 3 }\) + \(\sqrt { 5 }\) = a जहाँ a, एक परिमेय संख्या है।

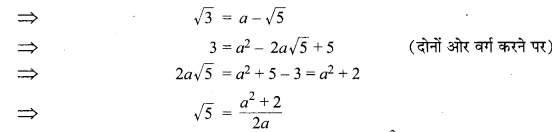
जो एक विरोधाभास है क्योंकि \(\sqrt { 5 }\) एक अपरिमेय संख्या तथा \(\frac{a^{2}+2}{2 a}\) एक परिमेय संख्या है।
अतः, \(\sqrt { 3 }\) + \(\sqrt { 5 }\) एक अपरिमेय संख्या है। इति सिद्धम्

प्रश्न 6.
दर्शाइए कि 12 का किसी संख्या के लिए अन्तिम अंक 0 अथवा 5 नहीं होगा।
हल:
∵ (12)ⁿ = (2 × 2 × 3)ⁿ = 2²ⁿ × 3n
चूँकि इसमें 5 की कोई घात नहीं है तथा किसी संख्या में अन्तिम अंक 0 अथवा 5 होने के लिए उसके गुणनखण्डों में 5 की घात होना आवश्यक है।
अतः, (12)ⁿ के मान में n के किसी मान के लिए अन्तिम अंक 0 या 5 पर समाप्त नहीं होगा। इति सिद्धम्

प्रश्न 7.
प्रातः भ्रमण (Morning Walk) पर तीन व्यक्ति एक साथ कदम बढ़ाते हैं। उनके कदमों की माप क्रमशः 40 cm, 42 cm एवं 45 cm है। वह लघुतम दूरी क्या होगी जिससे प्रत्येक व्यक्ति समान दूरी पूर्ण कदमों में तय कर सकें।
हल:
इसके लिए हमको 40, 42, एवं 45 का LCM ज्ञात करना होगा।

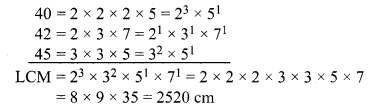
अतः, वह अभीष्ट लघुतम दूरी होगी, 2520 cm अर्थात् 25.20 m.

प्रश्न 8.
परिमेय संख्या \(\frac { 257 }{ 5000 } \) के हर को 2m × 5n के रूप में व्यक्त कीजिए, जहाँ m एवं n ऋणात्मक पूर्णांक हैं। इस प्रकार बिना भाग की क्रिया किए इसका दशमलव प्रसार लिखिए।
हल:

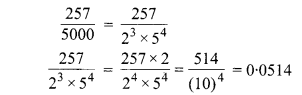
अतः, परिमेय संख्या का अभीष्ट रूपः = \(\frac{257}{2^{3} \times 5^{4}}\) होगा। तथा इसका दशमलव प्रसार 0.0514 होगा।

MP Board Class 10th Maths Chapter 1 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
क्या प्रत्येक धन पूर्णांक 4q + 2 के रूप का हो सकता है, जहाँ q एक पूर्णांक है। अपने उत्तर की पुष्टि कीजिए।
उत्तर:
नहीं, क्योंकि यूक्लिड की विभाजन प्रमेयिका के अनुसार a = 4q + 7; जहाँ 0 < r < 4 तथा r एक पूर्णांक है तथा का मान 0, 1, 2 और 3 हो सकता है। अर्थात् कोई भी धन पूर्णांक 4q, 4q + 1, 4q + 2 एवं 4q + 3 के रूप का हो सकता है।

प्रश्न 2.
“दो क्रमागत धनात्मक पूर्णांकों का गुणनफल 2 से विभाज्य होता है।” यह कथन सत्य है या असत्य। कारण दीजिए।
उत्तर:
कथन सत्य है।
क्योंकि दो क्रमागत पूर्णांकों का गुणनफल n(n + 1) होगा, जहाँ n एक पूर्णांक है और यदि n विषम है तो n + 1 सम और यदि n + 1 विषम है तोn सम होगा। इस प्रकार n(n + 1) एक सम पूर्णांक होगा, जो 2 से विभाज्य है।

प्रश्न 3.
“तीन क्रमागत धन पूर्णांकों का गुणनफल 6 से विभाज्य होता है।” क्या यह कथन सत्य है या असत्य? अपने उत्तर का औचित्य दीजिए।
उत्तर:
उक्त कथन सत्य है क्योंकि तीन क्रमागत धन पूर्णांकों में कम-से-कम एक पूर्णांक तीन से विभाज्य होगा तथा एक पद दो से विभाज्य होगा। अतः तीनों का गुणनफल 6 से विभाज्य होगा।

प्रश्न 4.
क्या किसी धन पूर्णांक का वर्ग 3m + 2 के रूप का होगा, जहाँ m एक प्राकृत संख्या है ? अपने उत्तर का औचित्य दीजिए।
उत्तर:
किसी धन पूर्णांक का वर्ग 3m + 2 के रूप का नहीं होगा। क्योंकि उसका रूप तो 3m या 3m + 1 हो सकता है।

प्रश्न 5.
एक धन पूर्णांक 3q + 1 के रूप का है, जहाँ एक प्राकृत संख्या है। क्या आप इसका वर्ग 3m + 1 के अतिरिक्त किसी अन्य रूप अर्थात् 3m या 3m + 2 के रूप में व्यक्त कर सकते हैं, जहाँ m कोई पूर्णांक है। अपने उत्तर का औचित्य दीजिए।
उत्तर:
नहीं। क्योंकि
(3q + 1)² = 9q² + 6q + 1 = 3(3q² + 2q) + 1 = 3m + 1
जहाँ m = 3q² + 2q एक पूर्णांक है।

प्रश्न 6.
संख्याएँ 525 और 3000 दोनों केवल 3, 5, 15, 25 एवं 75 से विभाज्य हैं। HCF (525, 3000) क्या होगा? अपने उत्तर का औचित्य दीजिए।
उत्तर:
HCF (525, 3000) का अभीष्ट मान 75 है, क्योंकि 75 ही महत्तम समापवर्तक (महत्तम सम गुणनखण्ड) है।

प्रश्न 7.
समझाइए कि 3 × 5 × 7 + 7 एक भाज्य संख्या है।
उत्तर:
चूँकि 3 × 5 × 7 + 7= 7 (3 × 5 + 1) = 7 × 16
जो कि एक भाज्य संख्या है।

प्रश्न 8.
क्या कोई दो संख्याओं का HCF = 18 एवं LCM = 380 हो सकता है? अपने उत्तर का कारण बताइए।
उत्तर:
कभी नहीं हो सकता क्योंकि दो संख्याओं का LCM उनके HCF से विभाज्य होता है जबकि संख्या 380 संख्या 18 से विभाज्य नहीं है।

प्रश्न 9.
बिना लम्बी भाग प्रक्रिया किए ज्ञात कीजिए कि \(\frac { 987 }{ 10500 } \) का दशमलव प्रसार सांत होगा अथवा असान्त आवर्ती होगा? अपने उत्तर का कारण बताइए।
उत्तर:
हाँ, उक्त संख्या का दशमलव प्रसार सांत होगा, क्योंकि

प्रश्न 10.
एक परिमेय संख्या अपने दशमलव प्रसार में 327.7081 है। आपके अभाज्य गुणनखण्डों के बारे में क्या कहना चाहेंगे यदि इस परिमेय संख्या को p/g के रूप में व्यक्त किया जाता है ? कारण दीजिए।
उत्तर:
q के अभाज्य गुणनखण्ड 2^m × 5ⁿ के रूप का होगा क्योंकि दशमलव प्रसार सांत है।

MP Board Class 10th Maths Chapter 1 वस्तुनिष्ठ प्रश्न

MP Board Class 10th Maths Chapter 1 बहु-विकल्पीय

प्रश्न 1.
किसी पूर्णांक m के लिए प्रत्येक सम पूर्णांक का रूप होगा :
(a) m
(b) m + 1
(c) 2m
(d) 2m + 1
उत्तर:
(c) 2m

प्रश्न 2.
किसी पूर्णांक q के लिए प्रत्येक विषम पूर्णांक का रूप होगा :
(a) q
(b) q + 1
(c) 2q
(d) 2q + 1
उत्तर:
(d) 2q + 1

प्रश्न 3.
n² – 1, 8 से विभाज्य होगा यदि n है :
(a) एक पूर्णांक
(b) एक प्राकृत संख्या
(c) एक विषम पूर्णांक
(d) एक सम पूर्णांक।
उत्तर:
(c) एक विषम पूर्णांक

प्रश्न 4.
यदि HCF (65, 117), 65m – 117 के रूप में व्यक्त किया जा सकता है, तब m का मान होगा :
(a) 4
(b) 2
(c) 1
(d) 3
उत्तर:
(b) 2

प्रश्न 5.
वह बड़ी-से-बड़ी संख्या जिससे 70 और 125 को विभाजित करने पर क्रमशः 5 एवं 8 शेषफल बचते हैं, निम्न है:
(a) 13
(b) 65
(c) 875
(d) 1750
उत्तर:
(a) 13

प्रश्न 6.
यदि दो धनात्मक पूर्णांक a एवं b निम्न रूप में लिखे हों : a = x³y² एवं b = xy³, जहाँ x एवं y अभाज्य संख्या हैं, तब HCF (a, b) होगा:
(a) xy
(b) xy²
(c) x³y³
(d) x³y²
उत्तर:
(b) xy²

प्रश्न 7.
यदि दो धनात्मक पूर्णांक p एवं निम्न की तरह व्यक्त किए जाएँ : p = ab(b) xy² एवं q = a(b) xy³b, जहाँ a एवं b अभाज्य संख्याएँ हैं, तब LCM (p,q) होगा:
(a) ab
(b) a²b²
(c) a³b²
(d) d³b³
उत्तर:
(c) a³b²

प्रश्न 8.
एक अशून्य परिमेय संख्या एवं एक अपरिमेय संख्या का गुणनफल होगा :
(a) सदैव अपरिमेय संख्या
(b) सदैव परिमेय संख्या
(c) परिमेय अथवा अपरिमेय
(d) एक।
उत्तर:
(a) सदैव अपरिमेय संख्या

प्रश्न 9.
वह छोटी-से-छोटी संख्या जो 1 से 10 की सभी संख्याओं (दोनों को सम्मिलित करते हुए) से विभाज्य है/हैं:
(a) 10
(b) 100
(c) 507
(d) 2520.
उत्तर:
(d) 2520.

प्रश्न 10.
परिमेय संख्या \(\frac { 14587 }{ 1250 } \) ……….. के बाद सांत होगी :
(a) एक दशमलव स्थान
(b) दो दशमलव स्थान
(c) तीन दशमलव स्थान
(d) चार दशमलव स्थान
उत्तर:
(d) चार दशमलव स्थान

प्रश्न 11.
96 और 404 का HCF होगा : (2019)
(a) 120
(b) 4
(c) 10
(d) 3
उत्तर:
(b) 4

रिक्त स्थानों की पूर्ति

प्रश्न 1.
एक सिद्ध किया हुआ कथन जिसे अन्य कथन को सिद्ध करने के लिए प्रयोग किया जाता है ………… कहलाता है।
उत्तर:
प्रमेयिका

प्रश्न 2.
\(\sqrt { P }\), जहाँ p एक अभाज्य संख्या होती है, एक ……………….. संख्या कहलाती है।
उत्तर:
अपरिमेय

प्रश्न 3.
संख्याओं में प्रत्येक उभयनिष्ठ अभाज्य गुणनखण्डों की सबसे छोटी घात का गुणनफल ……………….. कहलाता है।
उत्तर:
महत्तम समापवर्तक (HCF)

प्रश्न 4.
संख्याओं में सम्बद्ध प्रत्येक अभाज्य गुणनखण्ड की सबसे बड़ी घात का गुणनफल ……………….. कहलाता है।
उत्तर:
लघुतम समापवर्त्य (LCM)

प्रश्न 5.
कोई संख्या p/q, जहाँ p एवं q परस्पर अभाज्य पूर्णांक हैं तथा q ≠ 0, ……………….. कहलाती है।
उत्तर:
परिमेय संख्या

जोड़ी मिलाइए

उत्तर:

1. → (c)
2. → (d)
3. → (e)
4. → (a)
5. → (b)

सत्य/असत्य कथन

1. प्रत्येक प्राकृत संख्या पूर्ण संख्या होती है।
2. प्रत्येक पूर्णांक प्राकृत संख्या होती है।
3. प्रत्येक परिमेय संख्या वास्तविक संख्या होती है।
4. प्रत्येक वास्तविक संख्या अपरिमेय संख्या होती है।
5. प्रत्येक पूर्णांक को p/a के रूप में व्यक्त किया जा सकता है, जहाँ p एवं q कोई पूर्णांक हैं लेकिन q ≠ 0.

उत्तर:

1. सत्य
2. असत्य
3. सत्य
4. असत्य
5. सत्य

एक शब्द/वाक्य में उत्तर

प्रश्न 1.
4 एवं 5 का महत्तम समापवर्तक (HCF) क्या होगा ?
उत्तर:
(एक)

प्रश्न 2.
3 और 12 का लघुत्तम समापवर्त्य (LCM) क्या होगा ?
उत्तर:
12

प्रश्न 3.
दो संख्याओं a एवं b के LCM(a, b) एवं HCF(a, b) क्रमशः x एवं y हैं। a,b,x और y में क्या सम्बन्ध होगा?
उत्तर:
a × b = x × y

प्रश्न 4.
यदि a = bq तो a और b में क्या सम्बन्ध है?
उत्तर:
b, a का एक गुणनखण्ड है

प्रश्न 5.
यदि x = \(\frac { p }{ q } \) एक ऐसी संख्या है कि q के अभाज्य गुणनखण्ड 2n × 5m प्रकार के नहीं हैं, जहाँ n एवं m ऋणेत्तर पूर्णांक है, तो x का दशमलव प्रसार कैसा होगा?
उत्तर:
असांत आवर्ती।