Category: Class 9

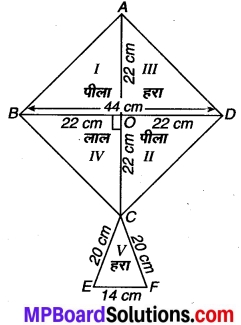
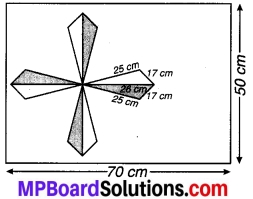
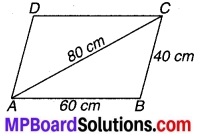
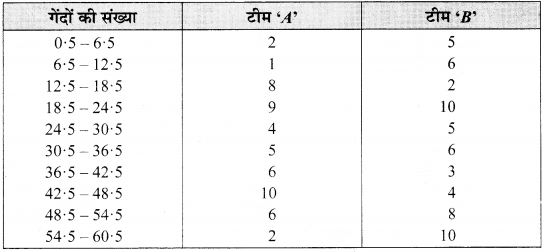
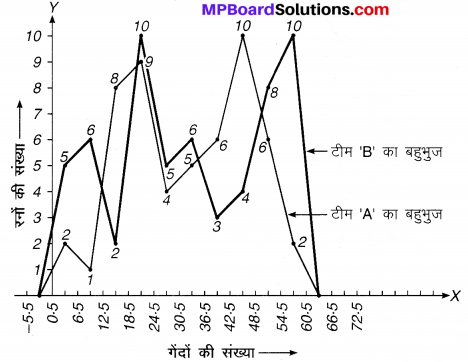
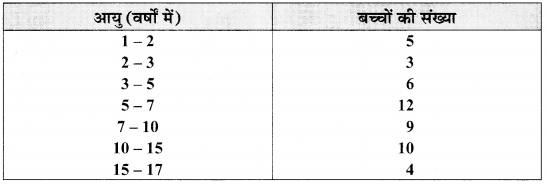
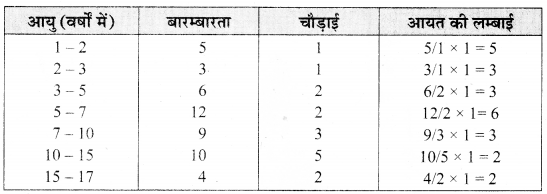
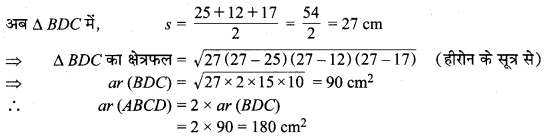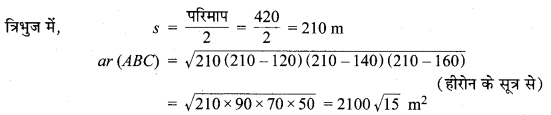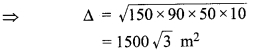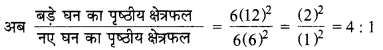MP Board Class 9th Maths Solutions Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल Additional Questions

MP Board Class 9th Maths Chapter 9 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 9th Maths Chapter 9 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
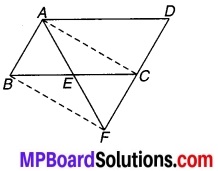
किसी समान्तर चतुर्भुज ABCD की भुजा BC पर कोई बिन्दु E लिया जाता है। AE और DC को बढ़ाया जाता है जिससे वे F पर मिलते हैं। सिद्ध कीजिए किar (ADF) = ar (ABFC) है।
हल:

चित्र 9.26
समान्तर चतुर्भुज ABCD दिया है जिसकी भुजा BC पर कोई बिन्दु E है। AE और DC को बढ़ाया गया है जो बिन्दु F पर मिलते हैं। AC और BF को मिलाइए।
चूँकि AC समान्तर चतुर्भुज ABCD का विकर्ण है
⇒ ar (ADC) = ar (ABC) …(1)
चूँकि उभयनिष्ठ आधार FC पर DF || AB के मध्य ∆ACF एवं ∆BCF स्थित हैं।
⇒ ar (ACF) = ar (BCF) …(2)
⇒ ar (ADC) + ar (ACF) = ar (ABC) + ar (BCF) [समी. (1) और (2) से]
ar (ADF) = ar (ABFC). (चित्रानुसार) इति सिद्धम्

प्रश्न 2.
संलग्न चित्र में ABCDE एक पंचभुज है। AC के समान्तर खींची गई BP बढ़ायी गई DC को P पर तथा AD के समान्तर खींची गई EQ बढ़ायी गई CD से Q पर मिलती है।
सिद्ध कीजिए कि-
ar (ABCDE) = ar (APQ)

चित्र 9.27
हल:
दिया है : ABCDE एक पंचभुज है। BP || AC और EQ || AD खींची गई हैं जो DC को दोनों ओर बढ़ाने पर क्रमशः P और Q बिन्दुओं पर मिलती हैं।
चूँकि उभयनिष्ठ आधार AC पर AC || BP के मध्य ∆ABC एवं ∆APC स्थित हैं। =
⇒ ar (ABC) = ar (APC) ….(1)
चूँकि उभयनिष्ठ आधार AD पर AD || EQ के मध्य ∆ADE और ∆ADO स्थित हैं।
⇒ ar (ADE) = ar (ADQ) …(2)
⇒ ar (ABC) + ar (ADE) = ar (APC) + ar (ADQ) [समीकरण (1) और (2) से]
⇒ ar (ABC) + ar (ACD) + ar (ADE) = ar (APC) + ar (ACD) + ar (ADQ) [दोनों ओर ar (ACD) जोड़ने पर]
अतः ar (ABCDE) = ar (APQ). (चित्रानुसार) इति सिद्धम्

प्रश्न 3.
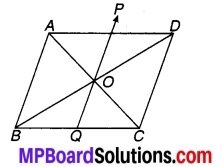
एक समान्तर चतुर्भुज ABCD के विकर्ण बिन्दु पर प्रतिच्छेद करते हैं। O से होकर एक रेखा खींची जाती है, जो AD को P और BC को Q पर मिलती है। दर्शाइए कि PQ इस समान्तर
चतुर्भुज ABCD को बराबर क्षेत्रफल वाले दो भागों में विभाजित करती है।
हल:

चित्र 9.28
ABCD एक दिया हुआ चतुर्भुज है जिसके विकर्ण AC और BD परस्पर O बिन्दु पर प्रतिच्छेद करते हैं। O से होकर रेखा POQ खींची गई है जो AD और BC को क्रमशः P और Q पर प्रतिच्छेद करती है। सिद्ध करना है कि PQ समान्तर चतुर्भुज ABCD को दो समान क्षेत्रफल वाले भागों में विभाजित करती है।
अर्थात् ar (ABQP) = ar (PQCD)
∆POA और ∆QOC में,
चूँकि ∠OAP = ∠OCQ (एकान्तर कोण हैं)
OA = OC (O, कर्ण AC का मध्य-बिन्दु है)
∠POA = ∠QOC (सम्मुख कोण हैं)
⇒ ∆POA = ∆QOC (ASA सर्वांगसमता प्रमेय से) …(1)
∆AOB और ∆COD में,
OA = OC (O, कर्ण AC का मध्य-बिन्दु है)
OB = OD (O, कर्ण BD का मध्य-बिन्दु है)
∠AOB = ∠COD (सम्मुख कोण हैं) AAOB = A COD (SAS सर्वांगसमता प्रमेय)…(2)
∆BOQ और ∆DOP में,
चूँकि ∠QOB = ∠POD (सम्मुख कोण हैं)
OB = OD (O कर्ण BD का मध्य-बिन्दु है)
∠OBQ = ∠ODP (एकान्तर कोण हैं)
∆BOQ ≅ ∆DOP (ASA सर्वांगसमता प्रमेय)…(3)
⇒ ar (POA) + ar (AOB) + ar (BOQ) = ar (QOC) + ar (COD) + ar (DOP) [समी (1) + (2) + (3) से]
अतः ar (ABQP) = ar (PQCD). (चित्रानुसार)
इति सिद्धम्

प्रश्न 4.
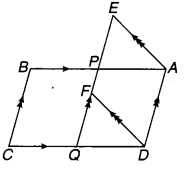
संलग्न चित्र में ABCD और AEFD दो समान्तर चतुर्भुज है। सिद्ध कीजिए कि ar (PEA) = ar (QFD).

चित्र 9.28
हल:
ABCD एवं AEFD दो समान्तर चतुर्भुज दिए हैं।
⇒ BA || CD तथा EA || FD (चित्रानुसार)
चूँकि BA || CD को EQ तिर्यक रेखा बिन्दु P और Q पर प्रतिच्छेद करती है।
⇒ ∠EPA = ∠FQD (संगत कोण हैं)…(1)
चूँकि EA || FD को EQ तिर्यक रेखा बिन्दु E और F पर प्रतिच्छेद करती है।
∠PEA = ∠QFD (संगत कोण हैं) …(2)
अब ∆PEA और ∆QFD में,
∠EPA = ∠FQD [समीकरण (1) से]
∠PEA = ∠QFD [समीकरण (2) से]
एवं EA = FD (समान्तर चतुर्भुज AEFD की सम्मुख भुजाएँ हैं)
⇒ ∆PEA ≅ ∆QFD
अतः ar (PEA) = ar (QFD) (सर्वांगसम त्रिभुज क्षेत्रफल में समान होते हैं) इति सिद्धम्

MP Board Class 9th Maths Chapter 9 लघु उत्तरीय प्रश्न

प्रश्न 1.
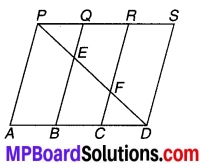
संलग्न चित्र में PSDA एक समान्तर चतुर्भुज है। PS पर P बिन्दुए और R इस प्रकार लिए गए हैं कि PQ = QR = RS है। तथा PA || QB || RC है। सिद्ध कीजिए कि-
ar (PQE) = ar (CFD) है।

चित्र 9.30
हल:
चूँकि PS | | AD को तिर्यक रेखा PD क्रमशः बिन्दु P और D पर प्रतिच्छेद करती है।
⇒ ∠SPD = ∠ADP अर्थात् ∠OPE = ∠CDF …(1) (एकान्तर कोण हैं)
चूँकि OP || RC को तिर्यक रेखा PD क्रमशः E और F पर प्रतिच्छेद करती है।
⇒ ∠PEQ = ∠EFR (संगत कोण हैं)
लेकिन ∠EFR = ∠DFC (सम्मुख कोण हैं)
∠PEQ = ∠DFC …(2)
अब ∆PEQ एवं ∆DFC में,
चूंकि ∠QPE = ∠CDF [समीकरण (1) से]
⇒ ∠PEQ = ∠DFC [समीकरण (2) से]
PQ = DC [PQ = RS दिया है RS = CD (RCDS एक समान्तर चतुर्भुज है)]
⇒ ∆PEQ = ∆DFC
अत: ar (PEQ) = ar (DFC). (सर्वांगसम त्रिभुजों के क्षेत्रफल बराबर होते हैं)
इति सिद्धम् वैकल्पिक विधि: PA || QB || RC || SD तिर्यक रेखा PS से PQ = QR = RS …(1)
अन्त:खण्ड काटते हैं, तो तिर्यक रेखा PD से PE = EF = FD …(2)
अन्त:खण्ड काटेंगे और तिर्यक रेखा AD से भी AB = BC = CD …(3)
अन्त:खण्ड काटेंगे।
चूँकि PS एवं AD समान्तर चतुर्भुज की सम्मुख भुजाएँ हैं।
⇒ PS = AD …(4)
अब ∆PQE और ∆CFD में,
चूँकि PQ = CD [समीकरण (1), (2) और (4) से]
∠QPE = ∠CDF (PS || AD एवं तिर्यक रेखा PD से बने एकान्तर कोण)
एवं PE = FD [समीकरण (2) से]
AQPE = ACFD (SAS सर्वांगसमता प्रमेय से)
अतः ar (POE) = ar (CFD). (सर्वांगसम के क्षेत्रफल बराबर होते हैं) इति सिद्धम्

प्रश्न 2.
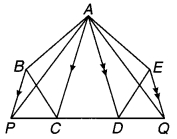
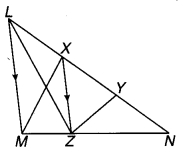
XY त्रिभुज LMN की भुजा LN पर स्थित दो बिन्दु इस प्रकार हैं कि LX = XY = YN है। Xसे होकर जाती हुई एक रेखा LM के समान्तर खींची गई है जो MNको zपर मिलती है देखिए संलग्न चित्र। सिद्ध कीजिए कि
ar (LZY) = ar (MZYX) है।

चित्र 9.31
हल:
दिया है : ∆LMN की भुजा पर स्थित दो बिन्दु X और Y इस M –
प्रकार कि LX=XY = YN एवं XZ|| LM रेखाखण्ड MN को Z पर मिलती है। LZ को मिलाया गया है।
अब उभयनिष्ठ आधार XZ पर XZ || LM के बीच दो ∆LXZ और ∆MXZ स्थित हैं।
ar (LXZ) = ar (MXZ) 2 ar (LXZ) + ar (XYZ) = ar (MXZ) + ar (XYZ) (ar (XYZ) को दोनों ओर जोड़ने पर)
⇒ ar (LZY) = ar (MZYX). (चित्रानुसार) इति सिद्धम्

प्रश्न 3.
संलग्न चित्र में समान्तर चतुर्भुज ABCD एवं ABEF हैं। यदि समान्तर चतुर्भुज ABCD का क्षेत्रफल 90 cm² है तो ज्ञात कीजिए
(i) ar (ABEF),
(ii) ar (ABD),
(iii) ar (BEF).

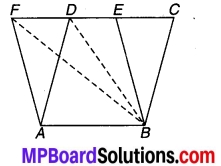
चित्र 9.32
हल:
दिया है : दो समान्तर चतुर्भुज ABCD एवं ABEF तथा समान्तर चतुर्भुज ABCD का क्षेत्रफल 90 cm² है। BF एवं BD को। मिलाया।

(i) उभयनिष्ठ आधार पर समान्तर चतुर्भुज ABCD और समान्तर चतुर्भुज ABEF एक ही AB || FC के मध्य स्थित हैं।
⇒ ar (ABEF) = ar (ABCD)
अतः ar (ABEF) = 90 cm² . (∵ ar (ABCD) = 90 cm²)

(ii) चूँकि BD समान्तर चतुर्भुज ABCD का विकर्ण है।
ar (ABD) = \(\frac { 1 }{ 2 }\) ar (ABCD)
अतः ar (ABD) = \(\frac { 1 }{ 2 }\) x 90 cm² = 45 cm². (∵ ar (ABCD) = 90 cm²)

(iii) चूँकि FB समान्तर चतुर्भुज ABEF का विकर्ण हैं।
⇒ ar (BEF) = \(\frac { 1 }{ 2 }\) ar (ABEF)
अतः ar (BEF) = \(\frac { 1 }{ 2 }\) x 90 cm² = 45 cm². (ar (ABEF) = 90 cm²)

प्रश्न 4.
संलग्न चित्र में त्रिभुज ABC की भुजा AB का मध्य-बिन्दु है। यदि रेखाखण्ड CQ || PD भुजा AB में Q पर मिलता है तो सिद्ध कीजिए कि ar (BPQ) = \(\frac { 1 }{ 2 }\)ar (ABC) है।

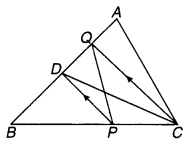
चित्र 9.33
हल:
∆ABC की भुजा AB का मध्य-बिन्दु D है तथा भुजा BC पर दिया हुआ कोई बिन्दु P है एवं CQ || PD भुजा AB से Q पर मिलता है।
PQ और CD को मिलाइए।
अब उभयनिष्ठ आधार DP पर DP || QC के मध्य ADPQ एवं ADPC स्थित हैं।
ar (DPQ) = ar (DPC) = ar (DPQ) + ar (DBP) = ar (DPC) + ar (DBP) [ar (DBP) को दोनों ओर जोड़ने पर]
⇒ ar (BPQ) = ar (DBC) (चित्रानुसार) …(2)
लेकिन ar (DBC) = \(\frac { 1 }{ 2 }\) ar (ABC) (DC, ∆ ABC की माध्यिका है) …(3)
अतः ar (BPQ) = \(\frac { 1 }{ 2 }\)ar (ABC). [समीकरण (2) एवं (3) से] इति सिद्धम्

प्रश्न 5.
संलग्न चित्र में ABCD एक वर्ग है। E और F क्रमशः BC और CD भुजाओं के मध्य-बिन्दु हैं। यदि R रेखाखण्ड EF का मध्य-बिन्दु है। सिद्ध कीजिए कि-
ar (AER) = ar (AFR) है।

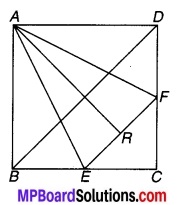
चित्र 9.34
हल:
ABCD एक वर्ग दिया है जिसकी भुजा BC और CD के मध्य-बिन्दु
क्रमशः E और F हैं तथा R रेखाखण्ड EF का मध्य-बिन्दु है।
अब ∆ABE और ∆ADF में,
चूँकि AB = AD (वर्ग की भुजाएँ हैं)
∠ABE = ∠ADF (वर्ग के कोण हैं)
एवं BE = DF (वर्ग की भुजाओं के आधे हैं)
⇒ ∆ABE ≅ ∆ADF (SAS सर्वांगसमता प्रमेय)
⇒ AE = AF (CPCT)
अब ∆AER और ∆AFR में,
चूंकि AE = AF (सिद्ध कर चुके हैं)
ER = FR (EF का मध्य-बिन्दु R दिया है)
AR = AR (उभयनिष्ठ है)
∆AER ≅ ∆AFR (SSS सर्वांगसमता प्रमेय)
अत: ar (AER) = ar (AFR). (सर्वांगसम क्षेत्रों के क्षेत्रफल बराबर होते हैं) इति सिद्धम्

वैकल्पिक विधि :
∆AEF की माध्यिका AR है (∵ R रेखाखण्ड EF का मध्य-बिन्दु है)
ar (AER) = ar (AFR). (माध्यिका त्रिभुज को दो बराबर क्षेत्रफल के क्षेत्रों में विभक्त करती हैं) इति सिद्धम्

प्रश्न 6.
एक समलम्ब ABCD में, AB || DC है तथा L भुजा BC का मध्य-बिन्दु है। L से होकर एक रेखा PQ || AD खींची गई है जो AB को P पर और बढ़ाई गई DC को Q पर मिलती है (देखिए संलग्न चित्र)। सिद्ध कीजिए कि-
ar (ABCD) = ar (APQD) है

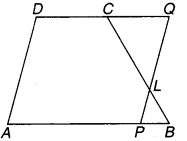
चित्र 9.35
हल:
ABCD एक समलम्ब चतुर्भुज दिया है जिसकी भुजा BC का A मध्य-बिन्दु L है। से होकर PQ || AD खींची गई है तथा
समलम्ब की भुजाएँ AB || DC है।
अब ∆LPB और ∆LOC में,
चूँकि ∠LPB = ∠LQC (एकान्तर कोण हैं, क्योंकि AB || DQ एवं PQ तिर्यक)
∠LBP ≅ ∠LCQ (एकान्तर कोण हैं, क्योंकि AB || DQ एवं CB तिर्यक)
एवं BL = LC (BC का मध्य-बिन्दु L दिया है)
⇒ ∆LPB ≅ ∆LQC (AAS सर्वांगसमता प्रमेय से)
⇒ ar (LPB) = ar (LQC) (सर्वांगसमता क्षेत्रों के क्षेत्रफल बराबर होते हैं)
⇒ ar (APLCD) + ar (LPB) = ar (APLCD) + ar (LQC) [ar (APLCD) को दोनों ओर जोड़ने पर]
अतः ar (ABCD) = ar (APQD). (चित्रानुसार) इति सिद्धम्

प्रश्न 7.
किसी समान्तर चतुर्भुज का आधार 20 सेमी तथा ऊँचाई (शीर्षलम्ब) 10 सेमी है, तो समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए। (2019)
हल:
समान्तर चतुर्भुज का क्षेत्रफल = आधार x ऊँचाई (शीर्षलम्ब)
= 20 x 10 = 200 सेमी²
अतः समान्तर चतुर्भुज का अभीष्ट क्षेत्रफल = 200 सेमी²

प्रश्न 8.
यदि किसी समान्तर चतुर्भुज का आधार 4 cm तथा शीर्षलम्ब (ऊँचाई) 2 cm है, तो समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए। (2019)
हल:
निर्देश : उपर्युक्त प्रश्न की तरह हल करें
उत्तर-अभीष्ट क्षेत्रफल = 8 cm

प्रश्न 9.
संलग्न चित्र में यदि AB || CD और ∆ABC का क्षेत्रफल 100 वर्ग सेमी है, तो ∆ABD का क्षेत्रफल ज्ञात कीजिए और कारण भी दीजिए। (2019)

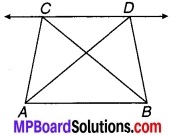
चित्र 9.36
हल:
चूँकि ∆ABC एवं ∆ABD दोनों ही समान आधार AB पर तथा AB || CD के मध्य स्थित हैं।
इसलिए, क्षेत्रफल (∆ABD) = क्षेत्रफल (∆ABC)
⇒ क्षेत्रफल (∆ABD) = 100 वर्ग सेमी
अतः ∆ABD का अभीष्ट क्षेत्रफल = 100 वर्ग सेमी।

प्रश्न 10.
केवल चित्र द्वारा प्रदर्शित कीजिए कि समान्तर चतुर्भुज के दोनों विकर्ण उसे बराबर (क्षेत्रफल वाले चार) त्रिभुजों में बाँटते हैं। (2019)

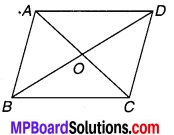
चित्र 9.37
हल:
ABCD एक समान्तर चतुर्भुज है जिसके विकर्ण AC एवं BD परस्पर O बिन्दु पर समद्विभाजित करके इसे चार बराबर-बराबर क्षेत्रफल वाले त्रिभुजों में विभाजित कर रहे हैं, अर्थात् क्षेत्रफल (∆ OBC) = क्षेत्रफल (∆ OCD) = क्षेत्रफल B (∆ODA) = क्षेत्रफल (∆OAB)

MP Board Class 9th Maths Chapter 9 अति लघु उत्तरीय प्रश्न

सत्य/असत्य लिखिए और अपने उत्तर का औचित्य दीजिए।

प्रश्न 1.
ABCD एक समान्तर चतुर्भुज और X- भुजा AB का मध्य-बिन्दु है। यदि ar(AXCD) = 24cm² है तो ar (ABC) = 24 cm है।
उत्तर:
असत्य कथन, क्योंकि ar (AXCD) ≠ ar (ABC).

प्रश्न 2.
PORS एक आयत है, जो त्रिज्या 13 cm वाले वृत्त के चतुर्थांश के अन्तर्गत है। A भुजा PQ पर स्थित कोई बिन्दु है। यदि PS = 5 cm है, तो ar (PAS) = 30 cm² है।
उत्तर:
कथन असत्य है, क्योंक

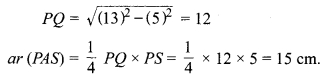
प्रश्न 3.
PQRS एक समान्तर चतुर्भुज है जिसका क्षेत्रफल 180 cm² है तथा A विकर्ण QS पर स्थित कोई बिन्दु है तब ∆ASR का क्षेत्रफल 90 cm² है।
उत्तर:
कथन असत्य है, क्योंकि ∆QSR का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x 180 = 90 cm² तथा
ar (ASR) < ar (QSR).

प्रश्न 4.
ABC और BDE दो समबाहु त्रिभुज इस प्रकार है कि D भुजा BC का मध्य-बिन्दु है। तब
ar (BDE) = \(\frac { 1 }{ 4 }\)ar (ABC).
उत्तर:

प्रश्न 5.
संलग्न चित्र में ABCD और EFGD दो समान्तर चतुर्भुज है तथा G भुजा CD का मध्य-बिन्दु है, तब
ar (DPC) = ar (EFGD).

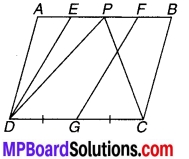
चित्र 9.38
उत्तर:
कथन असत्य है, क्योंकि ar(DPC) ≠ ar(EFGD) है।

MP Board Class 9th Maths Chapter 9 वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
12 cm और 16 cm विकर्णों वाले एक समचतुर्भुज की भुजाओं के मध्य-बिन्दुओं को मिलाने से बनी आकृति का क्षेत्रफल है :
(a) 48 cm² .
(b) 64 cm
(c) 96 cm²
(d) 192 cm².
उत्तर:
(a) 48 cm² .

प्रश्न 2.
त्रिभुज की माध्यिकाएँ उसे विभाजित करती हैं, दो :
(a) बराबर क्षेत्रफल वाले त्रिभुजों में
(b) सर्वांगसम त्रिभुजों में
(c) समकोण त्रिभुजों में
(d) समद्विबाहु त्रिभुजों में।
उत्तर:
(a) बराबर क्षेत्रफल वाले त्रिभुजों में

प्रश्न 3.
8 cm और 6 cm भुजाओं वाले एक आयत की आसन्न भुजाओं के मध्य-बिन्दुओं को मिलाने से बनी आकृति है :
(a) 24 cm² क्षेत्रफल का एक आयत
(b) 25 cm² क्षेत्रफल का एक वर्ग
(c) 24 cm² क्षेत्रफल का एक समलम्ब
(d) 24 cm² क्षेत्रफल एक समचतुर्भुज।
उत्तर:
(d) 24 cm² क्षेत्रफल एक समचतुर्भुज

प्रश्न 4.
संलग्न चित्र में समान्तर चतुर्भुज ABCD का क्षेत्रफल है :

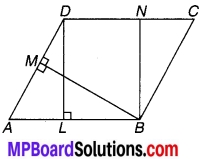
चित्र 9.39
(a) AB x BM
(b) BC – BN
(c) DC – DL
(d) AD x DL.
उत्तर:
(c) DC – DL

प्रश्न 5.
संलग्न चित्र में यदि समान्तर चतुर्भुज ABCD और आयत ABEM समान क्षेत्रफल वाले हैं, तो :

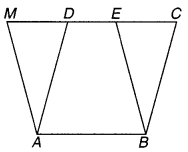
चित्र 9.40
(a) ABCD का परिमाप = ABEM का परिमाप
(b) ABCD का परिमाप < ABEM का परिमाप (c) ABCD का परिमाप > ABEM का परिमाप
(d) ABCD का परिमाप = = (ABEM का परिमाप)।
उत्तर:
(c) ABCD का परिमाप > ABEM का परिमाप

प्रश्न 6.
किसी त्रिभुज की भुजाओं के मध्य-बिन्दु किसी भी एक शीर्ष को चौथा बिन्दु लेकर एक समान्तर चतुर्भुज बनाते हैं जिसका क्षेत्रफल बराबर है :
(a) \(\frac { 1 }{ 2 }\)ar (ABC)
(b) \(\frac { 1 }{ 3 }\)Jar (ABC).
(c) \(\frac { 1 }{ 4 }\)ar (ABC)
(d) ar (ABC).
उत्तर:
(a) \(\frac { 1 }{ 2 }\)ar (ABC)

प्रश्न 7.
दो समान्तर चतुर्भज बराबर आधारों पर और एक ही समान्तर रेखाओं के मध्य स्थित हैं। उनके क्षेत्रफलों में अनुपात होगा :
(a) 1 : 2
(b) 1 : 1
(c) 2 : 1
(d) 3 : 1.
उत्तर:
(b) 1 : 1

प्रश्न 8.
ABCD एक चतुर्भुज है जिसका विकर्ण AC है, उसे बराबर क्षेत्रफल वाले दो भागों में विभाजित करता है। तब ABCD :
(a) एक आयत है
(b) सदैव एक सम चतुर्भुज है
(c) एक समान्तर चतुर्भुज है
(d) (a), (b) या (c) में से कोई भी होना आवश्यक नहीं।
उत्तर:
(d) (a), (b) या (c) में से कोई भी होना आवश्यक नहीं

प्रश्न 9.
एक त्रिभुज और एक समान्तर चतुर्भुज एक ही आधार पर और एक ही समान्तर रेखाओं के बीच स्थित हैं, तो त्रिभुज के क्षेत्रफल का समान्तर चतुर्भुज के क्षेत्रफल से अनुपात है :
(a) 1 : 3
(b) 1 : 2
(c) 3 : 1
(d) 1 : 4.
उत्तर:
(b) 1 : 2

प्रश्न 10.
ABCD एक समलम्ब है जिसकी समान्तर भुजाएँ AB = a cm और DC = b cm है (देखिए चित्र 9.41)। E और F समान्तर भुजाओं के मध्य-बिन्दु हैं। ar (ABFE) और ar (EFCD) का अनुपात है :

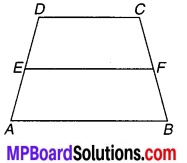
(a) a : b
(b) (3a + b) : (a + 3b)
(c) (a + 3b) : (3a + b)
(d) (2a + b) : (3a + b).
उत्तर:
(b) (3a + b) : (a + 3b)

प्रश्न 11.
समानान्तर चतुर्भुज का क्षेत्रफल होता है : (2018)
(a) आधार x ऊँचाई
(b) आधार + ऊँचाई
(c) 1/2 आधार x ऊँचाई
(d) आसन्न भुजाओं का गुणनफल
उत्तर:
(a) आधार x ऊँचाई

रिक्त स्थानों की पूर्ति

1. समचतुर्भुज का क्षेत्रफल उसके विकर्णों के गुणनफल का ……..होता है।
2. एक ही आधार और दो समान्तर रेखाओं के बीच बने समान्तर चतुर्भुज क्षेत्रफल में … होते हैं। (2019)
3. एक ही आधार पर व एक ही समान्तर रेखाओं के एक युग्म के बीच स्थित त्रिभुज क्षेत्रफल में ……. होते हैं।
4. एक ही आधार और उन्हीं समान्तर रेखाओं के मध्य स्थित आयत और समान्तर चतुर्भुज के क्षेत्रफल ……. होते हैं।
5. एक ही आधार और समान्तर रेखाओं के मध्य स्थित समान्तर चतुर्भुज का क्षेत्रफल त्रिभुज के क्षेत्रफल का ……… होता है।
उत्तर:
1. आधा,
2. बराबर,
3. बराबर,
4. बराबर,
5. दो गुना।

जोड़ी मिलान

उत्तर:
1. → (c),
2. → (d),
3. → (e),
4. → (a),
5. → (b).

सत्य/असत्य कथन
1. समान्तर चतुर्भुज जो एक ही आधार और समान्तर रेखाओं के बीच स्थित हों, क्षेत्रफल में बराबर नहीं होते।
2. समान्तर चतुर्भुज के विकर्ण उसे दो समान क्षेत्रफल वाले त्रिभुजों में विभक्त करते हैं।
3. प्रत्येक समान्तर चतुर्भुज समचतुर्भुज होता है।
4. प्रत्येक वर्ग एक आयत होता है लेकिन प्रत्येक आयत एक वर्ग नहीं होता।
5. आयत के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं।
उत्तर:
1. असत्य,
2. सत्य,
3. असत्य,
4. सत्य,
5. असत्य।

एक शब्द/वाक्य में उत्तर
1. एक सरल बन्द आकृति द्वारा घेरा गया तल क्या कहलाता है?
2. किसी बंद आकृति द्वारा घेरे गए तल का परिमाण क्या कहलाता है?
3. समान भुजाओं वाले समान्तर चतुर्भुज को क्या कहते हैं ?
4. यदि किसी चतुर्भुज की सम्मुख भुजाओं का एक युग्म समान्तर हो तो उसे क्या कहते हैं?
5. किसी समान्तर चतुर्भुज के विकर्ण उस समान्तर चतुर्भुज को चार त्रिभुजों में विभक्त करते हैं, उनके क्षेत्रफल में क्या सम्बन्ध होता है ?
6. यदि त्रिभुज का आधार एवं शीर्षलम्ब दिया हो, तो त्रिभुज का क्षेत्रफल ज्ञात करने का सूत्र लिखिए। (2019)
उत्तर:
1. तलीय क्षेत्र,
2. उस आकृति का क्षेत्रफल,
3. समचतुर्भुज,
4. समलम्ब चतुर्भुज या समलम्ब,
5. बराबर होते हैं।,
6. \(\frac { 1 }{ 2 }\) x आधार x शीर्षलम्ब।

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 12 हीरोन का सूत्र Additional Questions

MP Board Class 9th Maths अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 9th Maths दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
संलग्न चित्र में दी हुई पतंग को बनाने के लिए प्रत्येकरंग(शेड) के कितने कागज की आवश्यकता होगी यदि ABCD विकर्ण 44 cm वाला एक वर्ग है तथा नीचे 20 cm, 20 cm और 14 cm वाला एक समद्विबाहु त्रिभुज है।
हल:

ज्ञात है : एक पतंग जो एक वर्ग ABCD एवं एक समद्विबाहु ∆ CEF से बना है। वर्ग का विकर्ण AC = BD = 44 cm है जो परस्पर बिन्दु O पर समकोण पर समद्विभाजित करते हैं।
अर्थात् OA = OB = OC = OD = 22 cm
एवं ∠AOB = ∠ BOC = ∠COD = ∠DOA = 90°
समद्विबाहु त्रिभुज की भुजाएँ क्रमशः CE = 20 cm, CF = 20 cm एवं EF = 14 cm हैं। हम जानते हैं कि वर्ग के विकर्ण वर्ग को चार सर्वांगसम भागों में विभक्त करते हैं। पीला रंग का कागज वर्ग के दो चतुर्थांश I एवं II में है।
⇒ पीले रंग के कागज का क्षेत्रफल = 2 x \(\frac { 1 }{ 2 }\) x 22 x 22 = 484 cm
लाल रंग का कागज केवल वर्ग के एक चतुर्थांश IV में है
⇒ लाल रंग के कागज का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x 22 x 22 = 242 cm²
हरे रंग का कागज वर्ग के चतुर्थांश III एवं समद्विबाहु त्रिभुज (V) में है

∴ हरे रंग के कागज का क्षेत्रफल = ar (CEF) + ar (AOD)
= 131.14 + 242 = 373.14
अतः पीले रंग के कागज का अभीष्ट क्षेत्रफल = 484 cm²
लाल रंग के कागज का अभीष्ट क्षेत्रफल = 242 cm²
एवं हरे रंग के कागज का अभीष्ट क्षेत्रफल = 373.14 cm² .

प्रश्न 2.
एक त्रिभुज का परिमाप 50 cm है। त्रिभुज की एक भुजा छोटी भुजा से 4 cm लम्बी है तथा तीसरी भुजा छोटी भुजा के दुगने से 6 cm कम है। त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल:
मान लीजिए ∆ की छोटी भुजा = x cm तो प्रश्नानुसार दूसरी भुजा (x + 4) cm तथा तीसरी भुजा (2x – 6) cm होगी।
परिमाप = x + (x + 4) + (2x – 6)= 50 cm
⇒ 4x – 2 = 50 ⇒ 4x = 52
⇒ x = \(\frac { 52 }{ 4 }\) = 13 cm
अतः त्रिभुज की भुजाएँ क्रमशः 13 cm, 17 cm एवं 20 cm होंगी।

अतः त्रिभुज का अभीष्ट क्षेत्रफल = 109.54 cm².

प्रश्न 3.
संलग्न चित्र में ∆ABC की भुजाएँ AB = 7.5 cm, AC = 6.5 cm और BC = 7 cm हैं। आधार BC पर एक समान्तर चतुर्भुज DBCE की रचना की जाती है जो क्षेत्रफल में ∆ABC के बराबर है। इस समान्तर चतुर्भुज की ऊँचाई DF ज्ञात कीजिए।
हल:
दिया है : एक त्रिभुज जिसकी भुजा AB = 7.5 cm,
AC = 6.5 और BC = 7 cm
आधार BC = 7 cm पर एक समान्तर चतुर्भुज DBCE दिया है जिसका क्षेत्रफल ∆ABC के क्षेत्रफल के बराबर है। मान लीजिए समान्तर चतुर्भुज की ऊँचाई DF = d cm
∆ ABC में,


चूँकि ar (DBCE) = ar (ABC) (दिया है)
⇒ 7 x d = 21 ⇒ d = 2 = 3 cm
अतः समान्तर चतुर्भुज की अभीष्ट ऊँचाई DF = 3 cm.

प्रश्न 4.
संलग्न चित्र में 50 cm x 70 cm की विमाओं वाली एक आयताकार टाइल पर चित्र में दर्शाए गए अनुसार एक डिजाइन बनाया गया है। इस डिजाइन में 8 त्रिभुज हैं जिनमें से प्रत्येक की भुजाएँ 26 cm, 17 cm और 25 cm की हैं। डिजाइन का पूर्ण क्षेत्रफल ज्ञात कीजिए तथा टाइल के शेष भाग का क्षेत्रफल भी ज्ञात कीजिए।
हल:
दिया है : एक 50 cm x 70 cm विमाओं वाली 70cmटाइल जिसके अन्दर 26 cm, 17cm एवं 25 cm विमाओं वाली 8 सर्वांगसम त्रिभुजों से बनी आकृति।


∴ डिजाइन का क्षेत्रफल = 8 x त्रिभुज का क्षेत्रफल
= 8 x 204 = 1632 cm²
चूँकि आयताकार टाइल का क्षेत्रफल = लम्बाई x चौड़ाई
⇒ ar (आयताकार टाइल) = 70 x 50 = 3500 cm²
टाइल के शेष भाग का क्षेत्रफल = 3500 – 1632 = 1868 cm²
अतः टाइल की डिजाइन का अभीष्ट क्षेत्रफल = 1632 cm²
एवं शेष टाइल का अभीष्ट क्षेत्रफल = 1868 cm².

MP Board Class 9th Maths लघु उत्तरीय प्रश्न

प्रश्न 1.
भुजाओं 50 m, 65 m और 65 m वाले त्रिभुजाकार खेत में ₹ 7 प्रति m² की दर से घास लगवाने का व्यय ज्ञात कीजिए।
हल:
त्रिभुजाकार खेत के लिए,

चूँकि घास लगाने का व्यय = दर x क्षेत्रफल = 7 x 1500 = ₹ 10,500
अतः घास लगवाने का अभीष्ट व्यय = ₹ 10,500.

प्रश्न 2.
एक फ्लाई ओवर की त्रिभुजाकार दीवारों को विज्ञापन के लिए प्रयोग किया जाता है। दीवारों की भुजाएँ 13 m, 14 m और 15 m हैं। विज्ञापनों से एक वर्ष में ₹2,000 प्रति m² की दर से आय होती है। एक कम्पनी इनमें से एक दीवार को 6 महीने के लिए किराये पर लेती है। उस कम्पनी ने कितना किराया दिया ?
हल:

अतः विज्ञापन के लिए अभीष्ट किराया = ₹ 84,000.

प्रश्न 3.
एक समद्विबाहु त्रिभुज का परिमाप 32 cm है। एक बराबर भुजा और आधार का अनुपात 3 : 2 है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल:
दिया है : एक समद्विबाहु त्रिभुज जिसकी एक बराबर भुजा और आधार का अनुपात 3 : 2 है तथा परिमाप 32 cm है।
⇒ भुजाओं का अनुपात = 3 : 3 : 2
मान लीजिए भुजाएँ 3x, 3x एवं 2x हैं।
तो परिमाप 3x + 3x + 2x = 32 cm (दिया है)
⇒ x = 32 ⇒ x = \(\frac { 32 }{ 8 }\) = 4 cm
⇒ भुजाएँ क्रमश: 12 cm, 12 cm और 8 cm हैं। त्रिभुज में,

अतः त्रिभुज का अभीष्ट क्षेत्रफल = 32√2 cm².

प्रश्न 4.
संलग्न चित्र में दिए हुए समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए। साथ ही शीर्ष A से भुजा DC पर शीर्ष लम्ब की लम्बाई भी ज्ञात कीजिए।
हल:
दियाहैः एक समान्तर चतुर्भुज जिसकी भुजाएँ DC = 12 cm, BC = 17 cm और विकर्ण DB = 25 cm तथा A से DC पर शीर्षलम्ब = AE = d (मान लीजिए)
हम जानते हैं कि समान्तर चतुर्भुज का विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभक्त करता है।


चूँकि समान्तर चतुर्भुज का क्षेत्रफल = आधार (DC) x शीर्षलम्ब (AE)
⇒ 12 x d = 180 ⇒ d = \(\frac { 180 }{ 12 }\) = 15 cm
अतः समान्तर चतुर्भुज का अभीष्ट क्षेत्रफल = 180 cm²
एवं समान्तर चतुर्भुज का अभीष्ट शीर्षलम्ब = 15 cm.

प्रश्न 5.
एक खेत एक समान्तर चतुर्भुज के आकार का है जिसकी भुजाएँ 60 m और 40 m हैं तथा एक विकर्ण 80 m है। इस खेत का क्षेत्रफल ज्ञात कीजिए।
हल:
दिया है : एक समान्तर चतुर्भुज के आकार का खेत ABCDP
जिसकी भुजा AB = 60 m, BC = 40 m एवं विकर्ण AC = 80 m है।


अत: खेत का अभीष्ट क्षेत्रफल= 600√15 m².

प्रश्न 6.
एक त्रिभुजाकार का खेत का परिमाप 420 m हैं तथा इसकी भुजाओं का अनुपात 6 : 7 : 8 है। इस खेत का क्षेत्रफल ज्ञात कीजिए।
हल:
दिया है : एक त्रिभुजाकार खेत जिसकी परिमाप 420 m तथा भुजाओं का अनुपात 6 : 7 : 8 है।
चूँकि भुजाओं का अनुपात = 6 : 7 : 8 = भुजाएँ हैं 6x, 7x एवं 8x (मान लीजिए)
⇒ परिमाप = 6x + 7x + 8x = 420 ⇒ 21x = 420 ⇒ x = \(\frac { 420 }{ 21 }\) = 20 m
⇒ भुजाओं का वास्तविक मान a = 120 m, b = 140 m एवं c = 160 m

अतः खेत का अभीष्ट क्षेत्रफल = 2100√15 m².

प्रश्न 7.
किसी त्रिभुज की भुजाएँ क्रमश: 60 m, 100 m और 140 m हैं। त्रिभुज का क्षेत्रफल ज्ञात कीजिए। (2019)
हल:
दिया है : त्रिभुज की भुजाएँ क्रमश: a = 60 m, b = 100 m एवं c = 140 m


अतः त्रिभुज का अभीष्ट क्षेत्रफल = 1500√3 m.

प्रश्न 8.
किसी त्रिभुज ABC की भुजाएँ क्रमशः 40 m, 24 एवं 32 m हैं, तो त्रिभुज का क्षेत्रफल ज्ञात कीजिए। (2019)
हल:
निर्देशः उपर्युक्त प्रश्न की तरह हल करें
उत्तर:
अभीष्ट क्षेत्रफल = 384 m

MP Board Class 9th Maths अति लघु उत्तरीय प्रश्न

सत्य तथा असत्य कथन लिखिए तथा अपने उत्तर का औचित्व दीजिए।

प्रश्न 1.
आधार 4 cm और ऊँचाई 6 cm वाले त्रिभुज का क्षेत्रफल 24 cm² है।
उत्तर:
कथन असत्य है, क्योंकि ar (∆) = \(\frac { 1 }{ 4 }\) x 4 x 6 = 12 cm².

प्रश्न 2.
एक त्रिभुज ABC का क्षेत्रफल 8 cm है जिसमें AB = AC = 4 cm तथा ∠A = 90° है।
उत्तर:
कथन सत्य है, क्योंकि ar (ABC) = \(\frac { 1 }{ 2 }\) x 4 x 4 = 8 cm².

प्रश्न 3.
एक समद्विबाहु त्रिभुज का क्षेत्रफल \(\frac { 5 }{ 4 }\)√11 cm² होगा यदि उसका परिमाप 11 cm और आधार 5 cm है।
उत्तर:
कथन सत्य है, प्रत्येक बराबर भुजा 3 cm है।

प्रश्न 4.
एक समबाहु त्रिभुज का क्षेत्रफल 20√3 cm है जिसकी प्रत्येक भुजा 8 cm है।
उत्तर:
कथन असत्य है, क्योंकि समबाहु ∆ का क्षेत्रफल 16√3 cm² होगा।

प्रश्न 5.
यदि एक समचतुर्भुज की एक भुजा 10 cm और विकर्ण 16 cm है तो उस समचतुर्भुज का क्षेत्रफल 96 cm² है।
उत्तर:
कथन सत्य है, क्योंकि उसके विकर्ण से बने एक त्रिभुज का क्षेत्रफल = 48 cm².

प्रश्न 6.
एक समान्तर चतुर्भुज का आधार और संगत शीर्षलम्ब क्रमशः 10 cm और 3.5 cm हैं। उस समान्तर चतुर्भुज का क्षेत्रफल 30 cm है।
उत्तर:
कथन असत्य है, क्योंकि समान्तर चतुर्भुज का क्षेत्रफल = 10 x 3.5 = 35 cm².

प्रश्न 7.
भुजा a वाले एक समषद्भुज का क्षेत्रफल भुजा a वाले पाँच समबाहु त्रिभुज के क्षेत्रफल के बराबर होता है।
उत्तर:
कथन असत्य है, क्योंकि यह a भुजा वाले 6 समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होगा।

MP Board Class 9th Maths वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
एक समद्विबाहु समकोण त्रिभुज का क्षेत्रफल 8 cm है। इसके कर्ण की लम्बाई है:
(a) \(\sqrt { 32 }\) cm
(b) \(\sqrt { 16 }\) cm
(c) \(\sqrt { 48 }\) cm
(d) \(\sqrt { 24 }\) cm.
उत्तर:
(a) \(\sqrt { 32 }\) cm

प्रश्न 2.
एक समबाहु त्रिभुज का परिमाप 60 m है। इसका क्षेत्रफल है :
(a) 10√3 m²
(b) 15√3 m²
(c) 20√3 m²
(d) 100√3 m².
उत्तर:
(d) 100√3 m².

प्रश्न 3.
2√3 cm भुजा वाले समबाहु त्रिभुज का क्षेत्रफल है :
(a) 5.196 cm²
(b) 0.866 cm²
(c) 3:496 cm²
(d) 1:392 cm².
उत्तर:
(a) 5.196 cm²

प्रश्न 4.
क्षेत्रफल 9√3 cm वाले समबाहु त्रिभुज की प्रत्येक भुजा की लम्बाई है:
(a) 8 cm
(b) 36 cm
(c) 4 cm
(d) 6 cm.
उत्तर:
(d) 6 cm.

प्रश्न 5.
यदि एक समबाहु त्रिभुज का क्षेत्रफल 16/3 cm है तो इसकी परिमाप होगी :
(a) 48 cm
(b) 24 cm
(c) 12 cm
(d) 36 cm.
उत्तर:
(b) 24 cm

रिक्त स्थानों की पूर्ति

1. एक समकोण समद्विबाहु त्रिभुज की बराबर भुजा 10 cm है तो इसके विकर्ण लम्बाई …… होगी।
2. 10 cm और 6 cm भुजाओं वाले आयत का क्षेत्रफल …….. होगा।
3. एक समबाहु त्रिभुज की प्रत्येक भुजा 10 cm है तो इसका क्षेत्रफल ……… होगा।
4. एक आयत की भुजाएँ मीटर में मापी गई हैं। इसके क्षेत्रफल का मात्रक ………. होगा।
5. आधार 12 cm तथा शीर्षलम्ब 8 cm वाले त्रिभुज का क्षेत्रफल ……. है।
उत्तर:
1. 10√2 cm,
2. 60 cm²,
3. 25√3 cm²,
4. m²,
5. 48 cm².

जोड़ी मिलान

उत्तर:
1. → (c),
2. →(d),
3. → (e),
4. → (a),
5. → (b).

सत्य/असत्य कथन

1. हीरोन का सूत्र केवल समान्तर चतुर्भुज का क्षेत्रफल ज्ञात करने में प्रयुक्त होता है।
2. समान्तर चतुर्भुज की संलग्न भुजाएँ तथा एक विकर्ण दिया हो तो उसका क्षेत्रफल हीरोन के सूत्र से ज्ञात कर सकते हैं।
3. एक त्रिभुज का क्षेत्रफल होता है उसका आधार x शीर्षलम्ब।
4. आयत का क्षेत्रफल उसकी लम्बाई एवं चौड़ाई के गुणनफल के बराबर होता है।
5. समचतुर्भुज का क्षेत्रफल उसके विकर्णों के गुणनफल के बराबर होता है।
उत्तर:
1. असत्य,
2. सत्य,
3. असत्य,
4. सत्य,
5. असत्य।

एक शब्द/वाक्य में उत्तर
1. किसी त्रिभुज की परिमाप का मात्रक क्या होता है?
2. क्षेत्रफल को मापने का मात्रक क्या है?
3. किसी त्रिभुज की भुजाओं के योग को क्या कहते हैं?
4. किसी वर्ग की भुजा 4 सेमी है। उसके विकर्ण उसे चार त्रिभुजों में विभक्त करते हैं तो प्रत्येक त्रिभुज का क्षेत्रफल क्या होगा?
5. हीरोन का जन्म कहाँ हुआ था?
उत्तर:
1. सेमी या मीटर,
2. सेमी या मीटर,
3. परिमाप,
4. 4 cm²,
5. अलेक्जेण्ड्रिया (मिस्र) में।

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 11 रचनाएँ Additional Questions

MP Board Class 9th Maths Chapter 11 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 9th Maths Chapter 11 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
एक त्रिभुज की रचना कीजिए यदि उसका परिमाप 10-4 cm और दो कोण 45° और 120° है।
हल:
एक त्रिभुज ABC की रचना करनी है जिसमें ∠ B = 45°, ∠C = 120° तथा परिमाप AB + BC + CA = 10.4 cm
रचना:

चित्र 11.23
(i) रेखाखण्ड PQ = 10.4 cm खींचा
(ii) रेखाखण्ड PQ के बिन्दु P और Q पर क्रमशः 45° और 120° के कोण बनाते हुए किरण PR एवं QS खींचे।
(iii) ∠ RPQ और ∠SQP की समद्विभाजक किरणे PX और QY खींचे जो परस्पर बिन्दु A पर प्रतिच्छेद करती हैं।
(iv) AP एवं AQ के लम्ब समद्विभाजक खींचिए जो रेखाखण्ड PQ को क्रमशः B और C बिन्दुओं पर प्रतिच्छेद करते हैं।
(v) AB और AC को मिलाइए।
यही ∆ABC अभीष्ट त्रिभुज है।

प्रश्न 2.
त्रिभुज PQR की रचना कीजिए जिसमें QR = 3 cm, ∠ POR = 45° और QP – PR = 2 cm दिया है।
हल:
रचना :

चित्र 11.24
(i) रेखाखण्ड QR = 3 cm खींचा।
(ii) QR के बिन्दु Q पर 45° का कोण बनाती हुए किरण QX खींची।
(iii) किरण QX में से Qs = 2 सेमी का रेखाखण्ड काटा।
(iv) SR को मिलाया।
(v) SR का लम्ब समद्विभाजक खींचा जो किरण Qx को बिन्दु P पर प्रतिच्छेद करता है।
(vi) PR को मिलाया।
यही ∆POR अभीष्ट त्रिभुज है।

प्रश्न 3.
एक समकोण त्रिभुज की रचना कीजिए जिसकी एक भुजा 3.5 cm तथा अन्य भुजा और कर्ण का योग 5.5 cm है।
हल:
एक समकोण ∆ABC की रचना करनी है जिसका कोण B समकोण है। आधार BC = 3.5 cm, कर्ण AC + भुजा AB = 5.5 cm है।
रचना:

चित्र 11.25
(i) BC = 3.5 cm का एक रेखाखण्ड खींचिए।
(ii) बिन्दु B पर BC के साथ 90° का कोण बनाते हुए किरण BX खींचिए।
(iii) किरण BX में से BD = 5.5 cm का एक रेखाखण्ड काटिए।
(iv) DC को मिलाइए।
(v) DC का लम्ब समद्विभाजक खींचिए जो BD को बिन्दु A पर काटता है।
(vi) AC को मिलाइए।
यही ∆ABC अभीष्ट त्रिभुज है।

प्रश्न 4.
एक त्रिभुज ABC की रचना कीजिए जिसमें BC = 5 cm, ∠B = 60° और AC + AB = 7.5 cm है।
हल:
रचना :

चित्र 11.26
(i) एक रेखाखण्ड BC = 5 cm खींचिए।
(ii) BC के बिन्दु B पर 60° का कोण बनाते हुए एक किरण BX खींचिए।
(iii) किरण BX में से BD = 7.5 cm का रेखाखण्ड काटिए।
(iv) DC को मिलाइए।
(v) DC का लम्ब समद्विभाजक खींचिए जो BD को बिन्दु पर प्रतिच्छेद करता है।
(vi) AC को मिलाइए।
यही ∆ABC अभीष्ट त्रिभुज है।

MP Board Class 9th Maths Chapter 11 लघु उत्तरीय प्रश्न

प्रश्न 1.
चाँदे की सहायता से 110° का एक कोण खींचिए और फिर उसे समद्विभाजित कीजिए। प्रत्येक कोण को मापिए।
हल:
रचना:

चित्र 11.27
(i) एक रेखाखण्ड BC खींचिए।
(ii) B पर ∠ ABC = 110° का कोण बनाइए।
(iii) ∠ABC का समद्विभाजक BD खींचिए।
मापन करने पर प्रत्येक कोण का माप = 55° है।

प्रश्न 2.
3.6 cm, 3.0 cm और 4.8 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए।
हल:
एक त्रिभुज ABC की रचना करनी है जिसमें AB = 3.6 cm, BC = 3.0 cm और AC = 4.8 cm।
रचना :

चित्र 11.28
(i) AB = 3.6 cm का एक रेखाखण्ड खींचिए।
(ii) A को केन्द्र लेकर 4.8 cm की त्रिज्या से एक चाप खींचिए।
(iii) B को केन्द्र लेकर 3.0 cm की त्रिज्या से एक चाप खींचिए जो पहले चाप को बिन्दु C पर प्रतिच्छेद करता है।
(iv) AC और BC को मिलाइए।
यही ∆ABC अभीष्ट त्रिभुज है।

प्रश्न 3.
60° का कोण बनाकर इसका कोणार्द्धक खींचिए। (2019)
अथवा
60° का कोण बनाकर उसका समद्विभाजक खींचिए। (2019)
हल:
रचना :

चित्र 11.29
(i) एक किरण BC खींचिए।
(ii) B को केन्द्र लेकर किसी त्रिज्या से एक चाप खींचिए जो BC को बिन्दु P पर प्रतिच्छेद करता है।
(iii) P को केन्द्र लेकर उसी त्रिज्या से एक चाप खींचिए जो पूर्व से चाप को Q बिन्दु पर प्रतिच्छेद करता है।
(iv) BQ से होकर एक किरण BA खींचिए।
यही ∠ABC = 60° का अभीष्ट कोण है।
(v) P और Q को केन्द्र लेकर PQ के आधे से अधिक की त्रिज्या लेकर चाप खींचिए जो परस्पर बिन्दु R पर प्रतिच्छेद करते हैं।
(vi) BR से होकर किरण BD खींचिए।
यही BD अभीष्ट कोणार्द्धक (समद्विभाजक) है।

MP Board Class 9th Maths Chapter 11 अति लघु उत्तरीय प्रश्न

निम्नलिखित में प्रत्येक में सत्य या असत्य कथन लिखिए। अपने उत्तर का कारण दीजिए।

प्रश्न 1.
52.5° के कोण की रचना की जा सकती है।
उत्तर:
कथन सत्य है, क्योंकि 52.5° = 105°/2 की रचना की जा सकती है।

प्रश्न 2.
42.5° के कोण की रचना की जा सकती है।
उत्तर:
कथन असत्य है, क्योंकि 42.5° = 85°/2 और 85° के कोण की रचना नहीं की जा सकती है।

प्रश्न 3.
एक त्रिभुज ABC की रचना की जा सकती है जिसमें AB = 5 cm, ∠A = 45° और BC + AC = 5 cm ।
उत्तर:
कथन असत्य है, क्योंकि दो भुजाओं का योग तीसरी के बराबर है।

प्रश्न 4.
एक त्रिभुज ABC की रचना की जा सकती है जिसमें BC = 6 cm, ∠C = 30° और AC – AB = 4 cm है।
उत्तर:
कथन सत्य है, क्योंकि AC – AB < BC. प्रश्न 5. एक त्रिभुज ABC की रचना की जा सकती है जिसमें ∠B = 105°, ∠ C = 90° और AB + CA = 10 cm है। उत्तर: कथन असत्य है, क्योंकि ∠ B + ∠C = 105° + 90° = 195° > 180°.

प्रश्न 6.
एक त्रिभुज ABC की रचना की जा सकती है जिसमें ∠B = 60°, ∠C = 45° और AB+ BC + AC = 12 cm है।
उत्तर:
कथन सत्य है, क्योंकि ∠ B + ∠ C = 60° + 45° = 105° < 180°.

MP Board Class 9th Maths Chapter 11 वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
पटरी और परकार की सहायता से निम्न कोण की रचना सम्भव नहीं है :
(a) 37.5°
(b) 40°
(c) 22.5°
(d) 67.50.
उत्तर:
(b) 40°

प्रश्न 2.
एक त्रिभुज ABC जिसमें BC = 6 cm और ∠B = 45° दिया है, की रचना सम्भव नहीं है यदि AB और AC का अन्तर है:
(a) 6.9 cm
(b) 5.2 cm
(c) 5.0 cm
(d) 4.0 cm.
उत्तर:
(a) 6.9 cm

प्रश्न 3.
एक त्रिभुज ABC, जिसमें BC = 3 cm और ∠C = 60° की रचना सम्भव है जब AB और AC का अन्तर बराबर है :
(a) 3 : 2 cm
(b) 3.1 cm
(c) 3 cm
(d) 2.8 cm.
उत्तर:
(d) 2.8 cm.

प्रश्न 4.
पटरी और परकार की सहायता से निम्न कोण की रचना सम्भव है :
(a) 35°
(b) 40°
(c) 37.5°
(d) 47.5°
उत्तर:
(c) 37.5°

प्रश्न 5.
एक त्रिभुज ABC जिसमें AB = 4 cm और A = 60° है, की रचना सम्भव नहीं है, यदि BC और AC का अन्तर है:
(a) 3.5 cm
(b) 4.5 cm
(c) 3 cm
(d) 2.5 cm.
उत्तर:
(b) 4.5 cm

रिक्त स्थानों की पूर्ति
1. वह मापक यन्त्र जिसके एक ओर सेण्टीमीटर, मिलीमीटर तथा दूसरी ओर इंच और उसके भाग चिह्नित हों कहलाता है।
2. त्रिभुजाकार युग्म जिसमें एक के कोण 60°, 30° और 90° तथा दूसरे के 45°, 450 और 90° होते हैं कहलाता है।
3. मापक यन्त्र जिसकी दोनों भुजाओं में दो नुकीले सिरे होते हैं ……….. कहलाता है।
4. दो टाँगों वाला यन्त्र जिसके एक सिरे पर नुकीला सिरा तथा दूसरे सिरे पर पेंसिल लगाने की व्यवस्था हो …….. कहलाता है।
5. अर्द्धचन्द्राकार पारदर्शी मापक यन्त्र जिसकी वृत्तकार परिधि अंशांकित हो ..कहलाता है।
उत्तर:
1. अंशांकित पटरी (स्केल),
2. सेटस्क्वायर,
3. डिवाइडर,
4. परकार (कम्पास),
5. चाँदा।

सत्य/असत्य कथन

1. उस त्रिभुज की रचना सम्भव है जिसकी दो भुजाओं का योग तीसरी भुजा के बराबर हो।
2. पटरी एवं परकार की सहायता से 50° का कोण बनाना सम्भव नहीं है।
3. उस त्रिभुज की रचना सम्भव है जिसकी दो भुजाओं का अन्तर तीसरी भुजा के बराबर हो।
4. पटरी और परकार की सहायता से उस कोण की रचना सम्भव है जिसकी माप 7.5 के पूर्ण गुणक में हो।
5. उस त्रिभुज की रचना सम्भव है जिसकी दो भुजाओं का योग तीसरी भुजा से छोटा हो।
उत्तर:
1. असत्य,
2. सत्य,
3. असत्य,
4. सत्य,
5. असत्य।

एक शब्द/वाक्य में उत्तर

1. वह त्रिभुज क्या कहलाता है जिसकी भुजाएँ बराबर हों?
2. समबाहु त्रिभुज के प्रत्येक कोण का मान क्या होता है?
3. समकोण त्रिभुज में अधिकतर कितने समकोण हो सकते हैं?
4. किसी त्रिभुज के तीनों कोणों का योग कितना होता है?
5. वह रेखा क्या कहलाती है जो किसी रेखाखण्ड को समकोण पर दो बराबर भागों में विभक्त करती है।
उत्तर:
1. समबाहु त्रिभुज,
2. 60°,
3. एक
4. 180°
5. लम्ब समद्विभाजक।

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.6

प्रश्न 1.
एक बेलनाकार बर्तन के आधार की परिधि 132 cm है और उसकी ऊँचाई 25 cm है। इस बर्तन में कितने लीटर पानी आ सकता है ? (1000 cm³ = 1 लीटर) (2018)
हल :
बेलनाकार बर्तन के आधार की परिमाप = 2πr = 132
= \(2 \times \frac{22}{7} \times r=132 \Rightarrow r=\frac{132 \times 7}{2 \times 22}=21 \mathrm{cm}\)
बेलनाकार बर्तन का आयतन = \(\pi r^{2} h=\frac{22}{7} \times(21)^{2} \times 25 \mathrm{cm}^{2}\)
= 22 x 21 x 3 x 25 = 34650 cm³
= \(\frac { 34650 }{ 1000 }\)
= 34.650 लीटर
अत: बेलनाकार बर्तन में 34.650 लीटर पानी आ सकता है।

प्रश्न 2.
लकड़ी के एक बेलनाकार पाइप का आन्तरिक व्यास 24 cm है और बाहरी व्यास 28 cm है। इस पाइप की लम्बाई 35 cm है। इस पाइप का द्रव्यमान ज्ञात कीजिए यदि 1 cm³ लकड़ी का द्रव्यमान 0.6g है। (2019)
हल :
दिया है : d₁ = 28 cm ⇒ r₁ = \(\frac { 28 }{ 2 }\) = 14 cm, d₂ = 24 cm ⇒ r₂ = \(\frac { 24 }{ 2 }\) = 12 cm, लम्बाई l या h = 35 cm
पाइप की लकड़ी का आयतन = \(\pi\left(r_{1}^{2}-r_{2}^{2}\right) \times h=\frac{22}{7}\left(14^{2}-12^{2}\right) \times 35\)
= 22 (196 – 144) x 5 = 22 x 52 x 5 = 5720 cm³
पाइप की लकड़ी का द्रव्यमान = 5720 x 0.6 g = 3432 g
अतः पाइप का अभीष्ट द्रव्यमान = 3432 g या 3:432 kg

प्रश्न 3.
एक सोफ्ट ड्रिंक (soft drink) दो प्रकार के पैकों में उपलब्ध है :
(i) लम्बाई 5 cm और चौड़ाई 4 cm वाले एक आयताकार आधार का टिन का डिब्बा जिसकी ऊँचाई 15 cm है और
(ii) व्यास 7 cm वाले वृत्तीय आधार और 10 cm ऊँचाई वाला एक प्लास्टिक का बेलनाकार डिब्बा। किस डिब्बे की धारिता अधिक है और कितनी अधिक ?
हल :
(i) टिन के घनाभाकार डिब्बे की धारिता = 5 x 4 x 15 = 300 cm³
(ii) प्लास्टिक के बेलनाकार डिब्बे की धारिता = \(\frac{22}{7} \times\left(\frac{7}{2}\right)^{2} \times 10\) = 385 cm³
दोनों की धारिता का अन्तर = 385 – 300 = 85 cm³
अतः प्लास्टिक के डिब्बे की धारिता टिन के डिब्बे की धारिता से 85 cm³ अधिक है।

प्रश्न 4.
यदि एक बेलन का पार्श्व पृष्ठीय क्षेत्रफल 94.2 cm² है और उसकी ऊँचाई 5 cm है तो ज्ञात कीजिए:
(i) आधार की त्रिज्या,
(ii) बेलन का आयतन। (π = 3.14 लीजिए)
हल :
(i) चूँकि बेलन का पार्श्व पृष्ठीय क्षेत्रफल = 2πrh
⇒ 2 x 3.14 x r x 5 = 94.2 ⇒ r = \(\frac { 94.2 }{ 31.4 }\) = 3 cm
अतः बेलन के आधार की अभीष्ट त्रिज्या = 3 cm.

(ii) बेलन का आयतन = πr²h = 3.14 x 3² x 5 = 141.3 cm³
अतः बेलन का अभीष्ट आयतन = 141.3 cm³.

प्रश्न 5.
10 m गहरे एक बेलनाकार बर्तन के आन्तरिक वक्र पृष्ठ को पेंट कराने का व्यय Rs 2,200 है। यदि पेंट कराने की दर Rs 20 प्रति m² है, तो ज्ञात कीजिए
(i) बर्तन का आन्तरिक वक्र पृष्ठीय क्षेत्रफल
(ii) आधार की त्रिज्या
(iii) बर्तन की धारिता।
हल :
(i) चूँकि पेंट कराने का व्यय = दर x आन्तरिक वक्र पृष्ठीय क्षेत्रफल
⇒ 2200 = 20 x आन्तरिक वक्र पृष्ठीय क्षेत्रफल
⇒ आन्तरिक वक्र पृष्ठीय क्षेत्रफल = \(\frac { 2200 }{ 20 }\) = 110 m²
अतः बर्तन का अभीष्ट आन्तरिक वक्र पृष्ठीय क्षेत्रफल = 110 m².

(ii) बेलन का वक्रपृष्ठीय क्षेत्रफल = 2πrh = 2 x \(\frac { 22 }{ 7 }\) x r x 10 = 110
⇒ \(r=\frac{110 \times 7}{2 \times 22 \times 10}=\frac{7}{4} \mathrm{m}=1.75 \mathrm{m}\)
अत: बेलनाकार बर्तन के आधार की अभीष्ट त्रिज्या = 1.75 m.

(iii) बर्तन की धारिता = \(\pi r^{2} h=\frac{22}{7} \times\left(\frac{7}{4}\right)^{2} \times 10=\frac{22 \times 7 \times 10}{16}\)
बर्तन की धारिता = 96.25 m³ या 96.25 kL
अतः बेलनाकार बर्तन की अभीष्ट धारिता = 96.25 m³ (kL).

प्रश्न 6.
ऊँचाई 1 m वाले एक बेलनाकार बर्तन की धारिता 15.4 लीटर है। इसको बनाने के लिए कितने वर्ग मीटर धातु की शीट की आवश्यकता होगी ?
हल :
दी हुई धारिता = 15.4 लीटर = \(\frac { 15.4 }{ 1000 }\) m³ = πr²h

बेलनाकार बर्तन का पृष्ठीय क्षेत्रफल = 2πr (r + h)
= 2 x \(\frac { 22 }{ 7 }\) x 0.07 (0.07+ 1)= 44 x 0.01 x 1.07 m³
= 0.4708 m³
अतः धातु की शीट की अभीष्ट आवश्यकता = 0.4708 m³.

प्रश्न 7.
सीसे की एक पेंसिल (lead pencil) लकड़ी के एक बेलन के अभ्यन्तर में ग्रेफाइट (graphite) से बने ठोस बेलन को डालकर बनाई गई है। पेंसिल का व्यास 7 mm है और ग्रेफाइट का व्यास 1 mm है। यदि पेंसिल की लम्बाई 14 cm है तो लकड़ी का आयतन और ग्रेफाइट का आयतन ज्ञात कीजिए।
हल :
दिया है : पेंसिल का बाहरी व्यास d₁ = 7 mm
r₁ = \(\frac { 7 }{ 20 }\) cm
एवं पेंसिल का आन्तरिक (ग्रेफाइट) का व्यास d₂ = 1 mm
r₂ = \(\frac { 1 }{ 20 }\) cm
तथा पेंसिल की लम्बाई l = 14 cm

अतः लकड़ी का अभीष्ट आयतन = 5.28 cm³ एवं ग्रेफाइट का आयतन = 0.11 cm³.

प्रश्न 8.
एक अस्पताल (hospital) के एक रोगी को प्रतिदिन 7 cm व्यास वाले एक बेलनाकार कटोरे में सूप (soup) दिया जाता है। यदि यह कटोरा सूप से 4 cm ऊँचाई तक भरा जाता है, तो इस
अस्पताल में 250 रोगियों के लिए प्रतिदिन कितना सूप तैयार किया जाता है ?
हल :
दिया है : एक बेलनाकार कटोरे का व्यास d = 7 cm
r = \(\frac { 7 }{ 2 }\) cm
एवं कटोरे में सूप की ऊँचाई h = 4 cm
एक कटोरे में सूप का आयतन = \(\pi r^{2} h=\frac{22}{7} \times\left(\frac{7}{2}\right)^{2} \times 4=154 \mathrm{cm}^{3}\)
250 रोगियों के सूप का आयतन = 250 x 154 cm³ = 38500 cm³
= \(\frac { 38500 }{ 1000 }\)
= 38.5 लीटर
अतः प्रतिदिन तैयार किए गए सूप का अभीष्ट आयतन = 38.5 लीटर।

MP Board Class 9th Maths Solutions

zMP Board Class 9th Social Science Solutions Chapter 6 भारत : प्राकृतिक वनस्पति एवं वन्य जीव

MP Board Class 9th Social Science Chapter 6 पाठान्त अभ्यास

MP Board Class 9th Social Science Chapter 6 वस्तुनिष्ठ प्रश्न

सही विकल्प चुनकर लिखिए

प्रश्न 1.
भारत में सबसे कम वन क्षेत्र वाला राज्य है (2009, 11)
(i) असम
(ii) राजस्थान
(iii) झारखण्ड
(iv) हरियाणा।
उत्तर:
(iv) हरियाणा।

प्रश्न 2.
सुन्दरी वृक्ष पाया जाता है (2009, 10)
(i) उष्ण कटिबन्धीय वन में
(ii) हिमालयीन वन में
(iii) मैंग्रोव वन में,
(iv) उष्ण कटिबंधीय पर्णपाती वन में।
उत्तर:
(iii) मैंग्रोव वन में,

प्रश्न 3.
राजस्थान की प्राकृतिक वनस्पति है (2009)
(i) आर्द्र उष्ण कटिबन्धीय सदाबहार वन
(ii) अल्पाइन प्रकार के वन,
(iii) उष्ण कटिबन्धीय कंटीले वन
(iv) आर्द्र उष्ण कटिबन्धीय अर्द्ध सदाबहार वन।
उत्तर:
(iii) उष्ण कटिबन्धीय कंटीले वन

प्रश्न 4.
भारतीय सिंहों का प्राकृतिक आवास आरक्षित क्षेत्र है (2008, 09, 12, 15)
(i) गुजरात का गिर क्षेत्र
(ii) असम का काजीरंगा वन क्षेत्र
(iii) पश्चिम बंगाल का सुन्दरवन
(iv) नीलगिरि वन क्षेत्र।
उत्तर:
(i) गुजरात का गिर क्षेत्र

MP Board Class 9th Social Science Chapter 6 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
प्राकृतिक वनस्पति से क्या तात्पर्य है? (2017)
उत्तर:
प्राकृतिक रूप से मानव के हस्तक्षेप के बिना उगने वाले पेड़-पौधों को प्राकृतिक वनस्पति कहते हैं।

प्रश्न 2.
वन किसे कहते हैं? (2014, 16, 18)
उत्तर:
वन उस बड़े भू-भाग को कहते हैं, जो प्राकृतिक रूप से उगने वाले पेड़-पौधों तथा झाड़ियों द्वारा आच्छादित होता है।

प्रश्न 3.
मैंग्रोव वन किसे कहते हैं? (2017)
उत्तर:
भारत के तटवर्ती क्षेत्रों में जहाँ ज्वारभाटा आते हैं, वहाँ मैंग्रोव या ज्वारीय वन पाये जाते हैं।

प्रश्न 4.
देशज व विदेशज वनस्पति से क्या आशय है?
उत्तर:
जो वनस्पति मूलरूप से भारतीय है, उसे देशज वनस्पति कहते हैं लेकिन जो पौधे भारत के बाहर से आये हैं, उन्हें विदेशज वनस्पति कहते हैं।

प्रश्न 5.
अभ्यारण्य किसे कहते हैं? (2014, 16, 18)
उत्तर:
अभ्यारण्य राष्ट्रीय उद्यानों के समान ही होते हैं। ये वन्य प्राणियों को संरक्षित और प्रजातियों को सुरक्षित करने के लिए प्राकृतिक स्थल हैं यहाँ बिना अनुमति के शिकार करना मना होता है।

प्रश्न 6.
प्रशासनिक आधार पर वनों का वर्गीकरण कीजिए।
उत्तर:
प्रशासनिक आधार पर वनों को तीन श्रेणियों में बाँटा जा सकता है –

• आरक्षित वन :
  जो वन इमारती लकड़ी अथवा वन उत्पादों को प्राप्त करने के लिए स्थायी रूप से सुरक्षित किये गये हैं जिनमें पशुओं की चराई व कृषि करने की अनुमति प्राप्त नहीं होती है, आरक्षित वन कहलाते हैं।
• संरक्षित वन :
  ये वन जिनमें पशुओं को चराने व खेती करने की अनुमति सामान्य प्रतिबन्धों के साथ दे दी जाती है, संरक्षित वन कहलाते हैं।
• अवर्गीकृत वन :
  वे वन जो न तो आरक्षित हैं और न ही सुरक्षित हैं, अवर्गीकृत वन कहलाते हैं।

MP Board Class 9th Social Science Chapter 6 लघु उत्तरीय प्रश्न

प्रश्न 1.
प्रवासी पक्षी क्या है?
उत्तर:
उत्तरी एशिया से भारत में अल्पकाल के लिए आने वाले पक्षियों को प्रवासी पक्षी कहा जाता है। भारत के कुछ दलदली भाग प्रवासी पक्षियों के लिये प्रसिद्ध हैं। शीत ऋतु में साइबेरियन सारस बहुत संख्या में यहाँ आते हैं। इन पक्षियों का मनपसन्द स्थान कच्छ का रन है। जिस स्थान पर मरुभूमि समुद्र से मिलती है, वहाँ लाल सुन्दर कलगी वाले फ्लैमिंगो हजारों की संख्या में आते हैं।

प्रश्न 2.
वन संरक्षण से क्या तात्पर्य है?
उत्तर:
वन राष्ट्रीय सम्पदा हैं। यह मानव के लिये विभिन्न प्रकार से उपयोगी हैं। वनों से हमें प्रत्यक्ष एवं अप्रत्यक्ष लाभ प्राप्त होते हैं। मनुष्य की आवश्यकताएँ अनन्त होती हैं जबकि उन आवश्यकताओं को पूरा करने वाले प्रकृति प्रदत्त साधन सीमित हैं और यदि हम इन साधनों का अन्धाधुन्ध उपयोग करेंगे तो यह एक निश्चित समय के पश्चात् समाप्त हो जायेंगे। अतः वनों की देखभाल करना व उनको काटने से रोकना आदि ही वन संरक्षण कहलाते हैं। सरकार भी समय-समय पर अनेक कार्यक्रम शुरू करके वृक्षारोपण को प्रोत्साहित करती है जिससे हम जीवन-पर्यन्त तक वनों से लाभान्वित होते रहें।

प्रश्न 3.
भारत की हिमालयी क्षेत्र की वनस्पति का वर्णन कीजिए।
उत्तर:
हिमालयी क्षेत्रों में तापमान की कमी तथा ऊँचाई के कारण अन्य भागों की तुलना में वनस्पति में अधिक अन्तर होता है। शिवालिक श्रेणियों में 1000 मीटर की ऊँचाई पर, पर्वतपदीय क्षेत्र, भाबर व तराई में उष्ण कटिबन्धीय पर्णपाती वन पाये जाते हैं। 1000 से 2000 मीटर की ऊँचाई पर आर्द्र शीतोष्ण कटिबन्धीय सदाबहार वन पाये जाते हैं। ये लम्बे पेड़ों से युक्त घने वन हैं। पूर्वी हिमालय में ओक तथा चेस्टनट, पश्चिमी हिमालय में चीड़ तथा 2000 से 3000 मीटर की ऊँचाई वाले भागों में देवदार, सिल्वर, फर, स्यूस कम घने रूप में मिलते हैं। कम ऊँचाई वाले भागों में साल मुख्य वृक्ष है। जहाँ तापमान कम तथा वर्षा 100 सेमी से कम होती है; वहाँ जंगली जैतून, कठोर बबूल एवं कठोर सवाना घास के साथ ओक व देवदार के वृक्ष पाये जाते हैं। 3000 से 4000 मीटर की ऊँचाई पर अल्पाइन वनस्पति पाई जाती है।

प्रश्न 4.
राष्ट्रीय उद्यान एवं अभ्यारण्य में अन्तर स्पष्ट कीजिए।
उत्तर:
राष्ट्रीय उद्यान एवं अभ्यारण्य में अन्तर
राष्ट्रीय उद्यान तुलनात्मक रूप से एक विस्तृत क्षेत्र होता है। यह क्षेत्र मानव के शोषण और अधिग्रहण के द्वारा परिवर्तित नहीं हुआ है। विशिष्ट वैज्ञानिक शिक्षा और मनोरंजन के लिए इसके पेड़-पौधे, जीव-जन्तुओं की प्रजातियों को भू-आकृतिक स्थलों और आवासों के साथ संरक्षित किया गया है। राष्ट्रीय उद्यान में शिकार और चराई पूर्णतया वर्जित होते हैं। राष्ट्रीय उद्यानों में मानवीय हस्तक्षेप पूर्णतया प्रतिबन्धित होता है।

अभ्यारण्य राष्ट्रीय उद्यानों के समान ही होते हैं। ये वन्य प्राणियों को संरक्षित और प्रजातियों को सुरक्षित करने के प्रति समर्पित हैं। अभ्यारण्य में अनुमति के बिना शिकार करना मना है, लेकिन चराई और गौ-पशुओं का आना-जाना नियमित होता रहता है। अभ्यारण्य में मानवीय क्रिया-कलापों की अनुमति होती है।

प्रश्न 5.
भारत में पौधों तथा वनस्पति का वितरण किन तत्वों पर निर्भर करता है? लिखिए।
उत्तर:
भारत में पौधों तथा वनस्पति का वितरण निम्न तत्वों पर निर्भर करता है

• भूमि :
  भूमि का वनस्पति पर प्रत्यक्ष एवं अप्रत्यक्ष प्रभाव पड़ता है। ऊबड़-खाबड़ तथा असमान भू-भाग पर जंगल व घास के मैदान मिलते हैं जो कि वन्य प्राणियों के आश्रय स्थल हैं।
• मिट्टी :
  विभिन्न स्थानों की विभिन्न प्रकार की मिट्टियाँ विविध प्रकार की वनस्पति का आधार है। नदियों के डेल्टाई क्षेत्रों में मैंग्रोव वन, ऊँचे पर्वतों के ढलानों पर शंकुधारी वन पाये जाते हैं। मैदानी क्षेत्र कृषि के लिये अनुकूल है तो पठारी क्षेत्रों में पर्णपाती वन मिलते हैं।
• तापमान :
  प्रत्येक पौधे के अंकुरण, वृद्धि एवं प्रजनन के लिए अनुकूल तापमान की आवश्यकता होती है। उष्ण कटिबन्ध में उच्च तापमान और आर्द्रता के कारण विविध प्रकार के पेड़-पौधे उगते हैं। ऊँचे पर्वतों पर तापमान कम होने के कारण वनस्पति का वर्द्धन काल छोटा होता है।
• सूर्य का प्रकाश :
  सूर्य का प्रकाश अधिक समय तक मिलने के कारण वृक्ष गर्मी की ऋतु में जल्दी बढ़ते हैं। जैसे-हिमालय पर्वतीय क्षेत्र की दक्षिणी ढलानों पर अधिक सूर्यताप मिलने के कारण उत्तरी ढलानों की अपेक्षा अधिक सघन वनस्पति पायी जाती है।
• वर्षा :
  भारी वर्षा वाले क्षेत्रों में बड़े-बड़े पेड़ सघनता में पाये जाते हैं। कम वर्षा वाले क्षेत्रों में बौने वृक्ष, घास तथा झाड़ियाँ पायी जाती हैं। मरुस्थलीय क्षेत्रों में पेड़-पौधों की जड़ें लम्बी होती हैं। थार मरुस्थल की वनस्पति पानी की कमी के कारण काँटेदार होती है।

प्रश्न 6.
सदाबहार वन तथा पर्णपाती वन में अन्तर स्पष्ट कीजिए।
उत्तर:
सदाबहार वन तथा पर्णपाती वन

प्रश्न 7.
उष्ण आर्द्र सदाबहार वनों की प्रमुख विशेषताओं का उल्लेख कीजिए।
उत्तर:

1. ये वन भारत के उन प्रदेशों में पाये जाते हैं जहाँ वार्षिक वर्षा 300 सेमी से अधिक होती है तथा शुष्क ऋतु छोटी होती है।
2. ये वन अत्यधिक घने होते हैं। इनमें पेड़ों की लम्बाई 60 मीटर या इससे अधिक होती है।
3. इन वनों के पेड़ों के नीचे झाड़ियाँ, बेलें, लताएँ आदि का सघन जाल पाया जाता है। घास प्रायः अनुपस्थित होती है।
4. इनके पेड़ों की लकड़ी अधिक कठोर व भारी होती है।
5. वृक्षों में पतझड़ का कोई निश्चित समय नहीं होता है। अतः ये वन सदैव हरे-भरे लगते हैं।
6. भारत में ये वन पश्चिमी घाट के दक्षिणी भाग, केरल, कर्नाटक तथा उत्तर पूर्व की पहाड़ियों में प्रमुखता से पाये जाते हैं।

प्रश्न 8.
मानव के लिये वन किस प्रकार उपयोगी हैं? वर्णन कीजिए।
अथवा
वनों के प्रत्यक्ष लाभ की तुलना में अप्रत्यक्ष लाभ कैसे ज्यादा महत्त्वपूर्ण है? समझाइए।
उत्तर:
वन राष्ट्रीय सम्पदा हैं। यह मानव के लिए विभिन्न प्रकार से उपयोगी हैं। वन उत्पाद व संरक्षण दोनों प्रकार के कार्य करते हुए देश के आर्थिक विकास में योगदान देते हैं। वनों से हमें दो प्रकार के लाभ प्राप्त होते हैं-प्रत्यक्ष लाभ एवं अप्रत्यक्ष लाभ।
(A) प्रत्यक्ष लाभ :

1. वनों से पर्याप्त मात्रा में लकड़ी प्राप्त होती है। वनों की लकड़ियों का उपयोग ईंधन, फर्नीचर, खेल का सामान, दियासलाई तथा कागज आदि वस्तुएँ बनाने में किया जाता है।
2. वनों से अनेक प्रकार के गौण पदार्थ प्राप्त होते हैं, जिनमें बाँस, बेंत, लाख, राल, शहद, गोंद, चमड़ा रंगने के पदार्थ तथा जड़ी-बूटियाँ प्रमुख हैं।
3. वनों से हमें वस्त्र बनाने के लिए रेशम और समूर प्राप्त होता है।
4. खैर नामक वृक्ष से कत्था प्राप्त होता है।
5. वनों से अनेक लोगों को रोजगार प्राप्त होता है।

(B) अप्रत्यक्ष लाभ :

1. वन भूमि के कटाव को रोकते हैं, क्योंकि वृक्ष जल की बूंदों को सीधे भूमि पर गिरने से रोक देते हैं।
2. वनों द्वारा भूमि की उर्वरता में अत्यधिक वृद्धि होती है, क्योंकि वृक्षों की पत्तियाँ, घास व पेड़-पौधे, झाड़ियाँ आदि भूमि पर गिरकर व सड़कर ह्यूमस रूप में भूमि की उर्वरा-शक्ति को बढ़ाते हैं।
3. वन बाढ़ के प्रकोप को रोकते हैं, क्योंकि वृक्ष जल के तीव्र प्रवाह पर रोक लगा देते हैं जिससे जल का प्रवाह मन्द पड़ जाता है।
4. वायु-प्रदूषण भी वन रोकने में महत्त्वपूर्ण भूमिका निभाते हैं।
5. वन वर्षा करने में सहायक होते हैं।
6. वन जलवायु को मृदुल बनाते हैं। वन गर्मी और सर्दी की तीव्रता को कम करने में सहायक होते हैं।
7. वन पक्षियों तथा जीव-जन्तुओं के प्राकृतिक आश्रय स्थल हैं।
8. वन प्राकृतिक सौन्दर्य के प्रतीक हैं।
9. वन प्राकृतिक सन्तुलन के स्रोत हैं।

MP Board Class 9th Social Science Chapter 6 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
भारत के मुख्य वनस्पति प्रकारों का वर्णन कीजिए।
अथवा
भारत में कितने प्रकार के वन पाये जाते हैं। संक्षेप में वर्णन कीजिए।
उत्तर:
(1) उष्ण कटिबन्धीय सदाबहार वन :
इस प्रकार के वन भारत के उन भागों में पाये जाते हैं जहाँ वर्षा का वार्षिक औसत 200 सेमी या उससे अधिक रहता है। ये वृक्ष 60 मीटर या इससे भी अधिक ऊँचाई तक बढ़ जाते हैं। ये वन पश्चिमी घाट, मेघालय तथा उत्तरी-पूर्वी भारत के अन्य भागों में पाये जाते हैं। इस प्रकार के वनों में महोगनी, आबनूस तथा कपूरा जैसे अनेक प्रकार के वृक्ष पाये जाते हैं।

(2) उष्ण कटिबन्धीय पर्णपाती वन :
इस प्रकार के वन भारत के उन क्षेत्रों में पाये जाते हैं जहाँ वर्षा का औसत 75 से 200 सेमी के मध्य रहता है। इन वनों को मानसूनी वन’ भी कहते हैं। इन वनों के दो उपवर्ग हैं –

• आर्द्र पर्णपाती वन
• शुष्क पर्णपाती वन।

प्रथम वर्ग के वनों का विस्तार उत्तर में हिमालय की तराई व भावर प्रदेश, प्रायद्वीप के उत्तर-पूर्वी भागों तथा पश्चिमी घाट के पूर्वी भागों में पाया जाता है। सागौन इन वनों का महत्त्वपूर्ण वृक्ष है। आर्थिक दृष्टि से ये महत्त्वपूर्ण वन हैं। शुष्क पर्णपाती वनों के प्रमुख क्षेत्र दक्षिण-पश्चिमी बिहार, दक्षिणी उत्तर प्रदेश, पश्चिमी मध्य प्रदेश, पूर्वी महाराष्ट्र, गुजरात, कर्नाटक आदि में विस्तृत हैं। साल इन वनों का सर्वाधिक लाभदायक और महत्त्वपूर्ण वृक्ष है। इन्हें पर्णपाती (शुष्क और आर्द्र) इसलिए कहा जाता है क्योंकि ये ग्रीष्म ऋतु में 6 से लेकर 8 सप्ताह तक अपनी पत्तियाँ गिरा देते हैं। प्रत्येक जाति के वृक्षों के पतझड़ का समय अलग-अलग होता है।

(3) कँटीले वन तथा झाड़ियाँ :
इस प्रकार के वन भारत के उन भागों में उगते हैं जहाँ वर्षा का वार्षिक औसत 75 सेमी से कम है। ये वन प्रदेश के उत्तर-पश्चिमी भाग में, दक्षिण में सौराष्ट्र से लेकर उत्तर में पंजाब के मैदानों तक फैले हैं। पूर्व में ये वन उत्तरी मध्य प्रदेश प्रमुख रूप से मालवा का पठार तथा दक्षिण-पश्चिमी उत्तर प्रदेश के बुन्देलखण्ड के पठार पर फैले हैं। इन वनों में कीकर, बबूल, बेर, खजूर, रामबाँस, नागफनी, खजेड़ा आदि वृक्ष अधिक उगते हैं। आर्थिक दृष्टि से ये वन उपयोगी नहीं हैं, केवल खजूर ही उपयोगी है।

(4) पर्वतीय वन :
पर्वतीय क्षेत्रों में तापमान की कमी व ऊँचाई के कारण अन्य भागों की तुलना में वनस्पति में अधिक अन्तर पाया जाता है। शिवालिक श्रेणियों में 1000 मीटर की ऊँचाई पर पर्वतपदीय क्षेत्र, भावर व तराई में उष्ण कटिबन्धीय पर्णपाती वन पाये जाते हैं। 1000 से 2000 मीटर की ऊँचाई पर आर्द्र शीतोष्ण कटिबन्धीय सदाबहार वन पाये जाते हैं। ये लम्बे पेड़ों से युक्त घने वन हैं। पूर्वी हिमालय में ओक तथा चेस्टनट, पश्चिमी हिमालय में चीड़ तथा 2000 से 3000 मीटर की ऊँचाई वाले भागों में देवदार, सिल्वर फर, स्प्रूस कम घने रूप में मिलते हैं। कम ऊँचाई वाले भागों में साल मुख्य वृक्ष है। जहाँ तापमान कम तथा वर्षा 100 सेमी से कम होती है, वहाँ जंगली जैतून, कठोर बबूल एवं कठोर सवाना घास के साथ ओक व देवदार के वृक्ष पाये जाते हैं। 3000 से 4000 मीटर की ऊँचाई पर अल्पाइन वनस्पति पायी जाती है।

(5) मैंग्रोव या ज्वारीय वन :
भारत के तटवर्ती क्षेत्रों में जहाँ ज्वारभाटा आता है, ये वन पाये जाते हैं। इन वनों में ताड़, नारियल मैंग्रोव, नीपा, फोनेक्स, कैसटाइना आदि वृक्षों की प्रधानता होती है। गंगा तथा ब्रह्मपुत्र नदियों के डेल्टा में सुन्दरी वृक्ष पाये जाते हैं। इन वनों में सागरीय जल भरा रहता है। अतः इनमें आने-जाने के लिये नावों का प्रयोग किया जाता है। इन वनों में वृक्षों की छाल खारे जल के कारण नमकीन व कठोर हो जाती है। वृक्षों की लकड़ी का उपयोग नाव बनाने तथा नमकीन छाल का प्रयोग चमड़ा रंगने में किया जाता है।

प्रश्न 2.
वन संसाधनों के संरक्षण की आवश्यकता क्यों है ? उनके संरक्षण के प्रमुख उपाय बताइए।
उत्तर:
वन संसाधनों के संरक्षण की आवश्यकता :
वन राष्ट्रीय सम्पदा हैं। यह मानव के लिये विभिन्न प्रकार से उपयोगी हैं। मनुष्य की आवश्यकताएँ अनन्त होती हैं जबकि उनको पूरा करने के लिये प्रकृति प्रदत्त साधन सीमित हैं। यदि हम इन संसाधनों का तीव्रता से प्रयोग करते जाएँगे तो एक समय पश्चात् इन संसाधनों की कमी हो जाएँगी। अतः संसाधनों की कमी से उत्पन्न समस्याओं को देखते हुए इनका संरक्षण व संवर्द्धन आवश्यक है। इसके साथ-साथ हमें वनों से इमारती लकड़ी, ईंधन की लकड़ी, पशुओं के लिये चारा, लघु व कुटीर उद्योगों के लिये कच्चा माल तथा औषधियों हेतु कच्ची सामग्री प्राप्त होती है। अत: इनका संरक्षण आवश्यक है।

वन संरक्षण के उपाय :
वन संरक्षण हेतु निम्नलिखित उपाय किये गये –

1. सरकार द्वारा क्रियान्वित वन नीति का मुख्य उद्देश्य पर्यावरणीय स्थिरता और पारिस्थितिक सन्तुलन बनाये रखना है।
2. वन संरक्षण कानून-1980 वनों के विनाश तथा वनभूमि का वनों के अतिरिक्त दूसरे कार्यों के लिये उपयोग को रोकना है।
3. वन रोपण एवं बंजर भूमि का विकास।
4. मौजूदा वनों में पुनर्रोपण करना।
5. वनों की नियन्त्रित एवं वैज्ञानिक विधि से कटाई।
6. वनों को आग से बचाना और इसके निरीक्षण के लिये अनुवीक्षण मीनारों की स्थापना करना।
7. ईंधन के लिये वैकल्पिक स्रोत; जैसे-रसोई गैस, सौर चूल्हे आदि का प्रयोग करना।
8. भवन निर्माण में लकड़ी की अपेक्षा लोहा, टिन आदि का प्रयोग करना।
9. पशुचारण और ईंधन हेतु वृक्षों व झाड़ियों की कटाई पर रोक।
10. इमारती लकड़ी के व्यापार को सीमित करना।
11. दीमक, सँडी, झींगुर, गुबरेला जैसे हानिकारक कीटों पर नियन्त्रण।
12. कृषि वानिकी, विस्तार वानिकी, रक्षा पंक्ति वानिकी, वन संरक्षण, चिपको आन्दोलन एवं वन महोत्सव के प्रति लोगों में चेतना विकसित करना।

प्रश्न 3.
वन्य जीवों के संरक्षण के लिये किये गये उपायों को लिखिए।
अथवा
‘वन्य जीवों का संरक्षण’ पर टिप्पणी लिखिए।
उत्तर:
‘वन्य-जीवों का संरक्षण :
वन्य-प्राणी प्रकृति की धरोहर हैं। वन्य जीवों को संरक्षण प्रदान करने के लिए विशेष प्रयास किये जा रहे हैं। संकटापन्न वन्य-जीवों पर विशेष ध्यान दिया जा रहा है। इनकी अब गणना की जाने लगी है। बाघ परियोजना को सफलता मिल चुकी है। असम में गैंडे के संरक्षण की एक विशेष योजना चलायी जा रही है। सिंहों की घटती संख्या चिन्ता का विषय बन गयी है। अत: आरक्षित क्षेत्रों की संख्या और उनके क्षेत्रों के विस्तार पर बल दिया जा रहा है। वन्य-प्राणियों की सुरक्षा के लिए भारत में वन प्राणी संरक्षण क्षेत्रों की स्थापना की गयी है, जहाँ पशु-पक्षियों को प्राकृतिक वातावरण में फलने-फूलने का अवसर प्रदान किया जाता है।

“वर्तमान में संरक्षित क्षेत्र के अन्तर्गत 103 राष्ट्रीय उद्यानों और 535 अभ्यारण्यों की गिनती की जाती है जो देश के एक लाख 56 हजार वर्ग किमी क्षेत्र पर फैले हैं।” देश में प्राणी उद्यानों के प्रबन्धन की देख-रेख के लिए एक केन्द्रीय चिड़ियाघर प्राधिकरण स्थापित किया गया है। यह संस्था 200 से अधिक चिड़ियाघरों के कार्यों में तालमेल रखती है और जानवरों के आदान-प्रदान की वैज्ञानिक ढंग से देख-रेख करती है।

वन्य जीवों के संरक्षण हेतु उपाय-संसार की 5 लाख जीव प्रजातियों में से लगभग 75,000 भारत में है। पक्षियों की लगभग 12,000 प्रजातियाँ एवं 900 उपजातियाँ भारत में विद्यमान हैं। वन्य जीवों के संरक्षण हेतु निम्न उपाय किये गये हैं –

• बाघ परियोजना :
  1 अप्रैल, 1973 को ‘बाघ परियोजना’ की शुरूआत हुई। इस समय देश के 27 अभ्यारण्यों में यह परियोजना चल रही है।
• लाल पांडा परियोजना :
  हिमालय क्षेत्र में संरक्षण करने की परियोजना की शुरूआत वर्ष 1996 . में की। 1 भारत 2017, पृष्ठ 297.
• मणिपुर थामिन (ब्रो ऐन्टलर हिरण) परियोजना :
  1977 में मणिपुर थामिन परियोजना शुरू की गयी।
• गिर सिंह अभ्यारण्य योजना :
  1972 में गुजरात सरकार ने इनके संरक्षण, सुरक्षा एवं सुधार के लिए केन्द्र सरकार के सहयोग से यह परियोजना शुरू की।
• हिमालय कस्तूरी परियोजना :
  भारत सरकार के सहयोग से संरक्षण परियोजना उत्तर प्रदेश के ‘केदारनाथ अभ्यारण्य’ में आरम्भ की गयी।
• हाथी परियोजना :
  यह परियोजना झारखण्ड के सिंहभूमि जिले में 7 दिसम्बर, 1992 को शुरू की गयी।
• मगर प्रजनन परियोजना :
  भारत सरकार ने संयुक्त राष्ट्र विकास कार्यक्रम (यू.एन.डी. पी.) की सहायता से 1975 में उड़ीसा में मगर प्रजनन तथा प्रबन्ध की परियोजना आरम्भ की।
• प्रोजेक्ट हांगुल :
  ‘प्रोजेक्ट हांगुल’ 1970 में शुरू की गयी।
• देश में जीवमण्डल निचय (आरक्षित क्षेत्र) की स्थापना :
  देश में 14 जीवमण्डल निचय स्थापित किये गये हैं। इनमें से सुन्दर वन (पश्चिम बंगाल), नंदादेवी (उत्तराखण्ड), मन्नार की खाड़ी (तमिलनाडु) नीलगिरि (केरल, कर्नाटक तथा तमिलनाडु) की गणना विश्व के जीवमण्डल निचय में की जाती है। अन्य जीवमण्डल नाकरेक, ग्रेट निकोबार, मानस, सिमलीपाल, दिहांग-दिबांग, डिब्रु साइकवोबा, अगस्तमलाई, कंचनजंघा, पंचमढ़ी, अचनकमट-अभटूकंटक हैं।

MP Board Class 9th Social Science Chapter 6 अन्य परीक्षोपयोगी प्रश्न

MP Board Class 9th Social Science Chapter 6 वस्तुनिष्ठ प्रश्न

बहु-विकल्पीय प्रश्न

प्रश्न 1.
कौन-सी औषधीय वनस्पति नहीं हैं? (2008)
(i) तुलसी
(ii) नीम
(iii) सर्पगंधा
(iv) टीक।
उत्तर:
(iv) टीक।

प्रश्न 2.
संसार की 5 लाख जीव प्रजातियों में भारत में कितनी प्रजातियाँ पायी जाती हैं?
(i) 50,000 लगभग
(ii) 5,000 लगभग
(iii) 75,000 लगभग
(iv) 15,000 लगभग।
उत्तर:
(iii) 75,000 लगभग

प्रश्न 3.
बाघ विकास कार्यक्रम परियोजना कब प्रारम्भ की गई?
(i) 1971
(ii) 1973
(iii) 1975
(iv) 19791
उत्तर:
(ii) 1973

प्रश्न 4.
भारत में वन्य जीव सुरक्षा अधिनियम कब पारित हुआ? (2008,09)
(i) 1971
(ii) 1972
(iii) 1970
(iv) 19751
उत्तर:
(ii) 1972

प्रश्न 5.
मगर प्रजनन एवं प्रबन्ध परियोजना कब प्रारम्भ की गई?
(i) 1970
(ii) 1972
(iii) 1975
(iv) 19741
उत्तर:
(iii) 1975

प्रश्न 6.
कान्हा राष्ट्रीय उद्यान मध्य प्रदेश में कहाँ स्थित है? (2017)
(i) जबलपुर
(ii) नरसिंहपुर
(iii) होशंगाबाद,
(iv) मण्डला।
उत्तर:
(iv) मण्डला।

रिक्त स्थान पूर्ति

1. जो वनस्पति मूल रूप से भारतीय है, उसे …………. वनस्पति कहते हैं। (2008, 09)
2. जो वनस्पति भारत के बाहर से आती है, उन्हें …………. वनस्पति कहते हैं। (2008)
3. भारत में प्रथम जीव आरक्षित क्षेत्र …………. में स्थापित किया गया। (2008)
4. ………… में भारत में वन्य जीव सुरक्षा अधिनियम पारित हुआ। (2011)
5. …………. राष्ट्रीय उद्यान में बाघ नहीं पाये जाते हैं। (2008)
6. देश में सिंहों का प्राकृतिक आवास स्थल गुजरात का ………… जंगल है। (2010)
7. कान्हा राष्ट्रीय उद्यान …………. जिले में स्थित है। (2008, 09)
8. सतपुड़ा राष्ट्रीय उद्यान …………. जिले में हैं। (2009, 17)
9. ज्वारीय वन में ………… वृक्ष पाया जाता है। (2013)
10. सुन्दरी वृक्ष ………… में पाया जाता है। (2016)
11. राजस्थान की ………… प्राकृतिक वनस्पति है। (2016)

उत्तर:

1. देशज
2. विदेशज
3. नीलगिरि
4. 1972
5. माधव (शिवपुरी)
6. गिर क्षेत्र
7. मण्डला,
8. होशंगाबाद
9. सुन्दरी
10. मैंग्रोव वन
11. उष्ण कटिबन्धीय कटीले वन।

सत्य/असत्य

प्रश्न 1.
गंगा-ब्रह्मपुत्र डेल्टा में सुन्दरी वृक्ष पाये जाते हैं। (2008)
उत्तर:
सत्य

प्रश्न 2.
जो वनस्पति मूल रूप से भारतीय नहीं है, उसे देशज वनस्पति कहते हैं। (2013)
उत्तर:
असत्य

प्रश्न 3.
आरक्षित वनों में पशुओं को चराने की अनुमति दी जाती है।
उत्तर:
असत्य

प्रश्न 4.
मध्य प्रदेश में 45% क्षेत्र में वन है। (2008)
उत्तर:
असत्य

प्रश्न 5.
तुलसी वनस्पति का जुकाम व खाँसी के लिए उपयोग होता है। (2008)
उत्तर:
सत्य

सही जोड़ी मिलाइए

उत्तर:

1. → (ख)
2. → (ङ)
3. → (घ)
4. → (क)
5. → (ग)
6. → (च)।

एक शब्द/वाक्य में उत्तर

प्रश्न 1.
ऐसे वन जो न तो आरक्षित हैं और न ही सुरक्षित हैं। (2008)
उत्तर:
अवर्गीकृत वन

प्रश्न 2.
ऐसे वन जो एक ऋतु विशेष से पत्ते गिरा देते हैं। (2008, 09, 11)
उत्तर:
पर्णपाती

प्रश्न 3.
भाबर से लगा हुआ अधिक नम तथा दलदली क्षेत्र जहाँ घने वन तथा विविध वन्य जीव पाए जाते हैं। (2010)
उत्तर:
तराई

प्रश्न 4.
वृक्षारोपण को प्रोत्साहन देने का कार्यक्रम। (2009)
उत्तर:
सामाजिक वानिकी

प्रश्न 5.
सुन्दरी वृक्ष पाया जाता है। (2008)
उत्तर:
गंगा, ब्रह्मपुत्र डेल्टा में

प्रश्न 6.
अल्पकाल के लिए आने वाले पक्षी को कहते हैं। (2012, 15)
उत्तर:
प्रवासी पक्षी

प्रश्न 7.
प्रशासनिक आधार पर वनों को कितनी श्रेणियों में रखा गया है? (2013)
उत्तर:
तीन

प्रश्न 8.
भारतीय सिंहों का प्राकृतिक आवास आरक्षित क्षेत्र। (2013)
उत्तर:
गुजरात का गिर क्षेत्र

प्रश्न 9.
राजस्थान की प्राकृतिक वनस्पति है। (2014)
उत्तर:
उष्ण-कटिबन्धीय कँटीले वन

प्रश्न 10.
भारत में सबसे कम वन क्षेत्र वाला राज्य कौन-सा हैं? (2018)
उत्तर:
हरियाणा।

MP Board Class 9th Social Science Chapter 6 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
किसी क्षेत्र की वनस्पति को प्रभावित करने वाले तत्वों का नाम लिखिए।
उत्तर:
किसी क्षेत्र की वनस्पति को प्रभावित करने वाले तत्वों में वर्षा, तापमान, आर्द्रता, मिट्टी, समुद्र तल से ऊँचाई तथा भूगर्भिक संरचना महत्त्वपूर्ण है।

प्रश्न 2.
प्राकृतिक आधार पर वनों को कितने भागों में बाँटा जा सकता है?
उत्तर:
प्राकृतिक आधार पर वनों को पाँच भागों में बाँटा जा सकता है –

1. उष्ण कटिबन्धीय सदाबहार वन
2. उष्ण कटिबन्धीय पर्णपाती वन
3. पर्वतीय वन
4. मैंग्रोव वन
5. उष्ण कटिबन्धीय कँटीले वन।

प्रश्न 3.
उन वन्य प्राणियों के नाम लिखिए जो अब विलुप्त होने के कगार पर हैं?
उत्तर:
गैंडा, चीता, शेर, सोहन चिड़िया आदि वन्य प्राणी अब विलुप्त होने के कगार पर हैं।

प्रश्न 4.
भारत की वनस्पति में इतनी विविधता क्यों हैं? (2015)
उत्तर:
दक्षिण से लेकर उत्तर ध्रुव तक विविध प्रकार की जलवायु के कारण भारत में अनेक प्रकार की वनस्पतियाँ पाई जाती हैं जो समान आकार के अन्य देशों में बहुत कम मिलती हैं। यहाँ लगभग 46,000 प्रकार के पेड़-पौधे पाए जाते हैं।

प्रश्न 5.
पारिस्थितिक तन्त्र से क्या तात्पर्य है?
उत्तर:
भौतिक पर्यावरण और उसमें रहने वाले जीवों के सम्मिलित रूप को पारिस्थितिक तन्त्र या पारितन्त्र कहते हैं।

प्रश्न 6.
भाबर किसे कहते हैं?
उत्तर:
हिमालय क्षेत्र की पहाड़ियों के गिरीपाद प्रदेश में कंकड़ पत्थरों की एक पतली पेटी नदी की धारा के समानान्तर फैली है जो लगभग 8 से 16 किमी चौड़ी है, वह भाबर कहलाती है।

प्रश्न 7.
सागौन, बबूल, खैर और चन्दन वृक्षों का एक-एक मुख्य उपयोग लिखिए।
उत्तर:

1. बबूल – दन्त मंजन
2. सागौन – इमारती लकड़ी व फर्नीचर
3. खैर – कत्था
4. चन्दन – अगरबत्ती।

प्रश्न 8.
भारत के प्रमुख राष्ट्रीय उद्यानों के नाम लिखिए और बताइए कि ये किन-किन प्रदेशों में स्थित हैं? 1 भारत 2017, पृष्ठ 5 व 6
उत्तर:

1. काजीरंगा-असम
2. रणथम्भौर-राजस्थान
3. बांधवगढ़-मध्य प्रदेश
4. कान्हा किसली-मध्य प्रदेश
5. माधव (शिवपुरी)-मध्य प्रदेश
6. नन्दादेवी-उत्तराखण्ड।

प्रश्न 9.
मनुष्य के जीवित रहने के लिये पारितन्त्र का संरक्षण क्यों आवश्यक है?
उत्तर:
पारितन्त्र का विकास लाखों :
करोड़ों वर्षों में हुआ है। पारितन्त्र के अन्तर्गत आने वाले पौधों तथा जीव-जन्तुओं में गहरा सम्बन्ध होता है। मानव भी अपने अस्तित्व एवं विकास के लिये पारितन्त्र के जीव-जन्तुओं और वनस्पति पर आश्रित हो जाता है। पारितन्त्र से छेड़छाड़ करने से अत्यन्त गम्भीर परिणाम हो सकते हैं अतः पारितन्त्र का संरक्षण आवश्यक है।

MP Board Class 9th Social Science Chapter 6 लघु उत्तरीय प्रश्न

प्रश्न 1.
भारतीय वनस्पति के प्रमुख कटिबन्धों के नाम लिखिए। ज्वारीय वन का वर्णन कीजिए।
उत्तर:
भारतीय वनस्पति के चार प्रमुख कटिबन्ध निम्नलिखित हैं :

1. उष्ण कटिबन्धीय वर्षा वन
2. उष्ण कटिबन्धीय पर्णपाती वन
3. कँटीले वन तथा झाड़ियाँ
4. ज्वारीय वन।

ज्वारीय वन :
ये वन तट के सहारे नदियों के ज्वारीय क्षेत्र में पाये जाते हैं। ज्वारीय क्षेत्र में मिलने के कारण इन वनों को ज्वारीय वन कहा जाता है। इन वनों में ताड़, नारियल, मैंग्रोव, नीपा, फोनेक्स, कैज्युराइना आदि के वृक्षों की प्रधानता होती है। गंगा तथा ब्रह्मपुत्र नदियों के डेल्टा में सुन्दरी नामक वृक्ष पाये जाते हैं। इन वनों में सागरीय जल भरा रहता है, अतः इनमें आने-जाने के लिए नावों का प्रयोग किया जाता है। इन वनों के वृक्षों की छाल खारे जल के प्रभाव से नमकीन तथा लकड़ी कठोर हो जाती है। इन वृक्षों की कठोर लकड़ी का उपयोग नाव बनाने तथा नमकीन छाल का उपयोग चमड़ा रंगने में किया जाता है।

प्रश्न 2.
वनस्पति तथा जीव-जन्तु में अन्तर स्पष्ट कीजिए।
उत्तर:
वनस्पति तथा जीव-जन्तु

प्रश्न 3.
भारत में प्रायः औषधि के लिये प्रयोग होने वाले कुछ प्रमुख पादप-सर्पगंधा, तुलसी, नीम, जामुन, बबूल, कचनार व अर्जुन के उपयोग बताइए।
उत्तर:

1. सर्पगंधा-रक्तचाप के निदान के लिए
2. तुलसी-जुकाम और खाँसी के लिए
3. नीम-जैव व जीवाणु प्रतिरोध हेतु
4. जामुन-पाचन क्रिया को ठीक करने, मधुमेह में उपयोगी
5. बबूल-फुन्सी में लाभदायक व शारीरिक शक्ति में वृद्धि हेतु उपयोगी
6. कचनार-फोड़ा व दमा रोग के लिये उपयोगी
7. अर्जुन-कान का दर्द ठीक करने व रक्तचाप को नियन्त्रित करने के लिए।

प्रश्न 4.
प्रायद्वीपीय पर्वतीय वनों की विशेषताओं का वर्णन कीजिए।
उत्तर:

1. इन वनों में अधिक ऊँचाई वाले भागों में अविकसित वनों या झाड़ियों के साथ खुली हुई विकसित तरंगित घास भूमि पायी जाती है।
2. इन वनों में पेड़ों के नीचे वनस्पति का जाल पाया जाता है। इसमें परपोषी पौधे, काई व बारीक पत्तियों वाले पौधे प्रमुख होते हैं।
3. ये वन नीलगिरि, अन्नामलाई, पालनी, पश्चिमी घाट व महाबलेश्वर, सतपुड़ा व मैकल पहाड़ियों पर पाये जाते हैं।
4. इन वनों में पाया जाने वाले मैग्लोनिया, लारेल, एल्म सामान्य वृक्ष हैं। जबकि सिनकोना व यूकेलिप्टस वृक्षों को विदेश से लाकर लगाया गया है।

प्रश्न 5.
आर्द्र तथा शुष्क पर्णपाती वन में अन्तर स्पष्ट कीजिए।
उत्तर:
आर्द्र तथा शुष्क पर्णपाती वन

प्रश्न 6.
“वन पर्यावरण के महत्त्वपूर्ण अंग हैं।” इस कथन को स्पष्ट कीजिए।
अथवा
पर्यावरण सन्तुलन के लिए वन क्यों आवश्यक हैं? कोई चार कारण बताइए।
उत्तर:
वनों एवं पर्यावरण में घनिष्ठ सम्बन्ध है। यह निम्न तथ्यों से स्पष्ट है –

1. वन वायुमण्डल को शुद्ध रखते हैं और वायु प्रदूषण को कम करते हैं।
2. वन वायुमण्डल को ऑक्सीजन प्रदान करते हैं।
3. वन वायु के तापमान को बनाये रखते हैं, जिससे वर्षा होती है।
4. वन जलवायु को सम रखते हैं।
5. वन जल के बहाव को रोकते हैं, जिससे भूमि का कटाव रुक जाता है तथा भूगर्भीय जल-स्तर में वृद्धि होती है।

प्रश्न 7.
जीव-आरक्षित क्षेत्र (बायोस्फीयर रिजर्व) किसे कहते हैं? ऐसे दो क्षेत्रों के नाम बताइए। (2015)
उत्तर:
भारत में जैव-विविधता की सुरक्षा के लिए अनेक प्रयास किये जा रहे हैं। इस योजना के अन्तर्गत नीलगिरि में भारत का प्रथम जीव-आरक्षित क्षेत्र (बायोस्फीयर रिजर्व) स्थापित किया गया है। यह कर्नाटक, तमिलनाडु और केरल के सीमावर्ती क्षेत्रों में फैला है। इसका क्षेत्रफल 5500 वर्ग किमी है। इस योजना के अन्तर्गत प्रत्येक जन्तु तथा पौधे का रक्षण अनिवार्य है। इसकी स्थापना 1986 में की गयी थी। उत्तराखण्ड के हिमालय क्षेत्र में नन्दादेवी का जीव-आरक्षित क्षेत्र 1988 में स्थापित किया गया था।

प्रश्न 8.
पारिस्थितिक सन्तुलन के लिए वन क्यों आवश्यक हैं?
अथवा
वन संरक्षण क्यों आवश्यक है?
उत्तर:
वनों को काटे जाने के कारण पर्यावरण प्रदूषित हुआ है तथा पारिस्थितिकी में भी परिवर्तन आया है। इसी प्रकार वर्तमान युग में अधिकांश देशों में वनों का क्षेत्रफल कम हो रहा है। इस कमी के कारण भू-अपरदन, अनावृष्टि, बाढ़ आदि समस्याएँ आज मानव के समक्ष आ खड़ी हैं। अतः वायु प्रदूषण की समस्या आज के मानव के सामने सबसे बड़ी समस्या के रूप में उपस्थित हुई है। इसी कारण वन-संरक्षण पारिस्थितिक सन्तुलन के लिए आवश्यक है।

प्रश्न 9.
वनों के विनाश के क्या कारण हैं?
उत्तर:
वनों के विनाश के कारण –

1. जनसंख्या में तीव्र वृद्धि होने से कृषि भूमि की प्राप्ति के लिए वनों को काटकर खेती की जा रही है।
2. इमारती लकड़ी और चारे की बढ़ती माँग तथा वन्य भूमि के खेती के लिए उपयोग से वनों पर जबरदस्त प्रभाव पड़ा रहा है।
3. ईंधन के रूप में प्रयोग करने हेतु लकड़ी काटी जा रही है।
4. आवागमन के साधनों, रेल, सड़क मार्गों के विकास हेतु वनों को काटा जा रहा है।
5. आवास समस्या की पूर्ति के लिए वनों को काटकर रिहायशी भूमि का विस्तार किया जा रहा है।

प्रश्न 10.
कँटीले वनों की प्रमुख विशेषताएँ बताइए।
उत्तर:
जिन क्षेत्रों में 70 सेमी से भी कम वार्षिक वर्षा होती है। वहाँ कँटीले वन तथा झाड़ियाँ पायी जाती हैं। इस प्रकार की वनस्पति देश के उत्तर-पश्चिमी भागों में पायी जाती है। इसकी प्रमुख विशेषताएँ निम्न हैं –

1. इन वनों के वृक्षों का आकार छोटा, पत्तियाँ छोटी तथा जड़ें लम्बी होती हैं।
2. इन वनों के कीकर, बबूल, खैर तथा खजूर उपयोगी वृक्ष हैं।
3. इन वनों में वृक्ष दूर-दूर पाये जाते हैं।
4. कँटीली झाड़ियों में चूहे, खरगोश, लोमड़ी, भेड़िये, जंगली गधा, घोड़े, ऊँट तथा सिंह पाये जाते हैं।

MP Board Class 9th Social Science Chapter 6 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
मध्य प्रदेश में पाये जाने वाले जीव-जन्तुओं व प्रमुख वन्य-जीव अभ्यारण्यों के नाम लिखिए।
अथवा
मध्य प्रदेश में पाये जाने वाले जीव-जन्तुओं व प्रमुख राष्ट्रीय उद्यानों का वर्णन कीजिये।
उत्तर:
वन सम्पदा की दृष्टि से मध्य प्रदेश सम्पन्न राज्य है। यहाँ कुल भूमि का लगभग 30 प्रतिशत भाग वनों से घिरा हुआ है जिसमें विभिन्न प्रकार के वन्य-पशु एवं जीव-जन्तु पाये जाते हैं। मध्य प्रदेश के प्रमुख वन्य-पशु, जीव व पक्षी, काला हिरण, तेंदुआ, चिंकारा, बन्दर, गौर, नीलगाय, चीतल, साँभर, शेर, भालू, घड़ियाल, मगर, कछुआ, सोन चिड़िया, खरमौर आदि हैं। इन वन्य पशुओं, जीवों व पक्षियों को सुरक्षित आवास उपलब्ध कराने एवं प्रजातीय सुरक्षा हेतु वन्य जीव अभ्यारण्य एवं राष्ट्रीय उद्यान विकसित किये गये हैं जिनमें प्रमुख निम्नलिखित हैं –
मध्य प्रदेश के राष्ट्रीय उद्यान

मध्य प्रदेश के वन्य जीव अभ्यारण्य

MP Board Class 9th Social Science Solutions

MP Board Class 9th Maths Solutions Chapter 14 सांख्यिकी Ex 14.4

प्रश्न 1.
एक टीम ने फुटबॉल के 10 मैचों में निम्नलिखित गोल किए :(2018, 19)
2, 3, 4, 5, 0, 1, 3, 3, 4, 3.
इन गोलों के माध्य, माध्यक और बहुलक ज्ञात कीजिए।
हल :
आँकड़ों को आरोही क्रम में लगाने पर हम पाते हैं कि :
0, 1, 2, 3, 3, 3, 3, 4, 4, 5.

बहुलक = अधिकतम बारम्बारता वाला प्रेक्षण = 3
अत: अभीष्ट माध्य = 2.8, माध्यक = 3 एवं बहुलक = 3.

प्रश्न 2.
गणित की परीक्षा में 15 विद्यार्थियों ने (100 में से) निम्नलिखित अंक प्राप्त किए :
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60.
इन आँकड़ों के माध्य, माध्यक और बहुलक ज्ञात कीजिए। (2019)
हल :
आँकड़ों को आरोही क्रम में व्यवस्थित करने पर,
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98.

बहुलक = अधिकतम बारम्बारता वाला प्रेक्षण = 52
अतः अभीष्ट माध्य = 54.8, माध्यक = 52 एवं बहुलक = 52..

प्रश्न 3.
निम्नलिखित प्रेक्षणों को आरोही क्रम में व्यवस्थित किया गया है। यदि आँकड़ों का माध्यक 63 हो, तो x का मान ज्ञात कीजिए:
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95.
हल :
चूँकि

अत: का अभीष्ट मान = 62.

प्रश्न 4.
आँकड़ों 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18 का बहुलक ज्ञात कीजिए। (2018, 19)
हल :
आँकड़ों को आरोही क्रम में व्यवस्थित करने पर,
14, 14, 14, 14, 17, 18, 18, 18, 22, 23, 25, 28
बहुलक = अधिकतम बारम्बारता वाला प्रेक्षण = 14
अतः अभीष्ट बहुलक = 14.

प्रश्न 5.
निम्न सारणी से एक फैक्टरी में काम कर रहे 60 कर्मचारियाँ का माध्य वेतन ज्ञात कीजिए:

हल:


अत: 60 कर्मचारियों का अभीष्ट माध्य वेतन = Rs 508.33.

प्रश्न 6.
निम्न स्थिति पर आधारित एक उदाहरण दीजिए :
(i) माध्य ही केन्द्रीय प्रवृत्ति का उपयुक्त माप है।
(ii) माध्य केन्द्रीय प्रवृत्ति का उपयुक्त माप नहीं है जबकि माध्यक एक उपयुक्त माप है।
हल :
(i) मैरी और हरि के एक परीक्षा में पूछे गए 5 प्रश्नों में प्राप्तांक निम्न प्रकार हैं :
मैरी के प्राप्तांक 10, 8, 9, 8, 7
माध्य = \(\frac{\sum x}{n}=\frac{42}{5}=8 \cdot 4\)
एवं हरि के प्राप्तांक 4, 7, 10, 10, 10
माध्य = \(\frac{\sum x}{n}=\frac{41}{5}=5 \cdot 8.2\)
अतः मैरी का प्रदर्शन हरि से अच्छा है।

(ii) उपर्युक्त उदाहरण में मैरी और हरि के प्राप्तांकों को आरोही क्रम में व्यवस्थित करने पर,
मैरी के प्राप्तांक 7, 8, 8, 9, 10
माध्यक = तीसरा पद = 8
एवं हरि के प्राप्तांक 4, 7, 10, 10, 10
माध्यक = तीसरा पद = 10
अतः हरि का प्रदर्शन मैरी से अच्छा है।

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.5

प्रश्न 1.
माचिस की डिब्बी का माप 4 cm x 2.5 cm x 1.5 cm है। ऐसी 12 डिब्बियों के एक पैकेट का आयतन क्या होगा?
हल :
चूँकि एक माचिस की डिब्बी का आयतन V = 4 cm x 2.5 cm x 1.5 cm = 15 cm³
⇒ 12 डिब्बियों के एक पैकेट का आयतन = 12 x 15 = 180 cm³
अत: माचिस की डिब्बियों के पैकेट का अभीष्ट आयतन = 180 cm³.

प्रश्न 2.
एक घनाभाकार पानी की टंकी 6 m लम्बी, 5 m चौड़ी और 4.5 m गहरी है। इसमें कितने लिटर पानी आ सकता है ? (1 m³ = 1000 लीटर) (2019)
हल :
पानी की टंकी की धारिता = 6 x 5 x 4.5 = 135 m³
⇒ 135 x 1000 लीटर = 1,35,000 लीटर
अतः पानी की टंकी में अभीष्ट = 1,35,000 लीटर पानी आ सकता है।

प्रश्न 3.
एक घनाभाकार बर्तन 10 m लम्बा और 8 m चौड़ा है। इसको कितना ऊँचा बनाया जाए कि इसमें 380 घनमीटर द्रव आ सके।
हल :
मान लीजिए बर्तन की ऊँचाई h m रखी जाए।
चूँकि घनाभाकार बर्तन की धारिता = लम्बाई x चौड़ाई x ऊँचाई
380 = 10 x 8 x h ⇒ h = \(\frac { 380 }{ 10\times 8 }\) = 4.75 m
अत: बर्तन की अभीष्ट ऊँचाई = 4.75 m रखी जाए।

प्रश्न 4.
8 m लम्बा, 6 m चौड़ा और 3 m गहरा एक घनाभाकार गड्डा खुदवाने में Rs 30 प्रति m³ की दर से होने वाला व्यय ज्ञात कीजिए। (2019)
हल :
गड्डे का आयतन V = 8 m x 6 m x 3 m = 144 m³
खुदवाने का व्यय = दर x क्षेत्रफल = 30 x 144 = Rs 4,320
अत: गड्डा खुदवाने में अभीष्ट व्यय = Rs 4,320.

प्रश्न 5.
एक घनाभाकार टंकी की धारिता 50,000 लीटर पानी की है। यदि इस टंकी की लम्बाई और गहराई क्रमशः 2.5 m और 10 m है, तो इसकी चौड़ाई ज्ञात कीजिए।
हल :
दिया है : टंकी की धारिता V = 50,000 लीटर ⇒ V = 50 m³, लम्बाई l = 2.5 m, गहराई d = 10 m
पतन) V = l x b x h
⇒ 50 = 2.5 x b x 10 ⇒ b = \(\frac { 50 }{ 25 }\) = 2 m
अतः टंकी की अभीष्ट चौड़ाई = 2 m.

प्रश्न 6.
एक गाँव जिसकी जनसंख्या 4000 है, को प्रतिदिन प्रति व्यक्ति 150 लीटर पानी की आवश्यकता है। इस गाँव में 20 m x 15 m x 6 m मापों वाली एक टंकी बनी हुई है। इस टंकी का पानी वहाँ कितने दिन के लिए पर्याप्त होगा ?
हल :
टंकी की धारिता = 20 m x 15 m x 6 m = 1800 m³
⇒ धारिता (लीटर में) = 1800 x 1000 = 18,00,000 लीटर
एक दिन में जल की आवश्यकता = 4000 x 150 = 6,00,000 लीटर

अतः टंकी का पानी अभीष्ट 3 दिन के लिए पर्याप्त होगा।

प्रश्न 7.
किसी गोदाम की माप 40 m x 25 m x 15 m है। इस गोदाम में 1.5 m x 1.25 m x 0.5 m की माप वाली लकड़ी की कितनी अधिकतम क्रेट (crate) रखी जा सकती हैं?
हल :
चूँकि गोदाम की धारिता V = 40 m x 25 m x 15 m = 15,000 m³
एवं एक क्रेट का आयतन V1 = 1.5 m x 1.25 m x 0.5 m = 0.9375 m³

अतः क्रेटों की अभीष्ट संख्या = 16,000.

प्रश्न 8.
12 cm भुजा वाले एक ठोस घन को बराबर आयतन वाले 8 घनों में काटा जाता है। नए घन की भुजा क्या होगी ? साथ ही इन दोनों घनों के पृष्ठीय क्षेत्रफलों का अनुपात भी ज्ञात कीजिए। हल :
माना नए घन की भुजा = a cm
प्रश्नानुसार, (12)³ = 8a³ ⇒ a³ = \(\frac{12 \times 12 \times 12}{8}\) = (6)³ ⇒ a = 6 cm

अतः नए घन की अभीष्ट भुजा = 6 cm एवं उनके पृष्ठों के क्षेत्रफल का अनुपात = 4:1.

प्रश्न 9.
3 m गहरी और 40 m चौड़ी एक नदी 2 किमी प्रति घण्टा की चाल से बहकर समुद्र में गिरती है। एक मिनट में समुद्र में कितना पानी गिरेगा ?
हल :
1 मिनट में नदी द्वारा तय की गई दूरी l = \(\frac { 2000 }{ 60 }\) मीटर [∵ वेग = 2 किमी/घण्टा]
1 मिनट में समुद्र में नदी द्वारा गिरा पानी = \(\frac { 2000 }{ 60 }\) x 3 x 40 = 4,000 m³
अतः 1 मिनट में नदी द्वारा समुद्र में 4,000 m³ पानी गिरेगा।

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 14 सांख्यिकी Ex 14.3

प्रश्न 1.
एक संगठन ने पूरे विश्व में 15 – 44(वर्षों में) की आयु वाली महिलाओं में बीमारी और मृत्यु के कारणों का पता लगाने के लिए किए गए सर्वेक्षण में निम्नलिखित आँकड़े (% में) प्राप्त किए :
(i) ऊपर दी गई सूचनाओं को आलेखीय रूप में निरूपित कीजिए।
(ii) कौन-सी अवस्था पूरे विश्व की महिलाओं के खराब स्वास्थ्य और मृत्यु का बड़ा कारण हैं ?
(iii) अपनी अध्यापिका की सहायता से ऐसे दो कारणों का पता लगाने का प्रयत्न कीजिए जिनकी ऊपर (ii) में मुख्य भूमिका रही हो।
हल :
(i) अभीष्ट आलेख :

(ii) जनन स्वास्थ अवस्था
(iii) तन्त्रिका मनोविकारी अवस्था एवं अन्य कारण।

प्रश्न 2.
भारतीय समाज के विभिन्न क्षेत्रों में प्रति हजार लड़कों पर लड़कियों की (निकटतम 10 तक की) संख्या के आँकड़े नीचे दिए गए हैं :

(i) ऊपर दी गई सूचनाओं को एक दण्ड आलेख द्वारा निरूपित कीजिए।
(ii) कक्षा में चर्चा करके बताइए कि आप इस ओलख से कौन-कौन से निष्कर्ष निकाल सकते हैं?
हल :
(i) अभीष्ट दण्ड आलेख :

(ii) अनुसूचित जनजातियों में लड़कियों का लड़कों में अनुपात गैर-अनुसूचित जाति/जनजाति एवं अनुसूचित जातियों की अपेक्षा अच्छा है। इसी प्रकार पिछड़े जिलों में गैर-पिछड़े जिलों से तथा ग्रामीण क्षेत्रों में शहरी क्षेत्रों की अपेक्षा लड़कियों और लड़कों का अनुपात अच्छा है।

प्रश्न 3.
एक राज्य के विधान सभा के चुनाव में विभिन्न राजनैतिक पार्टियों द्वारा जीती गई सीटों के परिणाम नीचे दिए गए हैं : (2019)

(i) मतदान के परिणमों को निरूपित करने वाला दण्ड आलेख खींचिए।
(ii) किस राजनैतिक पार्टी ने सर्वाधिक (अधिकतम) सीटें जीती हैं ?
(iii) किस राजनैतिक पार्टी ने न्यूनतम सीटें जीती हैं?
हल :
(i) अभीष्ट दण्ड आलेख :

(ii) राजनैतिक पार्टी A ने अधिकतम सीटें जीती हैं।
(iii) राजनैतिक पार्टी E ने न्यूनतम सीटें जीती हैं।

प्रश्न 4.
एक पौधे की 40 पत्तियों की लम्बाइयाँ एक मिलीमीटर तक शुद्ध मापी गई और प्राप्त आँकड़ों को निम्नलिखित सारणी में निरूपित किया गया है :

(i) दिए हुए आँकड़ों को निरूपित करने वाला एक आयत चित्र खींचिए।
(ii) क्या इन्हीं आँकड़ों को निरूपित करने वाला कोई अन्य उपयुक्त आलेख है ?
(iii) क्या यह सही निष्कर्ष है कि 153 मिलीमीटर लम्बाई वाली पत्तियों की संख्या सबसे अधिक है ? क्यों ?
हल :
(i) संतत वर्ग सारणी बनाने पर हम प्राप्त करते हैं :

अभीष्ट आयत चित्र :

(ii) हाँ, इन आकड़ों को निरूपित करने वाला अन्य उपलब्ध आलेख बारम्बारता बहुभुज है।
(iii) यह निष्कर्ष सही नहीं है, गलत है क्योंकि पत्तियों की सर्वाधिक संख्या 153 मिली लम्बाई की न होकर 144.5 मिली से 153.5 मिली के बीच है।

प्रश्न 5.
नीचे की सारणी में 400 नियॉन लैम्पों के जीवन काल दिए गए हैं (2018, 19)

(i) एक आयत चित्र की सहायता से दी हुई सूचनाओं को निरूपित कीजिए।
(ii) कितने लैम्पों के जीवनकाल 700 घण्टों से अधिक है ?
हल :
(i) अभीष्ट आयत चित्र :

(ii) 700 घण्टों से अधिक जीवनकाल वाले लैम्पों की संख्या = 74 + 62 + 48 = 184
अत: अभीष्ट लैम्पों की संख्या = 184

प्रश्न 6.
नीचे की दो सारणियों में प्राप्त किए गए अंकों के अनुसार दो सेक्शनों के विद्यार्थियों का बंटन किया गया है:

दो बारम्बारता बहुभुजों की सहायता से एक ही आलेख पर दोनों सेक्शनों के विद्यार्थियों के प्राप्तांक निरूपित कीजिए। दोनों बहुभुजों का अध्ययन करके दोनों सेक्शनों के निष्पादनों की तुलना कीजिए।
हल :
अभीष्ट बारम्बारता बहुभुज :

20 अंक प्राप्त करने तक सेक्शन ‘B’ के छात्रों की संख्या सेक्शन ‘A’ के छात्रों से अधिक है, लेकिन इसके बाद अधिक अंक पाने के लिए सेक्शन ‘A’ की छात्र संख्या सेक्शन ‘B’ की छात्र संख्या से अधिक हो जाती है।

प्रश्न 7.
एक क्रिकेट मैच में दो टीमें ‘A’ और ‘B’ द्वारा प्रथम 60 गेंदों में बनाए गए रन नीचे दिए गए हैं : गेंदों की संख्या टीम ‘A’

बारम्बारता बहुभुजों की सहायता से एक ही आलेख पर दोनों टीमों के आँकड़े निरूपित कीजिए।
हल :
वर्ग अन्तरालों को संतत बनाने पर,

अभीष्ट बारम्बारता बहुभुज :

प्रश्न 8.
एक पार्क में खेल रहे विभिन्न आयु वर्गों के बच्चों की संख्या का एक यादृच्छिक सर्वेक्षण (random survey) करने पर निम्नलिखित आँकड़े प्राप्त हुए :

हल:

अभीष्ट आयत चित्र :

प्रश्न 9.
एक स्थानीय टेलीफोन निर्देशिका से 100 कुलनाम (surname) यादृच्छया लिए गए और उनसे वर्णमाला के अक्षरों की संख्या का निम्न बारम्बारता बंटन प्राप्त किया गया :

दी हुई सूचनाओं को निरूपित करने वाला एक आयत चित्र खींचिए एवं वह वर्ग अन्तराल बताइए जिसमें अधिकतम संख्या में कुलनाम हैं।
हल:

अभीष्ट आयत चित्र :

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 11 रचनाएँ Ex 11.2

प्रश्न 1.
एक त्रिभुज ABC की रचना कीजिए जिसमें BC = 7 cm, ∠B = 75° और AB + AC = 13 cm है। (2018, 19)
हल:
रचना :

चित्र 11.18
(i) BC = 7 cm का रेखाखण्ड खींचिए।
(ii) रेखाखण्ड BC के बिन्दु B पर ∠DBC = 75° का कोण बनाते हुए एक किरण BX खींचिए।
(iii) किरण BX में से BD = 13 cm का रेखाखण्ड लीजिए।
(iv) DC को मिलाइए।
(v) DC का लम्ब समद्विभाजक EF खींचिए।
(vi) जो BD को बिन्दु A पर प्रतिच्छेद करता है।
(vii) AC को मिलाइए।
यही ∆ABC अभीष्ट त्रिभुज है।

प्रश्न 2.
एक त्रिभुज ABC की रचना कीजिए जिसमें BC = 8 cm, ∠B = 45° और AB – AC = 3.5 cm है।
हल:
रचना :

चित्र 11.19
(i) BC = 8 cm का एक रेखाखण्ड खींचिए।
(ii) BC के साथ बिन्दु B पर ∠DBC = 45° का कोण बनाते हुए किरण BX खींचिए।
(iii) किरण BX में से BD = 3.5 cm का रेखाखण्ड लीजिए।
(iv) DC को मिलाइए।
(v) DC का लम्ब समद्विभाजक EF खींचिए जो Bx को B बिन्दु A पर प्रतिच्छेद करता है।
(vi) AC को मिलाइए।
यही ∆ABC अभीष्ट त्रिभुज है।

प्रश्न 3.
एक त्रिभुज PQR की रचना कीजिए जिसमें OR = 6 cm, ∠Q= 60° और PR – PQ = 2 cm हो।
हल:
रचना :

चित्र 11.20
(i) एक रेखाखण्ड QR = 6 cm खींचिए।
(ii) रेखाखण्ड QR के साथ 60° का कोण बनाते हुए किरण Qx खींचिए।
(iii) QS = 2 cm का एक रेखाखण्ड किरण Qx में से काटिए।
(iv) SR को मिलाइए।
(v) SR का लम्ब समद्विभाजक AB खींचिए जो Qx को बिन्दु P पर प्रतिच्छेद करता है।
(vi) PR को मिलाइए। यही ∠∆POR अभीष्ट त्रिभुज है।

प्रश्न 4.
एक त्रिभुज XYZ की रचना कीजिए जिसमें ∠Y = 30°, ∠Z = 90° और XY+ YZ + ZX = 11 cm हो।
हल:
रचना:

चित्र 11.21
(i) एक रेखाखण्ड PO = 11 cm खींचिए।
(ii) बिन्दु P पर 30° एवं बिन्दु O पर 90° का कोण बनाते हुए किरण PR एवं Qs खींचिए।
(iii) ∠RPO एवं ∠SOP के समद्विभाजक खींचिए जो परस्पर बिन्दु X पर प्रतिच्छेद करते हैं।
(iv) PX एवं QX के लम्ब समद्विभाजक खींचिए जो PQ को क्रमशः Y और Z बिन्दुओं पर प्रतिच्छेद करते हैं।
(v) XY एवं XZ को मिलाइए। यही ∆XYZ अभीष्ट त्रिभुज है।

प्रश्न 5.
एक समकोण त्रिभुज की रचना कीजिए जिसका आधार 12 cm और कर्ण तथा अन्य भुजा का योग 18 cm है।
हल:
एक समकोण ∆ABC की रचना करनी है जिसका ∠B समकोण है, आधार BC = 12 cm है तथा कर्ण AC + भुजा AB = 18 cm.
रचना:

चित्र 11.22
(i) BC = 12 cm का एक रेखाखण्ड खींचिए।
(ii) BC के बिन्दु B पर BC के साथ समकोण (90° का कोण) बनाते हुए एक किरण BP खींचिए।
(iii) किरण BP में से BD = 18 cm का एक रेखाखण्ड काटिए।
(iv) DC को मिलाइए।
(v) DC का लम्ब समद्विभाजक OR खींचिए जो BD को बिन्दु A पर प्रतिच्छेद करता है।
(vi) AC को मिलाइए।
यह ∆ABC अभीष्ट समकोण त्रिभुज है।

MP Board Class 9th Maths Solutions

MP Board Class 9th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.4

प्रश्न 1.
निम्न त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए :
(i) 10.5 cm (2018)
(ii) 5.6 cm
(iii) 14 cm.
हल :
(i) गोले का पृष्ठीय क्षेत्रफल = 4πR² = 4 x \(\frac { 22 }{ 7 }\) x (10.5)²
= 88 x 10.5 x 1.5
= 1386 cm²
अतः गोले का अभीष्ट पृष्ठीय क्षेत्रफल = 1386 cm².

(ii) गोले का पृष्ठीय क्षेत्रफल = 4πR² = 4 x \(\frac { 22 }{ 7 }\) x (5.6)²
= 88 x 5.6 x 0.8
= 394.24 cm²
अतः गोले का अभीष्ट पृष्ठीय क्षेत्रफल = 394.24 cm².

(iii) गोले का पृष्ठीय क्षेत्रफल = 4πR² = 4 x \(\frac { 22 }{ 7 }\) x (14)²
= 88 x 28
= 2464 cm²
अतः गोले का अभीष्ट पृष्ठीय क्षेत्रफल = 2464 cm².

प्रश्न 2.
निम्न व्यास वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए:
(i) 14 cm
(ii) 21 cm
(iii) 3.5 m.
हल :
(i) गोले का व्यास d = 14 cm (दिया है)
⇒ R = \(\frac { 14 }{ 2 }\) = 7 cm
गोले का पृष्ठीय क्षेत्रफल = 4πR² = 4 x \(\frac { 22 }{ 7 }\) x (7)² = 616 cm²
अतः गोले का अभीष्ट पृष्ठीय क्षेत्रफल = 616 cm².

(ii) गोले का व्यास d = 21 cm (दिया है)
⇒ R = \(\frac { 21 }{ 2 }\) = 10.5 cm
गोले का पृष्ठीय क्षेत्रफल = 4πR² = 4 x \(\frac { 22 }{ 7 }\) x (10.5)².
= 88 x 10.5 x 1.5 = 1386 cm²
अत: गोले का अभीष्ट पृष्ठीय क्षेत्रफल = 1386 cm².

(iii) गोले का व्यास d = 3.5 m (दिया है)
⇒ R = \(\frac { 3.5 }{ 2 }\) = 1.75 m
गोले का पृष्ठीय क्षेत्रफल = 4πR² = 4 x \(\frac { 22 }{ 7 }\) x (1.75)²
= 88 x 1.75 x 0.25 = 38.5 m²
अत: गोले का अभीष्ट पृष्ठीय क्षेत्रफल = 38.5 m².

प्रश्न 3.
10 cm त्रिज्या वाले एक अर्द्धगोले का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए)।
हल :
दिया है : अर्धगोले की त्रिज्या R = 10 cm
चूँकि अर्द्धगोले का कुल पृष्ठीय क्षेत्रफल = 3πR²
= 3 x 3.14 x 10²
= 942 cm²
अतः अर्द्धगोले का कुल पृष्ठीय क्षेत्रफल का अभीष्ट मान = 942 cm².

प्रश्न 4.
एक गोलाकार गुब्बारे में हवा भरने पर, उसकी त्रिज्या 7 cm से 14 cm हो जाती है। इन दोनों स्थितियों में गुब्बारे के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
दिया है : दोनों स्थितियों में गुब्बारे की त्रिज्याएँ क्रमशः R₁ = 7 cm एवं R₂ = 14 cm हैं।
चूँकि पहली स्थिति में गोले का पृष्ठीय क्षेत्रफल S₁ = 4πR₁²
⇒ S₁ = 4π(7)² cm²
एवं दूसरी स्थिति में गोले का पृष्ठीय क्षेत्रफल S₂ = 4πR₂²
⇒ S₂ = 4π(14)² cm²
∴ S₁ : S₂ = 4π (7)² : 4π (14)² = 1 : 4
अतः दोनों स्थितियों में अभीष्ट पृष्ठीय क्षेत्रफलों का अनुपात = 1 : 4.

प्रश्न 5.
पीतल के बने एक अर्द्धगोलाकार कटोरे का आन्तरिक व्यास 10.5 cm है। Rs 16 प्रति 100 cm² की दर से इसके आन्तरिक पृष्ठ पर कलई कराने का व्यय ज्ञात कीजिए।
हल :
दिया है : कटोरे का आन्तरिक व्यास, d = 10.5 cm ⇒ त्रिज्या R = 5.25 cm
कटोरे का आन्तरिक पार्श्व पृष्ठीय क्षेत्रफल = 2πR² = 2 x \(\frac { 22 }{ 7 }\) x (5.25)²
⇒ S_c = 44 x 5.25 x 0.75 cm² = 173.25 cm²
कलई का व्यय = दर x क्षेत्रफल = \(\frac { 16 }{ 100 }\) x 173.25 = Rs 27.72
अतः कलई कराने का अभीष्ट व्यय = Rs 27.72.

प्रश्न 6.
उस गोले की त्रिज्या ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 cm² है। (2018)
हल :
गोले का पृष्ठीय क्षेत्रफल = 154 cm² (दिया हुआ है)
चूँकि गोले का पृष्ठीय क्षेत्रफल S_c = 4πR²
4 x \(\frac { 22 }{ 7 }\) x R² = 154
R² = \(\frac { 154\times 7 }{ 4 \times 22 }\) = 12.25 cm²
R = √12.25 = 3.5 cm
अतः गोले की अभीष्ट त्रिज्या = 3.5 cm.

प्रश्न 7.
चन्द्रमा का व्यास पृथ्वी के व्यास का लगभग एक-चौथाई है। इन दोनों के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
दिया है : चन्द्रमा और पृथ्वी के व्यासों का अनुपात
\(=d_{m} : d_{e}=1 : 4 \Rightarrow R_{m} : R_{e}=1 : 4 \Rightarrow \frac{R_{m}}{R_{e}}=\frac{1}{4}\)
चूँकि चन्द्रमा एवं पृथ्वी के पृष्ठीय क्षेत्रफलों का अनुपात \(S_{m} : S_{e}=4 \pi R_{m}^{2} : 4 \pi R_{e}^{2}\)
\(\frac{S_{m}}{S_{e}}=\left(\frac{1}{4}\right)^{2}=\frac{1}{16} \Rightarrow S_{m} : S_{e}=1 : 16\)
अतः दोनों के पृष्ठीय क्षेत्रफलों का अभीष्ट अनुपात = 1:16.

प्रश्न 8.
एक अर्द्धगोलाकार कटोरा 0.25 cm मोटी स्टील से बना है। इस कटोरे की आन्तरिक त्रिज्या 5 cm है। कटोरे का बाहरी वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :
ज्ञात है : कटोरे की आन्तरिक त्रिज्या R_i = 5 cm एवं स्टील की मोटाई d = 0.25 cm
⇒ कटोरे की बाह्य त्रिज्या R_e = R_i + d = 5 + 0.25 = 5.25 cm
कटोरे का बाह्य वक्र पृष्ठीय क्षेत्रफल = \(2 \pi R_{e}^{2}=2 \times \frac{22}{7} \times(5 \cdot 25)^{2}\)
= 44 x 5.25 x 0.75 cm² = 173.25 cm²
अतः कटोरे का अभीष्ट बाहरी वक्र पृष्ठीय क्षेत्रफल = 173.25 cm².

प्रश्न 9.
एक लम्बवृत्तीय बेलन त्रिज्या r वाले एक गोले को पूर्णतया घेरे हुए हैं (देखिए संलग्न चित्र)। ज्ञात कीजिए
(i) गोले का पृष्ठीय क्षेत्रफल,
(ii) बेलन का वक्र पृष्ठीय क्षेत्रफल,
(iii) ऊपर (i) एवं (ii) में प्राप्त क्षेत्रफलों का अनुपात।

हल :
गोले की त्रिज्या r मात्रक दी गई है। चित्रानुसार बेलन की
त्रिज्या = r मात्रक तथा बेलन की ऊँचाई h = 2r मात्रक
(i) गोले का पृष्ठीय क्षेत्रफल = 4πR² (मात्रक)।
(ii) बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh = 2πr. 2r = 4πr²
अतः बेलन का वक्र पृष्ठीय अभीष्ट क्षेत्रफल = 4πr².
(iii) गोले का पृष्ठीय क्षेत्रफल : बेलन का वक्र पृष्ठीय क्षेत्रफल = 4πr² : 4πr² = 1 : 1
अतः दोनों पृष्ठों का अभीष्ट अनुपात = 1 : 1.

MP Board Class 9th Maths Solutions