MP Board Class 9th Maths Solutions Chapter 12 हीरोन का सूत्र Additional Questions
MP Board Class 9th Maths अतिरिक्त परीक्षोपयोगी प्रश्न
MP Board Class 9th Maths दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
संलग्न चित्र में दी हुई पतंग को बनाने के लिए प्रत्येकरंग(शेड) के कितने कागज की आवश्यकता होगी यदि ABCD विकर्ण 44 cm वाला एक वर्ग है तथा नीचे 20 cm, 20 cm और 14 cm वाला एक समद्विबाहु त्रिभुज है।
हल:
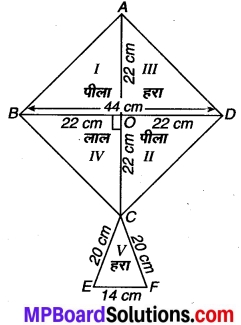
ज्ञात है : एक पतंग जो एक वर्ग ABCD एवं एक समद्विबाहु ∆ CEF से बना है। वर्ग का विकर्ण AC = BD = 44 cm है जो परस्पर बिन्दु O पर समकोण पर समद्विभाजित करते हैं।
अर्थात् OA = OB = OC = OD = 22 cm
एवं ∠AOB = ∠ BOC = ∠COD = ∠DOA = 90°
समद्विबाहु त्रिभुज की भुजाएँ क्रमशः CE = 20 cm, CF = 20 cm एवं EF = 14 cm हैं। हम जानते हैं कि वर्ग के विकर्ण वर्ग को चार सर्वांगसम भागों में विभक्त करते हैं। पीला रंग का कागज वर्ग के दो चतुर्थांश I एवं II में है।
⇒ पीले रंग के कागज का क्षेत्रफल = 2 x \(\frac { 1 }{ 2 }\) x 22 x 22 = 484 cm
लाल रंग का कागज केवल वर्ग के एक चतुर्थांश IV में है
⇒ लाल रंग के कागज का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x 22 x 22 = 242 cm2
हरे रंग का कागज वर्ग के चतुर्थांश III एवं समद्विबाहु त्रिभुज (V) में है
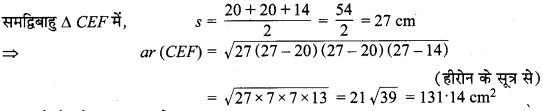
∴ हरे रंग के कागज का क्षेत्रफल = ar (CEF) + ar (AOD)
= 131.14 + 242 = 373.14
अतः पीले रंग के कागज का अभीष्ट क्षेत्रफल = 484 cm2
लाल रंग के कागज का अभीष्ट क्षेत्रफल = 242 cm2
एवं हरे रंग के कागज का अभीष्ट क्षेत्रफल = 373.14 cm2 .
प्रश्न 2.
एक त्रिभुज का परिमाप 50 cm है। त्रिभुज की एक भुजा छोटी भुजा से 4 cm लम्बी है तथा तीसरी भुजा छोटी भुजा के दुगने से 6 cm कम है। त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल:
मान लीजिए ∆ की छोटी भुजा = x cm तो प्रश्नानुसार दूसरी भुजा (x + 4) cm तथा तीसरी भुजा (2x – 6) cm होगी।
परिमाप = x + (x + 4) + (2x – 6)= 50 cm
⇒ 4x – 2 = 50 ⇒ 4x = 52
⇒ x = \(\frac { 52 }{ 4 }\) = 13 cm
अतः त्रिभुज की भुजाएँ क्रमशः 13 cm, 17 cm एवं 20 cm होंगी।

अतः त्रिभुज का अभीष्ट क्षेत्रफल = 109.54 cm2.
प्रश्न 3.
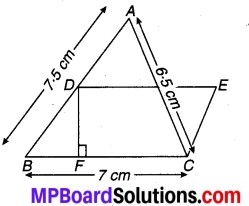
संलग्न चित्र में ∆ABC की भुजाएँ AB = 7.5 cm, AC = 6.5 cm और BC = 7 cm हैं। आधार BC पर एक समान्तर चतुर्भुज DBCE की रचना की जाती है जो क्षेत्रफल में ∆ABC के बराबर है। इस समान्तर चतुर्भुज की ऊँचाई DF ज्ञात कीजिए।
हल:
दिया है : एक त्रिभुज जिसकी भुजा AB = 7.5 cm,
AC = 6.5 और BC = 7 cm
आधार BC = 7 cm पर एक समान्तर चतुर्भुज DBCE दिया है जिसका क्षेत्रफल ∆ABC के क्षेत्रफल के बराबर है। मान लीजिए समान्तर चतुर्भुज की ऊँचाई DF = d cm
∆ ABC में,
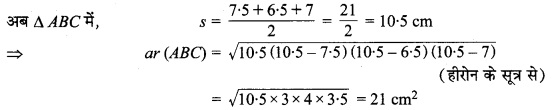
चूँकि ar (DBCE) = ar (ABC) (दिया है)
⇒ 7 x d = 21 ⇒ d = 2 = 3 cm
अतः समान्तर चतुर्भुज की अभीष्ट ऊँचाई DF = 3 cm.
प्रश्न 4.
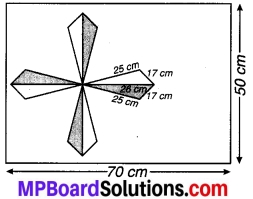
संलग्न चित्र में 50 cm x 70 cm की विमाओं वाली एक आयताकार टाइल पर चित्र में दर्शाए गए अनुसार एक डिजाइन बनाया गया है। इस डिजाइन में 8 त्रिभुज हैं जिनमें से प्रत्येक की भुजाएँ 26 cm, 17 cm और 25 cm की हैं। डिजाइन का पूर्ण क्षेत्रफल ज्ञात कीजिए तथा टाइल के शेष भाग का क्षेत्रफल भी ज्ञात कीजिए।
हल:
दिया है : एक 50 cm x 70 cm विमाओं वाली 70cmटाइल जिसके अन्दर 26 cm, 17cm एवं 25 cm विमाओं वाली 8 सर्वांगसम त्रिभुजों से बनी आकृति।
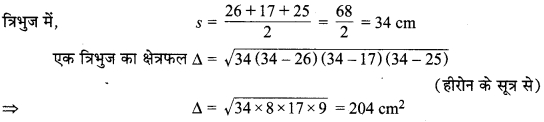
∴ डिजाइन का क्षेत्रफल = 8 x त्रिभुज का क्षेत्रफल
= 8 x 204 = 1632 cm2
चूँकि आयताकार टाइल का क्षेत्रफल = लम्बाई x चौड़ाई
⇒ ar (आयताकार टाइल) = 70 x 50 = 3500 cm2
टाइल के शेष भाग का क्षेत्रफल = 3500 – 1632 = 1868 cm2
अतः टाइल की डिजाइन का अभीष्ट क्षेत्रफल = 1632 cm2
एवं शेष टाइल का अभीष्ट क्षेत्रफल = 1868 cm2.
MP Board Class 9th Maths लघु उत्तरीय प्रश्न
प्रश्न 1.
भुजाओं 50 m, 65 m और 65 m वाले त्रिभुजाकार खेत में ₹ 7 प्रति m2 की दर से घास लगवाने का व्यय ज्ञात कीजिए।
हल:
त्रिभुजाकार खेत के लिए,

चूँकि घास लगाने का व्यय = दर x क्षेत्रफल = 7 x 1500 = ₹ 10,500
अतः घास लगवाने का अभीष्ट व्यय = ₹ 10,500.
प्रश्न 2.
एक फ्लाई ओवर की त्रिभुजाकार दीवारों को विज्ञापन के लिए प्रयोग किया जाता है। दीवारों की भुजाएँ 13 m, 14 m और 15 m हैं। विज्ञापनों से एक वर्ष में ₹2,000 प्रति m2 की दर से आय होती है। एक कम्पनी इनमें से एक दीवार को 6 महीने के लिए किराये पर लेती है। उस कम्पनी ने कितना किराया दिया ?
हल:

अतः विज्ञापन के लिए अभीष्ट किराया = ₹ 84,000.
प्रश्न 3.
एक समद्विबाहु त्रिभुज का परिमाप 32 cm है। एक बराबर भुजा और आधार का अनुपात 3 : 2 है। इस त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल:
दिया है : एक समद्विबाहु त्रिभुज जिसकी एक बराबर भुजा और आधार का अनुपात 3 : 2 है तथा परिमाप 32 cm है।
⇒ भुजाओं का अनुपात = 3 : 3 : 2
मान लीजिए भुजाएँ 3x, 3x एवं 2x हैं।
तो परिमाप 3x + 3x + 2x = 32 cm (दिया है)
⇒ x = 32 ⇒ x = \(\frac { 32 }{ 8 }\) = 4 cm
⇒ भुजाएँ क्रमश: 12 cm, 12 cm और 8 cm हैं। त्रिभुज में,
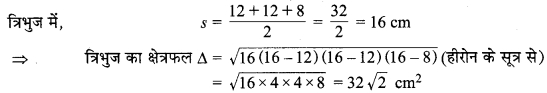
अतः त्रिभुज का अभीष्ट क्षेत्रफल = 32√2 cm2.
प्रश्न 4.
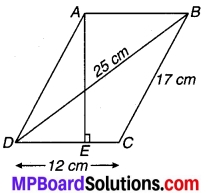
संलग्न चित्र में दिए हुए समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए। साथ ही शीर्ष A से भुजा DC पर शीर्ष लम्ब की लम्बाई भी ज्ञात कीजिए।
हल:
दियाहैः एक समान्तर चतुर्भुज जिसकी भुजाएँ DC = 12 cm, BC = 17 cm और विकर्ण DB = 25 cm तथा A से DC पर शीर्षलम्ब = AE = d (मान लीजिए)
हम जानते हैं कि समान्तर चतुर्भुज का विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभक्त करता है।
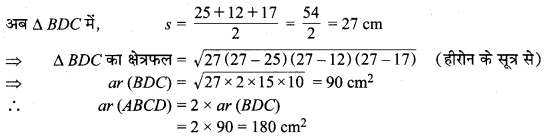
चूँकि समान्तर चतुर्भुज का क्षेत्रफल = आधार (DC) x शीर्षलम्ब (AE)
⇒ 12 x d = 180 ⇒ d = \(\frac { 180 }{ 12 }\) = 15 cm
अतः समान्तर चतुर्भुज का अभीष्ट क्षेत्रफल = 180 cm2
एवं समान्तर चतुर्भुज का अभीष्ट शीर्षलम्ब = 15 cm.
प्रश्न 5.
एक खेत एक समान्तर चतुर्भुज के आकार का है जिसकी भुजाएँ 60 m और 40 m हैं तथा एक विकर्ण 80 m है। इस खेत का क्षेत्रफल ज्ञात कीजिए।
हल:
दिया है : एक समान्तर चतुर्भुज के आकार का खेत ABCDP
जिसकी भुजा AB = 60 m, BC = 40 m एवं विकर्ण AC = 80 m है।
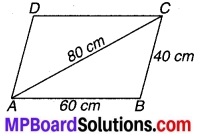

अत: खेत का अभीष्ट क्षेत्रफल= 600√15 m2.
प्रश्न 6.
एक त्रिभुजाकार का खेत का परिमाप 420 m हैं तथा इसकी भुजाओं का अनुपात 6 : 7 : 8 है। इस खेत का क्षेत्रफल ज्ञात कीजिए।
हल:
दिया है : एक त्रिभुजाकार खेत जिसकी परिमाप 420 m तथा भुजाओं का अनुपात 6 : 7 : 8 है।
चूँकि भुजाओं का अनुपात = 6 : 7 : 8 = भुजाएँ हैं 6x, 7x एवं 8x (मान लीजिए)
⇒ परिमाप = 6x + 7x + 8x = 420 ⇒ 21x = 420 ⇒ x = \(\frac { 420 }{ 21 }\) = 20 m
⇒ भुजाओं का वास्तविक मान a = 120 m, b = 140 m एवं c = 160 m
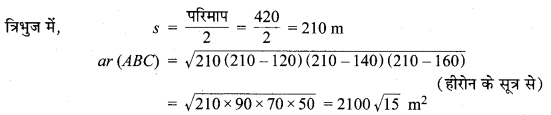
अतः खेत का अभीष्ट क्षेत्रफल = 2100√15 m2.
प्रश्न 7.
किसी त्रिभुज की भुजाएँ क्रमश: 60 m, 100 m और 140 m हैं। त्रिभुज का क्षेत्रफल ज्ञात कीजिए। (2019)
हल:
दिया है : त्रिभुज की भुजाएँ क्रमश: a = 60 m, b = 100 m एवं c = 140 m

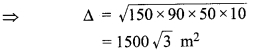
अतः त्रिभुज का अभीष्ट क्षेत्रफल = 1500√3 m.
प्रश्न 8.
किसी त्रिभुज ABC की भुजाएँ क्रमशः 40 m, 24 एवं 32 m हैं, तो त्रिभुज का क्षेत्रफल ज्ञात कीजिए। (2019)
हल:
निर्देशः उपर्युक्त प्रश्न की तरह हल करें
उत्तर:
अभीष्ट क्षेत्रफल = 384 m
MP Board Class 9th Maths अति लघु उत्तरीय प्रश्न
सत्य तथा असत्य कथन लिखिए तथा अपने उत्तर का औचित्व दीजिए।
प्रश्न 1.
आधार 4 cm और ऊँचाई 6 cm वाले त्रिभुज का क्षेत्रफल 24 cm2 है।
उत्तर:
कथन असत्य है, क्योंकि ar (∆) = \(\frac { 1 }{ 4 }\) x 4 x 6 = 12 cm2.
प्रश्न 2.
एक त्रिभुज ABC का क्षेत्रफल 8 cm है जिसमें AB = AC = 4 cm तथा ∠A = 90° है।
उत्तर:
कथन सत्य है, क्योंकि ar (ABC) = \(\frac { 1 }{ 2 }\) x 4 x 4 = 8 cm2.
प्रश्न 3.
एक समद्विबाहु त्रिभुज का क्षेत्रफल \(\frac { 5 }{ 4 }\)√11 cm2 होगा यदि उसका परिमाप 11 cm और आधार 5 cm है।
उत्तर:
कथन सत्य है, प्रत्येक बराबर भुजा 3 cm है।
प्रश्न 4.
एक समबाहु त्रिभुज का क्षेत्रफल 20√3 cm है जिसकी प्रत्येक भुजा 8 cm है।
उत्तर:
कथन असत्य है, क्योंकि समबाहु ∆ का क्षेत्रफल 16√3 cm2 होगा।
प्रश्न 5.
यदि एक समचतुर्भुज की एक भुजा 10 cm और विकर्ण 16 cm है तो उस समचतुर्भुज का क्षेत्रफल 96 cm2 है।
उत्तर:
कथन सत्य है, क्योंकि उसके विकर्ण से बने एक त्रिभुज का क्षेत्रफल = 48 cm2.
प्रश्न 6.
एक समान्तर चतुर्भुज का आधार और संगत शीर्षलम्ब क्रमशः 10 cm और 3.5 cm हैं। उस समान्तर चतुर्भुज का क्षेत्रफल 30 cm है।
उत्तर:
कथन असत्य है, क्योंकि समान्तर चतुर्भुज का क्षेत्रफल = 10 x 3.5 = 35 cm2.
प्रश्न 7.
भुजा a वाले एक समषद्भुज का क्षेत्रफल भुजा a वाले पाँच समबाहु त्रिभुज के क्षेत्रफल के बराबर होता है।
उत्तर:
कथन असत्य है, क्योंकि यह a भुजा वाले 6 समबाहु त्रिभुजों के क्षेत्रफलों के योग के बराबर होगा।
MP Board Class 9th Maths वस्तुनिष्ठ प्रश्न
बहु-विकल्पीय प्रश्न
प्रश्न 1.
एक समद्विबाहु समकोण त्रिभुज का क्षेत्रफल 8 cm है। इसके कर्ण की लम्बाई है:
(a) \(\sqrt { 32 }\) cm
(b) \(\sqrt { 16 }\) cm
(c) \(\sqrt { 48 }\) cm
(d) \(\sqrt { 24 }\) cm.
उत्तर:
(a) \(\sqrt { 32 }\) cm
प्रश्न 2.
एक समबाहु त्रिभुज का परिमाप 60 m है। इसका क्षेत्रफल है :
(a) 10√3 m2
(b) 15√3 m2
(c) 20√3 m2
(d) 100√3 m2.
उत्तर:
(d) 100√3 m2.
प्रश्न 3.
2√3 cm भुजा वाले समबाहु त्रिभुज का क्षेत्रफल है :
(a) 5.196 cm2
(b) 0.866 cm2
(c) 3:496 cm2
(d) 1:392 cm2.
उत्तर:
(a) 5.196 cm2
प्रश्न 4.
क्षेत्रफल 9√3 cm वाले समबाहु त्रिभुज की प्रत्येक भुजा की लम्बाई है:
(a) 8 cm
(b) 36 cm
(c) 4 cm
(d) 6 cm.
उत्तर:
(d) 6 cm.
प्रश्न 5.
यदि एक समबाहु त्रिभुज का क्षेत्रफल 16/3 cm है तो इसकी परिमाप होगी :
(a) 48 cm
(b) 24 cm
(c) 12 cm
(d) 36 cm.
उत्तर:
(b) 24 cm
रिक्त स्थानों की पूर्ति
1. एक समकोण समद्विबाहु त्रिभुज की बराबर भुजा 10 cm है तो इसके विकर्ण लम्बाई …… होगी।
2. 10 cm और 6 cm भुजाओं वाले आयत का क्षेत्रफल …….. होगा।
3. एक समबाहु त्रिभुज की प्रत्येक भुजा 10 cm है तो इसका क्षेत्रफल ……… होगा।
4. एक आयत की भुजाएँ मीटर में मापी गई हैं। इसके क्षेत्रफल का मात्रक ………. होगा।
5. आधार 12 cm तथा शीर्षलम्ब 8 cm वाले त्रिभुज का क्षेत्रफल ……. है।
उत्तर:
1. 10√2 cm,
2. 60 cm2,
3. 25√3 cm2,
4. m2,
5. 48 cm2.
जोड़ी मिलान

उत्तर:
1. → (c),
2. →(d),
3. → (e),
4. → (a),
5. → (b).
सत्य/असत्य कथन
1. हीरोन का सूत्र केवल समान्तर चतुर्भुज का क्षेत्रफल ज्ञात करने में प्रयुक्त होता है।
2. समान्तर चतुर्भुज की संलग्न भुजाएँ तथा एक विकर्ण दिया हो तो उसका क्षेत्रफल हीरोन के सूत्र से ज्ञात कर सकते हैं।
3. एक त्रिभुज का क्षेत्रफल होता है उसका आधार x शीर्षलम्ब।
4. आयत का क्षेत्रफल उसकी लम्बाई एवं चौड़ाई के गुणनफल के बराबर होता है।
5. समचतुर्भुज का क्षेत्रफल उसके विकर्णों के गुणनफल के बराबर होता है।
उत्तर:
1. असत्य,
2. सत्य,
3. असत्य,
4. सत्य,
5. असत्य।
एक शब्द/वाक्य में उत्तर
1. किसी त्रिभुज की परिमाप का मात्रक क्या होता है?
2. क्षेत्रफल को मापने का मात्रक क्या है?
3. किसी त्रिभुज की भुजाओं के योग को क्या कहते हैं?
4. किसी वर्ग की भुजा 4 सेमी है। उसके विकर्ण उसे चार त्रिभुजों में विभक्त करते हैं तो प्रत्येक त्रिभुज का क्षेत्रफल क्या होगा?
5. हीरोन का जन्म कहाँ हुआ था?
उत्तर:
1. सेमी या मीटर,
2. सेमी या मीटर,
3. परिमाप,
4. 4 cm2,
5. अलेक्जेण्ड्रिया (मिस्र) में।