Category: Class 7

MP Board Class 7th Maths Solutions Chapter 14 सममिति Ex 14.3

प्रश्न 1.
किन्हीं दो आकृतियों के नाम बताइए, जिनमें रैखिक सममिति और क्रम 1 से अधिक घूर्णन सममिति दोनों ही हों।
उत्तर:
समबाहु त्रिभुज और वृत्त।

प्रश्न 2.
जहाँ सम्भव हो, निम्नलिखित की एक रफ आकृति खींचिए:
(i) एक त्रिभुज जिसमें रैखिक सममिति और क्रम 1 से अधिक घूर्णन सममिति दोनों ही हों।
(ii) एक त्रिभुज, जिसमें केवल एक रैखिक सममिति और क्रम 1 से अधिक की घूर्णन सममिति न हों।
(iii) एक चतुर्भुज, जिसमें क्रम 1 से अधिक की घूर्णन सममिति हो, परन्तु रैखिक सममिति न हो।
(iv) एक चतुर्भुज, जिसमें केवल रैखिक सममिति हो और क्रम 1 से अधिक की घूर्णन सममिति न हो।
उत्तर:
(i) एक समबाहु त्रिभुज जिसमें 3 रैखिक सममिति होती हैं। समबाहु त्रिभुज में क्रम 3 की घूर्णन सममिति (1 से अधिक) होती है।
(चित्र : पृष्ठ 288 के प्रयास कीजिए का प्रश्न 1(a) का उत्तर देखिए।)

(ii) एक समद्विबाहु त्रिभुज में एक रैखिक सममिति तथा कोई भी घूर्णन सममिति क्रम 1 से अधिक नहीं होती है।

(iii) एक समान्तर चतुर्भुज में क्रम 2 की घूर्णन सममिति लेकिन कोई भी रैखिक सममिति नहीं है।

(iv) दिये हुए चतुर्भुज में एक रैखिक सममिति, लेकिन कोई भी घूर्णन सममिति नहीं है।

प्रश्न 3.
यदि किसी आकृति की दो या अधिक सममिति रेखाएँ हों, तो क्या यह आवश्यक है कि उसमें क्रम 1 से अधिक की घूर्णन सममिति होगी?
उत्तर:
हाँ, यह आवश्यक है यदि आकृति में दो या अधिक रैखिक सममिति हैं, तो उस आकृति में क्रम 1 से अधिक घूर्णन सममिति होगी।

प्रश्न 4.
रिक्त स्थानों को भरिए :
हल:

प्रश्न 5.
ऐसे चतुर्भुजों के नाम बताइए जिनमें रैखिक सममिति और क्रम 1 से अधिक की घूर्णन सममिति दोनों ही हों।
उत्तर:
वर्ग और समचतुर्भुज।

प्रश्न 6.
किसी आकृति को उसके केन्द्र के परितः 60° के कोण पर, घुमाने पर, वह उसकी प्रारम्भिक स्थिति जैसी ही दिखाई देती है। इस आकृति के लिए ऐसा कौन-से अन्य कोणों के लिए भी हो सकता है?
उत्तर:
ऐसे अन्य कोण होंगे – 120°, 180°, 240P, 300° और 360°

प्रश्न 7.
क्या हमें कोई ऐसी क्रम 1 से अधिक की घूर्णन सममिति प्राप्त हो सकती है, जिसके घूर्णन के कोण निम्नलिखित हों ?

1. 45°
2. 170

उत्तर:

1. हाँ
2. नहीं।

MP Board Class 7th Maths Solutions

MP Board Class 7th Hindi Sugam Bharti Solutions विविध प्रश्नावली 1

प्रश्न 1.
सही जोड़ी बनाइए
1. अमृत = (क) क्षमता
2. मनुष्य = (ख) महल
3. कार्य = (ग) घट
4. राज = (घ) समाज
उत्तर-
1. (ग),
2. (घ),
3. (क),
4. (ख)

प्रश्न 2.
उपयुक्त शब्द से रिक्त स्थानों की पूर्ति कीजिए
(क) जिन-जज भूखों की ………………………… दीनू ने बुझाई है, उनकी दुआएँ भी वह राजकुमार के लिए लाया है। (भूख/प्यास)
(ख) दुश्मन का मुख ………………………… करता, जन-जन की पीड़ा को हरता। (काला/पीला)
(ग) यदि एक तिहाई उम्र बिना कोई ………………………… गुजर भी जाए तो क्या फर्क पड़ेगा। (देखे/सोचे).
(घ) चक्रवात ………………………… दबाव में आकस्मिक पविर्तन के कारण होता है। (वायुमण्डलीय/ जैव.मण्डलीय)
उत्तर-
1. भूख
2. काला
3. देखे
4. वायुमण्डलीय।

प्रश्न 3.
निम्नलिखित प्रश्नों के उत्तर एक-एक वाक्य में लिखिए-
(अ) सिक्के की विश्वसनीयता और पहचान के लिए प्राचनी काल से राजा लोग क्या करते आए हैं।
उत्तर-
सिक्के की विश्वसनीयता और पहचान के लिए प्राचीन समय से ही राजाओं ने इसके एक ओर अपने राज्य की मुद्रा तथा दूसरी तरफ इसका मूल्य अंकित कर ढाला।

(ब) ‘महूरत न सोचो, मचलते चलो’ में ‘मचलते चलो’ का अर्थ क्या है?
उत्तर-
मचलते चलो = जिद करके अपनी धुन में बढ़े चलो।

(स) बाढ़ों के लिए कौन जिम्मेदार है?
उत्तर-
प्रकृति और मनुष्य बाढ़ो के लिए जिम्मेदार है।

(द) दीनू ने क्या सोचकर भिखारी को रोटियाँ दी?
उत्तर-
दीने के पास जो रोटियाँ थी उनमें से चार इसको दे दूंगा तो क्या फर्क पड़ जाएगा, उसने यह सोच कर चार रोटियाँ भिखारी को दी।

(इ) कर्मों के संकीर्तन में सबसे ऊँचा स्वर किसका है?
उत्तर-
कर्मों के संकीर्तन में सबसे ऊँचा स्वर उसका होता है जो समाज की सच्ची सेवा करता है।

प्रश्न 4.
निम्नलिखित प्रश्नों के उत्तर तीन से पाँच वाक्यों में लिखिए-
(अ) मनुष्य समाज के उन्नतिशील होने के कारण लिखिए।
उत्तर-
मनुष्य समाज के उन्नतिशील होने में सिक्के का महत्त्वपूर्ण योगदान है। पहले मनुष्य कुछ भी उत्पादित करता था, वह अपने उपयोग पर खर्च कर डालता था, परंतु सिक्कों के आने से वह अल्पबचत कर सकता है तथा भविष्य में उत्पन्न सभी समस्याओं से लड़ सकता

(ब) अविचल खड़ा हिमालय कौन-कौन से दायित्व निभा रहा है।
उत्तर-
प्रारंभिककाल से ही हिमालय भारत की रक्षा कर रहा है। हिमालय के उस पार कई बार दुश्मनों ने घुसपैठ करने की कोशिश की किंतु हिमालय ने अडिग रहकर हमारी मदद की। इसके अलावा हिमालय उत्तर दिशा में आने वाली बर्फ की आंधियों से हमारी रक्षा करता है। आज संपूर्ण विश्व में हिमालय ही हमारी पहचान है।

(स) ‘बहुमत के आधार पर दाँत सर्वोपरि है’ सिद्ध करो।
उत्तर-
बहुमत के आधार पर भी दाँत सर्वोपरि है। शरीर के अधिकतर अंग इकलौते हैं या फिर उनकी संख्या दो तक हो सकती है, पर दाँत संख्या में सर्वाधिक है।

(द) जल के बहाव को काम करने के लिए कौन-कौन से उपाय किए जाते हैं?
उत्तर-
जल के बहाव को कम करने के लिए निम्नलिखित उपाय किए गए जल के बहाव में कमी करने के लिए वन लगवाना। -जल प्रवाह मार्ग में नहरी तंत्र का विकास करना। -बाढ़ की भविष्यवाणी करना।

(इ) आर्थिक उन्नति में सिक्के की भूमिका पर प्रकाश डालिए।
उत्तर-
किसी भी समाज की आर्थिक उन्नति में सिक्कों का सबसे अधिक योगदान होता है। सिक्कों से व्यापार में उन्नति होती है। समाज की सभी छोटी-बड़ी आर्थिक इकाइयों में सिक्कों का लेनदेन होता है। सिक्कों का सबसे अधिक लाभ ‘अल्पबचत’ करना होता है। बचत से समाज का भविष्य सुरक्षित बना रहता है।

प्रश्न 5.
निम्नलिखित शब्दों के विलोम शब्द लिखिए-
स्वतंत्रता, बहुमत, हानि, दुश्मन, गरीब, उन्नति, ऊंचा, यश, उपेक्षा, आवश्यक, समर्थ
उत्तर-

प्रश्न 6.
निम्नलिखित तत्सम, तद्भव और आगत शब्दों को छाँटकर लिखिए-
प्यासा, जन, धड़ा, रास्ता, काम, जरूरत, कोशिश,। प्रयत्न, जड़ा, मुकाबला, मुस्कान, आँख, खिसकाना, किटकिट, गड़गड़ाहट, टकसाल, सिक्का, मुद्रा, बैंक, पेंसिल, अयस्क, दुआएँ, शताब्दी, जहान॥
उत्तर-

प्रश्न 7.
निम्नलिखित शब्दों के पर्यावाची लिखिएपथ, पग, शरीर, चेष्टा, हलचल, परहित, पीड़ा।
उत्तर-
शब्द – पर्यायवाची
पथ – मार्ग, रास्ता।
पग – पैर, कदम।
शरीर – तन, काया।
चेष्टा – प्रयत्न, कोशिश।
हलचल – कंपन
परहित – हितेषी।
पीड़ा – दुख, शोक।

प्रश्न 8.
निम्नलिखित अवतरण में से संज्ञा, सर्वनाम, विशेषण और क्रिया शब्द छाँटिए-
उसके झोले में तीन रोटियाँ ही बची थी। कुछ दूर चलने पर उसे एक गाय मिली। एक बछड़ा भी साथ था जो लगातार गौ के थन खींच रहा था। उनमें दूध नहीं था। दीनू गाय को हमेशा ही श्रद्धा से गो-माता के रूप में देखता था। उसने गो-माता को नमस्कार किया। एक रोटी उसे खिला दी। एक रोटी बछड़े को भी दे दी। सोचा-एक रोटी है मेरे पास। कौन ये मेरी रोटी खा ही – लेंगे। उपहार के लिए एक ही रोटी काफी है।
उत्तर-
संज्ञा शब्द : झोले, रोटियाँ, गाय, बछड़ा, गौ, दूध, दीनू।
सर्वनाम शब्द : उसके, कुछ, उसे, जो, उनमें आदि।
विशेषण : तीन, एक आदि।
क्रिया : बची, मिली, खींच, देखता नमस्कार करना, खिला, देना, खा लेना।

प्रश्न 9.
निम्नलिखित मुहावरों का वाक्य में प्रयोग कीजिए-
आँख फेरना, बन्दर धुड़की देना, मुँह में अँगुली दबाना, दाँत किट किटाना, जेब गर्म होना, हाथों-हाथ उठाना, फिसड्डी होना, खिल उठना।
उत्तर-

प्रश्न 10.
निम्नलिखित शब्दों में ग्रस्त, हीन और रहित शब्द जोड़कर नए सार्थक शब्द बनाइए-
बुद्धि, भेद-भाव, स्वार्थ, पंख, विचार, मर्यादा, अंग, रोग, शोक, मोह, लकवा, शर्म।
उत्तर-
शब्द = सार्थक शब्द
बुद्धि = बुद्धिहीन
भेदभाव = भेदभावरहित
स्वार्थ = स्वार्थरहित
पंख = पंखरहित
विचार = विचारहीन
मर्यादा = मर्यादाहीन
अंग = अंगहीन
रोग = रोगग्रस्त
शोक = शोकग्रस्त
मोह = मोहरहित
लकवा = लकवाग्रस्त
शर्म = शर्मरहित

प्रश्न 11.
निम्नलिखित अवतरण में संयुक्त क्रियाओं को रेखांकित कीजिए-
मेरे सर्वेक्षण में आँखों को इतना महत्त्व नहीं दिया जा सकता। आँखें सिर्फ देखने के काम आती हैं। मैंने दो-तिहाई उम्र इनसे काम ले लिया और इनमें जो-जो चीजें या हालात देखे, उन्हें देखकर इस निर्णय पर पहुँचा हूँ कि अब और कुछ देखने को जी नहीं चाहता॥
उत्तर-
मेरे सर्वेक्षण में आँखों को इतना महत्त्व नहीं दिया जा सकता। आँखें सिर्फ देखने के काम आती हैं। मैंने दो-तिहाई उम्र इनसे काम ले लिया और इनमें जो-जो चीजें या हालात देखे, उन्हें देखकर इस निर्णय पर पहुँचा हूँ कि अब और कुछ देखने को जी नहीं चाहता।

प्रश्न 12.
निम्नलिखित बिंदुओं को ध्यान में रखते हुए कहानी लिखिए-
बालक हलवाई की दुकान पर है। ललचाई आँखों से जलेबी को देखता है। कमीज-पेण्ट की जेबों में हाथ डालता है। कुछ भी न होने का भाव प्रकट करता है। हताश लौटने लगता है। हलवाई उसे जलेबियाँ देता है। बालक मुफ्त की चीज नहीं लूँगा। हलवाई मेहनत कर खाना अच्छी बात है। बालक-कमाकर लाऊँगा, तब खाऊँगा।
उत्तर-

“मेहनत ही इज्जत है”

सारे दिन कनिष्क शहर में इधर-उधर घूमता रहा। कभी इस गली से उस गली, कभी टूटी चप्पल से खाली प्लास्टिक की बोतल को लात मारता है। तभी बोतल पास के नत्थु हलवाई की दुकान के आगे लुढ़कती है। कनिष्क बोतल तक पहुँचता है। तभी उसकी नजर गर्म-गर्म जलेबी पर पड़ती है, उसके मुँह में पानी आ रहा है। वह नत्थु हलवाई की ओर देखते हुए अपनी जेबे टटोलता है। लेकिन उसके पास तो चवन्नी भी नहीं है। हलवाई उसकी ओर देखता है। कनिष्क हताश और अधूरे मन से वहाँ से लौटने के लिए मुड़ता है। नत्थु को बालक पर तरस आ जाता है, वह उसे रोककर दो जलेबी के टुकड़े देता है लेकिन कनिष्क अचानक जलेबी लेने से मना कर देता है, वह नत्थु से कहता है कि वह मुफ्त की चीज नहीं लेगा। हलवाई को बालक की खुद्दारी अच्छी लगती है। वह उसके सिर पर हाथ रखकर बोलता है-शाबाश बेटा, जिंदगी में कभी कोई चीज माँग कर मत लेना। खुद पैसा कमाकर चीजे खरीदना गर्व की बात है। बालक मुस्कराते हुए नत्थु से कहता है-ठीक है बाबा, अब तो ये जलेबियाँ तभी लूँगा जब मैं पैसे कमा कर लाऊँगा।

प्रश्न 13.
निम्नलिखित अवतरण में विराम लगाइए-
मैं जानता हूँ सभी बातें झटपट सिखाते नहीं बनती फिर भी हो सके तो उसके मन में जगाइए पसीना बहाकर कमाया हुआ एक पैसा भी फोकट में मिले खजाने से ज्यादा मूल्यवान है सिखाइए उसे कैसे झेलते हैं हार और सिखाकर जीत की खुशी में संयम बरतना अगर आपमें सामर्थ्य हो तो सिखाइए उसे ईर्ष्या द्वेष से दूर रहना
उत्तर-
मैं जानता हूँ सभी बातें झटपट सिखाते नहीं बनती फिर भी हो सके तो उसके मन में जगाइए। पसीना बहाकर कमाया हुआ एक पैसा भी फोकट में मिले खजाने से ज्यादा मूल्यवान है। सिखाइए उसे कैसे झेलते हैं हार और सिखाकर जीत की खुशी में संयम बरतना अगर आपमें सामर्थ्य हो तो सिखाइए उसे ईर्ष्या द्वेष से दूर रहना।

प्रश्न 14.
निम्नलिखित बिन्दुओं के आधार पर वर्षाऋतु पर निबंध लिखिए-
ऋतुएँ कितने प्रकार की होती हैं। ग्रीष्मकाल के बाद किस ऋतु का आगमन होता है। बादलों के बनने की प्रक्रिया क्या है। हिन्द महासागर तथा अरब सागर से उठने वाले बहाव कि दिशा में जाते हैं। मानसून से क्या आशय है। भारत वर्ष में मानसून की वर्षा का समय जुलाई से सितम्बर तक का है। वर्षा पर भारत वर्ष में कृषि की निर्भरता का उल्लेख कीजिए। यदि वर्णन हो तो देश की अर्थव्यवस्था पर क्या प्रभाव पड़ता है।

प्रश्न 15.
पत्र लेखन अपने मित्र को पत्र लिखिए जिससे उसे पर्वतों की रानी पचमढ़ी घूमने का निमंत्रण दीजिए।
परीक्षा भवन,
9 जून 2009
प्रिय रोहित
सप्रेम नमस्कार

हम सब कुशल से हैं। आशा है कि तुम भी ठीक से होंगे। तुम्हारा पत्र आज ही मिला है। इसे पढ़कर मैं बाग-बाग हो गया। जैसे कि तुम जानते हो कि हम हर वर्ष किसी पहाड़ी क्षेत्र की यात्रा करते हैं। इस वर्ष हम पर्वतों की रानी पंचमढ़ी घूमने गए। वहाँ के प्राकृतिक दृश्य देखने लायक थे। पर्वत को चोटी पर जब धूप पड़ रही थी, उस समय सोने की-सी छटा प्रतीत हो रही थी। यहाँ के लोग बड़े ही भोले और मासूम होते हैं। यहाँ परं एक झील भी है। जिसमें नाव का विशेष प्रबंध है। हमने वहाँ पर घुड़सवारी भी की। वहाँ पर खाने-पीने और ठहरने का विशेष प्रबंध है। सात दिन के टूर में हमने वहाँ बहुत लुत्क और ज्ञान अर्जित किया। मैं चाहता हूँ तुम भी अगली बार हमारे साथ पर्वतों की रानी पंचमढ़ी आओ!

अनेक शुभकामनाओं सहित,
तुम्हारा मित्र
क ख ग।

MP Board Class 7th Hindi Solutions

MP Board Class 7th Maths Solutions Chapter 14 सममिति Ex 14.2

प्रश्न 1.
निम्नलिखित आकृतियों में से किन आकृतियों में 1 से अधिक क्रम की घूर्णन सममिति है ?

हल:
यहाँ, आकृति (a), (b), (d), (e) और (f) में क्रम 1 से अधिक घूर्णन सममिति है।

प्रश्न 2.
पाठ्य-पुस्तक में दी गई आकृति में घूर्णन सममिति का क्रम बताइए।
हल:
(a) आकृति (i) में बिन्दु A अंकित किया। अब इस आकृति को X के अनुदिश दो स्थितियों (180° और 360°) में घुमाया जिससे कि यह अपनी मूल स्थिति में आ जाएगी।

∴ इसमें क्रम 2 की घूर्णन सममिति है।

(b) आकृति (i) में बिन्दु A अंकित किया। अब इस आकृति को X के अनुदिश दो स्थितियों (180° और 360°) में घुमाने पर प्राप्त आकृति ठीक मूल आकृति जैसी दिखाई देगी।

∴ इसमें क्रम 2 की घूर्णन सममिति है।

(c) आकृति (1) में बिन्दु A अंकित किया। अब इस आकृति को x के अनुदिश तीन स्थितियों (120°, 240° और 360°) में घुमाने पर प्राप्त आकृति ठीक मूल आकृति जैसी दिखाई देगी।

∴ इसमें क्रम 3 की घूर्णन सममिति है।

(d) आकृति (i) में बिन्दु A अंकित किया। अब इस आकृति को X के अनुदिश चार स्थितियों (90°, 180°, 270° और 360°) में घुमाने पर प्राप्त आकृति ठीक मूल आकृति जैसी दिखाई देगी।


∴ इसमें क्रम 4 की घूर्णन सममिति है।

(e) पाठ्य-पुस्तक में दी गई आकृति (e) को X के अनुदिश चार स्थितियों (90°, 180°, 270° और 360°) में घुमाने पर प्राप्त आकृति ठीक मूल आकृति जैसी दिखाई देगी।
∴ इसमें क्रम 4 की घूर्णन सममिति होगी।

(f) पाठ्य-पुस्तक में दी गई आकृति (f) को x के अनुदिश पाँच स्थितियों (72°, 144°, 216°, 288° और 360°) में घुमाने पर प्राप्त आकृति ठीक मूल आकृति जैसी दिखाई देगी।
∴ इसमें क्रम 5 की घूर्णन आकृति है।

(g) पाठ्य-पुस्तक में दी गई आकृति (g) में छः स्थितियाँ 60°, 120°, 180°, 240°, 300° और 360° घुमाने पर प्राप्त आकृति ठीक मूल आकृति जैसी दिखाई देगी।
∴ इसमें क्रम 6 की घूर्णन सममिति होगी।

(h) पाठ्य-पुस्तक में दी गई आकृति (h) में तीन स्थितियाँ 120°, 240° और 360° में घुमाने पर प्राप्त आकृति ठीक मूल आकृति जैसी प्राप्त होगी।
∴ इसमें क्रम 3 की घूर्णन सममिति होगी।

पाठ्य-पुस्तक पृष्ठ संख्या # 291-292

इन्हें कीजिए

प्रश्न 1.
अंग्रेजी वर्णमाला के कुछ अक्षरों में अद्भुत एवं आकर्षक सममितीय संरचनाएँ (structures) हैं। किन बड़े अक्षरों में केवल एक ही सममित रेखा है (जैसे E)? किन बड़े अक्षरों में क्रम 2 की घूर्णन सममिति है (जैसे I) ?
उपर्युक्त प्रकार से सोचते हुए, आप निम्नलिखित सारणी को भरने में समर्थ पाएँगे :
हल:

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 14 सममिति Ex 14.1

प्रश्न 1.
पाठ्य-पुस्तक में दी गई छेद की हुई आकृतियों की प्रतिलिपियाँ बनाकर (खींचकर) उनमें से प्रत्येक की सममित रेखाएँ ज्ञात कीजिए।
हल:
सममित रेखाएँ बिन्दुकित रेखाओं से निरूपित हैं।

प्रश्न 2.
पाठ्य-पुस्तक में दी गई आकृतियों में सममित रेखा (रेखाएँ) दी हुई हैं। अन्य छेद ज्ञात कीजिए।
हल:
निम्नांकित आकृतियों में अन्य छेद दर्शाए गए हैं :

प्रश्न 3.
पाठ्य-पुस्तक में दी हुई आकृतियों में दर्पण रेखा (अर्थात् सममित रेखा) बिन्दुकित रेखा के रूप में दी गई है। बिन्दुकित (दर्पण) रेखा में प्रत्येक आकृति का परावर्तन करके, प्रत्येक आकृति को पूरा कीजिए। (आप बिन्दुकित रेखा के अनुदिश एक दर्पण रख सकते हैं और फिर प्रतिबिम्ब (image) के लिए दर्पण में देख सकते हैं)। क्या आपको पूरी की गई आकृति का नाम याद है ?
हल:
प्रत्येक आकृति की पूर्ण आकृति (परावर्तित आकृति) दर्शाई गई है:

प्रश्न 4.
पाठ्य-पुस्तक में दी हुई आकृतियों में से प्रत्येक में विविध सममित रेखाओं (यदि हों तो) की पहचान कीजिए।
हल:
निम्नांकित आकृतियों में विविध सममित रेखाएँ दर्शाई गई हैं:

प्रश्न 5.
पाठ्य-पुस्तक में दी हुई आकृति की प्रतिलिपि बनाइए। किसी एक विकर्ण की सममित रेखा लीजिए तथा कुछ और वर्गों को इस तरह छायांकित कीजिए कि यह आकृति इस विकर्ण के अनुदिश सममित हो जाए। क्या ऐसा करने की एक से अधिक विधियाँ हैं ? क्या यह आकृति दोनों विकर्णों के अनुदिश सममित होगी?
हल:

1. आकृति विकर्ण AC के अनुदिश सममित है।
2. चूँकि आकृति EF और GH के अनुदिश सममित हैं। अत: यह एक से अधिक रेखा के अनुदिश सममित है।
3. यह आकृति विकर्ण BD के भी अनुदिश सममित है।
   

प्रश्न 6.
पाठ्य-पुस्तक में दिये हुए आरेखों की प्रतिलिपियाँ बनाइए तथा प्रत्येक आकार को इस तरह पूरा कीजिए ताकि वह आकार दर्पण रेखा (या रेखाओं) के अनुदिश सममित हो।
हल:
आरेखों की दर्पण रेखा के अनुदिश सममिति निम्न प्रकार है:

प्रश्न 7.
निम्नलिखित आकृतियों के लिए सममित रेखाओं की संख्याएँ बताइए:

(a) एक समबाहु त्रिभुज
(b) एक समद्विबाहु त्रिभुज
(c) एक विषमबाहु त्रिभुज
(d) एक वर्ग
(e) एक आयत
(f) एक समचतुर्भुज
(g) एक समान्तर चतुर्भुज
(h) एक चतुर्भुज
(i) एक समषट्भुज
(j) एक वृत्त

हल:

(a) एक समबाहु त्रिभुज – 3 सममित रेखाएँ
(b) एक समद्विबाहु त्रिभुज – 1 सममित रेखा
(c) एक विषमबाहु त्रिभुज – 0 (शून्य) समपित रेखा
(d) एक वर्ग – 4 सममित रेखाएँ
(e) एक आयत – 2 सममित रेखाएँ
(f) एक समचतुर्भुज – 2 सममित रेखाएँ
(g) एक समान्तर चतुर्भुज – 0 (शून्य) सममित रेखा
(h) एक चतुर्भुज – 0 (शून्य) सममित रेखा
(i) एक समषट्भुज – 6 सममित रेखाएँ
(j) एक वृत्त – असीमित सममित रेखाएँ

प्रश्न 8.
अंग्रेजी वर्णमाला के किन अक्षरों में निम्नलिखित के अनुदिश परावर्तन सममिति (दर्पण परावर्तन से सम्बन्धित सममिति) है :
(a) एक ऊर्ध्वाधर दर्पण
(b) एक क्षैतिज दर्पण
(c) ऊर्ध्वाधर और क्षैतिज दर्पण दोनों।
हल:
(a) एक ऊर्ध्वाधर दर्पण में निम्न अंग्रेजी वर्णमाला के अक्षरों में परावर्तन सममिति है :
A, H, I, M, O, T, U, V, W,X और Y.

(b) क्षैतिज दर्पण के अनुदिश अंग्रेजी अक्षर, जिनमें परावर्तन सममिति है:
B,C, D, E, H, I,O और X.

(c) अंग्रेजी अक्षर, जिनमें ऊर्ध्वाधर और क्षैतिज दर्पणों के अनुदिश परावर्तन्द सममिति है :
H, I, O और X.

प्रश्न 9.
ऐसे आकारों के तीन उदाहरण दीजिए, जिनमें कोई सममित रेखा न हो।
उत्तर:
ऐसे आकार जिनमें सममित रेखा नहीं है :

1. एक विषमबाहु त्रिभुज
2. एक अनियमित चतुर्भुज
3. अक्षर F.

प्रश्न 10.
आप निम्नलिखित आकृतियों की सममित रेखा के लिए अन्य क्या नाम दे सकते हैं ?
(a) एक समद्विबाहु त्रिभुज
(b) एक वृत्त।
उत्तर:

(a) माध्यिका
(b) वृत्त का व्यास।

पाठ्य-पुस्तक पृष्ठ संख्या # 288 प्रयास कीजिए

प्रश्न 1.
(a) क्या अब आप एक समबाहु त्रिभुज के लिए, घूर्णन सममिति के क्रम को बता सकते हैं (संलग्न आकृति) ?

(b) जब उपरोक्त त्रिभुज को उसके केन्द्र के परितः (चारों ओर) 120° के कोण पर घुमाया जाता है, तो कितनी स्थितियों में त्रिभुज (स्थिति के अनुसार) पहले जैसा ही लगता है ?
हल:
(a) ∵ ऐसी तीन स्थितियाँ हैं जहाँ कि त्रिभुज एक जैसे दिखाई देंगे। अतः इसमें क्रम 3 की घूर्णन स्थितियाँ हैं। (120°,240°,360°)
(b) यहाँ केवल एक स्थिति होगी, जबकि त्रिभुज ठीक पहले जैसी स्थिति में दिखाई देगा, जबकि इसे केन्द्र के परितः 120° पर घुमाया जाएगा।

प्रश्न 2.
निम्नलिखित में से कौन-से आकारों (संलग्न आकृति) में अंकित बिन्दुओं के परितः (चारों ओर) घूर्णन सममिति है।

हल:
क्योंकि हम जानते हैं कि जब कोई आकृति एक कोण के द्वारा एक बिन्दु पर घूर्णन करती है और पहले जैसी दिखाई देती है, तो उसे घूर्णन सममिति कहते हैं। इस प्रकार, आकृति (i), (ii) व (iv) में घूर्णन सममिति है।

इन्हें कीजिए

दो एक जैसे (सर्वांगसम चतुर्भुज खींचिए, एक समान्तर चतुर्भुज ABCD एक कागज पर तथा दूसरा समान्तर चतुर्भुज A’B’C’D’ एक पारदर्शक शीट (Transparent sheet) पर। उनके विकर्णों के प्रतिच्छेद बिन्दुओं को क्रमशः 0 और 0′ से अंकित (या व्यक्त) कीजिए। समान्तर चतुर्भुजों को इस प्रकार रखिए कि A’ शीर्ष A पर रहे, B’ शीर्ष B पर रहे, इत्यादि।

इन आकारों में, अब बिन्दु O पर एक पिन लगाइए। अब पारदर्शक शीट को दक्षिणावर्त दिशा में घुमाइए।

प्रश्न (i) एक पूरे चक्कर में पारदर्शकशीट पर बना आकार कागज पर बने आकार से कितनी बार संपाती होता है।
(ii) इसमें घूर्णन सममिति का क्या क्रम है ?
हल:
(i) जब हम पारदर्शक शीट को दक्षिणावर्त दिशा में घुमाते हैं, तो दो स्थितियाँ प्राप्त होती हैं। पहली स्थिति में जब शीर्ष A’ शीर्ष A पर होता है और दूसरी स्थिति में शीर्ष A’ शीर्ष C पर होता है। इससे स्पष्ट होता है कि पूरा चक्कर घुमाने (360°) पर समान्तर चतुर्भुज की दो स्थितियाँ हैं, जहाँ यह एक जैसा दिखाई देगा।
(ii) इसमें क्रम 2 की घूर्णन सममिति होगी।

पाठ्य-पुस्तक पृष्ठ संख्या # 289

प्रयास कीजिए

प्रश्न 1.
दी हुई आकृतियों के लिए x से अंकित बिन्दु के परितः घूर्णन सममिति का क्रम बताइए (संलग्न आकृति)।

हल:
जब आकृति (i) को अंकित बिन्दु के परितः घुमाया जाता है, तो यह आकृति चार स्थितियों (90°, 180°,270° और 360°) में मूल आकृति जैसी दिखती है। अतः आकृति (i) में क्रम 4 की घूर्णन सममिति होगी।

जब आकृति (ii) को अंकित बिन्दु के परितः घुमाया जाता है, तो यह आकृति तीन स्थितियों (120°, 240° और 360°) में | मूल आकृति जैसी दिखती है। अतः आकृति (ii) में क्रम 3 की घूर्णन सममिति होगी।

जब आकृति (iii) को अंकित बिन्दु के परितः घुमाया जाता है, तो यह आकृति दो स्थितियों (180° और 360°) में मूल आकृति जैसी दिखती है। अतः आकृति (iii) में क्रम 2 की घूर्णन सममिति होगी।

पाठ्य-पुस्तक पृष्ठ संख्या # 290

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 13 घातांक और घात Ex 13.3

प्रश्न 1.
निम्नलिखित संख्याओं को प्रसारित रूप में लिखिए :
279404, 3006194, 2806196, 120719, 20068
हल:
(i) 279404
= 2 × 100000 + 7 × 10000 + 9 × 1000
+ 4 × 100 + 0 × 10 + 4 × 1
= 2 × 105 + 7 × 104 + 9 × 103 + 4 × 10²
+ 0 × 101 + 4 × 100

(ii) 3006194
= 3 × 1000000 + 0 × 100000 + 0 × 10000
+ 6 × 1000 + 1 × 100 + 9 × 10 + 4 × 1
= 3 × 10⁶ + 0 × 10⁵ + 0 × 10⁴ + 6 × 10³
+ 1 × 10² + 9 × 10¹ + 4 × 10⁰

(ii) 2806196
= 2 × 1000000 + 8 × 100000 + 0 × 10000
+ 6 × 1000 + 1 × 100 + 9 × 10 + 6 × 1
= 2 × 10⁶ + 8 × 10⁵ + 0 × 10⁴ + 6 × 10³
+ 1 × 10² + 9 × 10¹ + 6 × 10⁰

(iv) 120719
= 1 × 100000 + 2 × 10000 + 0 × 1000
+ 7 × 100 + 1 × 10 + 9 × 1
= 1 × 10⁵ + 2 × 10⁴ + 0 × 10³ + 7 × 10²
+ 1 × 10¹ + 9 × 10⁰

(v) 20068
= 2 × 10000 + 0 × 1000 + 0 × 100
+ 6 × 10 + 8 × 1 = 2 × 10⁴ + 0 × 10³ + 0 × 10²
+ 6 × 10¹ + 8 × 10⁰

प्रश्न 2.
निम्नलिखित प्रसारित रूपों में से प्रत्येक के लिए संख्या ज्ञात कीजिए:
(a) 8 × 10⁴ + 6 × 10³ + 0 × 10² + 4 × 10¹ + 5 × 10⁰
(b) 4 × 10⁵ + 5 × 10³ + 3 × 10² + 2 × 10⁰
(c) 3 × 10⁴ + 7 × 10² + 5 × 10⁰
(d) 9 × 10⁵ + 2 × 10² + 3 × 10¹
हल:
(a) 8 × 10⁴ + 6 × 10³ + 0 × 10² + 4 × 10¹ + 5 × 10⁰
= 8 × 10000 + 6 × 1000 + 0 × 100 +4 × 10 + 5 × 1
= 80000 + 6000 + 0 + 40 + 5
= 86045

(b) 4 × 10⁵ + 5 × 10³ + 3 × 10² + 2 × 10⁰
= 4 × 100000 + 5 × 1000 + 3 × 100 + 2 × 1
= 400000 + 5000 + 300 + 2
= 405302

(c) 3 × 10⁴ + 7 × 10² + 5 × 10⁰
= 3 × 10000 + 7 × 100 + 5 × 1
= 30000 + 700 + 5
= 30705

(d) 9 × 10⁵ + 2 × 10² + 3 × 10¹
= 9 × 100000 + 2 × 100 + 3 × 10
= 900000 + 200 + 30
= 900230

प्रश्न 3.
निम्नलिखित संख्याओं को मानक रूप में व्यक्त कीजिए:
(i) 5,00,00,000
(ii) 70,00,000
(iii) 3,18,65,00,000
(iv) 3,90,878
(v) 39087.8
(vi) 3908.78
हल:
(i) 5,00,00,000 = 5 × 10000000
= 5 × 10⁷

(ii) 70,00,000 = 7 × 1000000
= 7 × 10⁶

(iii) 3,18,65,00,000 = 3.186500000 × 10⁹
= 3.1865 × 10⁹

(iv) 3,90,878 = 3.90878 × 10⁵

(v) 39087.8 = 3.90878 × 10⁴

(vi) 3908.78 = 3.90878 × 10³

प्रश्न 4.
निम्नलिखित कथनों में प्रकट होने वाली (आने वाली) संख्याओं को मानक रूप में व्यक्त कीजिए:
(a) पृथ्वी और चन्द्रमा के बीच की दूरी 3,84,000,000 m है।
(b) निर्वात स्थान में प्रकाश की चाल (या वेग) 3,00,000,000 m/sec है।
(c) पृथ्वी का व्यास 1,27,56,000 m है।
(d) सूर्य का व्यास 1,400,000,000 m है।
(e) एक आकाशगंगा में औसतन 100,000,000,000 तारे हैं।
(f) विश्व मण्डल (या सौर मण्डल) 12,000,000,000 वर्ष पुराना है।
(g) आकाशगंगा के मध्य से सूर्य की दूरी 300,000,000,000,000,000,000 m आंकलित की गई है।
(h) 1.8 g भार वाली पानी की एक बूंद में 60,230,000,000,000,000,000,000 अणु (molecules) होते हैं।
(i) पृथ्वी में 1,353,000,000 km³ समुद्र जल है।
(j) मार्च 2001 में भारत की जनसंख्या 1,027,000,000 थी।
हल:
(a) पृथ्वी और चन्द्रमा के बीच की दूरी
= 3,84,000,000 m
= 3.84000,000 × 10⁸ = 3.84 m × 10⁸ m

(b) निर्वात स्थान में प्रकाश की चाल
= 3.00,000,000 m/sec = 3 × 10⁸ m/sec

(c) पृथ्वी का व्यास = 12756000 m
= 1.2756000 × 10⁷ m = 1.2756 × 10⁷ m

(d) सूर्य का व्यास = 1,400,000,000m
= 1.400,000,000 × 10⁹ m
= 1.4 × 10⁹ m

(e) एक आकाशगंगा में औसतन तारे
= 1,00.000.000,000 = 1 × 10¹¹

(f) विश्वमण्डल पुराना है = 12,000,000,000
= 1.2 × 10¹⁰ वर्ष

(g) आकाश गंगा से सूर्य की दूरी
= 300,000,000,000,000,000,000 m
= 3 × 10²⁰ m

(h) 1.8g भार वाली पानी की बँद में अण
= 60,230,000,000,000,000,000,000
= 6.023 × 10²²

(i) पृथ्वी में समुद्र जल
= 1,353,000,000 km³
= 1.353 × 10⁹ km³

(j) मार्च 2001 में भारत की जनसंख्या
= 1,027,000,000 = 1.027 × 10⁹

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 13 घातांक और घात Ex 13.2

प्रश्न 1.
घातांकों के नियमों का प्रयोग करते हुए, सरल कीजिए और उत्तर को घातांकीय रूप में लिखिए :
(i) 3² × 3⁴ × 3⁸
(ii) 6¹⁵ ÷ 6¹⁰
(iii) a³ × a²
(iv) 7^x × 7²
(v) (5²)³ ÷ 5³
(vi) 2⁵ × 5⁵
(vii) a⁴ × b⁴
(viii) (3⁴)³
(ix) (2²⁰ ÷ 2¹⁵) × 2³
(x) 8^t ÷ 8²
हल:
(i) 3² × 3⁴ × 3⁸ = 3²⁺⁴⁺⁸ = 3¹⁴
(∵ a^m × aⁿ × a^r = a^m+n+r)

(ii) 6¹⁵ ÷ 6¹⁰ = 6^15-10
(∵ a^m ÷ aⁿ = a^m-n)
= 6⁵

(iii) a³ × a² = a³⁺²
(∵ a^m × aⁿ = a^m+n)
= a⁵

(iv) 7^x × 7² = 7^x+2
(∵ a^m × aⁿ = a^m+n)

(v) (5²)³ ÷ 5³ = 5^2×3 ÷ 5³ = 5⁶ ÷ 5³
[∵ (a^m)ⁿ = a^mn, a^m ÷ aⁿ = a^m-n)]
= 5^6-3 = 5³

(vi) 2⁵ × 5⁵ = (2 × 5)⁵ [∵ a^m × b^m = (ab)^m]
= 10⁵

(vii) a⁴ × b⁴ = (a × b)⁴ [∵ a^m × b^m = (ab)^m]
= (ab)⁴

(viii) (3⁴)³ = 3^4×3 [∵ (a) = (a^m)ⁿ = a^mn]
= 3¹²

(ix) (2²⁰ ÷ 2¹⁵) × 2³ = (2^20-15) × 2³
[∵ a^m ÷ aⁿ = a^m-n, a^m × aⁿ = a^m+n]
= 2⁵ × 2³ = 2⁵⁺³ = 28

(x) 8^t ÷ 8² = 8^t-2 (∵ a^m + aⁿ = a^m-n)

प्रश्न 2.
निम्नलिखित में से प्रत्येक को सरल करके घातांकीय रूप में व्यक्त कीजिए:

हल:

प्रश्न 3.
बताइए कि निम्नलिखित कथन सत्य हैं या असत्य तथा अपने उत्तर का कारण भी दीजिए :
(i) 10 × 10¹¹ = 100¹¹
(ii) 2³ > 5²
(iii) 2³ × 3² = 6⁵
(iv) 3⁰ = (1000)⁰
हल:
(i) L.H.S. = 10 × 10¹¹ = 10¹²
और R.H.S. = (100)¹¹ = (10²)¹¹
= 10^2×11 = 10²²
∴ 10 × 10¹¹ ≠ 100¹¹
अत: कथन असत्य है।
यहाँ L.H.S ≠ R. H. S.

(ii) L.H.S. = 2³ = 2 × 2 × 2 = 8
और R.H.S. = 5² = 5 × 5 = 25
यहाँ L.H.S. < R. H. S.
8 < 25 अर्थात् 2³ < 5²
अत: कथन असत्य है।

(iii) ∵ L.H.S. = 2³ × 3² = 2 × 2 × 2 × 3 × 3
= 72
R.H.S. = 6⁵ = 6 × 6 × 6 × 6 × 6
= 7,776
यहाँ L.H.S. ≠ R.H.S.
∴ 72 ≠ 7,776 अर्थात् 2³ × 3² ≠ 6⁵
अत: कथन असत्य है।

(iv) 3⁰ = (1000)⁰
∵ 3⁰ = 1 और (1000)⁰ = 1
यहाँ L.H.S. = R.H.S.
∴ 3⁰ = (1000)⁰
अत: कथन सत्य है।

प्रश्न 4.
निम्नलिखित में से प्रत्येक को केवल अभाज्य गुणनखण्डों की घातों के गुणनफल के रूप में व्यक्त कीजिए:
(i) 108 × 192
(ii) 270
(iii) 729 × 64
(iv) 768
हल:

∵ 108 = 2 × 2 × 3 × 3 × 3 = 22 × 33
और 192 = 2 × 2 × 2 × 2 × 2 × 2 × 3
= 2⁶ × 3
∴ 108 × 192 = 2² × 3³ × 2⁶ × 3
= 2⁸ × 3⁴

∴ 270 = 2 × 3 × 3 × 3 × 5
= 2 × 3³ × 5

∵ 729 = 3 × 3 × 3 × 3 × 3 × 3 = 3⁶
और 64 = 2 × 2 × 2 × 2 × 2 × 2 = 2⁶
∴ 729 × 64 = 3⁶ × 2⁶

∴ 768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
= 2⁸ × 3¹ = 2⁸ × 3

प्रश्न 5.
सरल कीजिए :

हल:

पाठ्य-पुस्तक पृष्ठ संख्या # 277

प्रयास कीजिए

प्रश्न 1.
10 की घातों का प्रयोग करते हुए घातांकीय रूप में प्रसारित कीजिए:
(i) 172
(ii) 5643
(iii) 56439
(iv) 176428
हल:
(i) 172 = 1 × 100 + 7 × 10 + 2 × 1
= 1 × 10² + 7 × 10¹ + 2 × 10⁰

(ii) 5643 = 5 × 1000 + 6 × 100 + 4 × 10 + 3 × 1
= 5 × 10³ + 6 × 10² + 4 × 10¹ + 3 × 10⁰

(iii) 56439 = 5 × 10000 + 6 × 1000 + 4 × 100 +3 × 10 + 9 × 1
= 5 × 10⁴ + 6 × 10³ + 4 × 10² + 3 × 10¹ + 9 × 10⁰

(iv) 176428 = 1 × 100000 + 7 × 10000 + 6 × 1000 +4 × 100 + 2 × 10 + 8 × 1
= 1 × 10⁵ + 7 × 10⁴ + 6 × 10³
+4 × 10² + 2 × 10¹ + 8 × 10⁰

पाठ्य-पुस्तक पृष्ठ संख्या # 279

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 13 घातांक और घात Ex 13.1

प्रश्न 1.
निम्नलिखित के मान ज्ञात कीजिए :
(i) 2⁶
(ii) 9³
(iii) 11²
(iv) 5⁴
हल:
(i) 2⁶ = 2 × 2 × 2 × 2 × 2 × 2 = 64
(iii) 9³ = 9 × 9 × 9 = 729
(iii) 11² = 11 × 11 = 121
(iv) 5⁴ = 5 × 5 × 5 × 5 = 625

प्रश्न 2.
निम्नलिखित को घातांकीय रूप में व्यक्त कीजिए:
(i) 6 × 6 × 6 × 6
(ii) t × t
(iii) b × b × b × b
(iv) 5 × 5 × 7 × 7 × 7
(v) 2 × 2 × a × a
(vi) a × a × a × c × c × c × c × d
हल:
(i) 6 × 6 × 6 × 6 = 6⁴
(ii) t × t = t²
(iii) b × b × b × b = b⁴
(iv) 5 × 5 × 7 × 7 × 7 = 5² × 7³
(v) 2 × 2 × a × a = 2² × a²
(vi) a × a × a × c × c × c × c × d = a³ × c⁴ × d

प्रश्न 3.
निम्नलिखित संख्याओं में से प्रत्येक को घातांकीय संकेतन में व्यक्त कीजिए :
(i) 512
(ii) 343
(iii) 729
(iv) 3125
हल:

प्रश्न 4.
निम्नलिखित में से प्रत्येक भाग में, जहाँ भी सम्भव हो, बड़ी संख्या को पहचानिए :
(i) 4³ या 3⁴
(ii) 5³ या 3⁵
(iii) 2⁸ या 8²
(iv) 100² या 2¹⁰⁰
(v) 2¹⁰ या 10²
हल:
(i) ∵ 4³ = 4 × 4 × 4 = 64
और 3⁴ = 3 × 3 × 3 × 3 = 81
∵ 81 > 64 ∴ 3⁴ > 4³
अतः 3⁴ बड़ा है।

(ii) ∵ 5³ = 5 × 5 × 5 = 125
और 3⁵ = 3 × 3 × 3 × 3 × 3 = 243
∵ 243 > 125 ∴ 3⁵ > 5³
अतः 3⁵ बड़ा है।

(iii) ∵ 2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 256
और 8² = 8 × 8 = 64
∵ 256 > 64 ∴ 2⁸ > 8²
अतः 28 बड़ा है।

(iv) ∵ 100² = 100 × 100 = 10000
और 2¹⁰⁰ = (2¹⁰)¹⁰
= (2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2)¹⁰
= (1024)¹⁰ = (1024)^5×2
= (1024 × 1024)⁵
= (1048576)⁵
∵ 1048576 > 10000
∴ (1048576)⁵ > 100²
या (2¹⁰)¹⁰ > 100² या 2¹⁰⁰ > 100²
अत: (2¹⁰)¹⁰ बड़ा है।

(v) ∵ 2¹⁰ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 1024
और 10² = 10 × 10 = 100
∵ 1024 > 100, ∴ 2¹⁰ > 10²
अतः 2¹⁰ बड़ा है।

प्रश्न 5.
निम्नलिखित में से प्रत्येक को उनके अभाज्य गुणनखण्डों की घातों के गुणनफल के रूप में व्यक्त कीजिए:
(i) 648
(ii) 405
(iii) 540
(iv) 3600
हल:
(i) 648

∴ 648 = 2 × 2 × 2 × 3 × 3 × 3 × 3
= 23 × 34

(ii)405

∴ 405 = 3 × 3 × 3 × 3 × 5
= 34 × 5

(iii) 540

∴ 540 = 2 × 2 × 3 × 3 × 3 × 5
= 22 × 33 × 5

(iv) 3600

∴ 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
= 2⁴ × 3² × 5²

प्रश्न 6.
सरल कीजिए:
(i) 2 × 10³
(ii) 7² × 2²
(iii) 2³ × 5
(iv) 3 × 4⁴
(v) 0 × 10²
(vi) 5² × 3³
(vii) 2⁴ × 3²
(viii) 3² × 10⁴
हल:
(i) 2 × 10³ = 2 × 1000 = 2000
(ii) 7² × 2² = 49 × 4 = 196
(iii) 2³ × 5 = 8 × 5 = 40
(iv) 3 × 4⁴ = 3 × 256 = 768
(v) 0 × 10² = 0 × 100 = 0
(vi) 5² × 3³ = 25 × 27 = 675
(vii) 2⁴ × 3² = 16 × 9 = 144
(viii) 3² × 10⁴ = 9 × 10000 = 90000

प्रश्न 7.
सरल कीजिए:
(i) (-4)³
(ii) (-3) × (-2)³
(iii) (-3)² × (-5)²
(iv) (-2)³ × (-10)³
हल:
(i) (-4)³ = (-4) × (-4) × (-4)
= -64

(ii) (-3) × (-2)³ = (-3) (-2) (-2) (-2)
= (-3) × (-8) = 24

(iii) (-3)² × (-5)² = (-3) (-3) (-5) (-5)
= 9 × 25 = 225

(iv) (-2)³ × (-10)3 = (-2)(-2)(-2) (-10) (-10) (- 10)
= (-8) × (-1000) = 8000

प्रश्न 8.
निम्नलिखित संख्याओं की तुलना कीजिए :
(i) 2.7 × 10¹²; 1.5 × 10⁸
(ii) 4 × 10¹⁴;3 × 10¹⁷
हल:
(i) ∵ 2.7 × 10¹² = \(\frac { 27 }{ 10 } \) × 10¹²
= 27 × 10¹¹ में 13 अंक होंगे।
और 1.5 × 10⁸ = \(\frac { 27 }{ 10 } \) × 10⁸
= 15 × 10⁷ में 9 अंक होंगे।
स्पष्ट है कि 27 × 10¹¹ > 15 × 10⁷
⇒ 2.7 × 10¹² > 1.5 × 10⁸

(ii) ∵ 4 × 10¹⁴ में 15 अंक होंगे
और 3 × 10¹⁷ में 18 अंक होंगे।
∴ 4 × 10¹⁴ < 3 × 10¹⁷

पाठ्य-पुस्तक पृष्ठ संख्या # 270

प्रयास कीजिए

प्रश्न 1.
सरल करके घातांकीय रूप में लिखिए :
(i) 2⁵ × 2³
(ii) p³ × p²
(iii) 4³ × 4²
(iv) a³ × a² × a⁷
(v) 5³ × 5⁷ × 5¹²
(vi) (-4)¹⁰⁰ × (-4)²⁰
हल:
(i) 2⁵ × 2³ = 2⁵⁺³ = 2⁸
(ii) p³ × p² = p³⁺² = p⁵
(iii) 4³ × 4² = 4³⁺² = 4⁵
(iv) a³ × a² × a⁷ = a³⁺²⁺⁷ = a¹²
(v) 5³ × 5⁷ × 5¹² = 5³⁺⁷⁺¹² = 5²²
(vi) (-4)¹⁰⁰ × (-4)²⁰ = (-4)¹⁰⁰⁺²⁰ = (-4)¹²⁰

पाठ्य-पुस्तक पृष्ठ संख्या # 271

प्रयास कीजिए

प्रश्न 1.
सरल करके घातांकीय रूप में लिखिए : उदाहरण के लिए, 116 + 113 = 114
(i) 2⁹ ÷ 2³
(ii) 10⁸ ÷ 10⁴
(iii) 9¹¹ ÷ 9⁷
(iv) 20¹⁵ ÷ 20¹³
(v) 7¹³ ÷ 7¹⁰
हल:
(i) 2⁹ ÷ 2³ = 2^9-3 = 2⁶
(ii) 10⁸ ÷ 10⁴ = 10^8-4 = 10⁴
(iii) 9¹¹ ÷ 9⁷ = 9^11-7 = 9⁴
(iv) 20¹⁵ ÷ 20¹³ = 20^15-13 = 20²
(v) 7¹³ ÷ 7¹⁰ = 7^13-10 = 7³

प्रयास कीजिए

प्रश्न 1.
सरल करके, उत्तर को घातांकीय रूप में व्यक्त कीजिए:
(i) (6²)⁴
(ii) (2²)¹⁰⁰
(iii) (7⁵⁰)²
(iv) (5³)⁷
हल:
(i) (6²)⁴ = 6^2×4 = 68
(ii) (2²)¹⁰⁰ = 2^2×100 = 2²⁰⁰
(iii) (7⁵⁰)² = 7^50×2 = 7¹⁰⁰
(iv) (5³)⁷ = 5^3×7 = 5²¹

पाठ्य-पुस्तक पृष्ठ संख्या # 273

प्रयास कीजिए

प्रश्न 1.
a^m × b^m = (ab)^m का प्रयोग करके, अन्य रूप में बदलिए:
(i) 4³ × 2³
(ii) 2⁵ × b⁵
(iii) a² × t²
(iv) 5⁶ × (-2)⁶
(v) (-2)⁴ × (-3)⁴
हल:
(i) 4³ × 2³ = (4 × 2)³ = (8)³
(ii) 2⁵ × b⁵ = (2 × b)⁵ = (2b)⁵
(iii) a² × t² = (a × t)² = (at)²
(iv) 56 × (-2)² = {5 × (-2)}²
= (-10)⁶ = (10)⁶
(v) (-2)⁴ × (-3)⁴ = {(-2) × (-3)}⁴ = (6)⁴

प्रयास कीजिए

प्रश्न 1.
a^m + b^m = (\(\frac { a }{ b } \))m का प्रयोग करके, अन्य रूप में बदलिए:
(i) 4⁵ ÷ 3⁵
(ii) 2⁵ ÷ b⁵
(iii) (-2)³ ÷ b³
(iv) p⁴ ÷ q⁴
(v) 5⁶ ÷ (-2)⁶
हल:

पाठ्य-पुस्तक पृष्ठ संख्या # 276

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.4

प्रश्न 1.
बराबर लम्बाई के रेखाखण्डों से बनाए गए अंकों के पैटर्न को देखिए। आप रेखाखण्डों से बने हुए इस प्रकार के अंकों को इलेक्ट्रॉनिक घड़ियों या कैलकुलेटरों पर देख सकते हैं।

यदि बनाए गए अंकों की संख्या n ली जाए, तो उसके लिए आवश्यक रेखाखण्डों की n संख्या दर्शाने वाला बीजीय व्यंजक पैटर्न के दाईं ओर लिखा गया है। 6,4,8 के प्रकार के 5, 10, 100 अंकों को बनाने के लिए कितने रेखाखण्डों की आवश्यकता होगी?
हल:
(i) ∵ 6 की तरह n अंकों को बनाने में लगे रेखाखण्डों की संख्या
= (5n + 1)
∴ 5 अंकों की संख्या के लिए रेखाखण्डों की संख्या
= 5 × 5 + 1 = 25 + 1 = 26
10 अंकों की संख्या के लिए रेखाखण्डों की संख्या
= 5 × 10 + 1 = 50 + 1 = 51
100 अंकों की संख्या के लिए रेखाखण्डों की संख्या
= 5 × 100 + 1 = 500 + 1 = 501

(ii) ∵ 4 की तरह n अंकों को बनाने के लिए रेखाखण्डों की संख्या = (3n + 1)
∴ 5, 10, 100 अंकों को बनाने के लिए रेखाखण्डों की संख्या क्रमशः
3 × 5 + 1 = 15 + 1 = 16
3 × 10 + 1 = 30 + 1 = 31
3 × 100 + 1 = 300 + 1 = 301

(iii) 8 की तरह n अंकों को बनाने में लगे रेखाखण्डों की संख्या = (5n + 2)
∴ 5, 10, 100 को बनाने में लगे रेखाखण्डों की संख्या क्रमशः
5 × 5 + 2 = 25 + 2 = 27
5 × 10 + 2 = 50 + 2 = 52
5 × 100 + 2 = 500 + 2 = 502

प्रश्न 2.
संख्या पैटों की निम्नलिखित सारणी को पूरा करने के लिए, दिए हुए बीजीय व्यंजकों का प्रयोग कीजिए:

हल:
(i) व्यंजक (2n – 1) के लिए
100 वाँ पद = 2 × 100 – 1 = 200 – 1 = 199

(ii) व्यंजक (3n + 2) के लिए
5 वाँ पद = 3 × 5 + 2 = 15 + 2 = 17
10 वाँ पद = 3 × 10 + 2 = 30 + 2 = 32
100 वाँ पद = 3 × 100 + 2 = 300 + 2 = 302

(iii) व्यंजक (4n + 1) के लिए
5 वाँ पद = 4 × 5 + 1 = 20 + 1 = 21
10 वाँ पद = 4 × 10 + 1 = 40 + 1 = 41
100 वाँ पद = 4 × 100 + 1 = 400 + 1 = 401

(iv) व्यंजक 7n + 20 के लिए
5 वाँ पद = 7 × 5 + 20 = 35 + 20 = 55
10 वाँ पद = 7 × 10 + 20 = 70 + 20 = 90
100 वाँ पद = 7 × 100 + 20 = 700 + 20 = 720

(v) व्यंजक n² + 1 के लिए
5 वाँ पद = (5)² + 1 = 25 + 1 = 26
10 वाँ पद = (10)² + 1 = 100 + 1 = 101

MP Board Class 7th Maths Solutions

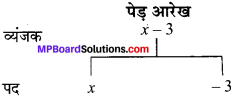
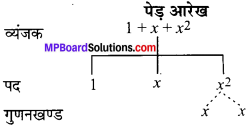
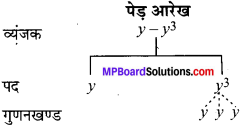
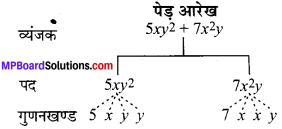
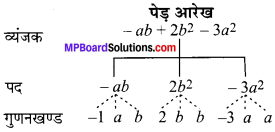
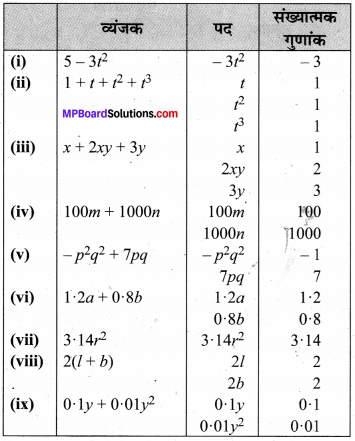
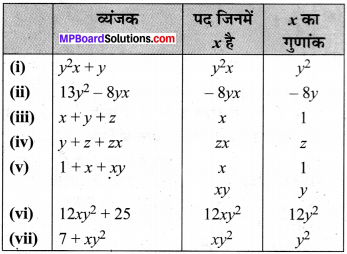
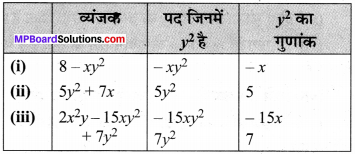
MP Board Class 7th Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.3

प्रश्न 1.
यदि m = 2 है, तो निम्नलिखित के मान ज्ञात कीजिए:
(i) m – 2
(ii) 3m – 5
(iii) 9 – 5m
(iv) 3m² – 2m – 7
(v) \(\frac { 5m }{ 2 } \) – 4
हल:
(i) m – 2 ∵ m = 2
∴ m – 2 = 2 – 2 = 0
(ii) 3m – 5 = 3 × 2 – 5 = 6 – 5 = 1

(iii) 9 – 5m = 9 – 5 × 2 = 9 – 10 = -1

(iv) 3m² – 2m – 7
= 3(2)² – 2 × 2 – 7
= 3 × 4 – 4 – 7 = 12 – 11 = 1

(v) \(\frac { 5m }{ 2 } \) – 4 = \(\frac{5 \times 2}{2}\) – 4 = 5 – 4 = 1

प्रश्न 2.
यदि p = -2 है, तो निम्नलिखित के मान ज्ञात कीजिए:
(i) 4p + 7
(ii) -3p + 4p + 7
(iii) -2p³ – 3p² + 4p + 7
हल:
यहाँ p = -2
(i) 4p + 7 = 4 × (-2) + 7 = – 8 + 7 = – 1

(ii) -3p² + 4p + 7
= -3(-2)² + 4(-2) + 7
= -3 × 4 – 8 + 7
= – 12 – 8 + 7 = – 13

(iii) -2p³ – 3p² + 4p + 7
= -2(-2)³ – 3(-2)² + 4(-2) + 7
= -2(-8) – 3 × 4 – 8 + 7
= 16 – 12 – 8 + 7 = 23 – 20 = 3

प्रश्न 3.
निम्नलिखित व्यंजकों के मान ज्ञात कीजिए, जब x = -1 है:
(i) 2x – 7
(ii) -x + 2
(iii) x² + 2x + 1
(iv) 2x² – x – 2
हल:
यहाँ x = -1
(i) 2x – 7 = 2 (-1) – 7 = – 2 – 7 = – 9
(ii) -x + 2 = – (-1) + 2 = 1 + 2 – 3
(iii) x² + 2x + 1 = (-1)² + 2(- 1) + 1
= 1 – 2 + 1 = 2 – 2 = 0
(iv) 2x² – x – 2 = 2 (-1)² – (-1) – 2
= 2 × 1 + 1 – 2 = 2 + 1 – 2 = 1

प्रश्न 4.
यदि a = 2 और b = -2 हो, तो निम्नलिखित के मान ज्ञात कीजिए:
(i) a² + b²
(ii) a² + ab + b²
(iii) a² – b²
हल:
यहाँ, a = 2 और b = -2
(i) a² + b² = (2)² + (-2)² = 4 + 4 = 8
(ii) a² + ab + b² = (2)² + 2 (-2) + (-2)²
= 4 – 4 + 4 = 4
(iii) a² – b² = (2)² – (-2)² = 4 – 4 = 0

प्रश्न 5.
जब a = 0 और b = -1 है, तो दिए हुए व्यंजकों के मान ज्ञात कीजिए:
(i) 2a + 2b
(ii) 2a² + b + 1
(iii) 2a²b + 2ab² + ab
(iv) a² + ab + 2
हल:
यहाँ, a = 0 और b = -1
(i) 2a + 2b = 2 × 0 + 2x (-1)
= 0 – 2 = – 2

(ii) 2a² + b² + 1 = 2 × (0)² + (-1)² + 1
= 2 × 0 + 1 + 1 = 2

(iii) 2a²b + 2ab² + ab = 2 (0)² (-1) + 2 (0) (-1)² + 0 × (-1)
= 0 + 0 + 0 = 0

(iv) a² + ab + 2 = (0) + 0 (-1) + 2
= 0 + 0 + 2 – 2

प्रश्न 6.
इन व्यंजकों को सरल कीजिए तथा इनके मान ज्ञात कीजिए, जब x का मान 2 है:
(i) x + 7 + 4 (x – 5)
(ii) 3(x + 2) + 5x – 7
(iii) 6x + 5(x – 2)
(iv) 4(2x – 1)+ 3x + 11
हल:
(i) x + 7 + 4 (x – 5) = x + 7 + 4x – 20
= x + 4x + 7 – 20
= 5x – 13
x = 2 रखने पर, 5x – 13 = 5 × 2 – 13
= 10 – 13 = -3

(ii) 3 (x + 2) + 5x – 7 = 3x + 6 + 5x – 7
= 3x + 5x + 6 – 7
= 8x – 1
x = 2 रखने पर,
8x – 1 – 8 × 2 – 1 = 16 – 1 = 15

(iii) 6x + 5(x – 2) = 6x + 5x – 10
= 11x – 10
x = 2 रखने पर,
11x – 10 = 11 × 2 – 10
= 22 – 10 = 12

(iv) 4(2x – 1) + 3x + 11
= 8x – 4 + 3x + 11
= 8x + 3x – 4 + 11
= 11x + 7
x = 2 रखने पर,
11x + 7 = 11 × 2 + 7 = 22 + 7 = 29

प्रश्न 7.
इन व्यंजकों को सरल कीजिए तथा इनके मान ज्ञात कीजिए, जब x = 3,4 = -1 और b = -2 है :
(i) 3x – 5 – x +9
(ii) 2 – 8x + 4x + 4
(iii) 3a + 5 – 8a + 1
(iv) 10 – 3b – 4 – 5b
(v) 2a – 2b – 4 – 5 + a
हल:
(i) 3x – 5 – x + 9 = 2x + 4
x = 3 रखने पर,
2x + 4 = 2 × 3 + 4
= 6 + 4 = 10

(ii) 2 – 8x + 4x + 4 = 6 – 4x
x = 3 रखने पर,
6 – 4x = 6 – 4 × 3
= 6 – 12 = -6

(iii) 3a + 5 – 8a + 1 = -5a + 6
a = -1 रखने पर,
-5a + 6 = -5 × (-1) + 6
= 5 + 6 = 11

(iv) 10 – 3b – 4 – 5b = 6 – 8b.
b – 2 रखने पर,
6 – 8b = 6 – 8 × (-2)
= 6 + 16 = 22

(v) 2a – 2b – 4 – 5 + a = 3a – 2b – 9
a = -1, b = – 2 रखने पर,
3a – 2b – 9 = 3(- 1)-2(- 2)- 9
= -3 + 4 -9 = -8

प्रश्न 8.
(i) यदि z = 10 है, तो z³ – 3(z – 10) का मान ज्ञात कीजिए।
(ii) यदि p = -10 है, तो p² – 2p – 100 का मान ज्ञात कीजिए।
हल:
(i) जब z = 10 है, तो 2
z³ – 3(z – 10) = (10)³ – 3(10 – 10)
= 1000 – 3 × 0
= 1000 – 0 = 1000

(ii) जब p = -10 है, तो
p² – 2p – 100 = (-10)2 – 2(-10) – 100
= 100 + 20 – 100
= 20

प्रश्न 9.
यदि x = 0 पर 2x² + x – a का मान 5 के बराबर है, तो a का मान क्या होना चाहिए ?
हल:
x = 0 पर, 2x² + x – a = 5
∴ 2 × (0)² + 0 – a = 5
या 0 + 0 – a = 5 ⇒ a = -5

प्रश्न 10.
व्यंजक 2(a² + ab) + 3 – ab को सरल कीजिए और इसका मान ज्ञात कीजिए, जब a = 5 और b = -3 है।
हल:
2 (a² + ab) + 3 – ab
= 2a² + 2ab + 3 – ab
= 2a² + 2ab – ab + 3
= 2a² + ab + 3
a = 5 और b = – 3 रखने पर,
2a² + ab + 3 = 2(5)2 + 5 × (-3) + 3
= 2 × 25 + (-15) + 3
= 50 – 15 + 3 = 38

पाठ्य-पुस्तक पृष्ठ संख्या # 261

प्रयास कीजिए

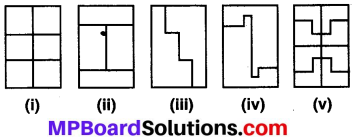
पाठ्य-पुस्तक में दिये गये आधारभूत आकारों को लेकर उपर्युक्त प्रकार के पैटर्न बनाइए :
आकारों को बनाने के लिए आवश्यक रेखाखण्डों की संख्या दाईं ओर लिखी हुई है। साथ ही n आकारों को बनाने के लिए आवश्यक रेखाखण्डों को दर्शाने वाला व्यंजक भी दाईं ओर दिया हुआ है। आगे बढ़िए और ऐसी ही और पैटर्नो की खोज कीजिए।
हल:

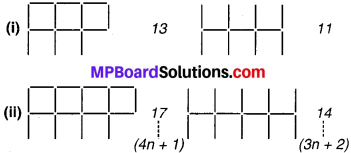
पाठ्य-पुस्तक पृष्ठ संख्या # 262

n भुजा वाले किसी बहुभुज के एक शीर्ष से हम कुल
(n – 3) विकर्ण खींच सकते हैं। एक सप्तभुज (7 भुजाएँ) और अष्टभुज (8 भुजाएँ) के लिए उनकी आकृतियाँ
खींच करके इसकी जाँच कीजिए। यह संख्या एक त्रिभुज (3 भुजाएँ) के लिए क्या है ?
हल:
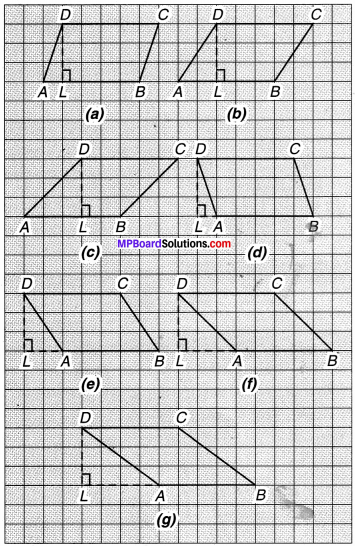
(i) सप्तभुज ABCDEFG में, विकर्ण AC, AD, AE, AF हैं, अर्थात् इसमें 4 विकर्ण हैं। यदि n – 3 में n = 7 रखें, तो विकर्ण = 7 – 3 = 4

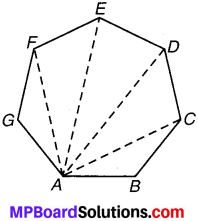
(ii) अष्टभुज ABCDEFGH में विकर्ण AC, AD, AE, AF, AG हैं अर्थात् इसमें 5 विकर्ण हैं। यदि n – 3 में n = 8 रखें, तो विकर्ण = 8 – 3 = 5

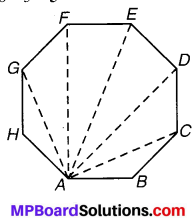
(iii) ∆ABC में कोई विकर्ण नहीं होता है। यदि n – 3 में n = 3 रखें, तो 3 – 3 = 0

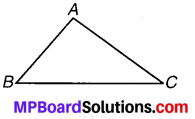
अतः प्रत्येक स्थिति में परिणाम सन्तुष्ट होता है।

पाठ्य-पुस्तक पृष्ठ संख्या # 262-263

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 12 बीजीय व्यंजक Ex 12.2

प्रश्न 1.
समान पदों को संयोजित (मिलान) करके सरल कीजिए:
(i) 21b – 32 + 7b – 20b
(ii) -z² + 13z² – 5z + 7z³ – 15z
(iii)p – (p – q) – q – (q – p)
(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
(v) 5x²y – 5x² + 3yx² – 3y² + x² – 8xy² – 3y²
(vi) (3y² + 5y – 4) – (8y – y² – 4)
हल:
(i) 21b – 32 + 7b – 20b
= 21b + 7b – 20b – 32
= (21 + 7 – 20) b – 32
= 8b – 32

(ii) – z² + 13z² – 5z + 7z³ – 15z
= 7z³ – z² + 13z² – 5z – 15z
= 7z³ + (-1 + 13)z² + (-5 -15) z
= 7z³ + 12z³ – 20z

(iii) p – (p – q) – q – (q – p)
= p – p + q – q – q + p
= p – p + p + q – q – q
= (1 – 1 + 1)p + (1 – 1 – 1)q
= p – q

(iv) 3a – 2b – ab – (a – b + ab) + 3ab + b – a
= 3a – 2b – ab – a + b – ab + 3ab + b – a
= (3a – a – a) + (-2b + b + b) + (-ab -ab + 3ab)
= (3 – 1 – 1)a + (-2 + 1 + 1) b + (- 1 – 1 + 3)ab
= (1)a + (0) b + (1) ab = a + ab

(v) 5x² y – 5x² + 3yx² – 3y² + x² – y² + 8xy²
= (5x²y + 3yx²) + (8xy²) + (-5x² + x²) + (-3y² – y² – 3y²)
= (5 + 3) x²y + 8xy² + (- 5 + 1)x² + (- 3 – 1 – 3) y²
= 8x²y + 8xy² – 4x² – 7y²

(vi) (3y² + 5y – 4) – (8y – y² – 4)
= 3y² + 5y – 4 – 8y + y² + 4
= (3y² + y²) + (5y – 8y) + (- 4 + 4)
= (3 + 1) y² + (5 – 8) y + (- 4 + 4)
= 4y² – 3y + 0 = 4y² – 3y

प्रश्न 2.
जोड़िए:
(i) 3mn, -5mn, 8mn, -4mn
(ii) t – 8tz, 3tz – z, z – 1
(iii) -7mn + 5,12mn + 2, 9mn – 8, -2 mn – 3
(iv) a + b – 3,b – a + 3,a – b + 3
(v) 14x + 10y – 12xy – 13, 18 – 7x – 10y + 8xy,4xy
(vi) 5m – 7n, 3n – 4m + 2, 2m – 3mn – 5
(vii) 4x²y, – 3xy², -5xy², 5x²y
(viii) 3p²q² – 4pq + 5, – 10p²q², 15 + 9pq + 7p²q²
(ix) ab – 4a, 4b – ab, 4a – 4b
(x) x² – y² – 1 – y² – 1 – x², 1 – x² – y²
हल:
(i) अभीष्ट योग
= 3mn + (-5mn) + 8mn + (-4mn)
= [3+ (-5) + 8 + (-4)] mn
= [11 – 9] mn = 2mn

(ii) अभीष्ट योग
= (1 – 8tz) + (3tz – z) + (z – t)
= t – 8tz + 3tz – z + z – t
= (t – t) + (-z + z) + (-8tz + 3tz)
= (1 – 1) t + (- 1 + 1) z + (- 8 + 3) tz
= (0) t + (0) z + (-5)tz = – 5tz

(iii) अभीष्ट योग = (-7mn + 5) + (12mn + 2) + (9mn – 8) + (-2mn – 3)
= -7mn + 5 + 12mn + 2 + 9mn – 8 – 2mm – 3
= (-7mm + 12mn + 9mn – 2mn) + (5 + 2 – 8 – 3)
= (-7 + 12 + 9 – 2) mn + (7 – 11)
= (21 – 9) mn + (-4) = 12mn – 4

(iv) अभीष्ट योग = (a + b – 3) + (b – a + 3) + (a – b + 3)
= a + b – 3 + b – a + 3 + a – b + 3
= ( a – a + a) + (b + b – b) + ( – 3 + 3 + 3)
= (1 – 1 + 1)a + (1 + 1 – 1) b + (- 3 + 6)
= (1) a + (1) b + (3)
= a + b + 3

(v) अभीष्ट योग
= (14x + 10y – 12xy – 13) + (18 – 7x – 10y + 8xy) + 4xy
= 14x + 10y – 12xy – 13 + 18 – 7x – 10y + 8xy + 4xy
= (14x – 7x) + (10y – 10y) + (- 12xy + 8xy + 4xy) + (- 13 + 18)
= (14 – 7) x + (10 – 10)y (- 12 + 8 + 4) xy + (5)
= (7)x + (0)y + (- 12 + 12) xy + (5)
= 7x + (0) y + (0) xy + 5
= 7x + 5.

(vi) अभीष्ट योग
= (5m – 7n) + (3n – 4m + 2) + (2m – 3mn – 5)
= 5m – 7n + 3n – 4m + 2 + 2m – 3mn – 5
= (5m – 4m + 2m) + (-7n + 3n) -3mn + (2 – 5)
= (5 – 4 + 2) m + (- 7 + 3) n – 3 mn – 3
= 3m – 4n – 3mn – 3

(vii) अभीष्ट योग
= 4x²y + (-3xy²) + (-5xy²) + 5x²y
= 4x²y – 3xy – 5xy² + 5x²y
= (4 + 5) x²y + (- 3 – 5) xy²
= 9x²y – 8xy²

(viii) अभीष्ट योग
= (3p²q² – 4pq + 5) + (-10 p²q²) + (15 + 9pq + 7p²q²)
= 3p²q² – 4pq + 5 – 10p²q² + 15 + 9pq + 7p²q²
= 3p²q² – 10p²q² + 7p²q² – 4pq + 9pq + 5 + 15
= (3 – 10 + 7)p²q² + (- 4 + 9) pq + (5 + 15)
= (0)p²q² + 5pq + 20
= 5pq + 20

(ix) अभीष्ट योग
= (ab – 4a) + (4b – ab) + (4a – 4b)
= ab – 4a + 4b – ab + 4a – 4b
= ab – ab – 4a + 4a + 4b – 4b
= (0) ab + (0) a + (0) b
= 0 + 0 + 0 = 0

(x) अभीष्ट योग
= (x² – y² – 1) + (y² – 1 – x²) + (1 – x² – y²)
= x² – y² – 1 + y² – 1 – x + 1 – x² – y²
= x² – x² – x² – y² + y² – y² – 1 – 1 + 1
= (1 – 1 – 1) x² + (- 1 + 1 – 1) y² + (- 1 – 1 + 1)
= – x² – y² – 1

प्रश्न 3.
घटाइए:
(i) y² में से – 5y²
(ii) – 12xy में से 6xy
(iii) (a + b) में से (a – b)
(iv) b (5 – a) में से a (b – 5)
(v) 4m² – 3mn + 8 में से – m² + 5mn
(vi) 5x – 10 में से – x² + 10x – 5
(vii) 3ab – 2a² – 2b² में से 5a² – 7ab + 5b²
(viii) 5p² + 3q² – Pq में से 4pq – 5q² – 3p²
हल:
(i) अभीष्ट अन्तर
y2 – (-5y2)
= y2 + 5 = 6y2

(ii) अभीष्ट अन्तर = – 12xy – 6xy = -18xy

(iii) अभीष्ट अन्तर
= (a + b) – (a – b) = a + b – a + b
= (1 – 1)a + (1 + 1) b = 2b

(iv) अभीष्ट अन्तर
= b (5 – a) – a (b – 5)
= 5b – ab – ab + 5a
= 5a + 5b + ( – 1 – 1) ab
= 5a + 5b – 2ab

(v) अभीष्ट अन्तर
= (4m² – 3mn + 8) – (- m² + 5mn)
= 4m² – 3mn + 8 + m² – 5mn
= 4m² + m² – 3mn – 5mn + 8
= (4 + 1)m + (- 3 – 5)mn + 8
= 5m² – 8mn + 8

(vi) अभीष्ट अन्तर
= (5x – 10) – (- x² + 10x – 5)
= 5x – 10 + x² – 10 x + 5
= x² + (5 – 10) x + (- 10 + 5)
= x² – 5x – 5

(vii) अभीष्ट अन्तर
= (3ab – 2a² – 2b²) – (5a² – 7ab + 5b²)
= 3ab – 2a² – 2b² – 5a² + 7ab – 5b²
= -2a² – 5a² – 2b² – 5b² + 3ab + 7ab
=(- 2 – 5) a² + (- 2 – 5) b² + (3 + 7) ab
= -7a – 7b² + 10ab

(viii) अभीष्ट अन्तर
= (5p² + 3q² – pq) – (4pq – 5q² – 3p²)
= 5p² + 3q² – pq – 4pq + 5q² + 3p²
= 5p² + 3p² + 3q² + 5q² – pq – 4pq
= (5 + 3)p² + (3 + 5) q² + (- 1 – 4)pq
= 8p² + 8q² – 5pq

प्रश्न 4.
(a) 2x² + 3xy प्राप्त करने के लिए x² + xy + ya में क्या जोड़ना चाहिए?
(b) -3a + 7b + 16 प्राप्त करने के लिए 2a + 8b + 10 में से क्या घटाना चाहिए ?
हल:
(a) अभीष्ट व्यंजक
= (2x² + 3xy) – (x² + xy + y²)
= 2x² + 3xy – x² – xy – y²
= 2x² – x² – y² + 3xy – xy
= (2 – 1) x² – y² + (3 – 1)xy
= x² – y² + 2xy

(b) अभीष्ट व्यंजक
= (2a + 8b + 10) – (- 3a + 7b + 16)
= 2a + 8b + 10 + 3a – 7b – 16
= 2a + 3a + 8b – 7b + 10 – 16
= (2 + 3)a + (8 – 7)b + (10 – 16)
= 5a + b – 6

प्रश्न 5.
-x² – y² + 6xy + 20 प्राप्त करने के लिए, 3x² – 4y² + 5xy + 20 में से क्या निकाल लेना चाहिए?
हल:
अभीष्ट व्यंजक = (3x² – 4y² + 5xy + 20) -(- x² – y² + 6xy + 20)
= 3x² – 4y² + 5xy + 20 + x² + y² – 6xy – 20
= 3x² + x² – 4y² + y² + 5xy – 6xy + 20 – 20
= (3 + 1)x² + (- 4 + 1) y² + (5 – 6) xy + (20 – 20)
= 4x² – 3y² – xy + 0
= 4x² – 3y² – xy

प्रश्न 6.
(a) 3x – y + 11 और – y – 11 के योग में से 3x – y – 11 को घटाइए।
(b) 4 + 3x और 5 – 4x + 2x² के योग में से 3x² – 5x और – x² + 2x + 5 के योग को घटाइए।
हल:
(a) 3x – y + 11 और – y – 11 का योग
= (3x – y + 11) + (- y – 11)
= 3x – y + 11 – y – 11
= 3x – y – y + 11 – 11
= 3x – 2y
अब 3x – 2y में से 3x – y – 11 को घटाने पर,
अभीष्ट अन्तर = (3x – 2y) – (3x – y – 11)
= 3x – 2y – 3x + y + 11
= (3x – 3x) + (-2y + y) + 11
= 0 – y + 11
= – y + 11

(b) 4 + 3x और 5 – 4x + 2x² का योग
= 4 + 3x + 5 – 4 x + 2x²
= (4 + 5) + (3x – 4x) + 2x²
= 9 – x + 2x²
3x² – 5x और = x² + 2x + 5 का योग
= 3x² – 5x – x² + 2x + 5
= 3x² – x² – 5x + 2x + 5
= (3 – 1)x² + (- 5 + 2)x + 5
= 2x² – 3x + 5
अब, प्रश्नानुसार
अभीष्ट अन्तर = (9 – x + 2x²) – (2x² – 3x + 5)
= 9 – x + 2x² – 2x² + 3x – 5
= (9 – 5) + (- x + 3x) + (2x² – 2x²)
= 4 + (- 1 + 3)x + (2 – 2) x²
= 4 + (2)x + (0) x²
= 4 + 2x ⇒ 2x +4
पाठ्य-पुस्तक पृष्ठ संख्या # 258

MP Board Class 7th Maths Solutions