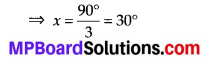Category: Class 7

MP Board Class 7th Maths Solutions Chapter 7 Congruence of Triangles Ex 7.1

Question 1.
Complete the following statements:
(a) Two line segments are congruent if ___ .
(b) Among two congruent angles, one has a measure of 70°; the measure of the other angle is ___.
(c) When we write ∠A = ∠B, we actually mean ___.
Solution:
(a) They have the same length.
(b) 70°
(c) m∠A = m∠B

Question 2.
Give any two real-life examples for congruent shapes.
Solution:
(i) Sheets of same letter pad.
(ii) Biscuits in the same packet.

Question 3.
If ∆ABC ≅ ∆FED under the correspondence ABC ⟷ FED, write all the corresponding congruent parts of the triangles.
Solution:
If ∆ABC ≅ ∆FED, then the corresponding angles and sides will be equal to each other.

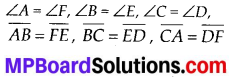
Question 4.
If ∆DEF ⟷ ∆BCA, write the part(s) of ∆BCA that correspond to
(i) ∠E
(ii) \(\overline{E F}\)
(iii) ∠F
(iv) \(\overline{D F}\)
Solution:
(i) ∠C
(ii) \(\overline{C A}\)
(iii) ∠A
(iv) \(\overline{B A}\)

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.5

Question 1.
PQR is a triangle, right-angled at P. If PQ= 10 cm and PR = 24 cm, find QR.
Solution:
By applying Pythagoras theorem in ∆PQR,
(PQ)² + (PR)² = (QR)²
⇒ (10)² + (24)² = (QR)2²
⇒ (QR)² = 100 + 576
= 676 = (26)²
∴ QR = 26 cm

Question 2.
ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Solution:
By applying Pythagoras theorem in AABC,
(AC)² + (BC)² = (AB)²
⇒ (BC)² = (AB)² – (AC)²
= (25)² – (7)²
= 625 – 49 = 576
= (24)²
∴ BC = 24 cm

Question 3.
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

Solution:
By applying Pythagoras theorem,
(15)² = (12)² + a²
⇒ 225 = 144 + a²
⇒ a² = 225 – 144 = 81 = 9²
⇒ a = 9 m
Therefore, the distance of the foot of the ladder from the wall is 9 m.

Question 4.
Which of the following can be the sides of a right triangle?
(i) 2.5 cm, 6.5 cm, 6 cm.
(ii) 2 cm, 2 cm, 5 cm.
(iii) 1.5 cm, 2 cm, 2.5 cm.
In the case of right-angled triangles, identify the right angles.
Solution:
(i) 2.5 cm, 6.5 cm, 6 cm
∴ (2.5)² = 6.25, (6.5)² = 42.25 and (6)² = 36
It can be observed that,
36 + 6.25 = 42.25
⇒ (6)² + (2.5)² = (6.5)²
The square of the length of one side is the sum of the squares of the lengths of the remaining two sides. Hence, these are the sides of a right-angled triangle. Right angle will be in front of the side of measure 6.5 cm.

(ii) 2 cm, 2 cm, 5 cm
∴ (2)² = 4, (2)² = 4 and (5)² = 25
Here, (2)² + (2)² ≠ (5)²
The square of the length of one side is not equal to the sum of the squares of the lengths of the remaining two sides. Hence, these sides are not of a right-angled triangle.

(iii) 1.5 cm, 2 cm, 2.5 cm
∴ (1.5)² = 2.25, (2)² = 4 and (2.5)² = 6.25
Here, 2.25 + 4 = 6.25
⇒ (1.5)² + (2)² = (2.5)²
The square of the length of one side is the sum of the squares of the lengths of the remaining
two sides. Hence, these are the sides of a right-angled triangle.
Right angle will be in front of the side of measure 2.5 cm.

Question 5.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Solution:
In the drawn figure, BC represents the unbroken part of the tree. Point C represents the point where the tree broke and CA represents the broken part of the tree. Triangle ABC, thus formed, is right-angled at B.

Applying Pythagoras C theorem in ∆ABC,
AC² = BC² + AB²
= (5)²+ (12)² BL
= 25 + 144 = 169
= (13)²
∴ AC = 13 m
Thus, original height of the tree = AC + CB = 13m + 5m = 18m

Question 6.
Angles Q and R of a ∆PQR are 25° and 65°. Write which of the following is true:
(i) PQ² + QR² = RP²
(ii) PQ² + RP² = QR²
(iii) RP² + QR² = PQ²

Solution:
The sum of the measures of all interior angles of a triangle is 180°.
∠P + ∠Q + ∠R = 180°
∠P + 25°+ 65° = 180°
∠P + 90° = 180°
∠P = 180° – 90° = 90°
Therefore, ∆PQR is right-angled at point P. Hence, (PR)² + (PQ)² = (QR)²
∴ (ii) is true.

Question 7.
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
Solution:
Let ABCD be the given rectangle with length AB = 40 cm and diagonal AC = 41 cm.
In ∆ABC,
(AC)² = (AB)² + (BC)²
⇒ (4)² = (40)²+ (BQ)²
⇒ (BC)² = 1681 – 1600 = 81 = 9²
∴ BC = 9 cm

∴ Perimeter of rectangle = 2(40 + 9)
= 2(49) = 98 cm.

Question 8.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Solution:
Let ABCD be the given rhombus with diagonals AC = 16 cm and BD = 30 cm.
We know that diagonals of a rhombus bisect each other at right angle.
Let diagonals AC and BD bisects at O.

Hence, perimeter of rhombus = 4 × (17) = 68 cm

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 13 Exponents and Powers Ex 13.3

Question 1.
Write the following numbers in the expanded forms:
279404, 3006194, 2806196, 120719, 20068
Solution:
279404 = 2 × 10⁵ + 7 × 10⁴ + 9 × 10³ + 4 × 10² + 0 × 10¹ + 4 × 10⁰
3006194 = 3 × 10⁶ + 0 × 10⁵ + 0 × 10⁴ + 6 × 10³ + 1 × 10² + 9 × 10¹ + 4 × 10⁰
2806196 = 2 × 10⁶ + 8 × 10⁵ + 0 × 10⁴ + 6 × 10³ + 1 × 10² + 9 × 10¹ + 6 × 10⁰
120719 = 1 × 10⁵ + 2 × 10⁴ + 0 × 10³ + 7 × 10² + 1 × 10¹ + 9 × 10⁰
20068 = 2 × 10⁴ + 0 × 10³ + 0 × 10² + 6 × 10¹ + 8 × 10⁰

Question 2.
Find the number from each of the following expanded forms:
(a) 8 × 10⁴ + 6 × 10³ + 0 × 10² + 4 × 10¹ + 5 × 10⁰
(b) 4 × 10⁵ + 5 × 10³ + 3 × 10² + 2 × 10⁰
(c) 3 × 10⁴ + 7 × 10² + 5 × 10⁰
(d) 9 × 10⁵ + 2 × 10² + 3 × 10¹
Solution:
(a) 8 × 10⁴ + 6 × 10³ + 0 × 10² + 4 × 10¹ + 5 × 10⁰ = 86045
(b) 4 × 10⁵ + 5 × 10³ + 3 × 10² + 2 × 10⁰ = 405302
(c) 3 × 10⁴ + 7 × 10² + 5 × 10⁰ = 30705
(d) 9 × 10⁵ + 2 × 10² + 3 × 10¹ = 900230

Question 3.
Express the following numbers in standard form:
(i) 5,00,00,000
(ii) 70,00,000
(iii) 3,18,65,00,000
(iv) 3,90,878
(v) 39087.8
(vi) 3908.78
Solution:
(i) 50000000 = 5 × 10⁷
(ii) 7000000 = 7 × 10⁶
(iii) 3186500000 = 3.1865 × 10⁹
(iv) 390878 = 3.90878 × 10⁵
(v) 39087.8 = 3.90878 × 10⁴
(vi) 3908.78 = 3.90878 × 1³

Question 4.
Express the number appearing in the following statements in standard form.
(a) The distance between Earth and Moon is 384.0. 000 m.
(b) Speed of light in vacuum is 300,000,000 m/s
(c) Diameter of the Earth is 1,27,56,000 m.
(d) Diameter of the Sun is 1,400,000,000 m.
(e) In a gala×y there are on an average 100,000,000,000 stars.
(f) The universe is estimated to be about 12,0,000,000 years old.
(g) The distance of the Sun from the centre of the Milky Way Gala×y is estimated to be 300,000,000,000,000,000,000 m.
(h) 60, 230, 000, 000, 000, 000, 000, 000 molecules are contained in a drop of water weighing 1.8 gm.
(i) The earth has 1, 353, 000,000 cubic km of sea water.
(j) The population of India was about 1,027,0,000 in March, 2001.
Solution:
(a) 3.84 × 10⁸ m
(b) 3 × 10⁸ m/s
(c) 1.2756 × 10⁷ m
(d) 1.4 × 10⁹ m
(e) 1 × 10¹¹ stars
(f) 1.2 × 10¹¹ years
(g) 3 × 10²⁰ m
(h) 6.023 × 10²² molecules
(i) 1.353 × 10⁹ cubic km
(j) 1.027 × 10⁹

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.4

Question 1.
Is it possible to have a triangle with the following sides?
(i) 2 cm, 3 cm, 5 cm
(ii) 3 cm, 6 cm, 7 cm
(iii) 6 cm, 3 cm, 2 cm
Solution:
In a triangle, the sum of the lengths of either two sides is always greater than the third side.
(i) Given that, the sides of the triangle are 2 cm, 3 cm, 5 cm.
It can be observed that,
(2 + 3) cm = 5 cm
However, 5 cm = 5 cm
Hence, this triangle is not possible.

(ii) Given that, the sides of the triangle are
3 cm, 6 cm, 7 cm.
Here, (3 + 6) cm = 9 cm > 7 cm
(6 + 7) cm = 13 cm > 3 cm
(3 + 7) cm = 10 cm > 6 cm
Hence, this triangle is possible.

(iii) Given that, the sides of the triangle are
6 cm, 3 cm, 2 cm.
Here, (6 + 3) cm = 9 cm > 2 cm
However, (3 + 2) cm = 5 cm < 6 cm Hence, this triangle is not possible.

Question 2.
Take any point 0 in the interior of a triangle PQR. Is

(i) OP + OQ > PQ?
(ii) OQ + OR > QR?
(iii) OR + OP > RP?
Solution:
If O is a point in the interior of a given triangle, then three triangles ∆OPQ, ∆OQR and ∆ORP can be constructed. In a triangle, the sum of the lengths of either two sides is always greater than the third side.
(i) Yes, as OQR is a triangle with sides OR, OQ and QR.

∴ OQ + OR> QR

(ii) Yes, as OQR is a triangle sides OR, OQ and QR.
∴ OQ + OR > QR

(iii) Yes, as A ORP is a triangle with sides OR, OP and PR.
∴ OR + OP > PR

Question 3.
AM is a median of a triangle ABC.
Is AB + BC + CA > 2AM?
(Consider the sides of ∆ABM and ∆AMC.)

Solution:
In a triangle, the sum of the lengths of either two sides is always greater than the third side.
In ∆ABM,
AB + BM > AM …(i)
Similarly, in ∆ACM,
AC + CM > AM …(ii)
Adding (i) and (ii), we obtain
AB + BM + MC +AC > AM + AM
AB + BC + AC > 2AM
Yes, the given expression is true.

Question 4.
ABCD is a quadrilateral.

Is AB + BC + CD + DA > AC + BD ?
Solution:
In a triangle, the sum of the lengths of either two sides is always greater than the third side.
In ∆ABC; AB + BC > CA …(i)
In ∆BCD; BC + CD > DB …(ii)
In ∆CDA; CD + DA > AC …(iii)
In ∆DAB; DA + AB > DB …(iv)
Adding (i), (ii), (iii) and (iv), we obtain
AB + BC + BC + CD + CD + DA + DA+ AB > AC + BD + AC + BD
⇒ 2AB + 2BC + 2CD + 2DA > 2AC + 2BD ⇒ 2{AB + BC + CD + DA) > 2(AC+BD)
⇒ (AB + BC + CD + DA) > (AC + BD)
Yes, the given expression is true.

Question 5.
ABCD is a quadrilateral.

Is AB + BC + CD + DA < 2(AC + BD)?
Solution:
In a triangle, the sum of the lengths of either two sides is always greater than the third side.
Let diagonals AC and BD of the quadrilateral ABCD intersects at O.

In ∆OAB, OA + OB > AB … (i)
In ∆OBC, OB + OC > BC … (ii)
In ∆OCD, OC + CD > CD … (iii)
In ∆ODA, OD + OA > DA … (iv)
OA + OB + OB + OC + OC + OD + OD + OA > AB + BC + CD + DA
⇒ 20A + 20B + 20C + 20D > AB + BC + CD + DA
⇒ 2(OA + OC) + 2(OB + OD) > AB + BC + CD + DA
⇒ 2(AC) + 2(BD) > AB + BC + CD + DA
⇒ 2(AC + BD) > AB + BC + CD + DA
Yes, the given expression is true.

Question 6.
The lengths of two sides of a triangle are 12 cm and 15 cm. Between what two measures should the length of the third side fall?
Solution:
In a triangle, the Sum of the lengths of either two side is always greater than the third side.
Lengths of two sides of a triangle are 12 cm and 15 cm.
Let the third side be x cm.
∴ x + 12 > 15 ⇒ x > 3
x + 15 > 12 ⇒ x > – 3 but side length never be negative.
and 12 + 15 > x ⇒ 27 > x
Hence, third side can measure between 3 and 27.

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 13 Exponents and Powers Ex 13.2

Question 1.
Using laws of exponents, simplify and write the answer in exponential form:
(i) 3² × 3⁴ × 3⁸
(ii) 6¹⁵ ÷ 6¹⁰
(iii) a³ × a²
(iv) 7^x × 7²
(v) (5²)³ 4 5³
(vi) 2⁵ × 5⁵
(vii) a⁴ × b⁴
(viii) (3⁴)³
(ix) (2²⁰ ÷ 2¹⁵) × 2³
(x) (8^t ÷ 8²)
Solution:
(i) 3² × 3⁴ × 3⁸ = (3)^{2 + 4 + 8} = 3¹⁴ [∵ a^m × aⁿ = a^m+n]
(ii) 6¹⁵ ÷ 6¹⁰ = (6)^{15 – 10} = 6⁵ [∵ a^m ÷ aⁿ = a^{m – n}]
(iii) a³ × a² = a^{3 + 2} = a⁵[∵ a^m × aⁿ = a^m+n]
(iv) 7^x × 7² = 7^{x + 2}[∵ a^m × aⁿ = a^m+n]
(v) (5²)³ ÷ 5³ = 5^{2 × 3} ÷ 5³ [∵ (a^m)ⁿ = a^mn]
= 5⁶ ÷ 5³ = 5^{(6 – 3)} [∵ a^m ÷ aⁿ = a^{m – n}]
= 5³
(vi) 2⁵ × 5⁵ = (2 × 5)⁵      [∵ a^m × b^m = (a × b)^m]
= 10⁵
(vii) a⁴ × b⁴ = (ab)⁴
(viii) (3⁴)³ = 3^{4 × 3} = 3¹²       [∵ (a^m)ⁿ = a^mn]
(ix) (2²⁰ ÷ 2¹⁵) × 2³ = (2^{20 – 15}) × 2³     [∵ a^m ÷ aⁿ = a^{m – n}]
= 2⁵ × 2³ = 2^{5 + 3} [∵ a^m × aⁿ = a^m+n]
(x) 8^t ÷ 8² = 8^{(t – 2)}    [∵ a^m ÷ aⁿ = a^{m – n}]

Question 2.
Simplify and express each of the following in exponential form:

Solution:

(ii) [(5²)³ × 5⁴] ÷ 5⁷
= [5^{2 × 3} × 5⁴] ÷ 5⁷ [∵ (a^m)ⁿ = a^mn]
= [5⁶ × 5⁴] ÷ 5⁷ [∵ a^m × aⁿ = a^{m + n}]
= [5^{6 + 4}] ÷ 5⁷
= 5¹⁰ ÷ 5⁷
= 5^{10 – 7} [∵ a^m ÷ aⁿ = a^{m – n}]
= 5³

(iii) 25⁴ ÷ 5³ = (5 × 5)⁴ ÷ 5³
= (5²)⁴ ÷ 5³ = 5^{2 × 4} ÷ 5³ [∵ (a^m)ⁿ = a^mn]
= 5⁸ ÷ 5³ = 5^{8 – 3} [∵ a^m ÷ aⁿ = a^{m – n}]
= 5⁵

(vi) 2⁰ + 3⁰ + 4⁰ = 1 + 1 + 1 = 3     [∵ a⁰ = 1]
(vii) 2⁰ × 3⁰ × 4⁰ = 1 × 1 × 1 = 1
(viii) (3⁰ + 2⁰) × 5⁰ = (1 + 1) × 1 = 2

Question 3.
Say true or false and justify your answer:
(i) 10 × 10¹¹ = 100¹¹
(ii) 2³ > 5²
(iii) 2³ × 3² = 6⁵
(iv) 3⁰ = (1000)⁰
Solution:
(i) L.H.S = 10 × 10¹¹
= 10^{1 + 11} = 10¹²
R.H.S = 100¹¹ = (10 × 10)¹¹ = (10⁰)¹¹ = 10^{2 × 11} = 10²²
⇒ L.H.S. ≠ R.H.S.
Hence, the given statement is false.

(ii) 2³ > 5²
L.H.S. = 2³ = 2 × 2 × 2 = 8
R.H.S. = 5³ = 5 × 5 = 25
⇒ L.H.S ≠ R.H.S
Hence, the given statement is false.

(iii) 2³ × 3² = 6⁵
L.H.S. = 2³ × 3² = 2 × 2 × 2 × 3 × 3 = 72
R.H.S. = 6⁵ = 6 × 6 × 6 × 6 × 6 = 7776
⇒ L.H.S. ≠ R.H.S.
Hence, the given statement is false.

(iv) 3⁰ = (1000)⁰
L.H.S. = 3⁰ = 1
R.H.S. = (1000)⁰ = 1
⇒ L.H.S. = R.H.S.
Hence, the given statement is true.

Question 4.
Express each of the following as a product of prime factors only in exponential form:
(i) 108 × 192
(ii) 270
(iii) 729 × 64
(iv) 768
Solution:
(i) 108 × 192
= (2 × 2 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2 × 3)
= (2² × 3³) × (2⁶ × 3)
= 2²⁺⁶ × 3³⁺¹ = 2⁸ × 3⁴
(ii) 270 = 2 × 3 × 3 × 3 × 5 = 2 × 3³ × 5
(iii) 729 × 64 = (3 × 3 × 3 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2) = 3⁶ × 2⁶
(iv) 768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 = 2⁸ × 3

Question 5.
Simplify:

Solution:

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.3

Question 1.
Find the value of the unknown x in the following diagrams:


Solution:
The sum of all interior angles of a triangle is 180°. By using this property, these problems can be solved as follows :
(i) x + 50° + 60° = 180°
⇒ x +110° = 180°
⇒ x = 180° -110° = 70°

(ii) x + 90° + 30° = 180°
⇒ x + 120° = 180°
⇒ x = 180° – 120° = 60°

(iii) x + 30° + 110° = 180°
⇒ x + 140° = 180°
⇒ x = 180° – 140° = 40°

(iv) 50° + x + x = 180°
⇒ 2x = 180° – 50° = 130°

(v) x + x + x = 180°
⇒ 3x = 180°

(vi) x + 2x + 90° = 180°
⇒ 3x = 180° – 90° = 90° = 90°

Question 2.
Find the values of the unknowns x and y in the following diagrams:

Solution:
(i) y + 120° = 180° (Linear pair)
⇒ y = 180° – 120° = 60°
Now, x + y + 50° = 180°
(Angle sum property)
⇒ x + 60° + 50° = 180° x = 180° – 60° – 50° = 70°

(ii) y = 80° (Vertically opposite angles)
Now, y + x + 50° = 180°
(Angle sum property)
⇒ 80° + x + 50° = 180°
⇒ x = 180° – 80°- 50° = 50°

(iii) y + 50° + 60° = 180°
(Angle sum property)
⇒ y = 180° – 60° – 50° = 70°
Now, x + y = 180° (Linear pair)
⇒ x = 180° – y = 180° – 70° = 110°

(iv) x = 60° (Vertically opposite angles)
Now, 30° + x + y = 180°
(Angle sum property)
⇒ 30° + 60° + y = 180° y = 180° – 30° – 60° = 90°

(v) y = 90° (Vertically opposite angles)
Now, x + x + y = 180°
(Angle sum property)
⇒ 2x + 90° = 180°
⇒ 2x = 180° – 90° = 90°

(vi) y = x (Vertically opposite angles)
a = x (Vertically opposite angles)
b = x (Vertically opposite angles)
Now, a + b + y = 180°
(Angle sum property)
⇒ x + x + x= 180°
⇒ 3x = 180°


Hence, y = x = 60°

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.2

Question 1.
Find the value of the unknown exterior angle x in the following diagrams:


Solution:
(i) x = 50° + 70° (Exterior angle property) = 120°
(ii) x = 65° + 45° (Exterior angle property)
= 110°
(iii) x = 40° + 30° (Exterior angle property)
= 70°
(iv) x = 60° + 60° (Exterior angle property)
= 120°
(v) x = 50° + 50° (Exterior angle property)
= 100°
(vi) x = 30° + 60° (Exterior angle property)
= 90°

Question 2.
Find the value of the unknown interior angle x in the following figures:


Solution:
(i) x + 50° = 115°
(Exterior angle property)
⇒ x = 115° – 50° = 65°
(ii) 70° + x = 100° (Exterior angle property) ⇒ x = 100° – 70° = 30°
(iii) x + 90° = 125° (Exterior angle property) ⇒ x = 125° – 90° = 35°
(iv) x + 60° = 120° (Exterior angle property) ⇒ x = 120° – 60° = 60°
(v) x + 30° = 80° (Exterior angle property) ⇒ x = 80° – 30° = 50°
(vi) x + 35° = 75° (Exterior angle property) ⇒ x = 75° – 35° = 40°

MP Board Class 7th Maths Solutions

MP Board Class 7th Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.1

Question 1.
In ∆PQR, D is the mid-point of \(\overline{Q R}\).
\(\overline{P M}\) is ___.
PD is ___.
Is QM = MR?

Solution:
(i) PM is an altitude
(ii) PD is a median
(iii) No, QM ≠ MR.

Question 2.
Draw rough sketches for the following:
(a) In ∆ABC, BE is a median.
(b) In ∆PQR, PQ and PR are altitudes of the triangle.
(c) In ∆XYZ, YL is an altitude in the exterior of the triangle.
Solution:

Question 3.
Verify by drawing a diagram, if the median and altitude of an isosceles triangle can be same.
Solution:

Draw a line segment AD perpendicular to BC. It can be observed that the length of BD and DC is also same. Therefore, AD is also a median of this triangle.

MP Board Class 7th Maths Solutions

MP Board Class 7th Social Science Solutions Chapter 19 Weather and Climate

MP Board Class 7th Social Science Chapter 19 Text Book Questions

Fill in the blanks:

1.  Weather affects a area.
2. Almost similar atmospheric condition is called
3. elements are found in climate and weather.

Answer:

1. small
2. season
3. Six.

MP Board Class 7th Social Science Chapter 19 Short Answer Type Questions

Question 1.
What is weather? What is difference between weather and season.
Answer:
Weather is the condition of atmosphere at a given place for a short-period with regard to its temperature, rainfall, pressure, humidity and direction of wind. Weather can change-many times in a day.
Difference between weather ans season.
Answer:
Weather:

• Weather Is a short duration atmospheric condition.
• Weather represents the atmospheric condition of a small area.
• Weather can change many time In a day.

Season:

• Season Is a long duration atmospheric condition.
• Season represents the atmospheric condition of a Large area.
• Season does not change for a long period.

Question 2.
To analyse the climate of an area how many years average data is taken?
Answer:
To analyse die climate of an area we have to take the average data of the weather conditions of the place of at least 30 years.

Question 3.
Which are the factors affecting the climate of a place?
Answer:
The factors affecting the climate of a place are:

1. The latitudinal position of a place.
2. Height from sea level.
3. The distribution of land and water.
4. Distance from sea.
5. Direction of wind.
6. Air pressure belts.
7. Situation of mountains.
8. Nature of land.
9. Ocean currents.

MP Board Class 7th Social Science Chapter 19 Long Answer Type Questions

Question 1.
Differentiate between weather and climate.
Answer:
The following are the difference of weather and climate.
Weather:

• Weather is a short durat – tion atmospheric condition.
• Weather represents the atmospheric condition of dsmall area.
• The weather can change many times in a day.
• In the weather of one sea – son any one element is prominent.

Climate

• Climate is a long duration atmospheric condition.
• Climate represents the wide area of atmo – spheric condition.
• The climate does not change for long periods.
• In one type of climate one or many seasons we there.

MP Board Class 7th Social Science Solutions

MP Board Class 7th Maths Solutions Chapter 13 Exponents and Powers Ex 13.1

Question 1.
Find the value of
(i) 2⁶
(ii) 9³
(iii) 11²
(iv) 5⁴
Solution:
(i) 2⁶ = 2 × 2 × 2 × 2 × 2 × 2 = 64
(ii) 9³ = 9 × 9 × 9 = 729
(iii) 11² = 11 × 11= 121
(iv) 5⁴ = 5 × 5 × 5 × 5 = 625

Question 2.
Express the following in exponential form:
(i) 6 × 6 × 6 × 6
(ii) t × t
(iii) b × b × b × b
(iv) 5 × 5 × 7 × 7 × 7
(v) 2 × 2 × a × a
(vi) a × a × a × c × c × c × c × d
Solution:
(i) 6 × 6 × 6 × 6 = 6⁴
(ii) t × t = t²
(iii) b × b × b × b = b⁴
(iv) 5 × 5 × 7 × 7 × 7 = 5² × 7³
(v) 2 × 2 × a × a = 2² × a²
(vi) a × a × a × c × c × c × c × d = a³ × c⁴ × d

Question 3.
Express each of the following numbers using exponential notation:
(i) 512
(ii) 343
(iii) 729
(iv) 3125
Solution:
(i) 512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2⁹
(ii) 343 = 7 × 7 × 7 = 7³
(iii) 729 = 3 × 3 × 3 × 3 × 3 × 3 = 3⁶
(iv) 3125 = 5 × 5 × 5 × 5 × 5 = 5⁵

Question 4.
Identify the greater number, wherever possible, in each of the following?
(i) 4³ or 3⁴
(ii) 5³ or 3⁵
(iii) 2⁵ or 8²
(iv) 100² or 2¹⁰⁰
(v) 2¹⁰ or 100²
Solution:
(i) 4³ = 4 × 4 × 4 = 64 and 3⁴ = 3 × 3 × 3 × 3 = 81
As 81 > 64, therefore 3⁴ > 4³

(ii) 5³ = 5 × 5 × 5 = 125,
3⁵ = 3 × 3 × 3 × 3 × 3 = 243
As 243 > 125, therefore, 3⁵ > 5³

(iii) 2⁸ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256,
8² = 8 × 8 = 64
As 256 > 64, therefore, 2⁸ > 8²

(iv) 2¹⁰⁰ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024
⇒ 2¹⁰⁰ = (2¹⁰)¹⁰ = 1024 × 1024 × 1024 × 1024 × 1024 × 1024 ×1024 ×1024 × 1024 × 1024 = (1024)¹⁰
and 100² = 100 × 100 = 10000
As (1024)¹⁰ > 10000, therefore 2¹⁰⁰ > 100²

(v) 2¹⁰ = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024
and 10² = 10 × 10 = 100
As 1024 > 100, therefore 2¹⁰ > 10²

Question 5.
Express each of the following as product of powers of their prime factors:
(i) 648
(ii) 405
(iii) 540
(iv) 3600
Solution:
(i) 648 = 2 × 2 × 2 × 3 × 3 × 3 × 3 = 2³ × 3⁴
(ii) 405 = 3 × 3 × 3 × 3 × 5 = 3⁴ ×5
(iii) 540 = 2 × 2 × 3 × 3 × 3 × 5 = 2² × 3³ × 5
(iv) 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5 = 2⁴ × 3² × 5²

Question 6.
Simplify:
(i) 2 × 10³
(ii) 7² × 2²
(iii) 2³ × 5
(iv) 3 × 4⁴
(v) 0 × 10²
(vi) 5² × 3³
(vii) 2⁴ × 3²
(viii) 32 × 104
Solution:
(i) 2 × 10³ = 2 × 10 × 10 × 10 = 2 × 1000 = 2000
(ii) 7² × 2² = 7 × 7 × 2 × 2 = 49 × 4 = 196
(iii) 2³ × 5 = 2 × 2 × 2 × 5 = 8 × 5 = 40
(iv) 3 × 4⁴ = 3 × 4 × 4 × 4 × 4 = 3 × 256 = 768
(v) 0 × 10² = 0 × 10 × 10 = 0
(vi) 5² × 3³ = 5 × 5 × 3 × 3 × 3 = 25 × 27 = 675
(vii) 2⁴ × 3⁴ = 2 × 2 × 2 × 2 × 3 × 3 = 16 × 9 = 144
(viii) 3² × 10⁴ = 3 × 3 × 10 × 10 × 10 × 10 = 9 × 10000 = 90000

Question 7.
Simplify:
(i) (-4)³
(ii) (-3) × (-2)³
(iii) (-3)² × (-5)²
(iv) (-2)³ × (-10)³
Solution:
(i) (-4)³ = (-4) × (-4) × (-4) = -64
(ii) (-3) × (-2)³ = (-3) × (-2) × (-2) × (-2) = (-3) × (-8) = 24
(iii) (-3)² × (-5)² = (-3) × (-3) × (-5) × (-5) = 9 × 25 = 225
(iv) (-2)³ × (-10)³ = (-2) × (-2) × (-2) × (-10) × (-10) × (-10) = (-8) × (-1000) = 8000

Question 8.
Compare the following numbers:
(i) 2.7 × 10¹²; 1.5 × 10⁸
(ii) 4 × 10¹⁴; 3 × 10¹⁷
Solution:
(i) 2.7 × 10¹²; 1.5 × 10⁸
Since, 10¹² > 10⁸
∴ 2.7 × 10¹² > 1.5 × 10⁸
(ii) 4 × 10¹⁴; 3 × 10¹⁷
Since, 10¹⁴ < 10¹⁷
∴ 4 × 10¹⁴ < 3 × 10¹⁷

MP Board Class 7th Maths Solutions