MP Board Class 7th Maths Solutions Chapter 13 Exponents and Powers Ex 13.2
Question 1.
Using laws of exponents, simplify and write the answer in exponential form:
(i) 32 × 34 × 38
(ii) 615 ÷ 610
(iii) a3 × a2
(iv) 7x × 72
(v) (52)3 4 53
(vi) 25 × 55
(vii) a4 × b4
(viii) (34)3
(ix) (220 ÷ 215) × 23
(x) (8t ÷ 82)
Solution:
(i) 32 × 34 × 38 = (3)2 + 4 + 8 = 314 [∵ am × an = am+n]
(ii) 615 ÷ 610 = (6)15 – 10 = 65 [∵ am ÷ an = am – n]
(iii) a3 × a2 = a3 + 2 = a5[∵ am × an = am+n]
(iv) 7x × 72 = 7x + 2[∵ am × an = am+n]
(v) (52)3 ÷ 53 = 52 × 3 ÷ 53 [∵ (am)n = amn]
= 56 ÷ 53 = 5(6 – 3) [∵ am ÷ an = am – n]
= 53
(vi) 25 × 55 = (2 × 5)5 [∵ am × bm = (a × b)m]
= 105
(vii) a4 × b4 = (ab)4
(viii) (34)3 = 34 × 3 = 312 [∵ (am)n = amn]
(ix) (220 ÷ 215) × 23 = (220 – 15) × 23 [∵ am ÷ an = am – n]
= 25 × 23 = 25 + 3 [∵ am × an = am+n]
(x) 8t ÷ 82 = 8(t – 2) [∵ am ÷ an = am – n]
Question 2.
Simplify and express each of the following in exponential form:

Solution:
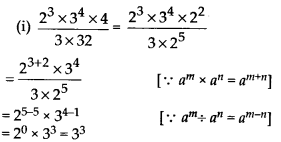
(ii) [(52)3 × 54] ÷ 57
= [52 × 3 × 54] ÷ 57 [∵ (am)n = amn]
= [56 × 54] ÷ 57 [∵ am × an = am + n]
= [56 + 4] ÷ 57
= 510 ÷ 57
= 510 – 7 [∵ am ÷ an = am – n]
= 53
(iii) 254 ÷ 53 = (5 × 5)4 ÷ 53
= (52)4 ÷ 53 = 52 × 4 ÷ 53 [∵ (am)n = amn]
= 58 ÷ 53 = 58 – 3 [∵ am ÷ an = am – n]
= 55

(vi) 20 + 30 + 40 = 1 + 1 + 1 = 3 [∵ a0 = 1]
(vii) 20 × 30 × 40 = 1 × 1 × 1 = 1
(viii) (30 + 20) × 50 = (1 + 1) × 1 = 2

Question 3.
Say true or false and justify your answer:
(i) 10 × 1011 = 10011
(ii) 23 > 52
(iii) 23 × 32 = 65
(iv) 30 = (1000)0
Solution:
(i) L.H.S = 10 × 1011
= 101 + 11 = 1012
R.H.S = 10011 = (10 × 10)11 = (100)11 = 102 × 11 = 1022
⇒ L.H.S. ≠ R.H.S.
Hence, the given statement is false.
(ii) 23 > 52
L.H.S. = 23 = 2 × 2 × 2 = 8
R.H.S. = 53 = 5 × 5 = 25
⇒ L.H.S ≠ R.H.S
Hence, the given statement is false.
(iii) 23 × 32 = 65
L.H.S. = 23 × 32 = 2 × 2 × 2 × 3 × 3 = 72
R.H.S. = 65 = 6 × 6 × 6 × 6 × 6 = 7776
⇒ L.H.S. ≠ R.H.S.
Hence, the given statement is false.
(iv) 30 = (1000)0
L.H.S. = 30 = 1
R.H.S. = (1000)0 = 1
⇒ L.H.S. = R.H.S.
Hence, the given statement is true.
![]()
Question 4.
Express each of the following as a product of prime factors only in exponential form:
(i) 108 × 192
(ii) 270
(iii) 729 × 64
(iv) 768
Solution:
(i) 108 × 192
= (2 × 2 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2 × 3)
= (22 × 33) × (26 × 3)
= 22+6 × 33+1 = 28 × 34
(ii) 270 = 2 × 3 × 3 × 3 × 5 = 2 × 33 × 5
(iii) 729 × 64 = (3 × 3 × 3 × 3 × 3 × 3) × (2 × 2 × 2 × 2 × 2 × 2) = 36 × 26
(iv) 768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 = 28 × 3
Question 5.
Simplify:
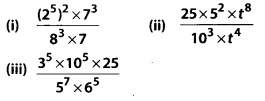
Solution:
