MP Board Class 7th Maths Solutions Chapter 6 The Triangles and Its Properties Ex 6.5
Question 1.
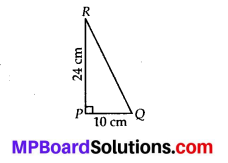
PQR is a triangle, right-angled at P. If PQ= 10 cm and PR = 24 cm, find QR.
Solution:
By applying Pythagoras theorem in ∆PQR,
(PQ)2 + (PR)2 = (QR)2
⇒ (10)2 + (24)2 = (QR)22
⇒ (QR)2 = 100 + 576
= 676 = (26)2
∴ QR = 26 cm
Question 2.
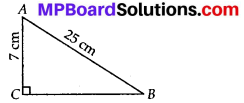
ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Solution:
By applying Pythagoras theorem in AABC,
(AC)2 + (BC)2 = (AB)2
⇒ (BC)2 = (AB)2 – (AC)2
= (25)2 – (7)2
= 625 – 49 = 576
= (24)2
∴ BC = 24 cm
![]()
Question 3.
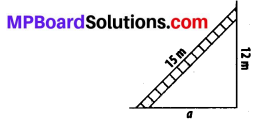
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
Solution:
By applying Pythagoras theorem,
(15)2 = (12)2 + a2
⇒ 225 = 144 + a2
⇒ a2 = 225 – 144 = 81 = 92
⇒ a = 9 m
Therefore, the distance of the foot of the ladder from the wall is 9 m.
![]()
Question 4.
Which of the following can be the sides of a right triangle?
(i) 2.5 cm, 6.5 cm, 6 cm.
(ii) 2 cm, 2 cm, 5 cm.
(iii) 1.5 cm, 2 cm, 2.5 cm.
In the case of right-angled triangles, identify the right angles.
Solution:
(i) 2.5 cm, 6.5 cm, 6 cm
∴ (2.5)2 = 6.25, (6.5)2 = 42.25 and (6)2 = 36
It can be observed that,
36 + 6.25 = 42.25
⇒ (6)2 + (2.5)2 = (6.5)2
The square of the length of one side is the sum of the squares of the lengths of the remaining two sides. Hence, these are the sides of a right-angled triangle. Right angle will be in front of the side of measure 6.5 cm.
(ii) 2 cm, 2 cm, 5 cm
∴ (2)2 = 4, (2)2 = 4 and (5)2 = 25
Here, (2)2 + (2)2 ≠ (5)2
The square of the length of one side is not equal to the sum of the squares of the lengths of the remaining two sides. Hence, these sides are not of a right-angled triangle.
(iii) 1.5 cm, 2 cm, 2.5 cm
∴ (1.5)2 = 2.25, (2)2 = 4 and (2.5)2 = 6.25
Here, 2.25 + 4 = 6.25
⇒ (1.5)2 + (2)2 = (2.5)2
The square of the length of one side is the sum of the squares of the lengths of the remaining
two sides. Hence, these are the sides of a right-angled triangle.
Right angle will be in front of the side of measure 2.5 cm.
![]()
Question 5.
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Solution:
In the drawn figure, BC represents the unbroken part of the tree. Point C represents the point where the tree broke and CA represents the broken part of the tree. Triangle ABC, thus formed, is right-angled at B.
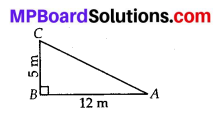
Applying Pythagoras C theorem in ∆ABC,
AC2 = BC2 + AB2
= (5)2+ (12)2 BL
= 25 + 144 = 169
= (13)2
∴ AC = 13 m
Thus, original height of the tree = AC + CB = 13m + 5m = 18m
Question 6.
Angles Q and R of a ∆PQR are 25° and 65°. Write which of the following is true:
(i) PQ2 + QR2 = RP2
(ii) PQ2 + RP2 = QR2
(iii) RP2 + QR2 = PQ2
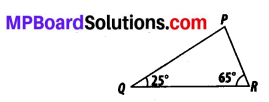
Solution:
The sum of the measures of all interior angles of a triangle is 180°.
∠P + ∠Q + ∠R = 180°
∠P + 25°+ 65° = 180°
∠P + 90° = 180°
∠P = 180° – 90° = 90°
Therefore, ∆PQR is right-angled at point P. Hence, (PR)2 + (PQ)2 = (QR)2
∴ (ii) is true.
![]()
Question 7.
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
Solution:
Let ABCD be the given rectangle with length AB = 40 cm and diagonal AC = 41 cm.
In ∆ABC,
(AC)2 = (AB)2 + (BC)2
⇒ (4)2 = (40)2+ (BQ)2
⇒ (BC)2 = 1681 – 1600 = 81 = 92
∴ BC = 9 cm
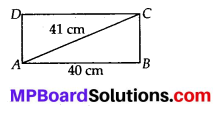
∴ Perimeter of rectangle = 2(40 + 9)
= 2(49) = 98 cm.
Question 8.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
Solution:
Let ABCD be the given rhombus with diagonals AC = 16 cm and BD = 30 cm.
We know that diagonals of a rhombus bisect each other at right angle.
Let diagonals AC and BD bisects at O.
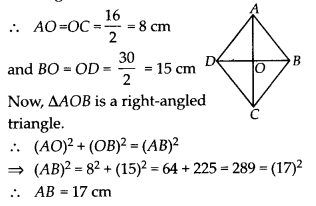
Hence, perimeter of rhombus = 4 × (17) = 68 cm
![]()