Category: Class 6

MP Board Class 6th Sanskrit Solutions Surbhi विविधप्रश्नावलिः 2

प्रश्न 1.
एकपदेन उत्तरं लिखत (एक शब्द में उत्तर लिखो)
(क) कः देशरक्षां करोति?
(ख) केभ्यः जयघोषः निःसरित?
(ग) मध्यप्रदेशस्य मध्यभागे का नदी प्रवहति?
(घ) दशरथस्य कति पुत्राः आसन्?
(ङ) जम्बूवृक्षः कुत्र आसीत्?
उत्तर:
(क) सैनिकः
(ख) भक्तजनमुखेभ्य
(ग) नर्मदा नदी
(घ) चत्वारः
(ङ) नद्याः तीरे।

प्रश्न 2.
एकवाक्येन उत्तरं लिखत (एक वाक्य में उत्तर लिखो)
(क) परोपकाराय के फलानि यच्छन्ति? (परोपकार के लिए कौन फल देते हैं?)
उत्तर:
परोपकाराय वृक्षाः फलानि यच्छन्ति। (परोपकार के लिए वृक्ष फल देते हैं।)

(ख) चन्द्रः कासां भूषणम् अस्ति? (चन्द्रमा किनका आभूषण है?)
उत्तर:
चन्द्रः ताराणां भूषणम् अस्ति। (चन्द्रमा तारों का आभूषण है।)

(ग) मध्यप्रदेशः कुत्र विराजते? (मध्यप्रदेश कहाँ विराजमान हैं?)
उत्तर:
मध्यप्रदेश: भारतदेशस्य मध्यभागे विराजते। (मध्यप्रदेश भारत देश के मध्य भाग में विराजमान है।)

(घ) आदिकविः कः अस्ति? (आदिकवि कौन हैं?)
उत्तर:
आदिकवि वाल्मीकिः अस्ति। (आदिकवि वाल्मीकि हैं।)

(ङ) कः उच्चैः गर्जति? (कौन ऊँचे स्वर में गरजता है?)
उत्तर:
सिंहः उच्चैः गर्जति। (शेर ऊँचे स्वर में गरजता है।)

प्रश्न 3.
रिक्तस्थानं पूरयत (रिक्त स्थान की पूर्ति करो)
(क) शास्त्रं ………… अस्ति। (पण्डिताः/पण्डिताय)
(ख) श्रीरामः …………पुत्रः। (दशरथस्य/दशरथेन)
(ग) भोपालनगरं मध्यप्रदेशस्य ………… अस्ति। (राजधानी/राजधानीम्)
(घ) सीतायाः विवाहः ……….. सह अभवत्। (रामस्य/रामेण)
(ङ) मयूरः अस्माकं ………… पक्षी अस्ति। (राष्ट्रियः/राष्ट्रीयम्)
(च) सिंह उच्चैः …………। (गर्जति/गर्जेत)
उत्तर:
(क) पण्डिताय
(ख) दशरथस्य
(ग) राजधानी
(घ) रामेण
(ङ) राष्ट्रियः
(च) गर्जति।

प्रश्न 4.
समीचीनं चिनुत (आम्/न) (उपयुक्त का चुनाव करो हाँ/न)
(क) अस्माभिः जलसंरक्षणं, वायुसंरक्षणं, भूसंरक्षणम् च अवश्यं करणीयम्।
(ख) स्वास्थ्यं ज्ञानाय परिश्रमाय न भवति।
(ग) प्राचीनकालात् आरभ्य उज्जयिनीक्षेत्रं संस्कृतविद्या केन्द्रमस्ति।
(घ) विद्या सर्वस्य भूषणं नास्ति।
(ङ) संस्कृतभाषा वेदानाम् उपनिषदां शास्त्राणांच भाषा वर्तते।
(च) नर्मदायाः दक्षितटे विन्ध्याचलः अस्ति।
(छ) मध्यप्रदेशस्य मध्ये नर्मदा नदी अस्य मेखला इव प्रवहति।
(ज) दशरथस्य आज्ञया रामः राज्यं त्यक्त्वा वनम् अगच्छत्।
(झ) लक्ष्मणेन रामः युद्धे घातितः।
उत्तर:
(क) आम्
(ख) न
(ग) आम्
(घ) न
(ङ) आम्
(च) न
(छ) आम्
(ज) आम्
(झ) न

प्रश्न 5.
अधोलिखितानि पदानि प्रयुज्यवाक्यानि लिखत(निम्नलिखित शब्दों का प्रयोग करके वाक्यों को लिखो)

उत्तर:
(क) सूर्यः लोकहिताय तपति।
(ख) नद्यः परोपकाराय वहन्ति।
(ग) मन्दिरात् घण्टानादः श्रूयते।
(घ) यात्रिकाः उज्जयिनीम् आगच्छन्ति ।

प्रश्न 6.
अक्षराणि प्रयुज्य पदचक्र पूरयत (अक्षरों का प्रयोग करके पदचक्र को पूरा करो)
ला, धु, भा, भा, स, षा

उत्तर:
(क) मधुरा भाषा
(ख) भारतभूषा
(ग) सरला भाषा।

प्रश्न 7.
अधोलिखितानि वाक्यानि यथाक्रमं लिखत (नीचे लिखे वाक्यों को क्रमानुसार लिखो)
(क) वने राक्षसराजः रावणः सीतां कपटेन अहरत्।
(ख) रामः सीता लक्ष्मणः च अयोध्याम् प्रत्यगच्छन्।
(ग) वानराः सागरे सेतुनिर्माणम् अकुर्वन।
(घ) रामेण रावणः युद्धे घातितः।
(ङ) विश्वामित्रः रामलक्ष्मणौ स्वाश्रमम् अनयत्।
उत्तर:
(1) ङ
(2) क
(3) ग
(4) घ
(5) ख

प्रश्न 8.
योजयत (जोड़ो)

उत्तर:
(क) → 3
(ख) → 1
(ग) → 4
(घ) → 2

प्रश्न 9.
रेखांकितपदानि लङ्लकारे परिवर्तयत (रेखांकित शब्दों को लङ् लकार में बदलो)-
एकः पिपासितः काकः अस्ति। सः जलं पातुम् इच्छति। ग्रीष्मकालः अस्ति, सः बहुत्र विहरति, पश्यति, किन्तु जलं न मिलति। काकः एकंघटं पश्यति, समीपं गच्छति। तस्मिन् घटे किञ्चित जलम् अस्ति। परितः पश्यति। जलं पातुंन पारयति। घटस्य पार्वे शिलाखण्डान् पश्यति। तान् घटे पातयति। जलम् उपर्युपरि आगच्छति। काकः जलम् पिबति। प्रसन्नः भवति। तत: गच्छति।
उत्तर:
एकः पिपासितः काकः आसीत्। सः जलं पातुं इच्छति। ग्रीष्मकालः अस्ति, स: बहुत्र विहरति, पश्यति, किन्तु जलं न अमिलत्। एकत्र एकं घटं अपश्यत्, समीपं अगच्छत्। तस्मिन् घटे किञ्चित जलम् आसीत्। परितः पश्यति। जलं पातुं न पारयति। घटस्य पार्वे शिलाखण्डान् पश्यति। तान् घटे अपातयत्। जलम् उपर्युपरि आगच्छत्। काकः जलम् अपिबत्। प्रसन्नः भवति। ततः अगच्छत्।

प्रश्न 10.
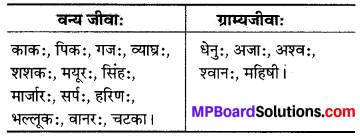
योगशब्दं चित्वा उचितस्थाने लिखत (उचित शब्द चुनकर उचित स्थान पर लिखें)
काकः, पिकः, गजः, व्याघ्रः, धेनुः, शशकः, मयूरः, सिंहः, अजाः, मार्जारः, सर्पः, अश्वः, हरिणः, भल्लूकः, वानरः, श्वानः, महिषी, चटका।

प्रश्न 11.
विभक्त्यनुसारं वाक्यानि लिखत (विभक्ति के अनुसार वाक्यों को लिखो)

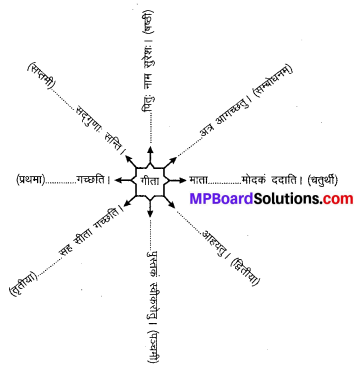
उत्तर:

1. गीतायाः पितुः नाम सुरेशः। (षष्ठी विभक्ति)
2. भो गीते! अत्र आगच्छतु। (सम्बोधन)
3. माता गीतायै मोदकं ददाति। (चतुर्थी)
4. गीतां आह्वयतु। (द्वितीया)
5. गीतायाः पुस्तकं स्वीकरोतु। (पंचमी)
6. गीतया सह गीता गच्छति। (तृतीया)
7. गीता गच्छति। (प्रथमा)
8. गीतायाम् सद्गुणः सन्ति। (सप्तमी)

MP Board Class 6th Sanskrit Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.6

पाठ्य-पुस्तक पृष्ठ संख्या # 313

प्रश्न 1.
75° माप वाले कोण ∠POQ की रचना कीजिए।
हल :
रचना के पद :
(1) किरण OP’ खींचते हैं।
(2) ∠BOQ = 90° बनाते हैं जबकि ∠LOQ = 60° और ∠BOL = 30°

(3) ∠BOL का समद्विभाजक \(\overline { OP } \) खींचते हैं।
इस प्रकार ∠LOP = \(\frac { 1 }{ 2 }\) ∠BOL
या ∠LOP = \(\frac { 1 }{ 2 }\) (30°) = 15°
(4) ∵ 60° + 15 = 75°
अतः ∠QOL + ∠LOP = ∠POQ
∴∠POQ = 75°

प्रश्न 2.
147° माप वाले एक कोण की रचना कीजिए और उसका समद्विभाजक खींचिए।
हल :
रचना के पद :
(1) किरण \(\overrightarrow{O A}\) खीचते हैं।
(2) चाँदे की सहायता से ∠AOB = 147° बनाते हैं।

(3) O को केन्द्र मानकर और सुविधाजनक त्रिज्या लेकर एक चाप लगाते हैं जो भुजा \(\overrightarrow{O A}\) और \(\overrightarrow{O B}\) को क्रमशः Q तथा पर काटता है।
(4) P को केन्द्र मानकर और PQ के आधे से अधिक त्रिज्या लेकर एक चाप लगाते हैं।
(5) पुनः Q को केन्द्र मानकर और इसी त्रिज्या से दूसरा चाप लगाते हैं, जो पहले चाप को R पर काटता है।
(6) O और R को मिलाते हुए आगे बढ़ाते हैं।
इस प्रकार OR, ∠AOB का अभीष्ट समद्विभाजक है।

प्रश्न 3.
एक समकोण खींचिए और उसके समद्विभाजक की रचना कीजिए।
हल :
रचना के पद :
(1) सर्वप्रथम एक रेखा l खीचते हैं और इस पर कोई बिन्दु O लेते हैं।
(2) O को केन्द्र मानकर और सुविधाजनक त्रिज्या लेकर एक चाप लगाते हैं, जो l को A और B पर काटता है।

(3) अब A और B को केन्द्र मानकर और AB के आधे से अधिक त्रिज्या लेकर दो चाप लगाते हैं, जो परस्पर C पर काटते हैं।
(4) O और C को मिलाते हैं।
इस प्रकार ∠AOC = 90° प्राप्त होता है।
(5) A और D को केन्द्र मानकर और AD के आधे से अधिक त्रिज्या लेकर दो चाप लगाते हैं, जो परस्पर E पर काटते
(6) O और E को मिलाते हुए इसे आगे बढ़ाते हैं।
इस प्रकार \(\overrightarrow{O E}\) , ∠AOC का अभीष्ट समद्विभाजक है, अर्थात् \(\overrightarrow{O E}\) समकोण का समद्विभाजक है।

प्रश्न 4.
153° का एक कोण खींचिए और इसके चार बराबर भाग कीजिए।
हल :
रचना के पद:
(1) किरण \(\overrightarrow{ AB }\) खींची।

(2) A पर चाँदे की सहायता से ∠BAC = 153° बनाया।
(3) ∠BAC का समद्विभाजक \(\overrightarrow{ AD }\) खींचा।
(4) पुनः ∠DAC का समद्विभाजक \(\overrightarrow{ AE }\) खींचा।
(5) ∠BAD का समद्विभाजक \(\overrightarrow{ AF }\) खींचा।
इस प्रकार \(\overrightarrow{A E}, \overrightarrow{A D}\) और \(\overrightarrow{ AF }\) दिए हुए कोण ∠BAC को चार समान भागों में विभाजित करते हैं।

प्रश्न 5.
रूलर और परकार की सहायता से निम्न मापों के कोणों की रचना कीजिए :
(a) 60°
(b) 300
(c) 90°
(d) 120°
(e) 45°
(f) 135°
हल :
(a) रचना के पद :
(1) सर्वप्रथम किरण \(\overrightarrow{ OA }\) खींचते हैं।
(2) O को केन्द्र मानकर तथा उपयुक्त त्रिज्या लेकर एक चाप लगाया जो OA को P पर काटता है।

(3) P को केन्द्र मानकर तथा उसी त्रिज्या से चाप लगाया जो पहले चाप को R पर काटता है।
(4) O को R से मिलाया और B तक आगे बढ़ाया।
इस प्रकार ∠AOB = 60°

(b) (1) सर्वप्रथम किरण \(\overrightarrow{ OA }\) खीचते हैं।
(2) O को केन्द्र मानकर और उपयुक्त त्रिज्या लेकर एक चाप PS लगाया जो OA को P पर काटता है।
(3) P को केन्द्र मानकर उसी त्रिज्या से चाप लगाया जो पहले चाप को Q पर काटता है।
(4) O को Q से मिलाते हुए आगे B तक बढ़ाया।
इस प्रकार ∠AOB = 60°
(5) अब ∠AOB का समद्विभाजक \(\overrightarrow{ OC }\) ज्ञात किया।

इस प्रकार ∠AOC = \(\frac { 1 }{ 2 }\) ∠AOB
= \(\frac { 1 }{ 2 }\) x 60° = 30°
अतः अभीष्ट ∠AOC = 30°

(c) (1) सर्वप्रथम किरण \(\overrightarrow{ OA }\) खींचते हैं।
(2) O को केन्द्र मानकर और उपयुक्त त्रिज्या लेकर एक चाप लगाते हैं, जो OA को P पर काटता है।

(3) P को केन्द्र मानकर और उसी त्रिज्या से एक चाप लगाया जो पहले चाप को R पर काटता है।
(4) अब R को केन्द्र मानकर उसी त्रिज्या से दूसरा चाप लगाया जो पहले चाप को S पर काटता है।
(5) अब R और S को केन्द्र मानकर दो चाप लगाए जो परस्पर Q पर काटते हैं।
(6) O को Q से मिलाते हुए आगे बढ़ाया।
इस प्रकार अभीष्ट कोण ∠AOQ = 90°

(d) (1) सर्वप्रथम किरण OA खींचते हैं।
(2) O को केन्द्र मानकर और उपयुक्त त्रिज्या लेकर एक चाप लगाया जो OA को P पर काटता है।
(3) P को केन्द्र मानकर उसी त्रिज्या से एक चाप लगाया जो पहले चाप को R पर काटता है।

(4) R को केन्द्र मानकर उसी त्रिज्या से दूसरा चाप लगाते हैं जो पहले चाप को S पर काटता है।
(5) O को S से मिलाते हुए आगे B तक बढ़ाया।
इस प्रकार अभीष्ट ∠AOB = 120°

(e) (1) सर्वप्रथम ∠AOQ = 90° बनाते हैं।
(2) ∠AOQ का समद्विभाजक OR ज्ञात करते हैं।
इस प्रकार ∠AOR = 45°

(f) चूँकि 135° = 90° + 45°
अर्थात् 90° + \(\frac { 1 }{ 2 }\) (90°) = 135°
आकृति में, ∠BOD = 90°

∠BOD का समद्विभाजक OC ज्ञात करते हैं।
इस प्रकार ∠BOC = 45°
अतः ∠AOC = 135°

प्रश्न 6.
45° का कोण खींचिए और उसके समद्विभाजक कीजिए।
हल :
रचना के पद :
(1) सर्वप्रथम किरण \(\overrightarrow{ OA }\) खींचते हैं।
(2) ∠AOQ = 45° बनाते हैं।

(3) C को केन्द्र मानकर और CD के आधे से अधिक त्रिज्या लेकर एक चाप लगाते हैं।
(4) D को केन्द्र मानकर और उसी त्रिज्या से लेकर एक दूसरा चाप लगाते हैं जो पहले चाप को B पर काटता है।
(5) O को B से मिलाया और आगे बढ़ाया।
इस प्रकार \(\overrightarrow{ OB }\) , ∠AOQ को दो समान भागों में विभाजित करता है।
∠AOB = \(\frac { 1 }{ 2 }\) (45°) = 22\(\frac { 1 }{ 2 }\)°

प्रश्न 7.
135° का कोण खींचिए और उसे समद्विभाजित कीजिए।
हल :
रचना के पद :
(1) सर्वप्रथम रेखा AB खींचते हैं और इस पर कोई बिन्दु O लेते हैं।

(2) बिन्दु O पर ∠AOC = 135° बनाते हैं।
(3) ∠AOC का समद्विभाजक \(\overrightarrow{ OD }\) खींचते हैं।
इस प्रकार ∠AOD = \(\frac { 1 }{ 2 }\) (135°) = 67\(\frac { 1 }{ 2 }\)°

प्रश्न 8.
70° का कोण खींचिए। इस कोण के बराबर रूलर और परकार की सहायता से एक कोण बनाइए।
हल:

रचना के पद-
(1) रेखाखण्ड \(\overrightarrow{ OA }\) खींचा।
(2) बिन्दु O पर चाँद की सहायता से ∠AOB = 70° बनाया।
(3) अब किरण \(\overrightarrow{ PQ }\) खींचते हैं।
(4) O को केन्द्र मानकर और उपयुक्त त्रिज्या लेकर एक चाप लगाया जो \(\overrightarrow{ OA }\) और \(\overrightarrow{ OB }\) को क्रमशः E और F पर काटता है।
(5) P को केन्द्र मानकर और उसी त्रिज्या से एक दूसरा चाप लगाया जो \(\overrightarrow{ PQ }\) को R पर काटता है।
(6) R को केन्द्र मानकर और EF के बराबर त्रिज्या लेकर पहले चाप को S पर काटते हुए एक चाप लगाते हैं।
(7) P को 5 से मिलाते हुए आगे बढ़ाते हैं।
इस प्रकार ∠QPS = ∠AOB = 70°

प्रश्न 9.
40° का एक कोण खींचिए। इसके सम्पूरक के बराबर एक कोण बनाइए।
हल:

रचना के पद :
(1) चाँद की सहायता से ∠AOB = 40° बनाते हैं। इसका सम्पूरक कोण ∠COB है।
(2) एक किरण OL खींचते हैं।
(3) O को केन्द्र मानकर और उपयुक्त त्रिज्या लेकर एक चाप लगाते हैं जो \(\overrightarrow{ OC }\) और \(\overrightarrow{ OB }\) को क्रमश: E और F पर काटता है।
(4) P को केन्द्र मानकर और उसी त्रिज्या को लेकर एक चाप लगाते हैं जो \(\overrightarrow{ OP }\) को N पर काटता है।
(5) अब N को केन्द्र मानकर और EF त्रिज्या लेकर एक चाप लगाते हैं, जो पहले चाप को M पर काटता है।
(6) P को M से मिलाया और आगे बढ़ाया।
इस प्रकार ∠OPM = सम्पूरक ∠COB

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.5

पाठ्य-पुस्तक पृष्ठ संख्या # 307-308

प्रश्न 1.
7.3 सेमी लम्बाई का एक रेखाखण्ड \(\overline { AB } \) खींचिए और उसकी सममित अक्ष ज्ञात कीजिए।
हल :
रचना के पद :
(1) एक रेखाखण्ड \(\overline { AB } \) = 7.3 सेमी खींचा।
(2) A को केन्द्र मानकर AB के आधे से अधिक त्रिज्या लेकर AB के दोनों ओर एक-एक चाप लगाते हैं।
(3) अब B को केन्द्र मानकर और AB के आधे से अधिक त्रिज्या लेकर AB के दोनों ओर दो चाप और लगाते हैं जो पहले वाले चापों को C और D पर काटते हैं।
(4) C को D से मिलाया। रेखा CD रेखाखण्ड \(\overline { AB } \) को M पर काटती है।

(5) बिन्दु M रेखाखण्ड \(\overline { AB } \) को समद्विभाजित करता है। इस प्रकार प्राप्त रेखाखण्ड सममित अक्ष है।

प्रश्न 2.
9.5 सेमी लम्बा एक रेखाखण्ड खींचिए और उसका लम्ब समद्विभाजक खींचिए।
हल :
रचना के पद :
(1) एक रेखाखण्ड AB = 9.5 सेमी खींचा।
(2) A को केन्द्र मानकर AB के आधे से अधिक दूरी की. त्रिज्या लेकर AB के दोनों ओर चाप लगाते हैं।

(3) अब B को केन्द्र मानकर इतनी ही त्रिज्या लेकर AB के दोनों ओर चाप लगाते हैं, जो पहले चापों को क्रमशः C और D पर काटते हैं।
(4) C को D से मिलाया।
रेखाखण्ड CD अभीष्ट लम्ब समद्विभाजक है।

प्रश्न 3.
एक रेखाखण्ड \(\overline { XY } \) का लम्ब समद्विभाजक खींचिए जिसकी लम्बाई 10.3 सेमी है।
(a) इस लम्ब समद्विभाजक पर कोई बिन्दु P लीजिए। जाँच कीजिए कि PX = PY है।
(b) यदि M रेखाखण्ड XY का मध्य-बिन्दु है, तो MX और XY के विषय में आप क्या कह सकते हैं ?
हल :
रचना के पद :
(1) रेखाखण्ड \(\overline { XY } \) = 10.3 सेमी खींचते हैं।
(2) X और Y को केन्द्र मानकर और XY के आधे से अधिक त्रिज्या लेकर दो चाप लगाते हैं, जो एक-दूसरे को A और B पर काटते हैं।

(3) A को B से मिलाया।
इस प्रकार AB ⊥ \(\overline { XY } \)
(4) \(\overline { AB } \) पर कोई बिन्दु P लेते हैं और PX तथा PY को जोड़ते हैं।
(a) मापने पर, \(\overline { PX } \) = \(\overline { PY } \)
(b) \(\overline { XY } \) का मध्य-बिन्दु M है। मापने पर,
\(\overline{X M}=\overline{M Y}=\frac{1}{2} \overline{X Y}\)

प्रश्न 4.
लम्बाई 12.8 सेमी वाला एक रेखाखण्ड खींचिए। रूलर और परकार की सहायता से इसके चार बराबर भाग कीजिए। मापन द्वारा अपनी रचना की जाँच कीजिए।
हल :
(1) रेखाखण्ड AB = 12.8 सेमी खींचा।
(2) AB का लम्ब समद्विभाजक ज्ञात किया जो AB को O पर काटता है।

(3) \(\overline { AO } \) का लम्ब समद्विभाजक खींचते हैं जो \(\overline { AB } \) को P पर काटता है।
(4) अब \(\overline { BO } \) का लम्ब समद्विभाजक खींचते हैं जो \(\overline { AB } \) को Q पर काटता है। (Q, \(\overline { OB } \) का मध्य-बिन्दु है।)
(5) रेखाखण्ड \(\overline { AB } \) बिन्दुओं P, O, Q द्वारा चार भागों में विभाजित हो जाता है।
मापने पर, \(\overline{A P}=\overline{P O}=\overline{O Q}=\overline{Q B}=3 \cdot 2\) सेमी

प्रश्न 5.
6.1 सेमी लम्बाई का एक रेखाखण्ड \(\overline { PQ } \) खींचिए फिर \(\overline { PQ } \) को व्यास मानकर एक वृत्त खींचिए।
हल :
रचना के पद :
(1) एक रेखाखण्ड \(\overline { PQ } \) = 6.1 सेमी खींचा।
(2) \(\overline { PQ } \) का लम्ब समद्विभाजक खींचा जो कि \(\overline { PQ } \) को O पर काटता है। (अर्थात् O, \(\overline { PQ } \) का मध्य-बिन्दु है।)

(3) O को केन्द्र मानकर और OP या OQ त्रिज्या लेकर P और Q से जाता हुआ एक वृत्त खींचा।।
वृत्त जिसका कि \(\overline { PQ } \) व्यास है, अभीष्ट वृत्त है।

प्रश्न 6.
केन्द्र C और त्रिज्या 3.4 सेमी लेकर एक वृत्त खींचिए। इसकी कोई जीवा \(\overline { AB } \) खींचिए। इस जीवा \(\overline { AB } \) का लम्ब समद्विभाजक खींचिए। जाँच कीजिए कि क्या यह वृत्त के केन्द्र C से होकर जाता है ?
हल :
रचना के पद:
(1) कागज पर कोई बिन्दु C लेते हैं।
(2) C को केन्द्र मानकर तथा 3.4 सेमी त्रिज्या लेकर एक वृत्त खींचते हैं।

(3) वृत्त की एक जीवा \(\overline { AB } \) खींचते हैं।
(4) वृत्त की जीवा का लम्ब समद्विभाजक PQ खींचते हैं।
हाँ, हम देखते हैं कि यह लम्ब समद्विभाजक वृत्त के केन्द्र से होकर जाता है।

प्रश्न 7.
प्रश्न 6.
की उस स्थिति के लिए दोबारा कीजिए जब \(\overline { AB } \) एक व्यास है।
हल :
रचना के पद :
(1) कागज पर कोई बिन्दु O लेते हैं।

(2) O को केन्द्र मानकर और 3.4 सेमी त्रिज्या लेकर एक वृत्त खींचते हैं।
(3) वृत्त का व्यास \(\overline { AB } \) खींचते हैं।
(4) \(\overline { AB } \) का लम्ब समद्विभाजक खींचते हैं। हम देखते हैं कि PQ, केन्द्र C से होकर जाता है और O व्यास \(\overline { AB } \) का मध्य-बिन्दु है।

प्रश्न 8.
4 सेमी त्रिज्या का एक वृत्त खींचिए। इसकी कोई दो जीवाएँ खींचिए। इन दोनों जीवाओं के लम्ब समद्विभाजक खींचिए। ये कहाँ मिलते हैं ?
हल :
रचना के पद :
(1) कागज पर कोई बिन्दु O अंकित करते हैं।
(2) O को केन्द्र मानकर और 4 सेमी त्रिज्या लेकर एक वृत्त खीचते हैं।

(3) वृत्त की दो जीवाएँ \(\overline { AB } \) और \(\overline { CD } \) खींचते हैं।
(4) जीवा \(\overline { AB } \) का लम्ब समद्विभाजक \(\overline { PQ } \) खींचते है।
(5) जीवा \(\overline { CD } \) का लम्ब समद्विभाजक \(\overline { RS } \) खींचते हैं।
ये दोनों लम्ब समद्विभाजक वृत्त के केन्द्र से होकर जाते हैं।

प्रश्न 9.
शीर्ष O वाला कोई कोण खींचिए। इसकी एक भुजा पर बिन्दु A और दूसरी भुजा पर एक अन्य बिन्दु B इस प्रकार लीजिए कि OA = OB है। \(\overline { OA } \) और \(\overline { OB } \) के लम्ब समद्विभाजक खींचिए। मान लीजिए ये Pपर प्रतिच्छेद करते हैं। क्या PA = PB है ?
हल :
रचना के पद :
(1) कोई कोण XOY बनाते हैं। इसका शीर्ष O है।
(2) \(\overline { OX } \) पर एक बिन्दु A तथा \(\overline { OY } \) पर एक अन्य बिन्दु B लेते हैं।
(3) \(\overline { OA } \) और \(\overline { OB } \) के लम्ब समद्विभाजक CD और EF खीचते हैं। माना कि ये P पर मिलते हैं।

(4) \(\overline { PA } \) और \(\overline { PB } \) को मिलाया
मापने पर, \(\overline{P A}=\overline{P B}\)

पाठ्य-पुस्तक पृष्ठ संख्या # 311

प्रयास कीजिए

प्रश्न 1.
पाठय-पुस्तक में दिए गए चरण 2 में, यदि हम त्रिज्या BC के आधे से कम लें, तो क्या कोण होगा?
उत्तर-
यदि हम BC के आधे से कम त्रिज्या लेंगे तो B तथा C को केन्द्र मानकर खींचे गए चाप आपस में नहीं काटेंगे। अतः कोण नहीं बनेगा।

पाठ्य-पुस्तक पृष्ठ संख्या # 312

प्रश्न 1.
ऊपर दर्शाए अनुसार 60° के कोण की रचना कीजिए। अब इस कोण को समद्विभाजित कीजिए। प्रत्येक कोण 30° का है। मापन द्वारा अपनी रचना की जाँच कीजिए।
हल :
रचना के पद :
(1) सर्वप्रथम एक किरण OA खींचते हैं।

(2) O को केन्द्र मानकर कोई भी उचित त्रिज्या लेकर एक चाप PS लगाते हैं, जो OA को P पर काटता है।
(3) P को केन्द्र मानकर इसी त्रिज्या से एक चाप लगाते हैं जो पहले चाप को Q पर काटता है।
(4) OQ को मिलाकर आगे बढ़ाते हैं और किरण OB प्राप्त करते हैं। तब ∠AOB = 60°
(5) P को केन्द्र मानकर और त्रिज्या > \(\frac { 1 }{ 2 }\) PQ लेकर, ∠AOB के अन्तः भाग में एक चाप लगाते हैं।
(6) Q को केन्द्र मानकर इसी त्रिज्या से (चरण 5) एक दूसरा चाप लगाते हैं जो पहले चाप को R पर काटता है।
(7) OR को मिलाते हुए C तक आगे बढ़ाते हैं।
तब ∠AOC = 30°

पाठ्य-पुस्तक पृष्ठ संख्या # 312

प्रयास कीजिए

प्रश्न 1.
15° के कोण की रचना आप किस प्रकार करेंगे?
हल :
रचना के पद :
(1) सर्वप्रथम 60° का ∠ABC बनाते हैं।
(2) ∠ABC को संमद्विभाजित करके 30° का कोण प्राप्त करते हैं। अर्थात् ∠ABD = 30°

(3) अब ∠ABD को इस प्रकार समद्विभाजित करते हैं कि \(\overline { BE } \) ∠ABD का समद्विभाजिक हो।
इस प्रकार ∠ABE = \(\frac { 1 }{ 2 }\) x 30° = 15°

पाठ्य-पुस्तक पृष्ठ संख्या # 313

प्रयास कीजिए

प्रश्न 1.
150° के कोण की रचना आप किस प्रकार करेंगे?
हल :
रचना के पद :
(1) सर्वप्रथम एक रेखा l खींचते हैं और इस पर कोई बिन्दु O लेते हैं।
(2) O को केन्द्र मानकर और उचित त्रिज्या लेकर एक चाप लगाते हैं, जो l को A पर काटता है।
(3) अब A को केन्द्र मानकर इसी त्रिज्या से एक चाप लगाते हैं जो पहले चाप को B पर काटता है।

(4) पुनः इसी त्रिज्या से B को केन्द्र मानकर दूसरा चाप लगाते हैं जो पहले चाप को C पर काटता है।
(5) एक बार पुनः इसी त्रिज्या से C को केन्द्र मानकर चाप लगाते हैं जो पहले चाप को D पर काटता है।
(6) अब ∠COD को समद्विभाजित करते हैं,
इस प्रकार ∠COE = ∠EOD = 30°
(7) चूँकि 150° = 120° + 30°
अतः ∠AOC + ∠COE = ∠AOE
अतः अभीष्ट ∠AOE = 150°

प्रयास कीजिए

प्रश्न 1.
45° के कोण की रचना आप किस प्रकार करेंगे?
हल :
रचना के पद:
(1) सर्वप्रथम 90° का ∠POQ बनाते हैं।
(2) ∠POQ का समद्विभाजक OR खींचते हैं।

इस प्रकार \(\frac { 1 }{ 2 }\)∠POQ = \(\frac { 1 }{ 2 }\) (90°) = 45°
अतः अभीष्ट ∠POR = 45°

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.4

पाठ्य-पुस्तक पृष्ठ संख्या # 305

प्रश्न 1.
एक रेखाखण्ड \(\overline { AB } \) खींचिए। इस पर कोई बिन्दु M अंकित कीजिए। M से होकर \(\overline { AB } \) पर एक लम्ब रूलर और परकार द्वारा खींचिए।
हल :
रचना के पद :
(1) एक रेखाखण्ड \(\overline { AB } \) खींचा और इस पर कोई बिन्दु M अंकित किया।
(2) परकार के नुकीले सिरे को M पर रखकर और कोई सुविधाजनक त्रिज्या लेकर एक चाप लगाते हैं जो AB को P और Q पर काटता है।

(3) अब P और Q को केन्द्र मानकर और PM से अधिक त्रिज्या लेकर दो चाप इस प्रकार लगाते हैं कि वे परस्पर बिन्दु C पर काटते हैं।
C को M से मिलाया।
इस प्रकार CM ⊥ AB

प्रश्न 2.
एक रेखाखण्ड \(\overline { PQ } \) खींचिए। कोई बिन्दु R लीजिए जो PQ पर न हो। R से होकर PQ पर एक लम्ब खींचिए (रूलर और सेट स्क्वे यर द्वारा)।
हल :
रचना के पद :
(1) रेखाखण्ड \(\overline { PQ } \) खींचा और इसके बाहर कोई बिन्दु R लिया।
(2) एक सेट स्क्वे यर को \(\overline { PQ } \) पर इस प्रकार रखते हैं कि उसके समकोण का एक किनारा रेखाखण्ड के अनुदिश हो।

(3) अब सेट स्क्वेयर के समकोण के सम्मुख किनारे के अनुदिश एक रूलर को रखते हैं।
(4) रूलर को कसकर पकड़ते हैं और सेट स्क्वेयर को रूलर के अनुदिश तब तक सरकाते हैं जब तक कि R समकोण बनाने वाले दूसरे किनारे को स्पर्श न करने लगे।
(5) अब R को सेट स्क्वे यर के किनारे के अनुदिश M से मिलाते हुए रेखा खींचते हैं।
अब रेखा RM ⊥ PQ है।

प्रश्न 3.
एक रेखा l खींचिए और उस पर स्थित एक बिन्दु X से होकर, रेखा l पर एक लम्ब रेखाखण्ड \(\overline { XY } \) खींचिए।
अब Y से होकर \(\overline { XY } \) पर एक लम्ब रूलर और परकार द्वारा खींचिए।
हल :
रचना के पद :
(1) एक रेखा l खींचते हैं और इस पर एक बिन्दु X अंकित करते हैं।

(2) X को केन्द्र मानकर और उचित त्रिज्या लेकर एक चाप लगाते हैं जो l को P और Q पर काटता है।
(3) P और Q को केन्द्र मानकर और PX से अधिक त्रिज्या लेकर दो और चाप लगाते हैं, जो एक-दूसरे को M पर काटते हैं।
(4) X को M से मिलाते हुए Z तक बढाते हैं। XZ रेखा l पर अभीष्ट लम्ब है।
(5) अब XZ पर एक बिन्दु Y लेते हैं। Y को केन्द्र मानकर और उचित त्रिज्या लेकर एक चाप लगाते हैं जो XY को R और S पर काटता है।
(6) R और S को केन्द्र मानकर और YR से अधिक त्रिज्या लेकर दो और चाप लगाते हैं, जहाँ एक-दूसरे को N पर काटते हैं।
(7) Y को N से मिलाते हैं।
इस प्रकार YN ⊥ XY.

पाठ्य-पुस्तक पृष्ठ संख्या # 307

प्रयास कीजिए

प्रश्न 1.
रूलर और परकार की रचना के चरण 2 में, यदि हम त्रिज्या \(\overline { AB } \) के आधे से कम लें तो क्या होगा?
उत्तर-
चरण 2 में यदि हम त्रिज्या \(\overline { AB } \) के आधे से कम लें तो A और B को केन्द्र मानकर खींचे गए चाप आपस में नहीं काटेंगे और रचना सम्भव नहीं होगी।

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.3

पाठ्य-पुस्तक पृष्ठ संख्या # 300

प्रश्न 1.
कोई रेखाखण्ड \(\overline { PQ } \) खींचिए। बिना मापे हुए \(\overline { PQ } \) के बराबर एक रेखाखण्ड की रचना कीजिए।
हल :
रचना के पदः
(i) एक रेखाखण्ड \(\overline { PQ } \) खींचा जिसकी लम्बाई ज्ञात नहीं है

(2) l एक रेखा खींची और इस पर एक बिन्दु R लिया।
(3) परकार को \(\overline { PQ } \) के बराबर खोलते हैं।
(4) अब परकार के फैलाव में बिना कोई परिवर्तन किए हुए उसके नुकीले सिरे को R पर रखते हैं।
(5) अब एक चाप लगाते हैं जो l को S पर काटता है। अतः \(\overline { RS } \) ही \(\overline { PQ } \) के बराबर अभीष्ट रेखाखण्ड है।

प्रश्न 2.
एक रेखाखण्ड \(\overline { AB } \) दिया हुआ है, जिसकी लम्बाई ज्ञात नहीं है। एक रेखाखण्ड \(\overline { PQ } \) की रचना कीजिए जिसकी लम्बाई \(\overline { AB } \) की लम्बाई की दो गुनी है।
हल :
रचना के पद:
(1) रेखाखण्ड \(\overline { AB } \) दिया हुआ है, जिसकी लम्बाई ज्ञात नहीं है।
(2) परकार के नुकीले सिरे को A पर रखकर परकार को B तक फैलाकर पेंसिल को B पर रखते हैं। परकार का यह फैलाव \(\overline { AB } \) की लम्बाई दर्शाता है।

(3) अब कोई रेखा l खींचते हैं और इस पर कोई बिन्दु P लेते हैं।
(4) परकार के फैलाव में बिना कोई परिवर्तन किए हुए, उसके नुकीले सिरे को P पर रखते हैं, और पेंसिल वाले सिरे से l पर एक चाप लगाते हैं जो रेखा l को Q पर काटता है।
(5) अब परकार के नुकीले सिरे को Q पर रखकर परकार के उसी फैलाव का एक दूसरा चाप लगाते हैं जो रेखा l को R पर काटता है।

अत: \(\overline { PR } \) अभीष्ट रेखाखण्ड है, जिसकी लम्बाई \(\overline { AB } \) की लम्बाई की दो गुनी है।
अर्थात् \(\overline { PR } \) = 2 \(\overline { AB } \)

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.2

पाठ्य-पुस्तक पृष्ठ संख्या # 299

प्रश्न 1.
रूलर का प्रयोग करके 7.3 सेमी लम्बाई का एक रेखाखण्ड खींचिए।
हल :
रचना के पद:
(1) कागज पर एक बिन्दु A लेते हैं।
(2) अब पैमाने को सीधा रखकर उसका शून्य A पर रखते हैं।

(3) पेंसिल की सहायता से A से 7.3 सेमी की दूरी पर बिन्दु B पर निशान लगाते हैं।
(4) A को B से मिलाते हैं। इस प्रकार प्राप्त रेखाखण्ड AB वांछित रेखाखण्ड है।

प्रश्न 2.
रूलर और परकार का प्रयोग करते हुए 5.6 सेमी लम्बाई का एक रेखाखण्ड खींचिए।
हल :
रचना के पद :
(1) एक रेखा l खींचते हैं और इस पर एक बिन्दु P लेते हैं।

(2) परकार की नोंक को पैमाने के शून्य पर रखते हैं और परकार को इस प्रकार खोलते हैं कि पेंसिल पैमाने के 5.6 सेमी तक पहुँचे।
(3) परकार की नोंक को बिन्दु P पर रखते हैं।
(4) अब परकार में भरी दूरी से रेखा l पर एक चाप लगाते हैं, जो l को बिन्दु Q पर काटता है।
इस प्रकार रेखाखण्ड \(\overline { PQ } \) अभीष्ट रेखाखण्ड है।

प्रश्न 3.
7.8 सेमी लम्बाई का रेखाखण्ड \(\overline { AB } \) खींचिए। इसमें से \(\overline { AC } \) काटिए जिसकी लम्बाई 4.7 सेमी हो। BC को मापिए।
हल :
रचना के पदः

(1) 7.8 सेमी लम्बाई का एक रेखाखण्ड AB खींचा।
(2) यहाँ, \(\overline { AB } \) = 7.8 सेमी और \(\overline { AC } \) = 4.7 सेमी
अब परकार की सहायता से इस रेखाखण्ड पर बिन्दु C इस प्रकार काटते हैं कि AC = 4.7 सेमी।
(3) \(\overline { BC } \) को मापने पर, \(\overline { BC } \) = 3.1 सेमी।

प्रश्न 4.
3.9 सेमी लम्बाई का एक रेखाखण्ड \(\overline { AB } \) दिया हुआ है। एक रेखाखण्ड \(\overline { PQ } \) खींचिए जो रेखाखण्ड \(\overline { AB } \) का दो गुना हो। मापन से अपनी रचना की जाँच कीजिए।

(संकेत: \(\overline { PX } \) खींचिए ताकि \(\overline { PX } \) लम्बाई \(\overline { AB } \) की लम्बाई के बराबर हो। फिर \(\overline { XQ } \) काटिए ताकि \(\overline { XQ } \) की लम्बाई भी \(\overline { AB } \) की लम्बाई के बराबर हो। इस प्रकार \(\overline { PX } \) और \(\overline { XQ } \) की लम्बाई मिलकर \(\overline { AB } \) की लम्बाई का दो गुना हो जाएगी।)
हल :
रचना के पद :
(i) एक रेखा l खींचते हैं।
(ii) AB = 3.9 सेमी खींची।

(iii) रेखा l में से \(\overline { PX } \) = \(\overline { AB } \) = 3.9 सेमी काटा।
(iv) अब \(\overline { XQ } \) = \(\overline { AB } \) = 3.9 सेमी काटा।
अत: \(\overline { AB } \) की दो गुनी लम्बाई के लिए \(\overline { PX } \) और \(\overline { XQ } \) लम्बाई जोड़ते हैं।
जाँच : \(\overline { AB } \) + \(\overline { AB } \) = 3.9 सेमी + 3.9 सेमी
2 \(\overline { AB } \) = 7.8 सेमी = \(\overline { PQ } \)
अत: \(\overline { AB } \) का दो गुना = \(\overline { PQ } \)

प्रश्न 5.
7.3 सेमी लम्बाई का रेखाखण्ड \(\overline { AB } \) और 3.4 सेमी लम्बाई का रेखाखण्ड \(\overline { CD } \) दिया हुआ है। एक रेखाखण्ड \(\overline { XY } \) खींचिए ताकि \(\overline { XY } \) की लम्बाई \(\overline { AB } \) और \(\overline { CD } \) की लम्बाइयों के अन्तर के बराबर हो।
हल :
रचना के पद :
(1) सर्वप्रथम रेखाखण्ड \(\overline { AB } \) = 7.3 और \(\overline { CD } \) = 3.4 सेमी खींचते हैं।

(2) एक रेखा l खींचते हैं और इस पर कोई बिन्दु X लेते हैं।

(3) अब \(\overline { XR } \) इस प्रकार लेते हैं कि \(\overline { XR } \) की लम्बाई = \(\overline { AB } \) की लम्बाई = 7.3 सेमी

(4) अब \(\overline { RY } \) = \(\overline { CD } \) की लम्बाई (3.4 सेमी) इस प्रकार काटते हैं कि
\(\overline { XY } \) की लम्बाई = \(\overline { AB } \) की लम्बाई – \(\overline { CD } \) की लम्बाई
जाँच : मापने पर, हम प्राप्त करते हैं
\(\overline { XY } \) = 3.9 सेमी = 7.3 सेमी – 3.4 सेमी
= \(\overline { AB } \) – \(\overline { CD } \)
अतः \(\overline { XY } \) = \(\overline { AB } \) – \(\overline { CD } \)

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Ex 14.1

प्रश्न 1.
3.2 सेमी त्रिज्या का एक वृत्त खींचिए।
हल :
रचना के पद :
(1) कागज पर एक बिन्दु O लेते हैं।
(2) परकार को वांछित त्रिज्या 3.2 सेण्टीमीटर तक खोलते हैं।
(3) परकार की नोंक को स्थिर बिन्दु O पर रखते हैं तथा दूसरे पेंसिल वाले सिरे को घुमाते हैं। पेंसिल वाले सिर को घुमाने पर वांछित वृत्त प्राप्त होता है।

प्रश्न 2.
एक ही केन्द्र O लेकर 4 सेमी और 2.5 सेमी त्रिज्या वाले दो वृत्त खींचिए।
हल :
रचना के पद:
(1) कागज पर एक बिन्दु O लेते हैं।
(2) परकार को 2.5 सेमी तक खोलते हैं।
(3) परकार की नोंक को बिन्दु O पर रखकर पेंसिल वाले सिरे को घुमाकर वृत बनाते हैं। इस प्रकार प्राप्त वृत्त 2.5 सेमी त्रिज्या का वृत्त होगा।

(4) अब परकार को 4 सेमी के लिए खोलते हैं।
(5) परकार की नोंक को बिन्दु O पर रखकर पेंसिल वाले सिरे को घुमाते हैं। इस प्रकार प्राप्त वृत्त 4 सेमी त्रिज्या का वृत्त होगा।

प्रश्न 3.
एक वृत्त और उसके कोई दो व्यास खींचिए। यदि आप इन व्यासों के सिरों को जोड़े दें तो कौन-सी आकृति प्राप्त होती है ? यदि व्यास परस्पर लम्ब हों, तो कौन-सी आकृति प्राप्त होगी?
आप अपने उत्तर की जाँच किस प्रकार करेंगे ?
हल :
रचना के पदः
(1) O केन्द्र लेकर किसी भी त्रिज्या का एक वृत्त खींचा।
(2) दो व्यास AC और BD खींचे।
(3) AC और BD को मिलाकर चतुर्भुज ABCD बनाते हैं।
मापने पर, AB = CD और AD = BC
और ∠A = ∠B = ∠C = ∠D = 90°
अत: ABCD एक आयत है।

पुनः यदि व्यास AC और BD लम्बवत् हैं, तब
(1) AC और BD के सिरों को मिलाते हैं।
हम एक चतुर्भुज प्राप्त करते हैं।

मापने पर, हम प्राप्त करते हैं :
AB = BC = CD = DA
और ∠A = ∠B और ∠C = ∠D
अत: ABCD एक वर्ग है।

प्रश्न 4.
एक वृत्त खींचिए और बिन्दु A, B और C इस प्रकार अंकित कीजिए कि
(a) A वृत्त पर स्थित हो।
(b) B वृत्त के अभ्यंतर में स्थित हो।
(c) C वृत्त के बहिर्भाग में स्थित हो।
हल :

प्रश्न 5.
मान लीजिए A और B समान त्रिज्याओं वाले दो वृत्तों के केन्द्र हैं। इन्हें इस प्रकार खींचिए ताकि एक वृत्त दूसरे के केन्द्र से होकर जाए। इन्हें C और D पर प्रतिच्छेद करने दीजिए। जाँच कीजिए कि \(\overline { AB } \) और \(\overline { CD } \) परस्पर समकोण पर हैं।

उत्तर-
हाँ, रेखाखण्ड \(\overline { AB } \) और \(\overline { CD } \) परस्पर समकोण पर हैं।

MP Board Class 6th Maths Solutions

MP Board Class 6th Maths Solutions Chapter 14 प्रायोगिक ज्यामिती Intext Questions

पाठ्य-पुस्तक पृष्ठ संख्या # 297-298

सोचिए, चर्चा कीजिए और लिखिए

प्रश्न 1.
आप केन्द्र O लेकर, एक बिन्दु मान लीजिए P से कितने वृत्त खींचे सकते हैं?
उत्तर-
एक।

MP Board Class 6th Maths Solutions

MP Board Class 6th Sanskrit Solutions Surbhi Chapter 20 श्रमस्य महत्वम्

MP Board Class 6th Sanskrit Chapter 20 अभ्यासः

प्रश्न 1.
एकपदेन उत्तरं लिखत (एक शब्द में उत्तर लिखो)
(क) सिक्खधर्मस्य प्रवर्तकः कः? (सिक्ख धर्म के प्रवर्तक कौन थे?)
उत्तर:
गुरुनानकदेवः

(ख) गुरुनानकदेवः कस्मिन् प्रान्ते अभवत्? (गुरुनानक देव किस प्रान्त में हुए?)
उत्तर:
पञ्जाब प्रान्ते

(ग) श्रमिकः काः समर्पितवान्? (श्रमिक ने क्या समर्पित किया?)
उत्तर:
रोटिकाः

(घ) धनिकः किम् अयच्छत्? (धनवान ने क्या प्रदान किया?)
उत्तर:
मिष्टान्नम्

(ङ) गुरुनानकः कस्य भोजनं स्वीकृतवान्? (गुरुनानक ने किसका भोजन स्वीकार किया?)
उत्तर:
श्रमिकस्य।।

प्रश्न 2.
एकवाक्येन उत्तरं लिखत (एक वाक्य में उत्तर लिखो)
(क) गुरुनानकः किमर्थं ग्रामम् अगच्छत्। (गुरुनानक किसलिए ग्राम को गये थे?)
उत्तर:
गुरुनानक: धर्मप्रचारार्थम् ग्रामम् अगच्छत्। (गुरुनानक धर्म के प्रचार के लिए ग्राम को गये।)

(ख) धनिकः किमर्थम् उत्तेजितः अभवत्? (धनिक किसलिए उत्तेजित हो गया?)
उत्तर:
धनिकस्य मिष्टान्नम् गुरुणा नानकेन अस्वीकृतः तेन सः धनिकः उत्तेजितः अभवत्। (धनिक का मिष्ठान्न गुरुनानक ने अस्वीकृत कर दिया। उससे वह धनवान उत्तेजित हो गया।)

(ग) गुरु धनिकं किम् उक्तवान्? (गुरू ने धनिक से क्या कहा?)
उत्तर:
गुरुः धनिकम् उक्तवान् यत् संसारे जात्या, धनेन च न कः अपि जन: उच्च: निम्नो वा। सर्वेजनाः समानाः। चरित्रेण एव श्रेष्ठता भवति। (गुरु ने धनवान से कहा कि संसार में जाति से और धन से कोई भी मनुष्य ऊँचा या नीचा नहीं होता है। सभी लोग समान होते हैं। चरित्र से श्रेष्ठता होती है।)

(घ) लक्ष्मी: शुद्धा कथं भवति? (लक्ष्मी शुद्ध किस तरह होती है?)
उत्तर:
श्रमेण अर्जिता लक्ष्मी: शुद्धा भवति। (परिश्रम से कमाई लक्ष्मी शुद्ध होती है।)

(ङ) मनुष्यस्य श्रेष्ठता केन भवति? (मनुष्य की श्रेष्ठता किससे होती है?)
उत्तर:
मनुष्यस्य श्रेष्ठता चरित्रेण भवति। (मनुष्य की श्रेष्ठता चरित्र से होती है।)

प्रश्न 3.
उचितशब्देन रिक्तस्थानं पूरयत (उचित शब्द से रिक्त स्थान को पूरा करो)
(क) “श्रम एव जयति” इति ध्येय …………. अस्ति। (वाक्यम्/वाक्यानि)
(ख) श्रमेण ……….. उन्नतिः भवति। (राष्ट्रस्य/राष्ट्रात्)
(ग) मम ………… सरसभोजनम् आनीतम्। (गृह/गृहात्)
(घ) एतत् …………. धनिकः सक्रोधम् अवदत्। (दृष्ट्वा /दृष्टम्)
(ङ) धनिकस्य भोजनं ……………… शुष्करोटिकाः स्वीकृतवान्। (त्यक्त्वा/त्यक्तुम्)
उत्तर:
(क) वाक्यम्
(ख) राष्ट्रस्य
(ग) गृहात्
(घ) दृष्ट्वा
(ङ) त्यक्त्वा।

प्रश्न 4.
उचितं मेलयत (उचित को मिलाओ)

उत्तर:
(क) → 3
(ख) → 4
(ग) → 1
(घ) → 2

प्रश्न 5.
क्त्वा प्रत्ययं योजयित्वा वाक्यनिर्माणं कुरुत (क्त्वा प्रत्यय जोड़कर वाक्य निर्माण करो)
(क) श्रमिकः गुरुं नमति, भोजनं यच्छति।
(ख) धनिकः गुरुं पश्यति, मिष्टान्नं यच्छति।
(ग) धनिकः गुरुवाक्यं शृणोति, सन्तुष्टः भवति।
(घ) धनिकः अभिमानं त्यजति, विनम्रः भवति।
उत्तर:
(क) श्रमिकः गुरुम नंत्वा भोजनं यच्छति।
(ख) धनिकः गुरुम् दृष्ट्वा मिष्टान्नं यच्छति।
(ग) धनिकः गुरुवाक्यं श्रुत्वा सन्तुष्टः भवति।
(घ) धनिकः अभिमानम् त्यक्त्वा विनम्रः भवति।

योग्यताविस्तारः

1. “श्रमस्य महत्वम्” विषयोपरि पञ्च वाक्यानि लिखत। (“श्रम के महत्व” विषय पर पाँच वाक्य लिखो)
उत्तर:
श्रमस्य महत्वम् :

• अपारे खलु संसारे सर्वे एव जनाः सुखमयं जीवनं कामयन्ते। इस अपार संसार में सभी लोग सुखमय जीवन की कामना करते हैं।
• जीवन सुखमयं विधातुं सुखं शान्तिश्च अपेक्षेते। जीवन को सुखमय बनाने के लिए सुख और शान्ति की अपेक्षा होती है।
• जीवनं पुरुषार्थेन एव चलति, अत: मानव पुरुषार्थी, उद्यमी श्रमशीलः च भवेत्। जीवन पुरुषार्थ से ही चलता है। अतः मनुष्य को पुरुषार्थी, उद्यमी और श्रमशील होना चाहिए।
• अकर्मणि कदापि प्रवृत्तिः न विधेया। अकर्म (निकम्मेपन में) प्रवृत्ति नहीं होनी चाहिए।
• उद्योगशीलः एव जनः सर्व दुःखानि विहाय सुखानि समृद्धिं च अनुभवति। उद्योगशील मनुष्य ही सभी दुःखों का त्याग करके सुख और समृद्धि का अनुभव करता है।
• संसारे परिश्रमस्य उद्योगस्य वा महत्वं सर्वैः स्वीकृतमस्ति। संसार में परिश्रम का अथवा उद्योग का महत्व सभी के द्वारा स्वीकारा गया है।

2. श्लोकं स्मरत (श्लोक को कण्ठाग्र करो)उद्यमः, साहस, धैर्य, बुद्धिः, शक्तिः, पराक्रमः। षडेते यत्र वर्तन्ते, तत्र देवः सहायकः॥

श्रमस्य महत्वम् हिन्दी अनुवाद

“श्रम एव जयति” इति अस्माकं ध्येयवाक्यम् अस्ति। श्रमेण राष्ट्रस्य उन्नतिः भवति। श्रमेण अर्जितं धनं श्रेष्ठं भवति। सिक्खधर्मस्यप्रवर्तकः गुरुनानकदेवः पञ्जाबप्रान्ते अभवत्। एकदा सः धर्मप्रचारार्थं एकं ग्रामम् अगच्छत्। तत्र एकः श्रमिकः गुरुं दृष्ट्वा स्वागतम् अकरोत् एवं च भोजनार्थं रोटिकाः समर्पयत्। एकः उच्चवर्गीयः धनिकः अपि गुरवे मिष्टान्नंअयच्छत्। नानकः किश्चित् विचार्य श्रमिकस्यरोटिकाः स्वीकृतवान्। एतत् दृष्ट्वा धनिकः सक्रोधम् अवदत्”महाराज! किमेतत् ? मम गृहात् आनीतं सरसभोजनं त्यक्त्वा भवान् श्रमिकस्य शुष्करोटिकाः स्वीकरोति। एतत् समीचीनं नास्ति। अहं प्रतिष्ठितः अस्मि। भवान् मम अपमानम् अकरोत्। किं मयि गुरुकृपा नास्ति? माम् अपि गौरवान्वितं करोतु।”

अनुवाद :
“परिश्रम ही विजय प्राप्त करता है।” यह हमारा ध्येय वाक्य है। परिश्रम से राष्ट्र की उन्नति होती है। श्रम से कमाया धन श्रेष्ठ होता है। सिक्ख पन्थ के प्रवर्तक गुरुनानक देव पंजाब प्रान्त में हुए थे। एक बार वे धर्म के प्रचार के लिए एक गाँव को गये। वहाँ एक श्रमिक (मजदूर) ने गुरु को देखकर स्वागत किया और भोजन के लिए रोटियाँ समर्पित कर दीं। एक उच्च वर्ग के धनवान ने भी गुरुजी को मिष्ठान (मीठे पकवान या मिठाइयाँ) दी। नानक ने कुछ विचार करके श्रमिक की रोटियों को स्वीकार कर लिया। इसे देखकर धनवान व्यक्ति क्रोधपूर्वक बोला-“महाराज! यह क्या है? मेरे घर से लाये गये सरस भोजन (स्वादिष्ट भोजन) को त्यागकर आपने श्रमिक की सूखी रोटियाँ स्वीकार की हैं। यह उचित नहीं है। मैं प्रतिष्ठावान् हूँ। आपने मेरा अपमान किया। क्या मुझ पर गुरु की कृपा नहीं है? मुझे भी गौरवान्वित कीजिए।”

गुरुनानकः क्षणं विचार्य मधुरवाण्या अवदत्-“संसारे जात्या, धनेन च न कोऽपि जन: उच्चः निम्नो वा। सर्वेजनाः समानाः। चरित्रेण एव श्रेष्ठता भवति। श्रमिकेण तु बहुश्रमेण धनं अर्जितम्। अतः तस्य भोजनं पवित्रम् अस्ति। अहं तस्य भोजनं स्वीकृतवान्। गुरुवाणीं श्रुत्वा प्रभावितः धनिकः अभिमानं त्यक्त्वा विनम्रः भूत्वा गुरुचरणयोः भूमौ अपतत्। उक्तं च “श्रमेण उपार्जिता लक्ष्मी: शुद्धा भवति।”

अनुवाद :
गुरुनानक क्षण भर विचार करके मधुर वाणी में बोले-“संसार में जाति से और धन से कोई भी व्यक्ति ऊँचा अथवा नीचा नहीं होता है। सभी लोग समान ही होते हैं। चरित्र से श्रेष्ठता होती है। श्रमिक ने बहुत परिश्रम से धन कमाया है। इसलिए उसका भोजन पवित्र है। मैंने उसका भोजन स्वीकार कर लिया। गुरु की वाणी को सुनकर प्रभावित हुआ धनवान अभिमान का त्याग करके विनम्र होकर गुरु के चरणों में जमीन पर गिर गया और कहा “परिश्रम से उपार्जित लक्ष्मी शुद्ध होती है।”

श्रमस्य महत्वम् शब्दार्थाः।

प्रवर्तक = चलाने वाले। विचार्य = विचार करके। श्रमिकः = मेहनत करने वाला, मजदूर। अयच्छत् = दिया। गौरवान्वितम् = धन्य।

MP Board Class 6th Sanskrit Solutions

MP Board Class 6th Maths Solutions Chapter 13 सममिति Ex 13.3

पाठ्य-पुस्तक पृष्ठ संख्या # 292-293

प्रश्न 1.
पाठ्य-पुस्तक में दी गई आकृतियों में सममित रेखाओं की संख्या ज्ञात कीजिए। आप अपने उत्तर की जाँच कैसे करोगे?
हल :
(a)

चार सममित रेखाएँ

(b)

एक सममित रेखा

(c)

दो सममित रेखाएँ

(d)

दो सममित रेखाएँ

(e)

एक सममित रेखा

(f)

दो सममित रेखाएँ .

प्रश्न 2.
पाठ्य-पुस्तक में दिए गए आरेखण को वर्गांकित पेपर पर बनाइए। प्रत्येक को पूरा कीजिए जिससे -प्राप्त आकृति में दो बिन्दुकित रेखाएँ दो सममित रेखाओं के रूप में हों।
हल :
आकृतियों को पूरा करने पर,

प्रश्न 3.
पाठ्य-पुस्तक में दी गई प्रत्येक आकृति में, अंग्रेजी वर्णमाला के एक अक्षर को ऊर्ध्वाधर रेखा के साथ दिखाया गया है। इस अक्षर का दी हुई दर्पण रेखा में प्रतिबिम्ब लीजिए। बताइए कौन-सा अक्षर परावर्तन के बाद समान रहता है (जैसे कौन-सा अक्षर प्रतिबिम्ब में समान दिखाई देता है) और कौन-सा नहीं ? क्या आप कल्पना कर सकते हैं, क्यों ?
O E M N P H L T S V X के लिए प्रयास कीजिए।
हल :
स्पष्ट है कि A प्रतिबिम्ब के बाद भी समान दिखता है, जबकि B समान नहीं दिखता है।

स्पष्ट है कि अक्षर O, M, H, T, V और X प्रतिबिम्ब में समान दिखाई देते हैं, जबकि E, N, P, L और S प्रतिबिम्ब में समान दिखाई नहीं देते हैं।

MP Board Class 6th Maths Solutions