Category: Class 12

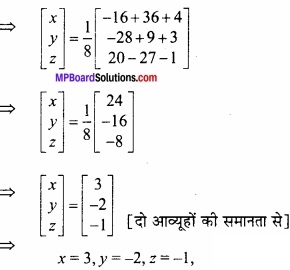
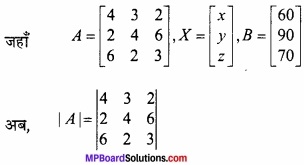
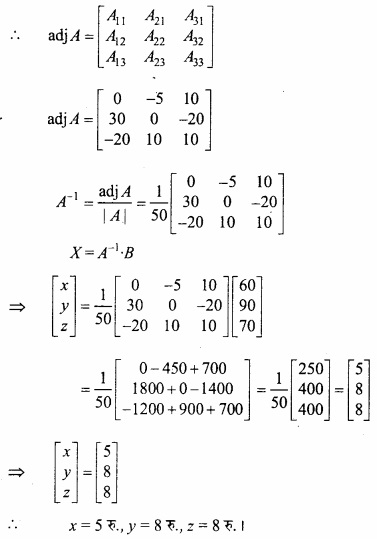
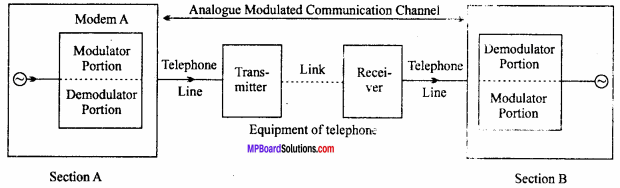
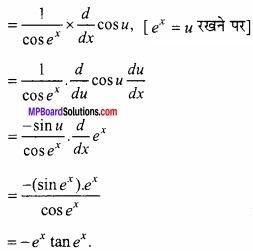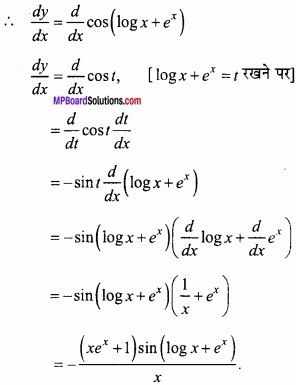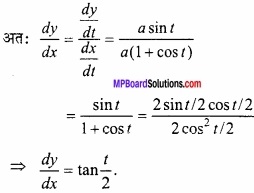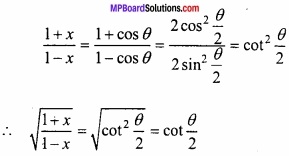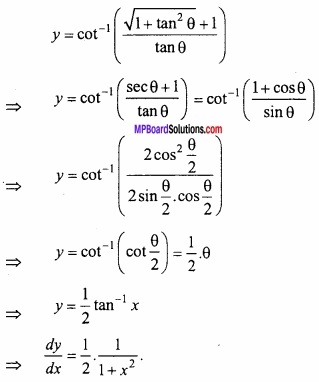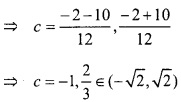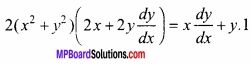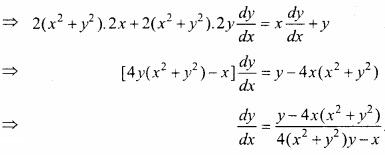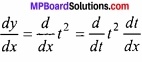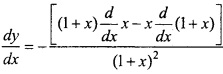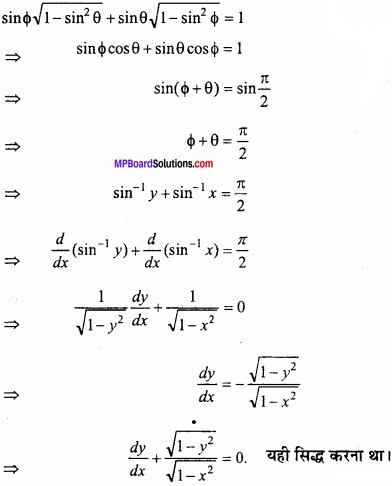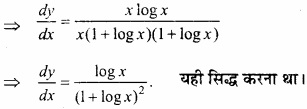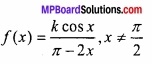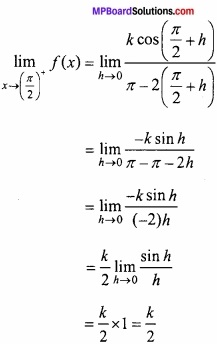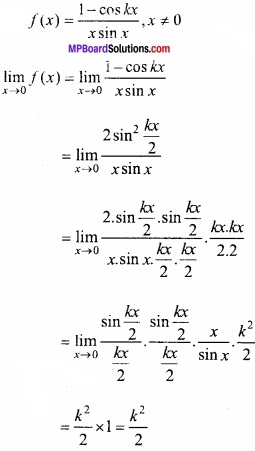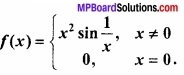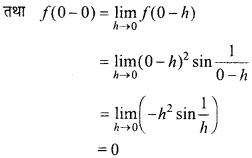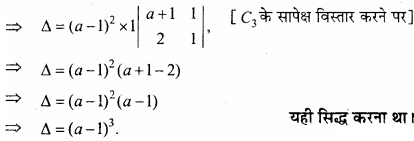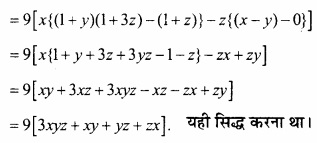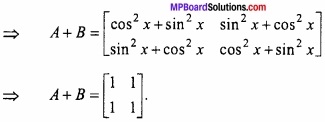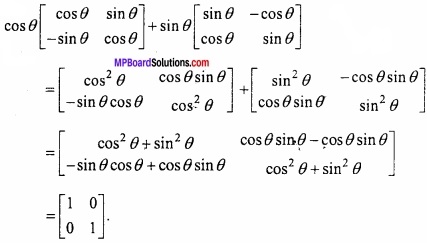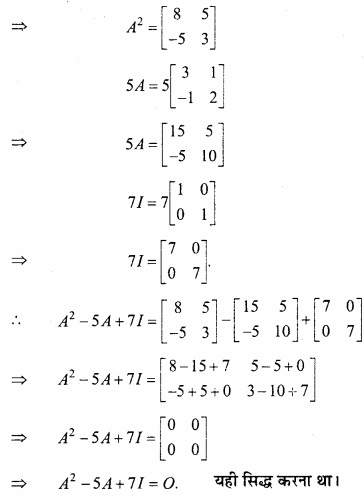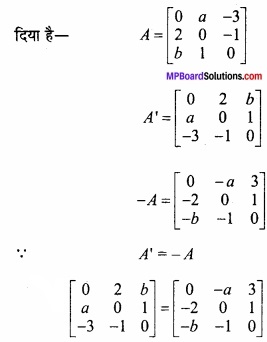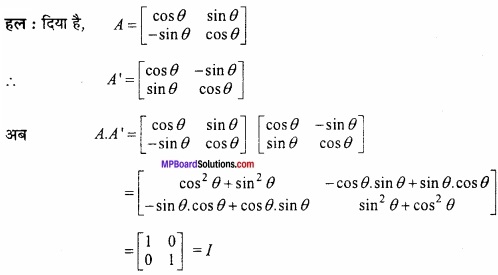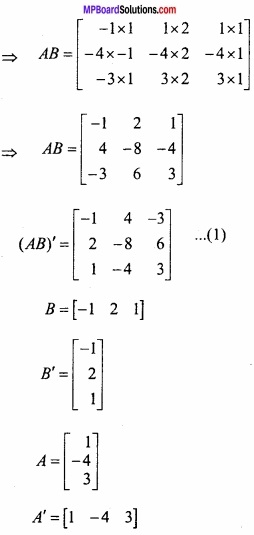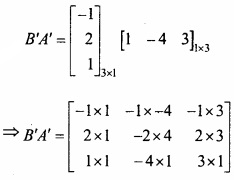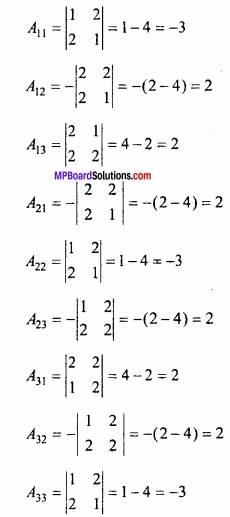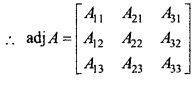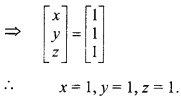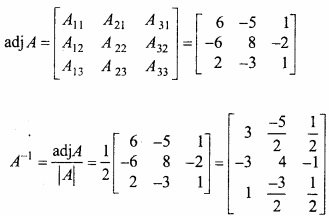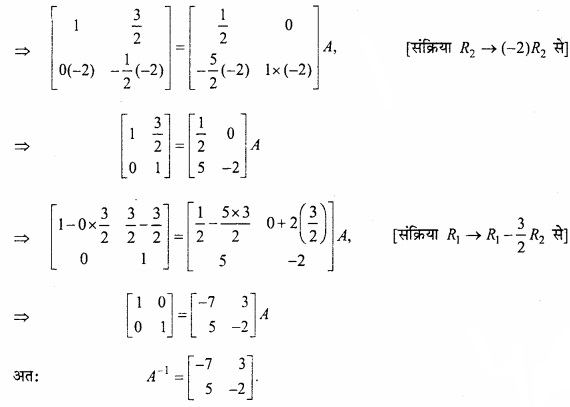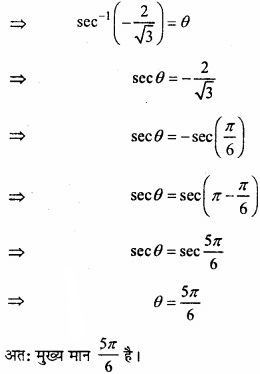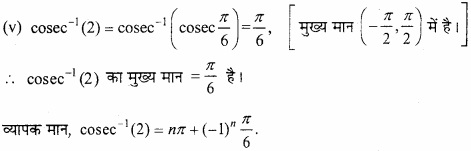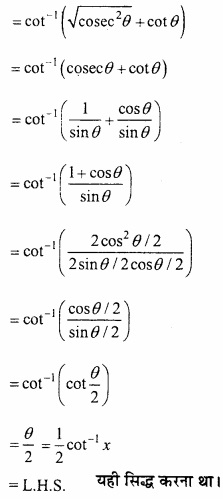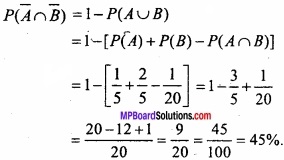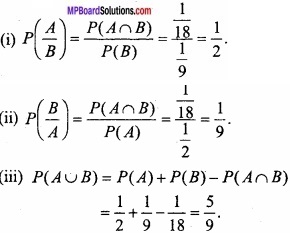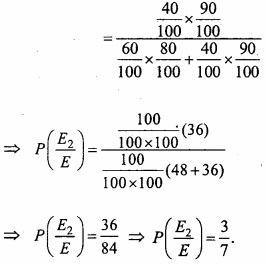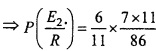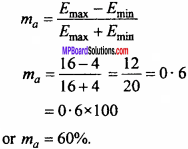MP Board Class 12th Maths Important Questions Chapter 6 अवकलज के अनुप्रयोग

अवकलज के अनुप्रयोग Important Questions

अवकलज के अनुप्रयोग वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सही विकल्प चुनकर लिखिए –

प्रश्न 1.
एक वृत्त की त्रिज्या r = 6 cm पर r के सापेक्ष क्षेत्रफल में परिवर्तन की दर है –
(a) 10π
(b) 12π
(c) 8π
(d) 11π
उत्तर:
(b) 12π

प्रश्न 2.
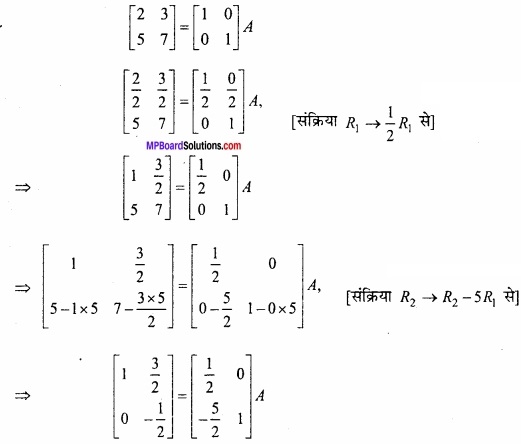
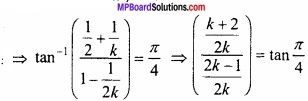
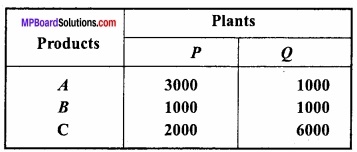
किसी बिन्दु पर y = x + 1, वक्र y² = 4x की स्पर्श रेखा है –
(a) (1, 2)
(b) (2, 1)
(c) (1, -2)
(d) (- 1, 2)
उत्तर:
(a) (1, 2)

प्रश्न 3.
x मीटर भुजा वाले घन की भुजा में 2% की वृद्धि के कारण से घन के आयतन में सन्निकट परिवर्तन ज्ञात कीजिए।
(a) 0.03 x³
(b) 0.02 x³
(c) 0.06 x³
(d) 0.09 x³
उत्तर:
(c) 0.06 x³

प्रश्न 4.
वक्र x² = 2y पर (0, 5) से न्यूनतम दूरी पर स्थित बिन्दु है –
(a) (2\(\sqrt{2}\), 4)
(b) (2\(\sqrt{2}\), 0)
(c) (0, 0)
(d) (2, 2)
उत्तर:
(a) (2\(\sqrt{2}\), 4)

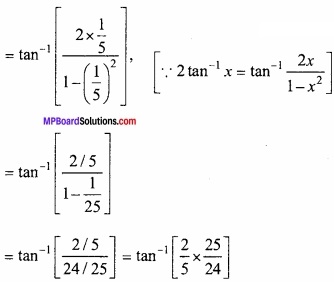
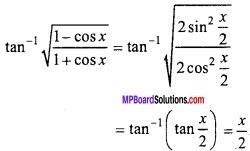
प्रश्न 5.
f (x) = x⁴ – x² – 2x+6 का न्यूनतम मान होगा –
(a) 6
(b) 4
(c) 8
(d) इनमें से कोई नहीं।
उत्तर:
(b) 4

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए –

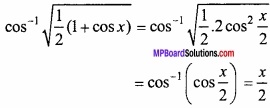
1. 0 ≤ x ≤ π के लिए फलन f (x) = cosx ………………….. फलन होगा।
2. एक वृत्तीय प्लेट की त्रिज्या 0.2 सेमी/सेकण्ड की दर से बढ़ रही है। जब r = 10 सेमी हो, तो क्षेत्रफल के परिवर्तन की दर ………………….. है।
3. फलन y = x(5 – x), x = ………………. पर उच्चिष्ठ है।
4. 2x + 3y का न्यूनतम मान, जब xy = 6, है ……………………… है।
5. sin x + cos x का उच्चिष्ठ मान ……………….. है।
6. रेखा y = mx + 1 वक्र y² = 4x की स्पर्श रेखा है, तो m का मान …………………………….
7. वक्र y = x² के बिन्दु (1, 1) पर स्पर्श रेखा की प्रवणता ………………………. है।
8. अवकलों के प्रयोग द्वारा 10.6 का सन्निकटतम मान ………………………. है।

उत्तर:

1. ह्रासमान
2. 4π cm²/ sec
3. \(\frac{5}{2}\)
4. 12
5. \(\sqrt{2}\)
6. 1
7. 2
8. 0.8

प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –

1. फलन f (x) = e^x – e^-x, x के सभी वास्तविक मानों के लिए वर्धमान फलन \(\frac{1}{2}\) x² है।
2. यदि किसी समद्विबाहु त्रिभुज की समान भुजाओं की लम्बाई x हो, तो उसका महत्तम क्षेत्रफल \(\frac{1}{2}\) x² होगा।
3. फलन f (x) = 3x² – 4x अंतराल (- ∞, \(\frac{2}{3}\) ) में वर्द्धमान है।
4. फलन f (x) = x – cot x सदैव ह्रासमान है।
5. वक्र y = e^x के बिन्दु (0, 1) पर अभिलम्ब का समीकरण x + y = 1 है।

उत्तर:

1. सत्य
2. सत्य
3. असत्य
4. असत्य
5. सत्य।

प्रश्न 4.
एक शब्द/वाक्य में उत्तर दीजिए –

1. \(\sqrt{49.5}\) का सन्निकट मान ज्ञात कीजिए।
2. परवलय y² = 4ax के बिन्दु (x’, y’) पर स्पर्श रेखा का समीकरण ज्ञात कीजिए।
3. वक्र y = x² + 1 के बिन्दु (1, 2) पर स्पर्श रेखा की प्रवणता ज्ञात कीजिए।
4. फलन sin x + cos x का उच्चिष्ठ मान ज्ञात कीजिए।
5. एक बर्फ का गोला चर त्रिज्या रखता है, उसके आयतन में परिवर्तन क्या होगा, जब उसकी त्रिज्या 1 मीटर हो।
6. किसी वर्ग की एक भुजा में 0.2 सेमी/सेकण्ड की दर से वृद्धि होती है। वर्ग के परिमाप की दर ज्ञात कीजिए।

उत्तर:

1. 7.0357
2. yy’ = 2a (x + x’)
3. 3, 3
4. \(\sqrt{2}\)
5. 4π घन मीटर/सेकण्ड
6. 0.8 सेमी/सेकण्ड।

अवकलज के अनुप्रयोग दीर्घ उत्तरीय प्रश्न – I

प्रश्न 1.
एक वृत्त की त्रिज्या 2 सेमी/सेकण्ड की एकसमान दर से बढ़ रही है। क्षेत्रफल में वृद्धि किस दर से होगी जबकि त्रिज्या 10 सेमी हो?
हल:
दिया है:
\(\frac{dr}{dt}\) = 2 सेमी/सेकण्ड
माना कि वृत्त का क्षेत्रफल A वर्ग सेमी है।
तब [ \(\frac{dA}{dt}\) ]_r=10 = ?
∵ वृत्त का क्षेत्रफल A = πr²
∴ \(\frac{dA}{dt}\) = π(2r). \(\frac{dr}{dt}\) = π(2r).(2)
⇒ \(\frac{dA}{dt}\) = 4πr
∴ [ \(\frac{dA}{dt}\) ]_r=10 = 4π(10)
= 40π वर्ग सेमी/सेकण्ड
अर्थात् क्षेत्रफल 40π वर्ग सेमी/सेकण्ड की दर से बढ़ रहा है।

प्रश्न 2.
एक हवा के बुलबुले की त्रिज्या 1/2 से.मी. प्रति सेकण्ड की दर से बढ़ रही है। जब बुलबुले की त्रिज्या 1 से.मी. है तब किस दर से बुलबुले का आयतन बढ़ रहा है?
हल:
बुलबुले की त्रिज्या r हो, तो
∴ आयतन V = \(\frac{4}{3}\) πr³

प्रश्न 3.
एक गुब्बारे की त्रिज्या 10 सेमी/सेकण्ड की दर से बढ़ रही है, जब गुब्बारे की त्रिज्या 15 सेमी है तब किस दर पर गुब्बारे की सतही क्षेत्रफल बढ़ रहा है?
हल:
माना गुब्बारे की त्रिज्या । है। यदि समय । पर उसकी सतही क्षेत्रफल A हो, तो
A = 4πr ²
समय t के साथ गुब्बारे के त्रिज्या में वृद्धि दर \(\frac{dr}{dt}\) = 10 सेमी/सेकण्ड
समय t के साथ गुब्बारे की क्षेत्रफल में वृद्धि के दर = \(\frac{dA}{dt}\)

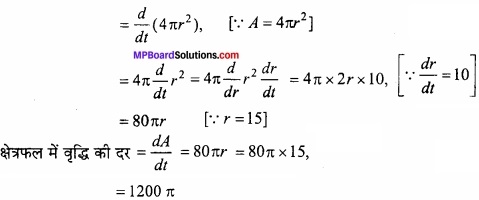
अतः जब गुब्बारे की त्रिज्या 15 सेमी है, तब उसका क्षेत्रफल = 1200π वर्ग सेमी/सेकण्ड की दर से बढ़ रहा है।

प्रश्न 4.
वे अन्तराल ज्ञात कीजिये जिनमें फलन f (x) = 2x³ – 15x² + 36x + 1 वर्धमान या ह्रासमान है।
हल:
f (x) = 2x³ – 15x² + 36x + 1
⇒ f'(x) = 6x² – 30x + 36
= 6(x² – 5x + 6)
= 6(x – 2)(x – 3)
फलन f (x) के वर्धमान होने के लिए,
f'(x) > 0 = (x – 2 )(x – 3) > 0
⇒ या तो x – 2 > 0 तथा x – 3 > 0
⇒ x > 2 तथा x > 3
⇒ x > 3 स्पष्ट है फलन, अन्तराल (3, ∞) में वर्धमान होगा।
पुनः (x – 2)(x – 3) > 0
या तो x – 2 < 0 तथा x – 3 < 0
⇒ x < 2 तथा x < 3
⇒ x < 2
स्पष्ट है फलन, अन्तराल (-∞, 2) में वर्धमान होगा।
अतः दिया गया फलन, अन्तराल (-∞, 2)∪(3, ∞) में वर्धमान होगा।
पुनः f (x) के एक ह्रासमान फलन होने के लिए,
f'(x) < 0
⇒ (x – 2)(x – 3) < 0
या तो x – 2 < 0 तथा x – 3 > 0
⇒ x < 2 तथा x > 3, जो असम्भव है।
या x – 2 > 0 तथा x – 3 < 0 ⇒ x > 2 तथा x < 3
⇒ 2 < x < 3
अत: फलन f (x) एक ह्रासमान फलन है, जबकि 2 < x < 3.
अर्थात् फलन f (x) अन्तराल (2, 3) में ह्रासमान होगा।

प्रश्न 5.
(A) यदि x + y = 8 हो, तो xy का महत्तम मान ज्ञात कीजिए।
हल:
माना
P = xy
⇒ x + y = 8
⇒ y = 8 – x
∴ P = x(8 – x) = 8x – x²
⇒ \(\frac{dP}{dx}\) = 8 – 2x
⇒ \(\frac { d^{ 2 }P }{ dx^{ 2 } } \) = -2
महत्तम और न्यूनतम मान के लिए,
8 – 2x = 0
⇒ x = 4
अब x = 4 पर \(\frac { d^{ 2 }P }{ dx^{ 2 } } \) = -2, जो ऋणात्मक है।
∴ x = 4 पर P का मान महत्तम है।
जब x = 4 तब y = 4
P का महत्तम मान = xy, जब x = 4, y = 4
= 4 × 4 = 16.

(B) यदि x + y = 10 हो, तो xy का महत्तम मान ज्ञात कीजिए।
हल:
प्रश्न क्र. 5 (A) की भाँति हल करें।

प्रश्न 6.
यदि वृत्त की त्रिज्या 3 सेमी/सेकण्ड की दर से बढ़ रही है। जब वृत्त की त्रिज्या 10 सेमी है, तब किस दर से वृत्त का क्षेत्रफल बढ़ रहा है?
हल:
माना कि वृत्त की त्रिज्या है।
यदि समय t पर उसका क्षेत्रफल A हो, तो –
A = πr²
समय t के साथ वृत्त की त्रिज्या में वृद्धि की दर = \(\frac{dr}{dt}\) = 3 सेमी/सेकण्ड।
समय t के साथ वृत्त के क्षेत्रफल में वृद्धि की दर = \(\frac{dA}{dt}\)
= \(\frac { d }{ dx } \) (πr²)
= \(\frac { d }{ dr } \) (πr²). \(\frac { dr }{ dt } \)
= π.2r.3 [∵ \(\frac { dr }{ dt } \) = 3]
= 6πr
अतः वृत्त के क्षेत्रफल में अभीष्ट वृद्धि की दर = \(\frac{dA}{dt}\) = 6πr
= 6π × 10,
= 60π [r = 10 पर]
अतः r = 10 सेमी पर वृत्त का क्षेत्रफल 607 वर्ग सेमी/सेकण्ड की दर से बढ़ रहा है।

प्रश्न 7.
एक घन का आयतन 9 सेमी/सेकण्ड की दर से बढ़ रहा है। यदि इसके कोर की लंबाई 10 सेमी है, तो इसके पृष्ठ का क्षेत्रफल किस दर से बढ़ रहा है? (NCERT)
हल:
माना घन का आयतन V है तथा घन की कोर की लंबाई a सेमी है।
घन का आयतन V = a³
∴ \(\frac{dV}{dt}\) = \(\frac{d}{dt}\)a³
दिया है:
\(\frac{dV}{dt}\) = 9 सेमी³/सेकण्ड

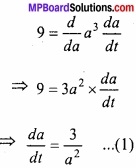
माना घन का पृष्ठ S है।
S = 6a²

प्रश्न 8.
(A) एक आदमी जिसकी ऊँचाई 180 सेमी है, एक बिजली के खम्भे से 1.2 मीटर प्रति सेकण्ड की दर से दूर हट रहा है। यदि बिजली के खम्भे की ऊँचाई 4.5 मीटर है, तो वह दर ज्ञात कीजिए जिस पर उसकी छाया बढ़ रही है।
हल:
AB = बिजली का खम्भा, PQ = आदमी, QC = x = छाया की लम्बाई, माना BQ = y
\(\frac{dy}{dx}\) = 1.2 = वह दर जिससे आदमी दूर हट रहा है।
\(\frac{dx}{dt}\) = वह दर जिससे छाया बढ़ रही है।

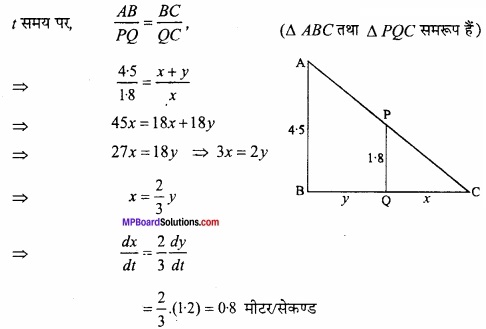
0.8 मीटर/सेकण्ड 0.8 मीटर/सेकण्ड छाया बढ़ने की दर होगी।

(B) 2 मीटर ऊँचाई का आदमी 6 मीटर ऊँचे बिजली के खंभे से दूर 5 किमी/घण्टा की समान चाल से चलता है। उसकी छाया की लंबाई की वृद्धि दर ज्ञात कीजिये। (NCERT)
हल: प्रश्न 8 (A) की भाँति हल करें।
[उत्तर: \(\frac{5}{2}\) किमी/घण्टा।]

प्रश्न 9.
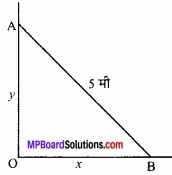
एक सीढ़ी जो 5 मीटर लम्बी है, एक दीवार से झुकी है। सीढ़ी का निचला सिरा दीवार से दूर धरातल के सहारे 2 मीटर/सेकण्ड की दर से खींचा जाता है। जब सीढ़ी का निचला सिरा दीवार से 4 मीटर दूर है, तब किस दर से दीवार पर इसकी ऊँचाई घट रही है? (NCERT)
हल:
माना, किसी समय सीढ़ी का निचला सिरा दीवार से x मीटर की दूरी पर है तथा इस समय दीवार की ऊँचाई ” मीटर है। तब चित्रानुसार,
x² + y² = 25 …………………. (1)
t के सापेक्ष अवकलन करने पर,
2x \(\frac{dx}{dt}\) + 2y\(\frac{dy}{dt}\) = 0
⇒ x\(\frac{dx}{dt}\) + y\(\frac{dy}{dt}\) = 0 …………………….. (2)
सीढ़ी के निचले सिरे की दीवार से दूर खींचे जाने की दर,
\(\frac{dx}{dt}\) = 2 मीटर/सेकण्ड।
∴ x.2 + y\(\frac{dy}{dt}\) = 0
⇒ y\(\frac{dy}{dt}\) = -2x
⇒ \(\frac{dy}{dt}\) = \(\frac{-2x}{y}\)
जब x = 4 मीटर, तब समी. (1) से,
16 + y² = 25
⇒ y² = 25 – 16 = 9
⇒ y = 3 मीटर
∴ समी. (3) से,
\(\frac{dy}{dt}\) = –\(\frac { 2\times 4 }{ 3 } \) = –\(\frac{8}{3}\)
अतः दीवार पर सीढ़ी की ऊँचाई 8/3 मीटर/सेकण्ड की दर से घट रही है।

प्रश्न 10.
वे अन्तराल ज्ञात कीजिए जिनमें फलन, f (x) = 5x² + 7x – 13 वर्धमान या ह्रासमान है।
हल:
दिया है:
f (x) = 5x² + 7x – 13
∴ f'(x) = 10x + 7
फलन f(x) के वर्धमान होने के लिए,
f'(x) > 0
⇒ 10x + 7 > 0
⇒ x > \(\frac{-7}{10}\)
∴ फलन. f (x), अन्तराल ( \(\frac{-7}{10}\), ∞) में एक वर्धमान फलन है।
पुनः फलन f (x) के ह्रासमान होने के लिए,
f'(x) < 0
⇒ 10x + 7 < 0
⇒ x < \(\frac{-7}{10}\)
∴ फलन. f (x), अन्तराल (- ∞, \(\frac{-7}{10}\) ) में एक वर्धमान फलन है।

प्रश्न 11.
वे अन्तराल ज्ञात कीजिए, जिनमें फलन f (x) = 2x³ – 24x + 5 वर्धमान या हासमान है।
हल:
दिया गया फलन है:
f (x) = 2x³ – 24x + 5
x के सापेक्ष अवकलन करने पर,
f'(x) = 6x² – 24
⇒ f'(x) = 6(x² – 4)
⇒ f'(x) = 6(x + 2)(x – 2)

(A) फलन f (x) के वर्धमान होने के लिए शर्त,
f'(x) > 0
6(x + 2)(x – 2) > 0 ⇒ 6(x + 2)(x – 2) < 0
∴ f (x), x ∈ (-2,-2) में वर्धमान है।

(B) फलन f (x) के ह्रासमान होने के लिए शर्त,
f'(x) < 0 ⇒ 6(x + 2)(x – 2) < 0 ∴ f (x), x ∈ (-2, 2) में ह्रासमान है।

प्रश्न 12.
सिद्ध कीजिए x के सभी वास्तविक मानों के लिए फलन f (x) = x – cos x वर्धमान फलन है। हल: दिया गया फलन है: f (x) = X – cos x f'(x) = 1- (- sin x) ⇒ f'(x) = 1 + sin x हम जानते हैं x के सभी वास्तविक मानों के लिए, -1 ≤ sin x ≤ 1 – 1 + 1 ≤ 1 + sin x ≤ 1 + 1 0 ≤ 1 + sin x ≤ 2
अत:
x के सभी वास्तविक मानों के लिए 1 + sin x धनात्मक है स्पष्टतः f'(x) भी धनात्मक होगा। अर्थात् f'(x) > 0. यही सिद्ध करना था।

प्रश्न 13.
a का वह न्यूनतम मान ज्ञात कीजिए जिसके लिए अंतराल [1, 2] में f (x) = x² + ax + 1 से प्रदत्त फलन निरंतर वर्धमान है। (NCERT)
हल:
दिया है:
f (x) = x² + ax + 1
∴ f'(x) = 2x + a
अब, 1 < x < 2
⇒ 2 < 2x < 4
⇒ 2 + a < 2x + a < 4 + a
⇒ 2 + a < f'(x) < 4 + a f (x) के निरंतर वर्धमान होने के लिए हम जानते हैं कि f'(x) > 0
अर्थात् 2 + a > 0 ⇒ a > -2
अत: a का न्यूनतम मान -2 है।

प्रश्न 14.
मान लीजिए [-1, 1] से असंयुक्त एक अन्तराल I हो, तो सिद्ध कीजिए कि f (x) = x + \(\frac{1}{x}\) से प्रदत्त फलन निरंतर वर्धमान है। (NCERT)
हल:
f (x) = x + \(\frac{1}{x}\)

अन्तराल [-1, 1] असंयुक्त है
यदि x < -1 तब f'(x) > 0
यदि x > 1 तब f'(x) > 0
अतः अन्तराल I में f (x) निरंतर वर्धमान है। यही सिद्ध करना था।

प्रश्न 15.
वे अन्तराल ज्ञात कीजिये जिनमें निम्न फलन वर्धमान या ह्रासमान है –
f (x) = x⁴ – \(\frac { x^{ 3 } }{ 3 } \)
हल:
f (x) = x⁴ – \(\frac { x^{ 3 } }{ 3 } \)
⇒ f'(x) = 4x³ – \(\frac { 3.x^{ 2 } }{ 3 } \)
⇒ f'(x) = x² (4x – 1)
f'(x) = 0 लेने पर,
x² (4x – 1) = 0
⇒ x = 0 या x = \(\frac{1}{4}\)

अत: 0 तथा \(\frac{1}{4}\), X अक्ष को तीन असंयुक्त अंतराल में बाँटते है –
(-∞, 0), (0, \(\frac{1}{4}\) ), ( \(\frac{1}{4}\), ∞)
अन्तराल (-∞, 0) मे –
f'(x) = x² (4x – 1), [∵ x² = +ve]
[तथा 4x – 1 = 0 ]
⇒ f'(x) < 0
अन्तराल (-∞, 0) मे –
f'(x) = x² (4x – 1), [∵ x² = +ve]
[तथा 4x – 1 = 0 ]
⇒ f'(x) < 0
∴ अन्तराल (-∞, 0) मे f (x) हसमान है।
अन्तराल (0, \(\frac{1}{4}\) ) मे –
f'(x) = x² (4x – 1), [∵ x² = +ve]
[तथा 4x – 1 = 0 ]
⇒ f'(x) > 0
∴ अन्तराल ( \(\frac{1}{4}\), ∞) मे f (x) वर्धमान है।

प्रश्न 16.
एक आयत का परिमाप 100 सेमी है। अधिकतम क्षेत्रफल के लिए आयत की भुजाएँ ज्ञात कीजिए।
हल:
माना कि आयत की लम्बाई x और चौड़ाई y है। तब,
आयत का परिमाप = 2(x + y)
⇒ 2x + 2y = 100
⇒ x + y = 50
माना आयत का क्षेत्रफल A है। तब
A = xy = x (50 – x) = 50x – x², [समी. (1) से]
∴ \(\frac{dA}{dx}\) = 50 – 2x
और \(\frac { d^{ 2 }A }{ dx^{ 2 } } \) = -2
A अधिकतम अथवा न्यूनतम होगा जब
\(\frac{dA}{dx}\) = 0
⇒ 50 – 2x = 0 या x = 25
x के प्रत्येक मान के लिए \(\frac { d^{ 2 }A }{ dx^{ 2 } } \) ऋण है।
∴ x = 25 पर आयत का क्षेत्रफल अधिकतम है।
समी. (1) से,
y = 50 – x = 50 – 25 = 25
अत: आयत की प्रत्येक भुजा 25 सेमी हुई।

प्रश्न 17.
एक आयत का क्षेत्रफल 25 वर्ग सेमी है, इसकी लम्बाई और चौड़ाई ज्ञात कीजिए जबकि इसका परिमाप न्यूनतम हो।
हल:
माना आयत की लम्बाई x व चौड़ाई y इकाई है।
दिया है: आयत का क्षेत्रफल A = 25 वर्ग इकाई
xy = 25 …………………… (1)
आयत का परिमाप

उच्चिष्ठ या निम्निष्ठ के लिये \(\frac{dP}{dx}\) = 0

जो x = 5 के लिये + ve है।
∴ न्यूनतम परिमाप के लिये x = 5 सेमी।
y = \(\frac{25}{x}\) = \(\frac{25}{5}\) = 5 सेमी।

प्रश्न 18.
सिद्ध कीजिए कि sin x + cos x का उच्चिष्ठ मान \(\sqrt{2}\) है।
हल:
माना f (x) = sin x + cos x ………………. (1)
∴ f'(x) = cos x – sin x ………………… (2)
तथा f”(x) = – sinx – cox ……………….. (3)
उच्चिष्ठ या निम्निष्ठ मान के लिए,
f”(x) = 0
∴ cos x – sin x = 0
⇒ sin x = cos x
⇒ tan x = 1
∴ x = \(\frac { \pi }{ 4 } \), \(\frac { 3\pi }{ 4 } \), \(\frac { 5\pi }{ 4 } \)
अब समी. (3) में x = \(\frac { \pi }{ 4 } \) रखने पर,

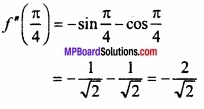
चूंकि f”( \(\frac { \pi }{ 4 } \) )ऋणात्मक है। अत: x = \(\frac { \pi }{ 4 } \) पर दिया गया फलन उच्चिष्ठ है। इसी प्रकार दिया गया फलन x = \(\frac { 3\pi }{ 4 } \), \(\frac { 5\pi }{ 4 } \) ………………. पर भी उच्चिष्ठ होगा।
समी. (1) में x = \(\frac { \pi }{ 4 } \) रखने पर,
उच्चिष्ठ मान f ( \(\frac { \pi }{ 4 } \) ) = sin \(\frac { \pi }{ 4 } \) + cos \(\frac { \pi }{ 4 } \)
= \(\frac { 1 }{ \sqrt { 2 } } \) + \(\frac { 1 }{ \sqrt { 2 } } \) = \(\frac { 2 }{ \sqrt { 2 } } \) = \(\sqrt{2}\) यही सिद्ध करना था।

प्रश्न 19.
दो धनात्मक संख्याएँ इस प्रकार ज्ञात कीजिए कि x + y = 60 तथा xy³ उच्चिष्ठ हो। (NCERT)
हल:
दिया हुआ है:
x + y = 60
माना u = xy³
समी. (1) से x का मान समी. (2) में रखने पर,
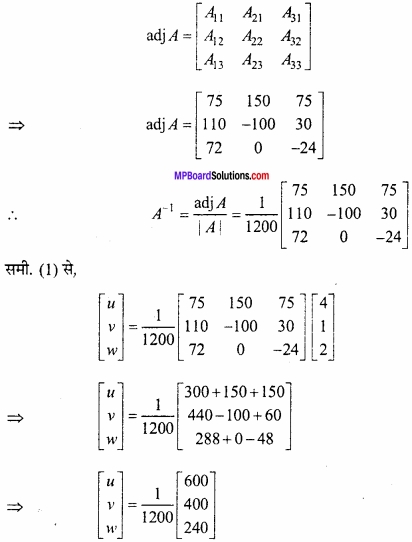
image 16
∴ u के उच्चिष्ठ व निम्निष्ठ मान के लिए \(\frac{du}{dy}\) = 0
∴ 180y² – 4y³ = 0
⇒ 4y² (45 – y) = 0
⇒ y = 0, y = 45
⇒ y = 45 (∵ y ≠ 0)
अब y = 45 पर \(\frac { d^{ 2 }u }{ dy^{ 2 } } \) का मान
= 360 × 45 – 12 × 45 × 45
= 12 × 45(30 – 45), (∵y ≠ 0)
जो सप्तस्ततः ऋणात्मक है।
अतिएव y = 45 पर, u उच्चिष्ठ है।
∴ समी. (1) से,
x + 45 = 60
⇒ x = 60 – 45 = 15
अतः अभीष्ट 15 और है 45 है।

प्रश्न 20.
वक्र y = x³ – x + 1 की स्पर्श रेखा की प्रवणता उस बिन्दु पर ज्ञात कीजिए जिसकाx निर्देशांक 2 है। (NCERT)
हल:
दिये गये वक्र का समीकरण है –
y = x³ – x + 1
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) (x³ – x + 1)
= \(\frac{d}{dx}\) x³ – \(\frac{d}{dx}\) x + \(\frac{d}{dx}\) 1
⇒ \(\frac{dy}{dx}\) = 3x² – 1 + 0
⇒ \(\frac{dy}{dx}\) = 3x² – 1
x = 2 पर स्पर्श रेखा की प्रवणता
( \(\frac{dy}{dx}\) )_x=2 = 3(2)² – 1
= 3 × 4 – 1 = 11

प्रश्न 21.
वक्र y = \(\frac { x-1 }{ x-2 } \), x ≠ 2 के x = 10 परस्पर्श रेखा की प्रवणता ज्ञात कीजिए। (NCERT)
हल:
दिये गये वक्र का समीकरण है –
y = \(\frac { x-1 }{ x-2 } \)
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) = ( \(\frac { x-1 }{ x-2 } \) )

प्रश्न 22.
वक्र y = x³ – 3x² – 9x + 7 पर उन बिन्दुओं को ज्ञात कीजिए जिन पर स्पर्श रेखा X अक्ष के समान्तर है। (NCERT)
हल:
दिये गये वक्र का समीकरण है –
y = x³ – 3x² – 9x + 7
image 18
स्पर्श रेखा X – अक्ष के समान्तर है।
∴ \(\frac{dy}{dx}\) = 0
3(x – 3)(x + 1) = 0
⇒ x = 3, -1
जब x = 3 तब y = (3)³ – 3(3)² – 9 × 3 + 7
y = 27 – 27 – 27 + 7
y = – 20
जब x = -1 तब y = (-1)³ – 3(-1)² – 9(-1) + 7
y = – 1 – 3 + 9 + 7
y = 12
बिन्दुओं (3, -20) और (-1, 12) पर स्पर्श रेखाएँ x – अक्ष के समान्तर होगी।

प्रश्न 23.
परवलय y² = 4ax के बिन्दु (at², 2at) पर स्पर्श रेखा का समीकरण ज्ञात कीजिए। (NCERT)
हल:
परवलय का समीकरण है –
y² = 4ax


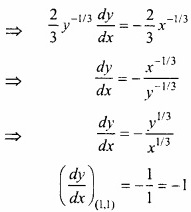
(_x1y1) स्पर्श रेखा का समीकरण है –
y – y₁ = \(\frac{dy}{dx}\) (x – x₂)
जँहा x₁ = at², y₁ = 2at, \(\frac{dy}{dx}\) = \(\frac{1}{t}\)
y – 2at = \(\frac{1}{t}\)(x – at²)
⇒ yt – 2at² = x – at²
⇒ x – ty + at² = 0.

प्रश्न 24.
वक्र x^2/3 + y^2/3 = 2 के बिन्दु (1, 1) पर स्पर्श रेखा का समीकरण ज्ञात कीजिए। (NCERT)
हल:
वक्र का समीकरण है –
x^2/3 + y^2/3 = 2

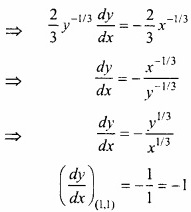
(_x1y1) पर स्पर्श रेखा का समीकरण है
y – y₁ = ( \(\frac{dy}{dx}\) ) (_x1y1) (x – x₁)
यहाँ x₁ = 1, y₁ = 1, \(\frac{dy}{dx}\) = -1
y – 1 = -(x – 1)
⇒ y – 1 = -x + 1
⇒ x + y – 2 = 0.

प्रश्न 25.
वक्र 2y + x² = 3 के बिन्दु (1, 1) पर अभिलम्ब का समीकरण ज्ञात कीजिए। (NCERT)
हल:
दिये गये वक्र का समीकरण है:
2y + x² = 3

(x₁, y₁) पर अभिलम्ब का समीकरण होगा –

प्रश्न 26.
(A) वक्र x = cost, y = sint के t = = पर अभिलम्ब का समीकरण ज्ञात कीजिए। (NCERT)
हल:
I वक्र का समीकरण है –
x = cos t
\(\frac{dx}{dt}\) = \(\frac{d}{dt}\)cos t
⇒ \(\frac{dx}{dt}\) = – sin t
II वक्र का समीकरण है –
y = sin t
\(\frac{dy}{dt}\) = \(\frac{d}{dt}\) sin t
⇒ \(\frac{dy}{dt}\) = cos t

(x₁, y₁) पर अभिलम्ब का समीकरण है –

(B) वक्र 16x² + 9y² = 145 के बिन्दु (x₁, y₁) पर स्पर्श रेखा तथा अभिलंब के समीकरण ज्ञात कीजिये, जहाँ x₁ = 2 तथा y₁ > 0। (CBSE 2018)
हल:
वक्र का समीकरण है –
16x² + 9y² = 145

समी. (1) में x = 2 रखने पर,
16. (2)² + 9y² = 145
⇒ 64 + 9y² = 145
⇒ 9y² = 145 – 64 = 81
⇒ y² = 9 [y ≠ -3 ∵y₁ > 0]
⇒ y = 3
बिन्दु (2, 3) पर \(\frac{dy}{dx}\) = – \(\frac{16}{9}\).\(\frac{2}{3}\) = – \(\frac{32}{27}\)
बिन्दु (2, 3) पर वक्र (1) की स्पर्श रेखा
y – y₁ = \(\frac{dy}{dx}\) (x – x₁)
⇒ y – 3 = \(\frac{-32}{7}\) (x – 2)
⇒ 27y – 81 = -32x + 64
⇒ 32x + 27y = 145
बिन्दु (2, 3) पर वक्र (1) का अभिलम्ब

⇒ 32y – 96 = 27x – 54
⇒ 27x – 32y = 42

प्रश्न 27.
(25)^1/3 का सन्निकट करने के लिए अवकल का प्रयोग कीजिए। (NCERT)
हल:
माना y = x^1/3
जहाँ x = 27 और ∆x = -2

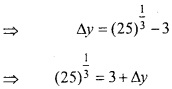
∆y सन्निकटतः dy के बराबर है।

(25)^1/3 का सन्निकट मान
= 3 + ∆y
= 3 – 0.074
= 2.926.

प्रश्न 28.
\(\sqrt { 36.6 } \) का सन्निकटन करने के लिए अवकल का प्रयोग कीजिए।
हल:
माना y = \(\sqrt{x}\)
जहाँ x = 36 और ∆x = 0.6

∆y सन्निकटतः dy के बराबर है।

\(\sqrt { 36.6 } \) का सन्निकट मान = ∆y + 6
= 0.05 + 6 = 6.05.

प्रश्न 29.
(15)^1/4 का सन्निकट करने के लिए अवकल का प्रयोग कीजिए। (NCERT)
हल:
माना y = x^1/4
जहाँ x = 16 और ∆x = -1

∆y सन्निकटतः dy के बराबर है।

(15)^1/4 का सन्निकट मान = ∆y + 2 = 2 – 0.031 = 1.969.

प्रश्न 30.
(26)^1/3 का सन्निकट करने के लिए अवकलज का प्रयोग कीजिए। (NCERT)
हल:
माना y = x^1/3
जहाँ x = 27 और ∆x = -1


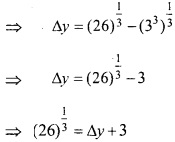
∆y सन्निकटतः dy के बराबर है।

(26)^1/3 का सन्निकट मान = ∆y+3
= 3 – 0.037 = 2.963.

प्रश्न 31.
एक गोले की त्रिज्या 9 सेमी मापी जाती है जिसमें 0.03 सेमी की त्रुटि है। इसके पृष्ठ के क्षेत्रफल के परिकलन में सन्निकट त्रुटि ज्ञात कीजिए। (NCERT)
हल:
माना गोले की त्रिज्या r तथा त्रिज्या मापन में त्रुटि ∆r है
दिया है:
r = 9 सेमी, ∆r = 0.03 सेमी
गोले का पृष्ठ S = 4πr²
\(\frac{dS}{dr}\) = 4π \(\frac{d}{dr}\)r²
⇒ \(\frac{dS}{dr}\) = 8πr
∆S = ( \(\frac{dS}{dr}\) ) ∆r
= (8πr) × 0.03 = 8π × 9 × 0.03 = 2.16 मी²
पृष्ठ क्षेत्रफल के परिकलन में सन्निकट त्रुटि 2.16 मी² है।

प्रश्न 32.
एक गोले की त्रिज्या 7 मी मापी जाती है जिसमें 0.02 मी की त्रुटि है। इसके आयतन के परिकलन में सन्निकट त्रुटि ज्ञात कीजिए। (NCERT)
हल:
माना गोले की त्रिज्या r तथा त्रिज्या मापन में त्रुटि ∆r है
दिया है:
r = 7 मी, ∆r = 0.02 मी
गोले का आयतन V = \(\frac{4}{3}\)πr³

आयतन के परिकलन में सन्निकट त्रुटि 3.9π मी³ है।

प्रश्न 33.
x मी भुजा वाले घन की भुजा में 1% वृद्धि के कारण घन के आयतन में होने वाला सन्निकट परिवर्तन ज्ञात कीजिए। (NCERT)
हल:
घन की भुजा x मी है
घन का आयतन V = x³, ∆x = x का 1% = \(\frac{x}{100}\)
\(\frac{dV}{dx}\) = \(\frac{d}{dx}\) x³ = 3x²
आयतन में परिवर्तन ∆V = ( \(\frac{dV}{dx}\) ) ∆x
= 3x² × \(\frac{x}{100}\) = 0.03 x³ मी³
आयतन में सन्निकट परिवर्तन 0.03x³ मी³ है।

प्रश्न 34.
x मीटर भुजा वाले घन की भुजा में 2% वृद्धि के कारण से घन के आयतन में सन्निकट परिवर्तन ज्ञात कीजिए। (NCERT)
हल:
घन की भुजा x मीटर है।
∆x = x का 2% = \(\frac { x\times 2 }{ 100 } \) = 0.02x
घन का आयतन V = x³
\(\frac{dV}{dx}\) = \(\frac{d}{dx}\) x³ = 3x²
dV = ( \(\frac{dV}{dx}\) ) ∆x = 3x² × 0.02x = 0.06 x³ मी³
आयतन में सन्निकट परिवर्तन 0.06x³ मी³ है।

MP Board Class 12 Maths Important Questions

MP Board Class 12th Maths Important Questions Chapter 5B अवकलन

अवकलन Important Questions

अवकलन लघु उत्तरीय प्रश्न

प्रश्न 1.
x के सापेक्ष sin [cos (x²) ] का अवकलन गुणांक ज्ञात कीजिए। (NCERT)
हल:
माना y = sin [cos (x²) ]
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) sin [cos (x²) ]
= \(\frac{d}{dx}\) sin t, [cos² = t, रखने पर]
= \(\frac{d}{dt}\) sin t \(\frac{dt}{dx}\) sin t
= cost \(\frac{d}{dx}\) cos x²
= cos (cos x²) \(\frac{d}{dx}\) cos u, [x² = u रखने पर]
= cos (cos x²) \(\frac{d}{du}\) cos u \(\frac{du}{dx}\)
= – cos(cos x²) sin u \(\frac{d}{dx}\) x²
= -2x cos(cos x²).sin x²

प्रश्न 2.
यदि y = sec [tan\(\sqrt{x}\) ] हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए।
हल:
दिया है:
y = sec [tan\(\sqrt{x}\) ]

प्रश्न 3.
यदि y = log [cos e^x] हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए। (NCERT)
हल:
दिया है:
y = log [cos e^x]
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) [log(cos e^x)]
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) log t, [cos e^x = t रखने पर]
= \(\frac{d}{dt}\) log t \(\frac{dt}{dx}\)
= \(\frac{1}{t}\). \(\frac{d}{dx}\) cos e^x

प्रश्न 4.
यदि y = cos [log x + e^x] हो, तो 4 का मान ज्ञात कीजिए। (NCERT)
हल:
दिया है:
y = cos [log x + e^x]

प्रश्न 5.
यदि y = cos^-1(e^x) हो, तो \(\frac{dy}{dx}\) ज्ञात कीजिए।
हल:
दिया है:
y = cos^-1(e^x)
∴ \(\frac{dy}{dx}\) = \(\frac{d}{dx}\) cos^-1(e^x)
e^x = t रखने पर,

प्रश्न 6.
यदि y + sin y = cos x हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए। (NCERT)
हल:
दिया गया फलन y + sin y = cos x
x के सापेक्ष अवकलन करने पर, का मान ज्ञात कीजिए।
\(\frac{d}{dx}\) (y + sin y) = \(\frac{d}{dx}\) cos x
⇒ \(\frac{dy}{dx}\) + cos y \(\frac{dy}{dx}\) = – sin x
⇒ \(\frac{dy}{dx}\) (1 + cos y) = – sin x
⇒ \(\frac{dy}{dx}\) = \(\frac { -sinx }{ 1+cosy } \)

प्रश्न 7.
यदि 2x + 3y = sinx हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए। (NCERT)
हल:
दिया है:
2x +3y = sin x
x के सापेक्ष अवकलन करने पर,
\(\frac{d}{dx}\) (2x + 3y) = \(\frac{d}{dx}\) sin x
2 \(\frac{d}{dx}\) x + 3 \(\frac{dy}{dx}\) = cos x
⇒ 2 + 3 \(\frac{dy}{dx}\) = cos x
⇒ 3 \(\frac{dy}{dx}\) = cos x – 2
∴ \(\frac{dy}{dx}\) = \(\frac { cosx-2 }{ 3 } \)

प्रश्न 8.
\(\frac{dy}{dx}\) का मान ज्ञात कीजिए यदि
x = a cos θ, y = a sin θ (NCERT)
हल:
दिया है:
x = a cos θ
y = a sin θ
अब समी. (1) का के सापेक्ष अवकलन करने पर,
\(\frac { dx }{ d\theta } \) = – a sin θ
पुनः समी. (2) का θ के सापेक्ष अवकलन करने पर,

प्रश्न 9.
\(\frac{dy}{dx}\) का मान ज्ञात कीजिए यदि (NCERT)
x = at², y = 2 at
हल:
दिया है:
x = at²
∴ \(\frac{dx}{dt}\) = 2 at
पुनः y = 2 at
\(\frac{dy}{dt}\) = 2a

प्रश्न 10.
यदि y = x² + 3x + 2 हो, तो \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) का मान ज्ञात कीजिए। (NCERT)
हल:
दिया है –
y = x² + 3x + 2

x के सापेक्ष पुनः अवकलन करने पर,

प्रश्न 11.
यदि y = x³ + tan x हो, तो का मान ज्ञात कीजिए। (NCERT)
हल:
दिया है:
y = x² + tan x
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) [x³ + tan x]
= \(\frac{d}{dx}\) x³ + \(\frac{d}{dx}\) tan x
⇒ \(\frac{dy}{dx}\) = 3x² + sec² x
x के सापेक्ष पुनः अवकलन करने पर,

अवकलन दीर्घ उत्तरीय प्रश्न – I

प्रश्न 1.
y = tan^-1 \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \) का x के सापेक्ष अवकलन कीजिए।
हल:
दिया है:
y = tan^-1 \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \)
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) tan^-1 \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \)

पुनः 1 + x² = u रखने पर,

प्रश्न 2.
\(\frac{dy}{dx}\) का मान ज्ञात कीजिए यदि
x = a (t + sint), y = a (1 – cost)
हल:
दिया है:
x = a (t + sint)
∴ \(\frac{dx}{dt}\) = a (1 + cos t)
पुनः y = a (1 – cos t)
∴ \(\frac{dy}{dt}\) = a (0 + sint) = a sint

प्रश्न 3.
यदि x = a (2θ – sin 2θ) तथा y = a (1 – cos 2θ), तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिये जबकि θ = \(\frac { \pi }{ 3 } \) (CBSE 2018) .
हल:
दिया है:
समी. (2) को θ के सापेक्ष अवकलन करने पर,
x = a (2θ – sin 2θ) ………………………. (1)
y = a (1 – cos 2θ) ………………………… (2)
\(\frac { dx }{ d\theta } \) = a (2.1 – cos 2θ.2)
= 2a (1- cos 2θ)
= 2a.2 sin²θ
= 4a sin²θ …………………….. (3) |
समी. (2) को θ के सापेक्ष अवकलन करने पर,
\(\frac { dy }{ d\theta } \) = a(0 + sin 2θ.2)
= 2a sin 2θ
= 2a. 2 sinθ cosθ
= 4a sinθcosθ ……………………….. (4)
समी. (4) ÷ (3) से,

जब θ = \(\frac { \pi }{ 3 } \), तब
\(\frac{dy}{dx}\) = cot \(\frac { \pi }{ 3 } \) = \(\frac { 1 }{ \sqrt { 3 } } \)

प्रश्न 4.
यदि y = a sin mx + b cos mx हो, तो सिद्ध कीजिए कि
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) + m² y = 0
हल:
दिया है:
y = a sin mx + b cos mx …………………….. (1)
समी. (1) के दोनों पक्षों में x के सापेक्ष अवकलन करने पर,
\(\frac{dy}{dx}\) = am cos mx – bm sin mx ……………… (2)
पुनः (2) का x के सापेक्ष अवकलन करने पर,

प्रश्न 5.
(A) यदि y = esin^{-1 x} हो, तो सिद्ध कीजिए कि (1 – x²), y₂ – xy₁ – m² y = 0
हल:
दिया है:

पुनः अवकलन करने पर,

(B)
यदि y = e^mtan-1x हो, तो सिद्ध कीजिए कि (1 + x²)y₂ + (2x – m) y₁ = 0
हल:
प्रश्न क्र. 5 (A) की भाँति हल करें।

(C)
यदि y = e^mcos-1x हो, तो सिद्ध कीजिए कि (1 – x²)y₂ + (2x – m)y₁ = 0
हल:
प्रश्न क्र. 5 (A) की भाँति हल करें।

प्रश्न 6.
sin^-1 \(\frac { 2x }{ 1+x^{ 2 } } \) का x के सापेक्ष अवकलन कीजिए।
हल:

प्रश्न 7.
यदि y = cot^-1 \(\sqrt { \frac { 1+x }{ 1-x } } \) हो, तो \(\frac{dy}{dx}\) ज्ञात कीजिए।
हल:
दिया है,
y = cot^-1 \(\sqrt { \frac { 1+x }{ 1-x } } \)
माना x = cos θ

समी. (1) में इसका मान रखने पर,

अब x के सापेक्ष दोनों पक्षों का अवकलन करने पर,
\(\frac{dy}{dx}\) = – \(\frac { 1 }{ 2\sqrt { 1-x^{ 2 } } } \)

प्रश्न 8.
यदि y = tan^-1 \(\sqrt { \frac { 1+x }{ 1-x } } \) हो, तो ज्ञात कीजिए।
हल: प्रश्न क्र. 7 की भाँति हल करें।
[उत्तर – \(\frac{dy}{dx}\) = \(\frac { 1 }{ 2\sqrt { 1-x^{ 2 } } } \)

प्रश्न 9.
यदि y = cot^-1 \(\frac { cosx+sinx }{ cosx-sinx } \) हो, तो \(\frac{dy}{dx}\) ज्ञात कीजिए।
हल:
दिया है:

प्रश्न 10.
y = tan^-1 \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) का x के सापेक्ष अवकलन कीजिए।
हल:
y = tan^-1 \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \)
समी. (1) x = tan θ में रखने पर, तब θ = tan^-1 x

प्रश्न 11.
यदि y = cot^-1 [ \(\frac { \sqrt { 1+x^{ 2 }+1 } }{ x } \) ] हो, तो \(\frac{dy}{dx}\) ज्ञात कीजिए।
हल:
y = cot^-1 [ \(\frac { \sqrt { 1+x^{ 2 }+1 } }{ x } \) ]
x = tan θ रखने पर,

प्रश्न 12.
यदि y = x^sinx हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए।
हल:
दिया है:
y = x^sinx
समी. (1) के दोनों पक्षों का log लेने पर, …………………………….. (1)
दोनों पक्षों का अवकलन करने पर,

प्रश्न 13.
यदि y = \(\sqrt { \frac { 1-x }{ 1+x } } \) हो, तो सिद्ध कीजिए \(\frac{dy}{dx}\) = \(\frac { y }{ x^{ 2 }-1 } \)
हल:
दिया है:

प्रश्न 14.
यदि y = (sin x)^{sinxsinx…………… ∞} हो, तो 4 का मान ज्ञात कीजिए।
हल:
दिया है:
y = (sin x)^{sinxsinx…………… ∞}
⇒ y = (sin x)^y
⇒ log y = y log sinx

x के सापेक्ष अवकलन करने पर,

प्रश्न 15.
(A) यदि y = \(\sqrt { sinx+\sqrt { sinx+……+\infty } } \) हो, तो सिद्ध कीजिए कि
\(\frac{dy}{dx}\) = \(\frac { cosx }{ 2y-1 } \)
हल:
दिया है:

(B)
यदि y = \(\sqrt { cotx\sqrt { cotx+\sqrt { cotx+…….+\infty } } } \) हो, तो सिद्ध कीजिए कि
\(\frac{dy}{dx}\) = \(\frac { cosec^{ 2 }x }{ 1-2y } \)
हल:
प्रश्न क्र. 15 (A) की भाँति हल करें।

(C) यदि y = \(\sqrt { tanx+\sqrt { tanx+\sqrt { tanx+…..\infty } } } \) हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए।
हल:
प्रश्न क्र. 15 (A) की भाँति हल करें।
[उत्तर: \(\frac { sec^{ 2 }x }{ (2y-1) } \) ]

प्रश्न 16.
यदि y = e^{x+ex+ex+e…………… ∞} हो, तो सिद्ध कीजिए कि
\(\frac{dy}{dx}\) = \(\frac{y}{1-y}\)
हल:
दिया है:
y = e^{x+ex+ex+e…………… ∞}
⇒ y = e^x+y
दोनों पक्षों में log लेने पर,
log y = loge^x+y
⇒ log y = x + y

प्रश्न 17.
फलन \(\frac { 1 }{ (x+a)(x+b)(x+c) } \) का x के सापेक्ष अवकलन कीजिये।
हल:
माना y = \(\frac { 1 }{ (x+a)(x+b)(x+c) } \)
दोनों पक्षों में log लेने पर
log y = log1 – log(x + a) – log(x + b) – log(x + c)
x के सापेक्ष अवकलन करने पर

प्रश्न 18.
log ( \(\sqrt{x}\) + \(\frac { 1 }{ \sqrt { x } } \) का x के सापेक्ष अवकल गुणांक ज्ञात कीजिये।
हल:

x के सापेक्ष अवकलन करने पर,

प्रश्न 19.
यदि y = tan^-1 ( \(\frac { sinx }{ 1+cosx } \) ) हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिये।
हल:
दिया है:
y = tan^-1 ( \(\frac { sinx }{ 1+cosx } \) )

दोनों पक्षों का x के सापेक्ष अवकलन करने पर,
अत:
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) ( \(\frac{x}{2}\) ) = \(\frac{1}{2}\)

प्रश्न 20.
फलन f (x) = x² के लिए अंतराल [-1, 1] में रोले प्रमेय का सत्यापन कीजिए। (NCERT)
हल:
यहाँ f (x) = x², a = -1, b = 1

1. चूँकि f (x) = x² एक बहुपद फलन है इसलिए f (x) संवृत अंतराल [-1, 1] में संतत है।
2. f’ (x) = 2x विवृत्त अंतराल (-1, 1) में परिभाषित है इसलिए f (x) विवृत अंतराल (-1, 1) में अवकलनीय है।
3. f (-1) = (-1)² = 1, f(1) = (1)² = 1

∴ f (-1) = f (1)
अतः फलन f (x) रोले प्रमेय के सभी प्रतिबंधों को संतुष्ट करता है।
∴ f'(c) = 0
⇒ 2c = 0 [∵ f'(x) = 2x]
⇒ (c) = 0 ∈ (-1, 1)
अतः रोले प्रमेय सत्यापित होता है।

प्रश्न 21.
फलन f (x) = x² + 2x – 8 के लिए अंतराल [-4, 2) में रोले प्रमेय का सत्यापन कीजिए। (NCERT)
हल:
यहाँ f (x) = x² + 2x – 8, a = – 4, b = 2.

1. f (x) = x² + 2x – 8 एक बहुपद फलन है इसलिए f (x) संवृत अंतराल [-4, 2] में संतत है।
2. f’ (x) = 2x + 2 विवृत्त अंतराल (-4, 2) में परिभाषित है इसलिए f (x) विवृत अंतराल (-4, 2) में अवकलनीय है।
3. f (-4) = (-4)² + 2 (-4) – 8

= 16 – 8 – 8 = 0
f (2) = (2)² + 2 × 2 – 8 = 0
f (- 4) = f (2)
अतः f(x) रोले प्रमेय की तीनों शर्तों को संतुष्ट करता है।
∴ f'(c) = 0
⇒ 2c + 2 = 0
⇒ c = -1 ∈ (-4, 2)
अतः रोले प्रमेय सत्यापित होता है।

प्रश्न 22.
फलन f (x) = 2x² + x² – 4x – 2 के लिए रोले प्रमेय का सत्यापन कीजिए।
हल:
चूँकि बहुपद फलन सभी वास्तविक संख्याओं के लिए संतत और अवकलनीय होता है इसलिए f (x) प्रत्येक अंतराल में संतत और अवकलनीय है।
अब f (x) = 0
⇒ 2x³ + x² – 4x – 2 = 0
⇒ x²(2x + 1) – 2 (2x + 1) = 0
⇒ (x² – 2) (2x + 1) = 0
⇒ x² = 2, 2x + 1 = 0
⇒ x = ± \(\sqrt{2}\), x = – \(\frac{1}{2}\)
⇒ x = – \(\sqrt{2}\), \(\sqrt{2}\), \(\frac{-1}{2}\)
अब अंतराल [-\(\sqrt{2}\), \(\sqrt{2}\) ] लेते हैं।

1. फलन f (x) संवृत अंतराल [-\(\sqrt{2}\), \(\sqrt{2}\) ] में संतत है।
2. f'(x) = 6x² + 2x – 4 का अस्तित्व विवृत अंतराल [-\(\sqrt{2}\), \(\sqrt{2}\) ] में है इसलिए f (x) विवृत अंतराल [-\(\sqrt{2}\), \(\sqrt{2}\) ] में अवकलनीय है।
3. f ( –\(\sqrt{2}\) ) = f ( \(\sqrt{2}\) ) = 0

अतः f (x) रोले प्रमेय के सभी प्रतिबंधों को संतुष्ट करता है।
∴ f'(c) = 0
⇒ 6c² + 2c – 4 = 0, [∵f'(x) = 6x² + 2x – 4]


अतः रोले प्रमेय सत्यापित होता है।

प्रश्न 23.
अंतराल [1,3] में फलन f (x) = x + \(\frac{1}{x}\) के लिए मध्यमान प्रमेय का सत्यापन कीजिए।
उत्तर
हल:
f (x) = x + \(\frac{1}{x}\) = \(\frac { x^{ 2 }+1 }{ x } \), x ∈ [1, 3]

1. चूँकि f(x), x ≠ 0 सहित एक परिमेय फलन है और प्रत्येक परिमेय फलन संतत होता है, इसलिए f (x), [1, 3] में संतत फलन है।
2. f'(x) = 1 – \(\frac { 1 }{ x^{ 2 } } \) विवृत अंतराल (1, 3) में परिभाषित है और प्रतेक परिमेय फलन संतत होता है इसलिए f (x), [1, 3] में संतत फलन है।
3. f (1) = 2, f (3) = \(\frac{10}{3}\)

अतः मध्यमान प्रमेय के दोनों प्रतिबंध संतुष्ट होते हैं।

अत: लैग्रांज का मध्यमान प्रमेय सत्यापित होता है।

प्रश्न 24.
फलन f (x) = log x का अंतराल [1, e] में मध्यमान प्रमेय का सत्यापन कीजिए।
हल:
f(x) = log x, x ∈ [1, e], x > 0.
a = 1, b = e

1. चूँकि f (x) = log x, x > 0 एक संतत फलन होता है इसलिए f (x), [1, e] में संतत फलन है।
2. f'(x) = \(\frac{1}{x}\), में परिभाषित है इसलिए f (x), (1, e) में अवकलनीय है।
3. f (1) = log 1 = 0, f (e) = log e = 1

अतः मध्यमान प्रमेय की दोनों शर्त संतुष्ट होती हैं।
∴ \(\frac { f(e)-f(1) }{ e-1 } \) = f'(c)
⇒ \(\frac { 1-0 }{ e-1 } \) = \(\frac{1}{e}\)
⇒ c = e – 1 ∈ (1, e)
अत: मध्यमान प्रमेय सत्यापित होता है।

प्रश्न 25.
मध्यमान प्रमेय के प्रयोग से अंतराल [2, 3] में परिभाषित वक्र y = \(\sqrt { x-2 } \) पर एक बिन्दु ज्ञात कीजिए जबकि स्पर्श रेखा वक्र के बिन्दुओं को मिलाने वाली जीवा के समांतर है।
हल:
f (x) = \(\sqrt { x-2 } \), a = 2, b = 3

1. चूँकि f(x) = \(\sqrt { x-2 } \), x ∈ [2,3] के लिए परिभाषित है इसलिए f (x), [2, 3] में संतत फलन है।
2. f'(x) = \(\frac { 1 }{ 2\sqrt { x-2 } } \) विवृत अंतराल (2, 3) में परिभाषित है इसलिए f (x), (2, 3) में अवकलनीय है।
3. f (2) = 0, f (3) = 1

अतः मध्यमान प्रमेय के दोनों प्रतिबंध संतुष्ट होते हैं।
∴ \(\frac { f(3)-f(2) }{ 3-2 } \) = f’ (c)

अभीष्ट निर्देशांक ( \(\frac{9}{4}\), \(\frac{1}{2}\) ) हैं।

अवकलन दीर्घ उत्तरीय प्रश्न – II

प्रश्न 1.
यदि y = sin^-1 \(\frac { 2^{ x+1 } }{ 1+4^{ x } } \) हो, तो \(\frac{dy}{dx}\) ज्ञात कीजिए। (NCERT)
हल:
दिया है:
y = sin^-1 \(\frac { 2^{ x+1 } }{ 1+4^{ x } } \)

प्रश्न 2.
यदि y = sin^-1 x हो, तो सिद्ध कीजिए कि (1 – x²) \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) – x \(\frac{dy}{dx}\) = 0? (NCERT)
हल:
दिया है:
y = sin^-1 x
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) (sin^-1 x)
\(\frac{dy}{dx}\) = \(\frac { 1 }{ \sqrt { 1-x^{ 2 } } } \)
\(\frac{d}{dx}\) ( \(\frac{dy}{dx}\) ) = \(\frac{d}{dx}\) (1 – x²)^-1/2
1 – x² = t रखने पर,

प्रश्न 3.
यदि y = tan x + sec x हो, तो सिद्ध कीजिए कि \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = \(\frac { cosx }{ (1-sinx)^{ 2 } } \)
हल:
दिया है:
y = tan x + sec x
\(\frac{dy}{dx}\) = sec² x + sec x tan x
⇒ \(\frac{dy}{dx}\) = sec x (sec x + tan x)
⇒ \(\frac{dy}{dx}\) = \(\frac{1}{cosx}\) = [ \(\frac { 1 }{ cosx } +\frac { sinx }{ cosx } \) ]

प्रश्न 4.
यदि y = sin (sin x) हो, तो सिद्ध कीजिए कि
y₂ + y₁ tan x + y cos² x = 0? (CBSE 2018)
हल:
y = sin (sin x) ………………………. (1)
x के सापेक्ष अवकलन करने पर,
y₁ = cos (sin x). cos x
पुनः x के सापेक्ष अवकलन करने पर,
y₂ = cos(sin x)\(\frac { d }{ dx } \) (cos x) + cos x \(\frac { d }{ dx } \) {cos(sin x)}
= cos(sin x)(- sin x) + (cos x) [- sin(sin x)]cos x
⇒ y₂ = – sin x cos(sin x) – cos² x sin(sin x)
⇒ y₂ = – sin x cos(sin x) – y cos² x, [ समी. (1) से ]
⇒ y₂ = [ – \(\frac { sinx }{ cosx } .cosx\) ] cos(sin x) – y cos² x
⇒ y₂ = (- tan x) y₁ – y cos² x, [ समी. (2) से ]
⇒ y₂ + y₁ tan x + y cos² x = 0. यही सिद्ध करना था।

प्रश्न 5.
\(\frac{dy}{dx}\) का मान ज्ञात कीजिए यदि (x² + y²)² = xy? (CBSE 2018)
हल:
(x² + y²)² = xy
दोनों पक्षों के प्रत्येक पद का x के सापेक्ष अवकलन करने पर,

प्रश्न 6.
यदि y = 500e^7x + 600e^-7x हो, तो सिद्ध कीजिए कि \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = 49 y? (NCERT)
हल:
दिया है:
y = 500e^7x + 600e^-7x

प्रश्न 7.
यदि y = (tan^-1 x)² हो, तो दर्शाइए कि (x² + 1)² y₂ + 2x(x² + 1) y₁ = 2 है। (NCERT)
हल:
दिया है:
y = (tan^-1 x)²
tan^-1 x = t रखने पर,

प्रश्न 8.
sec^-1 ( \(\frac { 1 }{ 2x^{ 2 }-1 } \) ) के सापेक्ष अवकल गुणांक ज्ञात कीजिए।
हल:
माना y₁ = sec^-1 = ( \(\frac { 1 }{ 2x^{ 2 }-1 } \) )
⇒ y₁ = cos^-1 (2x² – 1)

प्रश्न 9.
tan^-1 ( \(\frac { 2x }{ 1-x^{ 2 } } \) ) का sin^-1 ( \(\frac { 2x }{ 1+x^{ 2 } } \) ) के सापेक्ष अवकल गुणांक ज्ञात कीजिए।
हल:
माना y₁ = tan^-1 ( \(\frac { 2x }{ 1-x^{ 2 } } \) ) तथा y₂ = sin^-1 ( \(\frac { 2x }{ 1+x^{ 2 } } \) )
माना x = tan θ, अत: θ = tan^-1 x

प्रश्न 10.
tan^-1 ( \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ) का tan^-1 x के सापेक्ष अवकल गुणांक ज्ञात कीजिए।
हल:
माना y₁ = tan^-1 ( \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) )
x = tan θ रखने पर,

प्रश्न 11.
यदि x \(\sqrt { 1+y } \) + y \(\sqrt { 1+x } \) = 0 हो, तो सिद्ध कीजिए कि
\(\frac{dy}{dx}\) = – (1 + x)^-2
हल:
दिया है:
x \(\sqrt { 1+y } \) + y \(\sqrt { 1+x } \) = 0
⇒ x \(\sqrt { 1+y } \) = – y \(\sqrt { 1+x } \)
दोनों पक्षों का वर्ग करने पर,
x² (1 + y) = y² (1 + x)
⇒ x² + x²y = xy² + y²
⇒ x² – y² + x²y – xy² = 0
⇒ (x – y)(x + y) + xy (x – y) = 0
⇒ (x – y)(x + y + xy) = 0
अतः था तो  x – y = 0
⇒ x = y
किंतु  x ≠ y
∴ x + y+ xy = 0
⇒ y(1 + x) = -x
∴ y = –\(\frac { x }{ x+1 } \)
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

प्रश्न 12.
यदि y \(\sqrt { 1-x^{ 2 } } \) + x \(\sqrt { 1-y^{ 2 } } \) = 1 हो, तो सिद्ध कीजिए कि
\(\frac{dy}{dx}\) + \(\sqrt { \frac { 1-y^{ 2 } }{ 1-x^{ 2 } } } \) = 0?
हल:
दिया है:
y \(\sqrt { 1-x^{ 2 } } \) + x \(\sqrt { 1-y^{ 2 } } \) = 1
अब x = sin θ तथा y = sin ∅ लेने पर,

प्रश्न 13.
(A) यदि y = x^sin-1x + x^x
हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए।
हल:
दिया है:
y = x^sin-1x + x^x

(B)
यदि y = x^tan-1x + x^x हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए।
हल:
प्रश्न क्र. 13 (A) की भाँति हल करें।

प्रश्न 14.
यदि sin y = x sin (a + y) हो, तो सिद्ध कीजिए कि,
\(\frac{dy}{dx}\) = \(\frac { sin^{ 2 }(a+y) }{ sina } \)
हल:
दिया है:
sin y = x sin (a + y)
x = \(\frac { siny }{ sin(a+y) } \)

प्रश्न 15.
यदि x^y = e^x-y हो, तो सिद्ध कीजिए कि \(\frac{dy}{dx}\) = \(\frac { logx }{ (1+logx)^{ 2 } } \)?
हल:
दिया है:
x^y = e^x-y
दोनों पक्षों का लघुगणक लेने पर,
y log x = (x – y) log_e e
⇒ y log x = (x – y).1 = x – y
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

प्रश्न 16.
यदि x^y = e^y-x हो, तो सिद्ध कीजिए कि
\(\frac{dy}{dx}\) = \(\frac { 2-log_{ e }x }{ (i-log_{ e }x)^{ 2 } } \)?
हल:
दिया है:
x^y = e^y-x
दोनों पक्षों में log लेने पर,
∴ log_e x^y = log_e(e^y-x)
⇒ y log_e x = (y – x) log_e e
⇒ y log_e x = y – x,
⇒ y(1 – log_e x) = x
⇒ y = \(\frac { x }{ 1-log_{ e }x } \)
अब दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

MP Board Class 12 Maths Important Questions

MP Board Class 12th Maths Important Questions Chapter 5A सांतत्य तथा अवकलनीयता

सांतत्य तथा अवकलनीयता Important Questions

_{सांतत्य तथा अवकलनीयता वस्तुनिष्ठ प्रश्न}

प्रश्न 1.
सही विकल्प चुनकर लिखिए –

प्रश्न 1.
यदि x = at², y = 2at है, तो \(\frac{dy}{dx}\) होगा –
(a) t
(b) t²
(c) \(\frac{1}{t}\)
(d) \(\frac { 1 }{ t^{ 2 } } \)
उत्तर:
(c) \(\frac{1}{t}\)

प्रश्न 2.
यदि y = 2 \(\sqrt { cot(x^{ 2 }) } \) हो, तो \(\frac{dy}{dx}\) होगा –
(a) \(\frac { -2\sqrt { 2x } }{ sinx^{ 2 }\sqrt { sin2x^{ 2 } } } \)
(b) \(\frac { 2\sqrt { 2x } }{ sinx^{ 2 }\sqrt { sin2x^{ 2 } } } \)
(c) \(\frac { 2\sqrt { 2x } }{ sinx^{ 2 }\sqrt { sin2x^{ 2 } } } \)
(d) \(\frac { 2\sqrt { x } }{ sinx^{ 2 }\sqrt { sin2x^{ 2 } } } \)
उत्तर:
(a) \(\frac { -2\sqrt { 2x } }{ sinx^{ 2 }\sqrt { sin2x^{ 2 } } } \)

प्रश्न 3.
\(\frac{dy}{dx}\) (x³ + sinx²) का मान है –
(a) 3x² + cos x²
(b) 3x² + x sin²
(c) 3x² + 2x cos x²
(d) 3x² + x cos x²
उत्तर:
(c) 3x² + 2x cos x²

प्रश्न 4.
\(\frac{d}{dx}\) a^x का मान है –
(a) a^x
(b) a^xlog_ae
(c) a^xlog_ea
(d) \(\frac { a^{ x } }{ log_{ e }a } \)
उत्तर:
(c) a^xlog_ea

प्रश्न 5.
यदि y = 500e^7x + 6000e^-7x हो, तो, \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) का मान होगा –
(a) 45 y
(b) 47 y
(c) 49 y
(d) 50 y
(d) 50y.
उत्तर:
(c) 49 y

प्रश्न 2.
(a) रिक्त स्थानों की पूर्ति कीजिए –

1. cosx⁰ का x के सापेक्ष अवकल गुणांक ………………….. है।
2. e^{loge a}का x के सापेक्ष अवकल गुणांक ………………………..
3. log_e a का a के सापेक्ष अवकल गुणांक ……………………….
4. a^x का x के सापेक्ष अवकल गुणांक ……………………………… है।
5. sin 3x का 3x के सापेक्ष अवकल गुणांक …………………………… है।
6. यदि y = sin^-1(2x\(\sqrt { 1-x^{ 2 } } \) ) हो, तो \(\frac{dy}{dx}\) = ……………………… होगा।
7. sin x का cos.x के सापेक्ष अवकल गुणांक ………………… है।
8. \(\frac{d}{dx}\) (log tan x) का मान ………………………… है।
9. log(log sin x) का अवकलन गुणांक ……………………………….. होगा।

उत्तर:

1. – \(\frac { \pi }{ 180 } \) sin x⁰
2. 0
3. 0
4. log_ea.a^x
5. cos x
6. \(\frac { 2 }{ \sqrt { 1-x^{ 2 } } } \)
7. – cot x
8. cosec 2x
9. \(\frac { cotx }{ logsinx } \)

प्रश्न 2.
(b) रिक्त स्थानों की पूर्ति कीजिए –

1. यदि x = \(\sqrt { 1-y^{ 2 } } \) हो, तो \(\frac{dy}{dx}\) = ………………………. होगा।
2. sin x का n वाँ अवकलज ………………………………. होगा।
3. यदि y = \(\sqrt { x+\sqrt { x+………..\infty } } \) हो, तो \(\frac{dy}{dx}\) = ………………………. होगा।
4. यदि x = r cos θ, y = r sin θ हो, तो \(\frac{dy}{dx}\) = ………………………. होगा।
5. e^x का \(\sqrt{x}\) के सापेक्ष अवकलज ………………………………. होगा।

उत्तर:

1. \(\frac { \sqrt { 1-y^{ 2 } } }{ 1-2y^{ 2 } } \)
2. sin ( \(\frac { n\pi }{ 2 } \) + x )
3. \(\frac { 1 }{ 2y-1 } \)
4. -cot θ
5. 2\(\sqrt{x}\) e^x

प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –

1. e^{loge x} का अवकल गुणांक \(\frac{1}{x}\) है।
2. यदि f (x) = \(\sqrt{x}\); x > 0 तो f'(2) का मान \(\frac { 1 }{ 2\sqrt { 2 } } \) है।
3. कोई फलन f (x) किसी बिन्दु x = a पर अवकलनीय कहलाता है, जब Lf'(a) # Rf (a).
4. sec^-1a का x के सापेक्ष अवकल गुणांक 0 होता है।
5. यदि y = ae^mx + Be^-mx, तो = -m²y है।
6. यदि y = sin^-1 ( \(\frac { x-1 }{ x+1 } \) ) + cos^-1 ( \(\frac { x-1 }{ x+1 } \) ) हो, तो \(\frac{dy}{dx}\) = 0 होगा।
7. प्रत्येक अवकलनीय फलन सतत् होता है।
8. a^2x का अवकल गुणांक a^2xlog a.

उत्तर:

1. असत्य
2. सत्य
3. असत्य
4. असत्य
5. असत्य
6. सत्य
7. सत्य
8. असत्य।

प्रश्न 4.
सही जोड़ी बनाइये –

उत्तर:

1. (d)
2. (e)
3. (a)
4. (f)
5. (h)
6. (g)
7. (c)
8. (b)

प्रश्न 5.
एक शब्द/वाक्य में उत्तर दीजिए –

1. \(\frac { 6^{ x } }{ x^{ 6 } } \) का x के सापेक्ष अवकल गुणांक ज्ञात कीजिए।
2. y = e^{loge tanx} का x के सापेक्ष अवकल गुणांक ज्ञात कीजिए।
3. a^x का n वाँ अवकलज ज्ञात कीजिए।
4. y = sin(ax + b) हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए।
5. यदि x² + y² = sin xy, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए।
6. x के सापेक्ष log tan\(\frac{x}{2}\) का अवकल गुणांक ज्ञात कीजिए।
7. sin^-1 \(\frac { 2x }{ 1+x^{ 2 } } \) का x के सापेक्ष अवकल गुणांक ज्ञात कीजिए।
8. e -log_e^x का अवकल गुणांक ज्ञात कीजिए।

उत्तर:

1. \(\frac { 6^{ x } }{ x^{ 6 } } \) [ [log 6 – \(\frac{6}{x}\) ]
2. sec² x
3. a^x(log a)ⁿ
4. -a² y
5. \(\frac { ycosxy-2x }{ 2y-xcosxy } \)
6. cosec x
7. \(\frac { 2 }{ 1+x^{ 2 } } \)
8. \(\frac { -1 }{ x^{ 2 } } \)

सांतत्य तथा अवकलनीयता लघु उत्तरीय प्रश्न

प्रश्न 1.
फलन के सभी असांतत्य के बिन्दुओं को ज्ञात कीजिए, जबकि निम्नलिखित प्रकार से परिभाषित है –

हल:
x < 2 के लिए f (x) = 2x + 3 बहुपदी फलन है।
अत: x < 2 के लिए f (x) संतत फलन है। x > 2 के लिए f (x) = 2x – 3 बहुपदी फलन है।
अतः x > 2 के लिए f (x) संतत है।
अब हम केवल x = 2 पर f (x) की संततता का परीक्षण करेंगे।
x = 2 + h रखने पर
जब x → 2 तब h → 0
\(\underset { x\rightarrow 2^{ + } }{ lim } \) f(x) = \(\underset { h\rightarrow 0 }{ lim } \) 2(2 + h) – 3
= 2(2 + 0) – 3 = 4 – 3 = 1
x = 2 – h रखने पर
जब x → 2 तब h → 0
\(\underset { x\rightarrow 2^{ – } }{ lim } \) f(x) = \(\underset { h\rightarrow 0 }{ lim } \) 2(2 – h) + 3
= 2(2 – 0) + 3 = 7
f(2) = 2(2) + 3 = 7
\(\underset { x\rightarrow 2^{ – } }{ lim } \) f(x) = f(2) ≠ \(\underset { x\rightarrow 2^{ + } }{ lim } \) f(x)

प्रश्न 2.
फलन के सभी असातत्य बिन्दुओं को ज्ञात कीजिए, जबकि f निम्नलिखित प्रकार से परिभाषित है –

हल:
x ≠ 0 के लिए f (x) = \(\frac { |x| }{ x } \) संतत फलन है।
अत:
हम केवल x = 0 पर f (x) की संततता का परीक्षण करेंगे।
x = 0 + h रखने पर
जब x → 0 तब h → 0.

x = 0 – h रखने पर
जब x → 0 तब h → 0

दिया है:
f (0) = 0
\(\underset { x\rightarrow 0^{ + } }{ lim } \) f (x) ≠ \(\underset { x\rightarrow 0^{ – } }{ lim } \) f (x) ≠ f (0)
अत: दिया गया फलन f(x), x = 0 पर असंतत है।

प्रश्न 3.
बिन्दु x = 0 पर निम्नलिखित फलन f (x) के सातत्य की जाँच कीजिए –

हल:
f (x) = \(\frac { 1-cosx }{ x^{ 2 } } \), जब x ≠ 0
x = 0 + h रखने पर, x → 0 तो h → 0

पुनः x = 0 – h रखने पर, x → 0 तो h → 0

दिया है कि f (x) = \(\frac{1}{2}\) जब x = 0
या f (0) = \(\frac{1}{2}\)
इस प्रकार,
\(\underset { x\rightarrow 0^{ + } }{ lim } \) f(x) = \(\underset { x\rightarrow 0^{ + } }{ lim } \) f(x) = f(0)
अत: x = 0 पर f (x) संतत है।

प्रश्न 4.
फलन f निम्न प्रकार से परिभाषित है –

दर्शाइये कि बिन्दु x = 4 के अतिरिक्त प्रत्येक बिन्दु पर संतत है।
हल:

स्पष्ट है कि x = 4 के लिये फलन f (x) संतत नहीं है क्योंकि
\(\underset { x\rightarrow 4^{ – } }{ lim } \) f (x) ≠ \(\underset { x\rightarrow 4^{ + } }{ lim } \) तथा f (4) = 0
जब x < 4 तब f (x) = – 1 जो कि एक अचर फलन है। अत: यह संतत फलन है। जब x > 4 तब f (x) = 1 जो कि एक अचर फलन है। अत: यह संतत फलन है।
अतः f (x) बिन्दु x = 4 के अतिरिक्त सभी बिन्दुओं पर संतत है। यही सिद्ध करना था।

प्रश्न 5.
k का मान ज्ञात कीजिए यदि फलन –

बिन्दु x = \(\frac { \pi }{ 2 } \) + h रखने पर, जब x → \(\frac { \pi }{ 2 } \), तब h → 0

x = \(\frac { \pi }{ 2 } \) + h रखने पर, जब x → \(\frac { \pi }{ 2 } \) तब h → 0

x = \(\frac { \pi }{ 2 } \) – h रखने पर, जब x → \(\frac { \pi }{ 2 } \) तब h → 0

दिया है
f ( \(\frac { \pi }{ 2 } \) ) = 3
तथा दिया गया फलन संतत है।

⇒ \(\frac{k}{2}\) = \(\frac{k}{2}\) = 3
⇒ k = 6

प्रश्न 6.
k का मान ज्ञात कीजिए यदि फलन –

बिन्दु x = 2 पर संतत है।
हल: x = π + h रखने पर,
जब x → 7 तब h → 0

x = π – h रखने पर
जब x → π तब h → 0

दिया गया फलन x = π पर संतत है।

प्रश्न 7.
निम्न फलन बिन्दु x = 0 पर संतत है –

k का मान ज्ञात कीजिये।
हल:
दिया है

दिया है –
f (0) = \(\frac{1}{2}\)
चूँकि फलन f (x) बिन्दु x = 0 पर संतत है –

⇒ \(\frac { k^{ 2 } }{ 2 } \) = \(\frac { k^{ 2 } }{ 2 } \) = \(\frac{1}{2}\)
⇒ k² = 1 या k = ± 1

प्रश्न 8.
a और b के बीच संबंध स्थापित कीजिए जिनके लिए –

हल:
दिया है:

x = 3 + h रखने पर,
जब x → 3 तब h → 0

x = 3 – h रखने पर,
जब x → 3 तब h → 0

= a ( 3 – 0) + 1
= 3a + 1
f (3) = 3a + 1
∵ दिया गया पालन x = 3 पर संतत है।

⇒ 3a + 1 = 3b + 3
⇒ 3a = 3b + 2
⇒ a = b + \(\frac{2}{3}\)

प्रश्न 9.
सिद्ध कीजिए कि फलन f (x) = |x – 1|, x ∈ R, x = 1 पर अवकलनीय नहीं है। (NCERT)
हल:
दिया है:

x = 1 – h रखने पर, जब x → 1 तब h → 0

x = 1 + h रखने पर, जब x → 1 तब → 0

अतः दिया गया फलन x = 1 पर अवकलनीय नहीं है।

प्रश्न 10.
दर्शाइए कि फलन

पर अवकलनीय नहीं है।
हल:
हम जानते हैं,

प्रश्न 11.
सिद्ध कीजिए कि फलन

यही सिद्ध करना था।
x = 0 पर संतत है तथा अवकलनीय भी।
हल: यहाँ f (0) = 0


चूँकि f (0 + 0) = f (0 – 0) = f (0), अतएव x = 0 पर दिया हुआ फलन संतत है।
अब


स्पष्टतः Rf’ (0) = Lf’ (0)
अतः x = 0 पर दिया हुआ फलन अवकलनीय है।
अतः दिया हुआ फलन x = 0 पर संतत है तथा अवकलनीय भी है। यही सिद्ध करना था।

MP Board Class 12 Maths Important Questions

MP Board Class 12th Maths Important Questions Chapter 4 सारणिक

सारणिक Important Questions

सारणिक वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सही विकल्प चुनकर लिखिए –

प्रश्न 1.
यदि A, 3 × 3 कोटि का वर्ग आव्यूह है, तो |adj A| का मान है
(a) |A|
(b) |A|²
(c) |A|³
(d) 3 |A|

प्रश्न 2.
यदि a, b, c समांतर श्रेढी में हो, तो सारणिक \(\left|\begin{array}{ccc}
{x+2} & {x+3} & {x+2 a} \\
{x+3} & {x+4} & {x+2 b} \\
{x+4} & {x+5} & {x+2 c}
\end{array}\right|\) का मान होगा –
(a) 0
(b) 1
(c) x
(d) 2x

प्रश्न 3.
आव्यूह A = \(\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}\) हो, तो A^-1 होगा –
(a) A^-1 = \(\begin{bmatrix} 2 & -3 \\ -1 & 2 \end{bmatrix}\)
(b) A^-1 = \(\begin{bmatrix} 2 & -3 \\ 1 & -2 \end{bmatrix}\)
(c) A^-1 = \(\begin{bmatrix} -2 & 3 \\ -1 & 2 \end{bmatrix}\)
(d) A^-1 = \(\begin{bmatrix} -2 & 3 \\ 1 & -2 \end{bmatrix}\)

प्रश्न 4.
यदि ω इकाई का घनमूल हो, तो \(\left|\begin{array}{ccc}
{\mathbf{1}} & {\omega} & {\omega^{2}} \\
{\omega} & {\omega^{2}} & {1} \\
{\omega^{2}} & {1} & {\omega}
\end{array}\right|\) =
(a) 1
(b) 0
(c) ω
(d) ω²

प्रश्न 5.
सारणिक \(\left|\begin{array}{ccc}
{a+b} & {a+2 b} & {a+3 b} \\
{a+2 b} & {a+3 b} & {a+4 b} \\
{a+4 b} & {a+5 b} & {a+6 b}
\end{array}\right|\) =
(a) a² + b² + c² – 3abc
(b) 0
(c) a³ + b³ + c³
(d) इनमें से कोई नहीं।

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए –

1. यदि = \(\begin{bmatrix} 3 & m \\ 4 & 5 \end{bmatrix}\) हो, तो m = …………………………
2. सारणिक \(\begin{bmatrix} 2 & -3 \\ 1 & -2 \end{bmatrix}\) में अवयव – 3 का सहखण्ड ……………………….. है।
3. यदि A = \(\left|\begin{array}{lll}
   {1} & {0} & {1} \\
   {0} & {1} & {2} \\
   {0} & {0} & {4}
   \end{array}\right|\) हो, तो |3A| का मान ………………………………….. है।
4. सारणिक \(\begin{bmatrix} 1 & log_{ b }a \\ log_{ a }b & 1 \end{bmatrix}\) का मान …………………………….. है।
5. सारणिक \(\begin{bmatrix} cos70^{ \circ } & sin20^{ \circ } \\ sin70^{ \circ } & cos20^{ \circ } \end{bmatrix}\) का मान है।

प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –

1. सारणिक \(\left|\begin{array}{ccc}
   {0} & {a} & {-b} \\
   {-a} & {a} & {-c} \\
   {b} & {c} & {0}
   \end{array}\right|\) का मान abc है।
2. सारणिक \(\left|\begin{array}{ccc}
   {1} & {1} & {1} \\
   {1} & {1+\sin \theta} & {1} \\
   {1} & {1} & {1+\cos \theta}
   \end{array}\right|\) का उच्चिष्ठ मान \(\frac{1}{2}\) है।
3. यदि A एक 3 × 3 कोटि का आव्यूह हो, तो |kA| का मान k² |A| होगा।
4. यदि \(\begin{vmatrix} x & 2 \\ 18 & x \end{vmatrix}\) = \(\begin{vmatrix} 16 & 2 \\ 18 & 6 \end{vmatrix}\) तो x का मान ±3 है।
5. सारणिक \(\begin{vmatrix} 1 & \omega \\ \omega & -\omega \end{vmatrix}\) का मान 1 है।

उत्तर:

1. सत्य
2. सत्य
3. असत्य
4. असत्य
5. सत्य।

प्रश्न 4.
एक शब्द/वाक्य में उत्तर दीजिए –

1. k के कितने मानों के लिए रैखिक समीकरणों 4x + ky + 2x = 0, kx +4y + 2 = 0, 2x +2y + z = 0 का एक शून्येत्तर हल होगा।
2. यदि समीकरण 2x² + 3x + 5 = 0 के मूल α, β हों, तो \(\left|\begin{array}{lll}
   {0} & {\beta} & {\beta} \\
   {\alpha} & {0} & {\alpha} \\
   {\beta} & {\alpha} & {0}
   \end{array}\right|\) का मान ज्ञात कीजिए।
3. यदि शीर्षों (2, – 6), (5, 4) और (k, 4) वाले त्रिभुज का क्षेत्रफल 35 वर्ग एकांक हो, तो k का मान ज्ञात कीजिए।
4. यदि A = \(\begin{vmatrix} x+2 & -2 \\ -3x & 2x \end{vmatrix}\) = 8 हो, तो x का मान ज्ञात कीजिए।
5. सारणिक \(\left|\begin{array}{ccc}
   {1^{2}} & {2^{2}} & {3^{2}} \\
   {2^{2}} & {3^{2}} & {4^{2}} \\
   {3^{2}} & {4^{2}} & {5^{2}}
   \end{array}\right|\) का मान ज्ञात कीजिए।

उत्तर:

1. 2
2. –\(\frac{15}{4}\)
3. 12, -2
4. 2
5. -8.

सारणिक अति लघु उत्तरीय प्रश्न

प्रश्न 1.
\(\begin{vmatrix} 2 & 20 \\ 1 & 6 \end{vmatrix}\) का मान ज्ञात कीजिए।
उत्तर:
-8

प्रश्न 2.
\(\begin{vmatrix} -6 & 2 \\ 3 & y \end{vmatrix}\) = 24 तो y का मान ज्ञात कीजिए।
उत्तर:
-5

प्रश्न 3.
\(\begin{vmatrix} 2 & 4 \\ x & 0 \end{vmatrix}\) तो का मान ज्ञात कीजिए।
उत्तर:
4

प्रश्न 4.
यदि \(\begin{vmatrix} a & b \\ c & d \end{vmatrix}\) तो \(\begin{vmatrix} 3a & 3b \\ 3c & 3d \end{vmatrix}\) का मान ज्ञात कीजिए।
उत्तर:
45

प्रश्न 5.
यदि \(\begin{vmatrix} a & \omega \\ \omega & -\omega \end{vmatrix}\) हो, तो छ का मान ज्ञात कीजिए।
उत्तर:
1

प्रश्न 6.
यदि \(\begin{vmatrix} 3 & m \\ 4 & 5 \end{vmatrix}\) = 3 हो, तो m का मान ज्ञात कीजिए।
उत्तर:
3

प्रश्न 7.
यदि \(\begin{vmatrix} 2 & x \\ 4 & 9 \end{vmatrix}\) = 30 हो, तो x का मान ज्ञात कीजिए।
उत्तर:
-3

प्रश्न 8.
यदि \(\begin{vmatrix} 4 & -3 \\ m & m \end{vmatrix}\) = 21 तो m का मान ज्ञात कीजिए।
उत्तर:
3

प्रश्न 9.
यदि \(\begin{vmatrix} 2 & 4 \\ 3 & x \end{vmatrix}\) हो, तो x का मान ज्ञात कीजिए।
उत्तर:
9

प्रश्न 10.
यदि \(\begin{vmatrix} 4 & -3 \\ -m & m \end{vmatrix}\) = 21 हो, तो m का मान ज्ञात कीजिए।
उत्तर:
21

प्रश्न 11.
यदि \(\begin{vmatrix} -6 & 2 \\ 3 & m \end{vmatrix}\) = 12 हो, तो m का मान ज्ञात कीजिए।
उत्तर:
-3

प्रश्न 12.
यदि \(\begin{vmatrix} 4 & -6 \\ -2 & x \end{vmatrix}\) = 20 हो, तो x का मान ज्ञात कीजिए।
उत्तर:
8

प्रश्न 13.
यदि ω, ω² इकाई के सम्मिश्र घनमूल हों, तो \(\begin{vmatrix} 1 & \omega \\ \omega & -\omega \end{vmatrix}\) का मान ज्ञात कीजिए।
उत्तर:
1

प्रश्न 14.
\(\left|\begin{array}{ccc}
{224} & {777} & {32} \\
{735} & {888} & {105} \\
{812} & {999} & {116}
\end{array}\right|\) का मान ज्ञात कीजिए।
उत्तर:
0

प्रश्न 15.
यदि सारणिक \(\begin{vmatrix} x & 4 \\ 3 & 3 \end{vmatrix}\) = 0 हो, तो x का मान ज्ञात कीजिए।
उत्तर:
4

प्रश्न 16.
\(\begin{vmatrix} 2+3i & 4 \\ 1 & 2-3i \end{vmatrix}\) का मान ज्ञात कीजिए।
उत्तर:
9

प्रश्न 17.
सारणिक \(\begin{vmatrix} 2 & -3 \\ 1 & -2 \end{vmatrix}\) में अवयव – 3 का सहखण्ड क्या है?
उत्तर:
1

प्रश्न 18.
यदि \(\begin{vmatrix} 3 & -2 \\ -4 & x \end{vmatrix}\) = 16 हो, तो x का मान ज्ञात कीजिए।
उत्तर:
8

प्रश्न 19.
\(\begin{vmatrix} 1 & log_{ b }a \\ log_{ a }b & 1 \end{vmatrix}\) का मान ज्ञात कीजिए।
उत्तर:
0

प्रश्न 20.
सारणिक \(\begin{vmatrix} 1 & 3 \\ 2 & 4 \end{vmatrix}\) में अवयव 2 का उपसारणिक क्या होगा?
उत्तर:
3

प्रश्न 21.
\(\begin{vmatrix} 2+5i & 5 \\ 4 & 2-5i \end{vmatrix}\) का मान ज्ञात कीजिए।
उत्तर:
9

प्रश्न 22.
\(\begin{vmatrix} cotx & cosecx \\ cosecx & cotx \end{vmatrix}\) का मान ज्ञात कीजिए।
उत्तर:
-1

प्रश्न 23.
\(\begin{bmatrix} cos70^{ \circ } & sin20^{ \circ } \\ sin70^{ \circ } & cos20^{ \circ } \end{bmatrix}\) का मान ज्ञात कीजिए।
उत्तर:
0

सारणिक दीर्घ उत्तरीय प्रश्न – I

प्रश्न 1.
सिद्ध कीजिए –
\(\left|\begin{array}{ccc}
{a+b+2 c} & {a} & {b} \\
{c} & {b+c+2 a} & {b} \\
{c} & {a} & {c+a+2 b}
\end{array}\right|\) = 2(a + b + c)³?
हल:
माना

प्रश्न 2.
सिद्ध कीजिए कि \(\left|\begin{array}{ccc}
{a^{2}+1} & {a b} & {a c} \\
{a b} & {b^{2}+1} & {b c} \\
{a c} & {b c} & {c^{2}+1}
\end{array}\right|\) = 1 + a² + b² + c²? (NCERT; CBSE 2014)
हल:
माना

प्रश्न 3.
सिद्ध कीजिए कि \(\left|\begin{array}{ccc}
{a^{2}} & {b c} & {a c+c^{2}} \\
{a^{2}+a b} & {b^{2}} & {a c} \\
{a b} & {b^{2}+b c} & {c^{2}}
\end{array}\right|\) = 4a² b² c²? (NCERT; CBSE 2015)
हल:
माना

= 2abc² [-a(a – b) + a (a + b)]
= 2a²bc² [-a + b + a + b]
= 2a²bc². 2b = 4a² b² c²

प्रश्न 4.
निम्न सारणिक को हल कीजिए
\(\left|\begin{array}{ccc}
{x+1} & {3} & {5} \\
{2} & {x+2} & {5} \\
{2} & {3} & {x+4}
\end{array}\right|\) = 0?
हल:

प्रश्न 5.
सिद्ध कीजिए कि
\(\left|\begin{array}{ccc}
{\alpha} & {\beta} & {\lambda} \\
{\alpha^{2}} & {\beta^{2}} & {\lambda^{2}} \\
{\beta+\lambda} & {\lambda+\alpha} & {\alpha+\beta}
\end{array}\right|\) = (α – β) (β – λ) (λ – a) (α + β + λ)?
नोट -α = a,
β = b,
λ = c भी रखा जा सकता है।
हल:

प्रश्न 6.
सिद्ध कीजिए कि
\(\left|\begin{array}{ccc}
{1+a} & {1} & {1} \\
{1} & {1+b} & {1} \\
{1} & {1} & {1+c}
\end{array}\right|\) = (abc + ab + bc + ca) = (abc) (1 + \(\frac{1}{a}\) + \(\frac{1}{b}\) + \(\frac{1}{c}\) )? (NCERT; CBSE 2012, 14)
हल:

प्रश्न 7.
सिद्ध कीजिए –
\(\left|\begin{array}{ccc}
{-a^{2}} & {a b} & {a c} \\
{a b} & {-b^{2}} & {b c} \\
{a c} & {b c} & {-c^{2}}
\end{array}\right|\) = 4a²b²c²?
हल:

प्रश्न 8.
समीकरण हल कीजिए –
\(\left|\begin{array}{ccc}
{3 x-8} & {3} & {3} \\
{3} & {3 x-8} & {3} \\
{3} & {3} & {3 x-8}
\end{array}\right|\) = 0?
हल:

प्रश्न 9.
समीकरण \(\left|\begin{array}{lll}
{a+x} & {a-x} & {a-x} \\
{a-x} & {a+x} & {a-x} \\
{a-x} & {a-x} & {a+x}
\end{array}\right|\) = 0 को हल कीजिए।
हल:

प्रश्न 10.
सिद्ध कीजिए कि –
\(\left|\begin{array}{ccc}
{a} & {a+b} & {a+b+c} \\
{2 a} & {3 a+2 b} & {4 a+3 b+2 c} \\
{3 a} & {6 a+3 b} & {10 a+6 b+3 c}
\end{array}\right|\) = a³? (NCERT)
हल:

प्रश्न 11.
सिद्ध कीजिए कि –
\(\left|\begin{array}{ccc}
{x} & {x+y} & {x+2 y} \\
{x+2 y} & {x} & {x+y} \\
{x+y} & {x+2 y} & {x}
\end{array}\right|\) = -2(x³ + y³)? (NCERT)
हल:

प्रश्न 12.
सिद्ध कीजिए कि –
\(\left|\begin{array}{ccc}
{x+4} & {2 x} & {2 x} \\
{2 x} & {x+4} & {2 x} \\
{2 x} & {2 x} & {x+4}
\end{array}\right|\) = (5x + 4) (4 – x)²? (NCERT)
हल:
माना

प्रश्न 13.
सिद्ध कीजिए कि –
\(\left|\begin{array}{ccc}
{x} & {y} & {x+y} \\
{y} & {x+y} & {x} \\
{x+y} & {x} & {y}
\end{array}\right|\) = -2(x³ + y³)? (NCERT)
हल:

प्रश्न 14.
सिद्ध कीजिए कि –
\(\left|\begin{array}{ccc}
{a^{2}+2 a} & {2 a+1} & {1} \\
{2 a+1} & {a+2} & {1} \\
{3} & {3} & {1}
\end{array}\right|\) = (a – 1)³? (CBSE 2017)
हल:

प्रश्न 15.
सिद्ध कीजिए कि –
\(\left|\begin{array}{ccc}
{1} & {1} & {1+3 x} \\
{1+3 y} & {1} & {1} \\
{1} & {1+3 z} & {1}
\end{array}\right|\) = 9(3xyz + xy + yz + zx)? (CBSE 2018)
हल:
माना

MP Board Class 12 Maths Important Questions

MP Board Class 12th Maths Important Questions Chapter 3 आव्यूह

आव्यूह Important Questions

आव्यूह वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सही विकल्प चुनकर लिखिए –

प्रश्न 1.
यदि A = \(\begin{bmatrix} cos\alpha & -sin\alpha \\ sin\alpha & cos\alpha \end{bmatrix}\) तथा A + A’ = I, तो α का मान है –
(a) \(\frac { \pi }{ 6 } \)
(b) \(\frac { \pi }{ 3 } \)
(c) π
(d) \(\frac { 3\pi }{ 2 } \)
उत्तर:
(b) \(\frac { \pi }{ 3 } \)

प्रश्न 2.
यदि A = \(\left[\begin{array}{lll}
{2} & {0} & {0} \\
{0} & {2} & {0} \\
{0} & {0} & {2}
\end{array}\right]\) हो, तो A⁵ बराबर होगा –
(a) 5 A
(b) 10 A
(c) 16 A
(d) 32 A
उत्तर:
(c) 16 A

प्रश्न 3.
यदि एक आव्यूह सममित तथा विषम सममित दोनों ही है, तो –
(a) A एक विकर्ण आव्यूह है
(b) A एक शून्य आव्यूह है
(c) A एक वर्ग आव्यूह है
(d) A इनमें से कोई नहीं।
उत्तर:
(b) A एक शून्य आव्यूह है

प्रश्न 4.
यदि A = \(\begin{bmatrix} \alpha & \beta \\ \gamma & -\alpha \end{bmatrix}\) इस प्रकार है, कि A² = I तो –
(a) 1 + α² + βγ = 0
(b) 1 – α² + βγ = 0
(c) 1 – α² – βγ = 0
(d) 1 + α² – βγ = 0
उत्तर:
(c) 1 – α² – βγ = 0

प्रश्न 5.
यदि A = \(\begin{bmatrix} 2 & -1 \\ 3 & -2 \end{bmatrix}\) हो तो Aⁿ = ……………………………
(a) A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\), यदि n सम प्राकृत संख्या
(b) A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\), यदि n विषम प्राकृत संख्या
(c) A = \(\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\), यदि n ∈ N
(d) इनमें से कोई नहीं।
उत्तर:
(a) A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\), यदि n सम प्राकृत संख्या

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए –

1. यदि A = \(\begin{bmatrix} 2 & 4 \\ 3 & 2 \end{bmatrix}\) तथा B = \(\begin{bmatrix} 1 & 3 \\ 2 & 5 \end{bmatrix}\) हो, तो AB का मान.
   …………………………………. होगा।
2. यदि A = diag [1, – 1, 2] तथा B = diag [2, 3, – 1] हो, तो 3A + 4B का मान ……………………………. होगा।
3. एक वर्ग आव्यूह A समशम आव्यूह कहलाता है, यदि ……………………………….
4. एक वर्ग आव्यूह A लाम्बिक आव्यूह कहलाता है, यदि …………………………..
5. यदि [x, 1] \(\begin{bmatrix} 1 & 0 \\ -2 & 0 \end{bmatrix}\) = 0, तो x का मान…………. होगा।

उत्तर:

1. \(\begin{bmatrix} 10 & 26 \\ 7 & 19 \end{bmatrix}\)
2. diag [11, 9, 2]
3. A² = A
4. AA’ = A’A = I
5. x = 2

प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –

1. गुणन संक्रिया क्रम-विनिमेय नियम का सदैव पालन करती है।
2. दो आव्यूह तुलनीय कहलाते हैं यदि उनमें पंक्तियों और स्तम्भों की संख्या समान हो।
3. यदि A एक वर्ग आव्यूह हो, तो A.adj A = |A|I होता है।
4. वर्ग आव्यूह A सममित आव्यूह कहलाती है, यदि A = -A^T।
5. आव्यूह A तथा B एक-दूसरे के व्युत्क्रम होंगे यदि AB = BA

उत्तर:

1. असत्य
2. सत्य
3. सत्य
4. असत्य
5. असत्य।

प्रश्न 4.
सही जोड़ी बनाइये –

उत्तर:

1. (d)
2. (e)
3. (a)
4. (b)
5. (c).

प्रश्न 5.
एक शब्द/वाक्य में उत्तर दीजिए –

1. यदि A और B एक ही क्रम के वर्ग आव्यूह हों तो Adj (AB) का मान क्या होगा?
2. एक वर्ग आव्यूह A प्रतिकेन्द्रज कहलाता है, यदि –
3. यदि A = \(\begin{bmatrix} 0 & i \\ i & 0 \end{bmatrix}\) हो, तो A² का मान होगा।
4. यदि A = [1, 2, 3], तो AA^T का मान ज्ञात कीजिए।
5. यदि x + Y = \(\begin{bmatrix} 1 & -2 \\ 3 & 4 \end{bmatrix}\) तथा X – Y = \(\begin{bmatrix} 3 & 2 \\ -1 & 0 \end{bmatrix}\) तो X का मान ज्ञात कीजिए।

उत्तर:

1. Adj.(AB) = (Adj B).(Adj A)
2. A² = I
3. – 1
4. [14]
5. \(\begin{bmatrix} 2 & 0 \\ 1 & 2 \end{bmatrix}\)

आव्यूह लघु उत्तरीय प्रश्न

प्रश्न 1.
यदि A = \(\begin{bmatrix} a^{ 2 }+b^{ 2 } & b^{ 2 }+c^{ 2 } \\ a^{ 2 }+c^{ 2 } & a^{ 2 }+b^{ 2 } \end{bmatrix}\) हो, तो A + B ज्ञात कीजिए।
हल:
A+ B = \(\begin{bmatrix} a^{ 2 }+b^{ 2 } & b^{ 2 }+c^{ 2 } \\ a^{ 2 }+c^{ 2 } & a^{ 2 }+b^{ 2 } \end{bmatrix}\) + \(\begin{bmatrix} 2ab & 2bc \\ -2ac & -2ab \end{bmatrix}\)

प्रश्न 2.
यदि A = \(\begin{bmatrix} cos^{ 2 }x & sin^{ 2 }x \\ sin^{ 2 }x & cos^{ 2 }x \end{bmatrix}\) तथा B = \(\begin{bmatrix} sin^{ 2 }x & cos^{ 2 }x \\ cos^{ 2 }x & sin^{ 2 }x \end{bmatrix}\) हो, तो A + B ज्ञात कीजिए। (NCERT)
हल:
A + B = \(\begin{bmatrix} cos^{ 2 }x & sin^{ 2 }x \\ sin^{ 2 }x & cos^{ 2 }x \end{bmatrix}\) + \(\begin{bmatrix} sin^{ 2 }x & cos^{ 2 }x \\ cos^{ 2 }x & sin^{ 2 }x \end{bmatrix}\)

प्रश्न 3.
यदि A = \(\left[\begin{array}{lll}
{\frac{2}{3}} & {1} & {\frac{5}{3}} \\
{\frac{1}{3}} & {\frac{2}{3}} & {\frac{4}{3}} \\
{\frac{7}{3}} & {2} & {\frac{2}{3}}
\end{array}\right]\) तथा B = \(\left[\begin{array}{ccc}
{\frac{2}{5}} & {\frac{3}{5}} & {1} \\
{\frac{1}{5}} & {\frac{2}{5}} & {\frac{4}{5}} \\
{\frac{7}{5}} & {\frac{6}{5}} & {\frac{2}{5}}
\end{array}\right]\) हो, तो 3A – 5B परिकलित कीजिए।
हल:

प्रश्न 4.
सरल कीजिए –
cos θ \(\begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}\) + sin θ \(\begin{bmatrix} sin\theta & -cos\theta \\ cos\theta & sin\theta \end{bmatrix}\)
हल:

प्रश्न 5.
निम्नलिखित समीकरण से x तथा y के मानों को ज्ञात कीजिए – (NCERT)
2 \(\begin{bmatrix} x & 5 \\ 7 & y-3 \end{bmatrix}\) + \(\begin{bmatrix} 3 & -4 \\ 1 & 2 \end{bmatrix}\) = \(\begin{bmatrix} 7 & 6 \\ 15 & 14 \end{bmatrix}\)?
हल:
दिया है –

समान आव्यूह की परिभाषा से,
2x + 3 = 7
⇒ 2x = 4 ⇒ x = 2
⇒ 2y – 4 = 14
⇒ 2y = 18 ⇒ y = 9
∴ x = 2, y = 9

प्रश्न 6.
X तथा Y ज्ञात कीजिए यदि X + Y = \(\begin{bmatrix} 5 & 2 \\ 0 & 9 \end{bmatrix}\) तथा X – Y = \(\begin{bmatrix} 3 & 6 \\ 0 & -1 \end{bmatrix}\) है। (NCERT)
हल:
दिया है:
X + Y = \(\begin{bmatrix} 5 & 2 \\ 0 & 9 \end{bmatrix}\) ……………………………. (1)
तथा
X – Y = \(\begin{bmatrix} 3 & 6 \\ 0 & -1 \end{bmatrix}\) ……………………………….. (2)
समी. (1) और (2) को जोड़ने पर,
2X = \(\begin{bmatrix} 5 & 2 \\ 0 & 9 \end{bmatrix}\) + \(\begin{bmatrix} 3 & 6 \\ 0 & -1 \end{bmatrix}\)

समी. (1) में (2) को घटाने पर,

प्रश्न 7.
x तथा y ज्ञात कीजिए यदि
2 \(\begin{bmatrix} 1 & 3 \\ 0 & x \end{bmatrix}\) + \(\begin{bmatrix} y & 0 \\ 1 & 2 \end{bmatrix}\) = \(\begin{bmatrix} 5 & 6 \\ 1 & 8 \end{bmatrix}\)? (NCERT)
हल:
दिया है:
2 \(\begin{bmatrix} 1 & 3 \\ 0 & x \end{bmatrix}\) + \(\begin{bmatrix} y & 0 \\ 1 & 2 \end{bmatrix}\) = \(\begin{bmatrix} 5 & 6 \\ 1 & 8 \end{bmatrix}\)

समान आव्यूह की परिभाषा से,
2 + y = 5 ⇒ y = 3
2x + 2 = 8
⇒ x + 1 = 4
⇒ x = 3
∴ x = 3, y = 3.

प्रश्न 8.
यदि \(\left[\begin{array}{c}
{x+y+z} \\
{x+z} \\
{y+z}
\end{array}\right]\) = [ \(\begin{matrix} 9 \\ 5 \\ 7 \end{matrix}\) ] हो तो x, yतथा z के मान कीजिये
हल:
दिया है:
\(\left[\begin{array}{c}
{x+y+z} \\
{x+z} \\
{y+z}
\end{array}\right]\) = [ \(\begin{matrix} 9 \\ 5 \\ 7 \end{matrix}\) ]
सामान आतुयह की परोबाशा से
x + y + 2 = 9
x+ z = 5
y + z = 7
समी. (1) और (2) से,
x + z + y = 9
⇒ 5 + y = 9
⇒ y = 4
समी. (1) और (3) से,
x + (y + z) = 9
⇒ x + 7 = 9
⇒ x = 2
x का मान समी. (2) में रखने पर,
2 + z = 5
⇒ z = 3
∴ x = 2, y = 4, z = 3.

प्रश्न 9.
यदि
\(\begin{bmatrix} x+y & 2 \\ 5+z & xy \end{bmatrix}\) = \(\begin{bmatrix} 6 & 2 \\ 5 & 8 \end{bmatrix}\)
हो, तो x, y तथा z के मान ज्ञात कीजिए। (NCERT)
हल:
दिया है:
\(\begin{bmatrix} x+y & 2 \\ 5+z & xy \end{bmatrix}\) = \(\begin{bmatrix} 6 & 2 \\ 5 & 8 \end{bmatrix}\)
समान आव्यूह की परिभाषा से,
x + y = 6 …………………………. (1)
xy = 8 ………………………… (2)
5 + z = 5
⇒ z = 0
समी. (1) से,
y = 6 – x
xy = 8
⇒ x (6 – x) = 8
⇒ 6x – x² = 8
⇒ x² – 6x + 8 = 0
⇒ x² – 4x – 2x + 8 = 0
⇒ x(x – 4) – 2(x – 4) = 0
⇒ (x – 2) (x – 4) = 0
⇒ x = 2, 4
जब x = 2 तब y = 6 – 2 = 4
जब x = 4 तब y = 6 – 4 = 2
अतः
x = 2, y = 4, z = 0
x = 4, y = 2, z = 0.

प्रश्न 10.
यदि A = \(\begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}\) हो, तो सिद्ध कीजिए A² – 4A + 5I = 0?
हल:
दिया है
A = \(\begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}\)
A² = A. A = \(\begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}\) \(\begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}\)

प्रश्न 11.
यदि A = \(\begin{bmatrix} 2 & -3 \\ 3 & 4 \end{bmatrix}\) हो, तो सिद्ध कीजिए A² – 6A + 17I = 0?
हल:
A = \(\begin{bmatrix} 2 & -3 \\ 3 & 4 \end{bmatrix}\)
A² = A.A = \(\begin{bmatrix} 2 & -3 \\ 3 & 4 \end{bmatrix}\) \(\begin{bmatrix} 2 & -3 \\ 3 & 4 \end{bmatrix}\)

प्रश्न 12.
यदि A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}\) हो, तो सिद्ध कीजिए कि A² – 5A + 7I = 0? (NCERT)
हल:
A² = A.A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}\) × \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}\)

प्रश्न 13.
यदि A = \(\begin{bmatrix} 3 & -2 \\ 4 & -2 \end{bmatrix}\) और I = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\) हो, तो k का मान ज्ञात कीजिए यदि A² = KA – 2I? (NCERT)
हल:
माना A² = kA – 2I
⇒ kA = A² + 2I

प्रश्न 14.
यदि f (x) = x² – 2x – 3, तो f (A) ज्ञात कीजिए जब A = \(\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\)?
हल:
f (x) = x² – 2x – 3
∴ f (A) = A² – 24A – 3I

प्रश्न 15.
यदि आव्यूह A = \(\left[\begin{array}{ccc}
{0} & {a} & {-3} \\
{2} & {0} & {-1} \\
{b} & {1} & {0}
\end{array}\right]\) विषम सममित है तो ‘a’ तथा ‘b’ के मान ज्ञात कीजिये। (CBSE 2018)
हल:
यदि A आव्यूह विषम सममित है तो A’ = – A

2 = – a या a = – 2
– 3 = – b या b = 3.

प्रश्न 16.
यदि A = \(\begin{bmatrix} cos\alpha & -sin\alpha \\ sin\alpha & cos\alpha \end{bmatrix}\) है तो सिद्ध कीजिए –
AA^-1 = I?
हल:
दिया है:
A = \(\begin{bmatrix} cos\alpha & -sin\alpha \\ sin\alpha & cos\alpha \end{bmatrix}\)
A^-1 = \(\frac { adjA }{ |A| } \)
|A| = \(\begin{vmatrix} cos\alpha & -sin\alpha \\ sin\alpha & cos\alpha \end{vmatrix}\)
= cos² α – ( – sin² α)
= cos² α + sin² α = 1
∴ |A| = 1 …………………………….. (1)

प्रश्न 17.
यदि A = \(\begin{bmatrix} cos\alpha & -sin\alpha \\ sin\alpha & cos\alpha \end{bmatrix}\) है तो सिद्ध कीजिए –
A. (Adj A) = |A|I?
हल:

प्रश्न 18.
सिद्ध कीजिए कि वर्ग आव्यूह A = \(\begin{vmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{vmatrix}\) लाम्बिक आव्यूह है। [
हल:

इसी प्रकार A’. A = I
तब A. A’ = A’. A = I
अतः A लाम्बिक आव्यूह है। यही सिद्ध करना था।

प्रश्न 19.
यदि A = \(\begin{bmatrix} 3 & 2 \\ 7 & 5 \end{bmatrix}\) तथा B = \(\begin{bmatrix} 6 & 7 \\ 8 & 9 \end{bmatrix}\) हो, तो (AB)^-1 का मान ज्ञात कीजिए।
हल:
दिया है,
A = \(\begin{bmatrix} 3 & 2 \\ 7 & 5 \end{bmatrix}\), B = \(\begin{bmatrix} 6 & 7 \\ 8 & 9 \end{bmatrix}\)
A. B = \(\begin{bmatrix} 3 & 2 \\ 7 & 5 \end{bmatrix}\) \(\begin{bmatrix} 6 & 7 \\ 8 & 9 \end{bmatrix}\)

प्रश्न 20.
यदि A = \(\begin{bmatrix} 2 & -3 \\ -4 & 7 \end{bmatrix}\) हो, तो सिद्ध कीजिए कि
2A^-1 = 9I – A? (CBSE 2018)
हल:
दिया है,
A = \(\begin{bmatrix} 2 & -3 \\ -4 & 7 \end{bmatrix}\)

अतः समी (1) और (2) से,
2A^-1 = 9I – A

प्रश्न 21.
A तथा B आव्यूहों के लिए सत्यापित कीजिए कि (AB)’ = B’A’ जहाँ A = [ \(\begin{matrix} 1 \\ -4 \\ 3 \end{matrix}\) ] B = [-1 2 1]? (NCERT)
हल:
AB = [ \(\begin{matrix} 1 \\ -4 \\ 3 \end{matrix}\) ] _3×1 [ \(\begin{matrix} -1 & 2 & 3 \end{matrix}\) ] _1×3



अतः समी (1) और (2) से,
(AB)’ = B’A’

आव्यूह दीर्घ उत्तरीय प्रश्न – II

प्रश्न 1.
यदि A = \(\begin{bmatrix} 1 & 4 \\ 3 & 5 \end{bmatrix}\) हो, तो सिद्ध कीजिए कि –
A. adj A = (adjA). A = (adj A). A = |A| I?
हल:
दिया है,
A = \(\begin{bmatrix} 1 & 4 \\ 3 & 5 \end{bmatrix}\)
तब
|A| = \(\begin{bmatrix} 1 & 4 \\ 3 & 5 \end{bmatrix}\) = 5 – 12 = -7
A₁₁, A₁₂ = – 3, A₂₁ = – 4, A₂₂ = 1

⇒ (adj A). A = \(\begin{bmatrix} -7 & 0 \\ 0 & -7 \end{bmatrix}\)
⇒ (adj A). A = – 7 \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)
⇒ (adj A).A = |A| I ………………………….. (2)
अतः समी (1) और (2) से,
A.adj A = (adjA). A = |A| I. यही सिद्ध करना था।

प्रश्न 2.
यदि A = \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\) हो, तो सिद्ध कीजिए कि A^-1 = A?
हल:
प्रश्न क्र. 1 की भाँति हल करें।

प्रश्न 3.
यदि आव्यूह A = \(\left[\begin{array}{lll}
{0} & {0} & {1} \\
{0} & {1} & {0} \\
{1} & {0} & {0}
\end{array}\right]\) हो, तो सिद्ध कीजिए कि A^-1 = A?
हल:
दिया है:
A = \(\left[\begin{array}{lll}
{0} & {0} & {1} \\
{0} & {1} & {0} \\
{1} & {0} & {0}
\end{array}\right]\)

प्रश्न 4.
आव्यूह A = \(\left[\begin{array}{lll}
{2} & {3} & {1} \\
{3} & {4} & {1} \\
{3} & {7} & {2}
\end{array}\right]\) का प्रतिलोम ज्ञात कीजिए।
हल:
दिया है,
A = \(\left[\begin{array}{lll}
{2} & {3} & {1} \\
{3} & {4} & {1} \\
{3} & {7} & {2}
\end{array}\right]\)
∴ |A| = 2(4 × 2 – 7 × 1) – 3(3 × 2 – 3 × 1) + 1(3 × 7 – 3 × 4)
= 2(8 – 7) – 3(6 – 3) + 1(21 – 12)
= 2(1) – 3(3) + 1(9)
= 2 – 9 + 9 = 2
स्पष्ट है कि |A| ≠ 0
अतः A^-1 का अस्तित्व है।
अब |A| के अवयवों का सहखण्ड है –
A₁₁ = +(8 – 7) = 1, A₁₂ = -(6 – 3) = -3
A₁₃ = +(21 – 12) = 9, A₂₁ = -(6 – 7) = 1
A₂₂ = +(4 – 3) = 1, A₂₃ = -(14 – 9) = -5
A₃₁ = +(3 – 4) = -1, A₃₂ = -(2 – 3) = 1
A₃₃ = +(8 – 9) = -1

प्रश्न 5.
यदि A = \(\left[\begin{array}{lll}
{1} & {2} & {3} \\
{2} & {4} & {5} \\
{3} & {5} & {6}
\end{array}\right]\) हो, तो A^-1 का मान ज्ञात कीजिए।
हल: प्रश्न क्र. 4 की भाँति हल कीजिए।
उत्तर:
\(\left[\begin{array}{lll}
{1} & {2} & {3} \\
{2} & {4} & {5} \\
{3} & {5} & {6}
\end{array}\right]\)

प्रश्न 6.
यदि A = \(\left[\begin{array}{lll}
{1} & {2} & {2} \\
{2} & {1} & {2} \\
{2} & {2} & {1}
\end{array}\right]\) हो, तो A^-1 का मान ज्ञात कीजिए।
हल:
दिया है, A = \(\left[\begin{array}{lll}
{1} & {2} & {2} \\
{2} & {1} & {2} \\
{2} & {2} & {1}
\end{array}\right]\)
|A| = \(\left[\begin{array}{lll}
{1} & {2} & {2} \\
{2} & {1} & {2} \\
{2} & {2} & {1}
\end{array}\right]\)
⇒ |A| = 1(1 – 4) + 2(4 – 2) + 2 (4 – 2)
= – 3 + 4 + 4 = 5
|A| ≠ 0, इसलिए A^-1 का अस्तित्व है।

प्रश्न 7.
यदि A = \(\begin{bmatrix} 2 & 3 \\ -1 & 0 \end{bmatrix}\) हो, तो सिद्ध कीजिए कि –
A² – 2A + 3I = 0?17
हल:
दिया है,
A = \(\begin{bmatrix} 2 & 3 \\ -1 & 0 \end{bmatrix}\)

प्रश्न 8.
यदि A = \(\begin{bmatrix} 2 & -3 \\ 3 & 4 \end{bmatrix}\) हो, तो दर्शािइये कि A² – 6A + 17I = 0 तथा A^-1 का मान ज्ञात कीजिए।
हल:
दिया है:
A = \(\begin{bmatrix} 2 & -3 \\ 3 & 4 \end{bmatrix}\)

प्रश्न 9.
यदि A = \(\begin{bmatrix} -8 & 5 \\ 2 & 4 \end{bmatrix}\) हो, तो दर्शाइये A² + 4A – 42I = 0 तथा A^-1 का मान ज्ञात कीजिए।
हल:
प्रश्न क्र. 8 की भाँति हल कीजिए।
उत्तर:
A^-1 = \(\frac{1}{42}\) \(\begin{bmatrix} -4 & 5 \\ 2 & 0 \end{bmatrix}\)

प्रश्न 10.
आव्यूह विधि से निम्न समीकरणों को हल कीजिए –
x + y + 2 = 3
2x – y + z = 2
x – 2y + 3z = 2
हल:
यहाँ A = \(\left[\begin{array}{lll}
{1} & {1} & {1} \\
{2} & {-1} & {1} \\
{1} & {-2} & {3}
\end{array}\right]\), X = [ \(\begin{matrix} x \\ y \\ z \end{matrix}\) ] तथा B = [ \(\begin{matrix} 3 \\ 2 \\ 2 \end{matrix}\) ]

प्रश्न 11.
आव्यूह विधि से निम्न समीकरण हल कीजिये।
x + y + z = 6
x + 2y + 3z = 14
x + 4y + 9z = 36?
हल:
दिया गया समीकरण निकाय है –
x + y + z = 6
x + 2y + 3z = 14
x + 4y + 9z = 36.
उपरोक्त समीकरण निकाय का आव्यूह रूप है –
AX = B

प्रश्न 12.
यदि A’ = \(\left[\begin{array}{rr}
{3} & {4} \\
{-1} & {2} \\
{0} & {1}
\end{array}\right]\) तथा B = \(\left[\begin{array}{rrr}
{-1} & {2} & {1} \\
{1} & {2} & {3}
\end{array}\right]\) है तो सत्यापित कीजिये की

(i) (A + B)’ = A’ + B’
(ii) (A – B)’ = A’ – B’ (NCERT)

हल:




अतः समी (1) और (4) से,
(A – B)’ = A’ – B’ यही सिद्ध करना था।

प्रश्न 13.
यदि A = \(\left[\begin{array}{rrr}
{-1} & {2} & {3} \\
{5} & {7} & {9} \\
{-2} & {1} & {1}
\end{array}\right]\) तथा B = \(\left[\begin{array}{rrr}
{-4} & {1} & {-5} \\
{1} & {2} & {0} \\
{1} & {3} & {1}
\end{array}\right]\) हो, तो सत्यापित कीजिए कि
(i) (A + B)’ = A’ + B’
(ii) (A – B)’ = A’ – B’
हल:
प्रश्न क्र. 12 की भाँति हल करें। (NCERT)

प्रश्न 14.
आव्यूह A = \(\begin{bmatrix} 3 & 5 \\ 1 & -1 \end{bmatrix}\) को सममित और विषम सममित आव्यूह के योग के रूप में प्रदर्शित कीजिए? (NCERT)
हल:

प्रश्न 15.
(A) प्रारंभिक संक्रियाओं का प्रयोग करते हुए आव्यूह A = \(\begin{bmatrix} 2 & 3 \\ 5 & 7 \end{bmatrix}\) का व्युत्क्रम ज्ञात कीजिए? (NCERT)
हल:
A = AI के प्रयोग से,

(B)
प्रारंभिक संक्रियाओं का प्रयोग करते हुए आव्यूह A = \(\begin{bmatrix} 3 & 10 \\ 2 & 7 \end{bmatrix}\) का व्युत्क्रम ज्ञात कीजिए। (NCERT)
हल: प्रश्न क्र. 15 (A) की भाँति हल करें।
उत्तर- \(\begin{bmatrix} 7 & -10 \\ -2 & 3 \end{bmatrix}\)

प्रश्न 16.
आव्यूह विधि के प्रयोग से निम्नलिखित समीकरण निकाय को हल कीजिए – (NCERT)
\(\frac{2}{x}\) + \(\frac{3}{y}\) + \(\frac{10}{z}\) = 4 (CBSE 2011)
\(\frac{4}{x}\) – \(\frac{6}{y}\) + \(\frac{5}{z}\) = 1
\(\frac{6}{x}\) + \(\frac{9}{y}\) – \(\frac{20}{z}\) = 2, x, y, z, ≠ 0
हल:
माना
\(\frac{1}{x}\) = u, \(\frac{1}{y}\) = v, \(\frac{1}{z}\) = w, तब
2u+ 3v+ 10w = 4
4u – 6v + 5w = 1
6u + 9v – 20w = 2
उपरोक्त समीकरण निकाय का आव्यूह रूप है –
AX = B

⇒ |A| = 2 × (120 – 45) – 3(-80 – 30) + 10(36 + 36)
⇒ |A| = 150 + 330 + 720 = 1200
⇒ |A| ≠ 0 अर्थात् A व्युत्क्रमणीय है।
अतः समीकरण निकाय संगत है और अद्वितीय हल निम्न है –
X = A^-1 B
माना A में अवयव a_ij का सहखण्ड A_ij है, तब

प्रश्न 17.
A^-1 ज्ञात कीजिये जहाँ इसकी सहायता से निम्न निम्न समीकरण निकाय को हल कीजिये –
x + 2y – 3z = -4
2x + 3y + 2z = 2
3x – 3y – 4z = 11 (CBSE 2008, 10, 12)
हल:

प्रश्न 18.
\(\left[\begin{array}{ccc}
{-4} & {4} & {4} \\
{-7} & {1} & {3} \\
{5} & {-3} & {-1}
\end{array}\right]\) \(\left[\begin{array}{ccc}
{1} & {-1} & {1} \\
{1} & {-2} & {-2} \\
{2} & {1} & {3}
\end{array}\right]\) का गुणनफल ज्ञात कीजिए तथा इसकी सहायता से समीकरण निकाय को हल कीजिए – (CBSE 2012)
x – y + z = 4
x – 2y – 2x = 9
2x + y + 3z = 1.
हल:
माना B = \(\left[\begin{array}{ccc}
{-4} & {4} & {4} \\
{-7} & {1} & {3} \\
{5} & {-3} & {-1}
\end{array}\right]\) और A = \(\left[\begin{array}{ccc}
{1} & {-1} & {1} \\
{1} & {-2} & {-2} \\
{2} & {1} & {3}
\end{array}\right]\)

प्रश्न 19.
4kg प्याज, 3kg गेहूँ और 2kg चावल का मूल्य 60 रु. है। 2kg प्याज, 4kg गेहूँ और 6kg चावल का मूल्य 90 रु. है। 6kg प्याज, 2kg गेहूँ और 3kg चावल का मूल्य 70 रु. है। आव्यूह विधि द्वारा प्रत्येक का मूल्य प्रति kg ज्ञात कीजिए।
हल:
माना 1 kg प्याज का मूल्य = x रु.
1 kg गेहूँ का मूल्य = y रु.
1 kg चावल का मूल्य = zरु.
प्रश्नानुसार,
4x + 3y + 2z = 60
2x + 4y + 6z = 90
6x + 2y + 3z = 70
आव्यूह रूप है –
AX = B

⇒ |A| = 4(12 – 12) – 3(6 – 36) + 2(4 – 24)
⇒ |A| = 0 + 90 – 40 = 50 ≠ 0
⇒ A^-1 का अस्तित्व है।
अतः समीकरण निकाय का अद्वितीय हल है –
X = A^-1 B
माना A में a_ij का सहखण्ड A_ij है, तब

MP Board Class 12 Maths Important Questions

MP Board Class 12th Maths Important Questions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन

प्रतिलोम त्रिकोणमितीय फलन Important Questions

प्रतिलोम त्रिकोणमितीय फलन वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सही विकल्प चुनकर लिखिए –

प्रश्न 1.
यदि sin^-1x – cos^-1 x = \(\frac { \pi }{ 6 } \) हो, तो x का मान ज्ञात कीजिए –
(a) \(\frac{1}{2}\)
(b) \(\frac { \sqrt { 3 } }{ 2 } \)
(c) – \(\frac{1}{2}\)
(d) इनमें से कोई नहीं।
उत्तर:
(a) \(\frac{1}{2}\)

प्रश्न 2.
यदि tan^-1 3 + tan^-1 x = tan^-1 8 हो, तो x का मान होगा –
(a) 5
(b) \(\frac{1}{5}\)
(c) \(\frac{5}{14}\)
(d) \(\frac{14}{5}\)
उत्तर:
(b) \(\frac{1}{5}\)

प्रश्न 3.
tan^-1 ( \(\frac{x}{y}\) ) – tan^-1 ( \(\frac { x-y }{ x+y } \) ) का मान है –
(a) \(\frac { \pi }{ 2 } \)
(b) \(\frac { \pi }{ 3 } \)
(c) \(\frac { \pi }{ 4 } \)
(d) \(\frac { -3\pi }{ 4 } \)
उत्तर:
(c) \(\frac { -3\pi }{ 4 } \)

प्रश्न 4.
2 tan^-1 {cosec (tan^-1 x) – tan (cot^-1 x)} का मान है –
(a) cot^-1 x
(b) cot^-1 \(\frac{1}{x}\)
(c) tan^-1 x
(d) tan^-1 \(\frac{1}{x}\)
उत्तर:
(c) tan^-1 x

प्रश्न 5.
tan {cos^-1 \(\frac { 1 }{ 5\sqrt { 2 } } \) – sin^-1 \(\frac { 4 }{ \sqrt { 17 } } \) } का मान होगा –
(a) \(\frac { \sqrt { 29 } }{ 3 } \)
(b) \(\frac{29}{3}\)
(c) \(\frac { \sqrt { 3 } }{ 29 } \)
(d) \(\frac{3}{29}\)
उत्तर:
(d) \(\frac{3}{29}\)

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए –

1. tan^-1 (1) + tan^-1 (2) + tan^-1 (3) = ………………………….
2. tan^-1 (2) – tan^-1 (1) = …………………………….
3. cot^-1 3 + cosec^-1 \(\sqrt{5}\)
4. sin(sin^-1 x + 2 cos^-1 x) = …………………………..
5. यदि sin^-1 ( \(\frac { 2a }{ 1+a^{ 2 } } \) ) + sin ( \(\frac { 2b }{ 1+b^{ 2 } } \) ) = 2 tan^-1 x, तो x = ………………………….
6. यदि tan^-1 ( \(\frac { 1-x }{ 1+x } \) ) = \(\frac{1}{2}\) tan^-1 x (जब x > 0), तो x =
7. tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) + tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 c = ………………………..

उत्तर:

1. π
2. tan^-1 ( \(\frac{1}{3}\) )
3. \(\frac { \pi }{ 4 } \)
4. x
5. \(\frac { a+b }{ 1-ab } \)
6. \(\frac { 1 }{ \sqrt { 3 } } \)
7. tan^-1 (a)

प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –

1. tan^-1 x + tan^-1 y = tan^-1 \(\frac { x+y }{ 1-xy } \)
2. cos^-1(-x) = – cos^-1 x
3. sin^-1 (3x – 4x³) = sin^-1 \(\frac{x}{3}\)
4. cos^-1 ( \(\frac { 1-x^{ 2 } }{ 1+x^{ 2 } } \) ) = 2 tan^-1 x
5. sin^-1 x – sin^-1 y = sin^-1 [xy – \(\sqrt { 1-x^{ 2 } } \) \(\sqrt { 1-y^{ 2 } } \) ].

उत्तर:

1. सत्य
2. असत्य
3. असत्य
4. सत्य
5. असत्य।

प्रश्न 4.
सही जोड़ी बनाइये –

उत्तर:

1. (b)
2. (e)
3. (f)
4. (a)
5. (c)
6. (d)

प्रश्न 5.
एक शब्द/वाक्य में उत्तर दीजिए –

1. tan^-1\(\frac{1}{2}\) + tan^-1\(\frac{3}{2}\) का मान ज्ञात कीजिए।
2. tan^-1 \(\frac { x }{ \sqrt { 1-x^{ 2 } } } \) का मान ज्ञात कीजिए।
3. sin (2 sin^-1\(\frac{3}{5}\) ) का मान ज्ञात कीजिए।
4. समीकरण sin^-1 \(\frac{x}{5}\) + cosec^-1\(\frac{5}{4}\) = \(\frac { \pi }{ 2 } \) का मान ज्ञात कीजिए।
5. cos^-1 (cos \(\frac { 7\pi }{ 6 } \) ) का मुख्य मान लिखिए।
6. यदि cos^-1 ( \(\frac{1}{x}\) ) = θ हो, तो tan θ का मान लिखिए।

उत्तर:

1. tan^-1 8
2. sin^-1 x
3. \(\frac{24}{25}\)
4. x = 3
5. \(\frac { 5\pi }{ 6 } \)
6. \(\sqrt { x^{ 2 }-1 } \)

प्रतिलोम त्रिकोणमितीय फलन लाधु उतरिय प्रश्न

प्रश्न 1.
निम्नलिखित के मुख्य मान ज्ञात कीजिये – (CBSE 2014)

(i) tan^-1 [sin (- \(\frac { \pi }{ 2 } \) ) (CBSE 2014)

(ii) cot [ \(\frac { \pi }{ 2 } \) – 2 cot^-1 \(\sqrt{3}\) (CBSE 2014)

(iii) tan^-1 (-\(\sqrt{3}\) )

(iv) sec^-1 (-\(\frac{2}{3}\) \(\sqrt{3}\) ) (NCERT)

(v) cosec^-1 (2) (NCERT)

हल:
(i) tan^-1 [sin (- \(\frac { \pi }{ 2 } \) )
= tan^-1 [- sin \(\frac { \pi }{ 2 } \) ], [∵sin (- θ) = – sin θ]
= tan^-1 (-1), (∵ sin \(\frac { \pi }{ 2 } \) = 1)
= – tan^-1 (1), (∵ tan^-1 (-x) = – tan^-1 x)
= –\(\frac { \pi }{ 4 } \) (∵ tan^-1 (1) = \(\frac { \pi }{ 4 } \)
(ii) cot [ \(\frac { \pi }{ 2 } \) – 2cot^-1 \(\sqrt{3}\)

(iii) माना tan(-\(\sqrt{3}\)) = θ

(iv) sec^-1 \(\frac{-2}{3}\)\(\sqrt{3}\)) = θ

प्रश्न 2.
सिद्ध कीजिये –
(a) 2 cos^-1 \(\frac{4}{5}\) = cos^-1 \(\frac{7}{25}\)
(b) 2 sin^-1 \(\frac{3}{5}\) = sin^-1 \(\frac{24}{25}\)
(c) 2 sin^-1 \(\frac{5}{13}\) = sin^-1 \(\frac{120}{169}\)
हल:
(a) 2 cos^-1 \(\frac{4}{5}\) = cos^-1 \(\frac{7}{25}\)

(b) 2 sin^-1 \(\frac{3}{5}\) = sin^-1 \(\frac{24}{25}\)

(c) क्रमांक की 2(b) भाँती हल कीजिये।

प्रश्न 3.
मान ज्ञात कीजिये –
tan^-1 {2 cos (2 sin^-1 \(\frac{1}{2}\) )} (CBSE 2013, NCERT)
हल:
tan^-1 {2 cos (2 sin^-1 \(\frac{1}{2}\) )} = tan^-1 [2 cos (2 × \(\frac { \pi }{ 6 } \) ) ]
= tan^-1 [2 cos \(\frac { \pi }{ 3 } \) ] = tan^-1 [2 × \(\frac{1}{2}\) ]
= tan^-1 1
= \(\frac { \pi }{ 4 } \)

प्रश्न 4.
मान ज्ञात कीजिये –
sin [ \(\frac { \pi }{ 3 } \) – sin^-1 (- \(\frac{1}{2}\)) ] (CBSE 2008, 13)
हल:
sin [ \(\frac { \pi }{ 3 } \) – sin^-1 (- \(\frac{1}{2}\) ) ]
= sin [ \(\frac { \pi }{ 3 } \) + sin^-1 ( \(\frac{1}{2}\)) ], [∵sin^-1 (-x) = – sin^-1x]
= sin [ \(\frac { \pi }{ 3 } \) + \(\frac { \pi }{ 6 } \) ] = sin \(\frac { \pi }{ 2 } \) = 1

प्रश्न 5.
सिद्ध कीजिये –
2 tan^-1 \(\frac{1}{5}\) = tan^-1 \(\frac{5}{12}\)?
हल:
L.H.S = 2 tan^-1 \(\frac{1}{5}\)

प्रश्न 6.
मान ज्ञात कीजिये –
tan (2 tan^-1 \(\frac{1}{5}\) – \(\frac { \pi }{ 4 } \) )
हल:

प्रश्न 7.
सिद्ध कीजिये –
3 sin^-1 x = sin^-1 (3x – 4x³). (NCERT, CBSE 2018)
हल:
मानलो sin^-1 x = θ.
∴ x = sin θ
अब sin 3θ = 3 sinθ – 4sin³θ
= 3x – 4x³
∴ 3θ = sin^-1 (3x – 4x³)

यही सिद्ध करना था।

प्रश्न 8.
सिद्ध कीजिये –
3 cos^-1 x = cos^-1 (4x³ – 3x) (NCERT)
हल:
मानलो cos^-1 x = θ
∴ x = cos θ
अब cos 3θ = 4 cos³θ – 3 cos θ
= 4x³ – 3x
∴ 3θ = cos^-1 (4x³ – 3x)

यही सिद्ध करना था।

प्रश्न 9.
सिद्ध कीजिये –
(A) tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{3}\) = \(\frac { \pi }{ 4 } \)
(B) cos^-1\(\frac{12}{13}\) = tan^-1 \(\frac{5}{12}\)
(C) cos^-1\(\frac{3}{5}\) = sin^-1 \(\frac{4}{5}\)
हल:
(A) tan^-1 = \(\frac{1}{2}\) + tan^-1 \(\frac{1}{3}\) = \(\frac { \pi }{ 4 } \)
L.H.S = tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{3}\)

(B) cos^-1 \(\frac{12}{13}\) = tan^-1 \(\frac{5}{12}\)

समी. (1) तथा (2) L.H.S. = R.H.S. यही सिद्ध करना था।

(C) cos^-1 \(\frac{3}{5}\) = sin-1 \(\frac{4}{5}\)

समी. (1) तथा (2) L.H.S. = R.H.S. यही सिद्ध करना था।

प्रश्न 10.
सिद्ध कीजिये
(A) sec^-1 x + cosec^-1 x = \(\frac { \pi }{ 2 } \)
(B) sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \)
(C) tan^-1 x + cot^-1 x = \(\frac { \pi }{ 2 } \)
हल:
(A) sec^-1 x + cosec^-1 x = \(\frac { \pi }{ 2 } \)
माना sin^-1 x = θ ………………… (1)
⇒ x = sin θ
⇒ x = cos ( \(\frac { \pi }{ 2 } \) – θ) ………………………. (2)
समी. (1) तथा (2) को जोड़ने पर
sec^-1 x + cosec^-1 x = θ + \(\frac { \pi }{ 2 } \) – θ = \(\frac { \pi }{ 2 } \) यही सिद्ध करना था।

(B) sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \)
माना sin^-1 x = θ ………………….. (1)
⇒ x = sin θ
⇒ x = cos ( \(\frac { \pi }{ 2 } \) – θ)
⇒ cos^-1 x = \(\frac { \pi }{ 2 } \) – θ …………………………. (2)
समी. (1) तथा (2) को जोड़ने पर,
sin^-1 x + cos^-1 x = θ + \(\frac { \pi }{ 2 } \) – θ
⇒ sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \) यही सिद्ध करना था।

(C) tan^-1 x + cot^-1 x = \(\frac { \pi }{ 2 } \)
माना
⇒ tan^-1 x = θ …………………………… (1)
⇒ x = tan θ
⇒ x = cot ( \(\frac { \pi }{ 2 } \) – θ)
⇒ cot^-1 x = \(\frac { \pi }{ 2 } \) – θ ……………………… (2)

प्रश्न 11.
सिद्ध कीजिए कि
(A) tan^-1 5 – tan^-1 3 – tan^-1 \(\frac{1}{8}\)
(B) tan^-1 3 – tan^-1 2 = tan^-1 \(\frac{1}{7}\)
(C) tan^-1 7 – tan^-1 5 = tan^-1 \(\frac{1}{18}\)
हल:
(A) tan^-1 5 – tan^-1 3 = tan^-1 \(\frac{1}{8}\)
L.H.S = tan^-1 5 – tan^-1 3
= tan^-1 \(\frac { 5-3 }{ 1+5.3 } \) = tan^-1 \(\frac{2}{16}\) = tan^-1 \(\frac{1}{8}\)
= R.H.S. यही सिद्ध करना था।

(B) प्रश्न क्रमांक 11 (A) की भाँति हल कीजिये।

(C) प्रश्न क्रमांक 11 (A) की भाँति हल कीजिये।

प्रश्न 12.
सिद्ध कीजिये कि
(A) tan^-1 \(\frac{4}{7}\) – tan^-1 \(\frac{1}{5}\) = tan^-1 \(\frac{1}{3}\)
(B) tan^-1 \(\frac{1}{2}\) – tan^-1 \(\frac{2}{9}\) = tan^-1 \(\frac{1}{4}\)
(C) tan^-1 \(\frac{1}{7}\) + tan^-1 \(\frac{1}{8}\) = tan^-1 \(\frac{3}{11}\)
हल:
(A) tan^-1 \(\frac{4}{7}\) – tan^-1 \(\frac{1}{5}\) = tan^-1 \(\frac{1}{3}\)
L.H.S = tan^-1 \(\frac{4}{7}\) – tan^-1 \(\frac{1}{5}\)
= tan^-1 \(\frac { \frac { 4 }{ 7 } -\frac { 1 }{ 5 } }{ 1+\frac { 4 }{ 7 } .\frac { 1 }{ 5 } } \) = tan^-1 \(\frac{1}{3}\)
= tan^-1 \(\frac{13}{39}\) = tan^-1 \(\frac{1}{3}\)
= R.H.S यही सिद्ध करना था।

(B) प्रश्न क्रमांक 12 (A) की भाँति हल कीजिये।

(C) प्रश्न क्रमांक 12 (A) की भाँति हल कीजिये।

प्रश्न 13.
सिद्ध कीजिए कि
tan^-1 1 + tan^-1 2 + tan^-1 3 = π
हल: L.H.S. = tan^-1 1 + (tan^-1 2 + tan^-1 3)
= tan^-1 (1) + π + tan^-1 ( \(\frac { 2+3 }{ 1-2\times 3 } \) )
[∵ tan^-1 x + tan^-1 y = π + tan^-1 \(\frac { x+y }{ 1-xy } \), यदि x > 0, y > 0, xy > 1, यहाँ xy = 6 > 1]
= tan^-1 (1) + π + tan^-1 ( \(\frac{5}{5-6}\) )
= tan^-1 (1) + π + tan^-1 (-1)
= tan^-1 (1) + π – tan^-1 (1), [∵tan^-1(-x) = – tan^-1 x]
= π = R.H.S
∵ बाएँ पक्ष की राशियाँ धनात्मक कोण बनाती हैं, अतः बायाँ पक्ष शून्य नहीं हो सकता।
अत: बायाँ पक्ष = π = दायाँ पक्ष। यही सिद्ध करना था।

प्रश्न 14.
यदि tan^-1 ( \(\frac{1}{2}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) हो, तो k का मान ज्ञात कीजिए।
हल: tan^-1 ( \(\frac{1}{2}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \)

⇒ \(\frac { k+2 }{ 2k-1 } \) = 1
⇒ k + 2 = 2k – 1
⇒ 2 + 1 = 2k – k
⇒ k = 3.

प्रश्न 15.
यदि tan^-1 ( \(\frac{3}{4}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) हो, तो k का मान ज्ञात कीजिए।
हल:
प्रश्न क्रमांक 14 की भाँति हल कीजिये।
[उत्तर – k = 1.]

प्रश्न 16.
यदि tan^-1 ( \(\frac{4}{5}\) ) + tan^-1 ( \(\frac{1}{k}\) ) = \(\frac { \pi }{ 4 } \) हो, तो k का मान ज्ञात कीजिए।
हल:
प्रान क्रमांक 14 की भाँति हल कीजिये।
[उत्तर – k = 9.]

प्रश्न 17.
सिद्ध कीजिए कि
tan^-1 \(\sqrt{x}\) = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) )
हल:
R.H.S. = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) )
माना \(\sqrt{x}\) = tan θ
⇒ x = tan² θ
⇒ \(\frac { 1-x }{ 1+x } \) = \(\frac { 1-tan^{ 2 }\theta }{ 1+tan^{ 2 }\theta } \) = cos 2θ
∴ R.H.S = \(\frac{1}{2}\) cos^-1 (cos 2θ)
= \(\frac{1}{2}\) × 2θ = θ
= tan^-1 ( \(\sqrt{x}\) ), [∵ \(\sqrt{x}\) = tanθ ⇒ tan^-1 ( \(\sqrt{x}\) ) = θ]
= L.H.S. यही सिद्ध करना था।

प्रश्न 18.
सिद्ध कीजिए कि
sin (cos^-1x) = cos (sin^-1x)
हल:
L.H.S.= sin (cos^-1 x)
= sin [ \(\frac { \pi }{ 2 } \) – sin^-1 x], [∵sin^-1 x + cos^-1 x = \(\frac { \pi }{ 2 } \), cos^-1 x = \(\frac { \pi }{ 2 } \) – sin^-1 x] [∵ sin(90° – θ) = cos θ]
= cos (sin^-1 x),
= R.H.S यही सिद्ध करना था।

प्रश्न 19.
(A) सिद्ध कीजिए कि
tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 ( \(\frac { c-a }{ 1+ca } \) ) + tan^-1 a = tan^-1 b?
हल:
L.H.S = tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 ( \(\frac { c-a }{ 1+ca } \) ) + tan^-1 a
= tan^-1 b – tan^-1 c + tan^-1 c – tan^-1 a + tan^-1 a
= tan^-1 b = R.H.S. यही सिद्ध करना था।

(B) सिद्ध कीजिए कि
tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) + tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 c = tan^-1 a?
हल:
L.H.S = tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) + tan^-1 ( \(\frac { b-c }{ 1+bc } \) ) + tan^-1 c
= (tan^-1 a – tan^-1 b) + (tan^-1 b – tan^-1 c) + tan^-1 c
= tan^-1 a = R.H.S. यही सिद्ध करना था।

प्रश्न 20.
समीकरण हल कीजिए –
sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) + sin^-1 \(\frac { 2b }{ 1+b^{ 2 } } \) = 2 tan^-1 x?
हल:
दिया गया समीकरण है:
sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) + sin^-1 \(\frac { 2b }{ 1+b^{ 2 } } \) = 2 tan^-1 x
⇒ 2 tan^-1 a + 2 tan^-1 b = 2 tan^-1 x, [∵ sin^-1 \(\frac { 2x }{ 1+x^{ 2 } } \) = 2 tan^-1 x]
⇒ tan^-1 a + tan^-1 b = tan^-1 x
⇒ tan^-1 \(\frac { a-b }{ 1+ab } \) = tan^-1 x
x = \(\frac { a-b }{ 1+ab } \)

प्रश्न 21.
समीकरण हल कीजिए –
cos^-1 ( \(\frac { 1-a^{ 2 } }{ 1+a^{ 2 } } \) ) – cos^-1 ( \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) ) = 2 tan^-1 x?
हल:
दिया गया समीकरण है:
cos^-1 ( \(\frac { 1-a^{ 2 } }{ 1+a^{ 2 } } \) ) – cos^-1 ( \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) ) = 2 tan^-1 x
⇒ 2 tan^-1 a – 2 tan^-1 = 2 tan^-1 x
⇒ tan^-1 a – tan^-1 b = tan^-1 x
⇒ tan^-1 \(\frac { a-b }{ 1+ab } \) = tan^-1 x
∴ x = \(\frac { a-b }{ 1+ab } \)

प्रश्न 22.
(A) सिद्ध कीजिए –
2 tan^-1 \(\frac{1}{4}\) = tan^-1 \(\frac{8}{15}\)?
हल:
दिया है:
2 tan^-1 \(\frac{1}{4}\) = tan^-1 \(\frac{8}{15}\)
L.H.S = 2 tan^-1 \(\frac{1}{4}\)
= tan^-1 \(\frac { 2.1/4 }{ 1-(1/4)^{ 2 } } \) [∵ 2 tan^-1 x = tan^-1 \(\frac { 2x }{ 1-x^{ 2 } } \) ]
= tan^-1 \(\frac { 1/2 }{ 15/16 } \)
= tan^-1 \(\frac{8}{15}\) = R.H.S यही सिद्ध करना था।

(B) सिद्ध कीजिए –
2 tan^-1 ( \(\frac{1}{2}\) ) = tan^-1 ( \(\frac{4}{3}\) )
हल:
दिया है:
2 tan^-1 ( \(\frac{1}{2}\) ) = tan^-1 ( \(\frac{4}{3}\) )
L.H.S = 2 tan^-1 ( \(\frac{1}{2}\) )

यही सिद्ध करना था।

प्रश्न 23.
सरलतम रूप में लिखिए –
tan^-1 \(\sqrt { \frac { 1-cosx }{ 1+cosx } } \)?
हल:
दिया है:

प्रश्न 24.
सरलतम रूप में लिखिए –
cos^-1 \(\sqrt { \frac { 1 }{ 2 } (1+cosx) } \)?
हल:
दिया है:

प्रश्न 25.
यदि tan^-1 a + tan^-1 b + tan^-1 c = \(\frac { \pi }{ 2 } \) हो, तो सिद्ध कीजिए कि
ab + bc + ca = 1.
हल:
दिया है:
tan^-1 + tan^-1 b + tan^-1 c = \(\frac { \pi }{ 2 } \)
⇒ tan^-1a + tan^-1 b + tan^-1 c = tan^-1 a + cot^-1 a, [∵tan^-1 a + cot^-1 a = \(\frac { \pi }{ 2 } \) ]
⇒ tan^-1 b + tan^-1 c = cot^-1 a
⇒ tan^-1 ( \(\frac { b+c }{ 1-bc } \) ) = tan^-1 ( \(\frac{1}{a}\) )
⇒ \(\frac { b+c }{ 1-bc } \) = \(\frac{1}{a}\)
⇒ ab + ca = 1 – bc
⇒ ab + bc + ca = 1 यही सिद्ध करना था।

प्रश्न 26.
सिद्ध कीजिए –
यही सिद्ध करना था।
tan^-1 \(\frac{2}{11}\) + cot^-1 \(\frac{24}{7}\) = tan^-1 \(\frac{1}{2}\)?
हल:
L.H.S. = tan^-1 \(\frac{2}{11}\) + cot^-1 \(\frac{7}{24}\)
= tan^-1 \(\frac{2}{11}\) + tan^-1 \(\frac{7}{24}\)

= tan^-1 [ \(\frac{125}{250}\) ] = tan^-1 \(\frac{1}{2}\) = R.H.S. यही सिद्ध करना था।

प्रश्न 27.
सिद्ध कीजिए –
cos^-1 x = 2 cos^-1 \(\sqrt { \frac { 1+x }{ 2 } } \)
= 2 cos^-1 \(\sqrt { \frac { 1+cos\theta }{ 2 } } \), ( x = cos θ रखने पर)
= 2 cos^-1 \(\sqrt { \frac { 2cos^{ 2 }\frac { \theta }{ 2 } }{ 2 } } \) = 2. \(\frac { \theta }{ 2 } \)
= cos^-1 x = L.H.S. यही सिद्ध करना था।

प्रश्न 28.
सिद्ध कीजिए –
cos^-1 x = 2 tan^-1 \(\sqrt { \frac { 1-x }{ 1+x } } \)?
हल:
R.H.S = 2 tan^-1 \(\sqrt { \frac { 1-x }{ 1+x } } \)

= 2. \(\frac { \theta }{ 2 } \) = θ = cos^-1 x = L.H.S. यही सिद्ध करना था।

प्रश्न 29.
सिद्ध कीजिए कि
tan^-1 ( \(\frac{a}{b}\) ) – tan^-1 ( \(\frac { a-b }{ a+b } \) ) = \(\frac { \pi }{ 4 } \)?
हल:
L.H.S = tan^-1 ( \(\frac{a}{b}\) ) – tan^-1 ( \(\frac { a-b }{ a+b } \) )

= tan^-1 1
= \(\frac { \pi }{ 4 } \) = R.H.S. यही सिद्ध करना था।

प्रतिलोम त्रिकोणमितीय फलन दीर्घ उत्तरीय प्रश्न – I

प्रश्न 1.
(A) सिद्ध कीजिए कि
sin^-1 \(\frac { 1 }{ \sqrt { 5 } } \) + sin^-1 \(\frac { 1 }{ \sqrt { 10 } } \) = \(\frac { \pi }{ 4 } \)?
हल:
माना sin^-1 \(\frac { 1 }{ \sqrt { 5 } } \) = A, sin^-1 \(\frac { 1 }{ \sqrt { 10 } } \) = B
∴ A + B = \(\frac { \pi }{ 4 } \)
⇒ sin(A + B) = sin \(\frac { \pi }{ 4 } \)
⇒ sinA cosB + cosA sinB = \(\frac { 1 }{ \sqrt { 2 } } \)
L.H.S = sinA \(\sqrt { 1-sin^{ 2 }B } \) + \(\sqrt { 1-sin^{ 2 }A } \). sin B

(B) निम्न समीकरण को हल कीजिए:
sin^-1 x + sin^-1 (1 – x) = sin^-1 \(\sqrt { 1-x^{ 2 } } \)?
हल:
दिया गया समीकरण है:
sin^-1 x + sin^-1 (1 – x) = sin^-1 \(\sqrt { 1-x^{ 2 } } \)

वर्ग करने पर,
x² (2x – x²) = x² (1 – x²)
⇒ x² (2x – x² – 1 + x²) = 0
⇒ x² (2x – 1) = 0
अतः x = 0, \(\frac{1}{2}\).

प्रश्न 2.
(A) सिद्ध कीजिए कि tan^-1 \(\frac { x+1 }{ x } \) – tan^-1 \(\frac { 1 }{ 2x+1 } \) = \(\frac { \pi }{ 4 } \)?
(B) यदि tan^-1 x + tan^-1 y + tan^-1 z = \(\frac { \pi }{ 2 } \) हो, तो सिद्ध कीजिए xy + yz + zx = xyz.
(C) यदि tan^-1 x + tan^-1 y + tan^-1 z = \(\frac { \pi }{ 2 } \), हो, तो सिद्ध कीजिए xy + yz + zx = 1.
हल:
(A) tan^-1 \(\frac { x+1 }{ x } \) – tan^-1 \(\frac { 1 }{ 2x+1 } \) = \(\frac { \pi }{ 4 } \)

= R.H.S. यही सिद्ध करना था।
(B) tan^-1 x + tan^-1 z = π

⇒ x + y + z – xyz = 0 [∵ tan π = 0]
∴ x + y + z = xyz. यही सिद्ध करना था।
(C) प्रश्न क्रमांक 2 (B) की भाँति tan \(\frac { \pi }{ 2 } \) = ∞ = \(\frac{1}{0}\), रखकर विद्यार्थी स्वयं हल करें।

प्रश्न 3.
सरलतम रूप में लिखिए –
tan^-1 [ \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ]?
हल:
tan^-1 [ \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ]
माना x = tan θ

प्रश्न 4.
(A) सिद्ध कीजिए –
\(\frac{1}{2}\) sin^-1 x = cot^-1 \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \)?
हल:
R.H.S. = cot^-1 \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \)

(B) सिद्ध कीजिए –
\(\frac{1}{2}\) cot^-1 x = cot^-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )?
हल:
\(\frac{1}{2}\) cot^-1 x = cot^-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )
R.H.S. = cot^-1 ( \(\sqrt { 1+x^{ 2 }+x } \) )
माना x = cot θ

प्रश्न 5.
समीकरण को हल कीजिए –
tan^-1 (x + 1) + tan^-1 (x – 1) = tan^-1 ( \(\frac{6}{17}\) )?
हल:
दिया है:
tan^-1 (x + 1) + tan^-1 (x – 1) = tan^-1 ( \(\frac{6}{17}\) )?

⇒ 17x = 6 – 3x²
⇒ 3x² + 18 x – x – 6 = 0
⇒ 3x(x + 6) -1 (x + 6) = 0
⇒ (x + 6) (3x – 1) = 0
∴ x = – 6, x = \(\frac{1}{3}\)

प्रश्न 6.
सिद्ध कीजिए कि cos^-1 \(\frac{3}{5}\) + cos^-1 \(\frac{4}{5}\) = \(\frac { \pi }{ 2 } \)?
हल:
दिया है:
L.H.S = cos^-1 \(\frac{3}{5}\) + cos^-1 \(\frac{4}{5}\)

प्रश्न 7.
यदि cos^-1 x + cos^-1 y + cos^-1 z = π हो, तो सिद्ध कीजिए कि
x² + y² + z² + 2xyz = 1
हल:
दिया है:
cos^-1 x + cos^-1 y + cos^-1 z = π

दोनों पक्षों का वर्ग करने पर,
x²y² + z² + 2xyz = (1 – x²) (1 – y²)
⇒ x²y² + z² + 2xyz = 1 – y² – x² + x²y²
⇒ z² + 2xyz = 1 – y² – x²
⇒ x² + y² + z² + 2xyz = 1. यही सिद्ध करना था।

प्रश्न 8.
यदि sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) – cos^-1 \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) = tan^-1 \(\frac { 2x }{ 1-x^{ 2 } } \) हो, तो सिद्ध कीजिए कि x = \(\frac { a-b }{ 1+ab } \)?
हल:
यहाँ sin^-1 \(\frac { 2a }{ 1+a^{ 2 } } \) – cos^-1 \(\frac { 1-b^{ 2 } }{ 1+b^{ 2 } } \) = tan^-1 \(\frac { 2x }{ 1-x^{ 2 } } \) ………………………….. (1)
माना a = tan θ, b = tan ∅, x = tan Ψ
समी. (1) में इन मानों को रखने पर,

⇒ sin^-1 (sin 2θ) – cos^-1 (cos 2∅) = tan^-1 (tan 2Ψ)
⇒ 2θ – 2∅ = 2Ψ
⇒ θ – ∅ = Ψ
⇒ tan^-1 a – tan^-1 b = tan^-1 x
⇒ tan^-1 ( \(\frac { a-b }{ 1+ab } \) ) = tan^-1 x
⇒ x = \(\frac { a-b }{ 1+ab } \). यही सिद्ध करना था।

प्रश्न 9.
सिद्ध कीजिए कि
tan^-1 \(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\) = \(\frac { \pi }{ 4 } \) – \(\frac{1}{2}\) cos¹ x
हल:
माना कि x = cos θ, तब θ = cos^-1 x

प्रश्न 10.
सरलतम रूप में लिखिये –
tan^-1 ( \(\frac { x }{ \sqrt { 1+x^{ 2 }-1 } } \) )?
हल:
tan^-1 ( \(\frac { x }{ \sqrt { 1+x^{ 2 }-1 } } \) ) में x = tan θ रखने पर,

प्रश्न 11.
सिद्ध कीजिए कि –
tan^-1 \(\sqrt{x}\) = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) ) (NCERT)
हल:
R.H.S. = \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-x }{ 1+x } \) )

माना \(\sqrt{x}\) = tan θ
तब, θ = tan^-1 \(\sqrt{x}\)
= \(\frac{1}{2}\) cos^-1 ( \(\frac { 1-tan^{ 2 }\theta }{ 1+tan^{ 2 }\theta } \) )
= \(\frac{1}{2}\) cos^-1 (cos 2θ), [∵ cos^-1 (cos x) = x]
= \(\frac{1}{2}\) × 2θ
= θ
= tan^-1 \(\sqrt{x}\), [समी. (1) से]
= L.H.S. यही सिद्ध करना था।

प्रश्न 12.
सिद्ध कीजिए कि –
tan^-1 \(\frac { 6x-8x^{ 3 } }{ 1-12x^{ 2 } } \) – tan^-1 \(\frac { 4x }{ 1-4x^{ 2 } } \) = tan^-1 2x, जहाँ |2x| < \(\frac { 1 }{ \sqrt { 3 } } \) (CBSE 2016)
हल:
L.H.S. = tan^-1 \(\frac { 6x-8x^{ 3 } }{ 1-12x^{ 2 } } \) – tan^-1 \(\frac { 4x }{ 1-4x^{ 2 } } \)
= tan^-1 \(\frac { 3(2x)-(2x)^{ 3 } }{ 1-3(2x)^{ 2 } } \) – tan^-1 \(\frac { 2\times 2x }{ 1-(2x)^{ 2 } } \)
माना 2x = tanθ
तब,
θ = tan^-1 2x

= 3θ – 2θ = θ
= tan^-1 2x [समी. (1) से]
= R.H.S. यही सिद्ध करना था।

प्रश्न 13.
सिद्ध कीजिए कि –
cos^-1 \(\frac{4}{5}\) + cos^-1 \(\frac{12}{13}\) = cos^-1 \(\frac{33}{65}\)?
हल:
L.H.S. = cos^-1 \(\frac{4}{5}\) + cos^-1 \(\frac{12}{13}\)

MP Board Class 12 Maths Important Questions

MP Board Class 12th Maths Important Questions Chapter 1 संबंध एवं फलन

संबंध एवं फलन Important Questions

संबंध एवं फलन वस्तुनिष्ठ प्रश्न

प्रश्न 1.
सही विकल्प चुनकर लिखिए –

प्रश्न 1.
मान लीजिए कि f (x) = 8x द्वारा परिभाषित फलन f : R → R फलन है –
(a) f एकैकी आच्छादक है
(b) f बहुएक आच्छादक है
(c) f एकैकी है परन्तु आच्छादक नहीं है
(d) f न तो एकैकी है और न आच्छादक है।
उत्तर:
(a) f एकैकी आच्छादक है

प्रश्न 2.
फलन f(x) = \(\frac { e^{ x^{ 2 } }-e^{ -x^{ 2 } } }{ e^{ x^{ 2 } }+e^{ -x^{ 2 } } } \) द्वारा परिभाषित फलन f : R → R है –
(a) f एकैकी है परन्तु आच्छादक नहीं है
(b) f एकैकी आच्छादक है
(c) f न तो एकैकी है और न आच्छादक है
(d) f बहुएक आच्छादक है।
उत्तर:
(a) f एकैकी है परन्तु आच्छादक नहीं है

प्रश्न 3.
यदि f : R → R, f(x) = (3 – x³)^1/3 द्वारा प्रदत्त है तो fof(x) बराबर हैं –
(a) x^1/3
(b) x³
(c) x
(d) (3 – x³)
उत्तर:
(c) x

प्रश्न 4.
a * b = a³ + b³ प्रकार से परिभाषित N में एक द्विआधारी संक्रिया * पर विचार कीजिए –
(a) * साहचर्य तथा क्रमविनिमेय दोनों है
(b) * क्रमविनिमेय है, किन्तु साहचर्य नहीं है
(c) * साहचर्य है, किन्तु क्रमविनिमेय नहीं है
(d) * न तो क्रमविनिमेय है और न साहचर्य है।
उत्तर:
(b) * क्रमविनिमेय है, किन्तु साहचर्य नहीं है

प्रश्न 5.
समुच्चय {a, b} में द्विआधारी संक्रियाओं की संख्या है –
(a) 10
(b) 16
(c) 20
(d) 8
उत्तर:
(b) 16

प्रश्न 2.
रिक्त स्थानों की पूर्ति कीजिए –

1. यदि A = {1, 2, 3} हो, तो अवयव (1, 2) वाले तुल्यता सम्बन्धों की संख्या ……………………………….. होगी।
2. यदि f : R → R जहाँ f(x) = 5x – 7, ∀x ∈ R तो f^-1(7) का मान ………………………….. होगा।
3. यदि f : R → R तथा f(x) = x² – 3x + 2 से परिभाषित है, तो f(f(x)) का मान …………………………….. होगा।
4. यदि f : R → R; f (x) = 2x + 5 द्वारा परिभाषित है तब f^-1(y) का मान …………………………….. होता है।
5. f(x) = x³ द्वारा प्रदत्त फलन f : R → R …………………………. है।

उत्तर:

1. 2
2. 0
3. x⁴ – 6x³ + 10x² – 3x
4. \(\frac{1}{2}\) (y-5)
5. एकैकी है।

प्रश्न 3.
निम्न कथनों में सत्य/असत्य बताइए –

1. माना कि समुच्चय A = {1, 2, 3} पर एक सम्बन्ध R= {(1, 3), (3, 1), (3, 3)} है। तब R सममित, संक्रामक है, किन्तु स्वतुल्य नहीं है।
2. यदि f : A → B एकैकी आच्छादक फलन हो, तो f का प्रतिलोम f^-1 अद्वितीय होता है।
3. फलनों का संजोयन क्रमविनिमेयी होता है।
4. प्रत्येक फलन व्युत्क्रमणीय होता है।
5. माना कि समुच्चय Q⁺ पर एक द्विआधारी संक्रिया ^*, a * b = \(\frac{ab}{3}\), ∀a, b ∈ Q⁺ से परिभाषित है, तब 4 * 6 का प्रतिलोम \(\frac{9}{8}\) है।

उत्तर:

1. असत्य
2. सत्य
3. असत्य
4. असत्य
5. सत्य।

प्रश्न 4.
एक शब्द/वाक्य में उत्तर दीजिए –

1. समुच्चय A = {a, b, c} पर तत्समक संबंध लिखिए।
2. फलन f(x) = \(\frac { \left| x-1 \right| }{ x-1 } \) का परिसर क्या है?
3. फलन f(x) = \(\sqrt { 25-x^{ 2 } } \) से परिभाषित वास्तविक फलन का प्रान्त लिखिए।
4. माना कि एक द्विआधारी संक्रिया *, a * b = 3a + 4b – 2 से परिभाषित है तब 4 * 5 ज्ञात कीजिए।
5. माना कि f.g: R → R क्रमशः f(x) = 2x +1 और g(x) = x² – 2, ∀x ∈ R से परिभाषित है। तब gof (x) ज्ञात कीजिए।

उत्तर:

1. {(a, a), (b, b), (c, c)}
2. {-1, 1}
3. [-5, 5]
4. 30
5. 4x² + 4x – 1.

संबंध एवं फलन दीर्घ उत्तरीय प्रश्न – I

प्रश्न 1.
सिद्ध कीजिए कि पूर्णांकों के समुच्चय z में R = { (a, b ) : संख्या 2, (a – b) को विभाजित करती है } द्वारा प्रदत्त संबंध एक तुल्यता संबंध है। (NCERT)
हल: समस्त a ∈ Z के लिए 2,(a – a) को विभाजित करेगा अर्थात् (a, a) ∈ R अत: R स्वतुल्य है।
माना (a,b) ∈ R ⇒ 2, (a – b) को विभाजित करता है
⇒ 2,- (b – a) को विभाजित करता है
(a,b) ∈ R ⇒ (b,a) ∈ R
अत: R, सममित है।
माना (a,b) ∈ R = 2,(a – b) को विभाजित करता है।
(b, c) ∈ R → 2,(b – c) को विभाजित करता है।
a – b तथा b – C, 2 से भाज्य है
a – b + b – c, भी 2 से भाज्य है
अर्थात् a – c भी 2 से भाज्य है
इसलिए (a,b) ∈ R, (b,c) ∈ R ⇒ (a,c) ∈ R
अत: R संक्रमक है। अतः R, स्वतुल्य, सममित तथा संक्रमक है अतः यह एक तुल्यता संबंध है। यही सिद्ध करना था।

प्रश्न 2.
मान लीजिए कि समुच्चय A = {1, 2, 3, 4, 5, 6, 7} में R = {(a, b): a तथा b दोनों ही या तो विषम है या सम है } द्वारा परिभाषित एक संबंध है। सिद्ध कीजिए कि R एक तुल्यता संबंध है। साथ ही सिद्ध कीजिए कि उपसमुच्चय {1, 3, 5, 7} के सभी अवयव एक-दूसरे से संबंधित हैं और उपसमुच्चय {2, 4, 6} के सभी अवयव एक-दूसरे से संबंधित हैं। परंतु उपसमुच्चय {1, 3, 5, 7} का कोई भी अवयव उपसमुच्चय {2, 4, 6} के किसी भी अवयव से संबंधित नहीं है। (NCERT)
हल: A का दिया गया कोई अवयव a या तो विषम है या सम है अतः (a, a) ∈ R अत: R स्वतुल्य है।
माना (a,b) ∈ R ⇒ a तथा b दोनों ही या तो विषम है या सम है।
⇒ b तथा a दोनों ही या तो विषम है या सम है।
(a,b) ∈ D (b, a) ∈ R
अत: R सममित है।
(a,b) ∈ R तथा (b, c) ∈ R ⇒ अवयव a, b, c सभी या तो विषम हैं या सम हैं।
(a,b) ∈ R तथा (b, c) ∈ R = (a,c) ∈ R
अत: R संक्रमक है।
यहाँ R, स्वतुल्य, सममित तथा संक्रमक है इसलिए R एक तुल्यता संबंध है। यही सिद्ध करना था।
पुनः {1, 3, 5, 7} के सभी अवयव एक – दूसरे से संबंधित हैं क्योंकि इस उपसमुच्चय के सभी अवयव विषम हैं।
इसी प्रकार {2, 4, 6} के सभी अवयव एक – दूसरे से संबंधित हैं क्योंकि ये सभी सम हैं साथ ही उपसमुच्चय {1, 3, 5, 7} का कोई भी अवयव {2, 4, 6} के किसी भी अवयव से संबंधित नहीं हो सकता क्योंकि {1, 3, 5, 7} के अवयव विषम हैं जबकि {2, 4, 6} के अवयव सम हैं।

प्रश्न 3.
माना कि N प्राकृत संख्याओं का समुच्चय है। यदि समुच्चय N × N में परिभाषित एक संबंध R ऐसा हो कि (a, b) R (c, d) यदि ad (b + c) = bc (a + d) तो सिद्ध कीजिए कि R एक तुल्यता संबंध है। (CBSE 2015)
हल: स्वतुल्यता: प्रत्येक (a, b) ∈ N × N के लिए
ab (b + a) = ba (a + b)
⇒ (a, b) R (a, b)
अत: R स्वतुल्य होगा।
सममितता: माना (a, b)(c, d) ∈ N × N
(a, b) R (c, d) ⇒ ab(b + c) = bc(a + d)
⇒ bc (a + d) = ab (b + c)
(a,b) R (c,d) ⇒ (c, d) R (a, b)
अत: R सममित होगा।
उत्तर संक्रमकता: माना (a, b) R (c, d ) तथा (c, d) R (e, f)
⇒ ad ( b + c) = bc (a + d)
तथा cf (d + e) = de (c + f)

⇒ af (b + e) = bc (a + f)
(a, b) R (c, d) तथा (c, d) R (e, f) ⇒ (a, b) R (e, f)
अत: R संक्रमक है।
R, स्वतुल्य, सममित तथा संक्रमक है अत: R एक तुल्यता संबंध है। यही सिद्ध करना था।

प्रश्न 4.
माना A = {1, 2, 3, 4, 5} तथा R = {(a,b): |a – b| 2 से विभाजित है} तो सिद्ध कीजिए कि R एक तुल्यता संबंध है तथा तुल्यता वर्ग भी बनाइए।
हल: A = { 1, 2, 3, 4, 5 }
R = { (a, b) : |a – b| 2 से विभाजित है }
R = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (1, 3), (1, 5), (2, 4), (3, 5), (3, 1) (5, 1), (4, 2),(5, 3)}
∀ a ∈ A (a,a) ∈ R
इसलिए R स्वतुल्य होगा।
क्योंकि (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) ∈ R
(a,b) ∈ R ⇒ (b,a) ∈ R
(1, 3), (1, 5), (2, 4), (3, 5), (3, 1), (5, 1), (4, 2), (5, 3) ∈ R
इसलिए R सममित है।
∀ (a, b) ∈ R,(b, c) ∈ R ⇒ (a, c) ∈ R
क्योंकि (1, 3)(3, 1) ∈ R = (1, 1) ∈ R
R संक्रमक है।
R, स्वतुल्य, सममित तथा संक्रमक है इसलिए R एक तुल्यता संबंध है।
यही सिद्ध करना था।
तुल्यता वर्ग
[1] = { a : a तथा 2 |a – 1| से विभाजित है}
[1] = {a : a ∈ A तथा a – 1 = 2 k}
[1] = {1, 3, 5}
[2] = { a : a तथा 2, |a – 2| से विभाजित है}
[2] = {a : a तथा a – 2 = 2k}
[2] = {2, 4}.

प्रश्न 5.
मान लीजिए कि समस्त n ∈ N के लिए।

द्वारा परिभाषित एक फलन f : N → N है। बताइए कि क्या फलन f एकैकी आच्छादक है। अपने उत्तर का औचित्य भी बताइए। (NCERT)
हल: f : N → N में,

यहाँ f (1) = f (2) ⇒ 1 ≠ 2
डोमेन के दो अवयव 1 और 2 का सह – डोमेन में एक ही प्रतिबिम्ब 1 है।
अत: f एकैकी फलन नहीं है।

स्थिति I.
जब n विषम हो
n = 2r + 1, r ∈ N
तब 4r + 1 ∈ N इस प्रकार विद्यमान है कि
f (4r + 1) = \(\frac { 4r+1+1 }{ 2 } \) = \(\frac { 4r+2 }{ 2 } \) = 2r + 1
स्पष्ट है सह – डोमेन के प्रत्येक अवयव का डोमेन में पूर्व प्रतिबिम्ब है इसलिए / आच्छादक फलन है।

स्थिति II.
माना n = 2r (सम संख्या)
तब 4r ∈ N इस प्रकार विद्यमान है कि
f(4r) = \(\frac{4r}{2}\) = 2r
स्पष्ट है सह – डोमेन के प्रत्येक अवयव का डोमेन में पूर्व प्रतिबिम्ब है इसलिए f आच्छादक फलन है।
अतः f एकैकी आच्छादक फलन नहीं है।

प्रश्न 6.
मान लीजिए कि A = R – {3} तथा B = R – {1} है। f(x) = \(\frac { x-2 }{ x-3 } \) द्वारा परिभाषित फलन f : A → B पर विचार कीजिए। क्या f एकैकी तथा आच्छादक है? अपने उत्तर का औचित्य भी बताइए। (NCERT)
हल:
f : A → B, f (x) = \(\frac { x-2 }{ x-3 } \), A = R – {3} तथा B = R – {1}
मान लीजिए x, y∈A इस प्रकार है कि
f (x) = f (y)
⇒ \(\frac { x-2 }{ x-3 } \) = \(\frac { y-2 }{ y-3 } \)
⇒ (x – 2) (y – 3) = (y – 2) (x – 3)
⇒ xy – 3x – 2y + 6 = xy – 3y – 2x + 6
⇒ -3x – 2y = -3y – 2x
⇒ 3x – 2x = 3y – 2y
⇒ x = y
यहाँ f (x) = f (y) ⇒ x = y
अतः f एकैकी फलन है।
f आच्छादक फलन होगा यदि x∈A इस प्रकार विद्यमान है कि f(x) = y
\(\frac { x-2 }{ x-3 } \) = y
⇒ x – 2 = y (x – 3)
⇒ x – 2 = xy – 3y
⇒ xy – x = 3y – 2
⇒ x = \(\frac { 3y-2 }{ y-1 } \)∈A
प्रत्येक y ∈ B के लिए x ∈ A
f (x) = f ( \(\frac { 3y-2 }{ y-1 } \) )

∵ f(x) = y
अतः f अचधक पालन है।
अतः f एकोकी अचधक पालन है।

प्रश्न 7.
सिद्ध कीजिए कि नीचे परिभाषित फलन f : N → N एकैकी तथा आच्छादक दोनों ही।

हल: माना f (x₁) = f (x₂)
यदि x, विषम तथा x, सम है, तब
x₁ + 1 = x₂ – 1
X₁ – x₂ = -2
जो कि असंभव है।
इस प्रकार x₁ के सम तथा x₂ के विषम होने की संभावना नहीं है।
इसलिए x₁ तथा x₂, दोनों ही या तो सम होंगे या विषम होंगे।
माना x₁, x₂ दोनों विषम हैं।
f (x₁) = f (x₂)
⇒ x₁ – 1 = x₂ – 1
⇒ x₁ = x₂
अतः f एकैकी है।
सहप्रांत N की कोई भी विषम संख्या 2r + 1 प्रांत N की संख्या 2r + 2 का प्रतिबिंब है और सहप्रांत N की कोई भी सम संख्या 27, N की संख्या 2r – 1 का प्रतिबिंब है।
अतः f आच्छादक है। यही सिद्ध करना था।

प्रश्न 8.
f (x) = 4x + 3 द्वारा प्रदत्त फलन f: R → R पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है। f का प्रतिलोम फलन भी ज्ञात कीजिए? (NCERT)
हल: f : R → R, f (x) = 4x + 3
फलन का डोमेन तथा सह – डोमेन R है।
माना x, y ∈ R इस प्रकार है कि
f (x) = f (y)
4x + 3 = 4y + 3
⇒ 4x = 4y
⇒ x = y
इस प्रकार f (x) = f (y)
⇒ x = y
अतः f एकैकी है।
माना कि सह – डोमेन R का कोई अवयव y है
y = f (x)
y = 4x + 3
⇒ 4x = y – 3
⇒ x = \(\frac { y-3 }{ 4 } \)
∴ f^-1(y) = \(\frac { y-3 }{ 4 } \) तथा f^-1(x) = \(\frac { x-3 }{ 4 } \)

प्रश्न 9.
मान लीजिए कि y = {n² : n ∈ N}⊂N है। फलन f : N → y, जहाँ f (n) = n² पर विचार कीजिए। सिद्ध कीजिए कि व्युत्क्रमणीय है। का प्रतिलोम भी ज्ञात कीजिए। (NCERT)
हल:
y = f(n) = n²
n = \(\sqrt{y}\)
इससे g (y) = \(\sqrt{x}\) द्वारा परिभाषित फलन g : y → N प्राप्त होता है।
gof (n) = g [f (n)]
= g [n²]
= \(\sqrt { n^{ 2 } } \) [g(n) = \(\sqrt{n}\), g(n²) = \(\sqrt { n^{ 2 } } \) = n]
(gof) n = n
तथा
(fog)y = f [g(y)]
= f[ \(\sqrt{y}\) ], [f(n) = n², f( \(\sqrt{y}\) ) = ( \(\sqrt{y}\) )² = y]
= y
स्पष्ट है कि gof = I_n तथा fog = I_y
अतः f व्युत्क्रमणीय है तथा f^-1 = g.
यही सिद्ध करना था।

प्रश्न 10.
यदि f : R → R तथा g : R → R फलन क्रमशः f (x) = cosx तथा g(x) = 3x² द्वारा परिभाषित है, तो gof और fog ज्ञात कीजिए। सिद्ध कीजिए कि gof ≠ fog? (NCERT)
हल: दिया है: f(x) = cosx
g (x) = 3x²
(gof) x = g [f (x)]
(gof) x = g [cost]
दिया है:
f (x) = cosx ……………………….. (1)
g (x) = 3x²
g (cosx) = 3 cos²x ……………………………. (2)
समी. (1) और (2) से,
(gof )x = 3cos²x
(fog) x = f [g(x)]
= f [3x²] ………………………………… (3)
दिया है:
g (x) = 3x²
f (x) = cosx
f [3x²] = cos3x²
समी. (3) और (4) से,
(fog) x = cos3x²
x = 0 के लिए
3cos²x ≠ cos3x²
अतः gof ≠ fog. यही सिद्ध करना था।

प्रश्न 11.
f: {1,2,3} → {a,b,c}, f(1) = a, f(2) = b, f(3) = c द्वारा प्रदत्त फलन f पर विचार कीजिए-ज्ञात कीजिए ओर सिद्ध कीजिए कि (f^-1)^-1 = f है। (NCERT)
हल: दिया गया है:
f: {1, 2,3} → { a, b, c}
f(1) = a, f (2) = b, f (3) = c
माना g : { a, b, c } → {1, 2, 3} में
g (a) = 1, g (b) = 2, g (c) = 3
(fog) a = f [g (a)]
= f [1] = a
(fog) b = f [g (b)]
= f (2) = b
(fog) c = f [g (c)]
= f (3) = c
तथा (gof) (1) = g [f (1)]
= g (a) = 1
(gof) (2) = g [f(2)]
= g (b) = 2
(gof) (3) = g [f (3)]
= g (c) = 3
अत: gof = I_x, तथा fog = I_y
जहाँ x = {1, 2, 3} तथा y = {a, b, c}
f का प्रतिलोम विद्यमान है तथा।
तथा f^-1 = g
∴ f^-1 {a, b, c} → {1, 2, 3} में,
f^-1 (a) = 1, f^-1(b) = 2, f^-1(c) = 3
अतः f^-1 का प्रतिलोम अथरिथ का प्रतिलोम जात करेंगे
माना h: {1, 2, 3} → {a, b, c}
h(1) = a, h(2) = b, h(3) = c
(goh) 1 = g[h(1)] = g(a) = 1
(goh) 2 = g[h(2)] = g(b) = 2
(goh) 3 = g[h(3)] = g(c) = 3
तथा (hog) a = h[g(a)] = h(1) = a
(hog) b = h [ g(b)] = h(2) = b
(hog) c = h[g(c)] = h(3) = c
अत: goh = I_x तथा hog = I_y
जहाँ x = {1, 2, 3} तथा y = {a, b, c}
g का प्रतिलोम विद्यमान है तथा g^-1 = h = (f^-1)^-1 = f
अत: h = f
∴ (f^-1)^-1 = f यही सिद्ध करना था।

प्रश्न 12.
सिद्ध कीजिए कि समस्त बहुभुजों के समुच्चय A में R = { (P₁, P₂ ) : P₁ तथा P₂ की भुजाओं की संख्या समान है।} प्रकार से परिभाषित संबंध R एक तुल्यता संबंध है। 3, 4 और 5 की भुजाओं वाले समकोण त्रिभुज से संबंधित समुच्चय A के सभी अवयवों का समुच्चय ज्ञात कीजिए। (NCERT)
हल: दिया है:
A = समस्त बहुभुजों का समुच्चय
R = {(P₁, P₂) : P₁, तथा P₂ की भुजाओं की संख्या समान है।
प्रत्येक बहुभुज P में भुजाओं की संख्या, बहुभुज P की भुजाओं की संख्या के बराबर है।
∴ (P, P) ∈ R, ∀P∈A
माना (P₁,P₂)∈R ⇒ बहुभुज P₁ तथा P₂ मे भुजाओं की संख्या समान हैं।
⇒ बहुभुज P₂ तथा बहुभुज P₁ में भुजाओं की संख्या समान हैं।
अत: R संक्रमक संबंध है।
R, स्वतुल्य, सममित तथा संक्रमक है।
अतः R एक तुल्यता संबंध है।
भुजाओं 3, 4 तथा 5 वाले समकोण त्रिभुज से वह बहुभुज संबंधित होगा जिसमें भुजाओं की संख्या तीन होगी। इसलिए भुजाओं 3, 4 तथा 5 वाले समकोण त्रिभुज से संबंधित बहुभुज त्रिभुज है। यही सिद्ध करना था।

प्रश्न 13.
यदि f(x) = \(\frac { 4x+3 }{ 6x-4 } \), x ≠ \(\frac{2}{3}\) हो, तो सिद्ध कीजिए कि सभी x ≠ \(\frac{2}{3}\) के लिए fof(x) = xहै। f का प्रतिलोम फलन क्या है? (NCERT)
हल:
f (x) = \(\frac { 4x+3 }{ 6x-4 } \)
fof (x) = f {f (x)}
f{ \(\frac { 4x+3 }{ 6x-4 } \) }

माना f का प्रतिलोम फलान f^-1(x) = y हैं।
तब f (y) = x
∴ \(\frac { 4y+3 }{ 6y-4 } \) = x
⇒ 4y + 3 = 6xy – 4x
⇒ 6xy – 4y = 3 + 4x
⇒ y (6x – 4) = 3 + 4x
⇒ y = \(\frac { 3+4x }{ 6x-4 } \)
⇒ f^-1 (x) = \(\frac { 3+4x }{ 6x-4 } \) = f(x)
∴ f^-1 = f.

प्रश्न 14.
सिद्ध कीजिए कि f : [-1, 1] → R, f (x) = \(\frac { x }{ x+2 } \) द्वारा प्रदत्त फलन एकैकी है। फलन f : [-1, 1] → (f का परिसर) का प्रतिलोम फलन ज्ञात कीजिए। (NCERT)
हल: f (x) = \(\frac { x }{ x+2 } \)
f : [-1, 1] → R
यहाँ, f (x) = f (y)
⇒ \(\frac { x }{ x+2 } \) = \(\frac { y }{ y+2 } \)
⇒ xy + 2x = xy + 2y
⇒ 2x = 2y
⇒ x = y यही सिद्ध करना था।
∴ f एकैकी है।
माना f^-1 (x) = y
∴ f (y) = x
⇒ \(\frac { y }{ y+2 } \) = x
⇒ y = xy + 2x
⇒ y (1 – x) = 2x
∴ y = \(\frac { 2x }{ 1-x } \)
⇒ f^-1(x) = \(\frac { 2x }{ 1-x } \)

प्रश्न 15.
यदि f (x) = \(\frac { x }{ 1+|x| } \), ∀ x ∈ R जहाँ -1 < x < 1, तो gof तथा fog ज्ञात कीजिए। दिखाइए कि fog = gof?
हल: दिया है,
f (x) = \(\frac { x }{ 1+|x| } \)
g (x) = \(\frac { x }{ 1-|x| } \)
∴ fog (x) = f {g(x)}
= f ( \(\frac { x }{ 1-|x| } \) )

= x ………………….. (2)
fog = gof
यही सिद्ध करना था।

प्रश्न 16.
तीन फलन f : N → N, g : N → N तथा h : N → R पर विचार कीजिए f (x) = 2x, g (y) = 3y + 4, तथा h (z) = sin z ∀ x, y तथा z ∈ N सिद्ध कीजिये की ho(gof)n = (hog)of? (NCERT)
हल:
ho(gof) x = h[gof(x)]
= h {g[f(x)}
= h (g (2x))
= h [3(2x) + 4]
= h [6x + 4]
= sin (6x + 4) ………………………… (1)
इसी प्रकार ((hog)of) x = (hog) f(x)
= (hog) 2x
= h (g (2x))
= h [3 (2x) + 4]
= h [6x + 4]
= sin (6x + 4)
समी, (1) और (2) से स्पस्ट है की
ho(gof) = (hog)of. यही सिद्ध करना था।

MP Board Class 12 Maths Important Questions

MP Board Class 12th Maths Important Questions Chapter 13 Probability

Probability Important Questions

Probability Objective Type Questions

Question 1.
Choose the correct answer:

Question 1.
A bag contains 5 brown and 4 white socks. A man drawn two socks from the bag. The probability that both are of the same colour is:
(a) \(\frac { 5 }{ 108 } \)
(b) \(\frac { 18 }{ 108 } \)
(c) \(\frac { 30 }{ 108 } \)
(d) \(\frac { 48 }{ 108 } \)
Answer:
(d) \(\frac { 48 }{ 108 } \)

Question 2.
A die is roiled three times. The probability of getting a larger number then the previous number each time is:
(a) \(\frac { 5 }{ 72 } \)
(b) \(\frac { 5 }{ 54 } \)
(c) \(\frac { 13 }{ 216 } \)
(d) \(\frac { 1 }{ 18 } \)
Answer:
(d) \(\frac { 1 }{ 18 } \)

Question 3.
It is given that the events A and B are such that P(A) = \(\frac{1}{4}\), P( \(\frac{A}{B}\) ) = \(\frac{1}{2}\) and P ( \(\frac{B}{A}\) ) = \(\frac{2}{3}\), then P(B) is:
(a) \(\frac{1}{3}\)
(b) \(\frac{2}{3}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{1}{6}\)
Answer:
(a) \(\frac{1}{3}\)

Question 4.
A coin is tossed 4 times. Probability of getting at least one head is:
(a) \(\frac{1}{16}\)
(b) \(\frac{2}{16}\)
(c) \(\frac{14}{16}\)
(d) \(\frac{15}{16}\)
Answer:
(d) \(\frac{15}{16}\)

Question 5.
The probability of A speaking a truth is \(\frac{4}{5}\) and that of B speaking a truth is \(\frac{3}{4}\) The probability that they will contradict each other in answering a fact is:
(a) \(\frac{3}{10}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{7}{20}\)
(d) \(\frac{2}{5}\)
Answer:
(c) \(\frac{7}{20}\)

Question 2.
Fill in the blanks:

1. P( \(\frac { A∪B }{ C } \) ) = P ( \(\frac{A}{C}\) ) + ……………………….
2. P(A∩B) = ………………….. or ………………………….
3. If A and B are two independent events then, P (A ∩ B) = ………………………………..
4. If A and B are two independent events then, P ( \(\frac{A}{B}\) ) = ……………………………….
5. If the probability of random variable X is P (X), then mean E (X) will be ……………………………..
6. If probability of random variable X is P(X), then variance Var (X) will be ……………………………

Answer:

1. P( \(\frac{B}{C}\) ) – P ( \(\frac { A∩B }{ C } \) )
2. P(B).P ( \(\frac{A}{B}\) ) or P(A) . P ( \(\frac{B}{A}\) )
3. P(A).P(B)
4. P(A), P(B) ≠ 0
5. ΣX.P(X)
6. ΣX².P(X) – [ΣX.P(X)]².

Question 3.
Write True/False:

1. If A and B are any two events, then P (A – B) = P(A) – P (A∩B).
2. If A and B are any two events, then P (A ∪ B) – P (A∩B) = P(A) + P(B).
3. P( \(\frac{A}{B}\) ) = \(\frac { P(A∩B) }{ P(A) } \).
4. If A and B are any two events of a sample space S and F is another event such that P(F) ≠ 0, then P ( \(\frac { P(A∪B) }{ P(F) } \) ) = P ( \(\frac{A}{F}\) ) + P ( \(\frac{B}{F}\) ) – P ( \(\frac { P(A∪B) }{ P(F) } \) )
5. For any two events A and B. P (A∪B) = P (A∩B ) + P ( \(\bar { A } \) ∩ B) + P (A ∩\(\bar { B } \) )

Answer:

1. True
2. False
3. False
4. True
5. True.

Question 4.
Write the answer in one word/sentence :

1. Find the probability that a leap year has 53 Friday.
2. A coin is tossed 4 times. Find the probability of getting at least one head.
3. It is given that the events A and B are such that P (A) = \(\frac{1}{4}\), P ( \(\frac{A}{B}\) ) = \(\frac{1}{2}\) and P ( \(\frac{B}{A}\) ) = \(\frac{2}{3}\), then find the value of P(B).
4. There are 5 letters and 5 addressed envelops. If the letters are placed at random what is the probability that exactly 3 letters are placed in right envelops?
5. A problem in mathematics is given to 3 students whose chance of solving it are \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\). What is the probability that the problem is solved?

Answer:

1. \(\frac{2}{7}\)
2. \(\frac{15}{16}\)
3. \(\frac{1}{3}\)
4. \(\frac{1}{12}\)
5. \(\frac{3}{4}\)

Probability Short Answer Type Questions

Question 1.
(A) Two dice are thrown simultaneously. Find the probability of getting a sum?
Solution:
When two dice are thrown simultaneously.
n(S) = 6² = 36.
Sample space of getting a sum 8 is
A = {(2, 6); (6, 2); (5, 3); (3, 5); (4, 4)}
∴ n(A) = 5
∴ Required probability
P(A) = \(\frac { n(A) }{ n(S) } \) = \(\frac{5}{36}\).

(B) Two cubical dice are thrown simultaneously. Find the probability of getting a sum of 9?
Solution:
Solve as Q.No. 1 (A)

(C) Two cubical dice are thrown simultaneously. Find the probability of getting a sum of 7?
Solve as Q.No. 1 (A)

Question 2.
The odds against happening of an event is 3 : 4? Find the probability of its failing?
Solution:
The odds against the happening of an event = 3 : 4
∵ Probability of its failing P ( \(\bar { A } \) ) = \(\frac { b }{ a+b } \)
⇒ P ( \(\bar { A } \) ) = \(\frac { 4 }{ 3+4 } \) = \(\frac { 4 }{ 7 } \).

Question 3.
A card is drawn from a pack of 52 cards. Find the probability that its face?
Solution:
Here, n(S) = 52
∵Cards having face = 4 knave + 4 queens + 4 kings
∴ n(A) = 4 + 4 + 4 = 12
Required probability P(A) = \(\frac { 12 }{ 52 } \) = \(\frac { 3 }{ 13 } \)

Question 4.
What is the probability that a leap year selected at random will contain 53 Sundays?
Solution:
A leap year consists of 366 days. It has 52 complete weeks and 2 days extra. The equally likely cases for the occurrence of these extra days are:

1. Monday and Tuesday,
2. Tuesday and Wednesday,
3. Wednesday and Thursday,
4. Thursday and Friday,
5. Friday and Saturday,
6. Saturday and Sunday,
7. Sunday and Monday.

Out of these 7 exclusive cases, the last two cases are favourable.
∴ n(S) = 7 and n(E) = 2
∴ The required probability = \(\frac { n(E) }{ n(S) } \) = \(\frac{2}{7}\).

Question 5.
The probability of the horse A of winning a race is \(\frac{1}{4}\) and the probability of the horse B winning the same race is \(\frac{1}{8}\)? What is the probability that one of the horse will win the race?
Solution:
Given, P(A) = Probability of winning the horse A = \(\frac{1}{4}\)
and P(B) = Probability of winning the horse B = \(\frac{1}{8}\)
Since, the events of winning the race by A and B are mutually exclusive, therefore
P(A∪B)= P(A) + P(B)
\(\frac{1}{4}\) + \(\frac{1}{8}\) = \(\frac{2+1}{8}\) = \(\frac{3}{8}\).

Question 6.
(A) A card is drawn from an ordinary pack of cards, find the probability of getting a king or a spade?
Solution:
Let the event A denotes the event of drawing a king and B of drawing a spade. Then we
n(S) = 52, n(A) = 4, n(B) = 13, n(A∩B) = 1
[Since there are 4 kings in pack of cards the cards of spade are 13 includes its king]
∴ P(A) = \(\frac { n(A) }{ n(S) } \) = \(\frac{4}{52}\), P(B) = \(\frac { n(B) }{ n(S) } \) = \(\frac{13}{52}\)
P(A∩B) = \(\frac{1}{52}\)
∴ P(A∪B)= P(A) + P(B) = P(A∩B )
= \(\frac{4}{52}\) + \(\frac{13}{52}\) – \(\frac{1}{52}\) = \(\frac{16}{52}\) = \(\frac{4}{13}\).

(B) A card is drawn from a pack of cards, find the probability that neither it is an ace nor a King?
Solution:
Total No. of King = 4, No. of ace = 4
And drawing one card from 8 cards = ⁸_C1
And drawing one card from 52 cards = ⁵²_C1
∴ P(A) = \(\frac { ^{ 8 }{ C_{ 1 } } }{ ^{ 52 }{ C_{ 1 } } } \)
∴ Probability of neither ace nor king = P( \(\bar { A } \) ) = 1 – P(A)
= 1 – \(\frac{2}{13}\) = \(\frac{11}{13}\)

Question 7.
(A) A dice is thrown once. Find the probability of getting even No. “or ” No. less than 5?
Solution:
When a dice is thrown once the sample space is
S = {1, 2, 3, 4, 5, 6}
n(S) = 6
E₁ = {2,4,6}, [∴ n(E₁) = 3]
E₁ = {1, 2, 3, 4}, [∴ n(E₂) = 4]
E₁∩E₂= {2, 4}, [∴ n(E₁ ∩E₂)
= \(\frac { n(E_{ 1 }) }{ n(S) } \) + \(\frac { n(E_{ 2 }) }{ n(S) } \) – \(\frac { n(E_{ 1 }\cap E_{ 2 }) }{ n(S) } \)
= \(\frac{3}{6}\) + \(\frac{4}{6}\) – \(\frac{2}{6}\) = \(\frac{7-2}{6}\) = \(\frac{5}{6}\).

(B) A pair of dice is thrown. Find the probability that the sum is not 9 or 11?
Solution:
Total number of ways in which 2 dice can be thrown = 6 × 6 = 36
n(S) = 36
Event of getting sum 9 = {(3, 6), (4, 5), (5, 4), (6, 3)}
Total No. = 4.
∴ Probability of getting sum 9 = \(\frac{4}{36}\) = \(\frac{1}{9}\)
Now event of getting sum 11 = {(5, 6), (6, 5)}
∴ Probability of getting sum 11 = \(\frac{2}{36}\) = \(\frac{1}{18}\)
Now probability of getting sum 9 or 11
P(A) = \(\frac{1}{9}\) + \(\frac{1}{18}\) = \(\frac{2+1}{18}\) = \(\frac{3}{18}\) = \(\frac{1}{6}\)
∴ probability of not getting sum 9 or 11
P( \(\bar { A } \) ) = 1 – P(A)
= 1 – \(\frac{1}{6}\) = \(\frac{6 – 1}{6}\) = \(\frac{5}{6}\).

Question 8.
If 3 coins are tossed simultaneously, then find the probability of getting at least one head?
Solution:
Here, n(S) = 2³ = 8
If \(\bar { A } \) A denotes not getting a head then A = {{T, T, T)}
∴ n( \(\bar { A } \) ) = 1
Probability of not getting a head P( \(\bar { A } \) ) = \(\frac { n(\bar { A) } }{ n(S) } \) = \(\frac{1}{8}\)
∴ Probability of getting at least one head P(A) = 1 – P( \(\bar { A } \) )
= 1 – \(\frac{1}{8}\) = \(\frac{7}{8}\)

Question 9.
A coin is tossed twice. Find the probability of getting head, both the times?
Solution:
Let the event of getting head in first throw be E₂ and the second throw be E₂.
∴ P(E₁) = \(\frac{1}{2}\) = P(E₂) = \(\frac{1}{2}\)
Both the events are independent
∴ P(E₁ ∩ E₂) = P(E₁) × P(E₂)
= \(\frac{1}{2}\) × \(\frac{1}{2}\)
∴ Probability of getting head both the times = P(E₁ ∩ E₂)
= \(\frac{1}{4}\)

Question 10.
In a given race, the odds in favour of three horses A, B and C are 1 : 2, 1 : 3 and 1 : 4. Find the chance that one of them will win the race?
Solution:
The probability of winning the horse, A = \(\frac { 1 }{ 1+2 } \) = \(\frac { 1 }{ 3 } \)
P(B) = The probability of winning the horse, B = \(\frac { 1 }{ 1+3 } \) = \(\frac { 1 }{ 4 } \)
P(C) = The probability of winning the horse, C = \(\frac { 1 }{ 1+4 } \) = \(\frac { 1 }{ 5 } \)
These events are mutually exclusive, therefore the probabilities of winning any one horses
= P(A) + P(B) + P(C)
= \(\frac{1}{3}\) + \(\frac{1}{4}\) + \(\frac{1}{5}\)
= \(\frac{20+15+12}{60}\) = \(\frac{47}{60}\)

Question 11.
A problem in mathematics is given to three students A, B and C whose chances of solving it are \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\) respectively. Find the probability that the problem will not be solved?
Solution:
The chances of A, B, C solving the problem are respectively
\(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\)
∴ The chances of A, B, C not solving the problem are respectively
1 – \(\frac{1}{2}\), 1 – \(\frac{1}{3}\), 1 – \(\frac{1}{4}\), i.e; \(\frac{1}{2}\), \(\frac{2}{3}\), \(\frac{3}{4}\)
∴ The probability that none of the students A, B, C is able to solve the probelm
= \(\frac{1}{2}\) × \(\frac{2}{3}\) × \(\frac{3}{4}\) = \(\frac{1}{4}\).

Probability Long Answer Type Questions – I

Question 1.
In Raipur 20% persons read English newspaper 40% persons read Hindi newspaper and 5% person read both. What percentage of persons are not read any newspaper?
Solution:
P(A) = The probability of reading English newspaper
= \(\frac{20}{100}\) = \(\frac{1}{5}\)
P(B) = The probability of reading Hindi newspaper
= \(\frac{40}{100}\) = \(\frac{2}{5}\)
P(A∩B) = The probability of reading both English and Hindi newpaper
= \(\frac{5}{100}\) = \(\frac{1}{20}\)
No. of persons not reading any newspaper

Question 2.
A speaks truth in 75% of the cases and B in 80% of the cases. In what percentage of cases are they likely to contradict each other in stating the same fact?
Or
Mohan speaks truth in 75% of cases. Sohan speaks truth in 80% of the cases. In what percentage of cases did the Mohan speaks truth and Sohan speaks lie (or when they contradict each other)?
Solution:
P(A) = Probability that A speaks the truth = \(\frac{75}{100}\) = \(\frac{3}{4}\)
and P(B) = Probability that B speaks the truth = \(\frac{80}{100}\) = \(\frac{4}{5}\)
∴ P( \(\bar { A } \) ) = Probability that A does not speak the truth = 1 – \(\frac{3}{4}\) = \(\frac{1}{4}\)
and P( \(\bar { A } \) ) = Probability that B does not speak the truth = 1 – \(\frac{4}{5}\) = \(\frac{1}{5}\)
It is clear that A and B will contradict each other if one of them speaks the truth and the other does not.
∴ P(A and B contradict) = P(A) P( \(\bar { B } \) ) + P( \(\bar { A } \) ) P(B)
= \(\frac{3}{4}\) × \(\frac{1}{5}\) + \(\frac{1}{4}\) × \(\frac{4}{5}\) = \(\frac{7}{20}\) = \(\frac{35}{100}\)
Hence, in 35% cases, A and B will contradict each other.

Question 3.
Prove that P(A) + P( \(\bar { A } \) ) = 1?
Solution:
In total a + b trails, if an events can happen in a ways and fails in b ways, when all of these ways being equally likely to occur, then the probability of happening of event A,
P(A) = \(\frac { a }{ a+b } \)
and probability of failing of event A,
P( \(\bar { A } \) ) = \(\frac { b }{ a+b } \)
Adding eqns. (1) and (2), we get
P(A) + P( \(\bar { A } \) ) = \(\frac { a }{ a+b } \) + \(\frac { b }{ a+b } \)
= \(\frac { a+b }{ a+b } \) = 1.
∴ P(A) + P( \(\bar { A } \) ) = 1. Proved.

Question 4.
If P(A) = \(\frac{1}{2}\), P(B) = \(\frac{1}{9}\) and P(A∩B) = \(\frac{1}{18}\), then find the value of following:

(i) P( \(\frac{A}{B}\) ),

(ii) P( \(\frac{B}{A}\) )

(iii) P(A∪B)

Solution:
Given: P(A) = \(\frac{1}{2}\), P(B) = \(\frac{1}{9}\) and P(A∩B) = \(\frac{1}{18}\)

Question 5.
A group of 10 children contains 6 boys and 4 girls. Three children are chosen at random from this group. Find the probability that this group chosen:

1. Does not contain any girl.
2. Contains at least one girl.

Solution:
Total number of children = 6B + 4G = 10
3 children out of total 10 may be chosen in ¹⁰_{C3 ways}

1. 3 boys out of 6 boys may be chosen in ⁶_C3 ways
∴ Required probability = \(\frac { ^{ 6 }C_{ 3 } }{ ^{ 10 }C_{ 3 } } \) = \(\frac{1}{6}\)

2. At least 1 girl may be taken as follows
2 boys + 1 girl, number of ways = ⁶_C2 × ⁴_C1
or 3 girls, number of ways = ⁴_{C3
Hence, the required probability}

Question 6.
4 cards are fallen down by one during the shuffling of the cards. Find the probability that one card is heart, the other is diamond, the third is spade and the fourth is a club?
Solution:
Number of cards = 52
The first can fall in 52 ways.
The favourable ways for the first card to be heart = 13
Probability = \(\frac{13}{52}\) = \(\frac{1}{4}\)
The number of remaining cards = 52 – 1 = 51
Another card can be fall in 51 ways.
The favourable ways for this card to be a spade = 13
Probability = \(\frac{13}{50}\)
Number of remaining cards = 50 – 1 = 49
∴ Probability = \(\frac{13}{49}\)
Therefore, by compound probability principle, required probability
= \(\frac{1}{4}\) × \(\frac{13}{51}\) × \(\frac{13}{50}\) × \(\frac{13}{49}\)

Question 7.
A problem of Maths is given to three students whose chances of solving it are \(\frac{1}{2}\), \(\frac{1}{3}\) and \(\frac{1}{4}\). What is the probability that the problem is solved by all?
Solution:
Let the probabilities of solving the question by the three students be P₁, P₂, P₃ respectively.
Then given that P₁ = \(\frac{1}{2}\), P₂ = \(\frac{1}{3}\), P₃ = \(\frac{1}{4}\)
∴ The probabilities of not solving the problem by them are
q₁ = 1 – p₁ = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
q₂ = 1 – p₂ = 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
and q₃ = 1 – p₃ = 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\)
∴ Probability that all of the three students do not solve the problem
= q₁q₂q₃
= 1 – \(\frac{1}{4}\) = \(\frac{3}{4}\).

Question 8.
A bag contains 6 red, 4 white and 5 blue balls. If balls are drawn one by one from bag and they are not replaced, then what is the probability of 1st red, 2nd white and 3rd blue?
Solution:
A bag contains 6 red (R), 4 white (W), 5 blue (B) balls.
Total No. of balls = 6 + 4 + 5 = 15
∴ Probability of 1st ball is red,
P(R) = \(\frac{6}{15}\)
Now total balls in the bag 15 – 1 = 14
∴ Probability of 2nd ball is white,
P(W) = \(\frac{4}{14}\)
Now the total No. of balls in bag 14 – 1 = 13
∴ Probability of 3rd ball is blue,
P(B) = \(\frac{5}{13}\)
Hence, required probability
= \(\frac{6}{15}\) × \(\frac{4}{14}\) × \(\frac{5}{13}\)
= \(\frac{2}{5}\) × \(\frac{2}{7}\) × \(\frac{5}{13}\) = \(\frac{4×1}{91}\) = \(\frac{4}{91}\)

Question 9.
A bag contains 6 red, 4 white and 6 blue balls. If balls are drawn one by one from bag without replacement, then what is the probability of drawing 1st ball red, 2nd ball white and 3rd ball blue?
Solution:
Solve as Q. No. 8.

Question 10.
Two cubical dice are thrown simultaneously. Find the probability that the first dice shows an even number or both the dice show the sum 9?
Solution:
Here (S) = 6 × 6 = 36
The events of getting an even number on the first dice is
E₁ = {(2, 1), (2,-2), (2, 3), (2,4), (2, 5), (2, 6), (4, 1), (4, 2), (4, 3), (4,4), (4, 5), (4, 6), (6, 1), (6, 2), (6, 3), (6,4), (6, 5), (6, 6)}
∴ n(E₁) = 18
The event of getting a total of 9 on the two dice is
E₂ = {(3,6), (4, 5), (5,4), (6, 3)}
∴ n(E₂) = 4 .
Also, E₁∩E₂
⇒ n(E₁∩E₂) = 2
∴ P(E₁) = \(\frac{18}{36}\), P(E₂) = \(\frac{4}{36}\) and P(E₁∩E₂) = \(\frac{2}{36}\)
∴ The required probability = P(E₁∪E₂)
= P(E₁) + P(E₂) – P(E₁∩E₂)
= \(\frac{18}{36}\) + \(\frac{4}{36}\) – \(\frac{2}{36}\) = \(\frac{20}{36}\) = \(\frac{5}{9}\)

Question 11.
Out of two bags one contains 3 black and 4 red balls and the second bag contains 8 black and 10 red balls. If one bag is chosen and a ball is drawn from it, then find the probability that is a red ball?
Solution:
I bag
3B + 4R = 7 balls total

II bag
8B + 10R = 18 balls total
(i) Selecting the I bag:
Probability that one bag is chosen (out of two bags) = \(\frac{1}{2}\)
1 red ball is drawn from I bag probability = \(\frac{4}{7}\)
Hence, the probability that the I bag is chosen as well as 1 red ball is drawn from it
(Compound event) P₁ = \(\frac{1}{2}\) × \(\frac{4}{7}\) = \(\frac{2}{7}\) ………………… (1)

(ii) If selecting II bag:
Probability that Il bag is chosen = \(\frac{1}{2}\)
I red ball is drawn from II bag probability = \(\frac{10}{18}\) = \(\frac{5}{9}\)
Hence, the probability that the II bag is chosen as well as 1 red ball is drawn from it
(Compound event) P₂ = \(\frac{1}{2}\) × \(\frac{5}{9}\) = \(\frac{5}{18}\) ……………………… (2)
The above two event are mutually exclusive.
Hence, only one event out of these two will happen.
Hence, the required probability P = P₁ + P₂
= \(\frac{2}{7}\) + \(\frac{5}{18}\)
= \(\frac{36+35}{126}\) = \(\frac{71}{126}\).

Question 12.
There are two bags, one contains 5 red and 7 white balls and second bag contains 3 red and 12 white balls. One ball is drawn from any of these bags at random? Find the probability that the ball is red?
Solution:
Solve same as Q. No. 11.

Question 13.
A bag contains 50 bolts and 150 nuts. Half of the bolts and nuts are rusted. If one item is taken out at random find out the probability that ¡ts rusted o is a bolt?
Solution:

Question 14.
A can hit a target 4 times in 5 shots; B, 3 times in 4 shots and C, 2 times 3 shoots at one time. Find the probability of at least two shots hit?
Solution:
Probability of A hitting the target = \(\frac{4}{5}\)
Probability of B hitting the target = \(\frac{3}{4}\)
Probability of C hitting the target = \(\frac{2}{3}\)
At least 2 can hit the target in the following ways:
(i) Probability that A, B,C all hit the target = \(\frac{4}{5}\) × \(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{2}{5}\)

(ii) Probability that B and C hit the target and not A
= ( 1 – \(\frac{4}{5}\) ) × \(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{1}{5}\) × \(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{1}{10}\)

(iii) Probability that C and A hit the target and not B
= \(\frac{4}{5}\) × (1 – \(\frac{3}{4}\) × \(\frac{2}{3}\) = \(\frac{4}{5}\) × \(\frac{1}{4}\) × \(\frac{2}{3}\)
= \(\frac{2}{15}\)

(iv) Probability that A and B hit the target but not C
= \(\frac{4}{5}\) × \(\frac{3}{4}\) × (1 – \(\frac{2}{3}\)) = \(\frac{4}{5}\) × \(\frac{3}{4}\) × \(\frac{1}{3}\) = \(\frac{1}{5}\)
Since, all these events are mutually exclusive,
∴ Required probability = \(\frac{2}{5}\) + \(\frac{1}{10}\) + \(\frac{2}{15}\) + \(\frac{1}{5}\) = \(\frac{5}{6}\)

Question 15.
In a class 30% students fail in physics, 25% fails in maths and 10% fails in both. If one student selects at random, then And the probability of:

(i) Fail in maths when fail in physics also,
(ii) Fail in physics when fail in maths also,
(iii) Fail in maths or physics.

Solution:
Probability of fail in physics is
P(A) = \(\frac{30}{100}\)
Probability of fail in maths is
P(B) = \(\frac{25}{100}\)
Probability of fail in physics and maths both is
P(A∩B) = \(\frac{10}{100}\)

Question 16.
Two bags A and B contain 8 green and 9 white balls and 5 green and 4 white balls respectively. One ball is drawn at random from one of the bags and it is found to be green. Find the probability that it is drawn from bag B? (NCERT)
Solution:
Let E₁ : Event of choosing bag A
∴ P(E₁) = \(\frac{1}{2}\) ………………………. (1)
E₂ = \(\frac{1}{2}\) ………………………… (2)
Again, let C: Event of drawing a green ball
∴ By defnition of conditional probability

The required probability (i.e; the probability of obtaining a ball from bag B when it is green.)

Question 17.
A company has two plants to manufacture bicycles. The first plant manufacture 60% of the bicycles and second plant 40%. Also 80% of the bicycles are rated standard quality at the first plant and 90% of standard quality at the second plant. A bicycle is picked up at random and found to be standard quality? Find the probability that it comes from the second plant? (CBSE 2003)
Solution:
Let E₁: The event of choosing a bicycle from first plant.
∴ P(E₁) = \(\frac{60}{100}\) ………………….. (1)
Let E₂: The event of choosing a bicycle from first plant.
P(E₂) = \(\frac{40}{100}\) ……………………….. (2)
Let E be event of choosing a bicycycle of standard quality, then
P ( \(\frac { E }{ E_{ 1 } } \) ) = Probability of choosing a bicycle of standard quality, given that it is produced by the first plant.
⇒ P ( \(\frac { E }{ E_{ 1 } } \) ) = \(\frac{80}{100}\), (given 80%)
P( \(\frac { E }{ E_{ 2 } } \) ) = Probability of choosing a bicycle of standard quality, given that it is produced by the second plant.
⇒ P( \(\frac { E }{ E_{ 2 } } \) ) = \(\frac{90}{100}\) (given 90%)
∴ The required probability (i.e., probability of choosing a bicycle from the second plant, given that it is of standard quality,

Question 18.
A company manufactures T.V., machine A, B and C manufatures 30%, 20% and 50% T.V. of the total production of their outputs 7%, 5% and 2% are defec¬tive T.V. respectively. A T.V. is selected at random from the production and is found to be defective?
Find the probability that defective T.V. which is manufactured by machine A? (CBSE 2015)
Solution:
Let the events T₁, T₂ and T₃ are the following:
Event T₁ : T.V. manufactured by machined A.
Event T₂ : T.V. manufactured by mechine B.
Event T₃: T.V. manufactured by machine C.
It is noted that these events are mutually exclusive.
Again, let E : The event of defective T.V.
Given, P(T₁) = 30% = \(\frac{30}{100}\) ………………….. (1)
P(T₂) = 20% = \(\frac{20}{100}\) ………………….. (2)
P(T₃) = 50% = \(\frac{50}{100}\) ………………….. (3)
Again P( \(\frac { E }{ T_{ 1 } } \) ) = The probability that T.V. is defective when it is manufactured by machine A.
⇒ P(\(\frac { E }{ T_{ 1 } } \) ) = 7% = \(\frac{7}{100}\)
P( \(\frac { E }{ T_{ 2 } } \) ) = The probability that T.V. is defective when it is manufactured by machine B.
⇒ P( \(\frac { E }{ T_{ 3 } } \) ) = 5% = \(\frac{5}{100}\)
Similarly,
P( \(\frac { E }{ T_{ 3 } } \) ) = The probability that T.V. is defective when it is manufactured by machine C.
⇒ P( \(\frac { E }{ T_{ 3 } } \) ) = 2% = \(\frac{2}{100}\)
Now, from Bayes’s theorem
P( \(\frac { T_{ 1 } }{ E } \) ) = The probability that T.V. is defective when it is manufactured by machine A.

Question 19.
The probability that Mohan does not speak the truth is \(\frac{1}{5}\) Mohan speaks the head when a coin is thrown, find the probability that really gettting head by the throw of a coin? (NCERT)
Solution:
Let A: The event of getting head.
P(A) = \(\frac{1}{2}\)
B: The event of not getting head.
∴ P(B) = 1 – P(B) = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
Again, Let E: The event that really getting head by the throw of a coin and Mohan speaks.
P( \(\frac{E}{B}\) ) = \(\frac{1}{5}\)
and P( \(\frac{E}{A}\) ) = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
Now, from Bayes’s thoerem
P( \(\frac{A}{E}\) ) = Probability that the report of the Mohan that head has occured is actually head.

Question 20.
Bag A contains 3 white and 4 red balls and bag B contains 5 white and 6 red balls. One ball is drawn at random from one of the bags and it is found to be red. Find the probability that it is drawn from bag B?
Solution:
Let E₁ = Event of choosing bag A.
E₂ = Event of choosing bag B.
P(E₁) = \(\frac{1}{2}\); P(E₂) = \(\frac{1}{2}\) ………………….. (1)
⇒ P(E₁) = P(E₂) = \(\frac{1}{2}\)
Again, let R = Event of drawing a red ball.
According to the question.
P( \(\frac { R }{ E_{ 1 } } \) ) = The probability that a red ball is drawn when it is selected from bag A.
⇒ P( \(\frac { R }{ E_{ 1 } } \) ) = \(\frac{4}{3+4}\) = \(\frac{4}{7}\) …………………. (2) [since bag A contains 3 white and 4 red balls]
P( \(\frac { R }{ E_{ 2 } } \) ) = \(\frac{6}{5+6}\) = \(\frac{6}{11}\) ……………….. (3) [since bag B contains 5 white and 6 red balls]
Now, from Bayes’s theorem,
P( \(\frac { E_{ 2 } }{ R } \) ) = The probability that a ball is drawn from bag B when it is red.

Question 21.
Three different bags A, B and C are given, each bag contains 2-2 books. Bag A contains both 2 mathematics books, bag B contains 2 chemistry books and bag C contains, one mathematics and one chemistry book. The student select one bag ran¬domly and from that bag he randomly take out one book. The book he has taken out is that of mathematics. Find the probability that the second book he draws out from that bag is also of mathematics or that he is selected bag A given? (NCERT)
Solution:
Let events E₁, E₂ and E₃ represents the selection of bag A, B and C respctively.
P(E₁) = P(E₂) = P(E₃) = \(\frac{1}{3}\) …………………….. (1)
D: The event of mathematics book happen
P( \(\frac { D }{ E_{ 1 } } \) ) = P(A mathematics book chosen from bag A)
= \(\frac{2}{2}\) = 1 ……………….. (2)
P( \(\frac { D }{ E_{ 2 } } \) ) = P(A mathematics book chosen from bag B)
= \(\frac{0}{2}\) = 0 ………………… (3)
[∵according to the questions, both chemistry books are in bag B]
P( \(\frac { D }{ E_{ 3 } } \) ) = P(A mathematics book chosen from bag C)
= \(\frac{1}{2}\)
Now, the required probability
P( \(\frac { E_{ 1 } }{ D } \) )
Now, by Bayes’ thoerem,
P( \(\frac { E_{ 1 } }{ D } \) )

Question 22.
By examining about a student that he is known to speak the truth 2 out of 5 times. He throws a die and reports that it is a six. Find the probability that it is actually a six?
Solution:
Let E: Event that the student reports that it is a six.
A : Event of getting a six on the upper face of die.
B : Event of not getting a six on the upper face of die.
∴ P(A) = \(\frac{1}{6}\) ………………….. (1)
P(B) = P(Not A) = P( \(\bar { A } \) )
⇒ P(B) = 1 – P(A) = 1 – \(\frac{1}{6}\)
⇒ P(B) = \(\frac{5}{6}\) ………………… (2)
P( \(\frac{E}{A}\) ) = Probability that the student reports that six occurs, when six has actually occured.
P ( \(\frac{E}{A}\) ) = Probability that the student speaks the truth
= \(\frac{2}{5}\) …………………… (3)
Now, P ( \(\frac{E}{B}\) ) = Probability that the student reports that six occurs, when six that has not actually occured.
P ( \(\frac{E}{B}\) ) = Probability that the student does not speak the truth.
P( \(\frac{E}{B}\) ) = 1 – \(\frac{2}{5}\) = \(\frac{3}{5}\)
Now, by Bayes’s thoerem
P( \(\frac{A}{E}\) ) = Probability of getting six, given that the student reports it to be six.

MP Board Class 12 Maths Important Questions

MP Board Class 12th Physics Important Questions Chapter 15 Communication Systems

Communication Systems Important Questions 

Communication Systems Objective Type Questions

Question 1.
Choose the correct answer of the following:

Question 1.
The elements of communication system are :
(a) One transmitter
(b) Only receiver
(c) Only communication channel
(d) All of the above.
Answer:
(d) All of the above.

Question 2.
Sound wave are not directly transmitted after converting them into electric signals because:
(a) They propagates with speed of sound
(b) Their frequency does not remain constant
(c) For their transmission very high antenna is needed
(d) Their energy is very high.
Answer:
(c) For their transmission very high antenna is needed

Question 3.
The super imposing of audio waves with carrier wave is called :
(a) Transmission
(b) Reception
(c) Modulation
(d) Defection.
Answer:
(c) Modulation

Question 4.
The frequency range used for T.V. transmission is :
(a) 30 – 300 MHz
(b) 30 – 300 GHz
(c) 30 – 300 KHz
(d) 30 – 300 Hz.
Answer:
(a) 30 – 300 MHz

Question 5.
The periodic time of communication satellite is :
(a) 1 year
(b) 1 day
(c) 12 hours
(d) 12 minutes.
Answer:
(b) 1 day

Question 6.
T. V. signals are reflacted by :
(a) Mesosphere
(b) Ionosphere
(c) Troposphere
(d) None of these.
Answer:
(d) None of these.

Question 7.
The short wave band of radio waves are transmitted through :
(a) Sky wave propagation
(b) Ground wave propagation
(c) Artificial satellite
(d) Direct sending from transmitter to receiver.
Answer:
(a) Sky wave propagation

Question 8.
T.V. network uses :
(a) Microwaves
(b) Radio waves of very high frequency
(c) Gamma rays
(d) X – ray.
Answer:
(b) Radio waves of very high frequency

Question 9.
The waves used in telecommunication are :
(a) Infrared rays
(b) UV – rays
(c) Microwaves
(d) Cosmic rays.
Answer:
(c) Microwaves

Question 2.
Fill in the blanks :

1. …………….. is that signal which varies periodically with time.
2. Digital signal is represented by two binary number …………….. and……………..
3. The range of audio signals is ……………..
4. The frequency of carrier waves is of order of ……………..
5. The order of frequency of radio waves which can be transmitted by total internal reflection through ionosphere is ……………..
6. The band width of AM waves is ……………..
7. The T.V. transmission was invented by……………..
8. WWW means ……………..
9. …………….. is a device with the help of which the location of any place can be obtained.

Answer:

1. Analog signals
2. 0 and 1
3. 20 Hz to 20000 Hz
4. MHz
5. 30 – 300 MHz
6. Frequency of modulating wave
7. J. L. Baird
8. World Wide Web
9. GPS.

Question 3.
Match the columns:
I.

Answer:

1. (e)
2. (d)
3. (b)
4. (c)
5. (a)

II.

Answer:

1. (e)
2. (c)
3. (d)
4. (b)
5. (a)

Question 4.
Write the answer in one word/sentence:

1. Write any two light sources which are used in optical communication?
2. On what principle does the optical fibre work?
3. Who invented the T, V. transmission?
4. What is FAX?
5. What is meant by channel width? Write channel width of AM and FM radio station.
6. What is demodulation or detection?

Answer:

1. Light emitting diode (LED) and Diode LASER
2. Total internal reflection
3. J. L. Baird
4. The electronic reproduction of a document at a distant place is known as facsimile telegraphy or FAX
5. Channel width is that frequency range in which signals can be transmitted from a station. The channel width of AM is 10
6. kHz and of FM is 150 kHz
7. The process of extracting the audio signal from the modulated wave is known as demodulation or detection.

Communication Systems Very Short Answer Type Questions

Question 1.
What is principle of semiconductor LASER?
Answer:
In these LASER Gallium Arsenide (Ga – As) is used. This LASER the ability to produce LASER rays in the range 0.75 to 0.9 um.

Question 2.
Why is a parallel wire line not suitable for microwave transmission?
Answer:
In microwave transmission, half the operating wavelength approaches the separation between the two parallel wire lines. Therefore energy loss in the form of radiation becomes maximum.

Question 3.
What do you understand by channel and channel noise?
Answer:
The frequency range prescribed for a given transmission is called channel. The unwanted signals present by known or unknown reason in the transmitted signal is called noise.

Question 4.
What is importance of modulation index?
Answer:
The modulation index determines the strength and quality of the transmitted signal. If the modulation index is small the amount of variation in the carrier amplitude will be small.

Question 5.
Write full form of LED and LASER.
Answer:
Full form of LED is “Light Emitting Diode”. Full form of LASER is “Light Amplification by Stimulated Emission of Radiations”.

Question 6.
Which device is used to transmit the T.V. signals up to long distances?
Answer:
Communication satellites are used to transmit the T.V. signals up to long distances.

Question 7.
What is a communication system?
Answer:
Communication system is that system through which the signals are transmitted from one place and required at the other place.

Question 8.
What are message signals?
Answer:
A message signal is a single valued function of time that conveys the information. The electrical analog of information or basic message is called message signal. These are obtained by suitable transducers.

Question 9.
What are analog signals?
Answer:
An analog signal is continuous single value which at any instant lies within the range of a maximum and minimum value.

Question 10.
What is a digital signal?
Answer:
Digital signal is a discontinuous signal value which appears in steps in predetermined levels rather than having the continuous change.

Question 11.
What is noise?
Answer:
Noise refers to the unwanted signals that tends to disturb the transmission and processing of message signals in a communication system.

Question 12.
What is modulation?
Answer:
Modulation is a process in which the signal of low frequency (audio signals) are superimposed over a signal of high frequency (carrier signal).

Question 13.
What is FAX?
Answer:
Fax is a type of communication in which an electronic copy of a document is sent to a distance place.

Question 14.
Which type of signal is used in communication through computer?
Answer:
Digital Signal.

Question 15.
Write basic difference between the light emitted by LED and LASER.
Answer:
The light emitted by LASER is completely coherent and monochromatic while the light emitted by the LED is not coherent.

Question 16.
What is bandwidth? What is bandwidth of audio signals?
Answer:
The frequency range of a signal is called its bandwidth. The bandwidth audio signals is 20 Hz to 20 KHz.

Communication Systems Short Answer Type Questions

Question 1.
Write name of two system used for pulse modulation.
Answer:

1. PAM : Pulse Amplitude Modulation.
2. PCM : Pulse Code Modulation.

Question 2.
Write name of two systems which are used to convert the digital data into analog data.
Answer:

1. Amplitude Shift Keying (ASK)
2. Phase Shift Keying (PSK).

Question 3.
FM signals are less sensitive as compared to AM signals. Why?
Answer:
In FM transmission the information (message) in the carrier waves is in the form ofvariation (change) in frequency. In the AM the noise get amplitude modulated. Hence the amplitude carrier wave varies. That is why the FM signals are less sensitive as compared to AM signals.

Question 4.
Write limitations of frequency modulation.
Answer:

1. Area of reception for FM is much smaller.
2. About 10 times wider channel is required by FM.
3. FM receivers and transmitters are very complex and costly.

Question 5.
Write the meaning of LASER and two uses.
Answer:
Meaning of LASER:
Light Amplification by stimulated Emission of Radiations.

Uses:

1. Communication and
2. The medical field to determine vary long distances.

Question 6.
Write any two uses of optical communication.
Answer:

1. It is free from noise.
2. Its bandwidth is large, so number of channels can be transmitted simultaneously.

Question 7.
What is Light Emitting Diode?
Answer:
It is forward biased P – N junction which emits the light. It converts electrical energy into light energy.

Question 8.
What is optical fibre? On what principle does it work?
Answer:
An optical fibre is a device with the help of which the optical signals can be transmitted over through a zig-zag path without loss of energy. It is based on principle of total internal reflection.

Question 9.
What is meant by population inversion and optical pumping?
Answer:
Population inversion:
The process by which the number of atoms are increased . in the excited state as compared to ground state by stimulated absorption, is called population inversion.

Optical pumping:
The process by which population inversion is obtained, is called optical pumping.

Question 10.
Give two characteristics of LASER rays.
Answer:

1. LASER rays are monochromatic.
2. These are highly coherent.

Question 11.
What are the elements of communication system? Explain with the help of block diagram and also describe the different kinds of communication system.
Or
What is communication system? What are its main parts? Explain with block diagram.
Answer:
Communication system is that system through which the signals are transmitted from one place and received at the other place.

Elements of communication system : Following are the elements of a communication system:

1. Transmitter : Its function is to transmit the information after modifying it, to a form suitable for transmission.
Block diagram of transmitter :

2. Communication channel : The free space through which the electromagnetic waves sent by the transmitter, reach the receiver is called communication channel. It may be a coupled wire, coaxial cable or radio wave.

3. Receiver : Its function is to receive information.
Block diagram of receiver:

Question 12.
What is noise? Why digital communication is popular? What are A/D and D/A converter?
Answer:
Noise : Noise is unwanted disturbance or foreign element interfering with the desired information or signal. Noise can come up in any part of the communnication system but it has its worst effect when the signal is weakest.

The digital communication is popular nowaday because of the following characteristics :

1. Its quality is good.
2. Digital signals are in the form of pulses, they can produce easily by using logic gates.
3. These signals do not get distorted by noise.
4. These signals can be stored as digital data.
5. In this transmission many information can be transmitted using one channel.

A/D and D/A converter:
The electric circuit which can convert the analog signal to digital signal is called A/D converter. The electric circuit which can convert the digital signal into analog signal is called D/A converter.

Question 13.
Write difference between Analog and Digital signals.
Answer:
Difference between Analog and Digital signals :

Analog signal:

• In this signal value of current or voltage changes continuously with time.
• It is a continuous function of time.
• A simple analog signal is represented by a sine wave.
• The signal obtained by converting a speech, music or intensity of reflected light are analog signals.

Digital signal:

• In these signals the current or voltage has only two descrete levels 0 and 1.
• It is discontinuous function of time.
• Digital signal is represented in the form of pulses.
• The letters of a book, output of digital computers or the information obtained from a FAX are digital signals.

Communication Systems Long Answer Type Questions

Question 1.
Explain need of modulation and define the term modulation.
Or
What is modulation? Why it is needed for the transmission of signals?
Answer:
Modulation:
Modulation is a process in which the signal of low frequency (audio signals) superimposed over a signal of high frequency (carrier signal). Such that same properties of carrier wave like amplitude, frequency or phase varies in accordance with the instantaneous value of audio signals.

Need of Modulation:
Modulation is necessary for a low frequency signal when it is to be sent to a distant place so that the information may not die out in the way itself as well as for the proper identification of a signal and to keep the height of antenna small also.

For the transmission of electromagnetic waves the length of antenna should be of order of wavelength of the transmitted waves. Since, λ= \(\frac {c}{ ν}\) therefore the required length of antenna for the audible range should be equal to \(\frac { 3\times { 10 }^{ 8 } }{ 20,000 }\) = 1.5 x 10⁴m to \(\frac { 3\times { 10 }^{ 8 } }{ 20 }\) = 1.5 x 10⁷

This length of antenna is not possible in practical. Now if the waves of 300kHz or more than it are to be transmitted then the required length of antenna will be \(\frac { 3\times { 10 }^{ 8 } }{ 3,00,000 }\) = 100 m or less than it. The antenna of this size can be constructed easily. Hence to transmit the audio signals they are superimposed with the radio waves of frequency of order of Mega Hertz. These waves are called carrier waves and this process is called modulation.

Question 2.
How many types of modulation are there? Explain each types of modula-tion.
Answer:
The equation of carrier wave is given as :
e_c = E_c. cos (ω_ct + θ)
Where e_c is instantaneous value of carrier signal. E_c is amplitude of carrier wave, ω_c is angular frequency and θ is phase angle. Thus, there are three types of modulation corresponding to E_c, m_c and θ.

1. Amplitude modulation:
When an audio frequency (modulating) signal is superimposed that the amplitude of modulated wave is linear function of instantaneous value of modulating signal, then this type of modulation is called as amplitude modulation.

2. Frequency modulation:
Frequency modulation is that modulation in which the frequency of carrier wave varies in accordance with the instantaneous value of modulating signal. In this modulation the amplitude and phase of modulating signal are equal to that of carrier wave.

3. Phase Modulation:
In the phase modulation, the modulating waves are super imposed with carrier waves such that the phase of the modulated wave is the linear function of the amplitude of the modulating wave but the frequency and amplitude of the modulated signal remains same as the frequency and amplitude of the carrier wave.

Question 3.
What are limitations of amplitude modulation?
Answer:
The limitations (disadvantages) of amplitude modulation are as follows :

1. Efficiency of Amplitude modulation is smaller:
In AM modulation the message signals are contained in side bands, but not contained in the carrier wave. It is found that in amplitude modulation only one third power is contained inside bands, remaining power is contained in carrier wave. Hence efficiency decreases.

2. Amplitude modulation is more likely to suffer from noise.

3. In Amplitude modulation the fidelity of reception is less:
The range of audio signal is 20 Hz to 20 kHz. Hence the bandwidth must be 40 kHz. But the disturbance created by the nearby radio station should be taken into account and hence the bandwidth is kept only of about 20 kHz.

4. Its transmission range is low. Due to less power it is not possible to transmit the signals up to long distance. Inspite of these limitations the AM is mostly used for the transmission of audio signals.

Question 4.
Write advantages and disadvantages of frequency modulation.
Answer:
Advantages:

1. Frequency modulation is inherently and practically free from the effects of noise.
2. In frequency modulation, noise can further be decreased by increasing the deviation 8.
3. FM receiver can further be improved with the help of limiters to remove amplitude changes, if any which controls the noise level.
4. In FM it is possible to operate many independent transmitters on same frequency without interference.

Disadvantages:

1. A bout 10 times wider channel is required by FM.
2. Area of reception for FM is much smaller.
3. FM receivers and transmitters are very complicated and costly.

Question 5.
Explain the data transmission and retreival with the help of block diagram.
Answer:
The important use of data transmission and retrieval is in the microprocessor and computers. All the informations and signals which are to be transmitted are converted into digital signals by coding, which are then modulated with the carrier signals and are sent to far distant places. These signals are received by receivers. These received signals are amplified and demodulated in their original form. The block diagram of this process is shown in fig.

Question 6.
What is FAX machine? Draw its block diagram and explain its working.
Answer:

1. FAX : The electronic reproduction of a document at a distant place is known as facsimile telegraphy or Fax. To send the document through FAX following functions are performed.

• Optical scanning
• Conversion of data for transmission and reception.
• Printing a copy of images of the original document at the receiving end.

The block diagram of working of FAX is shown in fig.

Question 7.
Write notes on ‘MODEM’.
Or
What is MODEM? Write its working and uses.
Answer:
The block diagram of a modem is shown ahead : A modem is basically a modulator and a demodulator circuit.

Working:
At the transmitting end i.e., at section A, a modem change the digital data (obtained from source) into analogue form in audio frequency range.

So, it is easily modulated and transmitted by communication network through telephone lines and transmitter and sent to receiver for section B. At the receiving end i.e., at sermon B, the modem converts the analogue signal to digital signal.

Uses : It is used for short distance communication by connecting one computer to another through telephone lines.

Kinds of MODEM : MODEM are of two types.

• Internal MODEM : These are internally attached in the computer.
• External MODEM : These are connected externally with the computer.

Question 8.
Describe the following in short:

1. E – mail
2. Internet
3. World Wide Web
4. Celular phone
5. Pager.

Answer:
1. E – mail:
Its full form is electronic mail the message produced by using word processing, programs are transmitted over the world wide network called internet and they get stored in a computer called mail server. Any person connected to the internet can contact mail server. Any person connected to the internet can contact the mail server to check whether it is holding mail for him.

2. Internet:
Internet is a world wide network which connects the millions of computers which are linked together for data transmission. It is a global system of inter connected computer networks.

3. World Wide Web:
Its abreviation is WWW. It was invented by Tim Berners Lee in 1989 – 91 which is highly enlarged encylopedia which is accessible to every one for knowledge.

4. Celular Phone:
It is basically mini wireless phones for exchanging messages as well as for mobile telephonic conversation.

5. Pager:
It is a wireless device which records the messages in writing.

Question 9.
What is line communication? Explain.
Answer:
In a communication system the communication channel is a medium which provides the physicals path between transmitter and receiver. There are two types of communication medium:

1. Guided medium:
This medium connects transmitter and receiver in the case of point to point communication, double line cable, coaxial cable and optical fibre are the examples of guided medium.

2. Unguided medium:
This medium connects one transmitter and many receivers. Sky wave communication is an example of this medium. Its band frequency rays from few thousand kHz to few GHZ.

In the sky wave communication there is no point to point connection between transmitter and antenna. But in some communication applications the point to point connection is needed for example in telephone and telegraph the transmitter and receiver are connected by wire lines. It is called as line communication.

Question 10.
What is Global Positioning System (G.P.S.)? Write its applications.
Answer:
It is a space based satellite navigation system that provides users with accurate information on position time wherein the world even through the local streets and in all weather conditions.

To use GP.S. system of a satellite the user must have a GP.S. device fitted with transmitter and receiver for sending and receiving radio wave signal.

Applications of G.P.S

1. Navigation on land, water and air.
2. Keeping standard time all over the world.
3. Used in unmanned automatic vehicles movement and mobile telephony.
4. In desiging map of a location.

Communication Systems Numericals Questions

Question 1.
When there is 50% modulation the transmitter emits the 20 kW power calculate the power of carrier wave.
Solution:
Given : m_a = 50% = \(\frac {50}{100}\) = P_t = 20 kW = 20,000 W
Formula:

Question 2.
When a modulating of 500 Hz is given to a frequency modulation generator then it produces a frequency deviation of 2.25 kHz. Calculate modulation depth.
Solution:
Given : δ_max = 2.25 kHz = 2250 Hz, f_m = 500 Hz

Question 3.
The maximum and minimum amplitude of a amplitude modulated wave are 16 mV and 4 mV. What is the depth of modulation?
Solution:
Given : E_max = 16mV, E_min = 4mV
Formula:

Question 4.
A 20 kHz modulating signal is modulated with a carrier wave of 4 MHz. What will be the upper side band and lower side band? What will be the channel width?
Solution:
Given: f_m = 20 kHz, f_c = 4 MHz =4,000 kHz
f_USB = f_c + f_m = 4000 + 20 = 4020 kHz.
f_LSB = f_c – f_m= 4000 – 20 = 3980 kHz.
Channel width = f_USB – f_LSB
= 4020 – 3980 = 40 kHz.

Question 5.
Find out the modulation index of a frequency modulated wave whose modulating frequency is 2 kHz and maximum frequency deviation is 10 kHz.
Solution:
Given : f_m = 2 kHz and δ_max = 10 kHz
Formula : m_f = \(\frac { { \delta }_{ max } }{ { f }_{ m } }\)
m_f = \(\frac {10}{2}\) = 5

MP Board Class 12th Physics Important Questions

MP Board Class 12th Maths Important Questions Chapter 12 Linear Programming

Linear Programming Important Questions

Linear Programming Objective Type Questions

Question 1.
Choose the correct answer:

Question 1.
At which point the value of 3x + 2y is maximum under the constraints x + y ≤ 2, x ≥ 0, y ≥ 0:
(a) (0,0)
(b) (1.5, 1.5)
(c) (2, 0)
(d) (0,2).
Answer:
(c) (2, 0)

Question 2.
Variables of the objective function of linear programming problem are:
(a) negative
(b) zero or negative
(c) zero
(d) zero or positive.
Answer:
(d) zero or positive

Question 3.
Consider the inequalities x₁ + x₂ ≤ 3, 2x₁ + 5x₂ ≥ 10, x₁ ≥ 0, x₂ ≥ 0, which of the following points like in a feasible region:
(a) (2, 1)
(b) (4, 2)
(c) (2, 2)
(d) (1, 2).
Answer:
(d) (1, 2)

Question 4.
In linear constraints the maximum value of objective function will be:
(a) at centre of feasible region
(b) at (0,0)
(c) at one of the vertices of the feasible region
(d) at the vertex which is situated at maximum distance from (0,0).
Answer:
(c) at one of the vertices of the feasible region

Question 5.
Under constraints x – 2y ≤ 6, x + 2y ≥ 0, x ≤ 6 maximum value of P = 3x + 4y is:
(a) 16
(b) 17
(c) 18
(d) 19.
Answer:
(c) 18

Question 2.
Fill in the blanks:

1. The function whose maximum and minimum value is to be found subject to given linear constraints is called …………………………..
2. The maximum or minimum value of objective function is called …………………………..
3. The graph of x ≥ 0 is situated in the …………………… quadrant.
4. The process of doing certain specified step in a given order is called …………………………….
5. The common region determined by all constraints including the non – negative constraints x ≥ 0, y ≥ 0 of a linear programming problem is called the ……………………. for the problem.

Answer:

1. Objective function
2. Optimum value
3. First
4. Programming
5. Feasible region.

Question 3.
Match the Column:

Answer:

1. (b)
2. (a)
3. (d)
4. (c)
5. (f)
6. (e).

Question 4.
Write True/False:

1. If the variable x is such that its value lies between two fixed point a and b, then {x: a < x < b} is called closed interval.
2. The function whose maximum or minimum value is to be found is called objective function.
3. The set of values of the variables satisfying all constraints is called feasible solution of the problem.
4. If the feasible region is void, then the problem has bounded solution.
5. Graph of two or more than two equation is called linear inequation system.

Answer:

1. False
2. True
3. True
4. False
5. False.

Question 5.
Write the answer in one word/sentence:

1. Represent y ≤ – 2 graphically?
2. Represent 2x – 4 ≤ 0 graphically?
3. The graph of inequation x ≥ 0 and y ≥ 0 will be situated in which quadrant?
4. What word is used for the maximum or minimum value of the objective function?
5. P = 5x + 3y is an objective function. The coordinate of the vertices of feasible region are (3, 0), (12, 0), (0, 6). Write minimum value of objective function?

Answer:

1.
2.
3. First
4. Optimum value
5.15.

Linear Programming Long Answer Type Question – I

Question 1.
Find the maximum value of the function P = 2x + 3 y when the constraints are:
x ≥ 0, y ≥ 0,x + 2y ≤ 10; 2x + y ≤ 14?
Solution:
Because of the constraints x ≥ 0 and y ≥ 0, the graph of other linear inequation should be found on first quadrant only.

For x + 2y = 10, the table for values of x and y are given below:

For testing point (0, 0) the inequation x + 2y ≤ 10 therefore the region is towards origin 0 + 2 × 0 ≤ 10.
For 2x + y = 14 the table for the values of x and y are given below:

For origin (0, 0), 2x + y ≤ 14 is true because 2(0) + 0 ≤ 14. Therefore the region is towards the origin.
The required graph is the common region of the inequations shown by shaded portion OABD of the above graph whose vertices OABD the values of objective function P=2x + 3y is shown in the following table:

∴ The maximum value of P is 18 which is on point B (6, 2) for which x = 6, y = 2.

Question 2.
Find the minimum value of function P = x + y subject to constraints 3x + 2y ≥ 12, x + 3y ≥ 11, x ≥ 0, y ≥ 0?
Solution:
Because x ≥ 0, y ≥ 0 the graph of other constraints lies on first quadrant. They are
3x + 2y ≥ 12 ………………….. (1)
x + 3y ≥ 11 …………………… (2)

(i) For 3x + 2y = 12 the table for the values of x andy are given below:

(ii) For x + 3y = 11 the table for the values of x and y are given below:

The testing point (0, 0) does not satisfy both the inequations because
3 (0) +2 (0) ≥ 12 which is false
0 + 3(0) ≥ 11 which is false
Therefore the possible region in an open region whose vertices are A, B, D. The calculation of objective function according to the fundamental extreme point theorem is as below:

Therefore, minimum value of P is 5 when x = 2,y = 3.

Question 3.
Show graphically the fixed region by the inequations given below:
x ≥ 0, y ≥ 0, 2x + 5y ≤ 16, 2x + y ≤ 8?
and find the value of* andy for which the function P = 5x+ 4y has maximum value?
Solution:
2x + 5y ≤ 16 ……………………. (1)
and 2x + y ≤ 8 …………………………. (2)
\(\frac { 2x }{ 16 } \) + \(\frac { 5y }{ 16 } \) ≤ 1, [from inequation (1)]
⇒ \(\frac{x}{4}\) + \(\frac { y }{ \frac { 16 }{ 5 } } \) ≤ 1 ………………….. (3)
Similarly, \(\frac { 2x }{ 8 } \) + \(\frac { y }{ 8 } \) ≤ 1 [from inequation (2)]
⇒ \(\frac{x}{4}\) + \(\frac{y}{8}\) ≤ 1 ……………………….. (4)
The region x ≥ 0 and y ≥ 0 representing graphically the inequations (3) and (4),

Lines \(\frac{x}{4}\) + \(\frac{y}{8}\) = 1
and \(\frac{x}{4}\) + \(\frac { y }{ \frac { 16 }{ 5 } } \) = 1
Intersects each other at the point B(4, 2). Hence OABC is the region bounded by the lines, where the coordinates of the points O, A, B, C are 0 (0, 0), A (4, 0), B (3, 2), C (0, \(\frac{16}{5}\) ) respectively
On the vertices the value of P = 5x + 4y will be following:

From the above table the maximum, value of P is 23 on the point B (3, 2).
Hence the value is maximum at x = 3 and y = 2.

Question 4.
If a young man rides his motorcycle at 25 km per hour, he has to spend Rs. 2 per km on petrol, if he rides it in a faster speed of 40 km per hour, the petrol cost increases to Rs. 5 per km. He has Rs. 100 to spend on petrol and wishes to find what is maximum distance he can travel within one hour. Express this as a linear program¬ming problem and then solve it?
Solution:
Let the distance travelled at 25 km/hour = x km.
And distance travelled at 40 km/hour = y km.
We wish to maximize z = x + y subject to the constraints
2x + 5y ≤ 100 …………………….. (1)
\(\frac{x}{25}\) + \(\frac{y}{40}\) ≤ 1
Now let us solve the linear programme in the following way:
As x ≥ 0 and y ≥ 0 we shall shade the solution set of the other inequalities in the first quadrant.

For, eqn. (1),
2x + 5y = 100
x = \(\frac{100 – 5y}{2}\)
Now the test point O (0, 0) makes the inequation (1) true so we shade the half plane containing (0, 0).
For eqn.(2), \(\frac{x}{25}\) + \(\frac{y}{40}\) ≤ 1
or 8x + 5y ≤ 200
⇒ 8x + 5y = 200
⇒ x = \(\frac{200-5y}{8}\)
Again the test point (0, 0) makes the inequality (2) true so we shade the half plane containing (0, 0).

The vertices of feasible region are
0(0,0), D (25, 0), G ( \(\frac{50}{3}\), \(\frac{40}{3}\) ) , C (0, 20)
Let us caluculate z = x + y at these points.
At D (25, 0) z = 25 + 0 = 25
At G ( \(\frac{50}{3}\), \(\frac{40}{3}\) ) z = \(\frac{50}{3}\) + \(\frac{40}{3}\) = 30
At C (0, 20) z = 0 + 20 = 20
Hence, Maximum z = 30 km at ( \(\frac{50}{3}\), \(\frac{40}{3}\) ).

Question 5.
A manufacturer plants to install some new machines in his workshop. Type A machine costs Rs. 800 and occupies 3 square metre of floor space. Type B machine costs Rs. 1600 and occupies 1 \(\frac{1}{2}\) square metres of space. He can spend Rs. 20,000 altogether and the space available is 30 sq. metres. Type A turns out 10 components per hour where as type B 15 per hour. Trade restrictions compel him to have at least 3 machines of type A and 4 machines of type B?
What is the maximum number of machines he can install? Which arrangement gives him the maximum output?
Solution:
Let us assume that he buys x machines of type A and y machines of type B. Taking on account the costs of the machines and the total money available 800x + 1600y ≤ 20,000
or x + 2y ≤ 25 ………………. (1)
Again using the conditions of the space available and the space required for the machines
3x + \(\frac{3}{2}\) y ≤ 30
2x + y ≤ 20 …………………….. (2)
Also using the trade restrictions on having two types of machines
x ≥ 3 ……………………….. (3)
y ≥ 4 ……………………. (4)
The number of machines he buys will be x + y and the total output (10x + 15y) per hour.
Let N = x+y ……………………. (5)
and O = 10x + 15y ……………………… (6)
Now our problem is to maximize (5) and (6) subject to constraints (1) to (4).
The shaded region is the feasible region. The comers of the feasible region are the points (3, 4), (8, 4), (5, 10) and (3, 11).
At the point (3, 4)
N = 3+ 4 = 7,O = 30+ 60 = 90
At the point (8,4)
N = 8+ 4 = 12, O = 80 + 60 = 140
At the point (5, 10)
N = 5 + 10 = 15, O = 50 + 150 = 200
At the point (3, 11)
N = 3 + 11 = 14, O = 30 + 165 = 195

The maximum number of machines he can buy is 15. Also maximum output can be obtained by using 5 machines of type A and 10 machines of type B.

Question 6.
A soft drinks firm has two bottling plants one located at P and other at Q? Each plant produces three different soft drinks A, B and C? The capacities of two plants in number of bottles per day are as follows:

A market survey indicates that during the month of April there will be a demand for 24,000 bottles of A, 16,000 bottles of B and 48,000 bottles of C. The operating cost per day of running plants P and Q are respectively Rs. 6,000 and Rs. 4,000. Find graphi-cally how many days should the firm run each plant in April so that the production cost is minimized?
Solution:
Suppose that firm runs plant P for x days and plant Q for y days in April so the total operating cost of two plants is given by:
z = 6000x + 4000y (objective function)
As P plant produces 3000 bottles and Q plant produces 1000 bottles of drink A per day, so total production of drink A in the supposed period is
(3000x + 1000y) bottles
But there will be a demand for 24,000 bottles of this drink so the restriction 3000x + 1000y ≥ 24000 i.e., 3x + y ≥ 24
Similarly for the other two drink we have the constraints 1000x + 1000y ≥ 16000 i.e., x + y ≥ 16
2000 x + 6000 y ≥ 48000 i.e., x + 3y ≥ 24
Moreover x and y are non – negative. So x ≥ 0, y ≥ 0.
Mathematically, the given problem now reduces to minimize
z = 6000 x – 4000 y (objective function)
Subject to the conditions

The graph of the system or inequations can be easily obtained arid is as shown in figure, As (x ≥ 0 and y ≥ 0 the graph has been drawn in the first quadrant only). The points in the region which is common shaded area unbounded above constitutes the graph of the system of inequations.
Now the minimum value of the cost function z = 6000 x + 4000 y
As at one of the points A (24, 0), B (12,4), C (4, 12) and D (0, 24).

Hence P is minimum at x = 4 and y = 12. Therefore for minimum cost the firm P should run for 4 days and Q for 12 days.
Minimum cost will be Rs. 72,000.

Question 7.
A and B are the two tailor A earns Rs. 150 per day and B earns Rs. 200 per day? A can stich 6 shirts and 4 pants per day and B can stich 10 shirts and 4 pants per day? Formulate the above as a linear programming problem (L.P.P.) for minimizing the cost of at least 60 shirts and 32 pants? (CBSE 2005)
Solution:
Let, tailor works x days and tailor B works y day.
Hence, invest function is
Z = 150x + 200y
According to the function, tailor A, stich 6 shirts and B stich 10 shirts, for minimizing the cost of at least 60 shirts.
6x + 10 ≤ 60
and tailor A stich, 4 pants and B stich 4 pants, for minimizing the cost of at least 32 pants.
4x + 4y ≤ 32
and x ≥ 0, y ≥ 0
Similarly,
For minimizing invest function Z = 150x + 200y subject to the following contraints
6x + 10y ≤ 60
4x + 4y ≤ 32.
Note: For drawing the graph of constraints 6x + 10y ≤ 60, we will draw the graph of 6x + 1o y = 60.
\(\frac{6x}{60}\) + \(\frac{10y}{60}\) = 1
\(\frac{x}{10}\) + \(\frac{y}{6}\) = 1 ……………….. (1)
Line (1) cuts the intercepts 10 and 6 respectively with the coordinates axes.
i.e., By joining the points P(10,0) and Q( 0,6) get the graph of line 6x +10y = 60 easily.
Similarly draw the graph of 4x + 4y = 32
⇒ \(\frac{4x}{32}\) + \(\frac{4y}{32}\) = 1
⇒ \(\frac{x}{8}\) + \(\frac{y}{8}\) = 1 …………………….. (2)

Line (2) cuts the intercepts 8, 8 with the coordinates respectively i.e., graph of line 4x + 4y = 32 can be find by joining the points A(8, 0) and B(0, 8).
(i) x ≥ 0, all points above and on the X – axis in the solution set.
(ii) y ≥ 0, all points above and on the Y – axis in the solution set.
(iii) Taking testing point O (0, 0) for finding the solution set of 6x + 10y ≤ 60 we have, 6 × 0 + 10 × 0 < 60
⇒ 0 < 60 , which is true.
Hence all points on the line 6x + 10y = 60 including all points near to the origin is the solution set of 6x +10y ≤ 60.
(iv) Similarly, solution set of 4x + 4y ≤ 32 towards to the origin and each point on the line 4x + 4y = 32.
Hence, the common region of x ≥ 0, y ≥ 0, 6x + 10y ≤ 60 and 4x + 4y ≤ 32 shown in above graph by shaded region.
i.e., the required region is OACQ whose corner points are O (0, 0), A (8, 0), C (5, 3) and Q (0, 6).

Minimum value of invest Z = 150x + 200y is 0 and maximum invest cost of Rs. 1350 is corresponding to point (5, 3).

MP Board Class 12 Maths Important Questions