MP Board Class 12th Maths Important Questions Chapter 5B अवकलन

MP Board Class 12th Maths Important Questions Chapter 5B अवकलन

अवकलन Important Questions

अवकलन लघु उत्तरीय प्रश्न

प्रश्न 1.
x के सापेक्ष sin [cos (x²) ] का अवकलन गुणांक ज्ञात कीजिए। (NCERT)
हल:
माना y = sin [cos (x²) ]
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) sin [cos (x²) ]
= \(\frac{d}{dx}\) sin t, [cos² = t, रखने पर]
= \(\frac{d}{dt}\) sin t \(\frac{dt}{dx}\) sin t
= cost \(\frac{d}{dx}\) cos x²
= cos (cos x²) \(\frac{d}{dx}\) cos u, [x² = u रखने पर]
= cos (cos x²) \(\frac{d}{du}\) cos u \(\frac{du}{dx}\)
= – cos(cos x²) sin u \(\frac{d}{dx}\) x²
= -2x cos(cos x²).sin x²

प्रश्न 2.
यदि y = sec [tan\(\sqrt{x}\) ] हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए।
हल:
दिया है:
y = sec [tan\(\sqrt{x}\) ]

प्रश्न 3.
यदि y = log [cos e^x] हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए। (NCERT)
हल:
दिया है:
y = log [cos e^x]
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) [log(cos e^x)]
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) log t, [cos e^x = t रखने पर]
= \(\frac{d}{dt}\) log t \(\frac{dt}{dx}\)
= \(\frac{1}{t}\). \(\frac{d}{dx}\) cos e^x

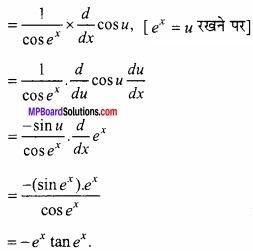
प्रश्न 4.
यदि y = cos [log x + e^x] हो, तो 4 का मान ज्ञात कीजिए। (NCERT)
हल:
दिया है:
y = cos [log x + e^x]

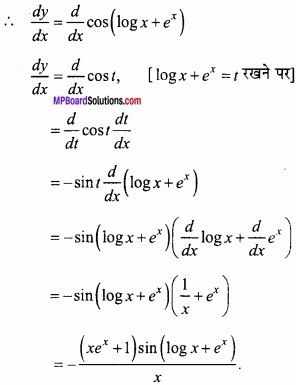
प्रश्न 5.
यदि y = cos^-1(e^x) हो, तो \(\frac{dy}{dx}\) ज्ञात कीजिए।
हल:
दिया है:
y = cos^-1(e^x)
∴ \(\frac{dy}{dx}\) = \(\frac{d}{dx}\) cos^-1(e^x)
e^x = t रखने पर,

प्रश्न 6.
यदि y + sin y = cos x हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए। (NCERT)
हल:
दिया गया फलन y + sin y = cos x
x के सापेक्ष अवकलन करने पर, का मान ज्ञात कीजिए।
\(\frac{d}{dx}\) (y + sin y) = \(\frac{d}{dx}\) cos x
⇒ \(\frac{dy}{dx}\) + cos y \(\frac{dy}{dx}\) = – sin x
⇒ \(\frac{dy}{dx}\) (1 + cos y) = – sin x
⇒ \(\frac{dy}{dx}\) = \(\frac { -sinx }{ 1+cosy } \)

प्रश्न 7.
यदि 2x + 3y = sinx हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए। (NCERT)
हल:
दिया है:
2x +3y = sin x
x के सापेक्ष अवकलन करने पर,
\(\frac{d}{dx}\) (2x + 3y) = \(\frac{d}{dx}\) sin x
2 \(\frac{d}{dx}\) x + 3 \(\frac{dy}{dx}\) = cos x
⇒ 2 + 3 \(\frac{dy}{dx}\) = cos x
⇒ 3 \(\frac{dy}{dx}\) = cos x – 2
∴ \(\frac{dy}{dx}\) = \(\frac { cosx-2 }{ 3 } \)

प्रश्न 8.
\(\frac{dy}{dx}\) का मान ज्ञात कीजिए यदि
x = a cos θ, y = a sin θ (NCERT)
हल:
दिया है:
x = a cos θ
y = a sin θ
अब समी. (1) का के सापेक्ष अवकलन करने पर,
\(\frac { dx }{ d\theta } \) = – a sin θ
पुनः समी. (2) का θ के सापेक्ष अवकलन करने पर,

प्रश्न 9.
\(\frac{dy}{dx}\) का मान ज्ञात कीजिए यदि (NCERT)
x = at², y = 2 at
हल:
दिया है:
x = at²
∴ \(\frac{dx}{dt}\) = 2 at
पुनः y = 2 at
\(\frac{dy}{dt}\) = 2a

प्रश्न 10.
यदि y = x² + 3x + 2 हो, तो \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) का मान ज्ञात कीजिए। (NCERT)
हल:
दिया है –
y = x² + 3x + 2

x के सापेक्ष पुनः अवकलन करने पर,

प्रश्न 11.
यदि y = x³ + tan x हो, तो का मान ज्ञात कीजिए। (NCERT)
हल:
दिया है:
y = x² + tan x
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) [x³ + tan x]
= \(\frac{d}{dx}\) x³ + \(\frac{d}{dx}\) tan x
⇒ \(\frac{dy}{dx}\) = 3x² + sec² x
x के सापेक्ष पुनः अवकलन करने पर,

अवकलन दीर्घ उत्तरीय प्रश्न – I

प्रश्न 1.
y = tan^-1 \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \) का x के सापेक्ष अवकलन कीजिए।
हल:
दिया है:
y = tan^-1 \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \)
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) tan^-1 \(\frac { x }{ \sqrt { 1+x^{ 2 } } } \)

पुनः 1 + x² = u रखने पर,

प्रश्न 2.
\(\frac{dy}{dx}\) का मान ज्ञात कीजिए यदि
x = a (t + sint), y = a (1 – cost)
हल:
दिया है:
x = a (t + sint)
∴ \(\frac{dx}{dt}\) = a (1 + cos t)
पुनः y = a (1 – cos t)
∴ \(\frac{dy}{dt}\) = a (0 + sint) = a sint

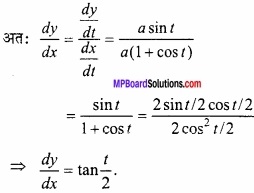
प्रश्न 3.
यदि x = a (2θ – sin 2θ) तथा y = a (1 – cos 2θ), तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिये जबकि θ = \(\frac { \pi }{ 3 } \) (CBSE 2018) .
हल:
दिया है:
समी. (2) को θ के सापेक्ष अवकलन करने पर,
x = a (2θ – sin 2θ) ………………………. (1)
y = a (1 – cos 2θ) ………………………… (2)
\(\frac { dx }{ d\theta } \) = a (2.1 – cos 2θ.2)
= 2a (1- cos 2θ)
= 2a.2 sin²θ
= 4a sin²θ …………………….. (3) |
समी. (2) को θ के सापेक्ष अवकलन करने पर,
\(\frac { dy }{ d\theta } \) = a(0 + sin 2θ.2)
= 2a sin 2θ
= 2a. 2 sinθ cosθ
= 4a sinθcosθ ……………………….. (4)
समी. (4) ÷ (3) से,

जब θ = \(\frac { \pi }{ 3 } \), तब
\(\frac{dy}{dx}\) = cot \(\frac { \pi }{ 3 } \) = \(\frac { 1 }{ \sqrt { 3 } } \)

प्रश्न 4.
यदि y = a sin mx + b cos mx हो, तो सिद्ध कीजिए कि
\(\frac { d^{ 2 }y }{ dx^{ 2 } } \) + m² y = 0
हल:
दिया है:
y = a sin mx + b cos mx …………………….. (1)
समी. (1) के दोनों पक्षों में x के सापेक्ष अवकलन करने पर,
\(\frac{dy}{dx}\) = am cos mx – bm sin mx ……………… (2)
पुनः (2) का x के सापेक्ष अवकलन करने पर,

प्रश्न 5.
(A) यदि y = esin^{-1 x} हो, तो सिद्ध कीजिए कि (1 – x²), y₂ – xy₁ – m² y = 0
हल:
दिया है:

पुनः अवकलन करने पर,

(B)
यदि y = e^mtan-1x हो, तो सिद्ध कीजिए कि (1 + x²)y₂ + (2x – m) y₁ = 0
हल:
प्रश्न क्र. 5 (A) की भाँति हल करें।

(C)
यदि y = e^mcos-1x हो, तो सिद्ध कीजिए कि (1 – x²)y₂ + (2x – m)y₁ = 0
हल:
प्रश्न क्र. 5 (A) की भाँति हल करें।

प्रश्न 6.
sin^-1 \(\frac { 2x }{ 1+x^{ 2 } } \) का x के सापेक्ष अवकलन कीजिए।
हल:

प्रश्न 7.
यदि y = cot^-1 \(\sqrt { \frac { 1+x }{ 1-x } } \) हो, तो \(\frac{dy}{dx}\) ज्ञात कीजिए।
हल:
दिया है,
y = cot^-1 \(\sqrt { \frac { 1+x }{ 1-x } } \)
माना x = cos θ

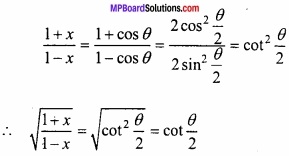
समी. (1) में इसका मान रखने पर,

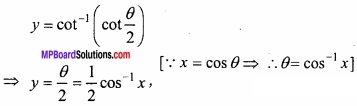
अब x के सापेक्ष दोनों पक्षों का अवकलन करने पर,
\(\frac{dy}{dx}\) = – \(\frac { 1 }{ 2\sqrt { 1-x^{ 2 } } } \)

प्रश्न 8.
यदि y = tan^-1 \(\sqrt { \frac { 1+x }{ 1-x } } \) हो, तो ज्ञात कीजिए।
हल: प्रश्न क्र. 7 की भाँति हल करें।
[उत्तर – \(\frac{dy}{dx}\) = \(\frac { 1 }{ 2\sqrt { 1-x^{ 2 } } } \)

प्रश्न 9.
यदि y = cot^-1 \(\frac { cosx+sinx }{ cosx-sinx } \) हो, तो \(\frac{dy}{dx}\) ज्ञात कीजिए।
हल:
दिया है:

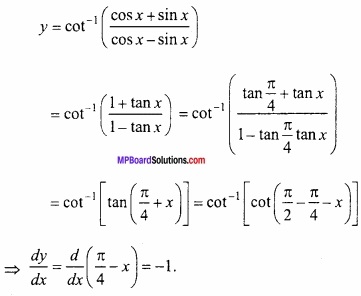
प्रश्न 10.
y = tan^-1 \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) का x के सापेक्ष अवकलन कीजिए।
हल:
y = tan^-1 \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \)
समी. (1) x = tan θ में रखने पर, तब θ = tan^-1 x

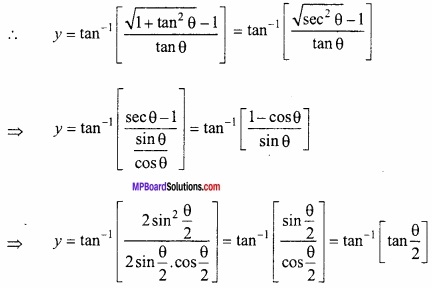
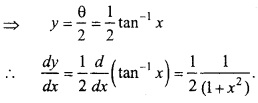
प्रश्न 11.
यदि y = cot^-1 [ \(\frac { \sqrt { 1+x^{ 2 }+1 } }{ x } \) ] हो, तो \(\frac{dy}{dx}\) ज्ञात कीजिए।
हल:
y = cot^-1 [ \(\frac { \sqrt { 1+x^{ 2 }+1 } }{ x } \) ]
x = tan θ रखने पर,

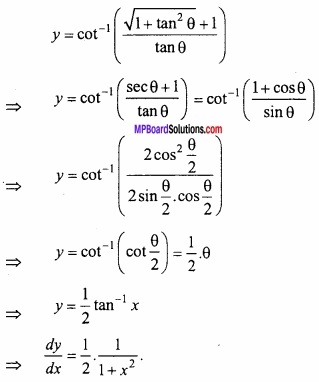
प्रश्न 12.
यदि y = x^sinx हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए।
हल:
दिया है:
y = x^sinx
समी. (1) के दोनों पक्षों का log लेने पर, …………………………….. (1)
दोनों पक्षों का अवकलन करने पर,

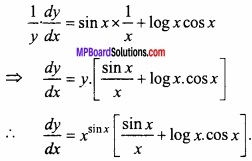
प्रश्न 13.
यदि y = \(\sqrt { \frac { 1-x }{ 1+x } } \) हो, तो सिद्ध कीजिए \(\frac{dy}{dx}\) = \(\frac { y }{ x^{ 2 }-1 } \)
हल:
दिया है:

प्रश्न 14.
यदि y = (sin x)^{sinxsinx…………… ∞} हो, तो 4 का मान ज्ञात कीजिए।
हल:
दिया है:
y = (sin x)^{sinxsinx…………… ∞}
⇒ y = (sin x)^y
⇒ log y = y log sinx

x के सापेक्ष अवकलन करने पर,

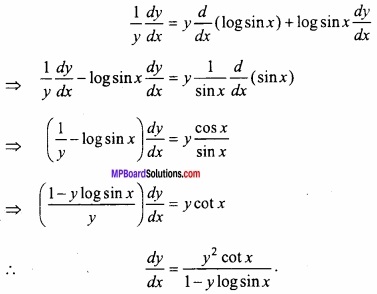
प्रश्न 15.
(A) यदि y = \(\sqrt { sinx+\sqrt { sinx+……+\infty } } \) हो, तो सिद्ध कीजिए कि
\(\frac{dy}{dx}\) = \(\frac { cosx }{ 2y-1 } \)
हल:
दिया है:

(B)
यदि y = \(\sqrt { cotx\sqrt { cotx+\sqrt { cotx+…….+\infty } } } \) हो, तो सिद्ध कीजिए कि
\(\frac{dy}{dx}\) = \(\frac { cosec^{ 2 }x }{ 1-2y } \)
हल:
प्रश्न क्र. 15 (A) की भाँति हल करें।

(C) यदि y = \(\sqrt { tanx+\sqrt { tanx+\sqrt { tanx+…..\infty } } } \) हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए।
हल:
प्रश्न क्र. 15 (A) की भाँति हल करें।
[उत्तर: \(\frac { sec^{ 2 }x }{ (2y-1) } \) ]

प्रश्न 16.
यदि y = e^{x+ex+ex+e…………… ∞} हो, तो सिद्ध कीजिए कि
\(\frac{dy}{dx}\) = \(\frac{y}{1-y}\)
हल:
दिया है:
y = e^{x+ex+ex+e…………… ∞}
⇒ y = e^x+y
दोनों पक्षों में log लेने पर,
log y = loge^x+y
⇒ log y = x + y

प्रश्न 17.
फलन \(\frac { 1 }{ (x+a)(x+b)(x+c) } \) का x के सापेक्ष अवकलन कीजिये।
हल:
माना y = \(\frac { 1 }{ (x+a)(x+b)(x+c) } \)
दोनों पक्षों में log लेने पर
log y = log1 – log(x + a) – log(x + b) – log(x + c)
x के सापेक्ष अवकलन करने पर

प्रश्न 18.
log ( \(\sqrt{x}\) + \(\frac { 1 }{ \sqrt { x } } \) का x के सापेक्ष अवकल गुणांक ज्ञात कीजिये।
हल:

x के सापेक्ष अवकलन करने पर,

प्रश्न 19.
यदि y = tan^-1 ( \(\frac { sinx }{ 1+cosx } \) ) हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिये।
हल:
दिया है:
y = tan^-1 ( \(\frac { sinx }{ 1+cosx } \) )

दोनों पक्षों का x के सापेक्ष अवकलन करने पर,
अत:
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) ( \(\frac{x}{2}\) ) = \(\frac{1}{2}\)

प्रश्न 20.
फलन f (x) = x² के लिए अंतराल [-1, 1] में रोले प्रमेय का सत्यापन कीजिए। (NCERT)
हल:
यहाँ f (x) = x², a = -1, b = 1

1. चूँकि f (x) = x² एक बहुपद फलन है इसलिए f (x) संवृत अंतराल [-1, 1] में संतत है।
2. f’ (x) = 2x विवृत्त अंतराल (-1, 1) में परिभाषित है इसलिए f (x) विवृत अंतराल (-1, 1) में अवकलनीय है।
3. f (-1) = (-1)² = 1, f(1) = (1)² = 1

∴ f (-1) = f (1)
अतः फलन f (x) रोले प्रमेय के सभी प्रतिबंधों को संतुष्ट करता है।
∴ f'(c) = 0
⇒ 2c = 0 [∵ f'(x) = 2x]
⇒ (c) = 0 ∈ (-1, 1)
अतः रोले प्रमेय सत्यापित होता है।

प्रश्न 21.
फलन f (x) = x² + 2x – 8 के लिए अंतराल [-4, 2) में रोले प्रमेय का सत्यापन कीजिए। (NCERT)
हल:
यहाँ f (x) = x² + 2x – 8, a = – 4, b = 2.

1. f (x) = x² + 2x – 8 एक बहुपद फलन है इसलिए f (x) संवृत अंतराल [-4, 2] में संतत है।
2. f’ (x) = 2x + 2 विवृत्त अंतराल (-4, 2) में परिभाषित है इसलिए f (x) विवृत अंतराल (-4, 2) में अवकलनीय है।
3. f (-4) = (-4)² + 2 (-4) – 8

= 16 – 8 – 8 = 0
f (2) = (2)² + 2 × 2 – 8 = 0
f (- 4) = f (2)
अतः f(x) रोले प्रमेय की तीनों शर्तों को संतुष्ट करता है।
∴ f'(c) = 0
⇒ 2c + 2 = 0
⇒ c = -1 ∈ (-4, 2)
अतः रोले प्रमेय सत्यापित होता है।

प्रश्न 22.
फलन f (x) = 2x² + x² – 4x – 2 के लिए रोले प्रमेय का सत्यापन कीजिए।
हल:
चूँकि बहुपद फलन सभी वास्तविक संख्याओं के लिए संतत और अवकलनीय होता है इसलिए f (x) प्रत्येक अंतराल में संतत और अवकलनीय है।
अब f (x) = 0
⇒ 2x³ + x² – 4x – 2 = 0
⇒ x²(2x + 1) – 2 (2x + 1) = 0
⇒ (x² – 2) (2x + 1) = 0
⇒ x² = 2, 2x + 1 = 0
⇒ x = ± \(\sqrt{2}\), x = – \(\frac{1}{2}\)
⇒ x = – \(\sqrt{2}\), \(\sqrt{2}\), \(\frac{-1}{2}\)
अब अंतराल [-\(\sqrt{2}\), \(\sqrt{2}\) ] लेते हैं।

1. फलन f (x) संवृत अंतराल [-\(\sqrt{2}\), \(\sqrt{2}\) ] में संतत है।
2. f'(x) = 6x² + 2x – 4 का अस्तित्व विवृत अंतराल [-\(\sqrt{2}\), \(\sqrt{2}\) ] में है इसलिए f (x) विवृत अंतराल [-\(\sqrt{2}\), \(\sqrt{2}\) ] में अवकलनीय है।
3. f ( –\(\sqrt{2}\) ) = f ( \(\sqrt{2}\) ) = 0

अतः f (x) रोले प्रमेय के सभी प्रतिबंधों को संतुष्ट करता है।
∴ f'(c) = 0
⇒ 6c² + 2c – 4 = 0, [∵f'(x) = 6x² + 2x – 4]


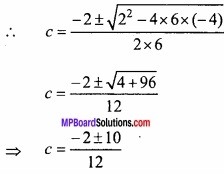
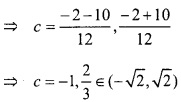
अतः रोले प्रमेय सत्यापित होता है।

प्रश्न 23.
अंतराल [1,3] में फलन f (x) = x + \(\frac{1}{x}\) के लिए मध्यमान प्रमेय का सत्यापन कीजिए।
उत्तर
हल:
f (x) = x + \(\frac{1}{x}\) = \(\frac { x^{ 2 }+1 }{ x } \), x ∈ [1, 3]

1. चूँकि f(x), x ≠ 0 सहित एक परिमेय फलन है और प्रत्येक परिमेय फलन संतत होता है, इसलिए f (x), [1, 3] में संतत फलन है।
2. f'(x) = 1 – \(\frac { 1 }{ x^{ 2 } } \) विवृत अंतराल (1, 3) में परिभाषित है और प्रतेक परिमेय फलन संतत होता है इसलिए f (x), [1, 3] में संतत फलन है।
3. f (1) = 2, f (3) = \(\frac{10}{3}\)

अतः मध्यमान प्रमेय के दोनों प्रतिबंध संतुष्ट होते हैं।

अत: लैग्रांज का मध्यमान प्रमेय सत्यापित होता है।

प्रश्न 24.
फलन f (x) = log x का अंतराल [1, e] में मध्यमान प्रमेय का सत्यापन कीजिए।
हल:
f(x) = log x, x ∈ [1, e], x > 0.
a = 1, b = e

1. चूँकि f (x) = log x, x > 0 एक संतत फलन होता है इसलिए f (x), [1, e] में संतत फलन है।
2. f'(x) = \(\frac{1}{x}\), में परिभाषित है इसलिए f (x), (1, e) में अवकलनीय है।
3. f (1) = log 1 = 0, f (e) = log e = 1

अतः मध्यमान प्रमेय की दोनों शर्त संतुष्ट होती हैं।
∴ \(\frac { f(e)-f(1) }{ e-1 } \) = f'(c)
⇒ \(\frac { 1-0 }{ e-1 } \) = \(\frac{1}{e}\)
⇒ c = e – 1 ∈ (1, e)
अत: मध्यमान प्रमेय सत्यापित होता है।

प्रश्न 25.
मध्यमान प्रमेय के प्रयोग से अंतराल [2, 3] में परिभाषित वक्र y = \(\sqrt { x-2 } \) पर एक बिन्दु ज्ञात कीजिए जबकि स्पर्श रेखा वक्र के बिन्दुओं को मिलाने वाली जीवा के समांतर है।
हल:
f (x) = \(\sqrt { x-2 } \), a = 2, b = 3

1. चूँकि f(x) = \(\sqrt { x-2 } \), x ∈ [2,3] के लिए परिभाषित है इसलिए f (x), [2, 3] में संतत फलन है।
2. f'(x) = \(\frac { 1 }{ 2\sqrt { x-2 } } \) विवृत अंतराल (2, 3) में परिभाषित है इसलिए f (x), (2, 3) में अवकलनीय है।
3. f (2) = 0, f (3) = 1

अतः मध्यमान प्रमेय के दोनों प्रतिबंध संतुष्ट होते हैं।
∴ \(\frac { f(3)-f(2) }{ 3-2 } \) = f’ (c)

अभीष्ट निर्देशांक ( \(\frac{9}{4}\), \(\frac{1}{2}\) ) हैं।

अवकलन दीर्घ उत्तरीय प्रश्न – II

प्रश्न 1.
यदि y = sin^-1 \(\frac { 2^{ x+1 } }{ 1+4^{ x } } \) हो, तो \(\frac{dy}{dx}\) ज्ञात कीजिए। (NCERT)
हल:
दिया है:
y = sin^-1 \(\frac { 2^{ x+1 } }{ 1+4^{ x } } \)

प्रश्न 2.
यदि y = sin^-1 x हो, तो सिद्ध कीजिए कि (1 – x²) \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) – x \(\frac{dy}{dx}\) = 0? (NCERT)
हल:
दिया है:
y = sin^-1 x
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) (sin^-1 x)
\(\frac{dy}{dx}\) = \(\frac { 1 }{ \sqrt { 1-x^{ 2 } } } \)
\(\frac{d}{dx}\) ( \(\frac{dy}{dx}\) ) = \(\frac{d}{dx}\) (1 – x²)^-1/2
1 – x² = t रखने पर,

प्रश्न 3.
यदि y = tan x + sec x हो, तो सिद्ध कीजिए कि \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = \(\frac { cosx }{ (1-sinx)^{ 2 } } \)
हल:
दिया है:
y = tan x + sec x
\(\frac{dy}{dx}\) = sec² x + sec x tan x
⇒ \(\frac{dy}{dx}\) = sec x (sec x + tan x)
⇒ \(\frac{dy}{dx}\) = \(\frac{1}{cosx}\) = [ \(\frac { 1 }{ cosx } +\frac { sinx }{ cosx } \) ]

प्रश्न 4.
यदि y = sin (sin x) हो, तो सिद्ध कीजिए कि
y₂ + y₁ tan x + y cos² x = 0? (CBSE 2018)
हल:
y = sin (sin x) ………………………. (1)
x के सापेक्ष अवकलन करने पर,
y₁ = cos (sin x). cos x
पुनः x के सापेक्ष अवकलन करने पर,
y₂ = cos(sin x)\(\frac { d }{ dx } \) (cos x) + cos x \(\frac { d }{ dx } \) {cos(sin x)}
= cos(sin x)(- sin x) + (cos x) [- sin(sin x)]cos x
⇒ y₂ = – sin x cos(sin x) – cos² x sin(sin x)
⇒ y₂ = – sin x cos(sin x) – y cos² x, [ समी. (1) से ]
⇒ y₂ = [ – \(\frac { sinx }{ cosx } .cosx\) ] cos(sin x) – y cos² x
⇒ y₂ = (- tan x) y₁ – y cos² x, [ समी. (2) से ]
⇒ y₂ + y₁ tan x + y cos² x = 0. यही सिद्ध करना था।

प्रश्न 5.
\(\frac{dy}{dx}\) का मान ज्ञात कीजिए यदि (x² + y²)² = xy? (CBSE 2018)
हल:
(x² + y²)² = xy
दोनों पक्षों के प्रत्येक पद का x के सापेक्ष अवकलन करने पर,

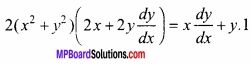
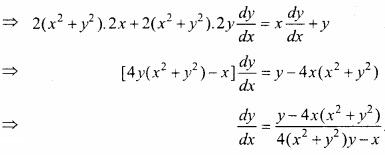
प्रश्न 6.
यदि y = 500e^7x + 600e^-7x हो, तो सिद्ध कीजिए कि \(\frac { d^{ 2 }y }{ dx^{ 2 } } \) = 49 y? (NCERT)
हल:
दिया है:
y = 500e^7x + 600e^-7x

प्रश्न 7.
यदि y = (tan^-1 x)² हो, तो दर्शाइए कि (x² + 1)² y₂ + 2x(x² + 1) y₁ = 2 है। (NCERT)
हल:
दिया है:
y = (tan^-1 x)²
tan^-1 x = t रखने पर,

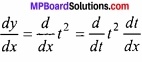
प्रश्न 8.
sec^-1 ( \(\frac { 1 }{ 2x^{ 2 }-1 } \) ) के सापेक्ष अवकल गुणांक ज्ञात कीजिए।
हल:
माना y₁ = sec^-1 = ( \(\frac { 1 }{ 2x^{ 2 }-1 } \) )
⇒ y₁ = cos^-1 (2x² – 1)

प्रश्न 9.
tan^-1 ( \(\frac { 2x }{ 1-x^{ 2 } } \) ) का sin^-1 ( \(\frac { 2x }{ 1+x^{ 2 } } \) ) के सापेक्ष अवकल गुणांक ज्ञात कीजिए।
हल:
माना y₁ = tan^-1 ( \(\frac { 2x }{ 1-x^{ 2 } } \) ) तथा y₂ = sin^-1 ( \(\frac { 2x }{ 1+x^{ 2 } } \) )
माना x = tan θ, अत: θ = tan^-1 x

प्रश्न 10.
tan^-1 ( \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) ) का tan^-1 x के सापेक्ष अवकल गुणांक ज्ञात कीजिए।
हल:
माना y₁ = tan^-1 ( \(\frac { \sqrt { 1+x^{ 2 }-1 } }{ x } \) )
x = tan θ रखने पर,

प्रश्न 11.
यदि x \(\sqrt { 1+y } \) + y \(\sqrt { 1+x } \) = 0 हो, तो सिद्ध कीजिए कि
\(\frac{dy}{dx}\) = – (1 + x)^-2
हल:
दिया है:
x \(\sqrt { 1+y } \) + y \(\sqrt { 1+x } \) = 0
⇒ x \(\sqrt { 1+y } \) = – y \(\sqrt { 1+x } \)
दोनों पक्षों का वर्ग करने पर,
x² (1 + y) = y² (1 + x)
⇒ x² + x²y = xy² + y²
⇒ x² – y² + x²y – xy² = 0
⇒ (x – y)(x + y) + xy (x – y) = 0
⇒ (x – y)(x + y + xy) = 0
अतः था तो  x – y = 0
⇒ x = y
किंतु  x ≠ y
∴ x + y+ xy = 0
⇒ y(1 + x) = -x
∴ y = –\(\frac { x }{ x+1 } \)
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

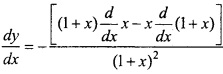
प्रश्न 12.
यदि y \(\sqrt { 1-x^{ 2 } } \) + x \(\sqrt { 1-y^{ 2 } } \) = 1 हो, तो सिद्ध कीजिए कि
\(\frac{dy}{dx}\) + \(\sqrt { \frac { 1-y^{ 2 } }{ 1-x^{ 2 } } } \) = 0?
हल:
दिया है:
y \(\sqrt { 1-x^{ 2 } } \) + x \(\sqrt { 1-y^{ 2 } } \) = 1
अब x = sin θ तथा y = sin ∅ लेने पर,

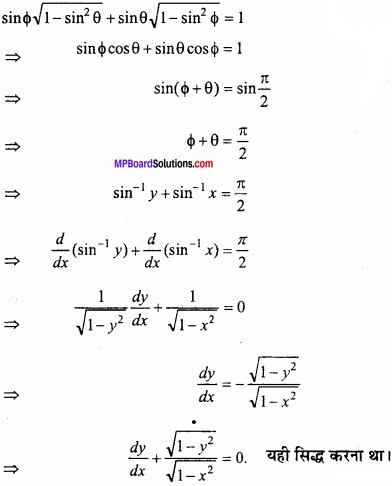
प्रश्न 13.
(A) यदि y = x^sin-1x + x^x
हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए।
हल:
दिया है:
y = x^sin-1x + x^x

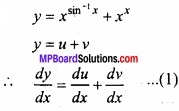
(B)
यदि y = x^tan-1x + x^x हो, तो \(\frac{dy}{dx}\) का मान ज्ञात कीजिए।
हल:
प्रश्न क्र. 13 (A) की भाँति हल करें।

प्रश्न 14.
यदि sin y = x sin (a + y) हो, तो सिद्ध कीजिए कि,
\(\frac{dy}{dx}\) = \(\frac { sin^{ 2 }(a+y) }{ sina } \)
हल:
दिया है:
sin y = x sin (a + y)
x = \(\frac { siny }{ sin(a+y) } \)

प्रश्न 15.
यदि x^y = e^x-y हो, तो सिद्ध कीजिए कि \(\frac{dy}{dx}\) = \(\frac { logx }{ (1+logx)^{ 2 } } \)?
हल:
दिया है:
x^y = e^x-y
दोनों पक्षों का लघुगणक लेने पर,
y log x = (x – y) log_e e
⇒ y log x = (x – y).1 = x – y
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

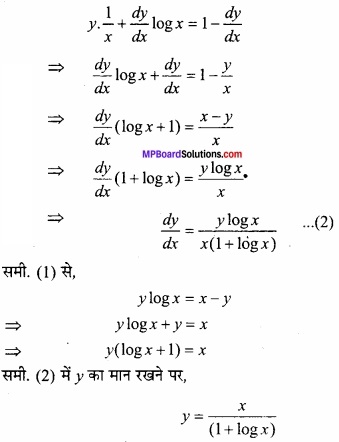
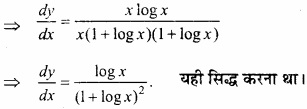
प्रश्न 16.
यदि x^y = e^y-x हो, तो सिद्ध कीजिए कि
\(\frac{dy}{dx}\) = \(\frac { 2-log_{ e }x }{ (i-log_{ e }x)^{ 2 } } \)?
हल:
दिया है:
x^y = e^y-x
दोनों पक्षों में log लेने पर,
∴ log_e x^y = log_e(e^y-x)
⇒ y log_e x = (y – x) log_e e
⇒ y log_e x = y – x,
⇒ y(1 – log_e x) = x
⇒ y = \(\frac { x }{ 1-log_{ e }x } \)
अब दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

MP Board Class 12 Maths Important Questions