Category: Class 12

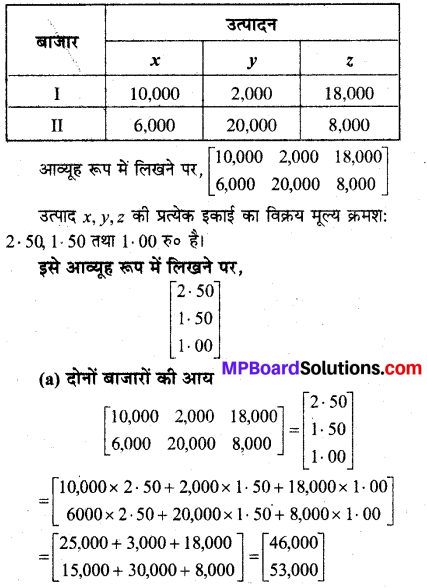
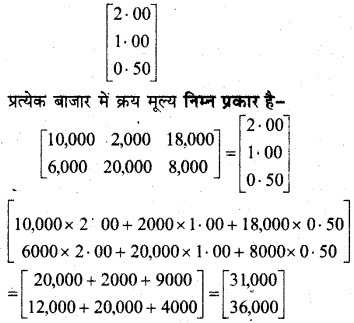
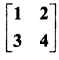
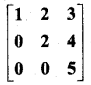
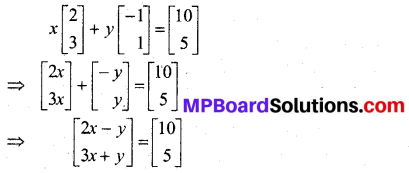
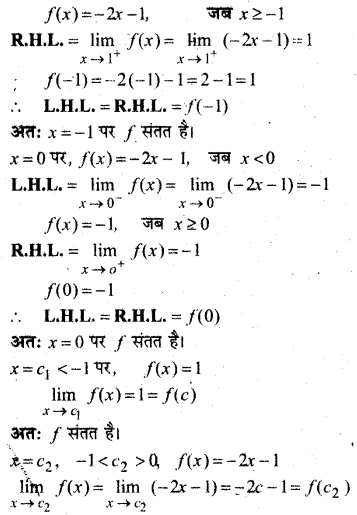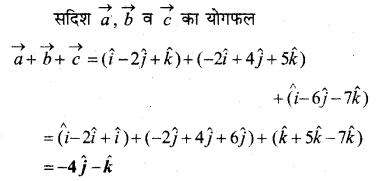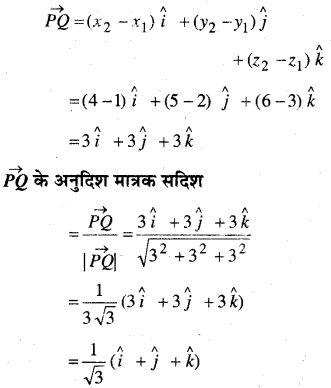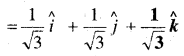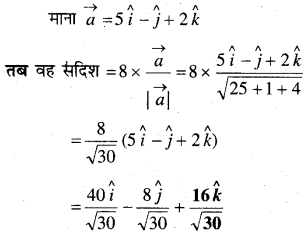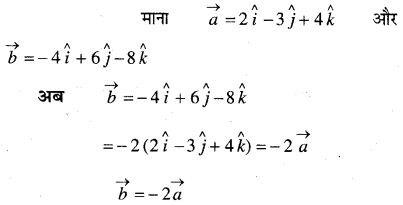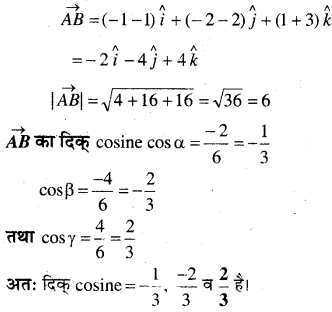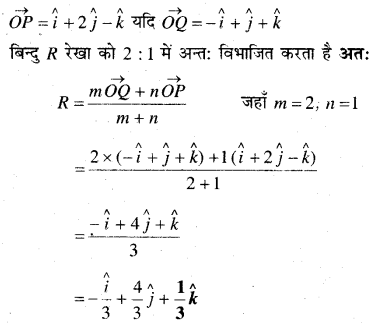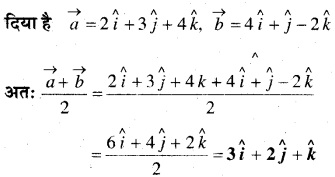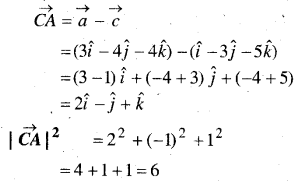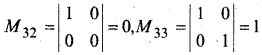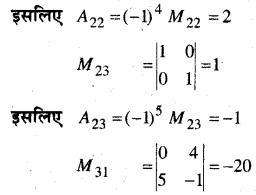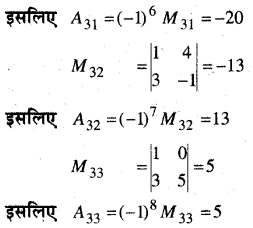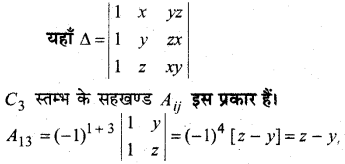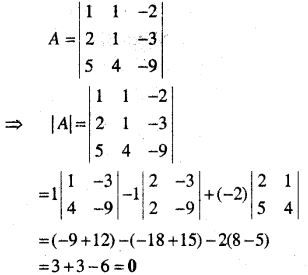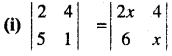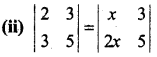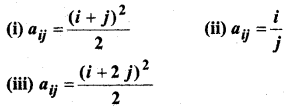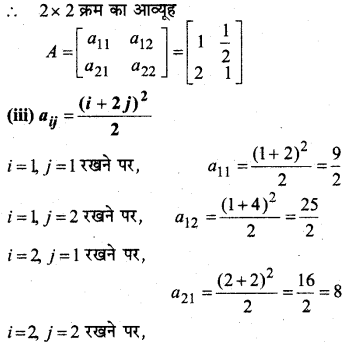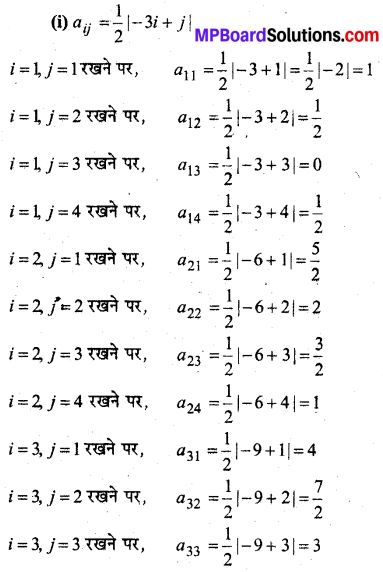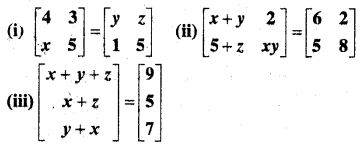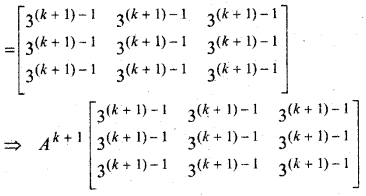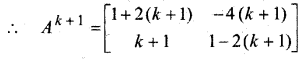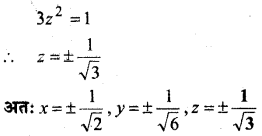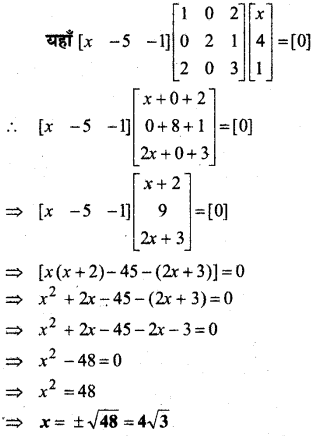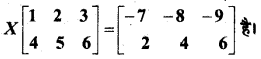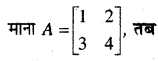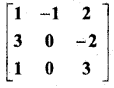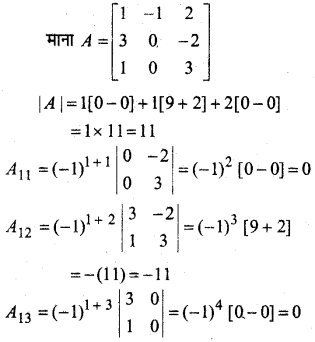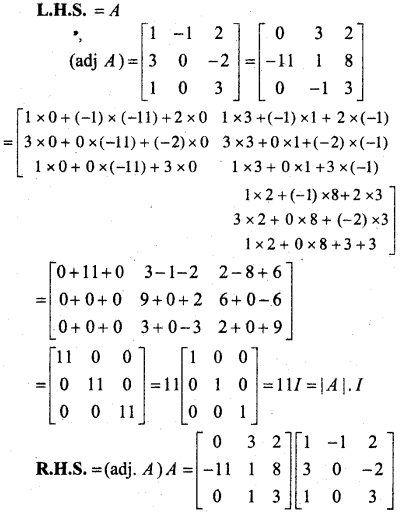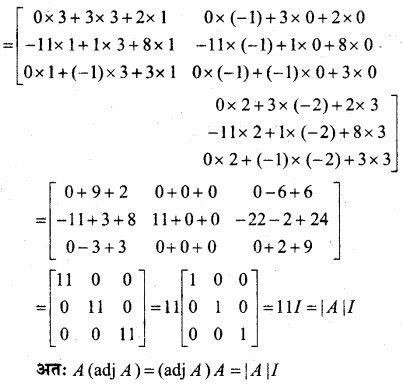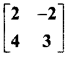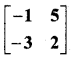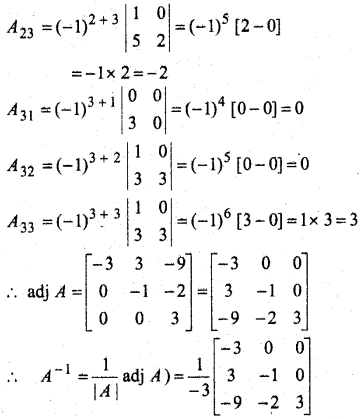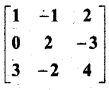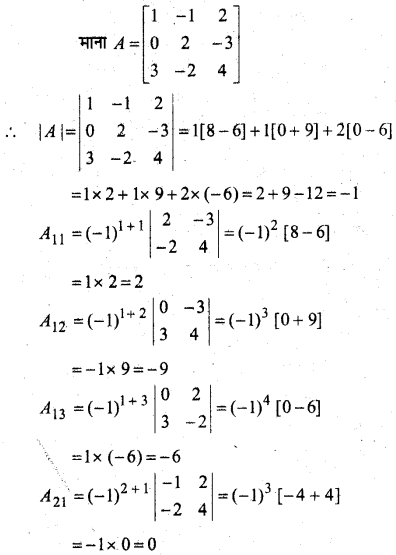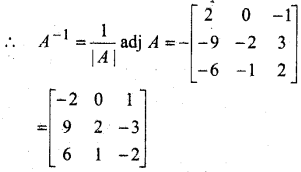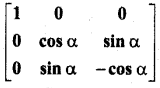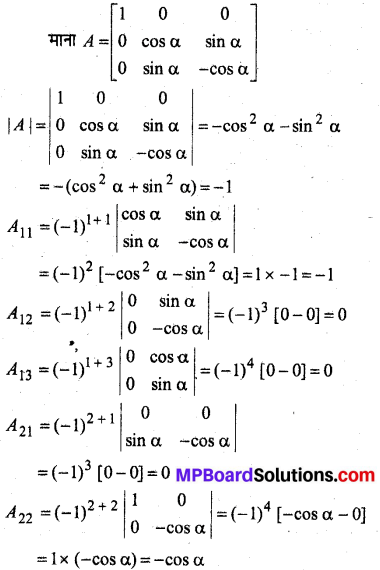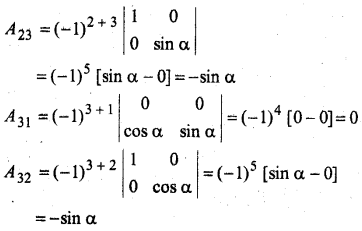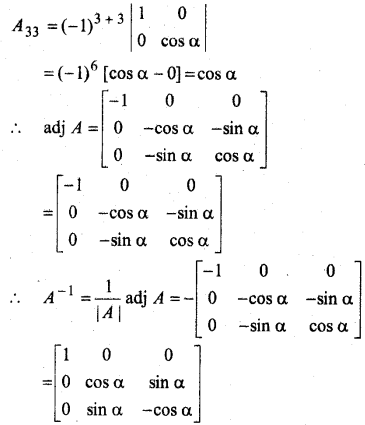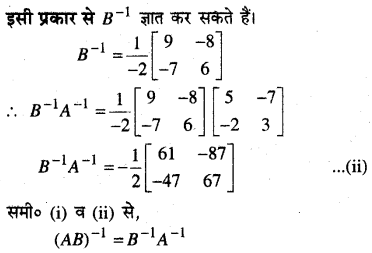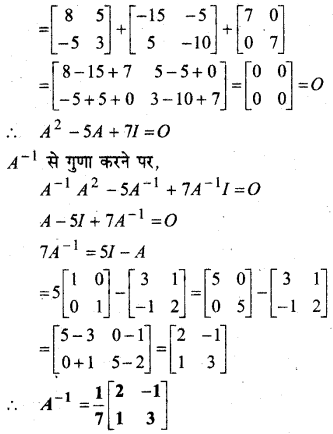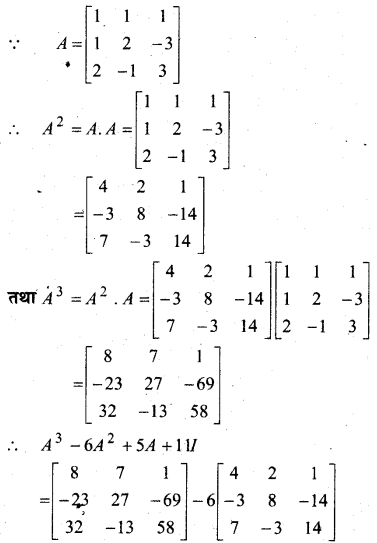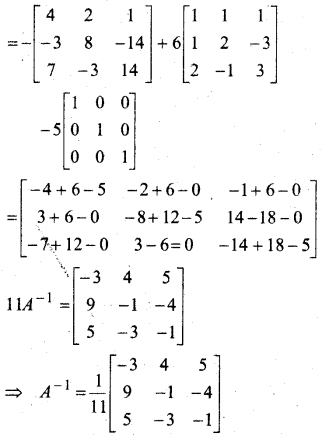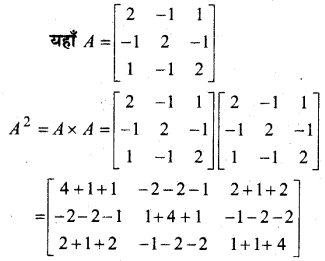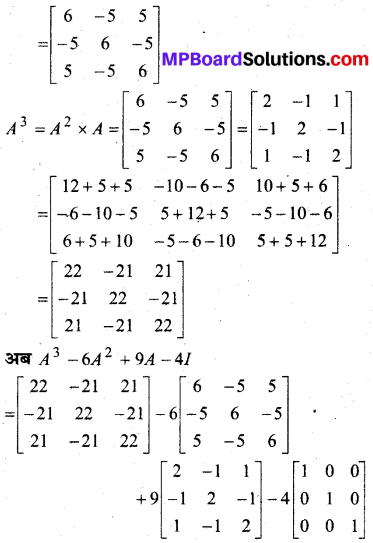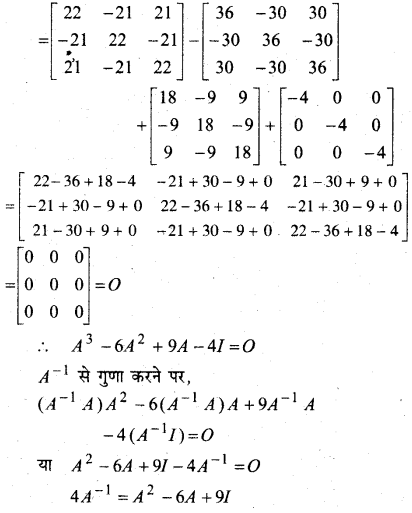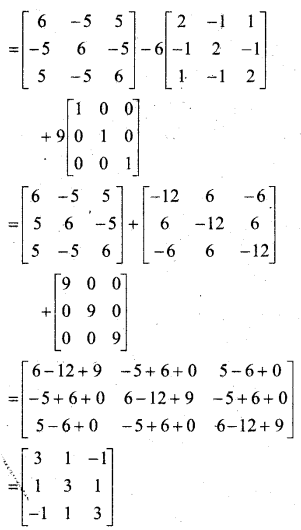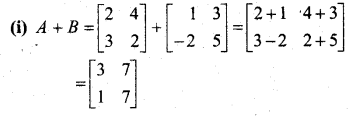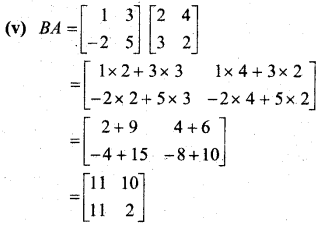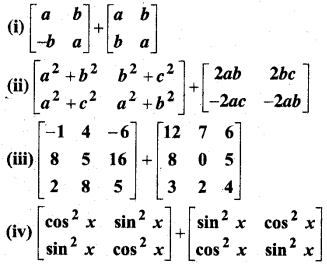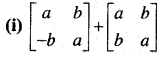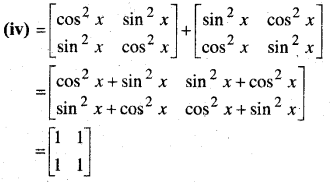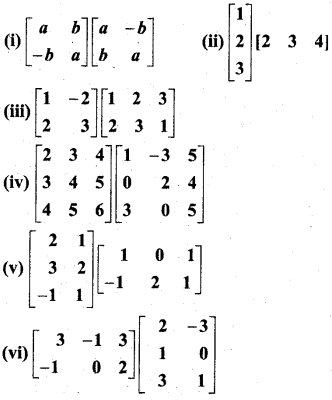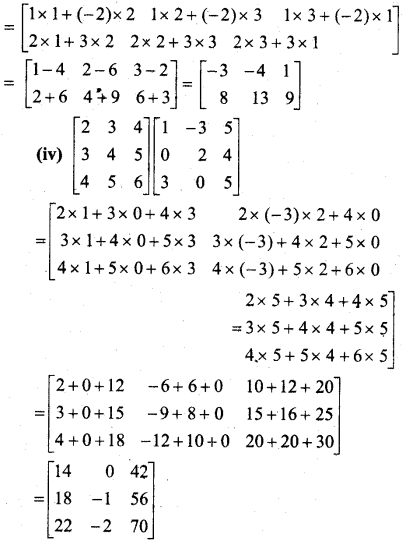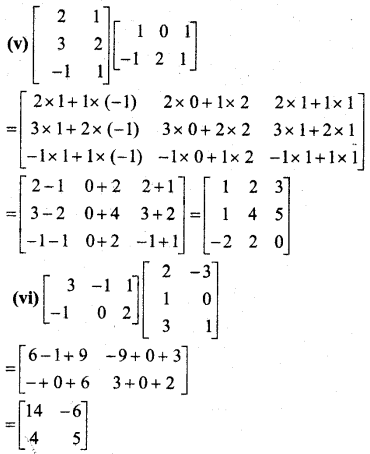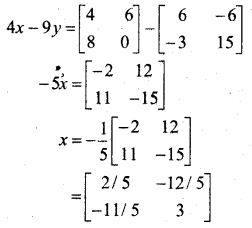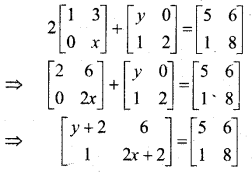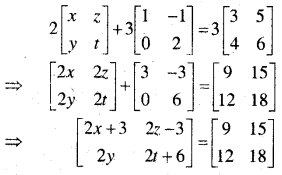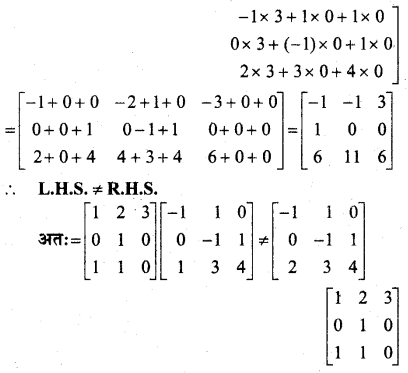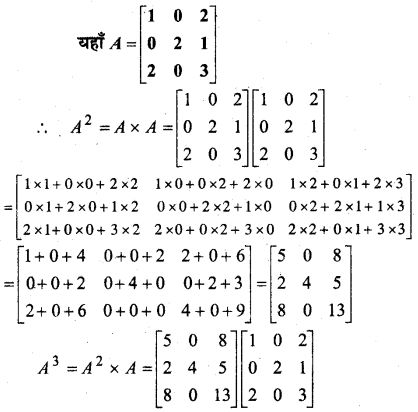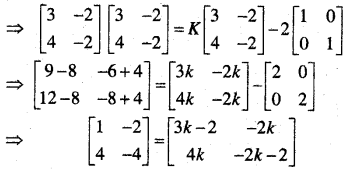In this article, we share MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.1

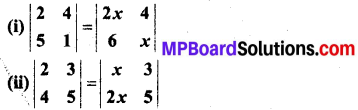
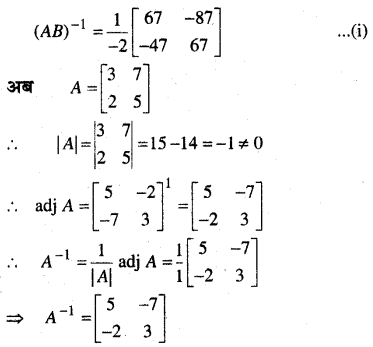
प्रश्न 1.
सिद्ध कीजिए कि फलन f(x) = 5x – 3, x = 0, x = – 3 तथा x = 5 पर संतत है।
हल:

प्रश्न 2.
x = 3 पर फलन f(x) = 2x² – 1 के सातत्य की जाँच कीजिए :
हल:
∵ f(x) = 2x² – 1
∴ f(3) = 2 x 3² – 1 = 17
\(\lim _{x \rightarrow 3} f(x)=\lim _{x \rightarrow 3}\left(2 x^{2} – 1\right)\)
= 2 × 9 – 1 = 17
अतः f(x), x = 3 पर सतत् है।

प्रश्न 3.
निम्नलिखित फलनों के सातत्य की जाँच कीजिए
हल:
(a) f(x) = x – 5
(x – 5) एक बहुपदीय व्यंजक है।
अतः हर बिन्दु x ϵ R पर संतत है।



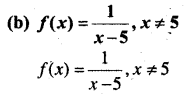
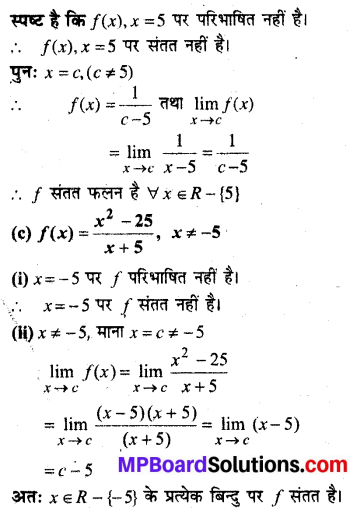
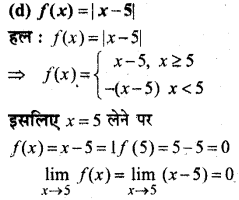
अतः f, x = 5 पर संतत है।
पुनः x < 5 पर f(x) = x – 5, जो कि एक बहुपद है इसलिए f, x > 5 पर संतत है
x < 5 पर
f(x) = – (x – 5) = 5 – x, जो कि एक बहुपद है
∴ f, x < 5 पर संतत है
अतः f, x की समस्त मान के लिए संतत है।

प्रश्न 4.
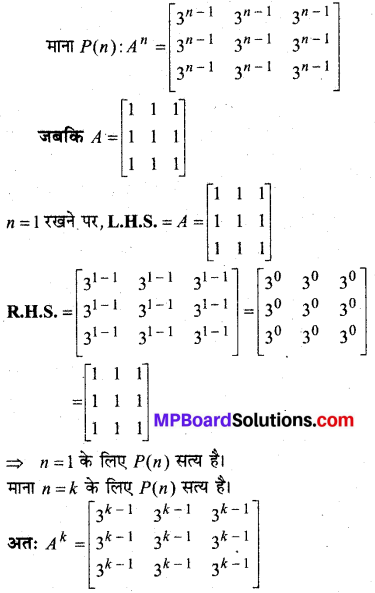
सिद्ध कीजिए कि फलन f(x) = xⁿ, x = n, संतत है, जहाँ n एक धन पूर्णांक है।
हल:
∵ n एक धन पूर्णांक है
∴ f(x) = xⁿ एक बहुपद हैं
इसलिए x = n पर f एक संतत है।

प्रश्न 5.
क्या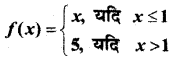
द्वारा परिभाषित फलन f, x = 0, x = 1 तथा x = 2 पर संतत है।
हल:

f के सभी असातत्य के बिन्दुओं को ज्ञात कीजिए, जबकि f निम्नलिखित प्रकार से परिभाषित है –
प्रश्न 6.

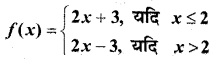
हल:

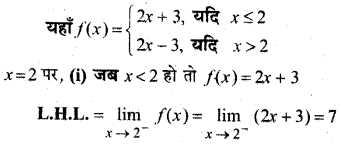
प्रश्न 7.

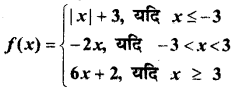
हल:

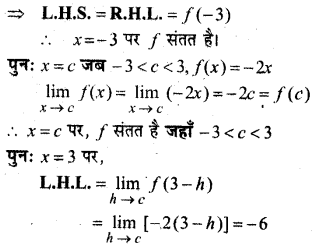
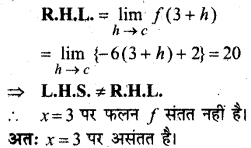
प्रश्न 8.

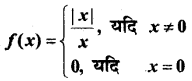
हल:

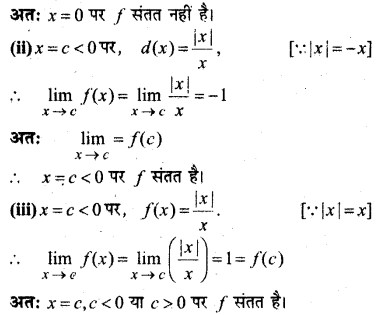
प्रश्न 9.

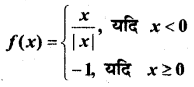
हल:

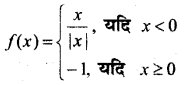
प्रश्न 10.

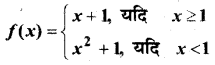
हल:

प्रश्न 11.

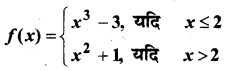
हल:

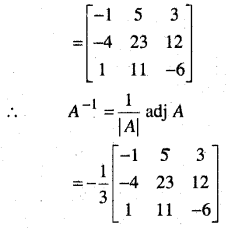
प्रश्न 12.

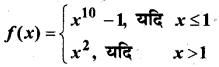
हल:

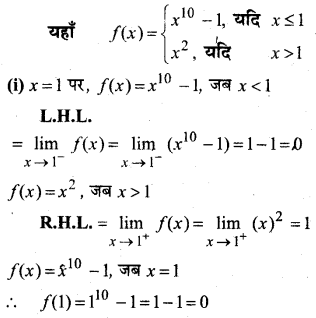
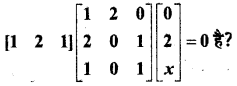
प्रश्न 13.
क्या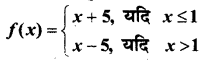
परिभाषित फलन, एक संतत फलन है?
हल:

फलन f के सातत्य पर विचार कीजिए, जहाँ f निम्नलिखित द्वारा परिभाषित है-
प्रश्न 14.

हल:

⇒ L.H.L. ≠ R.H.L.
∴ f बिन्दु x = 3 पर संतत नहीं है।
अतः x = 1 व x = 3 पर f असांत्यता है।

प्रश्न 15.

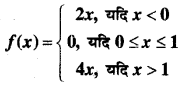
हल:


⇒ L.H.L. ≠ R.H.L.
अतः f (x), x = 1 पर संतत नहीं है। पुनः x > 1 के लिए,
f(x) = 4x, जो कि बहुपद है।
∴ x > 1 पर f सतत होगा।
अतः x = 1 के अतिरिक्त f सभी बिन्दुओं पर संतत होगा अथवा केवल x = 1 पर असांतत्य होगा।

प्रश्न 16.

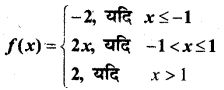
हल:

प्रश्न 17.
a और b के उन मानों को ज्ञात कीजिए। जिनके लिए

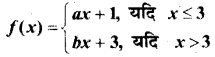
द्वारा परिभाषित फलन x = 3 पर संतत है।
हल:

अत: b के प्रत्येक मान के लिए इसके संगत a का मान ज्ञात कर सकते हैं।

प्रश्न 18.
λ के किस मान के लिए

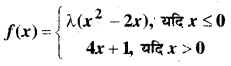
द्वारा परिभाषित फलन x = 0 पर संतत है। x = 1 पर इसके सांतत्य पर विचार कीजिए।
हल:

प्रश्न 19.
दर्शाइए कि g(x) = x – [x] द्वारा परिभाषित फलन समस्त पूर्णांक बिन्दुओं पर असंतत है। यहाँ [x] उस महत्तम पूर्णाक निरूपित करता है, जो x के बराबर या x से कम है।
हल:
x = c पूर्णांक पर, f(x) = x – [x]

प्रश्न 20.
क्या f(x) = x² – sin x + 5 द्वारा परिभाषित फलन x = π पर संतत है?
हल:
माना f(x) = x² – sin x + 5

प्रश्न 21.
निम्नलिखित फलनों के सातत्य पर विचार कीजिए –
(a) f(x) = sin x + cosx
(b) f(x) = sin x – cosx
(c) f(x) = sin x. cosx
हल:

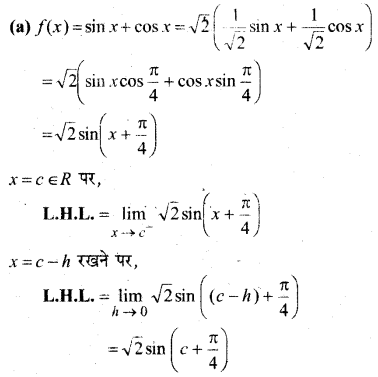
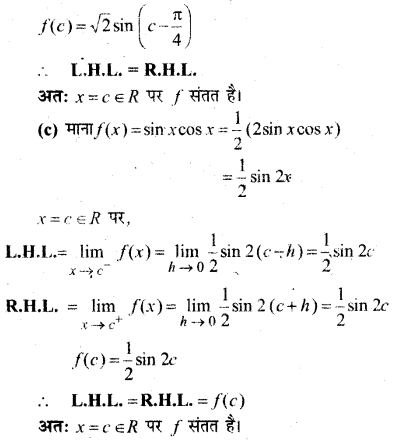
प्रश्न 22.
cosine, cosecant, secant और cotangent फलनों के सातत्य पर विचार कीजिए।
हल:
(a) माना f(x) = cos x

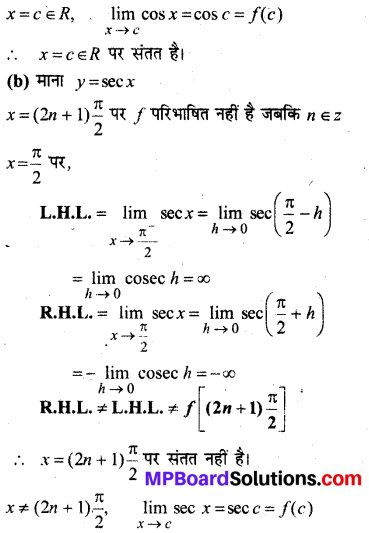
प्रश्न 23.
f के सभी असातत्यता के बिन्दुओं को ज्ञात कीजिए, जहाँ

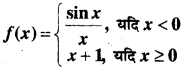
हल:

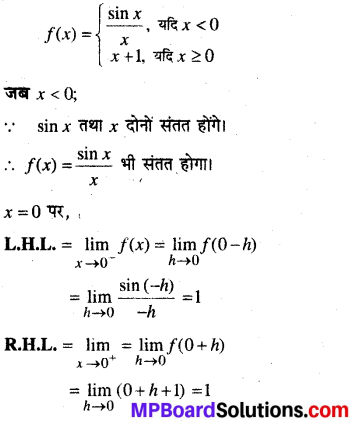
तथा f(0) = 0 + 1 = 1
∴ x = 0 पर f संतत फलन है।
जब x > 0, f(x) = x + 1, जो कि बहुपद है।
∴ f एक संतत फलन होगा।
अतः f प्रत्येक बिन्दु पर संतत फलन है।

प्रश्न 24.
निर्धारित कीजिए कि फलन f

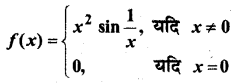
द्वारा परिभाषित एक संतत फलन है।
हल:

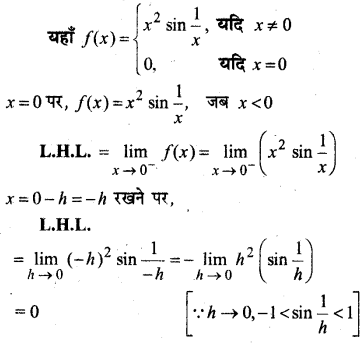
प्रश्न 25.
f के सातत्य की जाँच कीजिए, जहाँ f निम्नलिखित प्रकार से परिभाषित है-

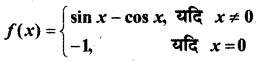
हल:

∴ x = c ≠ 0 पर f संतत है।
अत: x ϵ R, सभी बिन्दुओं पर f संतत है।

प्रश्न 26 से 29 में k के मानों को ज्ञात कीजिए ताकि प्रदत्त फलन निर्दिष्ट बिन्दु पर संतत हो-
प्रश्न 26.

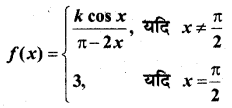
द्वारा परिभाषित फलन x = \(\frac{\pi}{2}\) पर।
हल:
x = \(\frac{\pi}{2}\) पर,

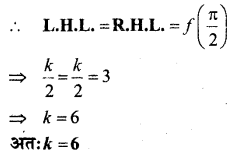
प्रश्न 27.

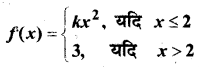
द्वारा परिभाषित फलन x = 2 पर।
हल:

प्रश्न 28.

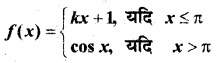
द्वारा परिभाषित फलन x = π पर।
हल:

प्रश्न 29.

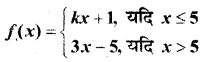
द्वारा परिभाषित फलन x = 5 पर
हल:

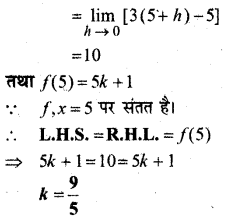
प्रश्न 30.
a तथा b के मानों को ज्ञात कीजिए ताकि

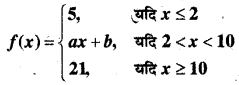
द्वारा परिभाषित फलन एक संतत फलन हो।
हल:
प्रश्न (15) की भाँति करें।
x = 3 पर
L.H.L. = 5
R.H.L. = 2a + b
तथा f(2) = 5
∵ f(x) x = 2 पर संतत फलन है।
∴ L.H.L. = R.H.L.
2a + b = 5
पुनः f (x), x = 10 पर संतत है।
∴ L.H.S. = R.H.S. = f(10)

प्रश्न 31.
दर्शाइए कि f(x) – cos (x²) द्वारा परिभाषित फलन एक संतत फलन है
हल:
f(x) = cos(x²)
माना g(x) = cosx तथा h (x) = x²
∴ goh (x) = g[h (x)] = g(x²)
= cos (x²) = f(x)
∵ g (x) एक कोज्या (cosine) का एक फलन है जो कि संतत होता है।
तथा h (x) एक बहुपद है।
इसलिए f(x) भी एक संतत फलन है।

प्रश्न 32.
दर्शाइए कि f(x) = | cos x| द्वारा परिभाषित फलन एक संतत फलन है।
हल:
यहाँ f(x) = |cosx|
सर्वप्रथम माना x = c ϵ R पर,
\(\lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c}|\cos x|=|\cos c|\)
f(c) = |cosc|
अतः x = C ϵ R पर एक संतत फलन है।

प्रश्न 33.
जाँचिए कि क्या sin |x|एक संतत फलन है।
हल:
माना f(x) = sin |x|
प्रथम विधि-
x = c ϵ R पर,
\(\lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c}(\sin |x|)=\sin |c|\)
f(c) = sin |c|
अतः x = c ϵ R पर एक संतत फलन है।
दूसरी विधि से-
माना g (x) = sin x, h (x) = |x|
f(x) = (goh)(x) = g (h (x)) = g (|x|) = sin |x|
g(x) = sin x 3ite h(x) = |x|
g और h दोनों संतत फलन हैं।
अतः f भी संतत फलन है।

प्रश्न 34.
f(x) = |x| – |x + 1| द्वारा परिभाषित फलन के सभी असांत्यता के बिन्दुओं को ज्ञात कीजिए।
हल:
यहाँ f(x) = |x| – |x + 1|
f(x) = -x[ – (x +1)], [जब x < – 1]
= – x + x + 1 = 1
f(x) = – x – (x + 1), [जब -1 ≤ x < 0]
= – x – x – 1
= – 2x – 1
f(x) = x – (x + 1), जब x ≥ 0
= x – x – 1 = – 1

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित Ex 10.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित Ex 10.2

प्रश्न 1.
निम्नलिखित सदिशों के परिमाण का परिकलन कीजिए-

हल:

प्रश्न 2.
समान परिमाण वाले दो विभिन्न सदिश लिखिए
हल:
माना \(\vec{a}=\hat{i}+2 \hat{j}+3 \hat{k}\) और \(\vec{b}=3 \hat{i}+\hat{j}+2 \hat{k}\) दो भिन्न वेक्टर हैं परन्तु इनके परिणाम समान हैं।

प्रश्न 3.
समान दिशा वाले दो विभिन्न सदिश लिखिए
हल:
माना दो सदिश वे \(\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=3 \hat{i}+3 \hat{j}+3 \hat{k}\)

प्रश्न 4.
x और y के मान ज्ञात कीजिए ताकि सदिश \(2 \hat{i}+3 \hat{j}\) और \(x \hat{i}+y \hat{j}\) समान हों।
हल:
\(2 \hat{i}+3 \hat{j}+x \hat{i}+y \hat{j}\)
\(\hat{i}\) और \(\hat{j}\) के गुणांकों की तुलना करने पर,
∴ x = 2, y = 3

प्रश्न 5.
एक सदिश का प्रारम्भिक बिन्दु (2, 1) और अन्तिम बिन्दु (-5, 7) है। इस सदिश के अदिश एवं सदिश घटक ज्ञात कीजिए।
हल:
माना सदिश के प्रारम्भिक व अन्तिम बिन्दु A (2, 1) व B (-5, 7) हैं। तब

अत: \(\overrightarrow{A B}\) के अदिश घटक –7 तथा 6 हैं व सदिश घटक \(-7 \hat{i}\) और \(6 \hat{j}\) हैं।

प्रश्न 6.
सदिश \(\vec{a}=\hat{i}-2 \hat{j}+\hat{k}, \quad \vec{b}=-2 \hat{i}+4 \hat{j}+5 \hat{k}\) और \(\vec{c}=\hat{i}-6 \hat{j}-7 \hat{k}\) का योगफल ज्ञात कीजिए।
हल:

प्रश्न 7.
सदिश \(\vec{a}=\hat{i}+\hat{j}+2 \hat{k}\) के अनुदिश एक मात्रक सदिश ज्ञात कीजिए।
हल:

प्रश्न 8.
सदिश \(\overrightarrow{P Q}\) के अनुदिश मात्रक सदिश ज्ञात कीजिए जहाँ बिन्दु P और Q क्रमशः (1, 2, 3) और (4, 5, 6) हैं।
हल:

प्रश्न 9.
दिए हुए सदिशों \(\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}\) और \(\vec{b}=-\hat{i}+\hat{j}-\hat{k}\) के लिए सदिश \(\vec{a}+\vec{b}\) के अनुदिश मात्रक सदिश ज्ञात कीजिए।
हल:

प्रश्न 10.
सदिश \(5 \hat{i}-\hat{j}+2 \hat{k}\) के अनुदिश एक ऐसा सदिश ज्ञात कीजिए जिसका परिमाण 8 इकाई है।
हल:

प्रश्न 11.
दर्शाइए कि सदिश \(2 \hat{i}-3 \hat{j}+4 \hat{k}\) और \(-4 \hat{i}+6 \hat{j}-8 \hat{k}\) संरेख हैं।
हल:

क्योंकि \(\vec{a}\) और \(\vec{b}\) की दिशा समान हैं अतः ये संरेख हैं।

प्रश्न 12.
सदिश \(\hat{i}+2 \hat{j}+3 \hat{k}\) की दिक् cosine ज्ञात कीजिए।
हल:

प्रश्न 13.
बिन्दुओं A (1, 2,-3) एवं B(-1, -2, 1) को मिलाने वाले एवं A से B की तरफ दिष्ट सदिश की दिक् cosine ज्ञात कीजिए।
हल:
A (1, 2, -3) एवं B (-1, – 2, 1)

प्रश्न 14.
दर्शाइए कि सदिश \(\hat{\boldsymbol{i}}+\hat{\boldsymbol{j}}+\hat{\boldsymbol{k}}\) अक्षों OX,OY तथा OZ के साथ बराबर झुका हुआ है।
हल:
माना A = \(\vec{A}=\hat{i}-\hat{j}+\hat{k}\)
माना सदिश \(\vec{a}\) अक्ष OX, OY एवं OZ के साथ क्रमश: α, β तथा γ कोण बनाता है तथा इनके दिक् cosine cos α, cos β तथा cos γ हैं।

प्रश्न 15.
बिन्दुओं P = \((\hat{i}+2 \hat{j}-\hat{k})\) और Q = \((-\hat{i}+\hat{j}+\hat{k})\) को मिलाने वाली रेखा को 2 : 1 के अनुपात में (i) अंत: (ii) बाह्य, विभाजित करने वाले बिन्दु R का स्थिति सदिश ज्ञात कीजिए।
हल:
(i) अन्त : विभाजन

(ii) बाह्य विभाजन
बिन्दु R रेखा को 2 : 1 में बाह्य विभाजित करता है अतः

प्रश्न 16.
दो बिन्दुओं P(2, 3, 4) और Q (4, 1, -2) को मिलाने वाले सदिश का मध्य बिन्दु ज्ञात कीजिए।
हल:
P और Q को मिलाने वाले सदिश का मध्य बिन्दु \(\frac{\vec{a}+\vec{b}}{2}\)

प्रश्न 17.
दर्शाइए कि बिन्दु A, B और C जिनके स्थिति सदिश क्रमश: \(\vec{a}=3 \hat{i}-4 \hat{j}-4 \hat{k}, \quad \vec{b}=2 \hat{i}-\hat{j}+\hat{k}\) और \(\vec{c}=\hat{i}-3 \hat{j}-5 \hat{k}\) हैं, एक समकोण त्रिभुज के शीर्षों का निर्माण करते हैं।
हल:

प्रश्न 18.
संलग्न चित्र में त्रिभुज ABC के लिए निम्नलिखित में से कौन-सा कथन सत्य नहीं है?

हल:
सदिशों के योगफल त्रिभुज नियम के अनुसार,

प्रश्न 19.
यदि \(\vec{a}\) और \(\vec{b}\) दो संरेख सदिश हैं तो निम्नलिखित में से कौन-सा कथन सही नहीं है?
(b) \(\vec{b}=\lambda \vec{a}\)किसी अदिश λ के लिए
(B) \(\vec{a}=\pm \vec{b}\)
(C) \(\vec{a}\) और \(\vec{b}\) के के क्रमागत घटक समानुपाती नहीं हैं।
(D) दोनों सदिशों के \(\vec{a}\) तथा \(\vec{b}\) की दिशा समान है परन्तु परिमाण विभिन्न हैं।
हल:
पहले तीन कथन (A), (B), (C) सही हैं परन्तु संरेख सदिश समान्तर होते हैं। यह आवश्यक नहीं है कि दिशा समान हो या परिमाण समान हों।
अतः विकल्प (D) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.4 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.4

निम्नलिखित सारणिकों के अवयवों के उपसारणिक एवं सहखण्ड लिखिए।
प्रश्न 1.

हल:
\(\left|\begin{array}{cc}{2} & {-4} \\ {0} & {3}\end{array}\right|\)
a₁₁ का उपसारणिक M₁₁ = 3
a₁₂ का उपसारणिक M₁₂ = 0
a₂₁ का उपसारणिक M₂₁ = -4
a₂₂ का उपसाराणिक M₂₂ = 2
a₁₁ का सहखण्ड = A₁₁ = (-1)¹⁺¹
M₁₁ = (-1)² × 3 =3
a₁₂ का सहखण्ड = A₁₂ = (-1)¹⁺²
M₁₂ = (-1)³ × 0 = 0
a₂₁ का सहखण्ड = A₁₃ = (-1)² + 1
M₂₁ = (-1)³ × (-4) = 4
a₂₂ का सहखण्ड = A₂₂ = (-1)²⁺²
M₂₂ = (-1)⁴ × 2 = 2

(ii) यहाँ \(\left|\begin{array}{ll}{a} & {c} \\ {b} & {d}\end{array}\right|\) सारणिक \(\left|\begin{array}{ll}{a} & {c} \\ {b} & {d}\end{array}\right|\) के अवयवों के उपसारणिक निम्न हैं-
M₁₁ = d
M₁₂ = b
M₂₁ = c
M₂₂ = a
इसलिए सहखंड निम्न होंगे-
A₁₁ = d
A₁₂ = -b
A₂₁ = -c
तथा A₂₂ = 1

प्रश्न 2.

हल:


A₁₁ = (-1)¹⁺¹ M₁₁ = (-1)² × 1 = 1
A₁₂ = 1¹⁺² M₁₂ = (-1)³ × 0= 0
A₁₃ = (-1)¹⁺³ M₁₃ = (-1)⁴ × 0 = 0
A₂₁ = (-1)²⁺¹ M₂₁ = (-1)³ × 0 = 0
A₂₂ = (-1)²⁺² M₂₂ = (-1)⁴ × 1 = 1
A₂₃ = (-1)²⁺³ M₂₃ = (-1)⁵ × 0 = 0
A₃₁ =(-1)³⁺¹ M₃₁ = (-1)⁴ × 0 = 0
A₃₂ = (-1)³⁺² M₃₂ = (-1)⁵ × 0= 0
A₃₃ = (-1)³⁺³ M₃₃ = (-1)⁶ × 1 = 1

(ii) यहाँ \(\left|\begin{array}{ccc}{1} & {0} & {4} \\ {3} & {5} & {-1} \\ {0} & {1} & {2}\end{array}\right|\) उपसारणिक और सहखण्ड की परिभाषां से a₁ का उपसारणिक M₁ = \(\left|\begin{array}{cc}{5} & {-1} \\ {1} & {2}\end{array}\right|\) = 10 + 1 = 11
हल:

प्रश्न 3.
दूसरी पंक्ति के अवयवों के सहखण्डों का प्रयोग करके ∆ = \(\left|\begin{array}{lll}{5} & {3} & {8} \\ {2} & {0} & {1} \\ {1} & {2} & {3}\end{array}\right|\) का मान ज्ञात कीजिए।
हल:

दूसरी पंक्ति से सारणिक का विस्तार करने पर,
∆ = a₂₁ A₂₁ + a₂₂ A₂₂ + a₂₃ A₂₃
= 2 × 7 + 0 × 7 + 1 × (-7)
= 14 + 0 – 7 = 7

प्रश्न 4.
तीसरे स्तम्भ के अवयवों के सहखण्डों का प्रयोग करके ∆ = \(\left|\begin{array}{ccc}{1} & {x} & {y z} \\ {1} & {y} & {z x} \\ {1} & {z} & {x y}\end{array}\right|\) का मान ज्ञात कीजिए।
हल:

A₂₃ = (-1)²⁺³ \(\left|\begin{array}{ll}{1} & {x} \\ {1} & {z}\end{array}\right|\) = (-1)⁵ [z – y]
= -(z – x)
A₃₃ = (-1)³⁺³ \(\left|\begin{array}{ll}{1} & {x} \\ {1} & {y}\end{array}\right|\) = (-1)⁶ [y – x] = (y – x)
∴ ∆ = a₁₃ A₁₃ + a₂₃ A₂₃ + a₃₃ A₃₃
= yz (z – y) + zx (-z + x) + xy(y – x)
= yz² – y²z – xz² + x²z + xy² – x²y
= (-y²z + yz²) + (y² – xz²) + (-x²y + x²z)
= – yz (y – z) + x(y² – z² ) – x²(y – z)
= (y – z)[-yz + x (y + z) – x²]
= (y – z)[z (x – y) – x(x – y)]
= (y – z)(x – y)(z – x)
= (x – y)(y – z)(z – x)

प्रश्न 5.
यदि ∆ = \(\left|\begin{array}{lll}{a_{11}} & {a_{12}} & {a_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right|\) और a_ij का सहखण्ड A_ij हो तो ∆ का मान निम्नलिखित रूप में व्यक्त किया जाता है
(A) A₁₁ A₃₁ + a₁₂ A₃₂ + a₁₃ A₃₃
(B) a₁₁ A₁₁ + a₁₂ A₂₁ + a₁₃ A₃₁
(C) a₂₁ A₁₁ + a₂₂ A₁₂ + a₂₃ A₁₃
(D) a₁₁ A₁₁ + a₂₁ A₂₁ + a₃₁ A₃₁
हल:
∆ = किसी पंक्ति (या स्तम्भ) के अवयवों तथा उनके संगत सहखण्डों के गुणन का योग
C₁ स्तम्भ के अवयव (a₁₁, a₂₁, a₃₁)
इनमें सहखण्ड a₁₁, A₂₁, A₃₁
⇒ ∆ = a₁₁ A₁₁ + a₂₁ A₂₁ + a₃₁ A₃₁
अत: विकल्प (D) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.1

प्रश्न 1 से 2 तक में सारणिकों का मान ज्ञात कीजिए
प्रश्न 1.
\(\left|\begin{array}{cc}{2} & {4} \\ {-5} & {-1}\end{array}\right|\)
हल:
\(\left|\begin{array}{cc}{2} & {4} \\ {-5} & {-1}\end{array}\right|\) = 2 × (-1) – 4 × (-5) = -2 + 20 = 18

प्रश्न 2.

हल:
(i) \(\left|\begin{array}{cc}{\cos \theta} & {-\sin \theta} \\ {\sin \theta} & {\cos \theta}\end{array}\right|\)
=cose θ cosθ – (sin θ) × (-sin θ)
= cos²θ + sin²θ
= 1

(ii) \(\left|\begin{array}{cc}{x^{2}-x+1} & {x-1} \\ {x+1} & {x+1}\end{array}\right|\)
= (x² – x + 1)(x + 1) – (x + 1)(x – 1)
= (x + 1) – (x² – 1) = x³ + 1 – x² + 1
= x³ – x² + 2

प्रश्न 3.
यदि A = \(\left[\begin{array}{ll}{1} & {2} \\ {4} & {2}\end{array}\right]\), तो दिखाइए |2A| = 4|A|
हल:

प्रश्न 4. यदि A = \(\left|\begin{array}{lll}{1} & {0} & {1} \\ {0} & {1} & {2} \\ {0} & {0} & {4}\end{array}\right|\) हो, तो दिखाइए |3A| = 27|A|
हलः

प्रश्न 5.
निम्नलिखित सारणिकों का मान ज्ञात कीजिए-

हल:



= 0[0-(-3) × 3][-1 × 0 – (-3) × (-2)] + 2[3 × (-1) – (-2) × 0]
= 0 × 9 – 1[0 – 6] + 2[-3 – 0]
= 0 – 1 × (-6) + 2 × (-3)
= 6 – 6 = 0

= 2[2 × 0 – (-1) × (-5)] + 1[0 × 0 – (-1) × 3] – 2[0 × (-5) – 2 × 3]
= 2[0 – 5] + 1[0 + 3] – 2 × [0 – 6]
= 2 × (-5) + 1 × 3 – 2 × (-6)
= -10 + 3 + 12 = -10 + 15 = 5

प्रश्न 6.
यदि A = \(\left|\begin{array}{ccc}{1} & {1} & {-2} \\ {2} & {1} & {-3} \\ {5} & {4} & {-9}\end{array}\right|\), हो तो |A| ज्ञात कीजिए।
हल:

प्रश्न 7.
x के मान ज्ञात कीजिए यदि

हल:

⇒ 2 – 20 = 2x² – 24
⇒ -18 = 2x² – 24
⇒ 2x² – 24 +18 = 0
⇒ 2x² -6 =0
⇒ x² = 3
⇒ x = ±\( \sqrt{{3}} \)

⇒ 10 – 12 = 5x – 6x
-2x³ = – x
x = 2

प्रश्न 8.
यदि \(\left|\begin{array}{cc}{x} & {2} \\ {18} & {x}\end{array}\right|=\left|\begin{array}{cc}{6} & {2} \\ {18} & {6}\end{array}\right|\) हो तो x बराबर है-
(A) 6
(B) ±6
(C) -6
(D) 0
हल:
\(\left|\begin{array}{cc}{x} & {2} \\ {18} & {x}\end{array}\right|=\left|\begin{array}{cc}{6} & {2} \\ {18} & {6}\end{array}\right|\)
⇒ x × x -2 × 18 = 6 × 6 – 2 × 18
⇒ x² – 36 = 36 – 36
⇒ x² – 36 = 0
⇒ x = 36
∴ x = ±6
अतः विकल्प (B) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 3 आव्यूह Ex 3.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 3 आव्यूह Ex 3.1

प्रश्न 1.
आव्यूह A = \(\left[\begin{array}{cccc}{2} & {5} & {19} & {-7} \\ {35} & {-2} & {5 / 2} & {12} \\ {\sqrt{3}} & {1} & {-5} & {17}\end{array}\right]\), के लिए ज्ञात कीजिए:
(i) आव्यूह की कोटि
(ii) अवयवों की संख्या
(iii) अवयव a₁₃, a₂₁, a₃₃, a₂₄, a₂₃
हल:
(i) आव्यूह A में पंक्तियों की संख्या = 3
तथा स्तम्भों की संख्या = 4
इसलिए आव्यूह की कोटि = 3 × 4
(ii) अवयवों की संख्या = 3 × 4 = 12 अवयव
(iii) a₁₃ = पहली पंक्ति व तीसरे स्तम्भ का अवयव = 19
इसी प्रकार,
a₂₁ = 35, a₃₃ =-5, a₂₄ = 12 तथा a₂₃ = \(\frac{5}{2}\)

प्रश्न 2.
यदि किसी आव्यूह में 24 अवयव हैं तो इसकी संभव कोटियाँ क्या हैं? यदि इसमें 13 अवयव हों तो कोटियाँ क्या होंगी?
हल:
(i) 24 अवयवों वाले आव्यूह की संभव कोटियाँ निम्न प्रकार हैं
1 × 24, 24 × 1, 2 × 12, 12 × 2, 3 × 8, 8 × 3, 4 × 6, 6 × 4
(ii) 13 अवयवों वाले आव्यूह की कोटियाँ = 1 × 13 और 13 × 1

प्रश्न 3.
यदि किसी आव्यूह में 18 अवयव हैं तो इसकी संभव कोटियाँ क्या हैं? यदि इसमें 5 अवयव हों तो क्या होगा?
हल:
(i) 8 अवयवों वाले आव्यूह की कोटियाँ निम्न प्रकार हैं- 18 × 1, 2 × 9, 3 × 6, 6 × 3, 9 × 2, 1 × 18
(ii) 5 अवयवों वाले आव्यूह की कोटियाँ = 1 × 5, 5 × 1

प्रश्न 4.
एक 2 × 2 आव्यूह A = [a_ij] की रचना कीजिए जिसके अवयव निम्नलिखित प्रकार से प्रदत्त हैं-

हल:

प्रश्न 5.
एक 3 × 4 आव्यूह की रचना कीजिए जिसके अवयव निम्नलिखित प्रकार से प्राप्त होते हैं-
(i) a_ij = \(\)|-3i + j|
(ii) a_ij = 2i – j
हल:

प्रश्न 6.
निम्नलिखित समीकरणों से x, y तथा z के माम ज्ञात कीजिए-

हल:
(i) \(\left[\begin{array}{ll}{4} & {3} \\ {x} & {5}\end{array}\right]=\left[\begin{array}{ll}{y} & {z} \\ {1} & {5}\end{array}\right]\)
∵ दोनों आव्यूह समान हैं
∴ संगत अवयवों को समान रखने पर
4 = y ⇒ y = 4
3 = z ⇒ 2 = 3
तथा x = 1
अतः x = 1, y = 4 तथा z = 3

(ii) \(\left[\begin{array}{cc}{x+y} & {2} \\ {5+z} & {x y}\end{array}\right]=\left[\begin{array}{ll}{6} & {2} \\ {5} & {8}\end{array}\right]\)
दो आव्यूहों की समानता परिभाषा. से संगत अवयवों को समान रखने पर,
x + y = 6 ⇒ y = 6 – x
तथा xy = 8
⇒ x (6 – x) = 8 ⇒ 6x – x² = 8
x² – 6x + 8 = 0
⇒ (x – 4)(x – 2) = 0 ⇒ x = 4, 2
∴ y = 2, 4
तथा 5 + z = 5 ⇒ z = 0
अत: x = 4, y = 2 तथा z = 0 अथवा x = 2, y = 4 व z = 0

(iii) \(\left[\begin{array}{c}{x+y+z} \\ {x+z} \\ {y+x}\end{array}\right]=\left[\begin{array}{c}{9} \\ {5} \\ {7}\end{array}\right]\)
दोनों आव्यूहों के संगत अवयवों को समान रखने पर,
x + y + z = 9 …. (i)
x + z = 5 … (ii)
y + z = 7 … (iii)
समी (i) व (iii) से,
x + 7 = 9 ⇒ x²
x का मान (ii) में रखने पर,
2 + z = 5 ⇒ z = 3
तथा y = 7 – 3 = 4
अतः x = 2, y = 4 तथा z = 3

प्रश्न 7.
समीकरण \(\) से a, b, c तथा d के मान ज्ञात कीजिए।
हल:
दोनों आव्यूह के संगत अवयवों को समान रखने पर,
a – b = -1 …(i)
2a – b = 0 ⇒ 2a = b …(ii)
2a + c = 5 ….(iii)
तथा 3c + d = 13 ….(iv)
समी० (i) व (ii) से,
a – 2a = -1 ⇒ a = -1
∴ b = 2
समी० (iii) से,
2 (1) + c = 5
⇒ c = 5 + 2 = 7
समी० (iv) 3c + d = 13
d = 13 – 21 = 8
अतः a = 1, b = -2, c = 7 तथा d = 8

प्रश्न 8.
A = [a_ij]_m×n एक वर्ग आव्यूह है यदि
(A) m < n (B) m > n
(C) m = n
(D) इनमें से कोई नहीं
हल:
वर्ग आव्यूह में पंक्तियों की संख्या स्तम्भों की संख्या के समान है।
m = n
अतः विकल्प (C) सही है।

प्रश्न 9.
x तथा y के प्रदत्त किन मानों के लिए आव्यूहों के निम्नलिखित युग्म समान हैं-

हल:
दिए हुए आव्यूह समान हैं।
3x + 7 = 0 ⇒ 3x = -7 ∴ x = \(-\frac{7}{3}\)
तथा 5 = y – 2 ⇒ 5 + 2 = y ∴ y = 7
2 – 3x = 4 ⇒ -3x = 4 – 2
⇒ -3x = 2 ∴ x = \(-\frac{2}{3}\)
x के दो मान \(-\frac{7}{3}\) और \(-\frac{2}{3}\) हैं। यह नहीं हो सकता।
अतः विकल्प (B) सही है।

प्रश्न 10.
3 × 3 कोटि के ऐसे आव्यूहों की कुल कितनी संख्या होगी जिनकी प्रत्येक प्रविष्टि 0 या 1 है?
(A) 27
(B) 18
(C) 81
(D) 512
हल:
3 × 3 कोटि के 9 अवयव हों तो प्रत्येक स्थान पर 0 या 1 रख सकते हैं।
0 के स्थानों को भरने के लिए 2⁹ = 512 तरीके हो सकते हैं।
∴ सम्भव आव्यूहों की संख्या = 512
अतः विकल्प (D) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 3 आव्यूह विविध प्रश्नावली Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Solutions Chapter 3 आव्यूह विविध प्रश्नावली

प्रश्न 1.
मान लीजिए कि A = \(\left[\begin{array}{ll}{0} & {1} \\ {0} & {0}\end{array}\right]\) हो तो दिखाइए कि सभी nEN के लिए (aI + bA)ⁿ = aⁿI + na^n-1 bA, जहाँ I कोटि 2 का तत्समक आव्यूह है।
हल:

प्रश्न 2.
यदि A = \(\left[\begin{array}{lll}{1} & {1} & {1} \\ {1} & {1} & {1} \\ {1} & {1} & {1}\end{array}\right]\), तो सिद्ध कीजिए कि

हल:



∴ P(n) सत्य है n = k +1 के लिए,
इसलिए गणितीय आगमन सिद्धान्त के अनुसार p(n), n के सभी n ϵ N मान के लिए सत्य है जब n ϵ N.

प्रश्न 3.
यदि A = \(\left[\begin{array}{ll}{3} & {-4} \\ {1} & {-1}\end{array}\right]\), तो सिद्ध कीजिए कि Aⁿ = \(\left[\begin{array}{cc}{1+2 n} & {-4 n} \\ {n} & {1-2 n}\end{array}\right]\) जहाँ n एक धन पूर्णांक है।
हल:


∴ P(n) सत्य है n = k + 1 के लिए
इसलिए गणितीय आगमन सिद्धान्त के अनुसार P(n), n ϵ N के सभी मानों के लिए सत्य है। n ϵ N.

प्रश्न 4.
यदि A तथा B सममित आव्यूह हैं तो सिद्ध कीजिए कि AB – BA एक विषम सममित आव्यूह है।
हल:
यदि A और B सममित आव्यूह हैं।
∴ A’ = A और B’ = B
(AB – BA) = (AB)’ – (BA)’ [∵ (X – Y) = X’ – Y’]
= B’A’ – A’B’ [∵ (XY) =Y’X’]
= BA – AB [∵ B’ = B, A’ = A]
= – (AB – BA)
∴ AB – BA एक विषम सममित आव्यूह है।

प्रश्न 5.
सिद्ध कीजिए कि आव्यूह B’ AB सममित अथवा विषम सममित है, यदि A सममित अथवा विषम सममित है।
हल:
(i) माना A सममित आव्यूह है।
तब A’ = A
∴ (B’ AB) = (B’ (AB)) =(AB)'(B’)’
= (B’A’)B
=B’ AB [∵ (AB)’ = B’A’ और A’ = A]
⇒ B’ AB एक सममित आव्यूह है।

(ii) माना A विषम सममित आव्यूह है।
∴ A’ = -A
अब, (B'(AB))’ = (AB)’ (B’)’ = (B’A’)B
= B'(-A)B = – B’ AB [∵ A’ = -A]
=-(B’ AB)
अत: B’ AB एक विषम सममित आव्यूह है।

प्रश्न 6.
x, y तथा z के मानों को ज्ञात कीजिए, यदि आव्यूह A = \(\left[\begin{array}{ccc}{0} & {2 y} & {z} \\ {x} & {y} & {-z} \\ {y} & {-y} & {z}\end{array}\right]\) समीकरण A’ A = I को सन्तुष्ट करता है।
हल:

प्रश्न 7.
x के किस मान के लिए

हल:

प्रश्न 8.
यदि A = \(\left[\begin{array}{cc}{3} & {1} \\ {-1} & {2}\end{array}\right]\) हो तो सिद्ध कीजिए कि A² – 5A + 7I = 0 है।
हल:

प्रश्न 9.
यदि [x -5 -1]\(\left[\begin{array}{lll}{1} & {0} & {2} \\ {0} & {2} & {1} \\ {2} & {0} & {3}\end{array}\right]\left[\begin{array}{l}{x} \\ {4} \\ {1}\end{array}\right]\) = 0 है तो x का मान ज्ञात कीजिए।
हल:

प्रश्न 10.
एक निर्माता तीन प्रकार की वस्तुएँ, x, y तथा z का उत्पादन करता है जिनका वह दो बाजारों में विक्रय करता है। वस्तुओं की वार्षिक बिक्री नीचे सूचित (निदर्शित) है-

(a) यदि x, y तथा z की प्रत्येक इकाई का विक्रय मूल्य क्रमश: Rs. 2.50, Rs. 1.50 तथा Rs. 1.00 है तो प्रत्येक बाजार में कुल आय (Revenue), आव्यूह बीजगणित की सहायता से ज्ञात कीजिए।
(b) यदि उपर्युक्त तीन वस्तुओं की प्रत्येक इकाई की लागत (Cost) क्रमश: Rs. 2.00, Rs. 1.00 तथा पैसे 50 है तो कुल लाभ (Gross Profit) ज्ञात कीजिए।
हल:
(a) वार्षिक बिक्री निम्नलिखित है-

अतः प्रत्येक बाजार से आय रु० 46,000 तथा 53,000 रु० है|

(b) प्रत्येक उत्पाद x, y, z की प्रत्येक इकाई का क्रय मूल्य क्रमशः 2.00,1: 00 तथा 0:50 रु० है।
आव्यूह रूप में लिखने पर,

पहले बाजार का लाभ = विक्रय मूल्य – क्रय मूल्य
46000 – 31000 = 15000 रु०
दूसरे बाजार का लाभ = 53000 – 36000 = 17000 रु०

प्रश्न 11.
आव्यूह X ज्ञात कीजिए, यदि

हल:

प्रश्न 12.
यदि A तथा B समान कोटि के वर्ग आव्यूह इस प्रकार हैं कि AB = BA है तो गणितीय आगमन द्वारा सिद्ध कीजिए कि ABⁿ = BⁿA होगा। इसके अतिरिक्त सिद्ध कीजिए कि समस्त n ϵ N के लिए (AB)ⁿ = AⁿBⁿ होगा।
हल:
माना P(n): ABⁿ = BⁿA, जबकि AB = BA
किन्तु n = 1, AB = BA (दिया है)
∴ P(n), n = 1 के लिए सत्य है।
माना P(n) सत्य है, n = k के लिए,
∴ AB^k = B^k A सत्य है।
दोनों ओर B से गुणा करने पर,
L.H.S. = AB^k . B = A (B^k B) = AB^k+1
R.H.S. = (B^k A)B = B^k (AB)
= B^k (BA)
= (B^k B) A = B^k+1A [∵ AB = BA दिया है]
∴ AB^k+1 = B^k+1A
⇒ P(n) सत्य है, n = k + 1 के लिए
इसलिए गणितीय · आगमन सिद्धान्त के अनुसार P(n), n ϵ N के सभी मानों के लिए सत्य है, जबकि n ϵ N
माना P(n): (AB)ⁿ = AⁿBⁿ
n = 1 रखने पर,
L.H.S. = (AB)’ = AB
R.H.S. = A’B’ = AB
P(n), n = 1 के लिए सत्य है।
माना P(n) सत्य है, n = k के लिए.
(AB)^k = A B^k
दोनों पक्षों को AB से गुणा करने पर,
L.H.S. = (AB)^k AB = (AB)^k+1
R.H.S. = A^k B^k . (AB)
= A^k B^k (BA) [∵ AB = BA दिया है।]
= A^k (B^k B)A
= A^k (B^k+1A) [∵ AB^k = B^kA]
= (A^k A)B^k+1 = A^k+1. B^k+1
अतः (AB)^k+1 = A^k+1. B^k+1
∴ P(n) सत्य है, n = k + 1 के लिए, . .
गणितीय आगमन सिद्धान्त के अनुसार P(n), n ϵ N के सभी मानों के लिए सत्य है जबकि n ϵ N.

निम्नलिखित प्रश्नों में सही उत्तर चुनिए-
प्रश्न 13.
यदि A = \(\left[\begin{array}{cc}{\alpha} & {\beta} \\ {\gamma} & {-\alpha}\end{array}\right]\) इस प्रकार है कि A² = I, तो:
(A) 1 + α² + βγ = 0
(B) 1 – α² + βγ = 0
(C) 1 – α² – βγ = 0
(D) 1 + α² + βγ = 0
हल:

α² + βγ = 1 या 1 – α² – βγ = 0
अतः विकल्प (C) सही है।

प्रश्न 14.
यदि एक आव्यूह सममित तथा विषम सममित दोनों ही है तो:
(A) A एक विकर्ण आव्यूह है।
(B) A एक शून्य आव्यूह है।
(C) A एक वर्ग आव्यूह है।
(D) इनमें से कोई नहीं।
हल:
सममित आव्यूह में, a_ij = a_ji …(1)
विषम सममित आव्यूह में, a_ij = -a_ji …(2)
सममित और विषम सममित आव्यूह में दोनों गुण होने चाहिए (1) और (2) को जोड़ने पर,
यदि 2a_ij = a_ij – a_ji = 0
⇒ a_ij = 0
a_ij = a_ji 0
∴ वर्ग आव्यूह एक शून्य आव्यूह (zero matrix) होगा।
अतः विकल्प (B) सही है।

प्रश्न 15.
यदि A एक वर्ग आव्यूह इस प्रकार है कि A = A तो (I + A)³ – 7A बराबर है-
(A) A
(B) I – A
(C) I
(D) 3A
हल:
दिया है : A² = A
∵ A³ = A². A
= A.A = A² = A
∴ (I + A)³ – 7A = I³ +3i² A + 3IA² + A³ – 7A
= I³ + 3IA + 3IA² + A³ – 7A
= I + 3A + 3A² + A³ – 7A
= I + 3A + 3A + A² . A – 7A
= I + 3A + 3A + A – 7A
= 7A – 7A + I
अतः विकल्प (C) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.5 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.5

प्रश्न 1 और 2 में प्रत्येक आव्यूह का सहखंडज E (adjoint) ज्ञात कीजिए।
प्रश्न 1.

हल:

प्रश्न 2.

हल:

प्रश्न 3 और 4 में सत्यापित कीजिए कि A (adj A) = (adj A). A =|A|. I है।
प्रश्न 3.

हल:

प्रश्न 4.

हल:

प्रश्न 5 से 11 में दिए गए प्रत्येक आव्यूहों के व्युत्क्रम (जिनका अस्तित्व हो) ज्ञात कीजिए।
प्रश्न 5.

हल:

प्रश्न 6.

हल:

प्रश्न 7.

हल:


प्रश्न 8.

हल:

प्रश्न 9.

हल:

प्रश्न 10.

हल:

प्रश्न 11.

हल:

प्रश्न 12.
यदि A = \(\left[\begin{array}{ll}{3} & {7} \\ {2} & {5}\end{array}\right]\) और B = \(\left[\begin{array}{ll}{6} & {8} \\ {7} & {9}\end{array}\right]\) है तो सत्यापति कीजिए कि (AB)^-1 = B^-1A^-1 है|
हल:

प्रश्न 13.
यदि A = \(\left[\begin{array}{cc}{3} & {1} \\ {-1} & {2}\end{array}\right]\) है तो दर्शाइए कि A² – 5A + 7I = 0 है। इसकी सहायता से A^-1 ज्ञात कीजिए।
हल:

प्रश्न 14.
आव्यूह A = \(\left[\begin{array}{ll}{3} & {2} \\ {1} & {1}\end{array}\right]\) के लिए a और b ऐसी संख्याएँ ज्ञात कीजिए ताकि A² + aA + bI = 0 हो।
हल:

संगत अवयवों की तुलना करने पर
8 + 2a = 0 ⇒ a = -4
11 + 3a + b = 0 ⇒ b = -11 + 12 = 1
अतः a = -4, b = 1

प्रश्न 15.
आव्यूह A = \(\left[\begin{array}{ccc}{1} & {1} & {1} \\ {1} & {2} & {-3} \\ {2} & {-1} & {3}\end{array}\right]\) के लिए दर्शाइए कि A³ – 6A² + 5A + 11I = 0 है। इसकी सहायता से A^-1 ज्ञात कीजिए।
हल:


अब A^-1 ज्ञात करने के लिए गणना
∵ A³ – 6A² + 5A + 11I = 0
दोनों और A^-1 से गुणा करने पर
(A^-1A)A² – 6(A¹ A)A + 5A^-1 A + 11A^-1I = 0
⇒ IA² – 6IA + 51 + 11A^-1 = 0
⇒ A² – 6A + 5I + 11A^-1 = 0
⇒ 11A^-1 = -A² + 6A – 5I

प्रश्न 16.
यदि A = \(\left[\begin{array}{ccc}{2} & {-1} & {1} \\ {-1} & {2} & {-1} \\ {1} & {-1} & {2}\end{array}\right]\), तो सत्यापित कीजिए कि A³ – 6A² + 9A – 4I =0 है तथा इसकी सहायता से A^-1 ज्ञात कीजिए।
हल:

प्रश्न 17.
यदि A, 3 × 3 कोटि का वर्ग आव्यूह है तो | adj A | का मान है
(A)|4|
(B)| A|²
(C)|A}³
(D) 3| A|
हल:
adj A = | A|^n-1, यहाँ n =3
∴ | adj A = | A²
अतः विकल्प (B) सही है।

प्रश्न 18.
यदि A कोटि 2 का व्युत्क्रमणीय आव्यूह है तो det (A^-1) बराबर है
(A) det(A)
(B) \(\frac { 1 }{ det\left( A \right) } \)
(C) 1
(D) 0
हल:
A व्युत्क्रमणीय आव्यूह है ⇒ |A | ≠ 0
∴ AA^-1 = I या |AA^-1| = |I| = 1
या |A || A^-1| = 1
|A^-1| = \(\frac{1}{|A|}\)
⇒ det (A^-1) = \(\frac { 1 }{ det\left( A \right) } \)
अतः विकल्प (B) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.3

प्रश्न 1.
निम्नलिखित प्रत्येक में दिए गए शीर्ष बिन्दुओं वाले त्रिभुजों का क्षेत्रफल ज्ञात कीजिए।
(i) (1, 0), (6, 0), (4, 3)
(ii) (2, 7), (1, 1), (10, 8)
(iii) (-2, -3), (3, 2), (-1, -8)
हल:
(i) (1, 0), (6, 0), (4, 3)
त्रिभुज का क्षेत्रफल :

= \(\frac{1}{2}\)[1(0 – 3) – 0(6 -4 ) + 1(18 – 0)]
= \(\frac{1}{2}\)[-3 + 18]
= \(\frac{1}{2}\) वर्ग इकाई

(ii) (2, 7), (1, 1), (10, 8) x₁ = 2 y₁ = 7, x₂ = 1, y₂ = 1, x₃ = 10, y₃ = 8

= \(\frac{1}{2}\)[2(1 × 1 – 1 × 8) – 7(1 × 1 – 10 × 1) + 1(1 × 8 – 10 × 1)]
= \(\frac{1}{2}\)[2 × (1 – 8) – 7(1 – 10) + 1(8 – 10)]
= \(\frac{1}{2}\)[2 × (-7) – 7 × (-9) + 1 × (-2)]
= \(\frac{1}{2}\)[-14 + 63 – 2] =\(\frac{1}{2}\)[63 – 16]
= \(\frac{1}{2}\) × 47 =\(\frac{47}{2}\) = 23\(\frac{1}{2}\) वर्ग इकाई

(iii) (-2, -3), (3, 2), (-1, -8) त्रिभुज का क्षेत्रफल

= \(\frac{1}{2}\)[-2(2 + 8) + 3 (3 + 1) + 1(-24 + 2)]
= \(\frac{1}{2}\)[-20 + 12 – 22]
= \(\frac{1}{2}\)[-30] = [30] ऋणात्मक चिन्ह को छोड़ने पर
= 15वर्ग इकाई

प्रश्न 2.
दर्शाइए कि बिन्दु A (a, b + c), B (b, c + a) और C(c, a + b) संरेख हैं।
हल:
यहाँ त्रिभुज के शीर्ष A (a, b+ c),B (b, c + a) और C(c, a + b)
x₁ = a x₂ = b x₃ = c y₁ = b + c y₂ = c + a y₃ = a + b

C₁ तथा C₃ समान हैं।
अतः बिन्दु A, B, C संरेख हैं।

प्रश्न 3.
प्रत्येक में k का मान ज्ञात कीजिए यदि त्रिभुजों का क्षेत्रफल 4 वर्ग इकाई है, जहाँ शीर्षबिन्दु निम्नलिखित हैं-
(i) (k, 0), (4, 0), (0, 2)
(ii) (-2, 0), (0, 4), (0, k)
हल:
(i) (k, 0), (4, 0), (0, 2)
त्रिभुज का क्षेत्रफल = 4 वर्ग इकाई

⇒ \(\frac{1}{2}\)[k(-2) + 0 + 1(8)] = ±4
⇒ -k + 5 = ±4
⇒ k= 0 या 8

(ii) त्रिभुज के शीर्ष (-2, 0), (0, 4), (0, k)
x₁ = -2, x₂ = 0, x₃ = 0
y₁ = 0, y₂₁ = 4, y₃ = k

±4 = \(\frac{1}{2}\)[-2(4 – k) + 1(0 – 0)]
±8 = -2(4 – k) ⇒ ±8 = k – 8
+ चिह्न लेने पर, 8 = 2k – 8 ⇒ 2k = 16 ∴ k = 8
-चिह्न लेने पर, -8 = 2k – 8 ∴ k = 0

प्रश्न 4.
(i) सारणिकों का प्रयोग करके (1, 2) और (3, 6) को मिलाने वाली रेखा का समीकरण ज्ञात कीजिए।
(ii) सारणिकों का प्रयोग करके (3, 1) और (9, 3) को मिलाने वाली,रेखा का समीकरण ज्ञात कीजिए।
हल:
(i) माना बिन्दु A (1, 2) व B(3, 6) से मिलाने वाले रेखाखण्ड पर स्थित बिन्दु P(x, y) हैं।
इसलिए बिन्दु A, B, P संरेख होंगे।
∴ ∆PAB का क्षेत्रफल = 0

⇒ x (2 – 6) – y(1 – 3) + 1(6 – 6) = 0
⇒ -4x + 2y = 0
⇒ 2x – y = 0
अतः अभीष्ट रेखा का समी० 2x – y = 0 है।

(ii) माना कोई बिन्दु (x, y) है।
तो त्रिभुज के शीर्ष (x, y), (3, 1) और (9, 3)

∆ = \(\frac{1}{2}\)[x × (-2) – y(-6) + 1 × 0]
∆ = \(\frac{1}{2}\)[-2x + 6y] = -x + 3y
बिन्दु (x, y), (3, 1), (9, 3) संरेख हैं।
यदि ∆ = 0
∴ 0 = -x + 3y ⇒ x – 3y = 0

प्रश्न 5.
यदि शीर्ष (2, -6), (5, 4) और (k, 4) वाले त्रिभुज का क्षेत्रफल 35 वर्ग इकाई है तो k का मान है
(A) 12
(B) -2
(C) -12, -2
(D) 12 ,-2
हल:
त्रिभुज के शीर्ष (2, -6), (5, 4) तथा (k, 4)

±35 = \(\frac{1}{2}\)[2(4 – 4) + 6(5 – k) + 1(20 -4k)]
±35 = \(\frac{1}{2}\) [2 x 0 + 6(5 – k) + 1(20 – 4k)]
±70 = 6(5 – k) + 20 – 4k
±70 = 30 – 6k + 20 – 4k
±70 = 50 = 10k ⇒ ±7 – 5 – k
+ चिह्न लेने पर, 7 = 5 – k
k = 5 – 7 = -2
– चिह्न लेने पर, -7 = 5 – k ⇒ -12 = -k
∴ k = 12
अतः k = -2, 12
अत: विकल्प (D) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन Ex 1.4 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन Ex 1.4

प्रश्न 1.
निर्धारित कीजिए कि क्या निम्नलिखित प्रकार से परिभाषित प्रत्येक संक्रिया से एक द्विआधारी संक्रिया प्राप्त होती है या नहीं। उस दशा में जब एक द्विआधारी संक्रिया नहीं है, औचित्य भी बतलाइए।
(i) Z⁺ में, a * b = a – b द्वारा परिभाषित संक्रिया
(ii) Z⁺ में, a* b = ab द्वारा परिभाषित संक्रिया
(iii) R में, संक्रिया *, a* b = ab² द्वारा परिभाषित
(iv) Z⁺ में, संक्रिया *, a* b = |a – b| द्वारा परिभाषित
(v) Z⁺ में, संक्रिया *, a* b = a द्वारा परिभाषित
हल:
(i) Z⁺ में, a* b = a – b द्वारा परिभाषित संक्रिया है
यदि a > b, a * b = a – b ϵ Z⁺
परन्तु यदि a < b, a * b = a – b < 0, Z⁺ में नहीं है।
अत:* संक्रिया द्विआधारी संक्रिया नहीं है।

(ii) Z⁺ पर * संक्रिया, a * b = ab द्वारा परिभाषित है।
यदि a, b ϵ Z⁺ ⇒ a और b दोनों धनात्मक हैं।
a * b = ab भी धनात्मक है।
ab ϵ Z⁺
अतः यह संक्रिया द्विआधारी है।

(iii) R पर * संक्रिया a* b = ab⁺ द्वारा परिभाषित है।
यदि a, b ϵ R, ab² भी R* में है।
अतः यह संक्रिया द्विआधारी है।

(iv) Z⁺ पर * संक्रिया a * b = |a – b| द्वारा परिभाषित है।
यदि a, b ϵ Z⁺ , |a – b | ϵ Z⁺
अंत: यह संक्रिया द्विआधारी है।

(v) Z⁺ पर * संक्रिया a* b = a द्वारा परिभाषित है।
यदि a, b ϵ Z⁺, ∴ a * b = a ϵ Z⁺
अत: यह संक्रिया द्विआधारी है।

प्रश्न 2.
निम्नलिखित परिभाषित प्रत्येक द्विआधारी संक्रिया के लिए निर्धारित कीजिए कि क्या द्वि आधारी क्रमविनिमेय है तथा क्या साहचर्य है।
(i) Z में, a * b = a – b द्वारा परिभाषित
(ii) Q में, a * b = ab + 1 द्वारा परिभाषित
(iii) Q में, a * b = \(\frac{a b}{2}\) द्वारा परिभाषित
(iv) Z⁺ में, a * b = 2^ab द्वारा परिभाषित
(v) Z⁺ में, a* b = a^b द्वारा परिभाषित
(vi) R – { – 1} में, a* b = \(\frac{a}{b+1}\) द्वारा परिभाषित
हल:
(i) Z पर संक्रिया a* b = a – b द्वारा परिभाषित है।
(a) यदि a * b = a – b और b * a = b – a
परन्तु a – b ≠ b – a ⇒ a* b + b * a
∴ यह संक्रिया क्रमविनिमेय नहीं है।

(b) यदि a * (b * c) = a * (b – c) = a * (b – c)
a – (b – c) = a – b + c
(a * b) * c = (a – b) * c = a – b – c
स्पष्ट है कि a * (b * c) (a * b) * c
∴ संक्रिया साहचर्य नहीं है। अतः संक्रिया न तो क्रमविनिमेय है और न ही साहचर्य है।

(ii) Q पर * संक्रिया, a * b = ab + 1 से परिभाषित है।
(a) a * b = ab + 1, b * a = ba + 1 = ab + 1
∴ a * b = b * a
∴ यह संक्रिया क्रमविनिमेय द्विआधारी है।

(b) यदि a * (b * c) = a * (bc + 1) = a (bc + 1) + 1
= abc + a + 1
(a * b) * c= (ab + 1) * c =(ab + 1)c + 1
= abc + c + 1
∴ (a * b) * c ≠ a + (b + c)
∴ यह संक्रिया साहचर्य द्विआधारी संक्रिया नहीं है। अतः यह संक्रिया क्रमविनिमेय है परन्तु साहचर्य नहीं है।

(iii) Q पर * संक्रिया, a * b = \(\frac{a b}{2}\) द्वारा परिभाषित है।

∴ यह संक्रिया साहचर्य द्विआधारी संक्रिया है।
अतः यह संक्रिया क्रमविनिमेय और साहचर्य दोनों हैं।

(iv) Z⁺ पर * संक्रिया a* b = 2^ab से परिभाषित है।
(a) ∴ a * b = 2^ab, b * a = 2^ba = 2^ab
⇒ a * b = b * a
अतः संक्रिया क्रमविनिमेय संक्रिया है।

(b) a * (b * c) = a * 2^bc = a^a.2^bc
(a * b) * c = 2^ab * c = 2^2ab.c
∴ a * (b * c) ≠ * (a * b) *c
∴ यह संक्रिया साहचर्य द्विआधारी संक्रिया नहीं है। अतः यह संक्रिया क्रमविनिमेय है परन्तु साहचर्य नहीं है।

(v) Z⁺ पर * संक्रिया, a * b = a^b से परिभाषित है।
(a) a * b = a^b, b * a = b^a
∴ a * b + b* a
अत: यह संक्रिया क्रमविनिमेय नहीं है।
(b) a * (b * c)=a * b^c = a^(bc)
(a * b) * c = ad * c = a^(b)c = a^bc
∴ (a * b) * c * a * (b * c)
∴ यह संक्रिया साहचर्य द्विआधारी संक्रिया नहीं है।
अत: यह संक्रिया न तो क्रमविनिमेय है और न ही साहचर्य

(vi) R – {-1} पर * संक्रिया, a * b = \(\frac{a}{b+1}\) द्वारा परिभाषित है।

∴ यह संक्रिया साहचर्य द्विआधारी संक्रिया नहीं है।
अत: यह संक्रिया क्रमविनिमेय है और न ही साहचर्य है।

प्रश्न 3.
समुच्चय {1, 2, 3, 4,5} में a ^ b= निम्नतम {a, b} द्वारा परिभाषित द्विआधारी संक्रिया पर विचार कीजिए। संक्रिया के लिए संक्रिया सारणी लिखिए।
हल:
समुच्चय {1, 2, 3, 4, 5} पर संक्रिया ^ सारणी निम्न है-

प्रश्न 4.
समुच्चय {1, 2, 3, 4, 5} में, निम्नलिखित संक्रिया सारणी (सारणी 1.2) द्वारा परिभाषित द्विआधारी संक्रिया पर विचार कीजिए तथा
(i) (2 * 3) * 4 तथा 2 * (3 * 4) का परिकलन कीजिए।
(ii) क्या * क्रम विनिमेय है?
(iii) (2 * 3) * (4 * 5) का परिकलन कीजिए। (संकेत : निम्न सारणी का प्रयोग कीजिए।)

हल:
(i) दी गई सारणी से
(2 * 3) * 4 = 1 * 4 = 1
तथा 2 * (3 * 4) = 2 * 1 = 1

(ii) माना a, b ϵ {1, 2, 3, 4, 5}
∴ सारणी से, a * a = a (a ≠ b) तथा a, b विषम संख्या है
a * b = b * a = 1
2 * 4 = 4 * 2 = 2 जहाँ a तथा b सम संख्या तथा a ≠ b
अतः a * b = b * a
अतः द्विआधारी संक्रिया क्रम विनिमेय है।

(iii) सारणी से,
(2 * 3) * (4 * 5) = 1 *1
= 1

प्रश्न 5.
मान लीजिए कि समुच्चय {1, 2, 3, 4, 5} में एक द्विआधारी संक्रिया *’, a *’ b = a तथा b का HCF द्वारा परिभाषित है। क्या संक्रिया *’ उपर्युक्त प्रश्न 4 में परिभाषित संक्रिया * के समान है? अपने उत्तर का औचित्य भी बतलाइए।
हल:
यहाँ समुच्चय {1, 2, 3, 4, 5} संक्रिया a*’ b H.C.F. a, b द्वारा परिभाषित है।
इस संक्रिया की निम्न सारणी दी गयी है-

प्रश्न 4 में दी गई सारणी और यह सारणी समान है।
अतः संक्रिया *’ तथा * समान है।

प्रश्न 6.
मान लीजिए कि N में एक द्विआधारी संक्रिया, a * b = a तथा b का LCM द्वारा परिभाषित है। निम्नलिखित ज्ञात कीजिए:
(i) 5 * 7, 20 * 16
(ii) क्या संक्रिय * क्रम विनिमेय है?
(iii) क्या * साहचार्य है?
(iv) N में * का तत्समक अवयव ज्ञात कीजिए।
(v) N के कौन-से अवयव * संक्रिया के लिए व्युत्क्रमणीय है?
हल:
द्विआधारी संक्रिया (Binary Operations) * इस प्रकार परिभाषित है कि
a * b = a तथा b का L.C.M.
(i) 5 * 7 =5 तथा 7 का L.C.M.
= 35
तथा 20 * 16 = 20 तथा 16 का L.C.M.
= 80

(ii) a * b = a तथा b का L.C.M.
= b तथा a का L.C.M
a * b = b * a
अतः द्विआधारी संक्रिया क्रम विनिमेय है।

(iii) a * (b * c) = a * (b तथा c का L.C.M.)
= a तथा (b तथा c का L.C.M.) का L.C.M.
= a, b तथा c का L.C.M.
इसी प्रकार
(a * b) * c =(a तथा b का L.C.M.) * c
=a, b, c of L.C.M.
⇒ a *(b * c) =(a * b) * c
अतः द्विआधारी संक्रिया * साहचर्य है।

(iv) N में * संक्रिया की तत्समक अवयव 1 है।
∵ 1 * a = a * 1 = a
= 1 तथा a का L.C.M.

(v) माना * : N × N → N इस प्रकार परिभाषित है कि a * b = a तथा b का L.C.M.
∴ a = 1, b = 1 के लिए,
a * b = 1 = b * a
अत: 1a* संक्रिया के लिए व्युत्क्रमणीय है।

प्रश्न 7.
क्या समुच्चय {1, 2, 3, 4, 5} में a * b = a तथा b का LCM द्वारा परिभाषित * एक द्विआधारी संक्रिया है? अपने उत्तर का औचित्य भी बतलाइए।
हल:
दिया गया समुच्चय = {1, 2, 3, 4, 5} द्विआधारी संक्रिया द्वारा परिभाषित है कि a * b = a और b का LCM 2 * 6 = 6 जो कि समुच्चय {1, 2, 3, 4, 5} में नहीं है इसलिए * एक द्विआधारी संक्रिया है।

प्रश्न 8.
मान लीजिए कि N में a * b = a तथा b का HCF द्वारा परिभाषित एक द्विआधारी संक्रिया है। क्या * क्रमविनिमेय है? क्या * साहचर्य है? क्या N में इस द्विआधारी संक्रिया के तत्समक का अस्तित्व है?
हल:
यहाँ N, प्राकृत संख्याओं का समुच्चय है।
द्विआधारी संक्रिया a * b = a, b का H.C.F. द्वारा परिभाषित
(i) a, b का H.C.F. = b, a के H.C.F.
a * b = b * a
अतः संक्रिया क्रमविनिमेय है।

(ii) a * (b * c)= a * (b, c का H.C.F.)
=a व b, c का H.C.F.
= a, b, c का H.C.F.
(a * b) * c = (a, b का H.C.F.) * c
= a, b व c का H.C.F.
= a, b, c का H.C.F.
a * (b * c)= (a * b) * c (∵ संक्रिया साहचर्य है)

(iii) 1 * a = a * 1 = 1 ≠ a
अतः तत्समक अवयव का अस्तित्व नहीं है।

प्रश्न 9.
मान लीजिए कि परिमेय संख्याओं के समुच्चय में निम्नलिखित प्रकार से परिभाषित * एक द्विआधारी संक्रिया है:
(i) a * b = a – b
(ii) a * b = a² + b²
(iii) a * b = a + ab
(iv) a * b = (a – b)²
(v) a * b = \(\frac{a b}{4}\)
(vi) a * b = ab²
ज्ञात कीजिए कि इनमें से कौन-सी संक्रियाएँ क्रमविनिमेय हैं और कौन-सी साहचर्य हैं।
हल:
यहाँ परिमेय संख्याओं का समुच्चय Q दिया है।
(i) a * b = ab – b, द्विआधारी संक्रिया है।
(a) b * a = b – a
∴ a – b ≠ b – a ⇒ a * b ≠ b * a
अत: यह संक्रिया क्रमविनिमेय नहीं है।
(b) a * (b * c) = a * (b – c) = a – (b – c) = a – b + c
(a * b) * c = (a-b)* c = a – b -c
∴ a – b + c ≠ a – b – c = a * (b * c) * (a * b) * c
अतः यह संक्रिया साहचर्य नहीं है।

(ii) (a) a * b = a² + b²
∴ b * a = b² + a² = a² + b²
⇒ a * b = b * a
अत: यह संक्रिया क्रमविनिमेय है।
(b) a * (b * c) = a * (b² + c²) = a² + (b² + c²)²
(a + b) * c = (a² + b²) * c = (a² + b²)² + c²
⇒ a * (b * c) ≠ (a * b) * c.
अतः यह * संक्रिया साहचर्य नहीं है।

(iii) संक्रिया a * b = a + ab द्वारा परिभाषित है।
(a) a * b = a (1 + b), b * a = b + ba = b (1 + a)
∴ a * b + b * a
अतः यह * संक्रिया क्रमविनिमेय नहीं है।
(a) a * (b * c) = a + (b + bc)= a + a (b + bc)
= a + ab + abc
(a * b) * c = (a + ab) * c = (a + ab) + (a + ab)c
= a + ab + ac + abc
∴ a * (b * c) (ab) * c
अतः यह * संक्रिया साहचर्य नहीं है।

(iv) दिया है : a * b = (a – b)²
(a) a * b = (a – b)², b * a = (b – a)² = (a – b)²
∴ a * b = b * a
अतः यह * संक्रिया क्रमविनिमेय है।
(b) a * (b * c) = a * (b – c) = [a – (b – c)²]²
(a * b) * c = (a – b)² * c = [(a – b)² – c]²
∴ a * (b * c) ≠ (a * b) * c
अतः यह * संक्रिया साहचर्य नहीं है।

(v) a * b = \(\frac{a b}{4}\)

अतः यह * संक्रिया साहचर्य है।

(vi) a * b = ab²
(a) a * b = ab², b * a = ba
∴ a * b ≠ b * a
अत: यह * संक्रिया क्रमविनिमेय नहीं है।
(b) a * (b * c) = a + bc² = a (bc²)² = ab²c⁴
(a * b) * c = ab² * c = ab²c² = ab²c²
∴ a + (b * c) ≠ (a * b) * c.
अतः यह * संक्रिया साहचर्य नहीं है।

प्रश्न 10.
सिद्ध कीजिए कि प्रश्न 9 में दी गई संक्रियाओं में किसी का तत्समक है, वह बतलाइए।
हल:
यहाँ (i) a * b = a – b
यदि e तत्समक अवयव हो तो
a * e = a – e, e * a = e – a
∴ a – e ≠ e – a ⇒ a * e ≠ e * a
अतः e का अस्तित्व नहीं है।

(ii) a * b = a² + b²
∴ a * e = a² + e², e * a = e² + a²
a * e = e * a ≠ a
अतः e का अस्तित्व नहीं है।

(iii) a * b = a + ab
a * e = a + ae, e * a = e + ea
∴ a * e # e * a # a
अत: e का अस्तित्व नहीं है।

(iv) a * b = (a – b)
a * e = (a – e)² # a, e * a = (e – a)² # a
a * e = e * a # a
अतः e का अस्तित्व नहीं है।

(v) a * b = \(\frac{a b}{4}\)
a * e = \(\frac{ae}{4}\) # a, e * a = \(\frac{ea}{4}\) # a
∴ a * e = e * a # a
अतः e का अस्तित्व नहीं है।

(vi) a * b = ab²
a * e = ae² # a, e * a = ea² # a
∴ a * e # e * a # a
अतः e का अस्तित्व नहीं है।

प्रश्न 11.
मान लीजिए कि A = N × N है तथा A में (a, b) * (c, d) = (a + c, b + d)द्वारा परिभाषित एक द्विआधारी संक्रिया है। सिद्ध कीजिए कि * क्रम विनिमेय तथा साहचर्य है। A में * का तत्समक अवयव, यदि कोई है, तो ज्ञात कीजिए।
हल:
माना A = N × N
द्विआधारी संक्रिया (Binary operation) * इस प्रकार परिभाषित है कि
(a, b) * (c, d) = (a + c, b + d)
इसलिए (c, d) * (a, b) = (c + a, d + b)
=(a + c, b + d)
=(a, b) * (c, d)
अतः द्विआधारी संक्रिया * क्रम विनिमेय है
पुनः (a, b)* [(c, d) * (e, f)]
= (a, b) * (c + e, d + f)
= (a + c + e, b + d + f)
तथा [(a, b) * (c, d)] * (e, f)
= (a + c, b + d) * (e, f)
= (a + c + e, b + d + f)
= (a, b) * [(c, d) * (e, f)]
= [(a, b) * (c, d)]* (e, f)
अतः दी गई संक्रिया * साहचर्य है।
A में तत्समक अवयव का अस्तित्व नहीं है।

प्रश्न 12.
बतलाइए कि क्या निम्नलिखित कथन सत्य हैं या असत्य हैं। औचित्य भी बतलाइए।
(i) समुच्चय N में किसी भी स्वेच्छ द्विआधारी संक्रिया* के लिए a * a = a, ∀a ϵ N
(ii) यदि N में * एक क्रमविनिमेय द्विआधारी संक्रिया है तो a * (b * c)=(c * b) * a
हल:
यहाँ द्विआधारी संक्रिया समुच्चय N पर इस प्रकार परिभाषित की गयी है कि
a * a = a ∀ a ϵ N
(i) यहाँ पर * संक्रिया में केवल एक ही अवयव का प्रयोग किया गया है।
अतः यह कथन असत्य है।
(ii) वास्तविक संख्याओं में समुच्चय पर संक्रिया क्रमविनिमेय है।
b * c = c * b
= (c * b) * a = (b * c) * a = a * (b * c)
∴ a * (b * c) = (c * b) * a
अतः यह कथन सत्य है।

प्रश्न 13.
a * b = a³ + b³ प्रकार से परिभाषित N में एक द्विआधारी संक्रिया * पर विचार कीजिए। अब निम्नलिखित में से सही उत्तर का चयन कीजिए।
(A) * साहचर्य तथा क्रमविनिमेय दोनों है
(B) * क्रमविनिमेय है किन्तु साहचर्य नहीं है
(C) * साहचर्य है किन्तु क्रमविनिमेय नहीं है
(D) * न तो क्रमविनिमेय है और न साहचर्य है
हल:
यहाँ द्विआधारी संक्रिया को समुच्चय पर इस प्रकार परिभाषित किया गया है कि
a * b = a³ + b³
(a) a * b = a³ + b³, b * a = b³ + a³ = a³ * b³
∴ a * b = b * a
अत: यह संक्रिया क्रमविनिमेय है।
(b) a * (b * c) = a * (b³ + c³) = a³ + (b³ + c³)³
(a * b) * c= (a³ + b³) * c = (a³ + b³) + c³
∴ a * (b * c) ≠ (a * b) * c
अतः यह * संक्रिया साहचर्य नहीं है।
∴ संक्रिया क्रमविनिमेय परन्तु साहचर्य नहीं है।
अतः विकल्प (B) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 3 आव्यूह Ex 3.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths BooK Solutions Chapter 3 आव्यूह Ex 3.2

प्रश्न 1.
मान लीजिए कि
A = \(\left[\begin{array}{ll}{2} & {4} \\ {3} & {2}\end{array}\right]\), B = \(\left[\begin{array}{rr}{1} & {3} \\ {-2} & {5}\end{array}\right]\), C = \(\left[\begin{array}{rr}{-2} & {5} \\ {3} & {4}\end{array}\right]\) तो निम्नलिखित ज्ञात कीजिए-
(i) A + B
(ii) A – B
(iii) 3A – C
(iv) AB
(v) BA
हल:

प्रश्न 2.
निम्नलिखित को परिकलित कीजिए-

हल:

प्रश्न 3.
निर्देशित गुणनफल परिकलित कीजिए-

हल:

प्रश्न 4.
यदि

तो (A + B) तथा (B – C) परिकलित कीजिए। साथ ही सत्यापित कीजिए कि A + (B – C) = (A + B) – C
हल:

प्रश्न 5.
यदि

तो 3A – 5B परिकलित कीजिए।
हल:

प्रश्न 6.
सरल कीजिए-

हल:

प्रश्न 7.
X तथा Y ज्ञात कीजिए यदि-
(i) X + Y = \(\left[\begin{array}{ll}{7} & {0} \\ {2} & {5}\end{array}\right]\) तथा X – Y = \(\left[\begin{array}{ll}{3} & {0} \\ {0} & {3}\end{array}\right]\)
हल:
दिया है

(ii) 2x + 3y = \(\left[\begin{array}{ll}{2} & {3} \\ {4} & {0}\end{array}\right]\) तथा 3x + 2y = \(\left[\begin{array}{rr}{2} & {-2} \\ {-1} & {5}\end{array}\right]\)

प्रश्न 8.
X तथा Y ज्ञात कीजिए यदि
Y = \(\left[\begin{array}{ll}{3} & {2} \\ {1} & {4}\end{array}\right]\) तथा 2X + Y = \(\left[\begin{array}{rr}{1} & {0} \\ {-3} & {2}\end{array}\right]\) दिया है
हल:

प्रश्न 9.
x तथा y ज्ञात कीजिए. यदि-
\(2\left[\begin{array}{ll}{1} & {3} \\ {0} & {x}\end{array}\right]+\left[\begin{array}{ll}{y} & {0} \\ {1} & {2}\end{array}\right]=\left[\begin{array}{ll}{5} & {6} \\ {1} & {8}\end{array}\right]\)
हल:

संगत अवयवों के गुणांकों की तुलना करने पर,
y + 2 = 5 ⇒ y = 3
तथा 2x + 2 = 8 ⇒ x = 3

प्रश्न 10.
प्रदत्त समीकरण को x, y, z तथा t के लिए हल कीजिए यदि
\(2\left[\begin{array}{ll}{x} & {z} \\ {y} & {t}\end{array}\right]+3\left[\begin{array}{cc}{1} & {-1} \\ {0} & {2}\end{array}\right]=3\left[\begin{array}{ll}{3} & {5} \\ {4} & {6}\end{array}\right]\)
हल:

संगत अवयवों के गुणांकों की तुलना करने पर,
2x + 3 = 9 ⇒ x = 3
2y = 12 ⇒ y = 6
तथा 2z – 3 = 15 ⇒ z = 9
2t + 6 = 18 ⇒ t = 6

प्रश्न 11.
यदि x\(\left[\begin{array}{l}{2} \\ {3}\end{array}\right]\) + y\(\left[\begin{array}{r}{-1} \\ {1}\end{array}\right]\) = \(\left[\begin{array}{c}{10} \\ {5}\end{array}\right]\) है तो x तथा y के मान ज्ञात कीजिए।
हल:

संगत अवयवों के गुणांक समान रखने पर,
⇒ -2x – y = 10 …(i)
3x + y = 5 …. (ii)
समी० (i) व (ii) को जोड़ने पर,
x = 15
x का मान समी० (ii) में रखने पर,
3 × 15 + y = 5
⇒ y = 5 – 45
y = -40
अतः x = 15, y = -40

प्रश्न 12.
यदि

x, y, z तथा w के मानों को ज्ञात कीजिए।
हल:

प्रश्न 13.
यदि F(x) = \(\left[\begin{array}{ccc}{\cos x} & {-\sin x} & {0} \\ {\sin x} & {\cos x} & {0} \\ {0} & {0} & {1}\end{array}\right]\) है तो सिद्ध कीजिए कि
F(x) F(y) = F(x + y)
हल:
F(x) = \(\left[\begin{array}{ccc}{\cos x} & {-\sin x} & {0} \\ {\sin x} & {\cos x} & {0} \\ {0} & {0} & {1}\end{array}\right]\)

प्रश्न 14.
दशाईए कि-

हल:

प्रश्न 15.
यदि A = \(\left[\begin{array}{ccc}{2} & {0} & {1} \\ {2} & {1} & {3} \\ {1} & {-1} & {0}\end{array}\right]\) है तो A² – 5A + 6I का मान ज्ञात कीजिए।
हल:

प्रश्न 16.
यदि A = \(\) है तो सिद्ध कीजिए कि A³ – 6A² + 7A + 2I = 0
हल:

प्रश्न 17.
यदि A = \(\left[\begin{array}{ll}{3} & {-2} \\ {4} & {-2}\end{array}\right]\) तथा I = \(\left[\begin{array}{ll}{\mathbf{1}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{1}}\end{array}\right]\) एवं
A² = AK – 2I हो तो k ज्ञात कीजिए।
हल:
A = \(\left[\begin{array}{ll}{3} & {-2} \\ {4} & {-2}\end{array}\right]\) तथा I = \(\left[\begin{array}{ll}{\mathbf{1}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{1}}\end{array}\right]\)
दिया है : A² = AK – 2I

संगत अवयवों के गुणांकों की तुलना करने पर,
3k – 2 = 1 ⇒ k = 1
4k = 4 ⇒ k = 1
-2k = -2 ⇒ k = 1
अतः k का मान =1
k = 1

प्रश्न 18.
यदि A = \(\left[\begin{array}{cc}{0} & {-\tan \frac{\alpha}{2}} \\ {\tan \frac{\alpha}{2}} & {0}\end{array}\right]\) तथा I कोटि 2 का एक तत्समक आव्यूह है तो सिद्ध कीजिए कि
I + A = (I – A)\(\left[\begin{array}{cc}{\cos \alpha} & {-\sin \alpha} \\ {\sin \alpha} & {\cos \alpha}\end{array}\right]\)
हल:

प्रश्न 19.
किसी व्यापार संघ के पास 30000 रुपयों का कोष है, जिसे दो भिन्न-भिन्न प्रकार के बांडों में निवेशित करना है। प्रथम बांड पर 5%वार्षिक तथा द्वितीय बांड पर 7% वार्षिक ब्याज प्राप्त होता है। आव्यूह गुणन के प्रयोग द्वारा यह निर्धारित कीजिए कि 30000 रुपयों के कोष को दो प्रकार के बांडों में निवेश करने के लिए किस प्रकार बांटें जिससे व्यापार संघको प्राप्त कुल वार्षिक ब्याज
(i) Rs. 1800 हो।
(ii) Rs. 2000 हो।
हल:
माना 30,000 रुपये के दो भाग क्रमश: x तथा (30000 – x) है।
माना इन्हें 1 × 2 की कोटि वाली आव्यूह A में प्रदर्शित किया मया है, तब
A =[x (30,000 – x)]
प्रथम बांड व द्वितीय बांड पर क्रमश: 5% व 7% वार्षिक है
माना इन्हें 2 × 1 की कोटि की आव्यूह R से प्रदर्शित किया गया है
∴ R = \(\left[\begin{array}{l}{5 / 100} \\ {7 / 100}\end{array}\right]=\left[\begin{array}{l}{0.05} \\ {0.07}\end{array}\right]\)
(i) ∴ AR = 1800
∴ [x 30,000 – x]\(\left[\begin{array}{l}{0.05} \\ {0.07}\end{array}\right]\) = [1,800]
⇒ [0.05x + (30,000 – x) 0.07] = [1,800]
⇒ 0.05x + (30,000 – x) × 0.07 = 1,800
⇒ 0.05x + 2,100 – 0.07x = 1,800
⇒ -0.02x = -300
⇒ x = \(\frac{300}{0.02}\) = 15,000
अतः प्रथम बांड में जमा धनराशि = 15,000
तथा दूसरे बांड में जमा धनराशि = 30,000 – 15,000
= 15,000 रु०

(ii) पुन: AR = 2,000
[x (30,000 – x] \(\left[\begin{array}{l}{0.05} \\ {0.07}\end{array}\right]\) = [2,000]
⇒ 0.05x + (30,000 – x) × 0.07 = 2000
⇒ 0.05x + 2,100 – 0.07x = 2000
⇒ 0.02x = -100
⇒ x = 5,000
अतः प्रथम बांड में निवेश धनराशि =5,000 रु०
तथा दूसरे बांड में निवेश धनराशि = 25,000 रु०

प्रश्न 20.
किसी स्कूल की पुस्तकों की दुकान में 10 दर्जन रसायन विज्ञान, 8 दर्जन भौतिक विज्ञान तथा 10 दर्जन अर्थशास्त्र की पुस्तकें हैं। इन पुस्तकों का विक्रय मूल्य क्रमशः Rs. 80, Rs. 60 तथा Rs. 40 प्रति पुस्तक है। आव्यूह बीजगणित प्रयोग द्वारा ज्ञात कीजिए कि सभी पुस्तकों को बेचने से दुकान को कुल कितनी धनराशि प्राप्त होगी?
हल:
विद्यालय में पुस्तकों की संख्या निम्न प्रकार है-
रसायन विज्ञान – 10 दर्जन- = 120 पुस्तकें
भौतिक विज्ञान – 8 दर्जन = 96 पुस्तकें
अर्थशास्त्र – 10 दर्जन = 120 पुस्तकें
ड्डसे आव्यूह A = [120 96 120] से व्यक्त करते हैं।
रसायन विज्ञान, भौतिक विज्ञान तथा अर्थशास्त्र की प्रत्येक पुस्तक का विक्रय मूल्य क्रमशः 80 रु०,60 रु० तथा 40 रु० है।
इसे आव्यूह R = \(\left[\begin{array}{l}{80} \\ {60} \\ {40}\end{array}\right]\) से व्यक्त करते हैं।
∴ प्राप्त राशि, AR = [120 96 120] \(\left[\begin{array}{l}{80} \\ {60} \\ {40}\end{array}\right]\)
= 120 × 80 + 96 × 60 + 120 × 40
= [9600 + 5760 + 4800] = [20160]
अतःकुल प्राप्त राशि = 20160 रु०
मान लीजिए कि X, Y, z,W तथा P क्रमशः 2 × n, 3 × k, 2 × p, n × 3 तथा px k कोटियों के आव्यूह हैं।

नीचे दिए प्रश्न संख्या 21 तथा 22 में सही उत्तर चुनिए।
प्रश्न 21.
PY + WY के परिभाषित होने के लिए n, k तथा p पर क्या प्रतिबन्ध होगा?
(A) k = 3, p = n
(B) k स्वेच्छ है, p = 2
(C) p स्वेच्छ है, k = 3
(D) k = 2, p = 3
हल:
दिया है : आव्यूह : X Y ZWP
कोटियाँ : 2 × n, 3 × k, 2 × p, n × 3, p × k
∴ P की कोटि = p × k, Y की कोटि = 3 × k
∴ PY संभव है यदि k = 3
PY की कोटि = p × k = p × 3
W और Y की कोटियाँ क्रमश: n × 3 और 3 × k = 3 × 3
WY की कोटि =n × 3
PY व WY का योग तभी संभव है जब यह दोनों एक ही कोटि के हों तो
p × 3 = n × 3 = P × n
∴ PY + WY परिभाषित हैं यदि p = n और k = 3
अतः विकल्प (A) सही है।

प्रश्न 22.
यदि n = p, तो आव्यूह 7X – 5Z की कोटि है
(A) p × 2
(B) 2 × n
(C) n × 3
(D) p × n
हल:
आव्यूह x तथा Z की कोटियाँ 2 × n और 2 × p हैं।
आव्यूह 7X – 5Z परिभाषित है यदि x तथा Z एक ही कोटि के हों, क्योंकि p = n दोनों की कोटि 2 × n है।
अतः विकल्प (B) सही है।