In this article, we share MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित Ex 10.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित Ex 10.2
प्रश्न 1.
निम्नलिखित सदिशों के परिमाण का परिकलन कीजिए-
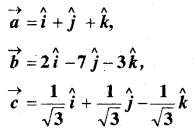
हल:

प्रश्न 2.
समान परिमाण वाले दो विभिन्न सदिश लिखिए
हल:
माना \(\vec{a}=\hat{i}+2 \hat{j}+3 \hat{k}\) और \(\vec{b}=3 \hat{i}+\hat{j}+2 \hat{k}\) दो भिन्न वेक्टर हैं परन्तु इनके परिणाम समान हैं।
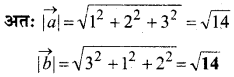
प्रश्न 3.
समान दिशा वाले दो विभिन्न सदिश लिखिए
हल:
माना दो सदिश वे \(\vec{a}=\hat{i}+\hat{j}+\hat{k}, \vec{b}=3 \hat{i}+3 \hat{j}+3 \hat{k}\)

प्रश्न 4.
x और y के मान ज्ञात कीजिए ताकि सदिश \(2 \hat{i}+3 \hat{j}\) और \(x \hat{i}+y \hat{j}\) समान हों।
हल:
\(2 \hat{i}+3 \hat{j}+x \hat{i}+y \hat{j}\)
\(\hat{i}\) और \(\hat{j}\) के गुणांकों की तुलना करने पर,
∴ x = 2, y = 3
![]()
प्रश्न 5.
एक सदिश का प्रारम्भिक बिन्दु (2, 1) और अन्तिम बिन्दु (-5, 7) है। इस सदिश के अदिश एवं सदिश घटक ज्ञात कीजिए।
हल:
माना सदिश के प्रारम्भिक व अन्तिम बिन्दु A (2, 1) व B (-5, 7) हैं। तब
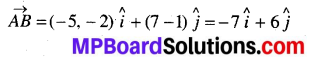
अत: \(\overrightarrow{A B}\) के अदिश घटक –7 तथा 6 हैं व सदिश घटक \(-7 \hat{i}\) और \(6 \hat{j}\) हैं।
प्रश्न 6.
सदिश \(\vec{a}=\hat{i}-2 \hat{j}+\hat{k}, \quad \vec{b}=-2 \hat{i}+4 \hat{j}+5 \hat{k}\) और \(\vec{c}=\hat{i}-6 \hat{j}-7 \hat{k}\) का योगफल ज्ञात कीजिए।
हल:
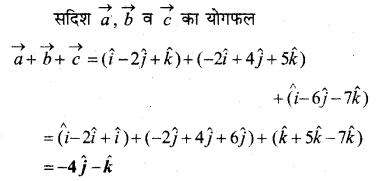
प्रश्न 7.
सदिश \(\vec{a}=\hat{i}+\hat{j}+2 \hat{k}\) के अनुदिश एक मात्रक सदिश ज्ञात कीजिए।
हल:

प्रश्न 8.
सदिश \(\overrightarrow{P Q}\) के अनुदिश मात्रक सदिश ज्ञात कीजिए जहाँ बिन्दु P और Q क्रमशः (1, 2, 3) और (4, 5, 6) हैं।
हल:
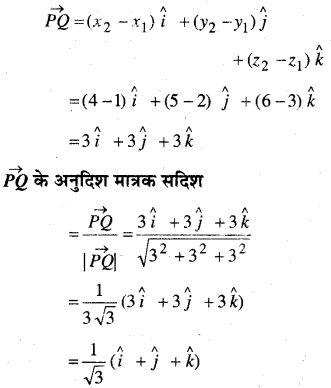
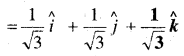
![]()
प्रश्न 9.
दिए हुए सदिशों \(\vec{a}=2 \hat{i}-\hat{j}+2 \hat{k}\) और \(\vec{b}=-\hat{i}+\hat{j}-\hat{k}\) के लिए सदिश \(\vec{a}+\vec{b}\) के अनुदिश मात्रक सदिश ज्ञात कीजिए।
हल:

प्रश्न 10.
सदिश \(5 \hat{i}-\hat{j}+2 \hat{k}\) के अनुदिश एक ऐसा सदिश ज्ञात कीजिए जिसका परिमाण 8 इकाई है।
हल:
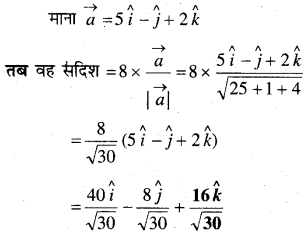
प्रश्न 11.
दर्शाइए कि सदिश \(2 \hat{i}-3 \hat{j}+4 \hat{k}\) और \(-4 \hat{i}+6 \hat{j}-8 \hat{k}\) संरेख हैं।
हल:
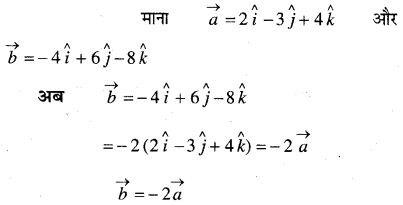
क्योंकि \(\vec{a}\) और \(\vec{b}\) की दिशा समान हैं अतः ये संरेख हैं।
प्रश्न 12.
सदिश \(\hat{i}+2 \hat{j}+3 \hat{k}\) की दिक् cosine ज्ञात कीजिए।
हल:

![]()
प्रश्न 13.
बिन्दुओं A (1, 2,-3) एवं B(-1, -2, 1) को मिलाने वाले एवं A से B की तरफ दिष्ट सदिश की दिक् cosine ज्ञात कीजिए।
हल:
A (1, 2, -3) एवं B (-1, – 2, 1)
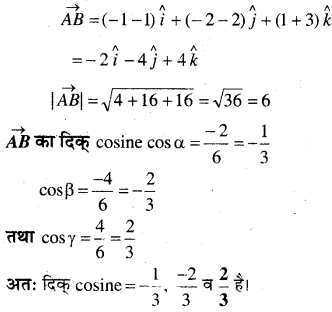
प्रश्न 14.
दर्शाइए कि सदिश \(\hat{\boldsymbol{i}}+\hat{\boldsymbol{j}}+\hat{\boldsymbol{k}}\) अक्षों OX,OY तथा OZ के साथ बराबर झुका हुआ है।
हल:
माना A = \(\vec{A}=\hat{i}-\hat{j}+\hat{k}\)
माना सदिश \(\vec{a}\) अक्ष OX, OY एवं OZ के साथ क्रमश: α, β तथा γ कोण बनाता है तथा इनके दिक् cosine cos α, cos β तथा cos γ हैं।

प्रश्न 15.
बिन्दुओं P = \((\hat{i}+2 \hat{j}-\hat{k})\) और Q = \((-\hat{i}+\hat{j}+\hat{k})\) को मिलाने वाली रेखा को 2 : 1 के अनुपात में (i) अंत: (ii) बाह्य, विभाजित करने वाले बिन्दु R का स्थिति सदिश ज्ञात कीजिए।
हल:
(i) अन्त : विभाजन
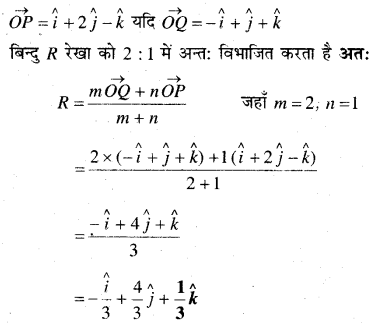
(ii) बाह्य विभाजन
बिन्दु R रेखा को 2 : 1 में बाह्य विभाजित करता है अतः

प्रश्न 16.
दो बिन्दुओं P(2, 3, 4) और Q (4, 1, -2) को मिलाने वाले सदिश का मध्य बिन्दु ज्ञात कीजिए।
हल:
P और Q को मिलाने वाले सदिश का मध्य बिन्दु \(\frac{\vec{a}+\vec{b}}{2}\)
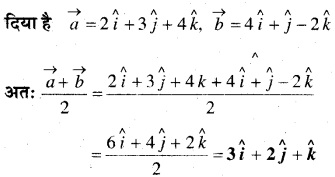
![]()
प्रश्न 17.
दर्शाइए कि बिन्दु A, B और C जिनके स्थिति सदिश क्रमश: \(\vec{a}=3 \hat{i}-4 \hat{j}-4 \hat{k}, \quad \vec{b}=2 \hat{i}-\hat{j}+\hat{k}\) और \(\vec{c}=\hat{i}-3 \hat{j}-5 \hat{k}\) हैं, एक समकोण त्रिभुज के शीर्षों का निर्माण करते हैं।
हल:

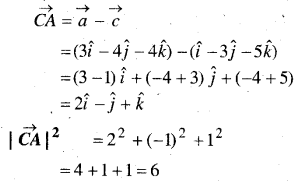
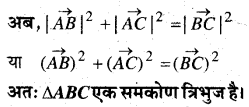
प्रश्न 18.
संलग्न चित्र में त्रिभुज ABC के लिए निम्नलिखित में से कौन-सा कथन सत्य नहीं है?
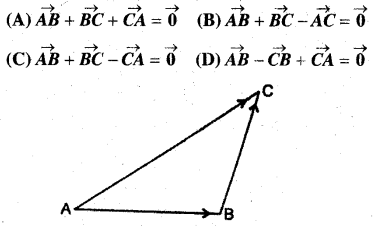
हल:
सदिशों के योगफल त्रिभुज नियम के अनुसार,
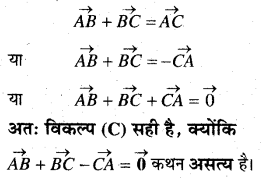
प्रश्न 19.
यदि \(\vec{a}\) और \(\vec{b}\) दो संरेख सदिश हैं तो निम्नलिखित में से कौन-सा कथन सही नहीं है?
(b) \(\vec{b}=\lambda \vec{a}\)किसी अदिश λ के लिए
(B) \(\vec{a}=\pm \vec{b}\)
(C) \(\vec{a}\) और \(\vec{b}\) के के क्रमागत घटक समानुपाती नहीं हैं।
(D) दोनों सदिशों के \(\vec{a}\) तथा \(\vec{b}\) की दिशा समान है परन्तु परिमाण विभिन्न हैं।
हल:
पहले तीन कथन (A), (B), (C) सही हैं परन्तु संरेख सदिश समान्तर होते हैं। यह आवश्यक नहीं है कि दिशा समान हो या परिमाण समान हों।
अतः विकल्प (D) सही है।