In this article, we share MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.1
प्रश्न 1 से 2 तक में सारणिकों का मान ज्ञात कीजिए
प्रश्न 1.
\(\left|\begin{array}{cc}{2} & {4} \\ {-5} & {-1}\end{array}\right|\)
हल:
\(\left|\begin{array}{cc}{2} & {4} \\ {-5} & {-1}\end{array}\right|\) = 2 × (-1) – 4 × (-5) = -2 + 20 = 18
प्रश्न 2.
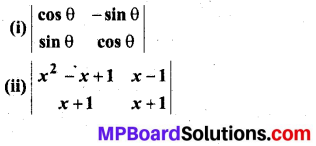
हल:
(i) \(\left|\begin{array}{cc}{\cos \theta} & {-\sin \theta} \\ {\sin \theta} & {\cos \theta}\end{array}\right|\)
=cose θ cosθ – (sin θ) × (-sin θ)
= cos2θ + sin2θ
= 1
(ii) \(\left|\begin{array}{cc}{x^{2}-x+1} & {x-1} \\ {x+1} & {x+1}\end{array}\right|\)
= (x2 – x + 1)(x + 1) – (x + 1)(x – 1)
= (x + 1) – (x2 – 1) = x3 + 1 – x2 + 1
= x3 – x2 + 2
प्रश्न 3.
यदि A = \(\left[\begin{array}{ll}{1} & {2} \\ {4} & {2}\end{array}\right]\), तो दिखाइए |2A| = 4|A|
हल:

प्रश्न 4. यदि A = \(\left|\begin{array}{lll}{1} & {0} & {1} \\ {0} & {1} & {2} \\ {0} & {0} & {4}\end{array}\right|\) हो, तो दिखाइए |3A| = 27|A|
हलः

![]()
प्रश्न 5.
निम्नलिखित सारणिकों का मान ज्ञात कीजिए-

हल:
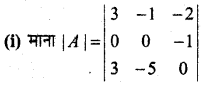

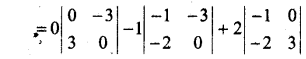
= 0[0-(-3) × 3][-1 × 0 – (-3) × (-2)] + 2[3 × (-1) – (-2) × 0]
= 0 × 9 – 1[0 – 6] + 2[-3 – 0]
= 0 – 1 × (-6) + 2 × (-3)
= 6 – 6 = 0
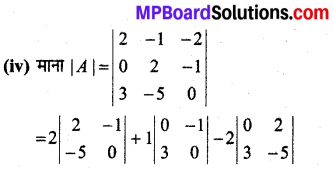
= 2[2 × 0 – (-1) × (-5)] + 1[0 × 0 – (-1) × 3] – 2[0 × (-5) – 2 × 3]
= 2[0 – 5] + 1[0 + 3] – 2 × [0 – 6]
= 2 × (-5) + 1 × 3 – 2 × (-6)
= -10 + 3 + 12 = -10 + 15 = 5
प्रश्न 6.
यदि A = \(\left|\begin{array}{ccc}{1} & {1} & {-2} \\ {2} & {1} & {-3} \\ {5} & {4} & {-9}\end{array}\right|\), हो तो |A| ज्ञात कीजिए।
हल:
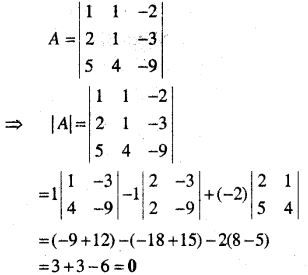
![]()
प्रश्न 7.
x के मान ज्ञात कीजिए यदि
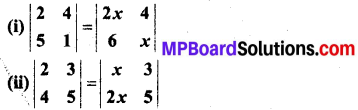
हल:
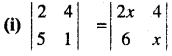
⇒ 2 – 20 = 2x2 – 24
⇒ -18 = 2x2 – 24
⇒ 2x2 – 24 +18 = 0
⇒ 2x2 -6 =0
⇒ x2 = 3
⇒ x = ±\( \sqrt{{3}} \)
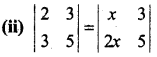
⇒ 10 – 12 = 5x – 6x
-2x3 = – x
x = 2
प्रश्न 8.
यदि \(\left|\begin{array}{cc}{x} & {2} \\ {18} & {x}\end{array}\right|=\left|\begin{array}{cc}{6} & {2} \\ {18} & {6}\end{array}\right|\) हो तो x बराबर है-
(A) 6
(B) ±6
(C) -6
(D) 0
हल:
\(\left|\begin{array}{cc}{x} & {2} \\ {18} & {x}\end{array}\right|=\left|\begin{array}{cc}{6} & {2} \\ {18} & {6}\end{array}\right|\)
⇒ x × x -2 × 18 = 6 × 6 – 2 × 18
⇒ x2 – 36 = 36 – 36
⇒ x2 – 36 = 0
⇒ x = 36
∴ x = ±6
अतः विकल्प (B) सही है।