In this article, we share MP Board Class 12th Maths Book Solutions Chapter 3 आव्यूह Ex 3.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths BooK Solutions Chapter 3 आव्यूह Ex 3.2
प्रश्न 1.
मान लीजिए कि
A = \(\left[\begin{array}{ll}{2} & {4} \\ {3} & {2}\end{array}\right]\), B = \(\left[\begin{array}{rr}{1} & {3} \\ {-2} & {5}\end{array}\right]\), C = \(\left[\begin{array}{rr}{-2} & {5} \\ {3} & {4}\end{array}\right]\) तो निम्नलिखित ज्ञात कीजिए-
(i) A + B
(ii) A – B
(iii) 3A – C
(iv) AB
(v) BA
हल:
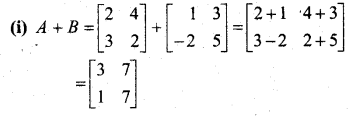

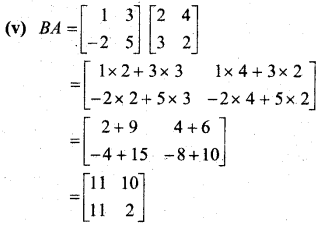
प्रश्न 2.
निम्नलिखित को परिकलित कीजिए-
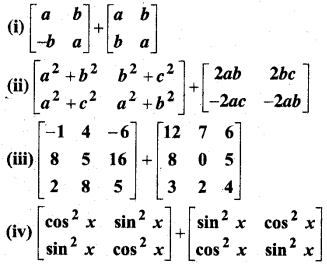
हल:
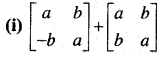

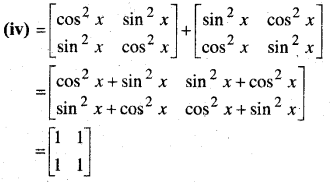
प्रश्न 3.
निर्देशित गुणनफल परिकलित कीजिए-
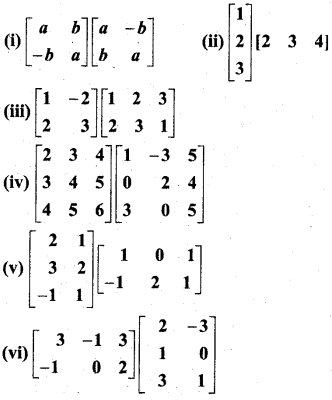
हल:

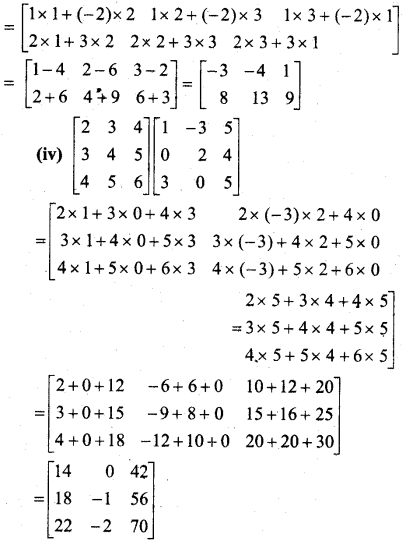
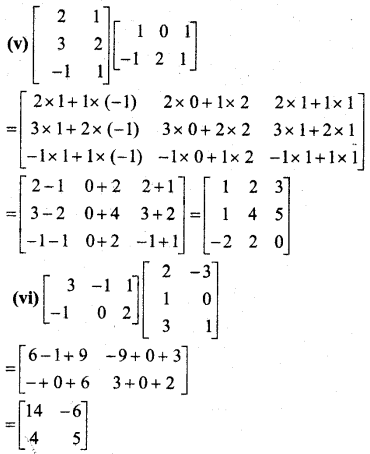
प्रश्न 4.
यदि
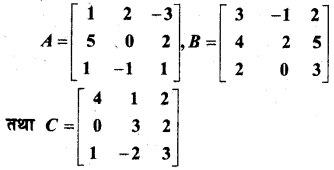
तो (A + B) तथा (B – C) परिकलित कीजिए। साथ ही सत्यापित कीजिए कि A + (B – C) = (A + B) – C
हल:


![]()
प्रश्न 5.
यदि
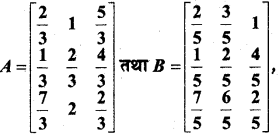
तो 3A – 5B परिकलित कीजिए।
हल:

प्रश्न 6.
सरल कीजिए-
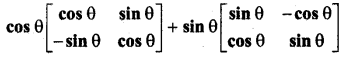
हल:
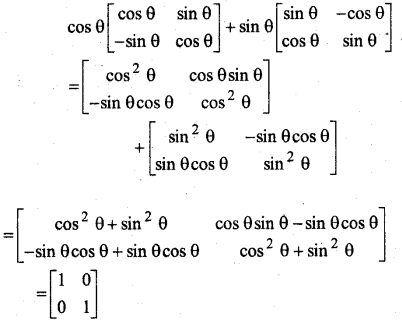
प्रश्न 7.
X तथा Y ज्ञात कीजिए यदि-
(i) X + Y = \(\left[\begin{array}{ll}{7} & {0} \\ {2} & {5}\end{array}\right]\) तथा X – Y = \(\left[\begin{array}{ll}{3} & {0} \\ {0} & {3}\end{array}\right]\)
हल:
दिया है

(ii) 2x + 3y = \(\left[\begin{array}{ll}{2} & {3} \\ {4} & {0}\end{array}\right]\) तथा 3x + 2y = \(\left[\begin{array}{rr}{2} & {-2} \\ {-1} & {5}\end{array}\right]\)

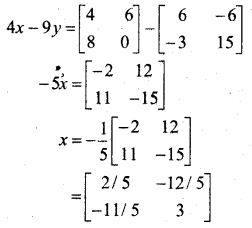
प्रश्न 8.
X तथा Y ज्ञात कीजिए यदि
Y = \(\left[\begin{array}{ll}{3} & {2} \\ {1} & {4}\end{array}\right]\) तथा 2X + Y = \(\left[\begin{array}{rr}{1} & {0} \\ {-3} & {2}\end{array}\right]\) दिया है
हल:

प्रश्न 9.
x तथा y ज्ञात कीजिए. यदि-
\(2\left[\begin{array}{ll}{1} & {3} \\ {0} & {x}\end{array}\right]+\left[\begin{array}{ll}{y} & {0} \\ {1} & {2}\end{array}\right]=\left[\begin{array}{ll}{5} & {6} \\ {1} & {8}\end{array}\right]\)
हल:
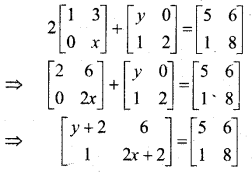
संगत अवयवों के गुणांकों की तुलना करने पर,
y + 2 = 5 ⇒ y = 3
तथा 2x + 2 = 8 ⇒ x = 3
![]()
प्रश्न 10.
प्रदत्त समीकरण को x, y, z तथा t के लिए हल कीजिए यदि
\(2\left[\begin{array}{ll}{x} & {z} \\ {y} & {t}\end{array}\right]+3\left[\begin{array}{cc}{1} & {-1} \\ {0} & {2}\end{array}\right]=3\left[\begin{array}{ll}{3} & {5} \\ {4} & {6}\end{array}\right]\)
हल:
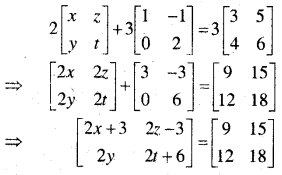
संगत अवयवों के गुणांकों की तुलना करने पर,
2x + 3 = 9 ⇒ x = 3
2y = 12 ⇒ y = 6
तथा 2z – 3 = 15 ⇒ z = 9
2t + 6 = 18 ⇒ t = 6
प्रश्न 11.
यदि x\(\left[\begin{array}{l}{2} \\ {3}\end{array}\right]\) + y\(\left[\begin{array}{r}{-1} \\ {1}\end{array}\right]\) = \(\left[\begin{array}{c}{10} \\ {5}\end{array}\right]\) है तो x तथा y के मान ज्ञात कीजिए।
हल:
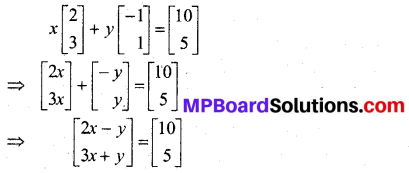
संगत अवयवों के गुणांक समान रखने पर,
⇒ -2x – y = 10 …(i)
3x + y = 5 …. (ii)
समी० (i) व (ii) को जोड़ने पर,
x = 15
x का मान समी० (ii) में रखने पर,
3 × 15 + y = 5
⇒ y = 5 – 45
y = -40
अतः x = 15, y = -40
प्रश्न 12.
यदि
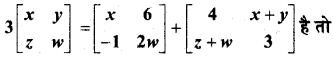
x, y, z तथा w के मानों को ज्ञात कीजिए।
हल:

प्रश्न 13.
यदि F(x) = \(\left[\begin{array}{ccc}{\cos x} & {-\sin x} & {0} \\ {\sin x} & {\cos x} & {0} \\ {0} & {0} & {1}\end{array}\right]\) है तो सिद्ध कीजिए कि
F(x) F(y) = F(x + y)
हल:
F(x) = \(\left[\begin{array}{ccc}{\cos x} & {-\sin x} & {0} \\ {\sin x} & {\cos x} & {0} \\ {0} & {0} & {1}\end{array}\right]\)
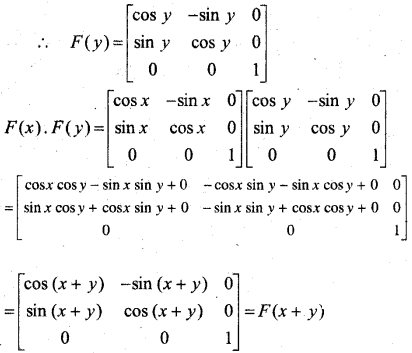
![]()
प्रश्न 14.
दशाईए कि-
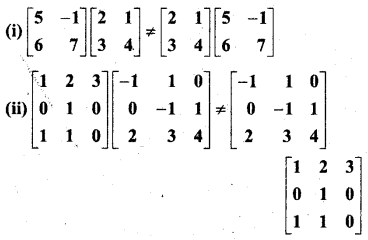
हल:

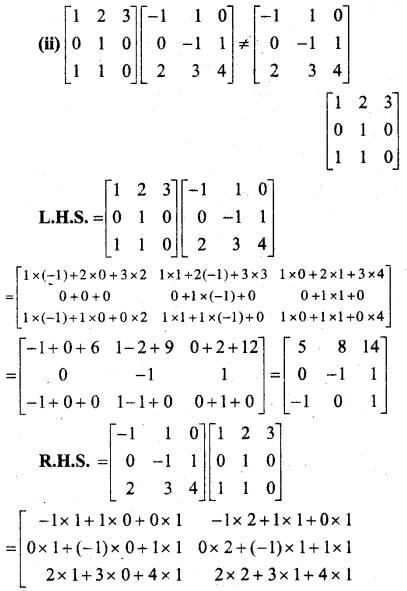
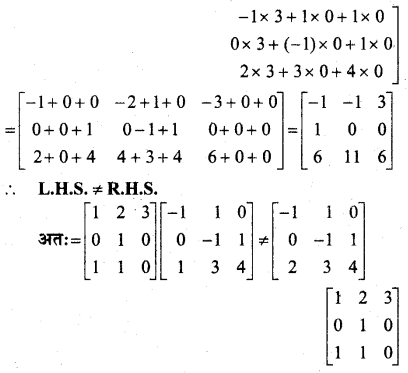
प्रश्न 15.
यदि A = \(\left[\begin{array}{ccc}{2} & {0} & {1} \\ {2} & {1} & {3} \\ {1} & {-1} & {0}\end{array}\right]\) है तो A2 – 5A + 6I का मान ज्ञात कीजिए।
हल:

प्रश्न 16.
यदि A = \(\) है तो सिद्ध कीजिए कि A3 – 6A2 + 7A + 2I = 0
हल:
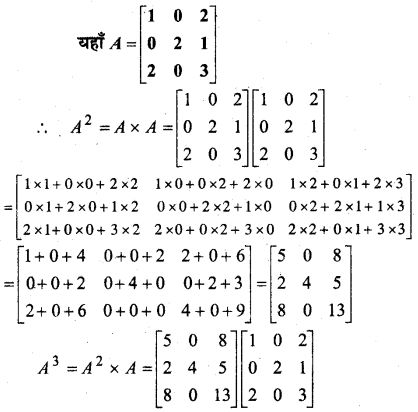


प्रश्न 17.
यदि A = \(\left[\begin{array}{ll}{3} & {-2} \\ {4} & {-2}\end{array}\right]\) तथा I = \(\left[\begin{array}{ll}{\mathbf{1}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{1}}\end{array}\right]\) एवं
A2 = AK – 2I हो तो k ज्ञात कीजिए।
हल:
A = \(\left[\begin{array}{ll}{3} & {-2} \\ {4} & {-2}\end{array}\right]\) तथा I = \(\left[\begin{array}{ll}{\mathbf{1}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{1}}\end{array}\right]\)
दिया है : A2 = AK – 2I
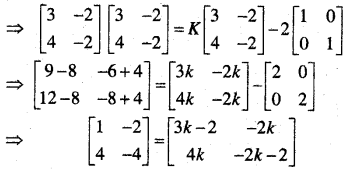
संगत अवयवों के गुणांकों की तुलना करने पर,
3k – 2 = 1 ⇒ k = 1
4k = 4 ⇒ k = 1
-2k = -2 ⇒ k = 1
अतः k का मान =1
k = 1
प्रश्न 18.
यदि A = \(\left[\begin{array}{cc}{0} & {-\tan \frac{\alpha}{2}} \\ {\tan \frac{\alpha}{2}} & {0}\end{array}\right]\) तथा I कोटि 2 का एक तत्समक आव्यूह है तो सिद्ध कीजिए कि
I + A = (I – A)\(\left[\begin{array}{cc}{\cos \alpha} & {-\sin \alpha} \\ {\sin \alpha} & {\cos \alpha}\end{array}\right]\)
हल:

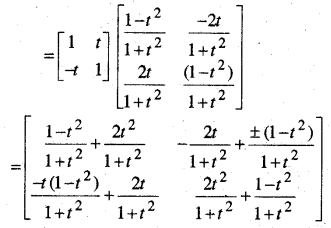
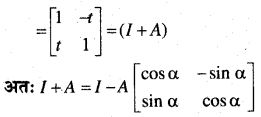
प्रश्न 19.
किसी व्यापार संघ के पास 30000 रुपयों का कोष है, जिसे दो भिन्न-भिन्न प्रकार के बांडों में निवेशित करना है। प्रथम बांड पर 5%वार्षिक तथा द्वितीय बांड पर 7% वार्षिक ब्याज प्राप्त होता है। आव्यूह गुणन के प्रयोग द्वारा यह निर्धारित कीजिए कि 30000 रुपयों के कोष को दो प्रकार के बांडों में निवेश करने के लिए किस प्रकार बांटें जिससे व्यापार संघको प्राप्त कुल वार्षिक ब्याज
(i) Rs. 1800 हो।
(ii) Rs. 2000 हो।
हल:
माना 30,000 रुपये के दो भाग क्रमश: x तथा (30000 – x) है।
माना इन्हें 1 × 2 की कोटि वाली आव्यूह A में प्रदर्शित किया मया है, तब
A =[x (30,000 – x)]
प्रथम बांड व द्वितीय बांड पर क्रमश: 5% व 7% वार्षिक है
माना इन्हें 2 × 1 की कोटि की आव्यूह R से प्रदर्शित किया गया है
∴ R = \(\left[\begin{array}{l}{5 / 100} \\ {7 / 100}\end{array}\right]=\left[\begin{array}{l}{0.05} \\ {0.07}\end{array}\right]\)
(i) ∴ AR = 1800
∴ [x 30,000 – x]\(\left[\begin{array}{l}{0.05} \\ {0.07}\end{array}\right]\) = [1,800]
⇒ [0.05x + (30,000 – x) 0.07] = [1,800]
⇒ 0.05x + (30,000 – x) × 0.07 = 1,800
⇒ 0.05x + 2,100 – 0.07x = 1,800
⇒ -0.02x = -300
⇒ x = \(\frac{300}{0.02}\) = 15,000
अतः प्रथम बांड में जमा धनराशि = 15,000
तथा दूसरे बांड में जमा धनराशि = 30,000 – 15,000
= 15,000 रु०
(ii) पुन: AR = 2,000
[x (30,000 – x] \(\left[\begin{array}{l}{0.05} \\ {0.07}\end{array}\right]\) = [2,000]
⇒ 0.05x + (30,000 – x) × 0.07 = 2000
⇒ 0.05x + 2,100 – 0.07x = 2000
⇒ 0.02x = -100
⇒ x = 5,000
अतः प्रथम बांड में निवेश धनराशि =5,000 रु०
तथा दूसरे बांड में निवेश धनराशि = 25,000 रु०
![]()
प्रश्न 20.
किसी स्कूल की पुस्तकों की दुकान में 10 दर्जन रसायन विज्ञान, 8 दर्जन भौतिक विज्ञान तथा 10 दर्जन अर्थशास्त्र की पुस्तकें हैं। इन पुस्तकों का विक्रय मूल्य क्रमशः Rs. 80, Rs. 60 तथा Rs. 40 प्रति पुस्तक है। आव्यूह बीजगणित प्रयोग द्वारा ज्ञात कीजिए कि सभी पुस्तकों को बेचने से दुकान को कुल कितनी धनराशि प्राप्त होगी?
हल:
विद्यालय में पुस्तकों की संख्या निम्न प्रकार है-
रसायन विज्ञान – 10 दर्जन- = 120 पुस्तकें
भौतिक विज्ञान – 8 दर्जन = 96 पुस्तकें
अर्थशास्त्र – 10 दर्जन = 120 पुस्तकें
ड्डसे आव्यूह A = [120 96 120] से व्यक्त करते हैं।
रसायन विज्ञान, भौतिक विज्ञान तथा अर्थशास्त्र की प्रत्येक पुस्तक का विक्रय मूल्य क्रमशः 80 रु०,60 रु० तथा 40 रु० है।
इसे आव्यूह R = \(\left[\begin{array}{l}{80} \\ {60} \\ {40}\end{array}\right]\) से व्यक्त करते हैं।
∴ प्राप्त राशि, AR = [120 96 120] \(\left[\begin{array}{l}{80} \\ {60} \\ {40}\end{array}\right]\)
= 120 × 80 + 96 × 60 + 120 × 40
= [9600 + 5760 + 4800] = [20160]
अतःकुल प्राप्त राशि = 20160 रु०
मान लीजिए कि X, Y, z,W तथा P क्रमशः 2 × n, 3 × k, 2 × p, n × 3 तथा px k कोटियों के आव्यूह हैं।
नीचे दिए प्रश्न संख्या 21 तथा 22 में सही उत्तर चुनिए।
प्रश्न 21.
PY + WY के परिभाषित होने के लिए n, k तथा p पर क्या प्रतिबन्ध होगा?
(A) k = 3, p = n
(B) k स्वेच्छ है, p = 2
(C) p स्वेच्छ है, k = 3
(D) k = 2, p = 3
हल:
दिया है : आव्यूह : X Y ZWP
कोटियाँ : 2 × n, 3 × k, 2 × p, n × 3, p × k
∴ P की कोटि = p × k, Y की कोटि = 3 × k
∴ PY संभव है यदि k = 3
PY की कोटि = p × k = p × 3
W और Y की कोटियाँ क्रमश: n × 3 और 3 × k = 3 × 3
WY की कोटि =n × 3
PY व WY का योग तभी संभव है जब यह दोनों एक ही कोटि के हों तो
p × 3 = n × 3 = P × n
∴ PY + WY परिभाषित हैं यदि p = n और k = 3
अतः विकल्प (A) सही है।
प्रश्न 22.
यदि n = p, तो आव्यूह 7X – 5Z की कोटि है
(A) p × 2
(B) 2 × n
(C) n × 3
(D) p × n
हल:
आव्यूह x तथा Z की कोटियाँ 2 × n और 2 × p हैं।
आव्यूह 7X – 5Z परिभाषित है यदि x तथा Z एक ही कोटि के हों, क्योंकि p = n दोनों की कोटि 2 × n है।
अतः विकल्प (B) सही है।