In this article, we share MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.3
प्रश्न 1.
निम्नलिखित प्रत्येक में दिए गए शीर्ष बिन्दुओं वाले त्रिभुजों का क्षेत्रफल ज्ञात कीजिए।
(i) (1, 0), (6, 0), (4, 3)
(ii) (2, 7), (1, 1), (10, 8)
(iii) (-2, -3), (3, 2), (-1, -8)
हल:
(i) (1, 0), (6, 0), (4, 3)
त्रिभुज का क्षेत्रफल :

= \(\frac{1}{2}\)[1(0 – 3) – 0(6 -4 ) + 1(18 – 0)]
= \(\frac{1}{2}\)[-3 + 18]
= \(\frac{1}{2}\) वर्ग इकाई
(ii) (2, 7), (1, 1), (10, 8) x1 = 2 y1 = 7, x2 = 1, y2 = 1, x3 = 10, y3 = 8

= \(\frac{1}{2}\)[2(1 × 1 – 1 × 8) – 7(1 × 1 – 10 × 1) + 1(1 × 8 – 10 × 1)]
= \(\frac{1}{2}\)[2 × (1 – 8) – 7(1 – 10) + 1(8 – 10)]
= \(\frac{1}{2}\)[2 × (-7) – 7 × (-9) + 1 × (-2)]
= \(\frac{1}{2}\)[-14 + 63 – 2] =\(\frac{1}{2}\)[63 – 16]
= \(\frac{1}{2}\) × 47 =\(\frac{47}{2}\) = 23\(\frac{1}{2}\) वर्ग इकाई
(iii) (-2, -3), (3, 2), (-1, -8) त्रिभुज का क्षेत्रफल

= \(\frac{1}{2}\)[-2(2 + 8) + 3 (3 + 1) + 1(-24 + 2)]
= \(\frac{1}{2}\)[-20 + 12 – 22]
= \(\frac{1}{2}\)[-30] = [30] ऋणात्मक चिन्ह को छोड़ने पर
= 15वर्ग इकाई
प्रश्न 2.
दर्शाइए कि बिन्दु A (a, b + c), B (b, c + a) और C(c, a + b) संरेख हैं।
हल:
यहाँ त्रिभुज के शीर्ष A (a, b+ c),B (b, c + a) और C(c, a + b)
x1 = a x2 = b x3 = c y1 = b + c y2 = c + a y3 = a + b

C1 तथा C3 समान हैं।
अतः बिन्दु A, B, C संरेख हैं।
![]()
प्रश्न 3.
प्रत्येक में k का मान ज्ञात कीजिए यदि त्रिभुजों का क्षेत्रफल 4 वर्ग इकाई है, जहाँ शीर्षबिन्दु निम्नलिखित हैं-
(i) (k, 0), (4, 0), (0, 2)
(ii) (-2, 0), (0, 4), (0, k)
हल:
(i) (k, 0), (4, 0), (0, 2)
त्रिभुज का क्षेत्रफल = 4 वर्ग इकाई
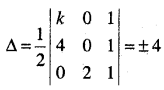
⇒ \(\frac{1}{2}\)[k(-2) + 0 + 1(8)] = ±4
⇒ -k + 5 = ±4
⇒ k= 0 या 8
(ii) त्रिभुज के शीर्ष (-2, 0), (0, 4), (0, k)
x1 = -2, x2 = 0, x3 = 0
y1 = 0, y21 = 4, y3 = k
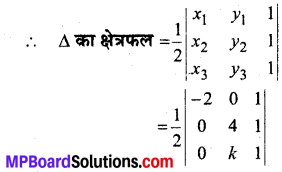
±4 = \(\frac{1}{2}\)[-2(4 – k) + 1(0 – 0)]
±8 = -2(4 – k) ⇒ ±8 = k – 8
+ चिह्न लेने पर, 8 = 2k – 8 ⇒ 2k = 16 ∴ k = 8
-चिह्न लेने पर, -8 = 2k – 8 ∴ k = 0
![]()
प्रश्न 4.
(i) सारणिकों का प्रयोग करके (1, 2) और (3, 6) को मिलाने वाली रेखा का समीकरण ज्ञात कीजिए।
(ii) सारणिकों का प्रयोग करके (3, 1) और (9, 3) को मिलाने वाली,रेखा का समीकरण ज्ञात कीजिए।
हल:
(i) माना बिन्दु A (1, 2) व B(3, 6) से मिलाने वाले रेखाखण्ड पर स्थित बिन्दु P(x, y) हैं।
इसलिए बिन्दु A, B, P संरेख होंगे।
∴ ∆PAB का क्षेत्रफल = 0
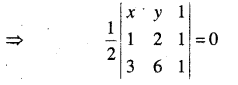
⇒ x (2 – 6) – y(1 – 3) + 1(6 – 6) = 0
⇒ -4x + 2y = 0
⇒ 2x – y = 0
अतः अभीष्ट रेखा का समी० 2x – y = 0 है।
(ii) माना कोई बिन्दु (x, y) है।
तो त्रिभुज के शीर्ष (x, y), (3, 1) और (9, 3)

∆ = \(\frac{1}{2}\)[x × (-2) – y(-6) + 1 × 0]
∆ = \(\frac{1}{2}\)[-2x + 6y] = -x + 3y
बिन्दु (x, y), (3, 1), (9, 3) संरेख हैं।
यदि ∆ = 0
∴ 0 = -x + 3y ⇒ x – 3y = 0
प्रश्न 5.
यदि शीर्ष (2, -6), (5, 4) और (k, 4) वाले त्रिभुज का क्षेत्रफल 35 वर्ग इकाई है तो k का मान है
(A) 12
(B) -2
(C) -12, -2
(D) 12 ,-2
हल:
त्रिभुज के शीर्ष (2, -6), (5, 4) तथा (k, 4)
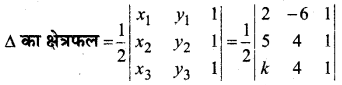
±35 = \(\frac{1}{2}\)[2(4 – 4) + 6(5 – k) + 1(20 -4k)]
±35 = \(\frac{1}{2}\) [2 x 0 + 6(5 – k) + 1(20 – 4k)]
±70 = 6(5 – k) + 20 – 4k
±70 = 30 – 6k + 20 – 4k
±70 = 50 = 10k ⇒ ±7 – 5 – k
+ चिह्न लेने पर, 7 = 5 – k
k = 5 – 7 = -2
– चिह्न लेने पर, -7 = 5 – k ⇒ -12 = -k
∴ k = 12
अतः k = -2, 12
अत: विकल्प (D) सही है।