Category: Class 12

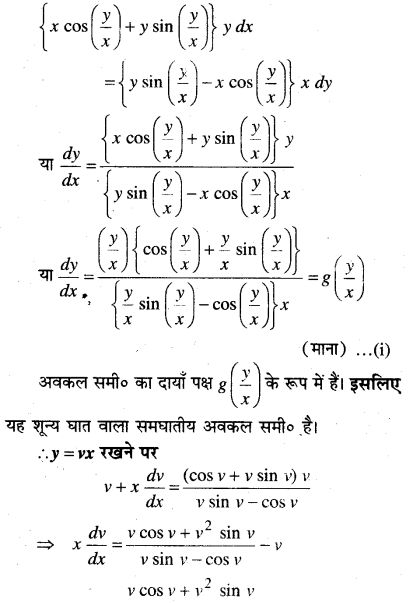
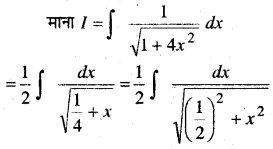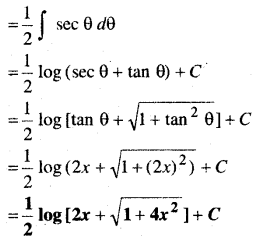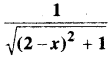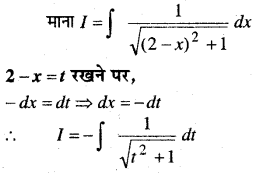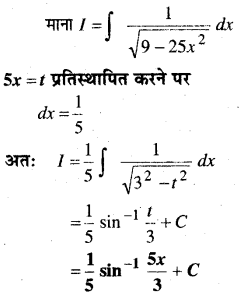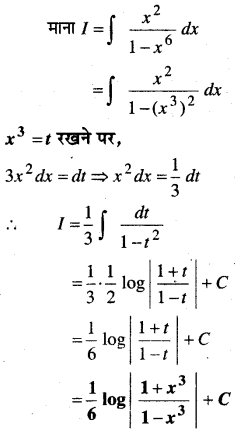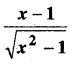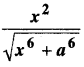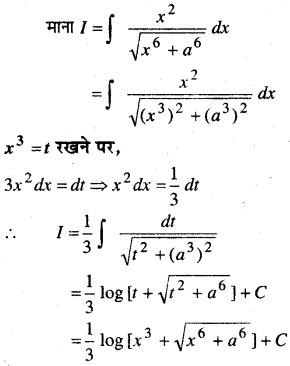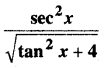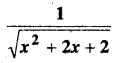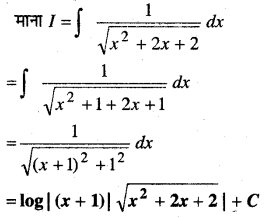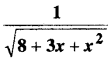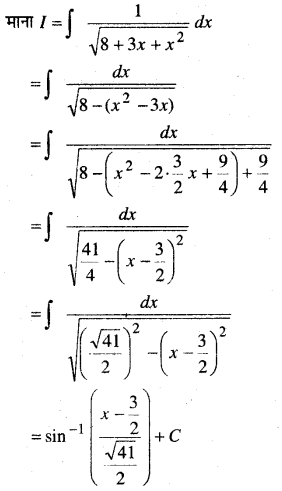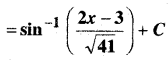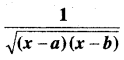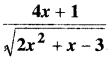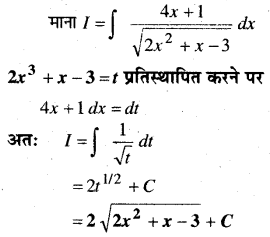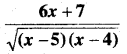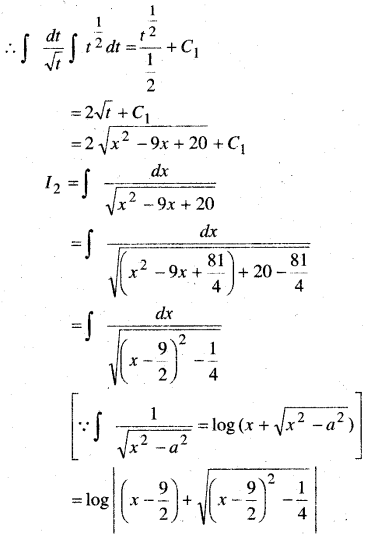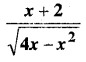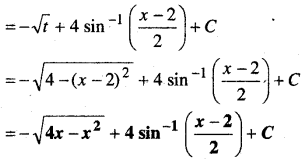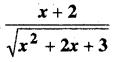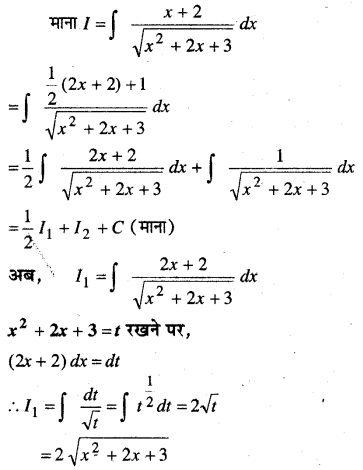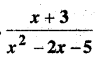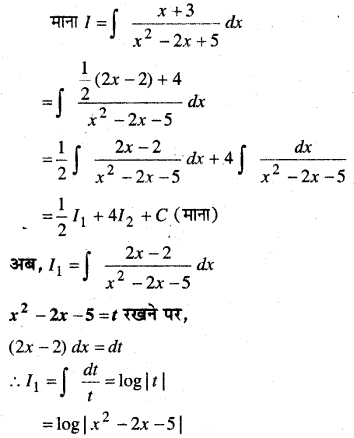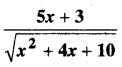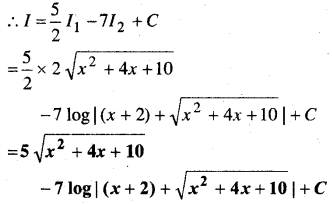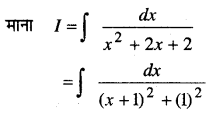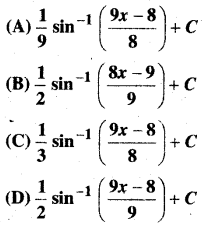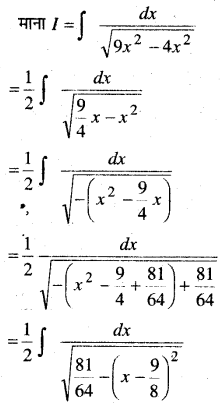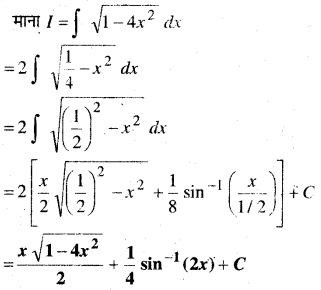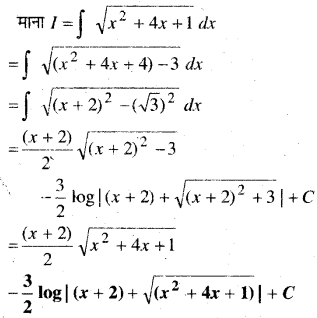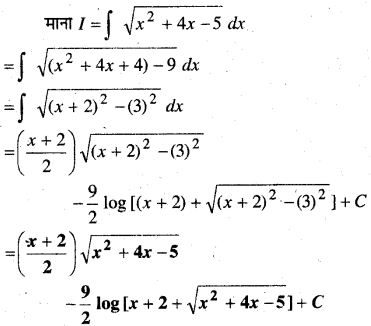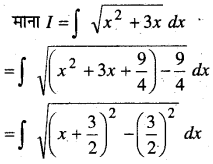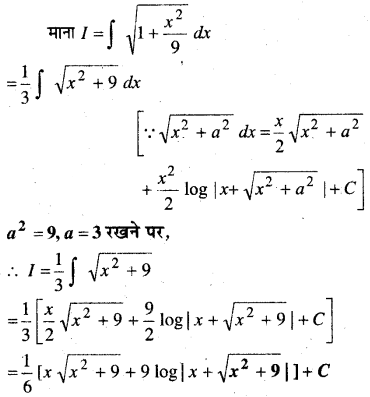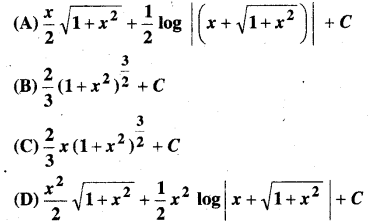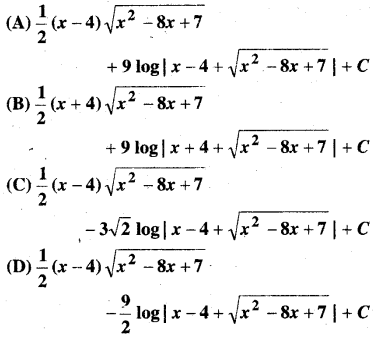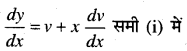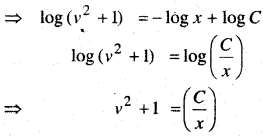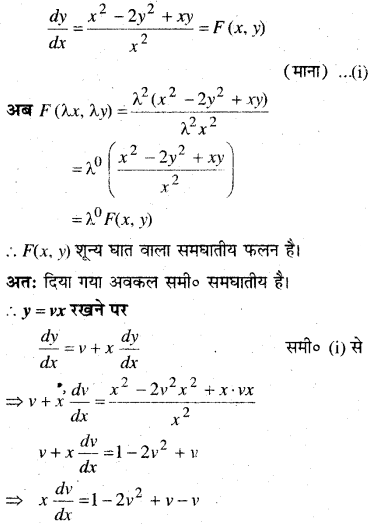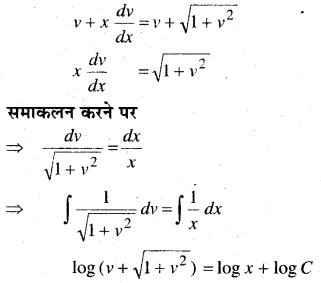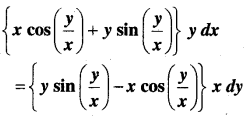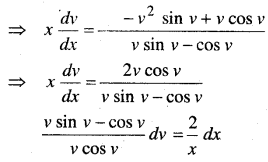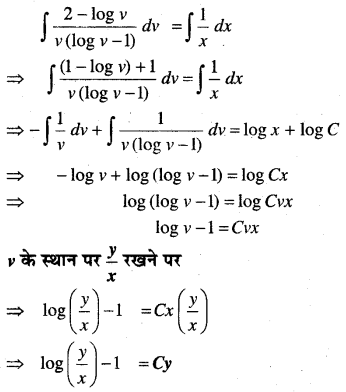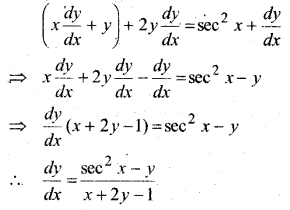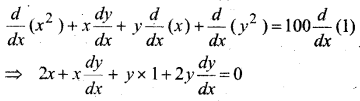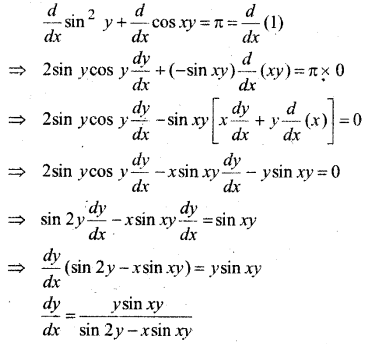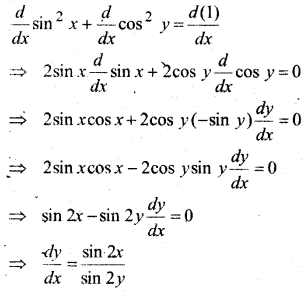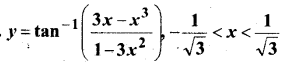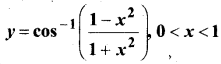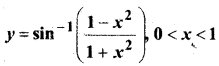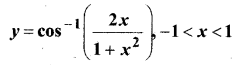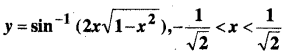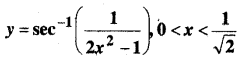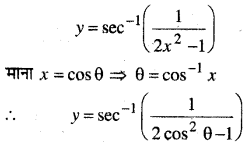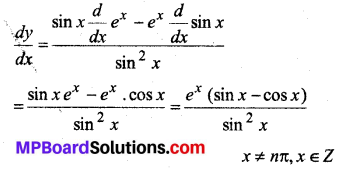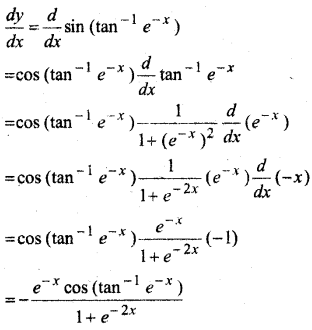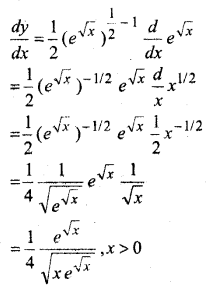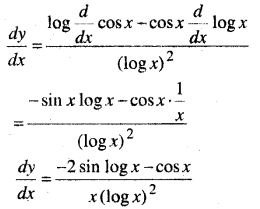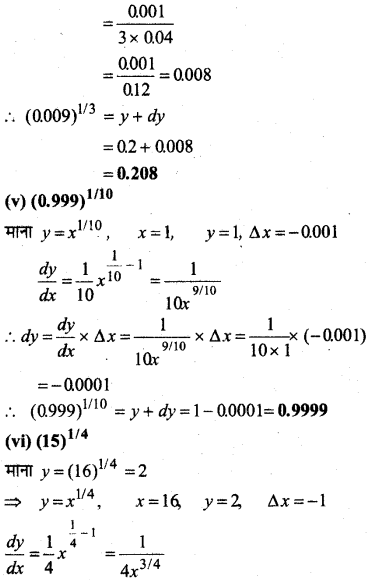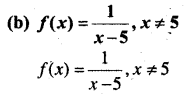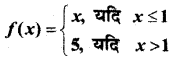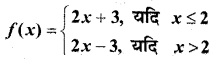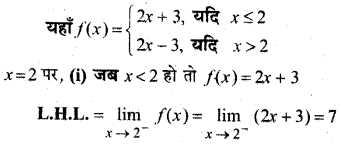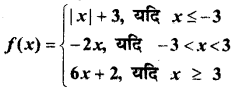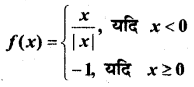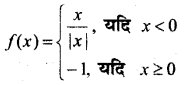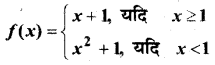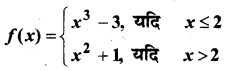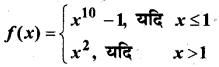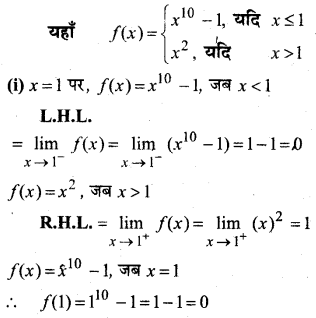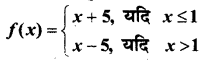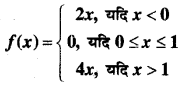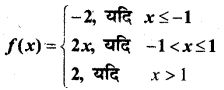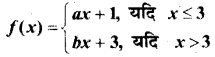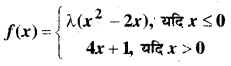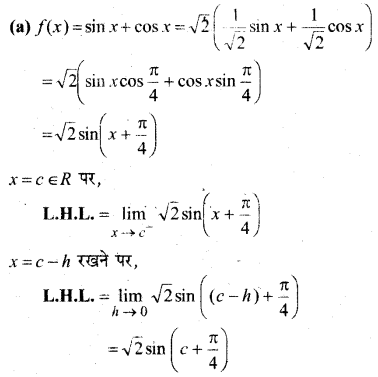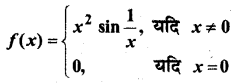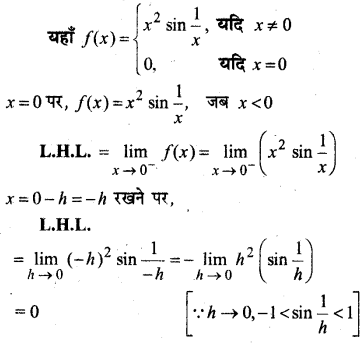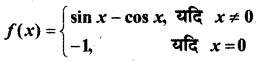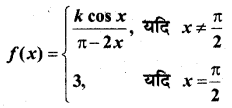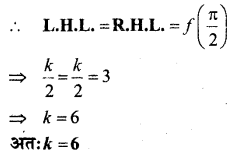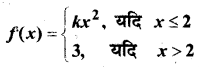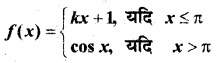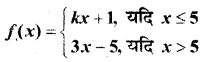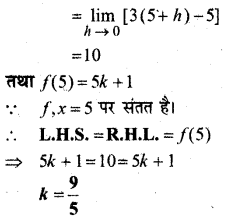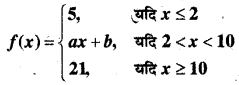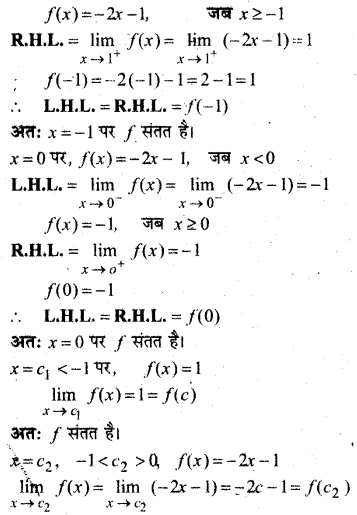In this article, we share MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.3

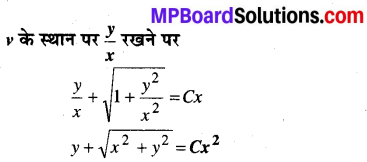
1 से 5 तक प्रत्येक प्रश्न में, स्वेच्छ अचरों a तथा b को विलुप्त करते हुए दिए हुए वक्रों के कुल को निरूपित करने वाला अवकल समीकरण ज्ञात कीजिए।
प्रश्न 1.
\(\frac{x}{a}+\frac{y}{b}=1\)
हल:

प्रश्न 2.
y² = a(b² – x²)
हल:
y = a(b² – x²) …(i)
x के सापेक्ष अवकलन करने पर

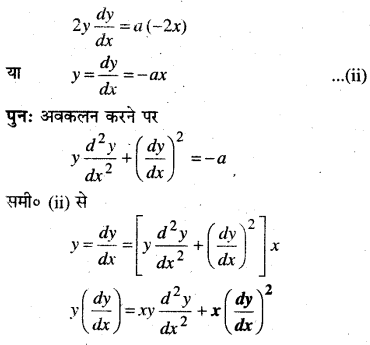
प्रश्न 3.
y = ae^3x + be^-2x
हल:
y = ae^3x + be^-2x …(i)
x के सापेक्ष अवकलन करने पर

प्रश्न 4.
y = e^2x(a + bx)
हल:
y = e^2x(a + bx) …(i)
x के सापेक्ष अवकलन करने पर

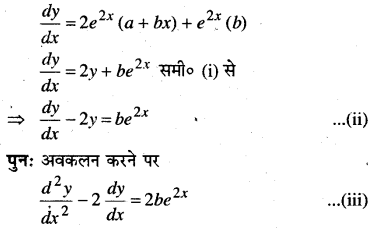
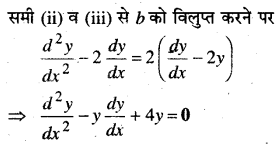
प्रश्न 5.
y = e^x (a cos x + b sin x)
हल:
ye^x(a cos x + b sin x) ….(i)
x के सापेक्ष अवकलन करने पर

प्रश्न 6.
y – अक्ष को मूल बिन्दु पर स्पर्श करने वाले वृत्तों के कुल का अवकल समीकरण ज्ञात कीजिए।
हल:
वृत्त का समी० जो y – अक्ष पर मूल बिन्दु पर स्पर्श करता है-
(x – a)² + (y – 0)² = a²
x² + y² – 2ax + a² = a²
⇒ x² + y² – 2ax = 0. …(i)
x के सापेक्ष अवकलन करने पर
2x + 2y\(\frac{d y}{d x}\) – 2a = 0
⇒ a = x + y\(\frac{d y}{d x}\) …(ii)
a का मान समी० (i) में रखने पर
x² + y² – 2\(\left(x+y \frac{d y}{d x}\right)\) = 0
⇒2xy\(\frac{d y}{d x}\) + x² – y² = 0

प्रश्न 7.
ऐसे परवलयों के कुल का अवकल समीकरण निर्मित कीजिए जिनका शीर्ष मूल बिन्दु पर है और जिनका अक्ष धनात्मक y – अक्ष की दिशा में है।
हल:
परवलय जिसका शीर्ष मूल बिन्दु तथा अक्ष OY है, का समीकरण
x² = 4ay …(i)
x के सापेक्ष अवकलन करने पर

प्रश्न 8.
ऐसे दीर्घवृत्तों के कुल का अवकल समीकरण ज्ञात कीजिए जिनकी नाभियाँ y – अक्ष पर हैं तथा जिनका केन्द्र मूल बिन्दु है।
हल:
इस प्रकार के दीर्घवृत्त के कुल का समी० निम्न होगा

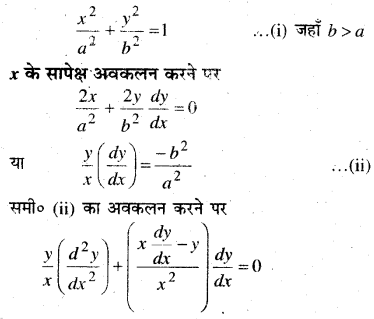
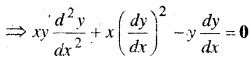
प्रश्न 9.
ऐसे अतिपरवलयों के कुल का अवकल समीकरण ज्ञात कीजिए जिनकी नाभियाँ x-अक्ष पर हैं तथा जिनका केन्द्र मूल बिन्दु है।
हल:
ऐसे अतिपरवलयों के कुल का समी० जिनकी नाभियाँ x – अक्ष पर तथा केन्द्र मूल बिन्दु हैं-

प्रश्न 10.
ऐसे वृत्तों के कुल का अवकल समीकरण ज्ञात कीजिए जिनका केन्द्र y-अक्ष पर है और जिनकी त्रिज्या 3 इकाई है।
हल:
ऐसे वृत्तों के कुल का समी० जिनका केन्द्र y – अक्ष पर हैं और त्रिज्या 3 इकाई हैं
x² + (y – b)² = 9 …(i)
x के सापेक्ष अवकलन करने पर
2x + 2 (y – b)\(\frac{d y}{d x}\) = 0
y – b = \(-\frac{x}{\left(\frac{d y}{d x}\right)}\) …(ii)
समी० (i) व (ii) से b को विलुप्त करने पर

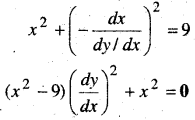
प्रश्न 11.
निम्नलिखित अवकल समीकरणों में से किस समीकरण का व्यापक हल y = c₁e^x + c₂e^-x है?

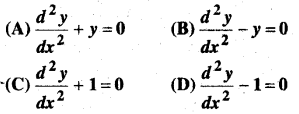
हल:
समीकरण y = c₁e^x + c₂e^-x
x के सापेक्ष अवकलन करने पर
y’ = c₁e^x – c₂e^-x
पुनः अवकलन करने पर …
y” = c₁e^x + c₂e^-x = y
∴ अवकल समीकरण y” – y = 0
या \(\frac{d^{2} y}{d x^{2}}\) – y = 0
अतः विकल्प (B) सही है।

प्रश्न 12.
निम्नलिखित समीकरणों में से किस समीकरण का एक विशिष्ट हल y = x है-

हल:
y = x
x के सापेक्ष अवकलन करने पर
y’ = 1
तथा y” = 0
y = x का मान \(\frac{d^{2} y}{d x^{2}}-x^{2} \frac{d y}{d x}+x y=0\) में रखने पर,
-x²·1 + x·x = 0 जो सत्य है
अतः विकल्प (C) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.4 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Book Maths Solutions Chapter 7 समाकलन Ex 7.4

प्रश्न 1 से 23 तक के फलनों का समाकलन कीजिए।
प्रश्न 1.
\(\frac{3 x^{2}}{x^{6}+1}\)
हल:

प्रश्न 2.
\(\frac{1}{\sqrt{1+4 x^{2}}}\)
हल:

प्रश्न 3.

हल:

प्रश्न 4.
\(\frac{1}{\sqrt{9-25 x^{2}}}\)
हल:

प्रश्न 5.
\(\frac{3 x}{1+2 x^{4}}\)
हल:

प्रश्न 6.
\(\frac{x^{2}}{1-x^{6}}\)
हल:

प्रश्न 7.

हल:

प्रश्न 8.

हल:

प्रश्न 9.

हल:

प्रश्न 10.

हल:

प्रश्न 11.

हल:

प्रश्न 12.

हल:

प्रश्न 13.

हल:

प्रश्न 14.

हल:

प्रश्न 15.

हल:

प्रश्न 16.

हल:

प्रश्न 17.

हल:

प्रश्न 18.

हल:

प्रश्न 19.

हल:

प्रश्न 20.

हल:

प्रश्न 21.

हल:

प्रश्न 22.

हल:

प्रश्न 23.

हल:

प्रश्न 24 एवं 25 में सही उत्तर का चयन कीजिए-
प्रश्न 24.
\(\int \frac{d x}{x^{2}+2 x+2}\) बराबर है
(A) x tan^-1(x + 1) + C
(B) tan^-1(x + 1) + C
(C) (x + 1) tan^-1 x + C
(D) tan^-1 x + C
हल:

प्रश्न 25.
\(\int \frac{d x}{\sqrt{9 x-4 x^{2}}}\) बराबर है-

हल:

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.7 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 7 समाकलन Ex 7.7

1 से 9 तक के प्रश्नों के फलनों का समाकलन कीजिए
प्रश्न 1.
\(\sqrt{4-x^{2}}\)
हल:

प्रश्न 2.
\(\sqrt{1-4 x^{2}}\)
हल:

प्रश्न 3.
\(\sqrt{x^{2}+4 x+6}\)
हल:
माना I = \(\int \sqrt{x^{2}+4 x+6} d x\)

प्रश्न 4.
\(\sqrt{x^{2}+4 x+1}\)
हल:

प्रश्न 5.
\(\sqrt{1-4 x-x^{2}}\)
हल:

प्रश्न 6.
\(\sqrt{x^{2}+4 x-5}\)
हल:

प्रश्न 7.
\(\sqrt{1+3 x-x^{2}}\)
हल:

प्रश्न 8.
\(\sqrt{x^{2}+3 x}\)
हल:

प्रश्न 9.
\(\sqrt{1+\frac{x^{2}}{9}}\)
हल:

प्रश्न 10 एवं 11 में सही उत्तर का चयन कीजिए-
प्रश्न 10.
\(\int \sqrt{1+x^{2}}\) बराबर है-

हल:
\(\int \sqrt{a^{2}+x^{2}} d x\)

प्रश्न 11.
\(\int \sqrt{x^{2}-8 x+7}\) dx बराबर है-

हल:

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 8 समाकलनों के अनुप्रयोग Ex 8.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 8 समाकलनों के अनुप्रयोग Ex 8.2

प्रश्न 1.
परवलय x² = 4y और वृत्त 4x² + 4y² = 9 के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
परवलय का समी० x² = 4y …(i)
तथा वृत्त का समी० x² + y² = \(\left(\frac{3}{2}\right)^{2}\) …(ii)
समी० (i) व (ii) को हल करने पर बिन्दु \(\left( \pm \sqrt{2}, \frac{1}{2}\right)\) प्रतिच्छेदन बिन्दु के रूप में प्राप्त होते हैं।
∴ दोनों वक्र x-अक्ष के सममित हैं।
∴ अभीष्ट क्षेत्रफल = 2 × ODCAO का क्षेत्रफल

प्रश्न 2.
वक्रों (x – 1)² + y = 1 एवं x² + y² = 1 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
वक्रों के समीकरण
x² + y = 1 …(i)
(x – 1)² + y² = 1
समी० (i) वृत्त का समी० है। जिसका केन्द्र (0, 0) तथा

त्रिज्या 1 इकाई है। जबकि समी० (ii) उस वृत्त का समीकरण है जिसका केन्द्र (1,0) तथा त्रिज्या 1 इकाई है।
समी० (i) व (ii) को हल करने पर प्रतिच्छेदन बिन्दु \(\left(\frac{1}{2}, \pm \sqrt{3} / 2\right)\) है।
∴ अभीष्ट क्षेत्रफल
= 2 × OCRAO का क्षेत्रफल
= 2 × [OCAO का क्षेत्रफल + CBAC का क्षेत्रफल]

प्रश्न 3.
वक्रों y = x² + 2, y = x, x = 0 एवं x = 3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
वक्र का समी० y = x² + 2
या x² = y – 1 यह एक परवलय का समी० है जिसका शीर्ष (0, 2) है।

प्रश्न 4.
समाकलन का उपयोग करते हुए एक ऐसे त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष (-1, 0), (1, 3) एवं (3, 2) हैं।
हल:
दिया है : शीर्ष बिन्दु (-1, 0), (1, 3) और (3, 2) रेखा AB का समी०

त्रिभुज ABC का क्षेत्रफल = (ANBA का क्षे० + NMCBN का क्षे०) – AMCA का क्षे०

प्रश्न 5.
समाकलन का उपयोग करते हुए एक ऐसे त्रिकोणीय क्षेत्र का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओं के ‘समीकरण y = 2x + 1, y = 3x + 1 एवं x = 4 हैं।
हल:
दिया है
भुजाओं के समी० y = 2x + 1 ….(i)
y = 3x + 1 …(ii)
x = 4 …(iii)

प्रश्न 6 एवं 7 में सही उत्तर का चयन कीजिए-
प्रश्न 6.
वृत्त x² + y² = 4 एवं रेखा x + y = 2 से घिरे छोटे भाग का क्षेत्रफल है-
(A) 2 (π – 2)
(B) (π – 2)
(C) 2π – 1
(D) 2(π + 2)
हल:
वृत्त का समी० x² + y² = 4
वृत्त का केन्द्र O है तथा त्रिज्या 2 है।

अतः विकल्प (B) सही है।

प्रश्न 7.
वक्रों y² = 4x एवं y = 2x के मध्यवर्ती क्षेत्र का क्षेत्रफल है-

हल:
वक्र कासमी० y² = 4x …(i)
रेखा का समी० y = 2x …(ii)
समी० (i) व (ii) से
(2x)² = 4x
4x² = 4x
⇒ x² – x = 0
⇒ x(x – 1) = 0
⇒ x = 0, x = 1

समी० (ii) से जब x = 0, y= 0 और जब x = 1, y = 2
समी० (i) व समी० (ii) का प्रतिच्छेदन बिन्दु (0, 0) तथा A(1, 2) हैं।
अभीष्ट क्षेत्रफल

अतः विकल्प (B) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.5 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.5

1 से 10 तक के प्रत्येक प्रश्न में दर्शाइए कि दिया हुआ अवकल समीकरण समघातीय है और इनमें से प्रत्येक को हल कीजिए-
प्रश्न 1.
(x² + xy) dy = (x² + y²)dx
हल:

प्रश्न 2.
y’ = \(\frac{x+y}{x}\)
हल:
\(\frac{d y}{d x}=\frac{x+y}{x}\)
∵ अंश व हर की घात समान है इसलिए दिया हुआ अवकल समी० समघातीय अवकल समी० हैं।
∴ y = vx रखने पर

प्रश्न 3.
(x – y)dy -(x + y)dx = 0
हल:
(x – y) dy – (x + y) dx =0
⇒ \(\frac{d y}{d x}=\frac{x+y}{x-y}\)
∵ अंश व हर की घात समान हैं अतः यह एक समघातीय अवकल समीकरण हैं।
∴ y = vx रखने पर

प्रश्न 4.
(x² – y) dx + 2xy dy = 0
हल:
(x² – y²) dx + 2xy dy = 0

प्रश्न 5.
x²\(\frac{d y}{d x}\) = x² – 2y² + xy
हल:

प्रश्न 6.
x dy – y dx = \(\sqrt{x^{2}+y^{2}}\) dx
हल:

प्रश्न 7.

हल:
दिया गया अवकल समीकरण

प्रश्न 8.
x\(\frac{d y}{d x}\) – y + x sin\(\left(\frac{y}{x}\right)\) = 0
हल:

प्रश्न 9.
y dx + x log\(\left(\frac{y}{x}\right)\)dy – 2x dy = 0
हल:
दिया गया अवकल समी०
y dx + x log\(\left(\frac{y}{x}\right)\)dy – 2x dy = 0 …(i)

प्रश्न 10.
(1 + e^x/y) dx + e^x/y (1 – \(\frac{x}{y}\)) dy = 0
हल:
दिया गया अवकल समी०

11 से 15 तक के प्रश्नों में प्रत्येक अवकल समीकरण के लिए दिए हुए प्रतिबन्ध को सन्तुष्ट करने वाला विशिष्ट हल ज्ञात कीजिए।
प्रश्न 11.
(x + y) dy + (x – y) dx = 0; y = 1 यदि x = 1
हल:
दिया है (x + y) dy + (x – y) dx = 0
⇒ \(\frac{d y}{d x}=\frac{y-x}{y+x}\) …(i)
∵ अंश व हर की घात समान हैं इसलिए यह एक समघातीय अवकल समी० है।
∴ y = vx रखने पर

प्रश्न 12.
x²dy + (xy + y²) dx = 0; y = 1 यदि x = 1
हल:
दिया गया अवकल समी०
x²dy + (xy + y²) dx = 0

प्रश्न 13.
[x sin² \(\left(\frac{y}{x}\right)\) – y] dx + x dy = 0: y = \(\frac{\pi}{4}\) यदि x = 1
हल:
दिया गया अवकल समी०

प्रश्न 14.
\(\frac{d y}{d x}-\frac{y}{x}\) + cosec \(\left(\frac{\boldsymbol{y}}{\boldsymbol{x}}\right)\) = 0; y = 0 यदि x = 1
हल:
दिया गया अवकल समी०

प्रश्न 15.
2xy + y² – 2x²\(\frac{d y}{d x}\) = 0; y = 2 यदि x = 1
हल:
दिया गया समी०

प्रश्न 16.
\(\frac{d x}{d y}=h\left(\frac{x}{y}\right)\) के रूप वाले समघातीय अवकल समीकरण को हल करने के लिए निम्नलिखित में से कौन-सा प्रतिस्थापन किया जाता है-
(A) y = vx
(B) v = yx
(C) x = vy
(D) x = y
हल:
जब \(\frac{d x}{d y}=h\left(\frac{x}{y}\right)\) हो तो x = yy प्रतिस्थापित करते हैं।
अत: विकल्प (C) सही है।

प्रश्न 17.
निम्नलिखित में से कौन-सा समघातीय अवकल समीकरण है
(A) (4x + 6y + 5)dy – (3y + 2x + 4)dx = 0
(B) (xy) dx – (x³ + y³)dy = 0
(C) (x³ + 2y²)dx + 2xy dy = 0
(D) y²dx + (x² – xy – y²)dy = 0
हल:
y²dx + (x² – xy – y²) dy = 0 पर विचार करते हैं।

इस प्रकार अवकल समीकरण समघातीय है।
अतः विकल्प (D) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.3

निम्नलिखित प्रश्नों में \(\frac{d y}{d x}\) ज्ञात कीजिए
प्रश्न 1.
2x + 3y = sin x
हल:
2x + 3y = sinx
x के सापेक्ष अवकलन करने पर,

प्रश्न 2.
2x + 3y = siny
हल:
यहाँ 2x + 3y = sin y
x के सापेक्ष अवकलन करने पर,

प्रश्न 3.
ax + by² = cosy
हल:
यहाँ ax + by² = cos y
x के सापेक्ष अवकलन करने पर,

प्रश्न 4.
xy + y² = tan x + y
हल:
यहाँ xy + y² = tan x + y
x के सापेक्ष अवकलन करने पर,

प्रश्न 5.
x² + xy + y² = 100
हल:
x² + xy + y² = 100
x के सापेक्ष अवकलन करने पर,

प्रश्न 6.
x² + x²y + xy² + y³ = 81
हल:
यहाँ x² + xy + xy² + y³ = 81
x के सापेक्ष अवकलन करने पर,

प्रश्न 7.
sin² y + cos xy = π
हल:
यहाँ sin ²y + cos xy = π
x के सापेक्ष अवकलन करने पर,

प्रश्न 8.
sin² x + cos²y = 1
हल:
∵ sin² x + cos² y = 1
दोनों ओर x के सापेक्ष अवकलन करने पर,

प्रश्न 9.
y = sin^-1\(\left(\frac{2 x}{1+x^{2}}\right)\)
हल:

प्रश्न 10.

हल:

प्रश्न 11.

हल:

प्रश्न 12.

हल:

प्रश्न 13.

हल:

प्रश्न 14.

हल:

प्रश्न 15.

हल:

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.4 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.4

निम्नलिखित का x के सापेक्ष अवकलन कीजिए-
प्रश्न 1.
\(\frac{e^{x}}{\sin x}\)
हल:
माना \(\frac{e^{x}}{\sin x}\)
x के सापेक्ष अवकलन करने पर,

प्रश्न 2.
esin^-1x
हल:
माना y = esin^-1x
x के सापेक्ष अवकलन करने पर,

प्रश्न 3.
e^x3
हल:
माना y = e^x3
x के सापेक्ष अवकलन करने पर,

प्रश्न 4.
sin (tan^-1e^-x)
हल:
माना y = sin (tan^-1e^-x)
के सापेक्ष अवकलन करने पर,

प्रश्न 5.
log (cos e^x)
हल :
माना y = log (cos e^x)
x के सापेक्ष अवकलन करने पर,

प्रश्न 6.
e^x + e^x2 + … + e^x2
हल :
माना y = e^x + e^x2 + e^x3 + e^x4 + e^x5
x के सापेक्ष अवकलन करने पर,

प्रश्न 7.
\(\sqrt{e^{\sqrt{x}}}\), x > 0
हल :
माना y = \(\sqrt{e^{\sqrt{x}}}\)
x के सापेक्ष अवकलन करने पर,

प्रश्न 8.
log (log x), x > 1
हल :
माना y = log (logx)
x के सापेक्ष अवकलन करने पर,

प्रश्न 9.
\(\frac{\cos x}{\log x}\), x > 0
हल:
माना y = \(\sqrt{\frac{\cos x}{\log x}}\)
x के सापेक्ष अवकलन करने पर,

प्रश्न 10.
cos (log x + e^x)
हल:
माना y = cos (log x + e^x)
x के सापेक्ष अवकलन करने पर,

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 6 अवकलज के अनुप्रयोग Ex 6.4 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 6 अवकलज के अनुप्रयोग Ex 6.4

प्रश्न 1.
अवकल का प्रयोग करके निम्नलिखित में से प्रत्येक का सन्निकट मान दशमलव के तीन स्थानों तक ज्ञात कीजिए-
(i) \( \sqrt{{25.3}} \)
(ii) \( \sqrt{{49.5}} \)
(iii) \( \sqrt{{0.6}} \)
(iv) (0.009)^1/3
(v) (0.999)^1/10
(vi) (15)^1/4
(vii) (26)^1/3
(viii) (255)^1/4
(ix) (82)^1/4
(x) (401)^1/2
(xi) (0.0037)^1/2
(xii) (26.57)^1/3
(xiii) (81.5)^1/4
(xiv) (3.968)^3/2
(xv) (32.15)^1/5
हल:

प्रश्न 2.
f (2.01) का सन्निकट मान ज्ञात कीजिए जहाँ f(x) = 4x + 5x + 2 है।
हल:
यदि f(x) = 4x² + 5x + 2 हो, तब
f(2) = 4(2)² + 5 × 2 + 2 = 16 + 10 + 2 = 28
∆x = 0.01
∴ f(x) = 8x + 5
df'(x) = f'(x) × ∆x = (x + 5) ∆x
= (8 × 2 + 5) × 0.01
= 21 × 0.01 = 0.21
∴ f(2.01) = f(2) = df (x)
= 28 + 0.21 = 28.21

प्रश्न 3.
f(5.001) का सन्निकट मान ज्ञात कीजिए जहाँ f(x) = x³ – 7x² + 15 है।
हल:
∵ f(x) = x³ – 7x² + 15
∴ f(5) = (5)³ – 7(5)² + 15 (x = 5 रखने पर)
= 140 – 175 = -35
∆x = 0.001
∴ f(x) = 3x² – 14x
∴ f(x) = f’ (x) × ∆x
= (3x² – 14x) × 0.001
= [3 (5)² – 14 × 5] × 0.001
= (75 – 70) × 0.001
= 5 × 0.001 = 0.005
∴ f(5.001) = f(5) + df (x)
= -35 + 0.005
= -34.995

प्रश्न 4.
xm भुजा वाले धन की भुजा में 1% वृद्धि के कारण घन के आयतन में होने वाला सन्निकट परिवर्तन ज्ञात कीजिए।
हल:
माना xm भुजा वाले घन का आयतन V है।
∴ v = x³
भुजा में होने वाली वृद्धि = भुजा का 1%

प्रश्न 5.
xm भुजा वाले घन की भुजा में 1% ह्रास के कारण घन के पृष्ठ क्षेत्रफल में होने वाले सन्निकट परिवर्तन ज्ञात कीजिए।
हल:
घन xm भुजा वाले घन का पृष्ठ = S
∴ S = 6x²
भुजा में हास = x का 1%
= x × \(\frac{1}{100}\) = 0.01x
∴ सन्निकट परिवर्तन = \(\frac{dS}{dx}\) × ∆x
= 12 × (-0.01x)
= -012x²m²
अतः क्षेत्रफल में सन्निकट परिवर्तन = 0.12x²m²

प्रश्न 6.
एक गोले की त्रिज्या 7 m मापी जाती है जिसमें 0.02 m की त्रुटि है। इसके आयतन के परिकलन में सन्निकट त्रुटि ज्ञात कीजिए।
हल:
गोले की त्रिज्या r = 7 m
त्रिज्या r में अशुद्धि ∆r = 0.03
माना r त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल S
∴ S = 4πr²
⇒ \(\frac{dS}{dx}\) = 8πr
अतः पृष्ठीय क्षेत्रफल में अशुद्धि = \(\frac{dS}{dx}\) × ∆x
= 8πr × ∆r
= 8 × π × 7 × 0.03
= 2.16πm²

प्रश्न 7.
एक गोले की त्रिज्या 9 m मापी जाती है जिसमें 0.03 cm की त्रुटि है। इसके पृष्ठ क्षेत्रफल के परिकलन में सन्निकट त्रुटि ज्ञात कीजिए।
हल:
यहाँ r= गोले की त्रिज्या = 9m
∆r त्रिज्या में अशुद्धि = 0.03
s = गोले का पृष्ठीय क्षेत्रफल = 4πr²
\(\frac{ds}{dx}\) = 8πr
पृष्ठीय क्षेत्रफल की गणना करने में अशुद्धि = \(\frac{ds}{dx}\) × ∆r
= 8πr × ∆r
= 8π × 9 × 003
= 2.16 πm³

प्रश्न 8.
यदि f(x) = 3x² + 15x + 5 हो तो f (3.02) का सन्निकट मान है-
(A) 47.66
(B) 57.66
(C) 67.66
(D) 77.66
हल:
यदि f(x) = 3x² + 15x + 5
f(x) = 6x + 15
f(3) = 3 × 9 + 15 × 3 + 5
= 27 + 45 + 5 = 77
df (x) = f'(x) × ∆x = (6x + 5) × ∆x
= (6 × 3 + 15) × 0.02 [∴ x = 3, ∆x = 0.02]
= (18 + 15) × 0.02
= 33 × 0.02 = 0.66
∴ f(3.02) = f(3) + df (3) = 77 + 0.66 = 77.66
अतः विकल्प (D) सही है।

प्रश्न 9.
भुजा में 3% वृद्धि के कारण भुजा x के धन के आयतन में सन्निकट परिवर्तन है
(A) 0.06 x³ m³
(B) 0.6 x³ m³
(C) 0.09 x³ m³
(D) 0.9 x³ m³
हल:
घन का आयतन V = x³ m³ (भुजा = x m)
भुजा में वृद्धि = 3% = x का 3% = 0.03x
आयतन में वृद्धि = \(\frac{d V}{d x}\) × ∆x
= 3x² × ∆x = 3x² × 003x
= 0.09x³ m³
अतः विकल्प (C) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित Ex 10.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 10 सदिश बीजगणित Ex 10.1

प्रश्न 1.
उत्तर से 30° पूर्व में 40 km के विस्थापन का आलेखीय निरूपण कीजिए।
हल:
20 km को 1 cm मानते हुए 2 cm का एक रेखाखण्ड OP, OY की दायीं ओर OY के साथ 30° का कोण बनाते हुए खींचा गया।
इस प्रकार सदिश \(\overrightarrow{O P}\) OY से 30° पूर्व में 40 km के विस्थापन को निरूपित करता है।

प्रश्न 2.
निम्नलिखित मापों को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।
(i) 10 kg,
(ii) 2 मीटर उत्तर-पश्चिम,
(iii) 40°,
(iv) 40 वॉट,
(v) 10^-19 कूलम्ब,
(vi) 20 m/s²
हल:
अदिश-
(i) 10 kg,
(iii) 40°,
(iv) 40 वॉट,
(v) 10^-19 कूलम्ब

सदिश-
(ii) 2 मीटर उत्तर-पश्चिम
(vi) 20 m/s²

प्रश्न 3.
निम्नलिखित को अदिश एवं सदिश राशियों के रूप में श्रेणीबद्ध कीजिए।
(i) समय कालांश
(ii) दूरी
(iii) बल
(iv) वेग
(v) कार्य
हल:
(a) अदिश राशि-
(i) समय कालांश,
(ii) दूरी,
(v) कार्य

(b) सदिश राशि-
(iii) बल,
(iv) वेग।।

प्रश्न 4.
संलग्न आकृति (एक वर्ग) में निम्नलिखित सदिशों को पहचानिए-
(i) सह-आदिम,
(ii) समान,
(iii) संरेख परन्तु असमान।

हल:
(i) सह-आदिम राशि : \(\overrightarrow{AB}\) = \(\overrightarrow{a}\) तथा AD = \(\overrightarrow{d}\)
(ii) समान : \(\overrightarrow{A D}=\vec{d}, \overrightarrow{B C}=\vec{b}\)
(iii) संरेख परन्तु असमान : \(\overrightarrow{A B}=\vec{a}, \overrightarrow{C D}=\vec{c}\)

प्रश्न 5.
निम्नलिखित का उत्तर सत्य अथवा असत्य के रूप में दीजिए।
(i) \(\overrightarrow{a}\) तथा \(-\overrightarrow{a}\) संरेख हैं।
(ii) दो संरेख सदिशों का परिमाण सदैव समान होता है।
(iii) समान परिमाण वाले दो सदिश संरेख होते हैं।
(iv) समान परिमाण वाले दो संरेख सदिश समान होते हैं।
हल:
(i) सत्य,
(ii) असत्य,
(iii) असत्य,
(iv) असत्य

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 5 सांतत्य तथा अवकलनीयता Ex 5.1

प्रश्न 1.
सिद्ध कीजिए कि फलन f(x) = 5x – 3, x = 0, x = – 3 तथा x = 5 पर संतत है।
हल:

प्रश्न 2.
x = 3 पर फलन f(x) = 2x² – 1 के सातत्य की जाँच कीजिए :
हल:
∵ f(x) = 2x² – 1
∴ f(3) = 2 x 3² – 1 = 17
\(\lim _{x \rightarrow 3} f(x)=\lim _{x \rightarrow 3}\left(2 x^{2} – 1\right)\)
= 2 × 9 – 1 = 17
अतः f(x), x = 3 पर सतत् है।

प्रश्न 3.
निम्नलिखित फलनों के सातत्य की जाँच कीजिए
हल:
(a) f(x) = x – 5
(x – 5) एक बहुपदीय व्यंजक है।
अतः हर बिन्दु x ϵ R पर संतत है।



अतः f, x = 5 पर संतत है।
पुनः x < 5 पर f(x) = x – 5, जो कि एक बहुपद है इसलिए f, x > 5 पर संतत है
x < 5 पर
f(x) = – (x – 5) = 5 – x, जो कि एक बहुपद है
∴ f, x < 5 पर संतत है
अतः f, x की समस्त मान के लिए संतत है।

प्रश्न 4.
सिद्ध कीजिए कि फलन f(x) = xⁿ, x = n, संतत है, जहाँ n एक धन पूर्णांक है।
हल:
∵ n एक धन पूर्णांक है
∴ f(x) = xⁿ एक बहुपद हैं
इसलिए x = n पर f एक संतत है।

प्रश्न 5.
क्या
द्वारा परिभाषित फलन f, x = 0, x = 1 तथा x = 2 पर संतत है।
हल:

f के सभी असातत्य के बिन्दुओं को ज्ञात कीजिए, जबकि f निम्नलिखित प्रकार से परिभाषित है –
प्रश्न 6.

हल:

प्रश्न 7.

हल:

प्रश्न 8.

हल:

प्रश्न 9.

हल:

प्रश्न 10.

हल:

प्रश्न 11.

हल:

प्रश्न 12.

हल:

प्रश्न 13.
क्या
परिभाषित फलन, एक संतत फलन है?
हल:

फलन f के सातत्य पर विचार कीजिए, जहाँ f निम्नलिखित द्वारा परिभाषित है-
प्रश्न 14.

हल:

⇒ L.H.L. ≠ R.H.L.
∴ f बिन्दु x = 3 पर संतत नहीं है।
अतः x = 1 व x = 3 पर f असांत्यता है।

प्रश्न 15.

हल:


⇒ L.H.L. ≠ R.H.L.
अतः f (x), x = 1 पर संतत नहीं है। पुनः x > 1 के लिए,
f(x) = 4x, जो कि बहुपद है।
∴ x > 1 पर f सतत होगा।
अतः x = 1 के अतिरिक्त f सभी बिन्दुओं पर संतत होगा अथवा केवल x = 1 पर असांतत्य होगा।

प्रश्न 16.

हल:

प्रश्न 17.
a और b के उन मानों को ज्ञात कीजिए। जिनके लिए

द्वारा परिभाषित फलन x = 3 पर संतत है।
हल:

अत: b के प्रत्येक मान के लिए इसके संगत a का मान ज्ञात कर सकते हैं।

प्रश्न 18.
λ के किस मान के लिए

द्वारा परिभाषित फलन x = 0 पर संतत है। x = 1 पर इसके सांतत्य पर विचार कीजिए।
हल:

प्रश्न 19.
दर्शाइए कि g(x) = x – [x] द्वारा परिभाषित फलन समस्त पूर्णांक बिन्दुओं पर असंतत है। यहाँ [x] उस महत्तम पूर्णाक निरूपित करता है, जो x के बराबर या x से कम है।
हल:
x = c पूर्णांक पर, f(x) = x – [x]

प्रश्न 20.
क्या f(x) = x² – sin x + 5 द्वारा परिभाषित फलन x = π पर संतत है?
हल:
माना f(x) = x² – sin x + 5

प्रश्न 21.
निम्नलिखित फलनों के सातत्य पर विचार कीजिए –
(a) f(x) = sin x + cosx
(b) f(x) = sin x – cosx
(c) f(x) = sin x. cosx
हल:

प्रश्न 22.
cosine, cosecant, secant और cotangent फलनों के सातत्य पर विचार कीजिए।
हल:
(a) माना f(x) = cos x

प्रश्न 23.
f के सभी असातत्यता के बिन्दुओं को ज्ञात कीजिए, जहाँ

हल:

तथा f(0) = 0 + 1 = 1
∴ x = 0 पर f संतत फलन है।
जब x > 0, f(x) = x + 1, जो कि बहुपद है।
∴ f एक संतत फलन होगा।
अतः f प्रत्येक बिन्दु पर संतत फलन है।

प्रश्न 24.
निर्धारित कीजिए कि फलन f

द्वारा परिभाषित एक संतत फलन है।
हल:

प्रश्न 25.
f के सातत्य की जाँच कीजिए, जहाँ f निम्नलिखित प्रकार से परिभाषित है-

हल:

∴ x = c ≠ 0 पर f संतत है।
अत: x ϵ R, सभी बिन्दुओं पर f संतत है।

प्रश्न 26 से 29 में k के मानों को ज्ञात कीजिए ताकि प्रदत्त फलन निर्दिष्ट बिन्दु पर संतत हो-
प्रश्न 26.

द्वारा परिभाषित फलन x = \(\frac{\pi}{2}\) पर।
हल:
x = \(\frac{\pi}{2}\) पर,

प्रश्न 27.

द्वारा परिभाषित फलन x = 2 पर।
हल:

प्रश्न 28.

द्वारा परिभाषित फलन x = π पर।
हल:

प्रश्न 29.

द्वारा परिभाषित फलन x = 5 पर
हल:

प्रश्न 30.
a तथा b के मानों को ज्ञात कीजिए ताकि

द्वारा परिभाषित फलन एक संतत फलन हो।
हल:
प्रश्न (15) की भाँति करें।
x = 3 पर
L.H.L. = 5
R.H.L. = 2a + b
तथा f(2) = 5
∵ f(x) x = 2 पर संतत फलन है।
∴ L.H.L. = R.H.L.
2a + b = 5
पुनः f (x), x = 10 पर संतत है।
∴ L.H.S. = R.H.S. = f(10)

प्रश्न 31.
दर्शाइए कि f(x) – cos (x²) द्वारा परिभाषित फलन एक संतत फलन है
हल:
f(x) = cos(x²)
माना g(x) = cosx तथा h (x) = x²
∴ goh (x) = g[h (x)] = g(x²)
= cos (x²) = f(x)
∵ g (x) एक कोज्या (cosine) का एक फलन है जो कि संतत होता है।
तथा h (x) एक बहुपद है।
इसलिए f(x) भी एक संतत फलन है।

प्रश्न 32.
दर्शाइए कि f(x) = | cos x| द्वारा परिभाषित फलन एक संतत फलन है।
हल:
यहाँ f(x) = |cosx|
सर्वप्रथम माना x = c ϵ R पर,
\(\lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c}|\cos x|=|\cos c|\)
f(c) = |cosc|
अतः x = C ϵ R पर एक संतत फलन है।

प्रश्न 33.
जाँचिए कि क्या sin |x|एक संतत फलन है।
हल:
माना f(x) = sin |x|
प्रथम विधि-
x = c ϵ R पर,
\(\lim _{x \rightarrow c} f(x)=\lim _{x \rightarrow c}(\sin |x|)=\sin |c|\)
f(c) = sin |c|
अतः x = c ϵ R पर एक संतत फलन है।
दूसरी विधि से-
माना g (x) = sin x, h (x) = |x|
f(x) = (goh)(x) = g (h (x)) = g (|x|) = sin |x|
g(x) = sin x 3ite h(x) = |x|
g और h दोनों संतत फलन हैं।
अतः f भी संतत फलन है।

प्रश्न 34.
f(x) = |x| – |x + 1| द्वारा परिभाषित फलन के सभी असांत्यता के बिन्दुओं को ज्ञात कीजिए।
हल:
यहाँ f(x) = |x| – |x + 1|
f(x) = -x[ – (x +1)], [जब x < – 1]
= – x + x + 1 = 1
f(x) = – x – (x + 1), [जब -1 ≤ x < 0]
= – x – x – 1
= – 2x – 1
f(x) = x – (x + 1), जब x ≥ 0
= x – x – 1 = – 1