In this article, we share MP Board Class 12th Maths Book Solutions Chapter 8 समाकलनों के अनुप्रयोग Ex 8.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.
MP Board Class 12th Maths Book Solutions Chapter 8 समाकलनों के अनुप्रयोग Ex 8.2
प्रश्न 1.
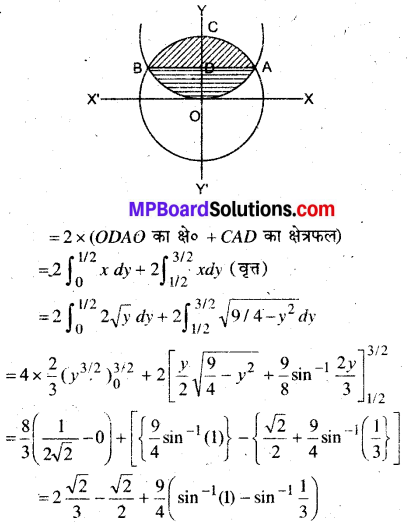
परवलय x2 = 4y और वृत्त 4x2 + 4y2 = 9 के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
परवलय का समी० x2 = 4y …(i)
तथा वृत्त का समी० x2 + y2 = \(\left(\frac{3}{2}\right)^{2}\) …(ii)
समी० (i) व (ii) को हल करने पर बिन्दु \(\left( \pm \sqrt{2}, \frac{1}{2}\right)\) प्रतिच्छेदन बिन्दु के रूप में प्राप्त होते हैं।
∴ दोनों वक्र x-अक्ष के सममित हैं।
∴ अभीष्ट क्षेत्रफल = 2 × ODCAO का क्षेत्रफल
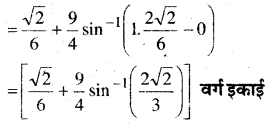
प्रश्न 2.
वक्रों (x – 1)2 + y = 1 एवं x2 + y2 = 1 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
वक्रों के समीकरण
x2 + y = 1 …(i)
(x – 1)2 + y2 = 1
समी० (i) वृत्त का समी० है। जिसका केन्द्र (0, 0) तथा
त्रिज्या 1 इकाई है। जबकि समी० (ii) उस वृत्त का समीकरण है जिसका केन्द्र (1,0) तथा त्रिज्या 1 इकाई है।
समी० (i) व (ii) को हल करने पर प्रतिच्छेदन बिन्दु \(\left(\frac{1}{2}, \pm \sqrt{3} / 2\right)\) है।
∴ अभीष्ट क्षेत्रफल
= 2 × OCRAO का क्षेत्रफल
= 2 × [OCAO का क्षेत्रफल + CBAC का क्षेत्रफल]

प्रश्न 3.
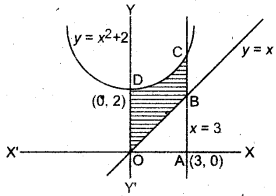
वक्रों y = x2 + 2, y = x, x = 0 एवं x = 3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल:
वक्र का समी० y = x2 + 2
या x2 = y – 1 यह एक परवलय का समी० है जिसका शीर्ष (0, 2) है।

![]()
प्रश्न 4.
समाकलन का उपयोग करते हुए एक ऐसे त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष (-1, 0), (1, 3) एवं (3, 2) हैं।
हल:
दिया है : शीर्ष बिन्दु (-1, 0), (1, 3) और (3, 2) रेखा AB का समी०
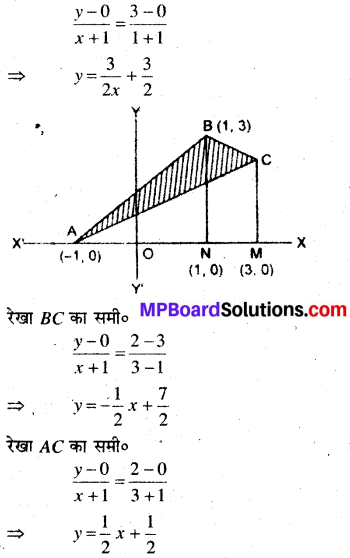
त्रिभुज ABC का क्षेत्रफल = (ANBA का क्षे० + NMCBN का क्षे०) – AMCA का क्षे०
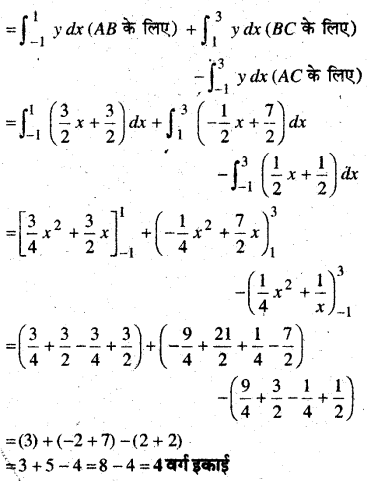
प्रश्न 5.
समाकलन का उपयोग करते हुए एक ऐसे त्रिकोणीय क्षेत्र का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओं के ‘समीकरण y = 2x + 1, y = 3x + 1 एवं x = 4 हैं।
हल:
दिया है
भुजाओं के समी० y = 2x + 1 ….(i)
y = 3x + 1 …(ii)
x = 4 …(iii)
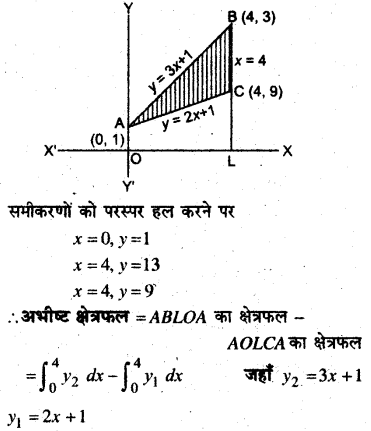

प्रश्न 6 एवं 7 में सही उत्तर का चयन कीजिए-
प्रश्न 6.
वृत्त x2 + y2 = 4 एवं रेखा x + y = 2 से घिरे छोटे भाग का क्षेत्रफल है-
(A) 2 (π – 2)
(B) (π – 2)
(C) 2π – 1
(D) 2(π + 2)
हल:
वृत्त का समी० x2 + y2 = 4
वृत्त का केन्द्र O है तथा त्रिज्या 2 है।

अतः विकल्प (B) सही है।
![]()
प्रश्न 7.
वक्रों y2 = 4x एवं y = 2x के मध्यवर्ती क्षेत्र का क्षेत्रफल है-

हल:
वक्र कासमी० y2 = 4x …(i)
रेखा का समी० y = 2x …(ii)
समी० (i) व (ii) से
(2x)2 = 4x
4x2 = 4x
⇒ x2 – x = 0
⇒ x(x – 1) = 0
⇒ x = 0, x = 1
समी० (ii) से जब x = 0, y= 0 और जब x = 1, y = 2
समी० (i) व समी० (ii) का प्रतिच्छेदन बिन्दु (0, 0) तथा A(1, 2) हैं।
अभीष्ट क्षेत्रफल
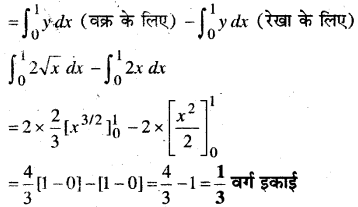
अतः विकल्प (B) सही है।