Prasanna

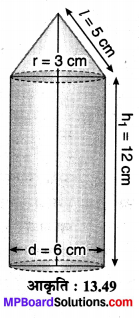
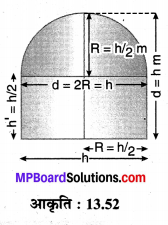
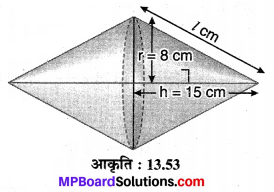
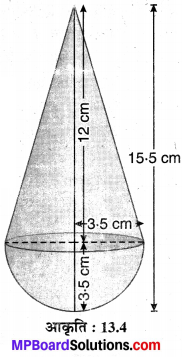
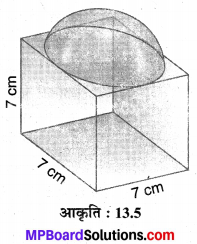
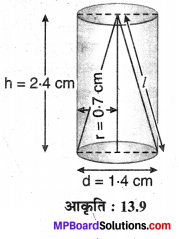
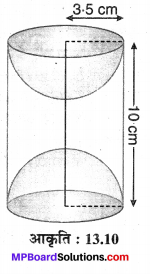
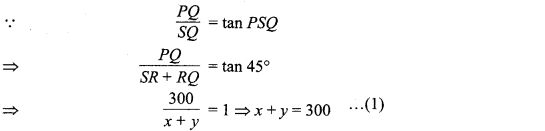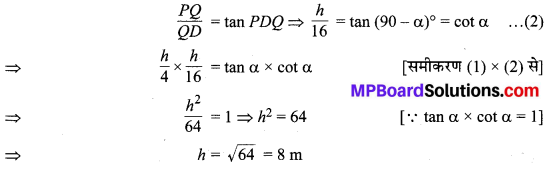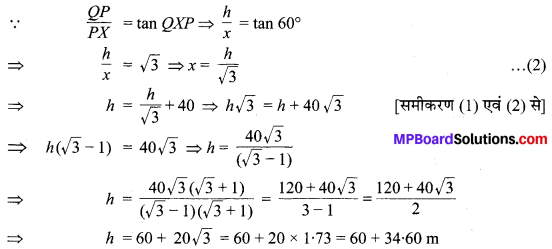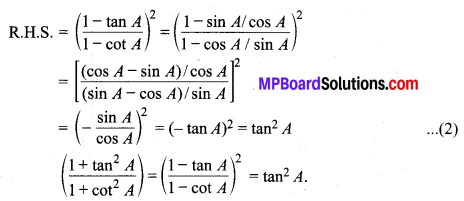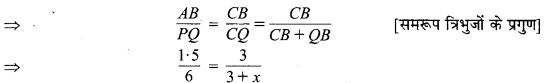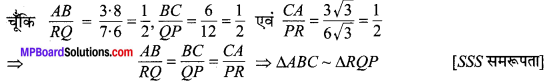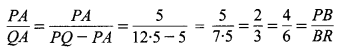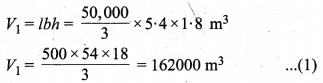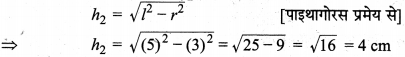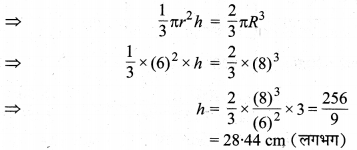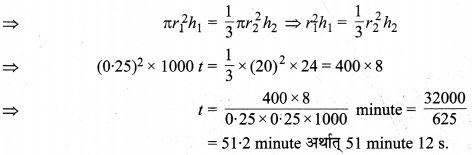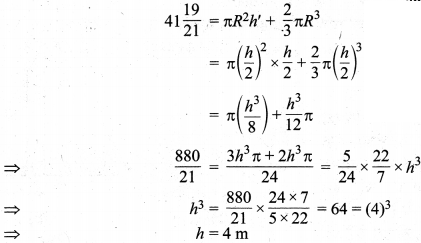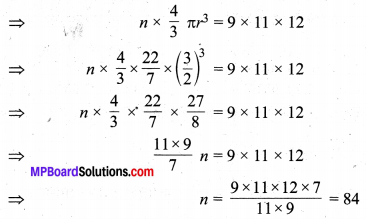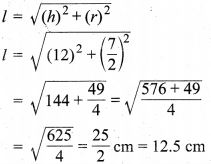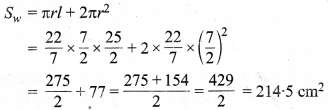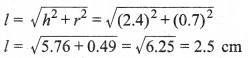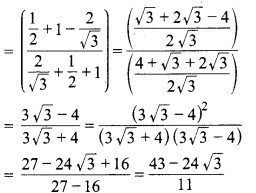In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 11 रचनाएँ Ex 11.1 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 11 रचनाएँ Ex 11.1

निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिए।

प्रश्न 1.
7.6 cm लम्बा एक रेखाखण्ड खींचिए और इसे 5 : 8 अनुपात में विभाजित कीजिए।
हल :

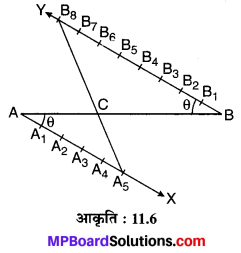
मान लीजिए AB = 7.6 cm लम्बा दिया हुआ रेखाखण्ड है जिसे 5 : 8 के अनुपात में विभाजित करना है।
रचना के चरण :

1. AB = 7.6 cm लम्बा एक रेखाखण्ड खींचिए।
2. रेखा AB के बिन्दु A पर नीचे की ओर ∠BAX = θ एक न्यूनकोण बनाते हुए किरण AX खींचिए।
3. रेखा AB के बिन्दु B पर ऊपर की ओर ∠ABY = ∠BAY = θ न्यूनकोण बनाते हुए किरण BY खींचिए।
4. AX एवं BY से क्रमश: AA1 = A1A2 = A2A3 = A3A4 = A4A5 = BB1 = B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7 = B7B8 रेखाखण्ड काटिए।
5. A6B8 रेखाखण्ड को मिलाइए जो AB को बिन्दु C पर प्रतिच्छेद करता है।

अत: AB के अभीष्ट विभाजित खण्ड AC : CB = 5 : 8 है।
एवं AC = 2.9 (लगभग)
तथा BC = 4.7 (लगभग)
उत्तर रचना का औचित्य : ∆CAA5 एवं ∆CBB8 में,
∵ ∠CAA5 = ∠CBB8 [रचना से हैं।
∵ ∠ACA5 = ∠BCB8 [शीर्षाभिमुख कोण हैं]
⇒ ∆CAA5 ~ ∆CBB8 [AA समरूपता]
⇒ \(\frac{A C}{B C}=\frac{A A_{5}}{B B_{8}}=\frac{5}{8}\)
⇒ AC : BC = 5 : 8.

प्रश्न 2.
4 cm, 5cm एवं 6 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और इसके समरूप अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac { 2 }{ 3 }\) गुनी हैं।
हल :

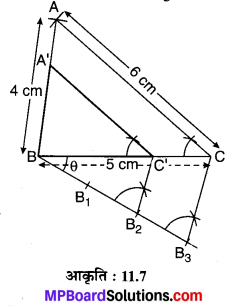
मान लीजिए कि एक दिए हुए त्रिभुज ABC की रचना करनी है जिसकी भुजाएँ AB = 4 cm, BC = 5 cm और CA = 6 cm हैं तथा इसके समरूप एक अन्य त्रिभुज की रचना दिए हुए स्केल गुणक \(\frac { 2 }{ 3 }\) के अनुसार करनी है।
रचना के पद :

1. एक रेखाखण्ड BC = 5 cm खींचिए।
2. B को केन्द्र मानकर AB = 4 cm की त्रिज्या एवं C को केन्द्र मानकर CA = 6 cm की त्रिज्या से चाप खींचिए जो परस्पर बिन्दु A पर प्रतिच्छेद करते हैं।
3. AB एवं AC को मिलाइए। इस प्रकार ∆ABC की रचना होती है।
4. BC रेखाखण्ड के बिन्दु B पर नीचे की ओर ∠CBX = θ एक न्यूनकोण बनाते हुए किरण BX खींचिए।
5. किरण BX से BB1 = B1B2 = B2B3 तीन बराबर रेखाखण्ड खींचिए।
6. B3C को मिलाइए।
7. B2 से B2C’||B3BC एक रेखाखण्ड खींचिए जो BC को बिन्दु C’ पर प्रतिच्छेद करता है।
8. C’ से C’ A’ || CA एक रेखाखण्ड खींचिए जो AB को बिन्दु A’ पर प्रतिच्छेद करता है।

अतः इस प्रकार बना अभीष्ट ∆A’BC’ ~ ∆ABC है जिसका स्केल गुणक \(\frac { 2 }{ 3 }\) है।
रचना का औचित्य : ∆BA’C’ एवं ∆BAC में
∵∠A’BC’ = ∠ABC [उभयनिष्ठ हैं]
∵∠A’C’B = ∠ACB रचना से (संगत कोण है)]
⇒ ∆A’BC’ ~ ∆ABC [AA समरूपता]
⇒ \(\frac{A^{\prime} B}{A B}=\frac{B C^{\prime}}{B C}=\frac{B B_{2}}{B B_{3}}=\frac{2}{3}\) [समरूप त्रिभुजों की संगत भुजाएँ]

प्रश्न 3.
5 cm, 6 cm और 7 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac { 7 }{ 5 }\) गुनी हैं।
हल :

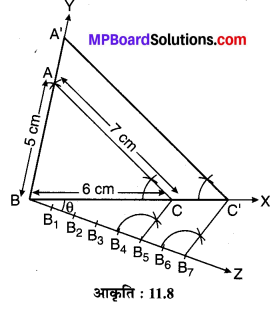
मान लीजिए एक दिए हुए ∆ABC की भुजाएँ क्रमश: AB = 5 cm, BC = 6 cm एवं CA = 7 cm की रचना करके एक अन्य ∆A’BC’ समरूप त्रिभुज की रचना करनी है जिसका स्केल गुणक \(\frac { 7 }{ 5 }\) हैं।
रचना के पद :

1. एक रेखाखण्ड BC = 6 cm खींचिए।
2. B को केन्द्र लेकर AB = 5 cm तथा C को केन्द्र लेकर CA = 7 cm की त्रिज्या से चाप खींचिए जो परस्पर बिन्दु A प्रतिच्छेद करते हैं।
3. AB एवं AC को मिलाइए। इस प्रकार ∆ABC की रचना होगी।
4. BC को आगे X तक तथा BA को आगे Y तक बढ़ाइए एवं बिन्दु B पर (नीचे की ओर) < XBZ = θ एक न्यूनकोण बनाते हुए किरण BZ खींचिए।
5. BZ से BB1 = B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7 रेखाखण्ड काटिए।
6. B5 को C से मिलाइए।
7. B7 से B7C’ || B5C रेखाखण्ड खींचिए जो BX को बिन्दु C’ पर प्रतिच्छेद करता है।
8. C’ से C’A’ || CA रेखाखण्ड खींचिए जो BY को बिन्दु A’ पर प्रतिच्छेद करता है।

अतः इस प्रकार बना अभीष्ट ∆A’BC’ ~ ∆ABC है जिसका स्केल गुणक \(\frac { 7 }{ 5 }\) है।
रचना का औचित्य : ∆A’ BC’ एवं ∆ABC में
∵ ∠A’BC’ = ∠ABC [उभयनिष्ठ हैं]
∵ ∠A’C’B = ∠ACB [रचना से (संगत कोण हैं)]
⇒ ∆A’BC’ ~ ∆ABC [AA समरूपता]
⇒ \(\frac{B A^{\prime}}{B A}=\frac{B C^{\prime}}{B C}=\frac{B B_{7}}{B B_{5}}=\frac{7}{5}\)[समरूप प्रमुख का संगत मुजाए ह]

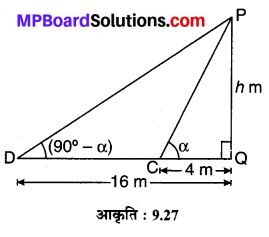
प्रश्न 4.
आधार 8 cm तथा ऊँचाई 4 cm के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की
\(1\frac { 1 }{ 2 }\), गुनी हैं।
हल :

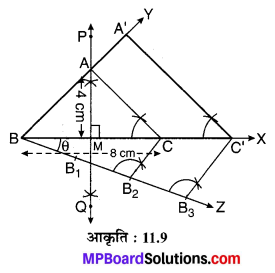
मान लीजिए एक दिए हुए समद्विबाहु त्रिभुज ABC का आधार BC = 8 cm एवं शीर्ष लम्ब (ऊँचाई) AD = 4 cm है तथा AB = AC की रचना करनी है तथा एक अन्य समरूप त्रिभुज A’BC’ की रचना करनी है जिसका स्केल गुणक \(1\frac { 1 }{ 2 }\) = \(\frac { 3 }{ 2 }\) हैं।
रचना के पदः

1. आधार BC = 8 cm का एक रेखाखण्ड खींचिए।
2. BC का लम्बार्द्धक PQ खींचिए जो आधार BC को बिन्दु M पर समद्विभाजित करता है।
3. MP में से MA = 4 cm का रेखाखण्ड काटिए।
4. AB एवं AC को मिलाइए।
   इस प्रकार अभीष्ट ∆ABC (एक समद्विबाहु त्रिभुज) की रचना होती है।
5. BC, BA को क्रमशः X एवं Y तक बढ़ाइए एवं बिन्दु B पर ∠CBZ = θ एक न्यूनकोण (नीचे की ओर) बनाते हुए किरण BZ खींचिए।
6. किरण BZ से BB1 = B1B2 = B2B3 रेखाखण्ड काटिए।
7. B2C को मिलाइए।
8. B3C’ || B2C खींचिए जो किरण BX को बिन्दु C’ पर प्रतिच्छेद करती है।
9. C’A’ || CA खींचिए जो किरण BY को बिन्दु A’ पर प्रतिच्छेद करती है।

अतः यही अभीष्ट ∆A’BC’ ~ ∆ABC है, जहाँ स्केल गुणक \(\frac { 3 }{ 2 }\) है अर्थात् ∆A’BC’ की भुजाएँ ∆ABC की संगत भुजाओं की \(1\frac { 1 }{ 2 }\) गुनी है।
रचना का औचित्य : ∆A’BC’ एवं ∆ABC में,
∵ ∠A’BC’ = ∠ABC [उभयनिष्ठ हैं]
∵ ∠A’C’B = ∠ACB [संगत कोण हैं-रचना से]
⇒ ∆A’BC’ ~ ∆ABC [AA समरूपता]
⇒ \(\frac{B A^{\prime}}{B A}=\frac{B C^{\prime}}{B C}=\frac{B B_{3}}{B B_{2}}=\frac{3}{2}\) [समरूप त्रिभुजों की संगत भुजाएँ हैं]

प्रश्न 5.
एक त्रिभुज ABC बनाइए जिसमें BC = 6 cm, AB = 5 cm और ∠ABC = 60° हैं। फिर एक त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac { 3 }{ 4 }\) गुनी हों।
हल :

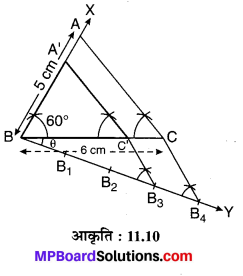
एक दिए हुए ∆ABC की रचना करनी है जिसमें BC = 6 cm, AB = 5 cm एवं ∠ABC = 60° है तथा इसके समरूप एक अन्य ∆A’BC’ खींचना है।
जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac { 3 }{ 4 }\) गुनी हो।
रचना के पद :

1. एक रेखाखण्ड BC = 6 cm खींचा।
2. BC के बिन्दु B पर ∠CBX = 60° का कोण बनाते हुए एक किरण BX खींची।
3. BX किरण में से BA = 5 cm का एक रेखाखण्ड काटा।
4. AC को मिलाया। इस प्रकार ∆ABC की रचना हुई।
5. BC के बिन्दु B पर ∠CBY = θ एक न्यूनकोण बनाते हुए किरण BY खींची।
6. किरण BY में से BB1 = B1B2 = B2B3 = B3B4 रेखाखण्ड काटे।
7. B4C को मिलाया।
8. बिन्दु B3 से ∠C’B3B = ∠CB4B संगत कोण बनाते हुए C’B3 || CB रेखाखण्ड खींचा जो BC को बिन्दु C’ पर प्रतिच्छेद करता है।
9. बिन्दु C’ से ∠A’C’B = ∠ACB संगत कोण बनाते हुए रेखाखण्ड, A’C’ खींचा जो AB को बिन्दु A’ पर प्रतिच्छेद करता है।

अतः यही अभीष्ट ∆A’BC’ ~ ∆ABC है जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac { 3 }{ 4 }\) गुनी हैं।
रचना का औचित्य : त्रिभुज ABC में A’C’ || AC [रचना से]
⇒ \(\frac{A^{\prime} B}{A B}=\frac{C B}{C B}\) …(1) [समरूप त्रिभुज के प्रगुण]
एवं ∆BCB4 में C’B3 || CBA [रचना से]
⇒ \(\frac{C^{\prime} B}{C B}=\frac{B_{3} B}{B_{4} B}=\frac{3}{4}\) ….(2) [समरूप त्रिभुज के प्रगुण]
⇒ \(\frac{A^{\prime} B}{A B}=\frac{C^{\prime} B}{C B}=\frac{3}{4}\) [समीकरण (1) और (2) से] ।

प्रश्न 6.
एक त्रिभुज ABC बनाइए जिसमें BC = 7 cm, ∠B = 45°, ∠A = 105° हो, फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac { 4 }{ 3 }\) गुनी हों।
हल :

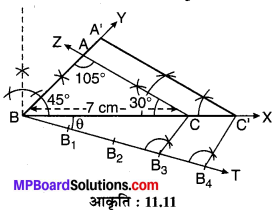
एक दिए हुए त्रिभुज ABC की रचना करनी है जिसमें BC = 7 cm, ∠B = 45° एवं ∠A = 105°, अतः ∠C = 180° – (45° + 105°) = 180° – 150° = 30° तथा स्केल गुणक \(\frac { 4 }{ 3 }\) वाले समरूप त्रिभुज की रचना करनी है।
रचना के पद :

1. एक किरण BY खींचिए।
2. किरण BX से BC = 7 cm का एक रेखाखण्ड काटिए।
3. बिन्दु B पर ∠CBY = 45° बनाते हुए किरण BY खींचिए।
4. बिन्दु C पर ∠BCZ = 30° बनाते हुए एक किरण CZ खींचिए जो किरण BY को बिन्दु A पर प्रतिच्छेद करती है। इस प्रकार ∆ABC की रचना होती है।
5. किरण BX के साथ नीचे की ओर ∠XBT = θ एक न्यूनकोण बनाते हुए किरण BT खींचिए।
6. किरण BT में से BB1 = B1B2 = B2B3 = B3B4. रेखाखण्ड काटिए।
7. B3C को मिलाइए।
8. B4 से B4C’ || B3C खींचिए जो BX को बिन्दु C’ पर प्रतिच्छेद करती है।
9. C’ से A’C’ || AC रेखाखण्ड खींचिए जो BY को बिन्दु A’ पर प्रतिच्छेद करता है।

अतः यही अभीष्ट ∆A’BC’ ~ ∆ABC है। जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac { 4 }{ 3 }\) गुनी हैं।
रचना का औचित्य : चूँकि ∆A’BC’ में AC || A’C’ है।
⇒ \(\frac{A^{\prime} B}{A B}=\frac{C^{\prime} B}{C B}\) …(1)[समरूप त्रिभुज के प्रगुण]
एवं ∆C’BB4 में CB3 || C’B4 है
⇒ \(\frac{C^{\prime} B}{C B}=\frac{B_{4} B}{B_{3} B}=\frac{4}{3}\) ….(2) [समरूप त्रिभुज के प्रगुण]
⇒ \(\frac{A^{\prime} B}{A B}=\frac{C^{\prime} B}{C B}=\frac{4}{3}\) [समीकरण (1) एवं (2) से]

प्रश्न 7.
एक समकोण त्रिभुज की रचना कीजिए जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 cm तथा 3 cm लम्बाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की \(\frac { 5 }{ 3 }\) गुनी हों।
हल :

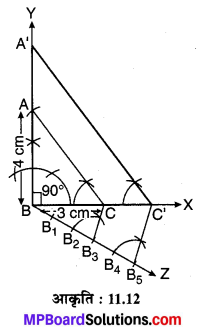
मान लीजिए एक दिए हुए समकोण ∆ABC की रचना करनी है जिसका ∠B समकोण है तथा भुजाएँ AB = 4 cm तथा BC = 3 cm हैं। इसके अतिरिक्त एक अन्य । त्रिभुज की रचना करनी है जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac { 5 }{ 3 }\) गुनी हों।
रचना के चरण :

1. एक किरण BX खींचिए तथा BX में से BC = 3 cm का रेखाखण्ड काटिए।
2. बिन्दु B पर BC के साथ ∠CBY = 90° (समकोण) बनाते हुए किरण BY खींचिए।
3. किरण BY में से BA = 4 cm का रेखाखण्ड काटिए।
4. AC को मिलाइए। इस प्रकार समकोण ∆ABC की रचना होती है।
5. बिन्दु B पर BX के साथ ∠XBZ = θ एक न्यूनकोण बनाते हुए किरण BZ खींचिए।
6. BZ में से BB1 = B1B2 = B2B3 = B3B4 = B4B5 काटिए।
7. B3C को मिलाइए।
8. B5 से B5C’ || B3C रेखाखण्ड खींचिए जो BX को बिन्दु C’ पर प्रतिच्छेद करता है।
9. C’ से C’A’ || CA एक रेखाखण्ड खींचिए जो BY को बिन्दु A’ पर प्रतिच्छेद करता है।

अतः यही ∆A’BC अभीष्ट समकोण त्रिभुज है जिसकी भुजाएँ ∆ABC की संगत भुजाओं की \(\frac { 5 }{ 3 }\) गुनी हैं।
रचना का औचित्य : चूँकि ∆A’BC’ में AC || A’C’ [रचना से]
⇒ \(\frac{A^{\prime} B}{A B}=\frac{C^{\prime} B}{C B}\) …(1) [समरूप त्रिभुजों के प्रगुण]
एवं ∆C’BB5 में, CB3 || C’B5 [रचना से]
⇒ \(\frac{C^{\prime} B}{C B}=\frac{B_{5} B}{B_{3} B}=\frac{5}{3}\) …..(2) [समरूप त्रिभुजों के प्रगुण]
⇒ \(\frac{A^{\prime} B}{A B}=\frac{C^{\prime} B}{C B}=\frac{5}{3}\) [समीकरण (1) एवं (2) से]

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग Additional Questions Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग Additional Questions

MP Board Class 10th Maths Chapter 9 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 10th Maths Chapter 9 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
एक मीनार के शीर्ष का उन्नयन कोण किसी बिन्द से 30° है। यदि प्रेक्षक 20 मीटर मीनार की ओर चलता है तो उस मीनार के शीर्ष का कोण 15° बढ़ जाता है। मीनार की ऊँचाई ज्ञात कीजिए।
हल :

मान लीजिए PQ एक मीनार है जिसके शीर्ष P का बिन्दु R पर उन्नयन कोण ∠PRQ = 30° है तथा मीनार की ओर RS = 20 m चलने पर उन्नयन कोण ∠PSQ = 30° + 15° = 45° हो जाता है। पुनः मान लीजिए मीनार की ऊँचाई PQ = hm तथा दूरी QS = x m है तो
समकोण ∆PQS में,
\(\frac { PQ }{ QS }\) = tan PSQ
⇒ \(\frac { h }{ x }\) = tan 45° = 1
⇒ h = x …(1)
एवं समकोण ∆PQR में,


अतः, मीनार की अभीष्ट ऊँचाई = 10 (√3 + 1) m है।

प्रश्न 2.
किसी मीनार के शीर्ष का उन्नयन कोण दो बिन्दुओं पर जो मीनार के पाद से क्रमशः s एवं t मात्रक की दूरी पर हैं, एक दूसरे के पूरक हैं तो सिद्ध कीजिए कि मीनार की ऊँचाई √st है।
हल :

जैसा कि संलग्न आकृति 9.21 में दिखाया गया है। मान लीजिए मीनार PQ = h मात्रक ऊँची है। RQ = s एवं SQ = t है तथा ∠PRQ = θ एवं ∠PSQ = (90° – θ) है। समकोण ∆PRQ में,
\(\frac { PQ }{ RQ }\) = tan PRQ
\(\frac { h }{ s }\) = tanθ …..(1)
समकोण ∆PSQ में,

h² = st
h = √st
अतः, मीनार की अभीष्ट ऊँचाई = √st है।
इति सिद्धम्

प्रश्न 3.
एक सड़क के ऊर्ध्वाधरतः स्थित एक गुब्बारे से एक ही दिशा में दो कारों के अवनमन कोण क्रमशः 45° एवं 60° पाये जाते हैं। यदि कारों के बीच की दूरी 100 m हो तो गुब्बारे की ऊँचाई ज्ञात कीजिए।
हल :

मान लीजिए गुब्बारे P की सड़क से ऊर्ध्वाधर ऊँचाई PQ = h m है तथा सड़क पर दो कारें A एवं B एक-दूसरे से AB = 100 m की दूरी पर हैं। P से A का अवनमन कोण ∠XPA = 45° एवं B का अवनमन कोण ∠XPB = 60° है। पुनः मान लीजिए कि BQ = x m तो चित्रानुसार ∠PAQ = ∠XPA = 45° (एकान्तर कोण हैं) एवं ∠PBQ = ∠XPB = 60° (एकान्तर कोण हैं)। समकोण त्रिभुज PQA में,

एवं समकोण ∆PQB में,
\(\frac { PQ }{ BQ }\) = tan PBQ
⇒ \(\frac { h }{ x }\) = tan 60° = √3 .
⇒ h = x√3 …(2)
⇒ h = (h – 100) √3 समीकरण (1) एवं (2) से]
⇒ h = h√3 – 100√3
⇒ (h√3 – h) = 100√3
⇒ h (√3 – 1) = 100√3

⇒ h = 50 (3 + √3) m
अतः, गुब्बारे की अभीष्ट ऊँचाई = 50 (3 + √3) m है।

प्रश्न 4.
एक हवाई जहाज भूतल से ऊपर 300 मीटर की ऊँचाई पर उड़ रहा है। इस ऊँचाई पर उड़ते हुए हवाई जहाज से एक नदी के दोनों किनारों पर परस्पर विपरीत दिशाओं में स्थित दो बिन्दुओं के अवनमन कोण क्रमशः 45° तथा 60° हैं। नदी की चौड़ाई ज्ञात कीजिए। [√3 = 1.732 का प्रयोग कीजिए।]
हल :

PQ = 300 m की ऊँचाई पर उड़ रहे हवाई जहाज से नदी के किनारे पर स्थित बिन्दुओं R एवं S के अवनमन कोण ∠XPR = 60° एवं ∠XPS = 45° है। ∠PRQ = ∠XPR = 60° एवं ∠PSQ = ∠XPS = 45° मान लीजिए कि SR = x m एवं RQ = y m हैं समकोण ∆PQS में,

एवं समकोण ∆PQR में,
\(\frac { PQ }{ RQ }\) = tan PRQ
\(\frac { 300 }{ y }\) = tan 60° = √3
y = \(\frac{300}{\sqrt{3}}\) = 100√3 = 100 x 1.732 = 173.2 m …(2)
x + 173.2 = 300 [समीकरण (1) एवं (2) से]
x = 300 – 173.2
= 126.8 m
अतः, नदी की अभीष्ट चौड़ाई = 126.8 m है।

प्रश्न 5.
एक मीनार के पाद से गुजरने वाली सीधी रेखा पर पाद से क्रमशः 4 m तथा 16 m की दूरियों पर स्थित दो बिन्दु C और D स्थित हैं। यदि C और D से मीनार के शिखर के उन्नयन कोण एक-दूसरे के पूरक हों, तो मीनार की ऊँचाई ज्ञात कीजिए।
हल :

मान लीजिए एक मीनार PQ = h m ऊँची है जिसके पाद Q से बिन्दुओं C एवं D की दूरियाँ क्रमशः QC = 4 m एवं QD = 16 m हैं तथा ∠PCQ = α° एवं ∠PDQ = (90 – α)° है। अब समकोण ∆PQC में,
\(\frac { PQ }{ QC }\) = tan PCQ ⇒ \(\frac { h }{ 4 }\) = tan a …(1)
एवं समकोण ∆PQD में,

अतः, मीनार की अभीष्ट ऊँचाई = 8 m है।

प्रश्न 6.
भूमि के एक बिन्दु Xसे एक ऊर्ध्वाधर मीनार PQ के शिखर Q का उन्नयन कोण 60° है। एक अन्य बिन्दु Y जो X से 40 m ऊर्ध्वाधर रूप में ऊँचा है, से शिखर Q का उन्नयन कोण 450
है। मीनार PQ की ऊँचाई तथा दूरी PX ज्ञात कीजिए। (√3 = 1.73 लीजिए)
हल :

मान लीजिए PQ = h m ऊँची मीनार के पास P से PX = x m की दूरी पर स्थित बिन्दु के ऊर्ध्वाधरतः XY = 40 m ऊपर बिन्दु Y है। X एवं Y पर मीनार के शिखर Q के उन्नयन कोण ∠QXP = 60° और ∠QYR = 45° दिए हैं।
चित्रानुसार,
YR = PX = x m
PR = XY = 40 m
⇒ QR = PQ – PR = (h – 40)
समकोण त्रिभुज ∆ORY में,
\(\frac { QR }{ YR }\) = tan QYR ⇒ \(\frac { h-40 }{ x }\) = tan 45°
h – 40 = x tan 45° = x ⇒ h = x + 40 …(1)
समकोण ∆QPX में,

अतः, मीनार की अभीष्ट ऊँचाई = 94.60 m है।

प्रश्न 7.
एक व्यक्ति एक जलयान के डैक जो पानी के स्तर से 10 m ऊँचा है, से एक पहाड़ी के शिखर का उन्नयन कोण 60° तथा पहाड़ी के तल का अवनमन कोण 30° पाता है। पहाड़ी से जलयान की दूरी तथा पहाड़ी की ऊँचाई ज्ञात कीजिए।
हल :

मान लीजिए PQ = h m ऊँची एक पहाड़ी से QB = x m की दूरी पर स्थित AB = 10 m ऊँचा जलयान का डैक है जिससे पहाड़ी के शिखर P का उन्नयन कोण ∠PAR = 60° एवं पहाड़ी के तल Q का अवनमन कोण RAQ = 30° है।
RQ = AB = 10 m
एवं AR = QB = x m
तथा PR = PQ – RQ = (h – 10) m
अब समकोण ∆ARO में,
\(\frac { RQ }{ AR }\) = tanRAQ
\(\frac { 10 }{ x }\) = tan 30° = \(\frac{1}{\sqrt{3}}\)
x = 10√3 …(1)
एवं समकोण ∆PRA में,
\(\frac { PR }{ AR }\) = tan PAR ⇒ \(\frac { h-10 }{ x }\) = tan 60° = √3
(h – 10) = x√3 …(2)
h – 10 = 10 √3 x 3 [समीकरण (1) एवं (2) से]
h = 30 + 10 = 40 m
अतः, पहाड़ी से जलयान की अभीष्ट दूरी = 10√3 m तथा पहाड़ी की ऊँचाई = 40 m है।

प्रश्न 8.
एक झील में पानी के तल से 20 m ऊँचे बिन्दु A से, एक बादल का उन्नयन कोण 30° है। झील में बादल के प्रतिबिम्ब का A से अवनमन कोण 60° है। A से बादल की दूरी ज्ञात कीजिए।
हल :
मान लीजिए एक बादल पानी के तल BC से PC = h m की ऊँचाई पर स्थित है जिसका प्रतिबिम्ब जल में बिन्दु Q पर बनेगा। इस प्रकार कि CQ = PC = h m (प्रकाश के परावर्तन के नियम से)। जल स्तर से AB = 20 m की ऊँचाई पर बिन्दु A से बादल P का उन्नयन कोण ∠PAD = 30° एवं बादल के प्रतिबिम्ब Q का अवनमन कोण ∠QAD = 60° एवं AD = x m है
⇒ DC = AB = 20 m

एाव PD = PC – DC = (h – 20) m
तथा QD = CQ + DC = (h + 20) m
अब समकोण ∆PDA में,

एवं समकोण ∆QDA में,

अब समकोण ∆PDA में,

अतः, बादल की बिन्दु A से अभीष्ट दूरी = 40 m है।

प्रश्न 9.
धरातल के एक बिन्दु A से हवाई जहाज का उन्नयन कोण 60° है। 15 सेकण्ड की उड़ान के पश्चात्, उन्नयन कोण 30° का हो जाता है। यदिहवाई जहाज एक निश्चित ऊँचाई 1500√3 m पर उड़ रहा हो, तो हवाई जहाज की गति किलोमीटर/घण्टा ज्ञात कीजिए।
हल :

मानलीजिए एक हवाईजहाज PR = 1500 √3 m की ऊँचाई पर बिन्दु P पर स्थित है तथा यह गति करते हुए 15 s में x m की दूरी तय करके बिन्दु Q पर आता है, जहाँ QS ऊँचाई = 1500 √3 m है। R से AR = y m की दूरी पर स्थित बिन्दु A से बिन्दु P का उन्नयन कोण ∠PAR = 60° एवं बिन्दु Q का उन्नयन कोण ∠QAS = 30° है।
RS = PQ = x m
एवं AS = AR + RS = (y + x) m
अब समकोण ∆PRA में,
\(\frac { PR }{ AR }\) = tan PAR ⇒ \(\frac{1500 \sqrt{3}}{y}\) = tan 60° = √3
⇒ y = 1500 m ……(1)
एवं समकोण ∆QAS में,
\(\frac { QS }{ AS }\) = tan QAS
\(\frac{1500 \sqrt{3}}{y+x}\) = tan 30° = \(\frac{1}{\sqrt{3}}\)
y + x = 1500√3 x √3 = 4500 m
1500 + x = 4500
x = 4500 – 1500 = 3000 m
हवाई जहाज द्वारा चली गयी दूरी = 3000m = 3 km
तथा यात्रा में लिया गया समय

चाल = 3 x 240 = 720 k/h
अतः, हवाई जहाज की अभीष्ट चाल = 720 k/h है।

MP Board Class 10th Maths Chapter 9 लघु उत्तरीय प्रश्न

प्रश्न 1.
सूर्य का उन्नतांश (उन्नयन कोण) ज्ञात कीजिए जबकि h m ऊँचे किसी खम्भे की छाया √3 h m लम्बी है।
हल :

मान लीजिए PQ = h m ऊँचे खम्भे की छाया QR = h√3 m है तथा सूर्य का उन्नतांश (उन्नयन कोण) ∠PRQ = θ है। तो समकोण त्रिभुज PQR में,
\(\frac { PQ }{ QR }\) = tan PRQ
\(\frac { 1 }{ 2 }\) = tanθ
tan θ = \(\frac { 1 }{ 2 }\) = tan 30°
θ = 30°
अतः, सूर्य का अभीष्ट उन्नतांश (उन्नयन कोण) = 30° है।

प्रश्न 2.
एक 15 m लम्बी सीढ़ी एक ऊर्ध्वाधर दीवार के शीर्ष तक ठीक-ठीक पहुँचती है। यदि सीढ़ी 60° का कोण दीवार के साथ बनाती है तो दीवार की ऊँचाई ज्ञात कीजिए।
हल :

मान लीजिए AB = 15 m लम्बी एक सीढ़ी दीवार के शीर्ष के साथ ∠ABC = 60° का कोण बनाते हुई खड़ी है। दीवार की ऊँचाई BC = h m है। समकोण ∆BCA में,
\(\frac { BC }{ AB }\) = COS ABC
⇒ \(\frac { h }{ 15 }\) = cos 60°= \(\frac { 1 }{ 2 }\)
⇒ h = \(\frac { 15 }{ 2 }\)
= 7.5 m
अतः, दीवार की अभीष्ट ऊँचाई = 7.5 m है।

प्रश्न 3.
1.5 m ऊँचा एक प्रेक्षक एक 22 m ऊँची मीनार से 20.5m की दूरी पर खड़ा है। मीनार के शिखर का उन्नयन कोण प्रेक्षक की आँख से ज्ञात कीजिए।
हल :

मान लीजिए PQ = 22 m एक मीनार है जिससे AR = BQ = 20.5 m की दूरी पर एक प्रेक्षक AB = 1.5 m ऊँचा खड़ा है। प्रेक्षक की आँख से मीनार के शिखर का उन्नयन कोण ∠PAR = θ°
PR = PQ – RQ
= PQ – AB
= 22 – 1.5
= 20.5 m.
समकोण ∆PRA में,

अतः, अभीष्ट उन्नयन कोण = 45° है।

प्रश्न 4.
यदि 30 m ऊँची एक मीनार भूमि पर 10√3 m लम्बी छाया बनाती है, तो सूर्य का उन्नयन कोण क्या है?
हल :

मान लीजिए PQ = 30 m ऊँची मीनार की छाया भूमि पर RQ = 10√3 m है तथा सूर्य का उन्नयन कोण ∠PRQ = θ है तो समकोण ∆PQR में,
tanθ = \(\frac{P Q}{R Q}=\frac{30}{10 \sqrt{3}}\) = √3
⇒ tanθ = tan 60°
⇒ θ = 60°
अतः, सूर्य का अभीष्ट उन्नयन कोण = 60° है।

प्रश्न 5.
एक दीवार के साथ लगी सीढ़ी क्षैतिज के साथ 60° का कोण बनाती है। यदि सीढ़ी का पाद दीवार से 2.5m की दूरी पर है तो सीढ़ी की लम्बाई ज्ञात कीजिए।
हल :

मान लीजिए AB = l m लम्बी एक सीढ़ी क्षैतिज के साथ ∠BAC = 60° का कोण बनाती है तथा बिन्दु A दीवार से AC = 2.5 m की दूरी पर है तो समकोण ∆ACB में,
cos BAC = \(\frac { AC }{ AB }\)
⇒ cos 60°= \(\frac{2 \cdot 5}{l}=\frac{1}{2}\)
⇒ l = 2 x 2.5 = 5m
अतः, सीढ़ी की अभीष्ट लम्बाई = 5 m है।

प्रश्न 6.
संलग्न आकृति 9.37 में एक मीनार AB की ऊँचाई 20 m है और इसकी भूमि पर परछाईं BC की लम्बाई 20√3 है। सूर्य का उन्नतांश ज्ञात कीजिए।
हल :

मान लीजिए AB = 20 m ऊँची मीनार की परछाई BC = 20√3 m है तथा सूर्य का उन्नातांश θ° है तो समकोण ∆ABC में,
tan ACB = \(\frac { AB }{ BC }\)
⇒ tan θ = \(\frac{20}{20 \sqrt{3}}=\frac{1}{\sqrt{3}}\)
⇒ tan θ = tan 30°
⇒ θ = 30°
अतः, सूर्य का अभीष्ट उन्नतांश = 30° है।

MP Board Class 10th Maths Chapter 9 अति लघु उत्तरीय प्रश्न

निम्नलिखित प्रश्नों में सत्य/असत्य कथन लिखिए तथा अपने उत्तर का औचित्य दीजिए।

प्रश्न 1.
एक मीनार की छाया की लम्बाई बढ़ने के साथ-साथ ही सूर्य का उन्नतांश भी बढ़ता जाता है।
हल :
कथन असत्य है, क्योंकि उन्नतांश बढ़ने पर छाया की लम्बाई घटती है।

प्रश्न 2.
एक मनुष्य एक झील के तल से 3 m ऊँचे प्लेटफार्म पर खड़ा एक बादल एवं उसके प्रतिबिम्ब का प्रेक्षण करता है तब वह देखता है कि बादल का उन्नयन कोण उसके प्रतिबिम्ब के अवनमन
कोण के बराबर है।
हल:
कथन असत्य है, क्योंकि प्रतिबिम्ब का अवनमन कोण बादल के उन्नयन कोण से अधिक होगा।

प्रश्न 3.
किसी मीनार के शीर्ष का उन्नयन कोण 30° है। यदि मीनार की ऊँचाई दूनी कर दी जाए तो इसके शीर्ष का उन्नयन कोण भी दूना हो जायेगा।
हल :
कथन असत्य है, क्योंकि उन्नयन कोण मीनार की ऊँचाई से तीन गुना करने पर दूना होगा।

प्रश्न 4.
किसी मीनार की ऊँचाई और इसके प्रेक्षक बिन्दु की दूरी में 10% वृद्धि कर दी जाए तो उन्नयन कोण समान रहेगा।
हल :
कथन सत्य है, क्योंकि दोनों भुजाओं का अनुपात समान रहने पर tanθ का मान और इसलिए कोण θ का मान वही रहेगा।

MP Board Class 10th Maths Chapter 9 वस्तुनिष्ठ प्रश्न

MP Board Class 10th Maths Chapter 9 बहु-विकल्पीय प्रश्न

प्रश्न 1.
यदि धूप में खड़े एक व्यक्ति की छाया उसकी ऊँचाई की √3 गुना हो, तो उस समय सूर्य का उन्नयन कोण होगा :
(a) 30°
(b) 45°
(c) 60°
(d) 75°
उत्तर:
(a) 30°

प्रश्न 2.
एक पेड़ की छाया 20√3 मीटर है। यदि पेड़ की ऊँचाई 20 मीटर हो, तो सूर्य का उन्नयन कोण होगा:
(a) 30°
(b) 45°
(c) 60°
(d) 75°
उत्तर:
(a) 30°

प्रश्न 3.
एक व्यक्ति किसी बिजली के खम्भे के शिखर से देखता है कि धरातल के एक बिन्दु का अवनमन कोण 60° है। यदि खम्भे के पाद से बिन्दु की दूरी 25 मीटर हो, तो खम्भे की ऊँचाई होगी :
(a) 25 मीटर
(b) 25√2 मीटर
(c) 25√3 मीटर
(d) 1 मीटर।
उत्तर:
(c) 25√3 मीटर

प्रश्न 4.
पुल पर बैठा एक व्यक्ति नदी में एक नाव देखता है, जिसका अवनमन कोण 45° है। यदि पुल की ऊँचाई 15 मीटर हो, तो नाव की पुल से दूरी होगी :
(a) 10 मीटर
(b) 15 मीटर
(c) 25 मीटर
(d) 5 मीटर।
उत्तर:
(b) 15 मीटर

प्रश्न 5.
पेड़ की छाया, उसकी ऊँचाई के बराबर है। सूर्य का उन्नतांश (उन्नयन) कोण होगा :
अथवा
यदि मीनार की ऊँचाई एवं छाया की लम्बाई समान हो, तो सूर्य के उन्नयन कोण का मान होगा :
(a) 30°
(b) 60°
(c) 90°
(d) 45.
उत्तर:
(d) 45.

प्रश्न 6.
एक भवन के पाद से 30 मीटर की दूरी से भवन के शिखर का उन्नयन कोण 45° है। भवन की ऊँचाई है:
(a) 25 मीटर
(b) 30 मीटर
(c) 25√2 मीटर
(d) 30√2 मीटर।
उत्तर:
(b) 30 मीटर

प्रश्न 7.
एक 6 m ऊँचे खम्भे की छाया 2√3 m लम्बी है तो सूर्य का उन्नतांश होगा :
(a) 60°
(b) 45°
(c) 30°
(d) 90°.
उत्तर:
(a) 60°

रिक्त स्थानों की पूर्ति

1. नीचे खड़े रहकर ऊपर की ओर देखने के लिए दृष्टि रेखा को क्षैतिज से जितना ऊपर की ओर घुमाना पड़ता है, वह कोण ……….. कहलाता है।
2. ऊपर के किसी बिन्दु से नीचे के किसी बिन्दु को देखने के लिए दृष्टि रेखा को क्षैतिज से जितना नीचे की ओर घुमाना पड़ता है, वह कोण ………… कोण कहलाता है।
3. यदि किसी मीनार (पेड़) की ऊँचाई एवं उसकी छाया (की लम्बाई) बराबर (समान) हो, तो उस समय उसका (सूर्य का) उन्नयन कोण ……….. होगा।
4. एक भवन के पास से 25 मीटर की दूरी से भवन के शिखर का उन्नयन कोण 45° है, तो भवन की ऊँचाई …………. होगी।
उत्तर-
1. उन्नयन कोण,
2. अवनमन,
3. 45°,
4.25 मीटर।

सत्य/असत्य कथन

1. क्षैतिज तल से ऊपर की ओर देखने पर दृष्टि रेखा क्षैतिज रेखा के साथ अवनमन कोण बनाती है।
2. वह रेखा जो हमारी आँख से वस्तु को जिसे हम देख रहे हैं, जोड़ती है, दृष्टि रेखा कहलाती है।
3. देखी गई वस्तु का उन्नयन कोण दृष्टि रेखा और क्षैतिज रेखा से बना कोण होता है, जबकि वस्तु को देखने के लिए अपने सिर को नीचे की ओर झुकाना पड़ता है। (2019)
उत्तर-
1. असत्य,
2. सत्य,
3. असत्य।

एक शब्द/वाक्य में उत्तर

1. उस मापक यन्त्र का नाम लिखिए जिसके द्वारा किसी दूरस्थ बिन्दु या ऊँचाई का कोण मापन किया जा सकता है।
2. वह रेखा क्या कहलाती है जो हमारी आँख से सीधे भूमि के समानान्तर जाती है?
3. हमारी आँख से उस वस्तु को जिसे हम देख रहे हैं, जोड़ने वाली रेखा क्या कहलाती है?
4. जब वस्तु आँख की क्षैतिज रेखा से ऊपर हो, तो उसे देखने के प्रक्रम में हमारी दृष्टि रेखा जिस कोण से ऊपर को मुड़ जाती है, उस कोण को क्या कहते हैं?
5. जब वस्तु आँख की क्षैतिज रेखा से नीचे हो, तो उसे देखने के प्रक्रम में हमारी दृष्टि रेखा जिस कोण से नीचे की ओर मुड़ जाती है, उस कोण को क्या कहते हैं?
6. एक वृक्ष की ऊँचाई एवं उसकी छाया बराबर हो, तो उस समय सूर्य का उन्नयन कोण कितना होगा?
उत्तर-
1. षष्टक,
2. क्षैतिज रेखा,
3. दृष्टि रेखा,
4. उन्नत (उन्नयन) कोण,
5. अवनत (अवनमन) कोण,
6. 45°

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.4

प्रश्न 1.
त्रिकोणमितीय अनुपातों sin A, sec A और tan A को cot A के पदों में व्यक्त कीजिए।
हल:

अत: cotA के पदों में \(\sin A=\frac{1}{\sqrt{1+\cot ^{2} A}}, \sec A=\frac{\sqrt{1+\cot ^{2} A}}{\cot A}\) एव \(\tan A=\frac{1}{\cot A}\) है।

प्रश्न 2.
∠A के अन्य सभी त्रिकोणमितीय अनुपातों को sec A के पदों में लिखिए।
हल :
मान लीजिए समकोण ∆ABC में ∠B समकोण है और sec A = x = \(\frac { AC }{ AB }\)
यदि कर्ण AC = x तो संलग्न भुजा AB = 1

अतः sec A के पदों में विभिन्न त्रिकोणमितीय अनुपात हैं :

प्रश्न 3.
मान निकालिए:
(i) \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)
(ii) sin 25° cos 65° + cos 25° sin 65°
हल :
(i) \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)

अतः अभीष्ट मान =1

(ii) sin 25°. cos 65° + cos 25°. sin 65°
= sin 25°. cos (90° – 25°) + cos 25°. sin (90° – 25°)
= sin 25°. sin 25° + cos 25°. cos 25°
= sin 25° + cos² 25° = 1 [∴ sin²θ + cos²θ = 1 (सर्वसमिका)]
अतः अभीष्ट मान = 1

प्रश्न 4.
सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिए :
(i) 9 sec²A – 9 tan² A बराबर है :
(A) 1
(B) 9
(C) 8
(D) 0.
हल :
सही विकल्प (B) 9 है,
क्योंकि 9 sec² A – 9 tan² A = 9 (sec²A – tan² A)
= 9 x 1
= 9

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) बराबर है :
(A) 0
(B) 1
(C) 2
(D) -1.
हल :
सही विकल्प (C) 2 है, क्योंकि
(1 + tan θ + sec θ) (1 + cot θ – cosec θ)

(iii) (sec A + tan A) (1 – sin A) बराबर है :
(A) sec A
(B) sin A
(C) coses A
(D) cos A.
हल :
सही विकल्प (D) cos A है,
क्योंकि (sec A + tan A)(1 – sin A)

(iv) \(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\) बराबर है :
(A) sec² A
(B) – 1
(C) cot² A
(D) tan² A.
हल :
सही विकल्प (D) tan² A है,
क्योंकि

प्रश्न 5.
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित है, न्यूनकोण हैं
(i) \((\csc \theta-\cot \theta)^{2}=\frac{1-\cos \theta}{1+\cos \theta}\)
(ii) \(\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}=2 \sec A\)
(iii) \(\frac{\tan \theta}{1-\cot \theta}+\frac{\cot \theta}{1-\tan \theta}=1+\sec \theta \cdot \csc \theta\)
(iv) \(\frac{1+\sec A}{\sec A}=\frac{\sin ^{2} A}{1-\cos A}\)
(v) cosec² A = 1 + cot² A \(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}=\csc A+\cot A\)
(vi) \(\sqrt{\frac{1+\sin A}{1-\sin A}}=\sec A+\tan A\)
(vii) \(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}=\tan \theta\)
(viii) (sin A + cosec A)² + (cos A + sec A)² = 7 + tan²A + cot² A
(ix) \((\csc A-\sin A)(\sec A-\cos A)=\frac{1}{\tan A+\cot A}\)
(x) \(\left(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\right)=\left(\frac{1-\tan A}{\cot A}\right)^{2}=\tan ^{2} A\)
हल :
(i) \((\csc \theta-\cot \theta)^{2}=\frac{1-\cos \theta}{1+\cos \theta}\)


LHS = RHS
इति सिद्धम

(ii) \(\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}=2 \sec A\)

LHS = RHS
इति सिद्धम

(iii) \(\frac{\tan \theta}{1-\cot \theta}+\frac{\cot \theta}{1-\tan \theta}=1+\sec \theta \cdot \csc \theta\)

LHS = RHS
इति सिद्धम

(iv) \(\frac{1+\sec A}{\sec A}=\frac{\sin ^{2} A}{1-\cos A}\)

LHS = RHS
इति सिद्धम

(v) cosec² A = 1 + cot² A \(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}=\csc A+\cot A\)

LHS = RHS
इति सिद्धम

(vi) \(\sqrt{\frac{1+\sin A}{1-\sin A}}=\sec A+\tan A\)

LHS = RHS
इति सिद्धम

(vii) \(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}=\tan \theta\)

LHS = RHS
इति सिद्धम

(viii) (sin A + cosec A)² + (cos A + sec A)² = 7 + tan²A + cot² A
L.H.S. = (sin A + cosec A)² + (cos A + sec A)²
= sin² A + 2 sin A cosec A + cosec² A + cos² A + 2 cos A sec A + sec² A
= sin² A + cos² A + 2 sin A cosec A + 2 cos A sec A + sec² A + cosec² A
= 1 + 2 + 2 + (1 + tan² A) + (1 + cot² A) [∵ sin² A + cos² A = 1, sin A coses A = 1 एाव cos A sec A = 1 एाव sec² A = 1 + tan² A तथा cosec² A = 1 + cot² A]
= 7 + tan² A + cot² A
= R.H.S.
L.H.S = R.H.S.
इति सिद्धम्

(ix) \((\csc A-\sin A)(\sec A-\cos A)=\frac{1}{\tan A+\cot A}\)

LHS = RHS
इति सिद्धम

(x) \(\left(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\right)=\left(\frac{1-\tan A}{\cot A}\right)^{2}=\tan ^{2} A\)


LHS = RHS
इति सिद्धम

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 6 त्रिभुज Additional Questions Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 6 त्रिभुज Additional Questions

MP Board Class 10th Maths Chapter 6 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 10th Maths Chapter 6 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
संलग्न आकृति 6.72 में यदि ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm और CP = 4 cm, तो PD और CD की लम्बाई ज्ञात कीजिए।
हल :

∆ABP एवं ∆CDP में,
∠A = ∠C (दिया है)
∠APB = ∠CPD (शीर्षभिमुख कोण हैं)
∆ABP ~ ∆CDP [AA समरूपता]


अतः PD की अभीष्ट लम्बाई = 5 cm एवं CD की अभीष्ट लम्बाई = 2 cm है।

प्रश्न 2.
∆ABC ~ ∆EDF दिए हैं जिनमें AB = 5 cm, AC = 7 cm, DF = 15 cm एवं DE = 12 cm. त्रिभुजों की शेष बची भुजाएँ ज्ञात कीजिए।
हल :
∵ ∆ABC ~ ∆EDF (दिया है)
\(\frac{A B}{E D}=\frac{B C}{D F}=\frac{A C}{E F}\) ….(1) (समरूप त्रिभुजों के प्रगुण)
AB = 5 cm, AC = 7 cm, DF = 15 cm एवं ED = DE = 12 cm के दिए हुए मान समीकरण (1) में रखने पर,

अतः शेष बची भुजाओं BC एवं EF की अभीष्ट लम्बाइयाँ क्रमशः 6.25 cm एवं 16.8 cm है।

प्रश्न 3.
एक त्रिभुज की एक भुजा के समानान्तर खींची गई रेखा अन्य दो भुजाओं को जिन दो बिन्दुओं पर प्रतिच्छेद करती है, वे बिन्दु उन भुजाओं को समान अनुपात में विभाजित करते हैं।
अथवा
यदि किसी त्रिभुज में एक भुजा के समानान्तर एक सरल रेखा खींची जाए तो वह अन्य दो भुजाओं को समान अनुपात में विभक्त करती है।
हल :

ज्ञात है : ∆ABC जिसमें रेखा DE || BC और रेखा DE, AB को D पर तथा AC को E पर प्रतिच्छेद करती है।
सिद्ध करना है: \(\frac{A D}{D B}=\frac{A E}{E C}\)
रचना : D को C से तथा B को E से मिलाइए एवं EF ⊥ AB खींचिए (देखिए आकृति 6.73)।

प्रश्न 4.
एक 5 m लम्बी सीढ़ी एक ऊर्ध्वाधर के सहारे इस प्रकार रखी है कि उसका शीर्ष दीवार की 4 m ऊँचाई तक पहुँचता है। यदि सीढ़ी के पाद को दीवार की तरफ 1.6 m विस्थापित कर दिया जाए तो वह दूरी ज्ञात कीजिए जिससे सीढ़ी का शीर्ष दीवार पर ऊपर की ओर खिसकता है।
हल :

AB = 5 m लम्बी एक सीढ़ी एक ऊर्ध्वाधर दीवार CA के सहारे खड़ी है जहाँ AC = 4 m है। अब सीढ़ी को दीवार की ओर BB’ = 1.6 m खिसकाने पर नई
स्थिति A’B’ हो जाती है।
अब समकोण ∆ACB में पाइथागोरस प्रमेय से,
BC² = AB² – AC²
BC² = (5)² – (4)²
= 25 – 16
= 9
BC = √9 = 3 m
एवं समकोण ∆A’CB’ में पाइथागोरस प्रमेय से,
A’C = A’B’² – B’C
लेकिन A’B’ = AB = 5 m
B’C = BC – BB’
= 3 m – 1.6 m
= 1.4 m
A’C² = (5)² – (1.4)²
= 25 – 1.96
= 23.04
A’C = √23.04
= 4.8 m
A’A = A’C – AC = 4.8 – 4 = 0.8 m
अतः दीवार के सहारे सीढ़ी का शीर्ष 0.8 m ऊपर की ओर खिसकेगा।

प्रश्न 5.
किसी शहर A से दूसरे शहर B तक जाने का रास्ता शहर C से होकर जाता है, इस प्रकार कि AC ⊥ CB एवं AC = 2x km तथा CB = 2 (x + 7) km. एक 26 km लम्बा राजमार्ग (हाईवे) बनाना प्रस्तवित है जो शहर A एवं B को सीधा जोड़ेगा। बताइए शहर A से शहर B तक जाने में राजमार्ग बनने पर कितनी दूरी की बचत होगी?
हल :

तीनों सड़कें समकोण त्रिभुज ACB की संरचना करती हैं, जहाँ AB = 26 km, AC = 2x km एवं CB = 2 (x + 7) km है।
अब समकोण ∆ACB में पाइथागोरस प्रमेय से,
AC² + BC² = AB²
(2x)² + [2 (x + 7)]² = (26)²
4x² + 4 (x² + 14x + 49) = 676
4x² + 4x² + 56x + 196 = 676
8x² + 56x – 480 = 0
x² + 7x – 60 = 0
x² + 12x – 5x – 60 = 0
x (x + 12) – 5 (x + 12) = 0
(x + 12) (x – 5) = 0
या तो x + 12 = 0 ⇒ x = – 12 km [जो असम्भव है]
अथवा
x – 5 = 0 ⇒ x = 5 km
राजमार्ग बनने से पहले तय की जाने वाली दूरी
= AC + CB = 2x + 2x + 14
= 4x + 14
= 4 × 5 + 14
= 20 + 14
= 34 km
दूरी में अन्तर = 34 km – 26 km = 8 km
अतः तय की गई दूरी में अभीष्ट बचत = 8 km.

प्रश्न 6.
संलग्न आकृति 6.76 में ABC एक समकोण त्रिभुज है जो B पर समकोण है एवं BD ⊥ AC. यदि AD = 4 cm एवं CD = 5 cm तो BD एवं AB के मान ज्ञात कीजिए।
हल :

समकोण त्रिभुज के समकोण वाले शीर्ष से कर्ण AC पर डाला गया लम्ब BD त्रिभुज को दो समरूप त्रिभुजों में विभाजित करता है जो मूल त्रिभुज के भी समरूप होते हैं (हम जानते हैं)।
⇒∆ADB ~ ∆BDC ~ ∆ABC [प्रमेय : 6.7 से]
⇒\(\frac{A D}{B D}=\frac{B D}{C D}\)
[समरूप त्रिभुजों के प्रगुण]
⇒\(\frac{4 \mathrm{cm}}{B D}=\frac{B D}{5 \mathrm{cm}}\)
⇒[∵ AD = 4 cm एवं CD = 5 cm दिया है।]
⇒BD² = 4 x 5 = 20
⇒BD = √20 = 2√5 cm
अब समकोण ∆ADB में पाइथागोरस प्रमेय से,
⇒AB² = AD² + BD² = (4)² + (2√5)²
= 16 + 20
= 36
⇒AB = √36 = 6 cm
अंत: BD एवं AB की अभीष्ट लम्बाइयाँ क्रमशः 2√5 cm एवं 6 cm हैं।

प्रश्न 7.
संलग्न आकृति 6.77 में ∆POR एक समकोण त्रिभुज है, जो बिन्दु Q पर समकोण है एवं QS ⊥ PR तथा PQ = 6 cm एवं PS = 4 cm तो QS, RS एवं QR के मान ज्ञात कीजिए।
हल :

∵ समकोण ∆PSQ में पाइथागोरस प्रमेय से,
QS² = PQ² – PS² = (6)² – (4)²
[∵ PQ = 6 cm एवं PS = 4 cm दिया है]
QS² = 36 – 16 = 20
QS = √20 = 2√5 cm
∵ समकोण ∆ में समकोण वाले शीर्ष पर डाला गया लम्ब त्रिभुज को दो समरूप त्रिभुजों में विभक्त करता है तथा प्रत्येक त्रिभुज मूल त्रिभुज के भी समरूप होता है। (हम जानते हैं)
∆PQS ~ ∆QRS ~ ∆PRQ

[समीकरण (1) में PQ = 6 cm, QS = 2√5 cm एवं RS = 5 cm मान रखने पर]
\(Q R=\frac{6 \times 5}{2 \sqrt{5}}=3 \sqrt{5} \mathrm{cm}\)
अत: QS, RS एवं QR के अभीष्ट मान क्रमश: 2√5 cm, 5 cm एवं 3√5 cm हैं।

प्रश्न 8.
एक चतुर्भुज ABCD में ∠A + ∠D = 90°, तो सिद्ध कीजिए कि : AC² + BD² = AD² + BC²
हल :

ज्ञात है : चतुर्भुज ABCD जिसमें ∠A + ∠D = 90°
तथा AC एवं BD को मिलाया गया है।
सिद्ध करना है : AC² + BD² = AD² + BC²
रचना : AB एवं DC को बढ़ाइए जो बिन्दु E पर मिलते हैं।
उपपत्ति : चूँकि ∆EAD में ∠A + ∠D = 90° (दिया है)
⇒∆AED, ∆AEC, ∆BEC एवं ∆DEB समकोण ∆ हैं, जिसमें ∠E = 90°
∵ समकोण ∆AEC में पाइथागोरस प्रमेय से,
AC² = AE² + CE² …(1)
∵ समकोण ∆DEB में पाइथागोरस प्रमेय से,
BD² = DE² + BE² …(2)
⇒AC² + BD² = AE² + DE² + BE² + CE² …(3)
[समीकरण (1) + (2) से]
∵ समकोण ∆AED में पाइथागोरस प्रमेय से,
AD² = AE² + DE² …(4)
∵ समकोण ∆BEC में पाइथागोरस प्रमेय से,
BC² = BE² + CE² ….(5)
⇒AD² + BC² = AE² + DE² + BE² + CE² …(6)
[समीकरण (4) + (5) से]
⇒AC² + BD² = AD² + BC². [समीकरण (3) एवं (6) से]
इति सिद्धम्

प्रश्न 9.
समलम्ब चतुर्भुज ABCD जिसमें AB || DC है के विकर्ण AC एवं BD का प्रतिच्छेद बिन्दु O है। O से होकर AB के समान्तर एक रेखाखण्ड PQ खींचा गया है जो AD को P पर तथा BC को Q पर मिलता है। सिद्ध कीजिए : PO = QO
हल :

∵ AB || DC एवं AB || PQ
PQ || DC अर्थात् OQ|| DC || AB
तथा PO || AB || DC
∵ ∆BDC में, OQ || DC


PO = QO.
इति सिद्धम्

प्रश्न 10.
संलग्न आकृति 6.80 में रेखाखण्ड DF, ∆ABC की भुजा AC को बिन्दु E पर इस प्रकार विभाजित करता है कि E बिन्दु भुजा CA का मध्य-बिन्दु है एवं ∠AEF = ∠AFE है तो सिद्ध कीजिए कि:
\(\frac{B D}{C D}=\frac{B F}{C E}\)
हल :

दिया है : रेखाखण्ड DE, ∆ABC की भुजा AC को बिन्दु E पर इस प्रकार प्रतिच्छेद करते हुए कि E, CA का मध्य-बिन्दु AB पर बिन्दु F पर मिलता है तथा ∠AEF = ∠AFE है। रचना : GC || DF खींचिए जो ∆ABC की भुजा AB के बिन्दु G पर मिलती है। चूँकि E, भुजा AC का मध्य-बिन्दु,
CE = AE (दिया है)
चूँकि ∠AEF = ∠AFE (दिया है)
AE = AF
AE = CE = AF
CG || DF खींचिए जो AB को बिन्दु G पर मिलती है।
∆ACG में, DF || CG

MP Board Class 10th Maths Chapter 6 लघु उत्तरीय प्रश्न

प्रश्न 1.
सिद्ध कीजिए कि किसी समकोण ∆ के कर्ण पर बने समाबाहु त्रिभुज का क्षेत्रफल शेष भुजाओं पर बने समबाहु त्रिभुजों के क्षेत्रफल के योग के बराबर होता है।
हल :

मान लीजिए ∆ABC एक समकोण त्रिभुज है जिसका ∠B समकोण है तथा कर्ण AC पर समबाहु ∆FAC, AB पर बना समबाहु ∆DAB एवं BC पर बना समबाहु त्रिभुज EBC है।
AB = p, BC = b एवं AC = h.
समकोण ∆ABC में पाइथागोरस प्रमेय से,
AB² + BC² = AC²
⇒ p² + b² = h² …(1)
ar (DAB) + ar (EBC)

अतः किसी समकोण त्रिभुज के कर्ण पर बने समबाहु त्रिभुज का क्षेत्रफल अन्य भुजाओं पर बने समबाहु त्रिभुजों के क्षेत्रफल के योग के बराबर होता है।
इति सिद्धम्

प्रश्न 2.
∆PQR में, PD ⊥ QR इस प्रकार है कि D बिन्दु QR पर स्थित है। यदि PQ = a, PR = b, QD = c तथा DR = d तो सिद्ध कीजिए कि : (a + b) (a – b) = (c + d) (c – d)
हल :

ज्ञात है : ∆PQR जिसमें PD ⊥ QR जहाँ D बिन्दु रेखा QR पर स्थित होगा। PQ = a, PR = b, QD = c एवं DR = d है।
सिद्ध करना है: (a + b)(a – b) = (c + d) (c – d)
अब समकोण ∆PDQ में पाइथागोरस प्रमेय से,
⇒ PD² = PQ² – QD² = a² – c² …(1)
एवं समकोण ∆PDR में पाइथागोरस प्रमेय से,
⇒ PD² = PR² – DR² = b² – d² ….(2)
⇒ a² – c² = b² – d² [समीकरण (1) एवं (2) से]
⇒ a² – b² = c² – d²
⇒ (a + b) (a – b) = (c + d) (c – d).
इति सिद्धम्

प्रश्न 3.
एक बल्ब एक खम्भे पर सड़क के तल से 6 m की ऊँचाई पर लगा है। एक 1.5 m ऊँचाई की स्त्री की छाया 3 m लम्बी पड़ती है। बताइए कि स्त्री खम्भे के आधार से कितनी दूरी पर खड़ी है?
हल :

मान लीजिए एक खम्भा PQ = 6 m ऊँचा है। एक स्त्री AB = 1.5 m ऊँचे खम्भे के आधार Q से QB = x m की दूरी पर खड़ी है जिसकी छाया CB = 3 m लम्बी पड़ती है।
चूँकि AB || PQ (ऊधर्वाधर है)
⇒ ∆ABC ~ ∆PQC [∠C उभयनिष्ठ ∠B = ∠Q = 90°]

⇒ 4.5 + 1.5x = 18
⇒ 1.5x = 18 – 4.5 = 13.5
⇒ x = \(\frac { 13.5 }{ 1.5 }\) = 9m
अतः स्त्री खम्भे के आधार से 9 m की दूरी पर खड़ी है।

प्रश्न 4.
18 m ऊँचे झण्डे के स्तम्भ की छाया 9.6 m लम्बी है। स्तम्भ के शीर्ष की छाया के दूर अन्त्यः बिन्दु से दूरी ज्ञात कीजिए।
हल :

मान लीजिए कि PQ = 18 m ऊँचे झण्डे के स्तम्भ की छाया QR = 9.6 m लम्बी पड़ती है।
बिन्दु R से खम्भे के शीर्ष P की दूरी PR = x m है।
समकोण ∆PQR में पाइथागोरस प्रमेय से,
PR² = PQ² + QR²
= (18)² + (9.6)²
= 324 + 92.16
= 416.16
PR = √416.16
= 20.4 m
अतः बिन्दु R से स्तम्भ के शीर्ष की अभीष्ट दूरी = 20.4m है।

प्रश्न 5.
संलग्न आकृति 6.85 में DE || AB तो x का मान ज्ञात कीजिए।
हल :

∆CAB में,
चूँकि DE || AB
⇒ \(\frac{C D}{D A}=\frac{C E}{E B}\) (प्रमेय : 6.1 से)
⇒ \(\frac{x+3}{3 x+19}=\frac{x}{3 x+4}\) (चित्रानुसार)
⇒ 3x² + 19x = 3x² + 4x + 9x + 12
⇒ 19x = 13x + 12
⇒ 6x = 12
⇒ x = \(\frac { 12 }{ 2 }\) = 2
अतः x का अभीष्ट मान = 2 है।

प्रश्न 6.
समलम्ब चतुर्भुज PQRS के विकर्ण परस्पर O बिन्दु पर प्रतिच्छेद करते हैं, जहाँ PQ || RS तथा PQ = 3RS, तो त्रिभुज POQ एवं ROS के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :

ज्ञात है PQRS एक समचतुर्भुज जिसमें PQ || RS एवं PQ = 3RS. इसके विकर्ण PR एवं QS परस्पर O बिन्दु पर प्रतिच्छेद करते हैं।
अब ∆POQ एवं ∆ROS में,
∵ ∠POQ = ∠ROS [शीर्षाभिमुख कोण हैं।]
⇒ ∠RPQ = ∠PRS
[एकान्तर कोण हैं जहाँ PQ || RS एवं RP तिर्यक रेखा है]
⇒ ∆POQ ~ ∆ROS [AA समरूपता]

अतः ∆POQ एवं ∆ROS के क्षेत्रफलों का अभीष्ट अनुपात 9:1 है।

प्रश्न 7.
∆ABC ~ ∆DEF, AB = 4 cm, DE = 6 cm, EF = 9 cm एवं FD = 12 cm. ∆ABC का परिमाप ज्ञात कीजिए।
हल :
चूंकि
∆ABC ~ ∆DEF

∆ABC की परिमाप = AB + BC + CA
= 4 cm + 6 cm + 8 cm
= 18 cm
अत: ∆ABC की अभीष्ट परिमाप = 18 cm है।

प्रश्न 8.
संलग्न आकृति 6.87 में, यदि DE || BC तो ∆ADE एवं ∆ABC के क्षेत्रफलों में अनुपात ज्ञात कीजिए।
हल :

⇒ ∆ADE एवं ∆ABC में
⇒ ∠A = ∠A [उभयनिष्ठ हैं।]
⇒ ∠D = ∠B [संगत कोण हैं]
चूँकि DE || BC एवं AB तिर्यक रेखा है।
⇒ ∆ADE ~ ∆ABC [AA समरूपता]

अत: ∆ADE एवं ∆ABC के क्षेत्रफलों में अभीष्ट अनुपात 1 : 4 है।

प्रश्न 9.
दो समरूप त्रिभुजों के क्षेत्रफल क्रमश: 36 cm² एवं 100 cm² हैं। यदि बड़े त्रिभुज की कोई भुजा की लम्बाई = 20 cm हो तो छोटे त्रिभुज की संगत भुजा की लम्बाई ज्ञात कीजिए।
हल :
मान लीजिए छोटी त्रिभुज की संगत भुजा की लम्बाई x cm है और हम जानते हैं कि समरूप त्रिभुजों में,

अतः छोटे त्रिभुज की संगत भुजा की अभीष्ट लम्बाई = 12 cm है।

प्रश्न 10.
एक 10 m लम्बी सीढ़ी एक ऊर्ध्वाधर दीवार के आधार से 6 m दूरी पर रखी हुई दीवार के साथ टिकी है। दीवार के उस बिन्दु की ऊँचाई ज्ञात कीजिए, जहाँ पर सीढ़ी का शीर्ष टिका है।
हल :

मान लीजिए एक सीढ़ी AB = 10 m लम्बी है और दीवार AC के आधार C से BC = 6 m की दूरी पर रखी हुई है तथा दीवार के साथ बिन्दु A पर टिकी है। A की ऊँचाई आधार से AC = h है तो समकोण ∆ACB में पाइथागोरस प्रमेय से,
⇒ AC² = AB² – BC²
⇒ h² = (10)² – (6)²
= 100 – 36
= 64
⇒ h = √64
= 8 m
अतः दीवार के अभीष्ट बिन्दु की ऊँचाई = 8 m

प्रश्न 11.
आकृति 6.89 में ∠P ज्ञात कीजिए।

हल :
∆ABC एवं ∆PQR में,

⇒ ∠A = ∠R, ∠A = ∠Q एवं ∠C = ∠P
लेकिन ∠C + 60° + 80° = 180° [त्रिभुज के अन्त:कोण हैं।]
⇒ ∠C = 180° + 140° = 40°
⇒ ∠P = ∠C = 40°
अतः ∠P का अभीष्ट मान = 40° है।

MP Board Class 10th Maths Chapter 6 अति लघु उत्तरीय प्रश्न

प्रश्न 1.
क्या त्रिभुज जिसकी भुजाएँ 25 cm, 5 cm और 24 cm हैं, समकोण त्रिभुज है? अपने उत्तर का कारण दीजिए।
हल :
नहीं, क्योंकि (24)² + (5)² = 576 + 25 = 601 ≠ (25)²

प्रश्न 2.
∆DEF ~ ∆RPQ दिया है। क्या यह कहना सत्य है कि ∠D = ∠R = एवं ∠F = ∠P.
हल :
कथन सत्य नहीं है, क्योंकि ∠F ≠ ∠P बल्कि ∠F = ∠Q.

प्रश्न 3.
किसी ∆POR की भुजाओं PQ एवं PR पर बिन्दु क्रमश: A एवं B इस प्रकार हैं कि PQ= 12.5 cm, PA = 5 cm, BR = 6 cm एवं PB = 4 cm. क्या AB || QR ? अपने उत्तर का कारण दीजिए।
हल :
हाँ AB || OR. क्योंकि

प्रश्न 4.
संलग्न आकृति 6.90 में BD एवं CF परस्पर बिन्द P पर प्रतिच्छेद करती हैं। क्या ∆PBC ~ ∆PDE और क्यों?
हल :

हाँ, ∆PBC ~ ∆PDE,
क्योकि \(\frac{P B}{P D}=\frac{5}{10}=\frac{1}{2}, \frac{P C}{P E}=\frac{6}{12}=\frac{1}{2}\)
एवं ∠BPC = ∠DPE [शीर्षाभिमुख कोण]
अर्थात् SAS समरूपता है।

प्रश्न 5.
∆PQR एवं ∆MST में ∠P = 55°, ∠Q = 25°, ∠M = 100° एवं ∠S = 25°, क्या ∆QPR ~ ∆TSM ? क्यों?
हल :
नहीं, क्योंकि ∆QPR ~ ∆STM.

प्रश्न 6.
क्या निम्न कथन सत्य है? और क्यों? “दो चतुर्भुज समरूप हैं अगर उनके संगत कोण बराबर हैं।”
हल :
नहीं, क्योंकि संगत भुजाएँ भी समानुपाती होनी चाहिए।

प्रश्न 7.
एक त्रिभुज की दो भुजाएँ एवं परिमाप क्रमशः दूसरे त्रिभुज की संगत भुजाओं और परिमाप का तीन गुना है। क्या दोनों त्रिभुज समरूप हैं? और क्यों?
हल :
हाँ, वे त्रिभुज समरूप हैं, क्योंकि दो संगत भुजाएँ एवं परिमाप समानुपाती हैं तो तीसरी भुजा भी समानुपाती होगी। (SSS समरूपता)

प्रश्न 8.
एक समकोण त्रिभुज का एक न्यूनकोण दूसरे समकोण त्रिभुज के एक न्यूनकोण के बराबर हो तो क्या दोनों त्रिभुज समरूप होंगे? और क्यों?
हल :
हाँ, समरूप होंगे। (AAA समरूपता)

प्रश्न 9.
दो समरूप त्रिभुजों के संगत शीर्ष लम्बों का अनुपात \(\frac { 3 }{ 5 }\) है तो क्या यह कहना सत्य है कि उनके क्षेत्रफलों का अनुपात \(\frac { 6 }{ 5 }\) होगा? और क्यों?
हल :
नहीं, यह कहना असत्य है क्योंकि क्षेत्रफलों का अनुपात \(\frac { 9 }{ 25 }\) होगा।

प्रश्न 10.
∆POR की भुजा QR पर बिन्दु D इस प्रकार है कि PD ⊥ QR, क्या यह कहना सत्य होगा कि ∆PQD ~ ∆RPD ? और क्यों?
हल :
नहीं, यह कहना असत्य है, क्योंकि यह तभी सम्भव है जब ∠P = 90° हो।

प्रश्न 11.
संलग्न आकृति 6.91 में ∠D = ∠C तो क्या यह कहना सत्य होगा कि ∆ADE ~ ∆ACB ? और क्यों?
हल :

हाँ, कथन सत्य है क्योंकि AA समरूपता है।

प्रश्न 12.
क्या यह कहना सत्य है कि यदि दो त्रिभुजों में एक त्रिभुज का एक कोण दूसरे त्रिभुज के एक कोण के बराबर हो एवं एक त्रिभुज की दो भुजाएँ दूसरे त्रिभुज की दो भुजाओं के समानुपाती हों तो त्रिभुज समरूप होंगे? अपने उत्तर का कारण दीजिए।
हल :
नहीं, कथन असत्य है क्योंकि दो जोड़े समानुपाती भुजाओं के मध्य कोण बराबर होने चाहिए।

प्रश्न 13.
∆ABC में, AB = 24 cm, BC = 10 cm एवं AC = 26 cm. क्या यह त्रिभुज एक समकोण त्रिभुज है? अपने उत्तर का कारण दीजिए।
हल :
हाँ, त्रिभुज समकोण त्रिभुज है क्योंकि
AB² + BC² = (24)² + (10)²
= 576 + 100
= 676
= (26)²
= AC²

प्रश्न 14.
एक त्रिभुज DEF की भुजाओं DE एवं DF पर क्रमशः बिन्दु P एवं Q इस प्रकार स्थित हैं कि DP = 5 cm, DE = 15 cm, DQ = 6 cm एवं DF = 18 cm. क्या PQ || EF ? अपने उत्तर का कारण दीजिए।
हल :

हाँ, क्योंकि

अत: PQ || EF है।

प्रश्न 15.
∆FED ~ ∆STU दिया है क्या \(\frac{D E}{S T}=\frac{E F}{T U}\) और क्यों?
हल :
नहीं, \(\frac{D E}{S T} \neq \frac{E F}{T U}\) क्योंकि \(\frac{D E}{T U}=\frac{E F}{S T}\) संगत भुजाओं का अनुपात समान होना चाहिए।

MP Board Class 10th Maths Chapter 6 वस्तुनिष्ठ प्रश्न

MP Board Class 10th Maths Chapter 6 बहु-विकल्पीय प्रश्न

प्रश्न 1.
दो त्रिभुज समरूप होंगे, यदि :
(a) त्रिभुजों के संगत कोण बराबर हैं,
(b) त्रिभुजों की संगत भुजाएँ आनुपातिक हों,
(c) त्रिभुजों के संगत क्षेत्रफल बराबर हों,
(d) त्रिभुजों के संगत कोण बराबर हों तथा संगत भुजाएँ आनुपातिक हों।
उत्तर:
(d) त्रिभुजों के संगत कोण बराबर हों तथा संगत भुजाएँ आनुपातिक हों।

प्रश्न 2.
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। इनमें से समकोण त्रिभुज नहीं है :
(a) 7 सेमी, 24 सेमी, 25 सेमी,
(b) 5 सेमी, 8 सेमी, 11 सेमी,
(c) 5 सेमी, 12 सेमी, 13 सेमी,
(d) 3 सेमी, 4 सेमी, 5 सेमी।
उत्तर:
(b) 5 सेमी, 8 सेमी, 11 सेमी,

प्रश्न 3.
“एक त्रिभुज की एक भुजा के समान्तर खींची गई रेखा अन्य दो भुजाओं को जिन दो बिन्दुओं पर प्रतिच्छेद करती है, वे बिन्दु भुजाओं को समान अनुपात में विभाजित करते हैं।” यह कथन है : (a) थेल्स प्रमेय का,
(b) पाइथागोरस प्रमेय का,
(c) थेल्स प्रमेय के विलोम का,
(d) पाइथागोरस प्रमेय के विलोम का।
उत्तर:
(a) थेल्स प्रमेय का,

प्रश्न 4.
“यदि कोई रेखा किसी त्रिभुज की दो भुजाओं को समान अनुपात में विभाजित करती है, तो यह रेखा तीसरी भुजा के समान्तर होती है।” यह कथन है :
(a) थेल्स प्रमेय का,
(b) पाइथागोरस प्रमेय का,
(c) थेल्स प्रमेय के विलोम का,
(d) पाइथागोरस प्रमेय के विलोम का।
उत्तर:
(c) थेल्स प्रमेय के विलोम का,

प्रश्न 5.
“एक समकोण त्रिभुज में कर्ण का वर्ग अन्य दो भुजाओं के वर्गों के योगफल के बराबर होता है।” यह कथन है:
(a) थेल्स प्रमेय का,
(b) पाइथागोरस प्रमेय का,
(c) थेल्स प्रमेय के विलोम का,
(d) पाइथागोरस प्रमेय के विलोम का।
उत्तर:
(b) पाइथागोरस प्रमेय का,

प्रश्न 6.
“एक त्रिभुज में यदि एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योगफल के बराबर हो, तो पहली भुजा के सामने का कोण समकोण होता है।” यह कथन है :
(a) थेल्स प्रमेय का,
(b) पाइथागोरस प्रमेय का,
(c) थेल्स प्रमेय का विलोम का,
(d) पाइथागोरस प्रमेय के विलोम का।
उत्तर:
(d) पाइथागोरस प्रमेय के विलोम का।

प्रश्न 7.
एक आदमी पूर्व की ओर 150 मीटर जाता है और फिर उत्तर की ओर 200 मीटर जाता है। आदमी की प्रारिम्भक बिन्दु से दूरी होगी :
(a) 150 मीटर,
(b) 25 मीटर,
(c) 15 मीटर,
(d) 250 मीटर।
उत्तर:
(d) 250 मीटर।

प्रश्न 8.
एक व्यक्ति पूर्व की ओर 15 मीटर जाता है और फिर उत्तर की ओर 8 मीटर जाता है। व्यक्ति की प्रारम्भिक बिन्दु से दूरी होगी :
(a) 23 मीटर,
(b) 17 मीटर,
(c) 7 मीटर,
(d) 25 मीटर।
उत्तर:
(b) 17 मीटर,

प्रश्न 9.
एक 25 मीटर लम्बी सीढ़ी एक भवन की जमीन से 20 मीटर ऊँची खिड़की तक जाती है। भवन से सीढ़ी के निचले सिरे की दूरी होगी :
(a) 45 मीटर,
(b) 5 मीटर,
(c) 15 मीटर,
(d) 25 मीटर।
उत्तर:
(c) 15 मीटर,

प्रश्न 10.
एक सीढ़ी इस तरह रखी गई है कि उसका निचला सिरा दीवार से 5 मीटर की दूरी पर है और उसका ऊपरी सिरा जमीन से 12 मीटर ऊँची खिड़की तक जाता है। सीढ़ी की लम्बाई होगी :
(a) 7 मीटर,
(b) 17 मीटर,
(c) 25 मीटर,
(d) 13 मीटर।
उत्तर:
(d) 13 मीटर।

प्रश्न 11.
दो समरूप त्रिभुजों के क्षेत्रफलों में 9 : 16 का अनुपात है, तो उनके शीर्ष लम्बों का अनुपात होगा :
(a) 3 : 4,
(b) 4 : 3,
(c) 9 : 1,
(d) 16 : 9.
उत्तर:
(a) 3 : 4,

प्रश्न 12.
समरूपता के लिए आवश्यक प्रतिबन्ध है :
(a), कोण-कोण-कोण समरूपता,
(b) कोण-कोण समरूपता,
(c) भुजा-कोण-भुजा समरूपता,
(d) ये सभी।
उत्तर:
(d) ये सभी।

प्रश्न 13.
एक ∆ABC की भुजाओं AB और AC पर क्रमश: दो बिन्दु एवं E इस प्रकार हैं कि: AD = 2 cm, BD = 3 cm, BC = 7.5 cm एवं DE || BC, तब DE की लम्बाई (cm में) होगी :
(a) 2.5,
(b) 3,
(c) 5,
(d) 6.
उत्तर:
(b) 3,

प्रश्न 14.
किसी समचतुर्भुज के विकर्णों की लम्बाई 16 cm एवं 12 cm है तो उसकी भुजा की लम्बाई है:
(a) 9 cm,
(b) 10 cm,
(c) 8 cm,
(d) 20 cm.
उत्तर:
(b) 10 cm,

प्रश्न 15.
यदि ∆ABC ~ ∆EDF एवं ∆ABC एवं ∆DEF समरूप नहीं हैं तब निम्न में से कौन सत्य नहीं है?
(a) BC.EF = AC.FD,
(b) AB.EF = AC.DE,
(c) BC.DE = AB. EF
(d) BC.DE = AB.FD.
उत्तर:
(c) BC.DE = AB. EF

प्रश्न 16.
यदि दो त्रिभुजों ABC एवं PQR में
(a) ∆PQR ~ ∆CAB,
(b) ∆PQR ~ ∆ABC,
(c) ∆CBA ~ ∆POR,
(d) ∆BCA ~ ∆POR.
उत्तर:
(a) ∆PQR ~ ∆CAB,

प्रश्न 17.
दो त्रिभुज DEF एवं PQR में ∠D = ∠Q एवं ∠R = ∠E तब निम्न में कौन सही नहीं है?

उत्तर:
(b) \(\frac{D E}{P Q}=\frac{E F}{R P}\)

प्रश्न 18.
∆ABC ~ ∆PQR दिया है एवं \(\frac{B C}{Q R}=\frac{1}{3}\) तब \(\frac{a r(P R Q)}{a r(B C A)}\) बराबर होगा :
(a) 9,
(b) 3,
(c) \(\frac { 1 }{ 3 }\).
(d) \(\frac { 1 }{ 9 }\).
उत्तर:
(a) 9,

प्रश्न 19.
∆ABC एवं ∆DEF में \(\frac{A B}{D E}=\frac{B C}{F D}\) तब ये दोनों त्रिभज समरूप होंगे जब :
(a) ∠B = ∠E,
(b) ∠A = ∠D,
(c) ∠B = ∠D,
(d) ∠A = ∠E
उत्तर:
(c) ∠B = ∠D,

प्रश्न 20.
यदि ∆ABC ~ ∆QRD एवं \(\frac{a r(A B C)}{a r(P Q R)}=\frac{9}{4}\), AB = 18 cm, BC = 15 cm तब PR बराबर
होगा :
(a) 10 cm,
(b) 12 cm,
(c) \(\frac { 20 }{ 3 }\) cm
(d) 8 cm.
उत्तर:
(a) 10 cm

रिक्त स्थानों की पूर्ति

1. यदि दो त्रिभुजों की संगत भुजाएँ आनुपातिक हों, तो वे त्रिभुज ……… होते हैं।
2. ………. त्रिभुज सदैव समरूप होते हैं।
3. सभी वर्ग ……….. होते हैं।
4. दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात किन्हीं दो संगत भुजाओं के ……….. के अनुपात के बराबर होता है।
5. किसी त्रिभुज के शीर्ष कोण का ………….. सम्मुख भुजा को शेष भुजाओं के अनुपात में विभाजित करता है।
6. यदि दो त्रिभुजों के संगत कोण बराबर हों, तो वे त्रिभुज ………… कहलाते हैं।
7. दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 9 : 16 के अनुपात में है, तो उन त्रिभुजों की संगत भुजाओं का अनुपात ………… होगा।
उत्तर-
1. समरूप,
2. समबाहु,
3. समरूप,
4. वर्गों,
5. समद्विभाजक,
6. समरूप त्रिभुज
7. 3 : 4

जोड़ी मिलाइए

उत्तर-
1.→(c),
2. →(d),
3.→(e),
4.→(a),
5. →(f),
6.→(b).

सत्य/असत्य कथन

1. समकोण त्रिभुज में कर्ण सबसे बड़ी भुजा होती है।
2. यदि त्रिभुज की संगत भुजाएँ आनुपातिक हों, तो वे त्रिभुज समरूप नहीं होते हैं।
3. समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के अनुपात के बराबर होता है।
4. यदि दो त्रिभुज समकोणिक हों तो त्रिभुज समरूप होंगे।
5. यदि किसी त्रिभुज में एक भुजा के समानान्तर एक सरल रेखा खींची जाए, तो वह अन्य दोनों भुजाओं को ___ समान अनुपात में विभक्त करती है।
6. थेल्स प्रमेय का कथन है-“यदि किसी त्रिभुज में कोई सरल रेखा उसकी दो भुजाओं को समान अनुपात __ में विभक्त करे, तो वह तीसरी भुजा के समानान्तर होती है।”
7. सभी वर्ग समरूप होते हैं। (2019)
8. समकोण त्रिभुज का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x आधार x शीर्ष लम्ब होता है। (2019)
उत्तर-
1. सत्य,
2. असत्य,
3. सत्य,
4. सत्य,
5. सत्य,
6. असत्य,
7. सत्य,
8. सत्य।

एक शब्द/वाक्य में उत्तर

1. एक त्रिभुज की एक भुजा के समानान्तर खींची गई रेखा अन्य दो भुजाओं को जिन दो बिन्दुओं पर प्रतिच्छेद करती है, वे बिन्दु उन भुजाओं को समान अनुपात में विभाजित करते हैं। यह प्रमेय किस नाम से जानी जाती है?
2. समकोण त्रिभुज प्रमेय का नाम लिखिए।
3. यदि किसी ∆ABC में AD ⊥ BC एवं AC² = AB² + BC² + 2BC.BD हो, तो यह प्रमेय किस नाम से जानी जाती है?
4. यदि किसी ∆ABC में AD ⊥BC एवं AC² = AB² + BC² – 2BC.BD हो, तो यह प्रमेय किस नाम से जानी जाती है?
5. यदि किसी ∆ABC की माध्यिका AD हो, तब AB² + AC² = 2 (AD² + BD²), तो यह प्रमेय किस नाम से जानी जाती है?
6. आकृतियों का वह गुण जिसमें उनका आकार समान हो तथा विस्तार भिन्न-भिन्न हो, क्या कहलाता है?
7. समरूप त्रिभुज, ∆ABC एवं ∆PQR के क्षेत्रफल एवं भुजाओं में सम्बन्ध लिखिए।
8. दो समरूप त्रिभुजों के शीर्षलम्बों की माप में 2 : 3 का अनुपात हो, तो उनके क्षेत्रफलों में क्या अनुपात होगा?
9. पाइथागोरस प्रमेय का कथन लिखिए।
उत्तर-
1. थेल्स प्रमेय,
2. पाइथागोरस प्रमेय,
3. अधिककोण त्रिभुज प्रमेय,
4. न्यूनकोण त्रिभुज प्रमेय,
5. अपोलोनियसपमेय
6. समरूपता
7.

8. 4 : 9
9.”समकोण त्रिभुज में कर्ण पर बना वर्ग शेष भुजाओं पर बने वर्गों के योग के बराबर होता है।”

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.2

प्रश्न 1.
एक ठोस एक अर्द्धगोले पर खड़े एक शंकु के आकार का है जिसकी त्रिज्याएँ 1 cm है तथा शंकु की ऊँचाई उसकी त्रिज्या के बराबार है। इस ठोस का आयतन π के पदों में ज्ञात कीजिए।
हल :

ज्ञात है: r = 1 cm त्रिज्या वाले अर्द्ध गोले पर उसी आधार त्रिज्या का एक शंकु जिसकी ऊँचाई h = r = 1 cm है।
चूँकि संयुक्त ठोस का आयतन = अर्द्ध गोले का आयतन + शंकु का आयतन

अतः, ठोस का अभीष्ट आयतन = π cm³ है

प्रश्न 2.
एक इन्जीनियरिंग के विद्यार्थी रचेल से एक पतली ऐलुमीनियम की शीट का प्रयोग करते हुए एक मॉडल बनाने को कहा गया, जो एक ऐसे बेलन के आकार का हो जिसके दोनों सिरों पर दो शंकु जुड़े हों। इस मॉडल का व्यास 3 cm और इसकी लम्बाई 12 cm है। यदि प्रत्येक शंकु की ऊँचाई 2 cm हो, तो रचेल द्वारा बनाए गए मॉडल में अन्तर्विष्ट हवा का आयतन ज्ञात कीजिए। यह मान लीजिए कि मॉडल की आन्तरिक तथा बाहरी विमाएँ लगभग बराबर हैं।
हल :

ज्ञात है : 12 cm लम्बा एक बेलनाकार मॉडल जिसके दोनों सिरों पर h’ = 2 cm ऊँचाई के शंकु। शंकु एवं बेलन के व्यास d = 3 cm
अर्थात् उनकी त्रिज्याएँ r = \(\frac { 3 }{ 2 }\) cm हैं।
बेलन की ऊँचाई h = 12 – 2 x 2
= 12 – 4
= 8 cm
मॉडल का आयतन (धारिता) = बेलन का आयतन + 2 x शंकु का आयतन
= πr²h + 2 x \(\frac { 1 }{ 3 }\) πr²h’
= हवा का आयतन
मॉडल का धारिता

अतः, मॉडल में अन्तर्विष्ट हवा का अभीष्ट आयतन = 66 cm³ है।

प्रश्न 3.
एक गुलाबजामुन में उसके आयतन की लगभग 30% चीनी की चासनी है। 45 गुलाबजामुनों में लगभग कितनी चासनी होगी यदि प्रत्येक गुलाबजामुन एक बेलन के आकार का है, जिसके दोनों सिरे अर्द्ध गोलाकार हैं तथा इसकी लम्बाई 5 cm एवं व्यास 2.8 cm है (देखिए सलंग्न आकृति)।
हल :

5 cm लम्बे तथा d= 2.8 cm व्यास वाले 45 ऐसे बेलनाकार गुलाबजामुन जिसके सिरे उसी व्यास के अर्द्ध गोलाकार हैं। गुलाबजामुनों में उनके आयतन का 30% चीनी की चासनी है। बेलनाकार भाग का व्यास = अर्द्धगोलाकार भाग का व्यास
d = 2.8 cm
बेलन एवं अर्द्ध गोले की त्रिज्याएँ r = \(\frac { 2.8 }{ 2 }\) = 1.4 cm
बेलनाकार भाग की लम्बाई h = 5 cm – 2 x 1.4 cm
= 2.2 cm
एक गुलाबजामुन का आयतन = बेलन का आयतन + 2 x अर्द्ध गोले का आयतन

अतः, चासनी का अभीष्ट आयतन = 338 cm³ (लगभग) है।

प्रश्न 4.
एक कलमदान घनाभ के आकार की एक लकड़ी से बना है, जिसमें कलम रखने के लिए चार शंक्वाकार गड्ढे बने हुए हैं। घनाभ की विमाएँ 15 cm x 10 cm x 3.5 cm हैं। प्रत्येक गड्ढे की त्रिज्या 0.5 cm है और गहराई 1.4 cm है। पूरे कलमदान की लकड़ी का आयतन ज्ञात कीजिए (देखिए संलग्न आकृति)।
हल :

दिया है : घनाभ की विमाएँ 15 cm x 10 cm x 3.5 cm जिसमें 4 शंक्वाकार गड्ढे प्रत्येक h = 1.4 cm गहरे तथा त्रिज्या r = 0.5 cm के हैं।
घनाभ का कुल आयतन = 15 cm x 10 cm x 3.5 cm
V1 = 525 cm³
4 शंक्वाकार गड्ढों का आयतन = 4 x \(\frac { 1 }{ 3 }\) πr²h
V2 = 4 x \(\frac { 1 }{ 3 }\) x \(\frac { 22 }{ 7 }\) x (0.5)² x 1.4 cm³
= \(\frac { 4.4 }{ 3 }\) cm³
= 1.47 cm³
लकड़ी का आयतन = V = V1 – V2
= 525 – 1.47
= 523.53 cm³
अतः, लकड़ी का अभीष्ट आयतन = 523.53 cm³ है।

प्रश्न 5.
एक बर्तन एक उल्टे शंकु के आकार का है। इसकी ऊँचाई 8 cm है और इसके ऊपरी सिरे (जो खुला हुआ है) की त्रिज्या 5 cm है। यह ऊपर तक पानी से भरा हुआ है। जब इस बर्तन में सीसे की कुछ गोलियाँ जिसमें प्रत्येक 0.5 cm त्रिज्या वाला एक गोला है, डाली जाती हैं, तो इसमें भरे हुए पानी का \(\frac { 1 }{ 4 }\) भाग बाहर निकल जाता है। बर्तन में डाली गयी सीसे की गोलियों की संख्या ज्ञात कीजिए।
हल :
शंक्वाकार बर्तन के ऊपरी तल की त्रिज्या r = 5 cm तथा इसकी ऊँचाई h = 8 cm दी है। मान लीजिए, सीसे की n गोलियाँ जिनमें प्रत्येक त्रिज्या r’ = 0.5 cm की गोलाकार गोली है डालने पर पूरे भरे बर्तन के पानी का \(\frac { 1 }{ 4 }\) आयतन बाहर निकल जाता है। प्रश्नानुसार,
n गोलियों का आयतन = \(\frac { 1 }{ 4 }\) शंक्वाकार बर्तन का आयतन (धारिता)

अतः, सीसे की गोलियों की अभीष्ट संख्या = 100 है।

प्रश्न 6.
ऊँचाई 220 cm और आधार व्यास 24 cm वाले एक बेलन जिस पर ऊँचाई 60 cm और त्रिज्या 8 cm वाला एक अन्य बेलन आरोपित है, से लोहे का एक स्तम्भ बना है। इस स्तम्भ का द्रव्यमान ज्ञात कीजिए जबकि दिया है 1 cm³ लोहे का द्रव्यमान 8g होता है (π = 3.14 लीजिए।)
हल :

एक लोहे का स्तम्भ दो बेलनों के संयोग से बना है जिसमें r₁ = \(\frac { 24 }{ 2 }\) = 12 cm,
h₁ = 220 cm, r₂ = 8 cm एवं h₂ = 60 cm दिए हैं।
∵ V₁ = πr₁²h₁
= π(12)² x 220
= 31680 π
∵ V₂ = πr₂²h₂
= π(8)² x 60
= 3840 π
कुल आयतन = 31680 π + 3840 π
= 35520 π
V = 35520 x 3.14
= 111532.8 cm³.
लोहे का द्रव्यमान = आयतन (cm³ में) x द्रव्यमान (g/cm³ में)
M = (111532.8 x 8)g = 892262.4 g
= 892.2624 kg
= 892.26 kg (लगभग)
अतः, लोहे का अभीष्ट द्रव्यमान = 892.26 kg (लगभग) है।

प्रश्न 7.
एक ठोस में, ऊँचाई 120 cm और त्रिज्या 60 cm वाला एक शंक सम्मिलित है, जो 60 cm त्रिज्या वाले एक अर्द्धगोले पर आरोपित है। इस ठोस को पानी से भरे हुए एक लम्बवृत्तीय बेलन में इस प्रकार सीधा डाल दिया जाता है कि यह बेलन की तली को स्पर्श करे। यदि बेलन की त्रिज्या 60 cm है और ऊँचाई 180 cm है, तो बेलन में शेष बचे पानी का आयतन ज्ञात कीजिए। हल :

मान लीजिए h = 180 cm ऊँचे तथा r = 60 cm त्रिज्या के बेलनाकार बर्तन में जल भरा है, जिसमें एक ठोस जो r = 60 cm त्रिज्या वाले अर्द्धगोले पर r = 60 cm त्रिज्या तथा h’ = 120 cm ऊँचाई का एक शंकु से मिलकर बना है, डाला जाता है जिसमें उसके आयतन के बराबर जल बाहर निकल जाता है।
∵ बेलन का आयतन = πr²h
= π(60)² x 180
V1 = 648000 π cm³
= 0.648 π m³
शंकु का आयतन = \(\frac { 1 }{ 3 }\) πr²h’
= π(60)² x 120
V2 = 144000 π cm³
= 0.144 π m³
अर्द्धगोलीय ठोस का आयतन = \(\frac { 2 }{ 3 }\) πr³
= \(\frac { 2 }{ 3 }\) π (60)³
V3 = 144000 π cm³
= 0.144 π m³.
ठोस का आयतन = V2 + V3
= 0.144 π m³ + 0.144 π m³
(V2 + V3) = 0.288π m³.
शेष जल का आयतन = बेलन का आयतन – ठोस का आयतन
= V1 – (V2+V3)
= 0.648π – 0.2881
= 0.360π m³
= 0.360 x \(\frac { 22 }{ 7 }\) m³
= 1.131 m³.
अतः, बेलनाकार बर्तन में अवशेष जल का आयतन = 1.131 m³ (लगभग) है।

प्रश्न 8.
एक गोलाकार काँच के बर्तन की एक बेलनाकार गर्दन है जिसकी लम्बाई 8 cm है और व्यास 2 cm है जबकि गोलाकार भाग का व्यास 8.5 cm है। इसमें भरे जा सकने वाली पानी का मात्रा मापकर एक बच्चे ने यह ज्ञात किया कि इस बर्तन का आयतन 345 cm³ है। जाँच कीजिए कि उस बच्चे का उत्तर सही है या नहीं। यह मानते हए कि उपरोक्त मापन आन्तरिक मापन है और π = 3.14 है।
हल :
गोलाकार भाग का व्यास 2R = 8.5 cm
R = \(\frac { 8.5 }{ 2 }\)
एवं बेलनाकार भाग का व्यास 2r = 2 cm
r = \(\frac { 2 }{ 2 }\) = 1 cm
गोलाकार भाग का आयतन

बेलनाकार भाग का आयतन = πr²h = 3.14 x (1)² x 8
V2 = 25.12 cm³
कुल आयतन V = V1+V2
= 321.39 + 25.12 .
= 346.51 cm³
अतः, बच्चे का उत्तर सही नहीं है क्योंकि सही आयतन 346.51 cm³ है।

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Additional Questions Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Additional Questions

MP Board Class 10th Maths Chapter 13 अतिरिक्त परीक्षोपयोगी प्रश्न

MP Board Class 10th Maths Chapter 13 दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
किसी वर्षा जल संग्रहण तन्त्र में, 22 m x 20 m की छत से वर्षा-जल बहकर 2 m आधार के व्यास तथा 3.5 m ऊँचाई के एक बेलनाकार टैंक में आता है। यदि टैंक भर गया हो, तो ज्ञात कीजिए कि सेमी में कितनी वर्षा हुई? जल संरक्षण पर अपने विचार व्यक्त कीजिए।
हल :
मान लीजिए वर्षा x cm हुई। छत की विमाएँ 22 m x 20 m दी हैं तथा दिए हुए बेलनाकार टैंक का व्यास d = 2r = 2 m ⇒ r = \(\frac { 2 }{ 2 }\) = 1 m तथा ऊँचाई h = 3.5 m दी है।
∵ वर्षा जल का आयतन = बेलनाकार टैंक का आयतन
⇒ छत की विमाएँ x वर्षा जल की ऊँचाई = πr²h.
= 22 m x 20 m x \(\frac { x }{ 100 }\) m
= \(\frac { 22 }{ 7 }\) x (1)² x 3.5
= \(x=\frac{22}{7} \times \frac{1 \times 3 \cdot 5 \times 100}{22 \times 20}\)
= 2.5
अतः अभीष्ट वर्षा कुल 2.5 cm हुई।
जल संरक्षण : विज्ञान में हमारे संसाधनों का प्रबन्धन’ अध्याय देखिए।

प्रश्न 2.
एकठोस लोहे के घनाभ की विमाएँ 4.4 m x 2.6 m x 1.0 m हैं। इसे पिघलाकार 30 cm आन्तरिक त्रिज्या और 5 cm मोटाई का एक खोखला बेलनाकार पाइप बनाया गया है। पाइप की लम्बाई ज्ञात कीजिए।
हल :

मान लीजिए खोखले बेलनाकार पाइप की लम्बाई = h cm है।
पाइप की मोटाई x = 5 cm तथा आन्तरिक त्रिज्या r_i = 30 cm
⇒ पाइप की बाह्य त्रिज्या r₀ = r_i + x = 30 + 5 = 35 cm
तथा ठोस लोहे के घनाभ की विमाएँ दी हैं।
4.4 m x 2.6 m x 1.0 m
⇒ 440 cm x 260 cm x 100 cm
ठोस घनाभ का आयतन V = 440 x 260 x 100 cm³ ….(1)
बेलनाकार पाइप का आयतन


अतः, बेलनाकार पाइप की अभीष्ट लम्बाई = 112.00 m है।

प्रश्न 3.
5.4m चौड़ी और 18 m गहरी एक नहर में पानी 25 km/h की गति से बह रहा है। इसमें 40 मिनट में कितने क्षेत्रफल की सिंचाई हो सकती है, यदि सिंचाई के लिए 10 cm गहरे पानी की आवश्यकता है?
हल :
दिया है : नहर की चौड़ाई b = 5.4 m, गहराई h = 1.8 m एवं जल की गति 25 km/h तथा धारा प्रवाह का समय 40 मिनट = \(\frac { 40 }{ 60 }\) घण्टे = \(\frac { 2 }{ 3 }\) घण्टे।
\(\frac { 2 }{ 3 }\) घण्टे में जल प्रवाह की लम्बाई l = 25 km/h x \(\frac { 2 }{ 3 }\) h
\(=\frac{50}{3} \mathrm{km}=\frac{50,000}{3} \mathrm{m}\)
∴ नहर में प्रवाहित कुल जल का आयतन

मान लीजिए सिंचाई हेतु क्षेत्र का क्षेत्रफल = A m²
तो क्षेत्र को सिंचाई के लिए आवश्यक जल का आयतन
⇒ V₂ = A × x (जहाँ x = 10 cm = 0.10 m दिया है)
⇒ V₂ = A × 0.10 = 0.10 A m² …(2)
∵ क्षेत्र की सिंचाई के लिए आवश्यक जल का आयतन = नहर द्वारा उस समय में उपलब्ध जल का आयतन
⇒ 0.10 A = 162000 [समी. (1) एवं (2) से]
⇒ \(A=\frac{162000}{0 \cdot 10}=1620000 \mathrm{m}^{2}\)
= 162
हेक्टेयर अतः, सिंचाई किए जा सकने वाले अभीष्ट क्षेत्र का क्षेत्रफल = 1620000 m² अथवा 162 हेक्टेअर है।

प्रश्न 4.
एक ठोस धातु के बेलन के दोनों किनारों से उसी व्यास के अर्द्धगोले के रूप में धातु निकाली गयी। बेलन की ऊँचाई 10 cm तथा आधार की त्रिज्या 4.2 cm है। शेष बचे बेलन को पिघलाकर 1.4 cm मोटी बेलनाकार तार बनायी गयी। तार की लम्बाई ज्ञात कीजिए। (π = \(\frac { 22 }{ 7 }\) लीजिए।)
हल :

दिया है: एक बेलनाकार धातु का ठोस जिसकी ऊँचाई h = 10 cm तथा आधार की त्रिज्या r = 4.2 cm है तथा इसके दोनों सिरों से एक अर्द्धगोला त्रिज्या 4.2 cm का काटकर निकाल दिया गया है। शेष भाग को पिघलाकर एक 1.4 cm मोटी अर्थात् व्यास d = 2r’ = 1.4 cm
⇒ r’ = \(\frac { 1.4 }{ 2 }\) = 0.7 cm त्रिज्या का तार बनाया गया है। मान लीजिए तार की लम्बाई l cm है, तो
तार का आयतन = πr’²l = \(\frac { 22 }{ 7 }\) x (0.7)² l
⇒ V = 1.54 l cm³ ..(1)
बेलन का आयतन V₁ = πr²h = \(\frac { 22 }{ 7 }\) x (4.2)² x 10
⇒ V₁ = 22 x 2.52 x 10
= 554.4 cm³.
दो अर्द्धगोलों का आयतन V₂ = 2 x \(\frac { 2 }{ 3 }\) πr³
⇒ \(V_{2}=\frac{4}{3} \times \frac{22}{7} \times(4 \cdot 2)^{3}=\frac{6519 \cdot 744}{21}\)
⇒ V₂ = 310.464 cm³
शेष बेलन का आयतन V = V₁ – V₂
⇒ V = 554.4 – 310.464
= 243.936 cm³ …(2)
⇒ 1.54 l = 243.936 [समीकरण (1) एवं (2) से]
⇒ l = \(\frac { 243.963 }{ 1.54 }\)
= 158.4 cm
= 1.584 m
अतः, तार की अभीष्ट लम्बाई = 158.4 cm अर्थात् 1.584 m है।

प्रश्न 5.
एक अर्द्धगोलीय बर्तन का आन्तरिक व्यास 36 cm है। वह तरल पदार्थ से भरा है। इस तरल को 72 बेलनाकार बोतलों में डाला गया है। यदि एक बेलनाकार बोतल का व्यास 6 cm हो, तो प्रत्येक बोतल की ऊँचाई ज्ञात कीजिए, जबकि इस क्रिया में 10% तरल गिर जाता है।
हल :
दिया है : एक अर्द्ध गोलीय बर्तन का व्यास d = 2r = 36 cm
r = \(\frac { 36 }{ 2 }\) = 18 cm.
इस बर्तन में भरे तरल के आयतन का 10% भाग बोतल भरने में गिर जाता है। एक बोतल का व्यास d = 2r’ = 6 cm
r’ = \(\frac { 6 }{ 2 }\) = 3 cm तथा बोतलों की संख्या n = 72 है।
मान लीजिए कि प्रत्येक बोतलों में तरल h ऊँचाई तक भरा जाता है।
∴अर्द्ध गोलाकार बर्तन में भरे तरल का आयतन V₁ = \(\frac { 2 }{ 3 }\) πr³
⇒ V₁ = \(\frac { 2 }{ 3 }\) π (18)³
= 3888 π
गिरने वाले तरल का आयतन = 10% V₁
⇒ V₂ = \(\frac { 10 }{ 100 }\) x 3888 π
= 388.8 π
शेष तरल का आयतन V = V₁ – V₂
= 3888 π – 388.8 π
⇒ V = 3499.2 π …..(1)
n बोतलों के तरल का आयतन = n x πr’² h
⇒ V = 72 x π x (3)²h
= 648 πh …(2)
⇒ 648 πh = 3499.2 π [समीकरण (1) एवं (2) से]
⇒ h = \(\frac { 3499.2 }{ 648 }\)
= 5.4 cm
अतः, बोतलों में तरल की अभीष्ट ऊँचाई = 5.4 cm है।

प्रश्न 6.
10 cm भुजा वाले एक घनाकार ब्लॉक के ऊपर एक अर्द्ध गोला रखा हुआ है। अद्ध गोल का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस के सम्पूर्ण पृष्ठीय क्षेत्र को पेंट करवाने का Rs 5 प्रति 100 वर्ग सेमी की दर से व्यय ज्ञात कीजिए। (π = 3.14 लीजिए।)
हल :

दिया है: a = 10 cm भुजा वाला एक घनाकार ब्लॉक जिसके ऊपरी तल पर एक अधिकतम व्यास का अर्द्ध गोला रखा है।
⇒ अर्द्ध गोले का अधिकतम व्यास d = घन की भुजा a = 10 cm
⇒ अर्द्ध गोले की त्रिज्या = \(\frac { 10 }{ 2 }\) = 5 cm
घन के ऊपरी तल पर r = 5 cm त्रिज्या का एक वृत्ताकार भाग अर्द्ध गोले से ढका है।
चूँकि घन का सम्पूर्ण पृष्ठीय क्षेत्रफल S_w = 6a²
S_w = 6(10)²
= 600 cm²
वृत्ताकार भाग का क्षेत्रफल A = πr² = π(5)² = 25π cm²
अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल S_C = 2πr²
= 2π(5)²
S_C = 50 π cm²

दिए संयुक्त ठोस का सम्पूर्ण पृष्ठ
S = घन का सम्पूर्ण पृष्ठ + अर्द्ध गोले का वक्र पृष्ठीय क्षेत्रफल – वृत्त का क्षेत्रफल
= S_w + S_C – A
= 600 + 50π – 25π
= 600 + 25π
= 600 + 25 x 3.14
= (600 + 78.50) cm²
S = 678.5 cm²
रंग करवाने का व्यय = क्षेत्रफल x दर
व्यय = 678.5 x \(\frac { 5 }{ 100 }\)
= Rs 33.93
अतः, अर्द्धवृत्त का अधिकतम व्यास = 10 cm
एवं ठोस पर रंग करवाने का कुल व्यय = Rs 33.93 है।

प्रश्न 7.
धातु के 3.5 cm व्यास तथा 3 cm ऊँचे 504 शंकुओं को पिघलाकर एक धात्विक गोला बनाया गया है। गोले का व्यास ज्ञात कीजिए। अतः इसका पृष्ठीय क्षेत्रफल भी ज्ञात कीजिए।
हल :
दिया है : 504 ठोस शंकु जिनमें प्रत्येक का व्यास d = 2r = 3.5 = \(\frac { 7 }{ 2 }\) = cm
r = \(\frac { 7 }{ 2 }\) cm तथा ऊँचाई h = 3 cm. इनको पिघलाकर एक ठोस गोला बनाया गया है। मान लीजिए गोले की त्रिज्या = R cm है, तो
गोले का आयतन V = \(\frac { 4 }{ 3 }\)πR³ ….(1)
एवं , 504 शंकुओं का आयतन

गोले का आयतन = 504 शंकुओं का आयतन

अतः, गोले का अभीष्ट व्यास = 21 cm एवं उसका पृष्ठीय क्षेत्रफल = 1386 cm² है।

प्रश्न 8.
अचानक बाढ़ आने पर कुछ कल्याणकारी संस्थाओं ने मिलकर सरकार को उसी समय 100 टैंट लगवाने के लिए कहा तथा इस पर आने वाले खर्च का 50% देने की पेशकश की। यदि प्रत्येक टेंट का निचला भाग बेलनाकार है जिसका व्यास 4.2 m है तथा ऊँचाई 4 m है तथा ऊपरी भाग उसी व्यास का शंकु है जिसकी ऊँचाई 2.8m है, और इस पर लगने वाले कैनवास की लागत Rs 100 प्रति वर्ग मीटर है, तो ज्ञात कीजिए कि इन संस्थाओं को कितनी राशि देनी होगी? इन संस्थाओं द्वारा किन मूल्यों का प्रदर्शन किया गया?
हल :

ज्ञात है टैंट का निचला भाग, व्यास d = 2r = 4.2 m
r = \(\frac { 4.2 }{ 2 }\) = 2.1
अर्थात् त्रिज्या r = 2.1 m का एक बेलन जिसकी ऊँचाई h₁ = 4 m
एवं ऊपरी भाग r = 2.1 m की त्रिज्या तथा ऊँचाई h₂ = 28 m का
एक शंकु l मान लीजिए शंकु की तिर्यक ऊँचाई = l m है।

बेलनाकार भाग का वक्रपृष्ठीय क्षेत्रफल
S_C1 = 2πrh
= 2 x \(\frac { 22 }{ 7 }\) x 2.1 x 4
= 52.8 m²
एवं शंक्वाकार भाग का वक्र पृष्ठीय क्षेत्रफल
S_C2 = πrl
= \(\frac { 22 }{ 7 }\) x 2.1 x 3.5
= 23.1 cm²
टेंट के कैनवास का कुल क्षेत्रफल = S_C = S_C1 + S_C2
S_C = 52.8 + 23.1 = 75.9 m²
100 टैंटों के लिए आवश्यक कैनवास का कुल क्षेत्रफल
= 100 x 75.9
= 7590 m²
कुल व्यय = कैनवास का क्षेत्रफल – दर
= 7590 x 100
= Rs 759000
संस्थाओं की हिस्सेदारी = 50% x Rs 759000
= Rs \(\frac { 50 }{ 100 }\) x 759000
= Rs 379500
अतः, संस्थाओं को Rs 379500 की धनराशि देनी होगी तथा ये संस्थाएँ मानवीय मूल्यों का प्रदर्शन कर रही हैं।

प्रश्न 9.
संलग्न आकृति में एक टैंट बेलन के ऊपर लगे उसी व्यास वाले शंकु के आकार का है। बेलनाकार भाग की ऊँचाई तथा व्यास क्रमश: 2.1 m तथा 3 m हैं तथा शंक्वाकार भाग की तिरछी ऊँचाई 2.8 m है। टैंट को बनाने में लगे कैनवास का मूल्य ज्ञात कीजिए, यदि कैनवास का भाव Rs 500 प्रति वर्ग मीटर है।
हल :

मान लीजिए टैंट का निचला भाग बेलनाकार है जिसकी ऊँचाई h = 2.1 m तथा व्यास d = 2r = 3 m है। अर्थात् त्रिज्या r = \(\frac { 3 }{ 2 }\) m है एवं ऊपरी शंक्वाकार भाग का व्यास बेलनाकार भाग के व्यास के बराबर अर्थात् त्रिज्या r = \(\frac { 3 }{ 2 }\) m है तथा त्रिर्यक ऊँचाई l = 2.8 m है।
बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल
\(S_{C_{1}}=2 \pi r h=2 \times \frac{22}{7} \times \frac{3}{2} \times 2 \cdot 1=19 \cdot 8 \mathrm{m}^{2}\)
एवं शंक्वाकार भाग का वक्रपृष्ठीय क्षेत्रफल
\(S_{C_{2}}=\pi r l=\frac{22}{7} \times \frac{3}{2} \times 2 \cdot 8=13 \cdot 2 \mathrm{m}^{2}\)
टैंट का कुल वक्र पृष्ठीय क्षेत्रफल S_C = S_C1 + S_C2
⇒ S_C = 19.8 + 13.2
= 33 m²
कैनवास का क्षेत्रफल = टैंट का कुल वक्र पृष्ठीय क्षेत्रफल
= 33 m²
कैनवास का कुल मूल्य = कैनवास का क्षेत्रफल x दर (भाव)
= 33 x 500
= Rs 16,500
अतः, कैनवास का अभीष्ट मूल्य = Rs 16,500 है।

प्रश्न 10.
एक शंक्वाकार बर्तन, जिसके आधार की त्रिज्या 5 cm तथा ऊँचाई 24 cm है, पानी से पूरा भरा है। उस पानी को एक बेलनाकार बर्तन, जिसकी त्रिज्या 10 cm है, में डाल दिया जाता है। बेलनाकार बर्तन में कितनी ऊँचाई तक पानी भर जायेगा?
हल :
मान लीजिए कि शंक्वाकार बर्तन के आधार की त्रिज्या r1 = 5 cm तथा ऊँचाई h1 = 24 cm है यह पूरा पानी से भरा है तथा इसका पानी एक बेलनाकार बर्तन जिसकी त्रिज्या r2 = 10 cm है में डाल . दिया जाता है। पुनः मान लीजिए कि बेलनाकार बर्तन में पानी के स्तर की अभीष्ट ऊँचाई h2 cm है, तो प्रश्नानुसार,
बेलनाकार बर्तन में पानी का आयतन = शंक्वाकार बर्तन की धारिता

अतः, बेलनाकार बर्तन में पानी के स्तर की अभीष्ट ऊँचाई = 2 cm है।

प्रश्न 11.
12 cm व्यास वाला एक गोला, एक लम्ब वृत्तीय बेलनाकार बर्तन में डाल दिया जाता है, जिसमें कुछ पानी भरा है। यदि गोला पूर्णतया पानी में डूब जाता है, तो बेलनाकार बर्तन में पानी का स्तर \(3\frac { 5 }{ 9 }\) सेमी ऊँचा उठ जाता है। बेलनाकार बर्तन का व्यास ज्ञात कीजिए।
हल :
मान लीजिए D = 12 cm व्यास अर्थात् R = \(\frac { 12 }{ 2 }\) = 6 cm त्रिज्या वाला एक गोला एक बेलनाकार बर्तन जिसका व्यास d cm है में डाला जाता है, जिसमें कुछ पानी भरा है। पानी का स्तर h = \(3\frac { 5 }{ 9 }\) cm = \(\frac { 32 }{ 9 }\) cm बढ़ जाता है। बेलनाकार बर्तन की त्रिज्या r = \(\frac { d }{ 2 }\), है।
चूँकि बेलनाकार बर्तन में बढ़े हुए जल स्तर का आयतन = गोले का आयतन

अतः, बेलनाकार बर्तन का अभीष्ट व्यास = 18 cm है।

प्रश्न 12.
किसी राज्य में भारी बाढ़ के कारण हजारों लोग बेघर हो गए। 50 विद्यालयों ने मिलकर राज्य सरकार को 1500 टैंट लगाने के लिए स्थान तथा कैनवास देने का प्रस्ताव किया जिसमें प्रत्येक विद्यालय बराबर का अंशदान देगा। प्रत्येक टैंट का निचला भाग बेलनाकार है जिसके आधार की त्रिज्या 2.8 m तथा ऊँचाई 3.5m है। प्रत्येक टैंट का ऊपरी भाग शंकु के आकार का है। जिसके आधार की त्रिज्या 2.8m तथा ऊँचाई 2.1m है। यदि टैंट बनाने वाले कैनवास का मूल्य Rs 120 प्रति वर्ग मीटर है, तो प्रत्येक विद्यालय द्वारा कुल व्यय में अंशदान ज्ञात कीजिए। इस प्रश्न का कौन-सा मूल्य जनित होता है?
हल :

मान लीजिए टैंट का निचला भाग त्रिज्या r1 = 2.8 m एवं ऊँचाई h1 = 3.5 m का बेलन है तथा ऊपरी भाग त्रिज्या r2 = 2:8 m एवं ऊँचाई h2 = 2.1 m का शंकु है और मान लीजिए शंकु की त्रिर्यक ऊँचाई l m है, तो

बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल
S_c1 = 2πr₁h₁
= 2π x 2.8 x 3.5
S_c1 = 19.6 π m²
एवं शंक्वाकार भाग का वक्र पृष्ठीय क्षेत्रफल
S_c2 = πrl
= π x 2.8 x 3.5 .
S_c1 = 9.8 π m²
टैंट का कुल वक्र पृष्ठीय क्षेत्रफल
S_c = S_c1 + S_c2
= 19.6 π + 9.8 π
= 29.47 π
= 29.4 x \(\frac { 22 }{ 7 }\) m²
S_c = 92.4 m² = कैनवास का क्षेत्रफल
1500 टैंटों के लिए आवश्यक कैनवास का कुल क्षेत्रफल
= 1500 x 92.4 m²
= 138600.0 m²
कुल व्यय = कैनवास का क्षेत्रफल – दर
= 138600 x 120
= Rs 16632000
प्रत्येक विद्यालय का व्यय में अंशदान

= Rs 3,32,640
अतः, प्रत्येक विद्यालय द्वारा कुल व्यय में अभीष्ट अंशदान = Rs 3,32,640 है।

प्रश्न 13.
तीन ठोस गोले जिनके व्यास क्रमशः 2 cm. 12 cm और 16 cm हैं. पिघलाकर एक ठोस गोला बनाया गया। इस प्रकार बने ठोस गोले का अर्द्धव्यास ज्ञात कीजिए।
हल :
यहाँ,
2R₁ = 2 cm
⇒ R₁ = \(\frac { 2 }{ 2 }\) = 1 cm
2R₂ = 12 cm
⇒ R₂ = \(\frac { 12 }{ 2 }\) = 6cm
2R₃ = 16 cm
⇒ R₃ = \(\frac { 16 }{ 2 }\) = 8 cm
माना गोले का अर्द्धव्यास = R cm हो, तो
प्रश्नानुसार,

= (1)³ + (6)³ + (8)³
= 1 + 216 + 512
R³ = 729 = (9)³
R = 9 cm
अतः, गोले की अभीष्ट त्रिज्या (अर्द्धव्यास) = 9 cm है।

प्रश्न 14.
एक 8 cm व्यास वाले धातु के बेलन को पिघलाकर 12 cm व्यास वाले कितने गोले बनाए जा सकते हैं? बेलन की ऊँचाई 90 cm है।
हल :
ज्ञात है : बेलन का व्यास d = 8 cm
r = 8/2 = 4 cm, ऊँचाई h= 90 cm, गोले का व्यास D = 12 cm
⇒ गोले की त्रिज्या R = \(\frac { 12 }{ 2 }\) = 6 cm
मान लीजिए बनाए गए गोले की संख्या = n प्रश्नानुसार,
∵ n गोलों का आयतन = बेलन का आयतन
⇒ n x \(\frac { 4 }{ 3 }\) πR³ = π(r)² x h
⇒ \(\frac { 4 }{ 3 }\)nR³ = r²h
⇒ \(\frac { 4 }{ 3 }\)n x (6)³ = (4)² x 90
⇒ \(\frac { 4 }{ 3 }\) x 216 n = 16 x 90
⇒ \(n=\frac{16 \times 90 \times 3}{4 \times 216}=5\) गोले
अतः, अभीष्ट गोलों की संख्या = 5 है।

प्रश्न 15.
6 cm व्यास के एक लोहे के गोले को पिघलाकार उससे एक बेलनाकार तार खींचा गया है। यदि तार का व्यास 0.2 cm हो, तो तार की लम्बाई ज्ञात कीजिए।
हल :
दिया है : गोले का व्यास D = 2R = 6 cm ⇒ R = \(\frac { 6 }{ 2 }\) cm = 3 cm
बेलनाकार तार का व्यास d = 2r = 0.2 cm
⇒ r = \(\frac { 0.2 }{ 2 }\) cm = 0.1 cm मान लीजिए कि बेलनाकार तार की लम्बाई = l cm
तो प्रश्नानुसार,
तार का आयतन = गोले का आयतन
⇒ πr²l = \(\frac { 4 }{ 3 }\)πR³
⇒ (0.1)²l = \(\frac { 4 }{ 3 }\)(3)³
⇒ 0.01 l = 4 x 9 = 36
⇒ l = \(\frac { 36 }{ 0.01 }\)
= 3600 cm
= 36.00 m
अतः, तार की अभीष्ट लम्बाई = 36 m है।

प्रश्न 16.
एक रॉकेट लम्ब वृत्तीय बेलन के आकार का है जिसका निचला सिरा बन्द है तथा ऊपरी सिरे पर एक शंकु है जिसकी त्रिज्या बेलन की त्रिज्या के बराबर है। बेलन का व्यास एवं उसकी ऊँचाई क्रमशः 6 cm एवं 12 cm है। यदि शंक्वाकार भाग की तिर्यक ऊँचाई 5 cm हो, तो रॉकेट का कुल पृष्ठीय क्षेत्रफल एवं आयतन ज्ञात कीजिए।
हल :

दिया है: एक बेलनाकार रॉकेट जिसका व्यास d = 2r = 6
⇒ r = \(\frac { 6 }{ 2 }\) cm
= 3 cm एवं ऊँचाई h1 = 12 cm जिसका निचला सिरा बन्द है तथा ऊपरी सिरे पर शंकु त्रिज्या r = 3 cm तथा तिर्यक ऊँचाई l = 5 cm है, जुड़ा है। मान लीजिए शंकु की ऊँचाई = h2 cm है, तो

शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl = π x 3 x 5 = 15π cm²
बेलनाकार वक्र पृष्ठीय क्षेत्रफल = 2πrh₁
= 2 x π x 3 x 12
= 72π cm²
आधार का क्षेत्रफल = πr² = π x (3)² = 9π cm²
कुल पृष्ठीय क्षेत्रफल = 15π + 72π + 9π = 96 π cm²
= 96 x 3.14
= 301.44 cm²
शंक्वाकार भाग का आयतन = \(\frac{1}{3} \pi r^{2} h_{2}=\frac{1}{3}(3)^{2} \times 4 \times \pi\)
= 12π cm³
बेलनाकार भाग का आयतन = πr²h₁ = π x (3)² x 12
= 108π cm³
रॉकेट का कुल आयतन = 12π + 108π
= 120π cm³
= 120 x 3.14
= 376.8 cm³
अतः रॉकेट का अभीष्ट सम्पूर्ण पृष्ठीय क्षेत्रफल = 301.44 cm²
एवं अभीष्ट आयतन = 376.8 cm³ है।

प्रश्न 17.
8 cm त्रिज्या वाला एक ठोस अर्द्ध गोला पिघलाकर उसे एक लम्ब वृत्तीय शंक में ढाला गया है। यदि शंकु के आधार की त्रिज्या 6 cm हो, तो उसकी ऊँचाई ज्ञात कीजिए।
हल :
ठोस अर्द्ध गोले की त्रिज्या R = 8 cm, दी है, इसको पिघलाकर एक आधार त्रिज्या r = 6 cm वाले
शंकु में ढाला गया है। मान लीजिए कि शंकु की ऊँचाई h cm है,
तो प्रश्नानुसार, शंकु का आयतन = अर्द्ध गोले का आयतन

अतः, शंकु की अभीष्ट ऊँचाई = 28.44 cm (लगभग) है।

प्रश्न 18.
एक आयताकार पानी की टंकी का आधार 11 m x 6m है तथा इसमें 5m की ऊँचाई तक पानी भरा हुआ है। यदि इस टंकी के पानी को 3.5m त्रिज्या की बेलनाकार टंकी में उडेल दिया जाए, तो इस टंकी में जल स्तर की ऊँचाई ज्ञात कीजिए।
हल :
आयताकार टंकी का आधार 11 m x 6 m तथा जल की ऊँचाई 5 m दी है तथा इस जल को r = 3.5 m त्रिज्या की बेलनाकार टंकी में उडेल दिया गया है।
मान लीजिए कि बेलनाकार टंकी में जल स्तर भी ऊँचाई h m हो, तो
प्रश्नानुसार, आयताकार टंकी के जल का आयतन = बेलनाकार टंकी के जल का आयतन
⇒ 11 m x 6 m x 5 m = πr²h = \(\frac { 22 }{ 7 }\) (3.5 m)² x h m
⇒ \(h=\frac{11 \times 6 \times 5 \times 7}{22 \times 3 \cdot 5 \times 3 \cdot 5}=\frac{60}{7}=8 \cdot 6 \mathrm{m}\)
अतः,बेलनाकार टंकी में जल स्तर की अभीष्ट ऊँचाई = 8.6 cm है।

प्रश्न 19.
1.5 cm मोटी लोहे की चद्दर के बने एक आयताकार ऊपर से खुले बॉक्स को बनाने में कितना cm लोहा लगेगा यदि उसकी बाहरी विमाएँ 36 cm x 25 cm x 16.5 cm है। यदि 1 cm³ लोहे का भार 7.5g हो, तो बक्से का भार ज्ञात कीजिए।
हल :
दिया है : बक्से की बाहरी विमाएँ 36 cm x 25 cm x 16.5 cm दी हैं तथा इसकी मोटाई 1.5 cm है, अत: बक्से की आन्तरिक विमाएँ
⇒ (36 – 3)cm x (25 – 3) cm x (16.5 – 1.5) cm अर्थात् 33 cm x 22 cm x 15 cm होंगी। लोहे का घनत्व d = 7:5 g/cm³
बक्से का बाह्य आयतन = 36 x 25 x 16.5 = 14850 cm³
बक्से का आन्तरिक आयतन = 33 x 22 x 15 = 10890 cm³
बक्से में लगे लोहे का आयतन = (14850 – 10890) cm³
आयतन V = 3960 cm³
एवं बक्से का भार = आयतन V x घनत्व d
= 3960 x 7.5 g
= 29700 g
= 29.7 kg
अतः लोहे का अभीष्ट आयतन = 3960 cm³ एवं
लोहे का अभीष्ट भार = 29700 g अर्थात् 29.7 kg होगा।

प्रश्न 20.
5 mm व्यास वाले एक बेलनाकार पाइप से जल का प्रवाह 10 m/minute है। आधार व्यास 40 cm एवं गहराई 24 cm वाले शंक्वाकार बर्तन को भरने में कितना समय लगेगा?
हल :
दिया है : बेलनाकार पाइप का व्यास d₁ = 2r₁ = 5 mm = 0.5 cm ⇒ r₁ = \(\frac { 0.5 }{ 2 }\) = 0.25 cm.
पाइप में जल प्रवाह v = 10 m/minute = \(\frac { 1000 }{ 60 }\) cm/s है। इससे शंक्वाकार बर्तन को भरना है जिसकी आधार व्यास d₂ = 2r₂ = 40 cm ⇒ r₂ = \(\frac { 40 }{ 2 }\) = 20 cm, गहराई h₂ = 24 cm दी है। मान लीजिए जल पाइप इस बर्तन को भरने में t minute का समय लेता है।
t minute में पाइप द्वारा निकली जल धारा की लम्बाई h₁ = 1000 t cm
प्रश्नानुसार, पाइप द्वारा t minute में दिया गया पानी = शंक्वाकार बर्तन का आयतन

अतः, अभीष्ट समय = 51.2 minute अर्थात 51 minute एवं 12 s है।

प्रश्न 21.
14 cm व्यास वाले एक बेलनाकार पाइप से होकर 15 km/h की दर से जल एक घनाभाकार गड्ढे में जिसकी लम्बाई 50 m एवं चौड़ाई 44 m है, गिरता है। कितने समय में गड्ढे में जलस्तर 21 cm चढ़ जायेगा?
हल :
मान लीजिए बेलनाकार पाइप का व्यास d = 2r = 14 cm = 0.14 m ⇒ r = \(\frac { 0.14 }{ 2 }\) = 0.07 m
दिया है जिसमें होकर जल की धारा 15 km/h की दर से अर्थात् 15,000 m/h की दर से प्रवाहित हो रही है, जो एक गड्ढे में गिरती है। गड्ढे की लम्बाई l = 50 m. चौड़ाई b = 44 cm एवं जलस्तर की ऊँचाई h = 21 cm = 0.21 m है। मान लीजिए इसको भरने में t घण्टे लगते हैं, तो प्रश्नानुसार, पाइप से निकला जल का आयतन = गड्ढे में जल का आयतन
lbh = πr² x दर x समय
50 x 44 x 0.21 = \(\frac { 22 }{ 7 }\) x (0.07)² x 15000 x 1
\(t=\frac{50 \times 44 \times 0.21 \times 7}{22 \times 0.07 \times 0.07 \times 15000}=\frac{50 \times 44 \times 21 \times 7}{22 \times 7 \times 7 \times 150}\)
= 2 घण्टे
अतः, अभीष्ट समय = 2 घण्टे है।

प्रश्न 22.
16 cm ऊँचाई वाला एक दूध का बर्तन किसी शंकु के छिन्नक के आकार का धातु की चद्दर से बना है जिसकी नीचे एवं ऊपर के सिरों की त्रिज्याएँ क्रमशः 8 cm एवं 20 cm हैं। इसमें भरे दूध का मूल्य ज्ञात कीजिए जबकि दूध की दर Rs 22 प्रति लीटर है।
हल :

बर्तन (छिन्नक) के दोनों सिरों की त्रिज्याएँ क्रमशः r1 = 8 cm एवं r2 = 20 cm तथा ऊँचाई h = 16 cm है। दूध की दर Rs 22 प्रति लीटर, दिया है।
दूध का आयतन = छिन्नक का आयतन

अतः, दूध का अभीष्ट मूल्य = Rs 230 (लगभग) है।

प्रश्न 23.
32 cm ऊँची तथा 18 cm आधार त्रिज्या वाली एक बेलनाकार बाल्टी रेत से पूरी भरी है। इसके रेत को जमीन पर उडेलकर एक शंकु के आकार में एकत्रित ! किया गया है। यदि इस शंक्वाकार ढेरी की ऊँचाई 24 cm हो, तो इस ढेरी की त्रिज्या एवं तिर्यक ऊँचाई ज्ञात कीजिए।

हल :
दिया है : एक बेलनाकार बाल्टी जिसकी आधार त्रिज्या r1 = 18 cm एवं ऊँचाई h1 = 32 cm जो रेत से भरी हुई है। इस रेत को जमीन पर उडेलकर एक शंक्वाकार ढेरी बनाई गई है जिसकी ऊँचाई h2 = 24 cm है। मान लीजिए ढेरी की आधार त्रिज्या r2 cm एवं तिर्यक ऊँचाई l cm है, तो प्रश्नानुसार शंक्वाकार ढेरी (रेत) का आयतन = बेलन के रेत का आयतन


अतः, शंक्वाकार ढेरी के आधार की अभीष्ट त्रिज्या = 36 cm
एवं ढेरी की अभीष्ट तिर्यक ऊँचाई = 43.27 cm (लगभग) है।

प्रश्न 24.
एक इमारत बेलनाकार है जिसके ऊपर एक अर्द्धगोलाकार गुम्बद है तथा इसमें \(41\frac { 19 }{ 21 }\) m³ वायु (हवा) है। यदि गुम्बद का आन्तरिक व्यास इस इमारत की कुल ऊँचाई के बराबर है, तो इस इमारत की कुल ऊँचाई ज्ञात कीजिए।
हल :

मान लीजिए कि दी हुई इमारत की कुल ऊँचाई = h है जो कि गुम्बद के व्यास के बराबर है, जो आधार के व्यास के बराबर है।
हवा का आयतन \(41\frac { 19 }{ 21 }\) m³ है। अतः बेलन की त्रिज्या = गुम्बद की त्रिज्या = R = \(\frac { h }{ 2 }\) m
तथा बेलनाकार भाग की ऊँचाई = h’ = h – h/2 = h/2 m
हवा का कुल आयतन V = बेलन का आयतन + गुम्बद का आयतन

अतः, इमारत की अभीष्ट कुल ऊँचाई = 4 m है।

प्रश्न 25.
लकड़ी से बना एक कलमदान घनाभ के आकार का है जिसकी विमाएँ 10 cm x 5 cm x 4 cm हैं। इसमें चार शंक्वाकार गड्ढे पैन (कलम) रखने के लिए तथा एक घनाकार गड्ढा पिन रखने के लिए बने हैं। प्रत्येक शंक्वाकार गड्ढे की त्रिज्या 0.5 cm एवं गहराई 2.1 cm है तथा घनाकार गड्ढे की कोर 3 cm है तो सम्पूर्ण कलमदान में लगने वाली लकड़ी का आयतन ज्ञात कीजिए।
हल :
दिया है: एक 10 cm x 5 cm x 4 cm विमाओं वाला लकड़ी का बना एक घनाभ के आकार का कलमदान जिसमें 4 शंक्वाकार गड्ढे प्रत्येक की त्रिज्या r = 0.5 cm एवं गहराई h = 2.1 cm तथा एक घनाकार गड्ढा जिसकी भुजा a = 3 cm है दिए हैं। कलमदान की कुल लकड़ी का आयतन
V = 10 x 5 x 4 = 200 cm³
4 शंक्वाकार गड्ढ़ों का आयतन = 4 x \(\frac { 1 }{ 3 }\) πr²h
V₁ = 4 x \(\frac { 1 }{ 3 }\) x \(\frac { 22 }{ 7 }\) x (0.5)² x 2.1 cm³
= 2.2 cm³
एवं घनाकार गड्ढे का आयतन V₂ = a³ = (3)³ = 27 cm
प्रयुक्त लकड़ी का आयतन = V – V₁ – V₂ = 200 – 2.2 – 27
= 200 – 29.2
= 170.8 cm³
अतः, कलमदान में प्रयुक्त अभीष्ट लकड़ी का आयतन = 170.8 cm³ है।

MP Board Class 10th Maths Chapter 13 लघु उत्तरीय प्रश्न

प्रश्न 1.
8 cm त्रिज्या के लोहे के एक गोले को गलाकार 1 cm त्रिज्या के कितने गोले बनाए जा सकते है?
हल :
ज्ञात है: बड़े गोले की त्रिज्या R = 8 cm
एवं छोटे प्रत्येक गोले की त्रिज्या r = 1 cm
मान लीजिए छोटे गोलों की संख्या n है तो
n छोटे गोलों का आयतन = 1 बड़े गोले का आयतन
\(n \times \frac{4}{3} \pi r^{3}=\frac{4}{3} \pi R^{3}\)
nr³ = R³
n (1)³ = (8)³ = 512
n = 512
अतः, अभीष्ट गोलों की संख्या = 512 है।

प्रश्न 2.
तीन धातु के घन जिनकी कोरों की लम्बाई क्रमश: 5 cm, 4 cm और 3 cm है, को पिघलाकर एक नए घन में बदल दिया गया है। इस प्रकार बने नए घन की कोर क्या होगी?
हल :
माना तीन घनों की कोरें क्रमशः a₁ = 5 cm, a₂ = 4 cm एवं a₃ = 3 cm हैं, इनको गलाकर नया घन बनाया गया है और मान लीजिए इस नए घन की कोर a cm हो तो बड़े घन का आयतन
V = V₁ + V₂ + V₃
a³ = a₁³ + a₂³ + a₃³
= (5)³ + (4)³ + (3)³
= 125 + 64 + 27
= 216 cm³
a³ = (6)³
a = 6 cm
अतः, नए घन की अभीष्ट कोर की लम्बाई = 6 cm है।

प्रश्न 3.
सीसे के बने एक 9 cm x 11 cm x 12 cm विमाओं वाले ठोस घनाभ से 3 cm व्यास वाली कितनी गोलियाँ बनेंगी?
हल :
सीसे के ठोस घनाभ की विमाएँ 9 cm x 11 cm x 12 cm हैं जिसे पिघलाकर व्यास
d = 2r = 3 cm
r = \(\frac { 3 }{ 2 }\) cm त्रिज्या वाली मान लीजिए n गोलियाँ बनेंगी।
प्रश्नानुसार, n गोलियाँ का आयतन = घनाभ का आयतन

अतः, गोलियों की अभीष्ट संख्या = 84 है।

प्रश्न 4.
एक बाल्टी एक शंकु छिन्नक के आकार की है जिसके दोनों सिरों की त्रिज्याएँ क्रमश: 28 cm एवं 21 cm हैं। इसमें 28.490 लीटर पानी भरा है। बल्टी की ऊँचाई ज्ञात कीजिए।
हल :
छिन्नक के आकार की बाल्टी के सिरों की त्रिज्याएँ क्रमशः r₁ = 28 cm एवं r₂ = 21 cm हैं तथा इसकी धारिता (आयतन) V = 28.490 लीटर = 28490 cm³ । मान लीजिए कि बाल्टी की ऊँचाई = h cm है तो प्रश्नानुसार,
V = \(\frac { 1 }{ 3 }\) πh (r₁² + r₂² + r₁r₂)
= \(\frac{1}{3} \times \frac{22}{7}\) [(28)² + (21)² + (28) (21)] h = 28490
= \(\frac{1}{3} \times \frac{22}{7}\) (784 + 441 + 588) h = 28490
\(\frac{1}{3} \times \frac{22}{7} \times 1813 h\) = 28490
\(h=\frac{28490 \times 3 \times 7}{22 \times 1813}\)
h = 15 cm
अतः, छिन्नक (बाल्टी) की अभीष्ट ऊँचाई = 15 cm है।

प्रश्न 5.
7 cm भुजा वाले एक घन में एक शंक्वाकार गुहा (cavity)7 cm गहरी तथा 3 cm त्रिज्या वाली बनायी गयी है। शेष ठोस का आयतन ज्ञात कीजिए।
हल :
मान लीजिए एक घन की भुजा a = 7 cm दिया है जिसमें गहराई h = 7 cm एवं त्रिज्या r = 3 cm वाली एक शंक्वाकार गुहा बनायी गयी है।
घन का आयतन V = a³ = (7)³ = 343 cm³
शंक्वाकार गुहा का आयतन \(V_{1}=\frac{1}{3} \pi r^{2} h\)
\(V_{1}=\frac{1}{3} \times \frac{22}{7} \times(3)^{2} \times 7\)
= 66 cm³
शेष ठोस का आयतन = 343 – 66 = 277 cm³
अतः, शेष ठोस का अभीष्ट आयतन = 277 cm³ है।

प्रश्न 6.
दो सर्वांगसम शंकु जिनकी आधार त्रिज्या r = 8 cm एवं ऊँचाई h = 15 cm है। आपस में आधार के साथ जोड़ दिए गए हैं। बने संयुक्त ठोस का सम्पूर्ण पृष्ठ ज्ञात कीजिए।
हल :

दो सर्वांगसम शंकु संलग्न आकृति के अनुसार आपस में जोड़े गए हैं। प्रत्येक शंकु की त्रिज्या r= 8 cm एवं ऊँचाई h = 15 cm है।
एक शंकु की तिर्यक ऊँचाई \(l=\sqrt{h^{2}+r^{2}}\)
[पाइथागोरस प्रमेय से]
\(l=\sqrt{(15)^{2}+(8)^{2}}=\sqrt{225+64}\)
= √289
= 17 cm
प्राप्त ठोस का सम्पूर्ण पृष्ठ = 2 x एक शंकु का वक्रपृष्ठ
S_w = 2 x πrl
= 2 x \(\frac { 22 }{ 7 }\) x 8 x 17
\(S_{w}=\frac{44 \times 8 \times 17}{7}=\frac{5984}{7}\)
= 854.86 cm² लगभग।
अतः, अभीष्ट सम्पूर्ण पृष्ठ = 854.86 cm² (लगभग) है।

प्रश्न 7.
7 cm व्यास वाले एक बीकर में कुछ पानी भरा है। इसमें 1.4cm व्यास वाले कुछ कंचे डाले जाते हैं। बीकर में डाले गए कंचों की संख्या ज्ञात कीजिए जिससे बीकर में पानी का स्तर 5.6cm चढ़ जाता है।
हल :
दिया है, व्यास d = 2r = 7 cm
r = \(\frac { 7 }{ 2 }\) = cm त्रिज्या वाले बेलनाकार बीकर में कुछ पानी है जिसमें मान लीजिए कि व्यास d₁ = 2r₁ = 1.4 cm
r = \(\frac { 1.4 }{ 2 }\) = 0.7 cm त्रिज्या वाले n गोलाकार कंचे डाले जाते हैं जिससे बीकर में जल स्तर h = 5.6 cm चढ़ जाता है, तो प्रश्नानुसार,
n कंचों का आयतन = बीकर में विस्थापित जल का आयतन

अतः, अभीष्ट कंचों की संख्या = 150 है।

प्रश्न 8.
एक 66 cm x 42 cm x 21 cm विमाओं वाले ठोस सीसे के घनाभ को पिघालकर 4.2 cm व्यास वाली कितनी सीसे की ठोस गोलियाँ प्राप्त की जा सकती हैं?
हल :
दिया है, 66 cm x 42 cm x 21 cm विमाओं वाले ठोस सीसे के घनाभ को पिघलाकार मान लीजिए n गोलियाँ बनाई जाती हैं जिनमें प्रत्येक का व्यास d = 2r = 4.2 cm अर्थात् त्रिज्या r = \(\frac { 4.2 }{ 2 }\) = 2.1 cm है तो प्रश्नानुसार,
n गोलियाँ का आयतन = घनाभ का आयतन

अतः, अभीष्ट गोलियों की संख्या = 1500 है।

प्रश्न 9.
सीसे के बने एवं 44 cm भुजा वाले एक ठोस धन से 4 cm व्यास वाली कितनी गोलियाँ बन सकती हैं?
हल:
दिया है, एक a = 44 cm भुजा वाला सीसे का ठोस घन जिसको पिघलाकर माना n गोलियाँ बनायी जाती हैं जिनमें प्रत्येक गोली का व्यास d = 2r = 4cm
⇒ r = \(\frac { 4 }{ 2 }\) = 2 cm अर्थात् त्रिज्या r = 2 cm दी है, तो प्रश्नानुसार,
n x गोलियाँ का आयतन = घन का आयतन


अतः, गोलियों की अभीष्ट संख्या = 2541 है।

प्रश्न 10.
एक दीवार 24 m लम्बी, 0.4 m मोटी एवं 6 m ऊँची बनानी है। इसको बनाने में 25 cm x 16 cm x 10 cm विमाओं वाली कितनी ईंटें लगेंगी जबकि दीवार के आयतन का \(\frac { 1 }{ 10 }\) भाग गारे द्वारा घेरा जायेगा?
हल :
दीवार की विमाएँ l = 24 m, b = 0.4m एवं h = 6 m तथा प्रत्येक ईंट की विमाएँ 25 cm x 16 cm x 10 cm दी हैं तथा दीवार के आयतन का \(\frac { 1 }{ 10 }\) भाग गारे द्वारा घेरा जाएगा। मान लीजिए ईंटों की संख्या n है तो
दीवार का आयतन V = lbh = 24 x 0.4 x 6 m³
V = 57.6 m³ = 57.6 x 10⁶ cm³
गारे द्वारा घेरा गया आयतन = \(\frac { 1 }{ 10 }\) V = 5.76 x 10⁶ cm³
दीवार का शेष आयतन = 57.6 x 10⁶ – 5.76 x 10⁶ cm³
= 51.84 x 10⁶ cm³
प्रश्नानुसार, n ईंटों का आयतन = शेष दीवार का आयतन
n x 25 x 16 x 10 = 51.84 x 10⁶ cm³
4 x 103 n = 51.84 x 10⁶ cm³
\(n=\frac{51 \cdot 84 \times 10^{6}}{4 \times 10^{3}}\)
n = 12.96 x 10³
= 12960 ईंटें
अतः, ईंटों की अभीष्ट संख्या = 12960 है।

प्रश्न 11.
आधार व्यास 1.5 cm एवं मोटाई (ऊँचाई) 0.2 cm वाली वृत्ताकार तस्तरियों की संख्या ज्ञात कीजिए जिनको पिघलाकर एक लम्ब वृत्तीय बेलन 4.5 cm व्यास एवं 10 cm ऊँचाई वाला बन सके।
हल :
वृत्ताकार तस्तरी का व्यास d₁ = 2r₁ = 1.5 cm = \(\frac { 3 }{ 2 }\)cm
त्रिज्या r₁ = \(\frac { 3 }{ 2 }\) cm एवं ऊँचाई (मोटाई) h₁ = 0.2 cm की संख्या n (मान लीजिए) को पिघलाकर h₂ = 10 cm ऊँचा एवं व्यास
d₂ = 2r₂ = 4.5 cm = \(\frac { 9 }{ 2 }\)
r₂ = \(\frac { 9 }{ 4 }\) cm वाला लम्ब वृत्तीय बनाया गया है, तो प्रश्नानुसार
n तस्तरियों का आयतन = बेलन का आयतन

अतः, तस्तरियों की अभीष्ट संख्या = 450 है।

MP Board Class 10th Maths Chapter 13 अति लघु उत्तरीय प्रश्न

निम्न कथनों में सत्य/असत्य लिखिए एवं अपने उत्तर का औचित्य दीजिए।

प्रश्न 1.
दो सर्वांगसम एवं समान आधार त्रिज्या वाले ठोस अर्द्धगोले आधार से आधार जोड़ दिए गए हैं। उनका सम्पूर्ण पृष्ठीय क्षेत्रफल 6πr² होगा।
हल :
असत्य कथन, क्योंकि उनका सम्पूर्ण पृष्ठीय क्षेत्रफल = 4πr² होगा वे एक गोला बनाएँगे।

प्रश्न 2.
r त्रिज्या एवं h ऊँचाई वाले एक ठोस बेलन को समान ऊँचाई एवं त्रिज्या वाले बेलन पर रखा जाता है तो इस प्रकार प्राप्त ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल = 4πrh + 4πr² होगा।
हल :
कथन असत्य है, क्योंकि प्राप्त ठोस एक 2h ऊँचाई एवं r त्रिज्या का बेलन होगा और उसका सम्पूर्ण पृष्ठीय क्षेत्रफल = 4πrh + 2πr² होगा।

प्रश्न 3.
h ऊँचाई एवं r त्रिज्या वाला एक ठोस शंकु एकसमान आधार त्रिज्या एवं समान ऊँचाई वाले बेलन पर रखा है। संयुक्त ठोस का कुल पृष्ठीय क्षेत्रफल है \(\pi r[\sqrt{r^{2}+h^{2}}+3 r+2 h]\).
हल :
कथन असत्य है, क्योंकि संयुक्त ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल \(\pi r[\sqrt{r^{2}+h^{2}}+r+2 h]\) होगा।

प्रश्न 4.
एक ठोस बॉल ठीक प्रकार एक a भुजा वाले घन के अन्दर रखी है तो बॉल का आयतन \(\frac{4}{3} \pi a^{3}\) होगा।
हल :
कथन असत्य है, क्योंकि बॉल का आयतन = \(\frac{1}{6} \pi a^{3}\) होगा।

प्रश्न 5.
एक शंकु के छिन्नक का आयतन \(\frac{1}{3} \pi h\left[r_{1}^{2}+r_{2}^{2}-r_{1} r_{2}\right]\) है, जहाँ h छिन्नक की ऊर्ध्वाधर ऊँचाई तथा r1, r2 उसके सिरों की त्रिज्याएँ हैं।
हल :
कथन असत्य है, क्योंकि छिन्नक का आयतन =\(\frac{1}{3} \pi h\left(r_{1}^{2}+r_{2}^{2}+r_{1} r_{2}\right)\) होता है।

प्रश्न 6.
एक बेलनाकार बर्तन में नीचे अन्दर की ओर एकसमान त्रिज्या का अर्द्ध गोलीय उभार है। इस बर्तन की ऊँचाई h एवं त्रिज्या r है उसकी धारिता है \(\frac{\pi r^{2}}{3}(3 h-2 r)\) है। हल :
कथन सत्य है, क्योंकि बर्तन की धारिता = बेलन का आयतन – अर्द्धगोले का आयतन
= \(\pi r^{2} h-\frac{2}{3} \pi r^{3}=\frac{\pi r^{2}}{3}(3 h-2 r)\) होगा।

प्रश्न 7.
एक शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल \(\pi l\left(r_{1}+r_{2}\right)\) है, जहाँ \(l=\sqrt{h^{2}+\left(r_{1}+r_{2}\right)^{2}}\) एवं r1 तथा r2 क्रमशः दोनों सिरों की त्रिज्याएँ।
हल :
कथन असत्य है, क्योंकि वक्र पृष्ठीय क्षेत्रफल तो \(\pi l\left(r_{1}+r_{2}\right)\) होगा लेकिन \(l=\sqrt{(h)^{2}+\left(r_{1}-r_{2}\right)^{2}}\) होगा, जहाँ r1, r2 क्रमशः सिरों की त्रिज्याएँ हैं।

प्रश्न 8.
एक धातु की खुली बाल्टी जो एक शंकु के छिन्नक के आकार की है, एक खोखले बेलनाकार आधार पर टिकी है जो उसी धातु का बना है। धातु की प्रयुक्त चद्दर का क्षेत्रफल बराबर है छिन्नक का वक्र पृष्ठीय क्षेत्रफल + वृत्ताकार आधार का क्षेत्रफल + बेलन का वक्र पृष्ठीय क्षेत्रफल।
हल :
कथन सत्य है, क्योंकि बाल्टी का सम्पूर्ण पृष्ठीय क्षेत्रफल इन क्षेत्रफलों से मिलकर बना है।

प्रश्न 9.
एक ठोस शंकु अपने समान ऊँचाई h एवं त्रिज्या r वाले बेलन पर रखा है तो संयुक्त ठोस का वक्र पृष्ठीय क्षेत्रफल \(\pi r \sqrt{h^{2}+r^{2}}+2 \pi r h\) है।
हल :
कथन सत्य है, क्योंकि संयुक्त ठोस का बक्रपृष्ठीय क्षेत्रफल बेलन के वक्रपृष्ठीय क्षेत्रफल 2πrh एवं शंकु के वक्रपृष्ठीय क्षेत्रफल πrl अर्थात \(\pi r \sqrt{h^{2}+r^{2}}\) के योग के बराबर होगा।

प्रश्न 10.
एक स्टील की गोलाकार बॉल पिघलाकार 8 नए सर्वांगसम बॉलों में ढाली गयी है तो प्रत्येक बॉल की त्रिज्या मूल बॉल की त्रिज्या का \(\frac { 1 }{ 8 }\) भाग होगा।
हल :
कथन असत्य है, क्योंकि उसकी त्रिज्या मूल त्रिज्या की \(\frac { 1 }{ 2 }\) होगी।

प्रश्न 11.
दो सर्वांगसम घन जिनमें प्रत्येक की भुजा a हो आपस में जोड़े गए हैं, तो कुल पृष्ठीय क्षेत्रफल 12a² है।
हल :
कथन असत्य है, क्योंकि कुल पृष्ठीय क्षेत्रफल 10a² होगा।

MP Board Class 10th Maths Chapter 13 वस्तुनिष्ठ प्रश्न

MP Board Class 10th Maths Chapter 13 बहु-विकल्पीय प्रश्न

प्रश्न 1.
संलग्न आकृति एक फनल की है जो एक संयुक्त आकृति है :

(a) एक शंकु एवं एक बेलन की
(b) एक शंकु छिन्नक एवं एक बेलन की
(c) एक अर्द्ध गोला एवं एक बेलन की
(d) एक अर्द्ध गोला एवं एक शंकु की।
उत्तर:
(b) एक शंकु छिन्नक एवं एक बेलन की

प्रश्न 2.
एक शंकु छिन्नक के सिरों की त्रिज्याएँ क्रमशः r1 cm एवं r2 cm तथा ऊँचाई h cm है तो आयतन cm³ में होगा :

उत्तर:
(a) \(\frac{1}{3} \pi h\left(r_{1}^{2}+r_{2}^{2}+r_{1} r_{2}\right)\)

प्रश्न 3.
एक सिरे पर छीली गई एक बेलनाकार पेन्सिल एक संयुक्त आकृति है:

(a) एक बेलन एवं एक शंकु की
(b) एक शंकु छिन्नक एवं एक बेलन की
(c) एक अर्द्ध गोला एवं एक बेलन की
(d) दो बेलनों की।
उत्तर:
(a) एक बेलन एवं एक शंकु की

प्रश्न 4.
एक सुराही संयुक्त आकृति है :

(a) एक गोले एवं एक बेलन की
(b) एक अर्द्ध गोला एवं एक बेलन की
(c) दो अर्द्ध गोलों की
(d) एक बेलन एवं एक शंकु की।
उत्तर:
(a) एक गोले एवं एक बेलन की

प्रश्न 5.
एक साहुल सूत्र (प्लम्ब लाइन) (देखिए संलग्न आकृति) एक संयुक्त आकृति है:

(a) एक शंकु एवं एक बेलन की
(b) एक अर्द्ध गोला एवं एक शंकु की
(c) एक शंकु छिन्नक एवं एक बेलन की
(d) एक गोला एवं एक बेलन की।
उत्तर:
(b) एक अर्द्ध गोला एवं एक शंकु की

प्रश्न 6.
एक गिलास प्रायः निम्न आकृति का होता है :

(a) एक शंकु की
(b) एक शंकु छिन्नक की
(c) एक बेलन की
(d) एक गोले की।
उत्तर:
(b) एक शंकु छिन्नक की

प्रश्न 7.
गिल्ली-डंडा खेल की गिल्ली संयुक्त आकृति होती है निम्न की :

(a) दो बेलनों की
(b) एक शंकु एवं एक बेलन की
(c) दो शंकु एवं एक बेलन की
(d) दो बेलन एवं एक शंकु की।
उत्तर:
(c) दो शंकु एवं एक बेलन की

प्रश्न 8.
बैडमिण्टन खेल में प्रयुक्त एक शटल कॉक एक संयुक्त आकृति

(a) एक बेलन एवं एक गोला की
(b) एक बेलन एवं एक अर्द्ध गोला की
(c) एक गोला एवं एक शंकु की
(d) एक शंकु-छिन्नक एवं एक अर्द्ध गोला की।
उत्तर:
(d) एक शंकु-छिन्नक एवं एक अर्द्ध गोला की।

प्रश्न 9.
एक शंक को उसके आधार के समान्तर एक तल द्वारा काटने पर एक सिरे पर प्राप्त छोटे शंकु को पृथक् कर दिया जाता है। इस प्रकार शेष बचा ठोस कहलाता है:
(a) एक शंकु का एक छिन्नक
(b) शंकु
(c) बेलन
(d) गोला।
उत्तर:
(a) एक शंकु का एक छिन्नक

प्रश्न 10.
एक ठोस 2 cm व्यास एवं 16 cm ऊँचाई वाले बेलन को पिघलाकर 12 सर्वांगसम गोले बनाए जाते हैं तो प्रत्येक गोले का व्यास होगा :
(a) 4 cm
(b) 3 cm
(c) 2 cm
(d) 6 cm.
उत्तर:
(c) 2 cm

प्रश्न 11.
यदि दो ठोस समान आधार त्रिज्या के r अर्द्ध गोले आपस में आधार से आधार सटाकर जोड़ दिए जाते हैं तो इस प्रकार प्राप्त नए ठोस का वक्र पृष्ठीय क्षेत्रफल होगा :
(a) 4πr²
(b) 6πr²
(c) 3πr²
(d) 8πr²
उत्तर:
(a) 4πr²

प्रश्न 12.
r cm त्रिज्या एवं h cm (h > 2r) ऊँचाई का एक लम्ब वृत्तीय बेलन एक गोले को ठीक-ठीक ढक लेता है तो इस गोले का व्यास होगा :
(a) r cm
(b) 2r cm
(c) h cm
(d) 2h cm.
उत्तर:
(b) 2r cm

प्रश्न 13.
एक ठोस को दूसरे ठोस में परिवर्तित करने पर नए ठोस का आयतन :
(a) बढ़ जायेगा
(b) घट जायेगा
(c) अपरिवर्तित रहेगा
(d) दूना होगा।
उत्तर:
(c) अपरिवर्तित रहेगा

प्रश्न 14.
एक लम्बवृत्तीय शंकु को आधार के समान्तर तल द्वारा काटने पर प्राप्त परिच्छेद होगा :
(a) वृत्त
(b) शंकु छिन्नक
(c) गोला
(d) अर्द्ध गोला।
उत्तर:
(a) वृत्त

प्रश्न 15.
दो गोलों के आयतनों का अनुपात 64 : 27 है तो उनके पृष्ठीय क्षेत्रफलों का अनुपात होगा :
(a) 3:4
(b) 4:3
(c) 9:16
(d) 16:9.
उत्तर:
(d) 16:9.

रिक्त स्थानों की पूर्ति

1. किसी शंकु को उसके आधार के समान्तर तल द्वारा काटकर छोटे शंकु को हटाने पर शेष बचा ठोस …………. कहलाता है।
2. शंकु छिन्नक के दोनों सिरे …………. होते हैं।
3. बाल्टी का आकार प्रायः एक …………. का होता है।
4. शंकु छिन्नक का आयतन दोनों शंकुओं के आयतनों के …………. के बराबर होता है।
5. शंकु छिन्नक का वक्र पृष्ठीय क्षेत्रफल दोनों शंकुओं के वक्र प्रष्ठीय क्षेत्रफलों के …………. के बराबर होता है।
उत्तर-
1.शंकु छिन्नक,
2. वृत्ताकार,
3. शंकु छिन्नक,
4. अन्तर,
5. अन्तर।

जोड़ी मिलाइए

उत्तर-
1.→(b),
2.→(c),
3.→(a).

सत्य/असत्य कथन

1. शंकु छिन्नक का आयतन संगत शंकुओं के आयतनों के योग के बराबर होता है।
2. यदि किसी बेलन के एक सिरे पर उसी त्रिज्या का एक अर्द्ध गोलाकार गड्ढा कर दिया जाए तो प्राप्त ठोस का वक्र पृष्ठीय क्षेत्रफल दोनों के वक्र पृष्ठीय क्षेत्रफल के योग के बराबर होता है। 3. शंकु छिन्नक का वक्रपृष्ठीय क्षेत्रफल संगत शंकुओं के वक्र पृष्ठीय क्षेत्रफलों के योग के बराबर होता है।
उत्तर-
1. असत्य,
2. सत्य,
3. असत्य।

एक शब्द/वाक्य में उत्तर

1. एक शंकु छिन्नक जिसके सिरों की त्रिज्याएँ क्रमशः r₁ एवं r₂ तथा तिर्यक ऊँचाई l तो उसका सम्पूर्ण पृष्ठीय क्षेत्रफल क्या होगा?
2. शंकु के छिन्नक के आयतन का सूत्र लिखिए। (2019)
उत्तर-
1. S_w = πl (r₁ + r₂) + πr₁² + πr₂²
2. V = \(\frac { 1 }{ 3 }\)πh(r₁² + r₂² + r₁r₂).

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.3 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.3

प्रश्न 1.
निम्नलिखित के मान निकालिए :
(i) \(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\)
(ii) \(\frac{\tan 26^{\circ}}{\cot 64^{\circ}}\)
(iii) cos 48° sin 42°
(iv) cosec 31° – sec 590.
हल :
(i) \(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\)
= 1.
अतः अभीष्ट मान = 1 (एक) है।

(ii) \(\frac{\tan 26^{\circ}}{\cot 64^{\circ}}\)
= 1
अतः अभीष्ट मान 1 (एक) है।

(iii) cos 48° sin 42° = cos (90° – 42°) – sin 42°
= sin 42° – sin 42°
= 0
अतः अभीष्ट मान 0 (शून्य) है।

(iv) cosec 31° – sec 59° = cosec (90° – 59°) – sec 59°
= sec 59° – sec 59°
= 0
अत: अभीष्ट मान 0 (शून्य) है।

प्रश्न 2.
दिखाइए कि:
(i) tan 48°. tan 23°. tan 42° tan 67° = 1
(ii) cos 38°. cos 52° – sin 38°. sin 52° = 0.
हल :
(i) L.H.S. = tan 48°. tan 23°. tan 42° tan 67°
= tan (90° – 42°). tan 23°. tan 42°. tan (90° – 23°)
= cot 42°. tan 23°. tan 42°. cot 23°
= \(\frac{\cos 42^{\circ}}{\sin 42^{\circ}} \cdot \frac{\sin 23^{\circ}}{\cos 23^{\circ}} \cdot \frac{\sin 42^{\circ}}{\cos 42^{\circ}} \cdot \frac{\cos 23^{\circ}}{\sin 23^{\circ}}\)
= 1
= R.H.S.
इति सिद्धम्

(ii) L.H.S. = cos 38°.cos 52° – sin 38°. sin 52°
= cos 38°. cos (90° – 38°) – sin 38° sin (90° – 38°)
= cos 38°.sin 38° – sin 38°. cos 38°
= cos 38°.sin 38° – cos 38°.sin 38°
= 0
= R.H.S.
इति सिद्धम्

प्रश्न 3.
यदि tan 2A = cot (A – 18°), जहाँ 2A एक न्यूनकोण है, तो A का मान ज्ञात कीजिए।
हल :
चूंकि tan 2A = cot (A – 18°) (दिया हुआ है)
cot (90° – 2A) = cot (A – 18°)
90° – 2A = A – 18°
3A = 90° + 18° = 108°
A = \(\frac { 108 }{ 3 }\)
= 36°
अतः A का अभीष्ट मान = 36° है।

प्रश्न 4.
यदि tan A = cot B, तो सिद्ध कीजिए कि A+ B = 90°.
हल :
चूँकि
⇒ tan A = cot B (दिया है)
⇒ tan A = tan (90° – B)
⇒ A = 90° – B
⇒ A + B = 90°.
इति सिद्धम्

प्रश्न 5.
यदि sec 4A = cosec (A – 20°) जहाँ 4A एक न्यनूकोण है, तो A का मान ज्ञात कीजिए।
हल :
चूंकि sec 4A = cosec (A – 20°) (दिया है)
⇒ cosec (90° – 4A) = cosec (A – 20°)
⇒ 90° – 4A = A – 20°
⇒ 4A + A = 90° + 20°
⇒ 5A = 110°
⇒ A = \(\frac { 110 }{ 5 }\) = 22°
अतः A का अभीष्ट मान = 22° है।

प्रश्न 6.
यदि A, B और C त्रिभुज ABC के अन्तः कोण हों, तो दिखाइए कि
\(\sin \left(\frac{B+C}{2}\right)=\cos \frac{A}{2}\)
हल :
चूंकि
A + B + C = 180° (त्रिभुज के अन्त:कोण हैं)

= cos \(\frac { A }{ 2 }\)
= RHS
इति सिद्धम्

प्रश्न 7.
sin 67° + cos 75° को 0° और 45° के बीच के कोणों के त्रिकोणमितीय अनुपातों के पदों में व्यक्त कीजिए।
हल :
sin 67° + cos 75° = sin (90° – 23°) + cos (90° – 15°)
= cos 23° + sin 15°
अतः अभीष्ट त्रिकोणमितीय अनुपात के पद cos 23° + sin 15°.

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 6 त्रिभुज Ex 6.4 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 6 त्रिभुज Ex 6.4

प्रश्न 1.
मान लीजिए ∆ABC ~ ∆DEF और इनके क्षेत्रफल क्रमश: 64 cm और 121 cm हैं। यदि EF = 15.4 cm हो, तो BC ज्ञात कीजिए।
हल :
चूँकि ∆ABC ~ ∆DEF [दिया है]

अतः BC का अभीष्ट मान = 11.2 cm.

प्रश्न 2.
एक समलम्ब ABCD जिसमें AB || DC है के विकर्ण परस्पर बिन्दु O पर प्रतिच्छेद करते हैं। यदि AB = 2CD हो, तो त्रिभुजों AOB और COD के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :

∆AOB और ∆COD में,
∵LOAB = ZOCD (एकान्तर कोण हैं)
[यहाँ AB || DC, AC तिर्यक रेखा]
∵ LOBA = ZODC (एकान्तर कोण हैं)
[यहाँ AB || DC, DB तिर्यक रेखा]
∆AOB ~ ∆COD [AA समरूपता]

अतः क्षेत्र. (∆AOB) : क्षेत्र. (∆COD) = 4 : 1.

प्रश्न 3.
संलग्न आकृति 6.29 में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं। यदि AD, BC को O पर प्रतिच्छेद करे, तो दर्शाइए कि \(\frac { ar(ABC) }{ ar(DBC) } =\frac { AO }{ DO } \) हैं।
हल :

दिया है : एक ही आधार BC पर दो ∆ABC एवं ∆DBC और AD, BC को बिन्दु O पर प्रतिच्छेद करती है।
रचना : AE ⊥ BC एवं DF ⊥ BC खींचिए।
अब ∆AEO और ∆DFO में,
चूँकि ∠AEO = ∠DFO = 90° [∵ AE ⊥ BC एवं DF ⊥ BC]
∠AOE = ∠DOF [शीर्षाभिमुख कोण हैं]
∆AEO ~ ∆DFO [AA समरूपता]
\(\frac{A E}{D F}=\frac{A O}{D O}\) [समरूप त्रिभुजों के प्रगुण]

[∵ त्रिभुज का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x आधार x शीर्षलम्ब]
\(\frac { ar(ABC) }{ ar(DBC) } =\frac { AO }{ DO } \) [समीकरण (1) एवं (2) से]
इति सिद्धम्

प्रश्न 4.
यदि दो समरूप त्रिभुजों के क्षेत्रफल समान हों, तो सिद्ध कीजिए कि वे त्रिभुज सर्वांगसम होते हैं।
हल :
मान लीजिए
∆ABC ~ ∆PQR

लेकिन
ar(ABC) = ar(PQR) = x वर्ग मात्रक।

(AB)² = (PQ)², (BC)² = (QR)² एवं (CA)² = (RP)²
AB = PQ, BC = QR एवं CA = RP …(1)
अब ∆ABC और ∆PQR में,
∵ AB = PQ, BC = QR एवं CA = RP [समीकरण (1) से]
∆ABC ≅ ∆PQR. [SSS सर्वांगसमता]
इति सिद्धम्

प्रश्न 5.
एक त्रिभुज ABC की भुजाओं AB, BC एवं CA के मध्य-बिन्दु क्रमश: D, E एवं F हैं। ∆DEF और ∆ABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :

दिया है : ∆ABC की भुजाओं AB, BC एवं CA के क्रमशः मध्य-बिन्दुओं D, E एवं F को मिलाने से ∆DEF बना है (देखिए संलग्न आकृति 6.30 में)
चूँकि किसी त्रिभुज की दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के आधा होता है।

ar(DEF) : ar(ABC) = 1 : 4.
अत: ∆DEF एवं ∆ABC के क्षेत्रफलों का अभीष्ट अनुपात 1 : 4 है।

प्रश्न 6.
सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है।
हल :

मान लीजिए कि दो समरूप ∆ABC ~ ∆PQR हैं, जिनकी संगत माध्यिकाएँ AD एवं PM हैं। (देखिए आकृति 6.31)
चूँकि ∆ABC ~ ∆PQR दिया है।
∠A = ∠P, ∠B = ∠Q
एवं ∠C = ∠R …(1)
एवं \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{C A}{R P}\) …(2)
[समरूप त्रिभुजों के प्रगुण]
∵ \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{2 B D}{2 Q M}=\frac{B D}{Q M}\) ….(3)
[D, BC का एवं M, QR का मध्य-बिन्दु है]
अब ∆ABD एवं ∆PQM में,
∠B = ∠Q [समीकरण (1) से]

अतः दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है।
इति सिद्धम्

प्रश्न 7.
सिद्ध कीजिए कि किसी वर्ग की किसी भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के एक विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
हल :

मान लीजिए ABCD एक वर्ग है। जिसका एक विकर्ण AC है। वर्ग की भुजा AD पर समबाहु ∆EAD एवं उसके विकर्ण AC पर समबाहु ∆FAC बने हैं।
चूँकि दो समबाहु त्रिभुज सदैव समरूप होते हैं।
∆EAD ~ ∆FAC

अतः किसी वर्ग की भुजा पर बने समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के विकर्ण पर बने समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
इति सिद्धम्

प्रश्न 8.
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिन्दु है। त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है :
(a) 2:1
(b) 1:2
(c) 4:1
(d) 1:4.
सही उत्तर चुनिए और अपने उत्तर का औचित्य दीजिए।
हल :
सही विकल्प (c) 4 : 1 है, क्योंकि ∆ABC ~ ∆BDE क्योंकि समबाहु त्रिभुज समरूप होते हैं एवं

यहाँ AB = 2BD क्योंकि D, AB का मध्य-बिन्दु है।

प्रश्न 9.
दो समरूप त्रिभुजों की भुजाएँ 4:9 के अनुपात में हैं। इन त्रिभुजों के क्षेत्रफलों का अनुपात है :
(a) 2:3
(b) 4:9
(c) 81:16
(d) 16:81
सही विकल्प चुनिए तथा अपने उत्तर का औचित्य दीजिए।
हल :
सही विकल्प (d) 16 : 81 है, क्योंकि समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात का वर्ग होता है। अत: 4 : 9 का वर्ग अनुपात 16 : 81 है।

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.1 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.1

प्रश्न 1.
दो घनों जिनमें से प्रत्येक का आयतन 64 cm³ है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

ज्ञात है : दो सर्वांगसम घन जिनमें से प्रत्येक का आयतन V = a³ = 64 cm³ है, जहाँ a = वर्ग की भुजा है। दोनों के संलग्न फलकों को मिलाकर एक घनाभ बनाया गया है जिसकी लम्बाई l = 2a cm चौड़ाई b = a cm एवं ऊँचाई h = a cm है।
∵ V = a³ = 64 = (4)³
⇒ a = 4 cm
⇒ l = 2a = 2 x 4 = 8cm,
b = 4 cm एवं h = 4 cm
∵ घनाभ का पृष्ठीय क्षेत्रफल
S_w = 2(lb + bh + hl) .
⇒ S_w = 2(8 x 4 + 4 x 4 + 4 x 8)
= 2(32 + 16 + 32)
= 2 x 80
= 160 cm²
अतः, घनाभ का अभीष्ट पृष्ठीय क्षेत्रफल = 160 cm² है।

प्रश्न 2.
कोई बर्तन खोखले अर्द्धगोले के आकार का है जिसके ऊपर एक खोखला बेलन अध्यारोपित है। अर्द्ध गोले का व्यास 14 cm है और इस बर्तन (पात्र) की कुल ऊँचाई 13 cm है। इसका आन्तरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

ज्ञात है : एक 14 cm व्यास वाला एक खोखला अर्द्धवृत्ताकार पात्र एवं उसके ऊपर अध्यारोपित समान व्यास के एक खोखले बेलन के अध्यारोपण के फलस्वरूप बना एक संयुक्त पात्र जिसकी कुल ऊँचाई 13 cm है (देखिए संलग्न आकृति 13.3)। चूँकि बेलन के आधार पर व्यास = अर्द्ध गोलाकार बर्तन का व्यास d= 14 cm
⇒ बेलन की त्रिज्या = अर्द्ध गोले की त्रिज्या r = 14/2 =7 cm
∵ पात्र की कुल ऊँचाई = 13 cm
⇒ बेलन की ऊँचाई h = 13 cm – 7 cm = 6 cm
∵ पात्र की आन्तरिक पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + अर्द्ध गोले का वक्र पृष्ठीय क्षेत्रफल
⇒ पात्र का आन्तरिक पृष्ठीय क्षेत्रफल = 2πrh + 2π²
= 2 x \(\frac { 22 }{ 7 }\) x 7 x 6 + \(\frac { 22 }{ 7 }\) x (7)²
= 264 + 308
= 572 cm²
अतः, पात्र का अभीष्ट आन्तरिक पृष्ठीय क्षेत्रफल = 572 cm² है।

प्रश्न 3.
एक खिलौना त्रिज्या 3.5 cm वाले एक शंकु के आकार का है जो उसी त्रिज्या वाले एक अर्द्ध गोले पर अध्यारोपित है। इस खिलौने की सम्पूर्ण ऊँचाई 15.5 cm है। इस खिलौने का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

ज्ञात है : संलग्न आकृति के अनुसार एक खिलौना जिसकी सम्पूर्ण ऊँचाई 15.5 cm तथा अर्द्ध गोले
एवं शंकु के आधार की त्रिज्या = 3.5 cm दी गयी है, अतः r = \(\frac { 7 }{ 2 }\) cm.
⇒ शंकु की ऊर्ध्वाधर ऊँचाई h = 15.5 – 3.5 = 12 cm.
∵ शंकु की तिर्यक ऊँचाई

चूँकि खिलौने का सम्पूर्ण पृष्ठीय क्षेत्रफल = शंकु का पार्श्व पृष्ठीय क्षेत्रफल + अर्द्ध गोले का पार्श्व पृष्ठीय क्षेत्रफल

अतः, खिलौने का अभीष्ट सम्पूर्ण पृष्ठीय क्षेत्रफल = 214.5 cm² है।

प्रश्न 4.
भुजा 7 cm वाले एक घनाकार ब्लॉक के ऊपर एक अर्द्धगोला रखा हुआ है। अर्द्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

चूँकि घनाकार ब्लॉक की भुजा a = 7 cm दी है। इसके ऊपर एक अर्द्धगोला रखा है, अतः अर्द्धगोले का अधिकतम व्यास d= घन की भुजा = a = 7 cm
⇒ अर्द्धवृत्त की त्रिज्या r = \(\frac { 7 }{ 2 }\) cm
चूँकि ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल = घन का सम्पूर्ण पृष्ठीय क्षेत्रफल + अर्द्धगोले का पार्श्व पृष्ठीय क्षेत्रफल – अर्द्धगोले के आधार द्वारा घेरे गए वृत्ताकार भाग का क्षेत्रफल
S_w = 6a² + 2πr² – πr²
= 6a² + πr²
\(S_{w}=6 \times(7)^{2}+\frac{22}{7} \times\left(\frac{7}{2}\right)^{2}\)
= 294 + 38.5
= 332.5 cm²
अतः, अर्द्धवृत्त का अधिकतम अभीष्ट व्यास = 7 cm
एवं ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल = 332.5 cm² है।

प्रश्न 5.
एक घनाकार ब्लॉक के एक फलक को अन्दर की ओर काटकर एक अर्द्ध गोलाकार गड्डा इस प्रकार बनाया गया है कि अर्द्धगोले का व्यास l घन के एक किनारे के बराबर है। शेष बचे ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

माना लीजिए दिए हुए घनाकार ब्लॉक की भुजा (l किनारा) a = l मात्रक।
इसके एक फलक को काटकर अर्द्ध गोलीय गड्ढा इस प्रकार बनाया गया है कि अर्द्ध गोले का व्यास d = l मात्रक।
⇒ अर्द्धगोले की त्रिज्या r = \(\frac { l }{ 2 }\) मात्रक।
चूंकि ठास का सम्पूर्ण पृष्ठीय क्षत्रफल = घन का सम्पूर्ण पृष्ठीय क्षेत्रफल + अर्द्ध गोलीय गड्ढे का पृष्ठीय क्षेत्रफल – काटे हुए वृत्त का क्षेत्रफल
S_w = 6l² + 2π² – πr²
= 6l² + πr²
= \(6 l^{2}+\pi\left(\frac{l}{2}\right)^{2}=6 l^{2}+\frac{1}{4} \pi l^{2}\)
S_w = \(\frac { 1 }{ 4 }\)l² (24 + π) वर्ग मात्रक।
अतः ठोस का अभीष्ट सम्पूर्ण पृष्ठीय क्षेत्रफल = \(\frac { 1 }{ 4 }\)l² (24 + π) वर्ग मात्रक।

प्रश्न 6.
दवा का एक कैप्सूल (Capsule) एक बेलन के आकार का है जिसके दोनों सिरों पर एक-एक अर्द्ध गोला लगा हुआ है (देखिए संलग्न आकृति)। पूरे कैप्सूल की लम्बाई 14 mm है और उसका व्यास 5 mm है। इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

मान लीजिए दवा का एक कैप्सूल कुल 14 mm लम्बा तथा d = 5 mm व्यास वाला एक इस प्रकार का बेलनाकार है जिसके दोनों सिरों पर उसी व्यास के एक-एक अर्द्ध गोले लगे हुए हैं। चूँकि बेलनाकार भाग एवं अर्द्धगोलीय भाग का व्यास d = 5 mm
⇒ बेलनाकार भाग एवं अर्द्ध गोलीय भाग की त्रिज्या r = \(\frac { 5 }{ 2 }\) mm
चूँकि कैप्सूल की कुल लम्बाई = बेलनाकार भाग की लम्बाई l + दो अर्द्धगोलीय त्रिज्या अर्थात् व्यास
⇒ l + 5 = 14 mm
⇒ l = 14 – 5 = 9 mm
∵ कैप्सूल का सम्पूर्ण पृष्ठीय क्षेत्रफल = बेलन का वृक्र पृष्ठीय क्षेत्रफल + 2 x अर्द्धगोलीय भाग का वक्र पृष्ठीय क्षेत्रफल

अतः कैप्सूल का अभीष्ट पृष्ठीय क्षेत्रफल = 220 mm² (लगभग) है।

प्रश्न 7.
कोई तम्बू एक बेलन के आकार का है जिस पर एक शंकु अध्यारोपित है। यदि बेलनाकार भाग की ऊँचाई और व्यास क्रमश: 2.1 m और 4 m है तथा शंकु की तिर्यक ऊँचाई 2.8 m है, तो इस तम्बू को बनाने में प्रयुक्त कैनवास (Canvas) का क्षेत्रफल ज्ञात कीजिए। साथ ही Rs 500 प्रति m² की दर से इसमें प्रयुक्त कैनवास की लागत ज्ञात कीजिए। (ध्यान दीजिए कि
तम्बू के आधार को कैनवास से नहीं ढका जाता है।)
हल :

ज्ञात है : तम्बू के बेलनाकार भाग की ऊँचाई h = 2.1 m तथा बेलनाकार भाग एवं शंक्वाकर भाग के व्यास d = 4 m
बेलन की त्रिज्या = शंकु की त्रिज्या
r = \(\frac { 4 }{ 2 }\)m = 2 m
शंकु की तिर्यक ऊँचाई l = 2.8 m.
चूँकि तम्बू का पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + शंकु का वक्र पृष्ठीय क्षेत्रफल
S_w = 2πrh x πrl
= 2 x \(\frac { 22 }{ 7 }\) 2 x 2.1 + \(\frac { 22 }{ 7 }\) x 2 x 2.8
= 26.4 + 17.6
= 44.0 m²
∵ व्यय = क्षेत्रफल x दर
= 44 x Rs 500
= Rs 22,000.
अतः, प्रयुक्त कैनवास का अभीष्ट क्षेत्रफल = 44 m²
एवं उसको लगाने में अभीष्ट व्यय = Rs 22,000 है।

प्रश्न 8.
ऊँचाई 2.4 cm और व्यास 1.4 cm वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल (Cavity) काट लिया जाता है। शेष बचे ठोस का निकटतम वर्ग सेण्टीमीटर तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

दिया है : h= 2.4 cm ऊँचाई एवं d = 1.4 cm व्यास वाले एक बेलन में से उसी ऊँचाई एवं उसी व्यास का शंक्वाकार खोल काट दिया जाता है। मान लीजिए शंकु की तिर्यक ऊँचाई = l cm है।
चूँकि व्यास = 1.4 cm
त्रिज्या = \(\frac { 1.4 }{ 2 }\) = 0.7 cm
चूँकि तिर्यक ऊँचाई

चूँकि प्राप्त ठोस का पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + शंकु का वक्र पृष्ठीय क्षेत्रफल + ऊपर के आधार का वृत्तीय क्षेत्रफल
S_w = 2πrh + πrl + πr²
= πr(2h + l + r)
= \(\frac { 22 }{ 7 }\) x 0.7(2 x 2.4 + 2.5 + 0.7)
= 2.2(4.8 + 2.5 + 0.7)
= 2.2 x 8.0
= 17.6 cm²
S_w = 18 cm² (निकटतम cm² में)
अतः, शेष बचे ठोस का अभीष्ट पृष्ठीय क्षेत्रफल
= 18 cm² (निकटतम cm² में) है।

प्रश्न 9.
लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्द्ध गोला खोदकर निकालते हुए एक वस्तु बनाई गई है जैसा कि संलग्न आकृति में दर्शाया गया है। यदि बेलन की ऊँचाई 10 cm है और आधार की त्रिज्या 3.5 cm है, तो इस वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल :

ज्ञात है : h = 10 cm ऊँचाई एवं r = 3.5 cm त्रिज्या वाला लकड़ी का एक बेलन जिसके दोनों सिरों से उसी त्रिज्या का एक-एक अर्द्ध गोलाकार भाग काटकर निकाल दिया गया है तो
∵ प्राप्त ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + 2 x अर्द्धगोले का पृष्ठीय क्षेत्रफल
S_w = 2πrh + 2 x 2πr²
= 2πr(h + 2r)
= 2 x \(\frac { 22 }{ 7 }\) x 3.5(10 + 2 x 3.5)
= 22 x 17
= 374 cm²
अतः, शेष प्राप्त ठोस का अभीष्ट सम्पूर्ण पृष्ठीय क्षेत्रफल = 374 cm² है।

In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.2 Pdf, These solutions are solved subject experts from the latest edition books.

MP Board Class 10th Maths Solutions Chapter 8 त्रिकोणमिति का परिचय Ex 8.2

प्रश्न 1.
निम्नलिखित के मान निकालिए :
(i) sin 60°. cos 30° + sin 30°. cos 60° (2019)
(ii) 2 tan² 45° + cos² 30° – sin² 60° (2019)
(iii) \(\frac{\cos 45^{\circ}}{\sec 30^{\circ}+\csc 30^{\circ}}\)
(iv) \(\frac{\sin 30^{\circ}+\tan 45^{\circ}-\csc 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}\)
(v) \(\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}\)
हल :
(i) sin 60°. cos 30° + sin 30°. cos 60°
\(=\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}+\frac{1}{2} \times \frac{1}{2}=\frac{3}{4}+\frac{1}{4}=\frac{4}{4}=1\)
अतः अभीष्ट मान = 1 है।

(ii) 2 tan² 45° + cos² 30° – sin² 60°
\(=2(1)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}-\left(\frac{\sqrt{3}}{2}\right)^{2}\)
\(=2+\frac{3}{4}-\frac{3}{4}\)
अतः अभीष्ट मान = 2 है।

(iii) \(\frac{\cos 45^{\circ}}{\sec 30^{\circ}+\csc 30^{\circ}}\)

अतः अभीष्ट मान \(\frac{3 \sqrt{2}-\sqrt{6}}{8}\) है।

(iv) \(\frac{\sin 30^{\circ}+\tan 45^{\circ}-\csc 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}\)

अतः अभीष्ट मान \(\frac{43-24 \sqrt{3}}{11}\) है।

(v) \(\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}\)

अतः अभीष्ट मान \(\frac { 67 }{ 12 }\) है।

प्रश्न 2.
सही विकल्प चुनिए और अपने विकल्प का औचित्य दीजिए :
(i) \(\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}\) = …………
(A) sin 60°
(B) cos 60°
(C) tan 60°
(D) sin 30°
हल :
सही विकल्प है (A) sin 60°.
क्योंकि

(ii) \(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}\) = ……….
(A) tan 90°
(B) 1
(C) sin 45°
(D) 0.
हल :
सही विकल्प (D) 0.
क्योंकि

(iii) sin 2A = 2 sin A तब सत्य होता है जबकि A बराबर है :
(A) 0°
(B) 30°
(C) 45°
(D) 60°.
हल :
सही विकल्प है (A) 0°.
क्योंकि sin 2A = 2 sin A ⇒ sin 2 x 0° = 2 sin 0
⇒ sin 0° = 2 sin 0° ⇒ 0 = 2 x 0 = 0.

(iv) \(\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}\) बराबर है:
(A) cos 60°
(B) sin 60°
(C) tan 60°
(D) sin 30°
हल :
सही विकल्प है (C) tan 60°.
क्योंकि

प्रश्न 3.
यदि tan (A + B) = √3 और tan (A – B) = \(\frac{1}{\sqrt{3}}\), 0° < A + B ≤ 90° ; A > B तो A और B के मान ज्ञात कीजिए।
हल : ∵ tan (A + B) = √3 = tan 60°
⇒ A + B = 60° ….(1)
∵ tan (A – B) = \(\frac{1}{\sqrt{3}}\) = tan 30°
⇒ A – B = 30° …(2)
⇒ 2A = 90°
⇒ A = \(\frac { 90 }{ 2 }\) = 45° [समीकरण (1) + (2) से]
A = 45° का मान समीकरण (1) में रखने पर,
⇒ A + 45° = 60°
⇒ A = 60° – 45° = 15°
अतः A एवं B के अभीष्ट मान हैं क्रमशः 45° एवं 150°.

प्रश्न 4.
बताइए कि निम्नलिखित में कौन-कौन सत्य है या असत्य है? कारण सहित अपने उत्तर की पुष्टि कीजिए:
(i) sin (A + B) = sin A + sin B.
(ii) θ में वृद्धि होने के साथ sin θ के मान में भी वृद्धि होती है।
(iii) θ में वृद्धि होने के साथ cos θ के मान में भी वृद्धि होती है।
(iv) θ के सभी मानों पर sinθ = cosθ.
(v) A = 0° पर cot A परिभाषित नहीं है।
हल :
(i) कथन असत्य है, sin (60° + 30°) = sin 90° = 1
एवं sin 60° + sin 30° = \(\frac{\sqrt{3}}{2}+\frac{1}{2}=\frac{\sqrt{3}+1}{2}\) जो बराबर नहीं है।

(ii) कथन सत्य है, क्योंकि sin 0° = 0, sin 30° = \(\frac { 1 }{ 2 }\), sin 45° = \(\frac{1}{\sqrt{2}}\), sin 60° = \(\frac{\sqrt{3}}{2}\), एवं sin 90° = 1.

(iii) कथन असत्य है, क्योंकि cos 0° = 1, cos 30° = \(\frac{\sqrt{3}}{2}\), cos 45° = \(\frac{1}{\sqrt{2}}\), Cos 60° = \(\frac { 1 }{ 2 }\), एवं cos 90° = 0.

(iv) कथन असत्य है, क्योंकि sin 30° = \(\frac { 1 }{ 2 }\) जबकि cos 30° = \(\frac{\sqrt{3}}{2}\).

(v) कथन सत्य है, क्योंकि cot A° = cot 0° = \(\frac{\cos 0^{\circ}}{\sin 0^{\circ}}=\frac{1}{0}\) जो कि अपरिश भाषित है।