In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग Additional Questions Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 9 त्रिकोणमिति के कुछ अनुप्रयोग Additional Questions
MP Board Class 10th Maths Chapter 9 अतिरिक्त परीक्षोपयोगी प्रश्न
MP Board Class 10th Maths Chapter 9 दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
एक मीनार के शीर्ष का उन्नयन कोण किसी बिन्द से 30° है। यदि प्रेक्षक 20 मीटर मीनार की ओर चलता है तो उस मीनार के शीर्ष का कोण 15° बढ़ जाता है। मीनार की ऊँचाई ज्ञात कीजिए।
हल :
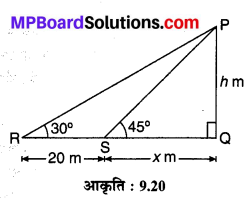
मान लीजिए PQ एक मीनार है जिसके शीर्ष P का बिन्दु R पर उन्नयन कोण ∠PRQ = 30° है तथा मीनार की ओर RS = 20 m चलने पर उन्नयन कोण ∠PSQ = 30° + 15° = 45° हो जाता है। पुनः मान लीजिए मीनार की ऊँचाई PQ = hm तथा दूरी QS = x m है तो
समकोण ∆PQS में,
\(\frac { PQ }{ QS }\) = tan PSQ
⇒ \(\frac { h }{ x }\) = tan 45° = 1
⇒ h = x …(1)
एवं समकोण ∆PQR में,
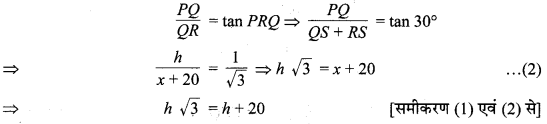

अतः, मीनार की अभीष्ट ऊँचाई = 10 (√3 + 1) m है।
प्रश्न 2.
किसी मीनार के शीर्ष का उन्नयन कोण दो बिन्दुओं पर जो मीनार के पाद से क्रमशः s एवं t मात्रक की दूरी पर हैं, एक दूसरे के पूरक हैं तो सिद्ध कीजिए कि मीनार की ऊँचाई √st है।
हल :
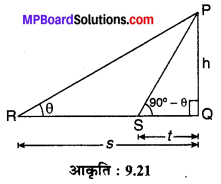
जैसा कि संलग्न आकृति 9.21 में दिखाया गया है। मान लीजिए मीनार PQ = h मात्रक ऊँची है। RQ = s एवं SQ = t है तथा ∠PRQ = θ एवं ∠PSQ = (90° – θ) है। समकोण ∆PRQ में,
\(\frac { PQ }{ RQ }\) = tan PRQ
\(\frac { h }{ s }\) = tanθ …..(1)
समकोण ∆PSQ में,
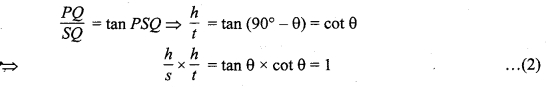
h² = st
h = √st
अतः, मीनार की अभीष्ट ऊँचाई = √st है।
इति सिद्धम्
प्रश्न 3.
एक सड़क के ऊर्ध्वाधरतः स्थित एक गुब्बारे से एक ही दिशा में दो कारों के अवनमन कोण क्रमशः 45° एवं 60° पाये जाते हैं। यदि कारों के बीच की दूरी 100 m हो तो गुब्बारे की ऊँचाई ज्ञात कीजिए।
हल :
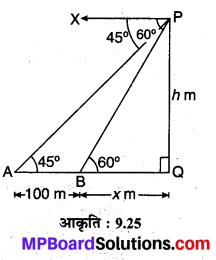
मान लीजिए गुब्बारे P की सड़क से ऊर्ध्वाधर ऊँचाई PQ = h m है तथा सड़क पर दो कारें A एवं B एक-दूसरे से AB = 100 m की दूरी पर हैं। P से A का अवनमन कोण ∠XPA = 45° एवं B का अवनमन कोण ∠XPB = 60° है। पुनः मान लीजिए कि BQ = x m तो चित्रानुसार ∠PAQ = ∠XPA = 45° (एकान्तर कोण हैं) एवं ∠PBQ = ∠XPB = 60° (एकान्तर कोण हैं)। समकोण त्रिभुज PQA में,
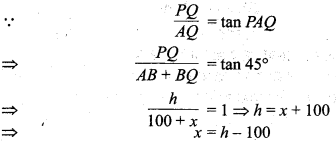
एवं समकोण ∆PQB में,
\(\frac { PQ }{ BQ }\) = tan PBQ
⇒ \(\frac { h }{ x }\) = tan 60° = √3 .
⇒ h = x√3 …(2)
⇒ h = (h – 100) √3 समीकरण (1) एवं (2) से]
⇒ h = h√3 – 100√3
⇒ (h√3 – h) = 100√3
⇒ h (√3 – 1) = 100√3
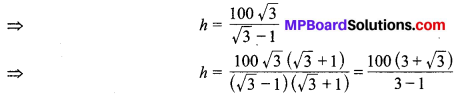
⇒ h = 50 (3 + √3) m
अतः, गुब्बारे की अभीष्ट ऊँचाई = 50 (3 + √3) m है।
प्रश्न 4.
एक हवाई जहाज भूतल से ऊपर 300 मीटर की ऊँचाई पर उड़ रहा है। इस ऊँचाई पर उड़ते हुए हवाई जहाज से एक नदी के दोनों किनारों पर परस्पर विपरीत दिशाओं में स्थित दो बिन्दुओं के अवनमन कोण क्रमशः 45° तथा 60° हैं। नदी की चौड़ाई ज्ञात कीजिए। [√3 = 1.732 का प्रयोग कीजिए।]
हल :
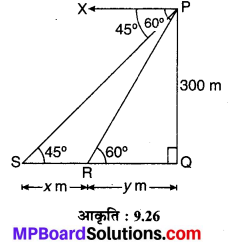
PQ = 300 m की ऊँचाई पर उड़ रहे हवाई जहाज से नदी के किनारे पर स्थित बिन्दुओं R एवं S के अवनमन कोण ∠XPR = 60° एवं ∠XPS = 45° है। ∠PRQ = ∠XPR = 60° एवं ∠PSQ = ∠XPS = 45° मान लीजिए कि SR = x m एवं RQ = y m हैं समकोण ∆PQS में,
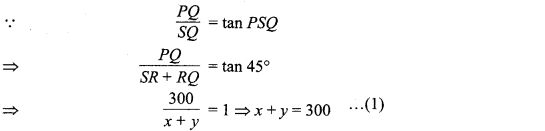
एवं समकोण ∆PQR में,
\(\frac { PQ }{ RQ }\) = tan PRQ
\(\frac { 300 }{ y }\) = tan 60° = √3
y = \(\frac{300}{\sqrt{3}}\) = 100√3 = 100 x 1.732 = 173.2 m …(2)
x + 173.2 = 300 [समीकरण (1) एवं (2) से]
x = 300 – 173.2
= 126.8 m
अतः, नदी की अभीष्ट चौड़ाई = 126.8 m है।
![]()
प्रश्न 5.
एक मीनार के पाद से गुजरने वाली सीधी रेखा पर पाद से क्रमशः 4 m तथा 16 m की दूरियों पर स्थित दो बिन्दु C और D स्थित हैं। यदि C और D से मीनार के शिखर के उन्नयन कोण एक-दूसरे के पूरक हों, तो मीनार की ऊँचाई ज्ञात कीजिए।
हल :
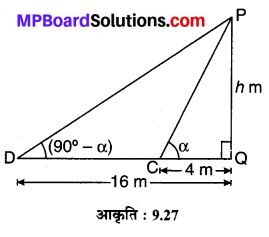
मान लीजिए एक मीनार PQ = h m ऊँची है जिसके पाद Q से बिन्दुओं C एवं D की दूरियाँ क्रमशः QC = 4 m एवं QD = 16 m हैं तथा ∠PCQ = α° एवं ∠PDQ = (90 – α)° है। अब समकोण ∆PQC में,
\(\frac { PQ }{ QC }\) = tan PCQ ⇒ \(\frac { h }{ 4 }\) = tan a …(1)
एवं समकोण ∆PQD में,
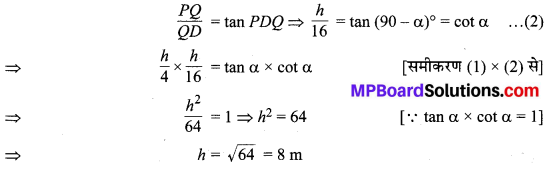
अतः, मीनार की अभीष्ट ऊँचाई = 8 m है।
प्रश्न 6.
भूमि के एक बिन्दु Xसे एक ऊर्ध्वाधर मीनार PQ के शिखर Q का उन्नयन कोण 60° है। एक अन्य बिन्दु Y जो X से 40 m ऊर्ध्वाधर रूप में ऊँचा है, से शिखर Q का उन्नयन कोण 450
है। मीनार PQ की ऊँचाई तथा दूरी PX ज्ञात कीजिए। (√3 = 1.73 लीजिए)
हल :
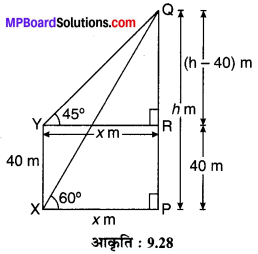
मान लीजिए PQ = h m ऊँची मीनार के पास P से PX = x m की दूरी पर स्थित बिन्दु के ऊर्ध्वाधरतः XY = 40 m ऊपर बिन्दु Y है। X एवं Y पर मीनार के शिखर Q के उन्नयन कोण ∠QXP = 60° और ∠QYR = 45° दिए हैं।
चित्रानुसार,
YR = PX = x m
PR = XY = 40 m
⇒ QR = PQ – PR = (h – 40)
समकोण त्रिभुज ∆ORY में,
\(\frac { QR }{ YR }\) = tan QYR ⇒ \(\frac { h-40 }{ x }\) = tan 45°
h – 40 = x tan 45° = x ⇒ h = x + 40 …(1)
समकोण ∆QPX में,
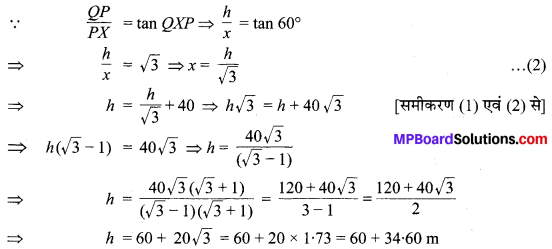
अतः, मीनार की अभीष्ट ऊँचाई = 94.60 m है।
प्रश्न 7.
एक व्यक्ति एक जलयान के डैक जो पानी के स्तर से 10 m ऊँचा है, से एक पहाड़ी के शिखर का उन्नयन कोण 60° तथा पहाड़ी के तल का अवनमन कोण 30° पाता है। पहाड़ी से जलयान की दूरी तथा पहाड़ी की ऊँचाई ज्ञात कीजिए।
हल :
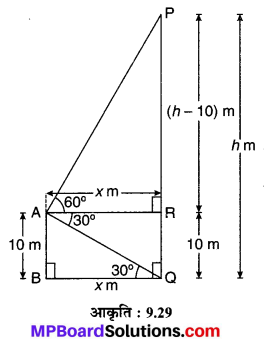
मान लीजिए PQ = h m ऊँची एक पहाड़ी से QB = x m की दूरी पर स्थित AB = 10 m ऊँचा जलयान का डैक है जिससे पहाड़ी के शिखर P का उन्नयन कोण ∠PAR = 60° एवं पहाड़ी के तल Q का अवनमन कोण RAQ = 30° है।
RQ = AB = 10 m
एवं AR = QB = x m
तथा PR = PQ – RQ = (h – 10) m
अब समकोण ∆ARO में,
\(\frac { RQ }{ AR }\) = tanRAQ
\(\frac { 10 }{ x }\) = tan 30° = \(\frac{1}{\sqrt{3}}\)
x = 10√3 …(1)
एवं समकोण ∆PRA में,
\(\frac { PR }{ AR }\) = tan PAR ⇒ \(\frac { h-10 }{ x }\) = tan 60° = √3
(h – 10) = x√3 …(2)
h – 10 = 10 √3 x 3 [समीकरण (1) एवं (2) से]
h = 30 + 10 = 40 m
अतः, पहाड़ी से जलयान की अभीष्ट दूरी = 10√3 m तथा पहाड़ी की ऊँचाई = 40 m है।
प्रश्न 8.
एक झील में पानी के तल से 20 m ऊँचे बिन्दु A से, एक बादल का उन्नयन कोण 30° है। झील में बादल के प्रतिबिम्ब का A से अवनमन कोण 60° है। A से बादल की दूरी ज्ञात कीजिए।
हल :
मान लीजिए एक बादल पानी के तल BC से PC = h m की ऊँचाई पर स्थित है जिसका प्रतिबिम्ब जल में बिन्दु Q पर बनेगा। इस प्रकार कि CQ = PC = h m (प्रकाश के परावर्तन के नियम से)। जल स्तर से AB = 20 m की ऊँचाई पर बिन्दु A से बादल P का उन्नयन कोण ∠PAD = 30° एवं बादल के प्रतिबिम्ब Q का अवनमन कोण ∠QAD = 60° एवं AD = x m है
⇒ DC = AB = 20 m
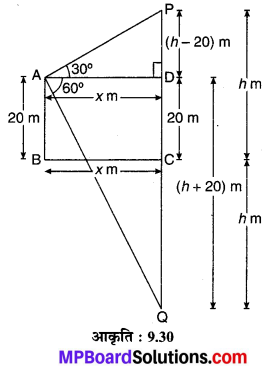
एाव PD = PC – DC = (h – 20) m
तथा QD = CQ + DC = (h + 20) m
अब समकोण ∆PDA में,
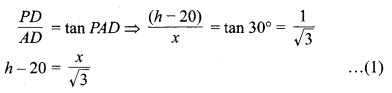
एवं समकोण ∆QDA में,

अब समकोण ∆PDA में,
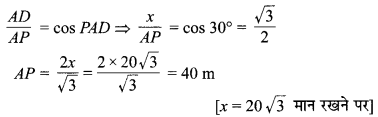
अतः, बादल की बिन्दु A से अभीष्ट दूरी = 40 m है।
प्रश्न 9.
धरातल के एक बिन्दु A से हवाई जहाज का उन्नयन कोण 60° है। 15 सेकण्ड की उड़ान के पश्चात्, उन्नयन कोण 30° का हो जाता है। यदिहवाई जहाज एक निश्चित ऊँचाई 1500√3 m पर उड़ रहा हो, तो हवाई जहाज की गति किलोमीटर/घण्टा ज्ञात कीजिए।
हल :
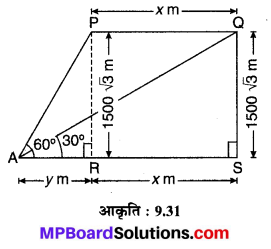
मानलीजिए एक हवाईजहाज PR = 1500 √3 m की ऊँचाई पर बिन्दु P पर स्थित है तथा यह गति करते हुए 15 s में x m की दूरी तय करके बिन्दु Q पर आता है, जहाँ QS ऊँचाई = 1500 √3 m है। R से AR = y m की दूरी पर स्थित बिन्दु A से बिन्दु P का उन्नयन कोण ∠PAR = 60° एवं बिन्दु Q का उन्नयन कोण ∠QAS = 30° है।
RS = PQ = x m
एवं AS = AR + RS = (y + x) m
अब समकोण ∆PRA में,
\(\frac { PR }{ AR }\) = tan PAR ⇒ \(\frac{1500 \sqrt{3}}{y}\) = tan 60° = √3
⇒ y = 1500 m ……(1)
एवं समकोण ∆QAS में,
\(\frac { QS }{ AS }\) = tan QAS
\(\frac{1500 \sqrt{3}}{y+x}\) = tan 30° = \(\frac{1}{\sqrt{3}}\)
y + x = 1500√3 x √3 = 4500 m
1500 + x = 4500
x = 4500 – 1500 = 3000 m
हवाई जहाज द्वारा चली गयी दूरी = 3000m = 3 km
तथा यात्रा में लिया गया समय

चाल = 3 x 240 = 720 k/h
अतः, हवाई जहाज की अभीष्ट चाल = 720 k/h है।
![]()
MP Board Class 10th Maths Chapter 9 लघु उत्तरीय प्रश्न
प्रश्न 1.
सूर्य का उन्नतांश (उन्नयन कोण) ज्ञात कीजिए जबकि h m ऊँचे किसी खम्भे की छाया √3 h m लम्बी है।
हल :
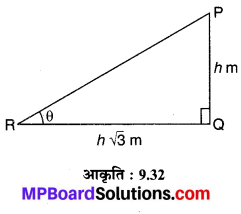
मान लीजिए PQ = h m ऊँचे खम्भे की छाया QR = h√3 m है तथा सूर्य का उन्नतांश (उन्नयन कोण) ∠PRQ = θ है। तो समकोण त्रिभुज PQR में,
\(\frac { PQ }{ QR }\) = tan PRQ
\(\frac { 1 }{ 2 }\) = tanθ
tan θ = \(\frac { 1 }{ 2 }\) = tan 30°
θ = 30°
अतः, सूर्य का अभीष्ट उन्नतांश (उन्नयन कोण) = 30° है।
प्रश्न 2.
एक 15 m लम्बी सीढ़ी एक ऊर्ध्वाधर दीवार के शीर्ष तक ठीक-ठीक पहुँचती है। यदि सीढ़ी 60° का कोण दीवार के साथ बनाती है तो दीवार की ऊँचाई ज्ञात कीजिए।
हल :
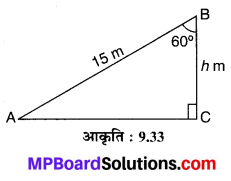
मान लीजिए AB = 15 m लम्बी एक सीढ़ी दीवार के शीर्ष के साथ ∠ABC = 60° का कोण बनाते हुई खड़ी है। दीवार की ऊँचाई BC = h m है। समकोण ∆BCA में,
\(\frac { BC }{ AB }\) = COS ABC
⇒ \(\frac { h }{ 15 }\) = cos 60°= \(\frac { 1 }{ 2 }\)
⇒ h = \(\frac { 15 }{ 2 }\)
= 7.5 m
अतः, दीवार की अभीष्ट ऊँचाई = 7.5 m है।
प्रश्न 3.
1.5 m ऊँचा एक प्रेक्षक एक 22 m ऊँची मीनार से 20.5m की दूरी पर खड़ा है। मीनार के शिखर का उन्नयन कोण प्रेक्षक की आँख से ज्ञात कीजिए।
हल :
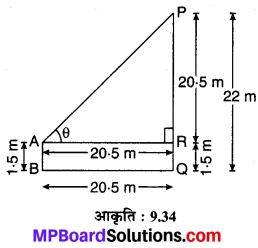
मान लीजिए PQ = 22 m एक मीनार है जिससे AR = BQ = 20.5 m की दूरी पर एक प्रेक्षक AB = 1.5 m ऊँचा खड़ा है। प्रेक्षक की आँख से मीनार के शिखर का उन्नयन कोण ∠PAR = θ°
PR = PQ – RQ
= PQ – AB
= 22 – 1.5
= 20.5 m.
समकोण ∆PRA में,

अतः, अभीष्ट उन्नयन कोण = 45° है।
![]()
प्रश्न 4.
यदि 30 m ऊँची एक मीनार भूमि पर 10√3 m लम्बी छाया बनाती है, तो सूर्य का उन्नयन कोण क्या है?
हल :
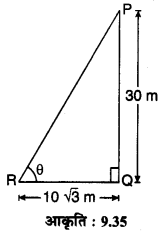
मान लीजिए PQ = 30 m ऊँची मीनार की छाया भूमि पर RQ = 10√3 m है तथा सूर्य का उन्नयन कोण ∠PRQ = θ है तो समकोण ∆PQR में,
tanθ = \(\frac{P Q}{R Q}=\frac{30}{10 \sqrt{3}}\) = √3
⇒ tanθ = tan 60°
⇒ θ = 60°
अतः, सूर्य का अभीष्ट उन्नयन कोण = 60° है।
प्रश्न 5.
एक दीवार के साथ लगी सीढ़ी क्षैतिज के साथ 60° का कोण बनाती है। यदि सीढ़ी का पाद दीवार से 2.5m की दूरी पर है तो सीढ़ी की लम्बाई ज्ञात कीजिए।
हल :
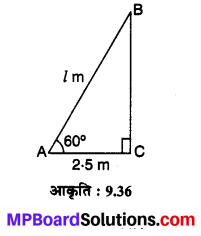
मान लीजिए AB = l m लम्बी एक सीढ़ी क्षैतिज के साथ ∠BAC = 60° का कोण बनाती है तथा बिन्दु A दीवार से AC = 2.5 m की दूरी पर है तो समकोण ∆ACB में,
cos BAC = \(\frac { AC }{ AB }\)
⇒ cos 60°= \(\frac{2 \cdot 5}{l}=\frac{1}{2}\)
⇒ l = 2 x 2.5 = 5m
अतः, सीढ़ी की अभीष्ट लम्बाई = 5 m है।
प्रश्न 6.
संलग्न आकृति 9.37 में एक मीनार AB की ऊँचाई 20 m है और इसकी भूमि पर परछाईं BC की लम्बाई 20√3 है। सूर्य का उन्नतांश ज्ञात कीजिए।
हल :
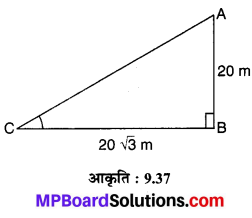
मान लीजिए AB = 20 m ऊँची मीनार की परछाई BC = 20√3 m है तथा सूर्य का उन्नातांश θ° है तो समकोण ∆ABC में,
tan ACB = \(\frac { AB }{ BC }\)
⇒ tan θ = \(\frac{20}{20 \sqrt{3}}=\frac{1}{\sqrt{3}}\)
⇒ tan θ = tan 30°
⇒ θ = 30°
अतः, सूर्य का अभीष्ट उन्नतांश = 30° है।
MP Board Class 10th Maths Chapter 9 अति लघु उत्तरीय प्रश्न
निम्नलिखित प्रश्नों में सत्य/असत्य कथन लिखिए तथा अपने उत्तर का औचित्य दीजिए।
प्रश्न 1.
एक मीनार की छाया की लम्बाई बढ़ने के साथ-साथ ही सूर्य का उन्नतांश भी बढ़ता जाता है।
हल :
कथन असत्य है, क्योंकि उन्नतांश बढ़ने पर छाया की लम्बाई घटती है।
प्रश्न 2.
एक मनुष्य एक झील के तल से 3 m ऊँचे प्लेटफार्म पर खड़ा एक बादल एवं उसके प्रतिबिम्ब का प्रेक्षण करता है तब वह देखता है कि बादल का उन्नयन कोण उसके प्रतिबिम्ब के अवनमन
कोण के बराबर है।
हल:
कथन असत्य है, क्योंकि प्रतिबिम्ब का अवनमन कोण बादल के उन्नयन कोण से अधिक होगा।
![]()
प्रश्न 3.
किसी मीनार के शीर्ष का उन्नयन कोण 30° है। यदि मीनार की ऊँचाई दूनी कर दी जाए तो इसके शीर्ष का उन्नयन कोण भी दूना हो जायेगा।
हल :
कथन असत्य है, क्योंकि उन्नयन कोण मीनार की ऊँचाई से तीन गुना करने पर दूना होगा।
प्रश्न 4.
किसी मीनार की ऊँचाई और इसके प्रेक्षक बिन्दु की दूरी में 10% वृद्धि कर दी जाए तो उन्नयन कोण समान रहेगा।
हल :
कथन सत्य है, क्योंकि दोनों भुजाओं का अनुपात समान रहने पर tanθ का मान और इसलिए कोण θ का मान वही रहेगा।
MP Board Class 10th Maths Chapter 9 वस्तुनिष्ठ प्रश्न
MP Board Class 10th Maths Chapter 9 बहु-विकल्पीय प्रश्न
प्रश्न 1.
यदि धूप में खड़े एक व्यक्ति की छाया उसकी ऊँचाई की √3 गुना हो, तो उस समय सूर्य का उन्नयन कोण होगा :
(a) 30°
(b) 45°
(c) 60°
(d) 75°
उत्तर:
(a) 30°
प्रश्न 2.
एक पेड़ की छाया 20√3 मीटर है। यदि पेड़ की ऊँचाई 20 मीटर हो, तो सूर्य का उन्नयन कोण होगा:
(a) 30°
(b) 45°
(c) 60°
(d) 75°
उत्तर:
(a) 30°
प्रश्न 3.
एक व्यक्ति किसी बिजली के खम्भे के शिखर से देखता है कि धरातल के एक बिन्दु का अवनमन कोण 60° है। यदि खम्भे के पाद से बिन्दु की दूरी 25 मीटर हो, तो खम्भे की ऊँचाई होगी :
(a) 25 मीटर
(b) 25√2 मीटर
(c) 25√3 मीटर
(d) 1 मीटर।
उत्तर:
(c) 25√3 मीटर
प्रश्न 4.
पुल पर बैठा एक व्यक्ति नदी में एक नाव देखता है, जिसका अवनमन कोण 45° है। यदि पुल की ऊँचाई 15 मीटर हो, तो नाव की पुल से दूरी होगी :
(a) 10 मीटर
(b) 15 मीटर
(c) 25 मीटर
(d) 5 मीटर।
उत्तर:
(b) 15 मीटर
![]()
प्रश्न 5.
पेड़ की छाया, उसकी ऊँचाई के बराबर है। सूर्य का उन्नतांश (उन्नयन) कोण होगा :
अथवा
यदि मीनार की ऊँचाई एवं छाया की लम्बाई समान हो, तो सूर्य के उन्नयन कोण का मान होगा :
(a) 30°
(b) 60°
(c) 90°
(d) 45.
उत्तर:
(d) 45.
प्रश्न 6.
एक भवन के पाद से 30 मीटर की दूरी से भवन के शिखर का उन्नयन कोण 45° है। भवन की ऊँचाई है:
(a) 25 मीटर
(b) 30 मीटर
(c) 25√2 मीटर
(d) 30√2 मीटर।
उत्तर:
(b) 30 मीटर
प्रश्न 7.
एक 6 m ऊँचे खम्भे की छाया 2√3 m लम्बी है तो सूर्य का उन्नतांश होगा :
(a) 60°
(b) 45°
(c) 30°
(d) 90°.
उत्तर:
(a) 60°
रिक्त स्थानों की पूर्ति
1. नीचे खड़े रहकर ऊपर की ओर देखने के लिए दृष्टि रेखा को क्षैतिज से जितना ऊपर की ओर घुमाना पड़ता है, वह कोण ……….. कहलाता है।
2. ऊपर के किसी बिन्दु से नीचे के किसी बिन्दु को देखने के लिए दृष्टि रेखा को क्षैतिज से जितना नीचे की ओर घुमाना पड़ता है, वह कोण ………… कोण कहलाता है।
3. यदि किसी मीनार (पेड़) की ऊँचाई एवं उसकी छाया (की लम्बाई) बराबर (समान) हो, तो उस समय उसका (सूर्य का) उन्नयन कोण ……….. होगा।
4. एक भवन के पास से 25 मीटर की दूरी से भवन के शिखर का उन्नयन कोण 45° है, तो भवन की ऊँचाई …………. होगी।
उत्तर-
1. उन्नयन कोण,
2. अवनमन,
3. 45°,
4.25 मीटर।
![]()
सत्य/असत्य कथन
1. क्षैतिज तल से ऊपर की ओर देखने पर दृष्टि रेखा क्षैतिज रेखा के साथ अवनमन कोण बनाती है।
2. वह रेखा जो हमारी आँख से वस्तु को जिसे हम देख रहे हैं, जोड़ती है, दृष्टि रेखा कहलाती है।
3. देखी गई वस्तु का उन्नयन कोण दृष्टि रेखा और क्षैतिज रेखा से बना कोण होता है, जबकि वस्तु को देखने के लिए अपने सिर को नीचे की ओर झुकाना पड़ता है। (2019)
उत्तर-
1. असत्य,
2. सत्य,
3. असत्य।
एक शब्द/वाक्य में उत्तर
1. उस मापक यन्त्र का नाम लिखिए जिसके द्वारा किसी दूरस्थ बिन्दु या ऊँचाई का कोण मापन किया जा सकता है।
2. वह रेखा क्या कहलाती है जो हमारी आँख से सीधे भूमि के समानान्तर जाती है?
3. हमारी आँख से उस वस्तु को जिसे हम देख रहे हैं, जोड़ने वाली रेखा क्या कहलाती है?
4. जब वस्तु आँख की क्षैतिज रेखा से ऊपर हो, तो उसे देखने के प्रक्रम में हमारी दृष्टि रेखा जिस कोण से ऊपर को मुड़ जाती है, उस कोण को क्या कहते हैं?
5. जब वस्तु आँख की क्षैतिज रेखा से नीचे हो, तो उसे देखने के प्रक्रम में हमारी दृष्टि रेखा जिस कोण से नीचे की ओर मुड़ जाती है, उस कोण को क्या कहते हैं?
6. एक वृक्ष की ऊँचाई एवं उसकी छाया बराबर हो, तो उस समय सूर्य का उन्नयन कोण कितना होगा?
उत्तर-
1. षष्टक,
2. क्षैतिज रेखा,
3. दृष्टि रेखा,
4. उन्नत (उन्नयन) कोण,
5. अवनत (अवनमन) कोण,
6. 45°