In this article, we will share MP Board Class 10th Maths Book Solutions Chapter 6 त्रिभुज Ex 6.4 Pdf, These solutions are solved subject experts from the latest edition books.
MP Board Class 10th Maths Solutions Chapter 6 त्रिभुज Ex 6.4
प्रश्न 1.
मान लीजिए ∆ABC ~ ∆DEF और इनके क्षेत्रफल क्रमश: 64 cm और 121 cm हैं। यदि EF = 15.4 cm हो, तो BC ज्ञात कीजिए।
हल :
चूँकि ∆ABC ~ ∆DEF [दिया है]

अतः BC का अभीष्ट मान = 11.2 cm.
प्रश्न 2.
एक समलम्ब ABCD जिसमें AB || DC है के विकर्ण परस्पर बिन्दु O पर प्रतिच्छेद करते हैं। यदि AB = 2CD हो, तो त्रिभुजों AOB और COD के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
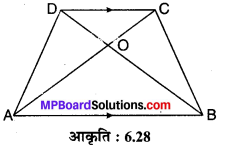
∆AOB और ∆COD में,
∵LOAB = ZOCD (एकान्तर कोण हैं)
[यहाँ AB || DC, AC तिर्यक रेखा]
∵ LOBA = ZODC (एकान्तर कोण हैं)
[यहाँ AB || DC, DB तिर्यक रेखा]
∆AOB ~ ∆COD [AA समरूपता]
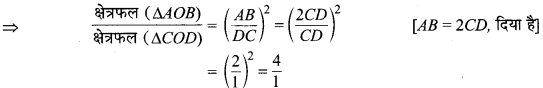
अतः क्षेत्र. (∆AOB) : क्षेत्र. (∆COD) = 4 : 1.
प्रश्न 3.
संलग्न आकृति 6.29 में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं। यदि AD, BC को O पर प्रतिच्छेद करे, तो दर्शाइए कि \(\frac { ar(ABC) }{ ar(DBC) } =\frac { AO }{ DO } \) हैं।
हल :
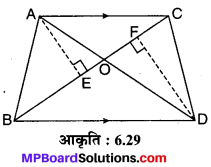
दिया है : एक ही आधार BC पर दो ∆ABC एवं ∆DBC और AD, BC को बिन्दु O पर प्रतिच्छेद करती है।
रचना : AE ⊥ BC एवं DF ⊥ BC खींचिए।
अब ∆AEO और ∆DFO में,
चूँकि ∠AEO = ∠DFO = 90° [∵ AE ⊥ BC एवं DF ⊥ BC]
∠AOE = ∠DOF [शीर्षाभिमुख कोण हैं]
∆AEO ~ ∆DFO [AA समरूपता]
\(\frac{A E}{D F}=\frac{A O}{D O}\) [समरूप त्रिभुजों के प्रगुण]
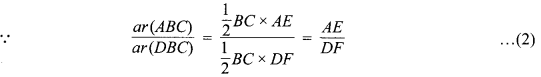
[∵ त्रिभुज का क्षेत्रफल = \(\frac { 1 }{ 2 }\) x आधार x शीर्षलम्ब]
\(\frac { ar(ABC) }{ ar(DBC) } =\frac { AO }{ DO } \) [समीकरण (1) एवं (2) से]
इति सिद्धम्
![]()
प्रश्न 4.
यदि दो समरूप त्रिभुजों के क्षेत्रफल समान हों, तो सिद्ध कीजिए कि वे त्रिभुज सर्वांगसम होते हैं।
हल :
मान लीजिए
∆ABC ~ ∆PQR
![]()
लेकिन
ar(ABC) = ar(PQR) = x वर्ग मात्रक।
![]()
(AB)² = (PQ)², (BC)² = (QR)² एवं (CA)² = (RP)²
AB = PQ, BC = QR एवं CA = RP …(1)
अब ∆ABC और ∆PQR में,
∵ AB = PQ, BC = QR एवं CA = RP [समीकरण (1) से]
∆ABC ≅ ∆PQR. [SSS सर्वांगसमता]
इति सिद्धम्
प्रश्न 5.
एक त्रिभुज ABC की भुजाओं AB, BC एवं CA के मध्य-बिन्दु क्रमश: D, E एवं F हैं। ∆DEF और ∆ABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
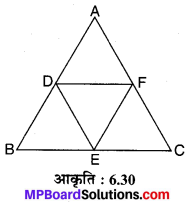
दिया है : ∆ABC की भुजाओं AB, BC एवं CA के क्रमशः मध्य-बिन्दुओं D, E एवं F को मिलाने से ∆DEF बना है (देखिए संलग्न आकृति 6.30 में)
चूँकि किसी त्रिभुज की दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के आधा होता है।
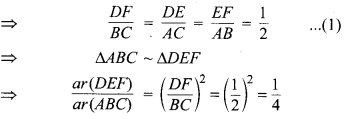
ar(DEF) : ar(ABC) = 1 : 4.
अत: ∆DEF एवं ∆ABC के क्षेत्रफलों का अभीष्ट अनुपात 1 : 4 है।
प्रश्न 6.
सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है।
हल :
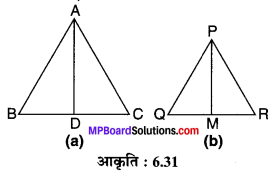
मान लीजिए कि दो समरूप ∆ABC ~ ∆PQR हैं, जिनकी संगत माध्यिकाएँ AD एवं PM हैं। (देखिए आकृति 6.31)
चूँकि ∆ABC ~ ∆PQR दिया है।
∠A = ∠P, ∠B = ∠Q
एवं ∠C = ∠R …(1)
एवं \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{C A}{R P}\) …(2)
[समरूप त्रिभुजों के प्रगुण]
∵ \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{2 B D}{2 Q M}=\frac{B D}{Q M}\) ….(3)
[D, BC का एवं M, QR का मध्य-बिन्दु है]
अब ∆ABD एवं ∆PQM में,
∠B = ∠Q [समीकरण (1) से]

अतः दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है।
इति सिद्धम्
![]()
प्रश्न 7.
सिद्ध कीजिए कि किसी वर्ग की किसी भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के एक विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
हल :
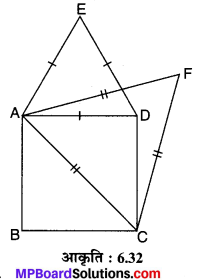
मान लीजिए ABCD एक वर्ग है। जिसका एक विकर्ण AC है। वर्ग की भुजा AD पर समबाहु ∆EAD एवं उसके विकर्ण AC पर समबाहु ∆FAC बने हैं।
चूँकि दो समबाहु त्रिभुज सदैव समरूप होते हैं।
∆EAD ~ ∆FAC

अतः किसी वर्ग की भुजा पर बने समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के विकर्ण पर बने समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
इति सिद्धम्
प्रश्न 8.
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिन्दु है। त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है :
(a) 2:1
(b) 1:2
(c) 4:1
(d) 1:4.
सही उत्तर चुनिए और अपने उत्तर का औचित्य दीजिए।
हल :
सही विकल्प (c) 4 : 1 है, क्योंकि ∆ABC ~ ∆BDE क्योंकि समबाहु त्रिभुज समरूप होते हैं एवं
![]()
यहाँ AB = 2BD क्योंकि D, AB का मध्य-बिन्दु है।
प्रश्न 9.
दो समरूप त्रिभुजों की भुजाएँ 4:9 के अनुपात में हैं। इन त्रिभुजों के क्षेत्रफलों का अनुपात है :
(a) 2:3
(b) 4:9
(c) 81:16
(d) 16:81
सही विकल्प चुनिए तथा अपने उत्तर का औचित्य दीजिए।
हल :
सही विकल्प (d) 16 : 81 है, क्योंकि समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के अनुपात का वर्ग होता है। अत: 4 : 9 का वर्ग अनुपात 16 : 81 है।
![]()