Bhagya

MP Board Class 8th Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.2

Question 1.
Find the product of the following pairs of monomials.
(i) 4, 7p
(ii) -4p, 7p
(iii) -4p, 7pq
(iv) 4p³, -3p
(v) 4p, 0
Solution:
(i) 4 × 7p = 28p
(ii) -4p × 7p = -28p
(iii) -4p × 7pq = -28p
(iv) 4p³ × -3p = -12p⁴
(v) 4p × 0 = 0

Question 2.
Find the areas of rectangles with the following pairs of monomials as their lengths and breadths respectively.
(p, q); d (10m, 5n); (20x², 5y²); (4x, 3x²); (3mn, 4np)
Solution:

Question 3.
Complete the table of products.

Solution:

Question 4.
Obtain the volume of rectangular boxes with the following length, breadth and height respectively.
(i) 5a, 3a², 7a⁴
(ii) 2p, 4q, 8r
(iii) xy, 2x²y, 2xy²
(iv) a, 2b, 3c
Solution:

Question 5.
Obtain the product of
(i) xy, yz, zx
(ii) a, -a², a²
(iii) 2, 4y, 8y², 16y³
(iv) a, 2b, 3c. 6abc
(v) m, – mn, mnp
Solution:
(i) xy × yz × zx = x²y²z²
(ii) a × (-a²) × a³ = – a⁶
(iii) 2 × ⁴y × 8y² × 16y³ = 1024y⁶
(iv) a × 2b × 3c × 6abc = 36a²b²c²
(v) m × (- mn) × mnp = – m³n²p

MP Board Class 8th Maths Solutions

MP Board Class 11th Maths Solutions Chapter 5 सम्मिश्र संख्याएँ और द्विघातीय समीकरण Ex 5.2

प्रश्न 1 से 2 तक सम्मिश्र संख्याओं में प्रत्येक का मापांक और कोणांक ज्ञात कीजिए :
प्रश्न 1.
z = -1 – i\( \sqrt{{3}} \).
हल:
मान लीजिए : = – 1 – i\( \sqrt{{3}} \) = r(cos θ + i sin θ)
अर्थात् r cos θ = -1, r sin θ = – \( \sqrt{{3}} \)
वर्ग करके जोड़ने पर, r² = 1 + 3 = 4 या r = 2
z का मापांक = 2
अब cosθ = \(-\frac{1}{2}\) = – cos \(\frac{\pi}{3}\)

प्रश्न 2.
–\( \sqrt{{3}} \) + i
हल:
मान लीजिए x = –\( \sqrt{{3}} \) + i = r (cos θ + i sin θ)
D r cos θ = –\( \sqrt{{3}} \), r sin θ = 1
वर्ग करके जोड़ने पर,
r²(cos²θ + sin²θ) = 3 + 1 = 4 ,
∴ r² = 4 या r = 2

प्रश्न 3 से 8 तक सम्मिश्र संख्याओं में प्रत्येक को ध्रुवीय रूप में रूपांतरित कीजिए :
प्रश्न 3.
1 – i.
हल:
मान लीजिए z = 1 – i = r(cos θ + i sinθ)
∴ r cos θ = 1 तथा rsin θ = -1
वर्ग करके जोड़ने पर,
r² cos² θ + r² sin²θ = 1 + 1 = 2
या r² (cos²θ + sin²θ) = 2
या r² = 2 या r = –\( \sqrt{{2}} \)
अब cos θ धनात्मक है और sin θ ऋणात्मक है।
∴ θ चौथे चतुर्थांश में है।

प्रश्न 4.
-1 + i.
हल:
मान लीजिए z = -1 + i = r(cos θ + isin θ)
⇒ r cosθ = – 1 और r sin θ = 1
इनका वर्ग करके जोड़ने पर,
r²cos²θ + r² sin²θ = 1
या (cos² θ + sin²θ) = 1
r² = 2 या r = \( \sqrt{{2}} \)
यहाँ cos θ ऋणात्मक तथा sin θ धनात्मक है
⇒ θ दूसरे चतुर्थांश में है।

प्रश्न 5.
-1 – i
हल:
मान लीजिए z = – 1 – i = r(cos θ + i sin θ)
∴ rcos θ = – 1, r sin θ = -1
इनका वर्ग करके जोड़ने पर,
∴ r² cos²θ + r² sin² θ = 1 + 1 = 2
या r²(cos² θ + sin²θ) = 2
∴ r² = 2 या r = \( \sqrt{{2}} \)
यहाँ cos θ और sin θ दोनों ही ऋणात्मक हैं।
∴ θ तीसरे चतुर्थांश में है।

प्रश्न 6.
-3.
हल:
मान लीजिए z = – 3 = r (cos θ + sin θ)
∴ r cos θ = – 3, r sin θ = 0
इनका वर्ग करके जोड़ने पर,
∴ r²cos²θ + r² sin² θ = 9
r² (cos²θ + sin² θ) = r² = 9 या r = 3
अब \(\frac{r \sin \theta}{r \cos \theta}=\frac{0}{-3}=0\) परन्तु r cos θ ऋणात्मक है।
∴ θ = π
∴ z का ध्रुवीय रूप = 3(cos π + i sin π).

प्रश्न 7.
\( \sqrt{{3}} \) + i.
हल:
मान लीजिए z = \( \sqrt{{3}} \) + i = r(cos θ + i sin θ)
∴ rcos θ = \( \sqrt{{3}} \), r sin θ = 1
वर्ग करके जोड़ने पर,
r² cos² θ + r² sin² θ = 3 + 1 = 4
या r²(cos² θ + sin² θ) = 4
r² = 4 या r = 2
∴ cos² = \(\frac{\sqrt{3}}{2}\) और sin θ = \(\frac{1}{2}\)
sin θ और cos θ दोनों ही धनात्मक है।
∴ θ पहले चतुर्थांश में है।

प्रश्न 8.
i.
हल:
मान लीजिए z = i = r(cos θ + i sin θ)
⇒ r cos θ = 0 और r sin θ = 1
वर्ग करके जोड़ने पर,
r²cos²θ + r² sin²θ = 0 + 1
या r²(sin²θ + cos²θ) = 1 .
या r² = 1 या r = 1

MP Board Class 11th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.1

Question 1.
Identify the terms, their coefficients for each of the following expressions.
(i) 5xyz² – 3zy
(ii) 1 + x + x²
(iii) 4x²y² – 4x²y²z² + z2
(iv) 3 – pq + qr – rp
(v) \(\frac{x}{2}+\frac{y}{2}-x y\)
(vi) 0.3a – 0.6ab + 0.5b
Solution:

Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?
x + y, 1000, x + x² + x³ + x⁴, 7 + y + 5x, 2y – 3y², 2y – 3y² + 4y³, 5x – 4y + 3xy, 4z – 15z², ab + bc + cd + da, pqr, p²q, 9a², 2p + 2q
Solution:

Question 3.
Add the following:
(i) ab – bc, bc – ca, ca – ab
(ii) a – b + ab, b – c + bc, c – a + ac
(iii) 2p²q² – 3pq + 4, 5 + 7pq – 3p²q²
(iv) l² + m², m² + n², n² + l², 2lm + 2mn + 2nl
Solution:

Question 4.
(a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
(b) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
(c) Subtract 4p²q – 3pq + 5pq² – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq² + 5p²q
Solution:

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 12 Exponents and Powers Ex 12.2

Question 1.
Express the following numbers in standard form.
(i) 0.0000000000085
(ii) 0.00000000000942
(iii) 6020000000000000
(iv) 0.00000000837
(v) 31860000000
Solution:
(i) 0.0000000000085 = 8.5 × 10^-12
(ii) 0.00000000000942 = 9.42 × 10^-12
(iii) 6020000000000000 = 6.02 × 10¹⁵
(iv) 0.00000000837 = 8.37 × 10^-9
(v) 31860000000 = 3.186 × 10¹⁰

Question 2.
Express the following numbers in usual form.
(i) 3.02 × 10^-6
(ii) 4.5 × 10⁴
(iii) 3 × 10^-8
(iv) 1.0001 × 10⁹
(v) 5.8 × 10¹²
(vi) 3.61492 × 10⁶
Solution:
(i) We have, 3.02 × 10^-6 = 0.00000302
(ii) We have, 4.5 × 10⁴ = 45000
(iii) We have, 3 × 10^-8 = 0.00000003
(iv) We have, 1.0001 × 10⁹ = 1000100000
(v) We have, 5.8 × 10¹² = 5800000000000
(vi) We have, 3.61492 × 10⁶ = 3614920

Question 3.
Express the number appearing in the following statements in standard form.
(i) 1 micron is equal to \(\frac{1}{1000000}\) m.
(ii) Charge of an electron is 0. 000,000,000,000,000,000,16 coulomb.
(iii) Size of a bacteria is 0.0000005 m.
(iv) Size of a plant cell is 0.00001275 m.
(v) Thickness of a thick paper is 0.07 mm.
Solution:
(i) Standard form of given statement = 1 × 10^-8.
(ii) Standard form of given statement = 1.6 × 10^-19.
(iii) Standard form of given statement = 5 × 10^-7.
(iv) Standard form of given statement = 1.275 × 10^-5.
(v) Standard form of given statement = 7 × 10^-2.

Question 4.
In a stack there are 5 books each of thickness 20 mm and 5 paper sheets each of thickness 0.016 mm. What is the total thickness of the stack.
Solution:
Total number of books = 5
Thickness of each book = 20 mm
∴ Thickness of 5 books = (5 × 20) mm = 100 mm
Thickness of each paper sheet = 0.016 mm
∴ Thickness of 5 paper sheets = (5 × 0.016) mm = 0.08 mm
Hence, total thickness of stack = 100 mm + 0.08 mm
= 100.08 mm = 1.0008 × 10² mm

MP Board Class 8th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 12 Exponents and Powers Ex 12.1

Question 1.
Evaluate
(i) 3^-2
(ii) (-4)^-2
(iii) \(\)
Solution:

Question 2.
Simplify and express the result in power notation with positive exponent.

Solution:

Question 3.
Find the value of
(i) (3⁰ + 4^-1) × 2²
(ii) (2^-1 × 4^-1) ÷ 2^-2
(iii) \(\left(\frac{1}{2}\right)^{-2}+\left(\frac{1}{3}\right)^{-2}+\left(\frac{1}{4}\right)^{-2}\)

Solution:

Question 4.
Evaluate

Solution:

Question 5.
Find the value of m for which 5^m ÷ 5^-3 = 5⁵.
Solution:
We have, 5^m ÷ 5^-3 = 5⁵
⇒ 5^m-(-3) = 5⁵ [∵ a^m + aⁿ =a^{m + n}]
⇒ 5^{m + 3} = 5⁵
⇒ m + 3 = 5 [∵ a^m = aⁿ ⇒ m = n]
⇒ m = 5 – 3 = 2

Question 6.
Evaluate

Solution:

Question 7.
Simplify.

Solution:

MP Board Class 8th Maths Solutions

MP Board Class 10th General Hindi अपठित अनुच्छेद

परीक्षा में अपठित गद्यांश का प्रश्न अनिवार्य रूप से पूछा जाता है। ऐसे प्रश्न पूछने का उद्देश्य यह जानना है कि विद्यार्थी किसी गद्यांश को पढ़कर उसमें निहित भावों को समझकर अपने शब्दों में लिख सकते हैं या नहीं। अपठित गद्यांश वे होते हैं, जिन्हें विद्यार्थी अपनी पाठ्यपुस्तकों में नहीं पढ़ते। अपठित गद्यांश के प्रश्न को हल करते समय निम्नलिखित बातों को ध्यान में रखना चाहिए:

1. गद्यांश को समझने के लिए यह आवश्यक है कि आप उसका वाचन कम-से-कम दो बार करें। यदि दो बार में भी गद्यांश का मूलभाव समझ में नहीं आता तो एक बार और उसे पढ़ें।
2. अपठित गद्यांश पर दो प्रश्न तो अनिवार्य रूप से पूछे ही जाते हैं-एक तो अपठित का सारांश और दूसरा उसका शीर्षक।
3. दो या तीन बार पढ़ने से अपठित का मूल भाव आपकी समझ में आ जाएगा। पहले उत्तर पुस्तिका के एक पृष्ठ पर उसका सारांश लिखिए। यह ध्यान रखिए कि कोई मूल भाव छूटने न पाए।
4. सारांश की भाषा आपकी अपनी हो, गद्यांश की भाषा का प्रयोग न करें। 5. सारांश मूल अंश का एक-तिहाई होना चाहिए।
5. सारांश में न तो आप अपनी तरफ से कोई बात जोड़ें और न कोई उदाहरण, किसी महापुरुष का कथन या किसी कवि की कोई उक्ति ही उद्धृत करें।
6. गद्यांश का शीर्षक गद्यांश के भीतर ही प्रारंभिक पंक्तियों या अंतिम पंक्तियों में रहता है। शीर्षक अत्यंत संक्षिप्त हो। वह गद्यांश के मुख्य भाव को प्रकट करे। मुख्य भाव को प्रकट करनेवाला कोई शीर्षक अपनी ओर से भी दिया जा सकता है।
7. अपठित का सारांश या उसके शीर्षक के अतिरिक्त भी कुछ प्रश्न पूछ जाते हैं। इन प्रश्नों के उत्तर गद्यांश में ही रहते हैं। इन प्रश्नों के उत्तर देते समय यह ध्यान रहे कि इनकी भाषा अपनी रहे। गद्यांश की भाषा में उत्तर देना ठीक नहीं। यहाँ अपठित गद्यांश के कुछ उदाहरण हल सहित दिए जा रहे हैं। उनके बाद अभ्यासार्थ कुछ अपठित गद्यांश दिए गए हैं।

I. गद्यांश

उदाहरण 1.
यह सच है कि विज्ञान ने मानव के लिए भौतिक सुख का द्वार खोल दिया है, किंतु यह भी उतना ही सच है कि उसने मनुष्य से उसकी मनुष्यता छीन ली है। भौतिक सुखों के लोभ में मनुष्य यंत्र की भाँति क्रियारत है, उसकी मानवीय भावनाओं का लोप हो रहा है और वह स्पर्धा के नाम पर ईर्ष्या और द्वेष से ग्रसित होकर स्वजनों का ही गला काट रहा है। इसी का परिणाम है, अशांति। मनुष्यता को दाँव पर हारकर भौतिक सुख की ओर बढ़ना अशुभ है।

प्रश्न-
(क) उपर्युक्त गद्य खण्ड का उपयुक्त शीर्षक लिखिए।
(ख) इस गद्य खण्ड का सारांश लगभग 25 शब्दों में लिखिए।
उत्तर-
(क) शीर्षक-विज्ञान : एक अभिशाप।
(ख) सारांश-विज्ञान ने मानव को सुख के बहुत-से साधन दिए हैं, किंतु उसके कारण मनुष्य की मनुष्यता भी छिन गई है। आज मनुष्य अपने ही भाइयों का विनाश कर रहा है, इसी के कारण सर्वत्र अशांति फैली है।

उदाहरण 2.
राष्ट्र की उन्नति पर ही व्यक्ति की उन्नति निर्भर है। यदि किसी के घोर संकुचित स्वार्थपूर्ण कामों के कारण राष्ट्रीय हित को क्षति पहुँचती हो अथवा राष्ट्र की निंदा होती हो तो ऐसे कुपुत्र का जन्म लेना निरर्थक है। राष्ट्रभक्त के लिए राष्ट्र का तिनका-तिनका मूल्यवान है। उसे राष्ट्र का कण-कण परम प्रिय है। वह अपने गाँव, नदी, पर्वत तथा मैदान को देख आनंद विभोर हो उठता है। जिसका मन, वाणी और शरीर सदा राष्ट्र-हित के कामों में तत्पर है, जिसे अपने पूर्वजों पर गर्व है, जिसको अपनी संस्कृति पर आस्था है तथा जो अपने देशवासियों को अपना समझता है, वही सच्चा राष्ट्रभक्त है।

प्रश्न-
(क) उपर्युक्त गद्य-खण्ड का उचित शीर्षक लिखिए।
(ख) इस गद्यांश का सारांश लगभग तीस शब्दों में लिखिए।
उत्तर-
(क) शीर्षक-सच्चा राष्ट्रभक्त कौन?
(ख) सारांश-एक राष्ट्रभक्त अपने राष्ट्र के तृण-तृण का आदर करता है। वह राष्ट्र की एक-एक वस्तु नदी, पर्वत, मैदान को देख आनन्दित होता है। राष्ट्रभक्त अपने पूर्वजों, अपनी संस्कृति पर गर्व करता है और अपने देशवासियों को अपना समझता है।

उदाहरण 3.
परोपकार-कैसा महत्त्वपूर्ण धर्म है। प्राणिपात्र के जीवन का तो यह लक्ष्य होना चाहिए। यदि विचारपूर्वक देखा जाए तो ज्ञात होगा कि प्रकृति के सारे कार्य परोपकार के लिए ही हैं नदियाँ स्वयं अपना पानी नहीं पीतीं। पेड़ स्वयं अपने फल नहीं खाते। गुलाब का फूल अपने लिए सुगन्ध नहीं रखता। वे सब दूसरों के हितार्थ हैं। महात्मा गांधी और अन्य महात्माओं का मत है कि परोपकार ही करना चाहिए, किंतु परोपकार निष्काम हो। यदि परोपकार किसी प्रत्युपकार की आशा से किया जाता है, तो उसका महत्त्व क्षीण हो जाता है।

भारत का प्राचीन इतिहास दया और परोपकार के उदाहरणों से भरा है। राजा शिवि ने कपोल की रक्षा के लिए अपने प्राण देने तक का संकल्प कर लिया था। परोपकार का इससे ज्वलंत उदाहरण और कौन-सा मिल सकता है? चाहे जो हो, परोपकार आदर्श गुण है। हमें परोपकारी बनना चाहिए।

प्रश्न-
(क) इस गद्यांश का मूल भाव बताइए।
(ख) इस गद्यांश का उचित शीर्षक दीजिए।
(ग) प्राणिमात्र के जीवन का लक्ष्य क्या होना चाहिए?
(घ) महात्मा गांधी जैसे महात्माओं ने परोपकार के सम्बन्ध में क्या मत व्यक्त किया है?
(ङ) हमें कैसा बनना चाहिए?
उत्तर-
(क) परोपकार महत्त्वपूर्ण धर्म है। यह प्राणिमात्र के जीवन का परम उद्देश्य होना चाहिए। प्रकृति के सारे कार्य परोपकार के लिए ही हैं। सभी महात्मा जन-जीवन में इसके महत्त्व की आवश्यकता का अनुभव करते हैं। पर यह होना कामना रहित चाहिए। भारत के प्राचीन इतिहास में अनेक उदाहरण देखे जा सकते हैं। अतः हमें यह परोपकार अवश्य करना चाहिए।
(ख) इस गद्यांश का शीर्षक ‘परोपकार’ है।
(ग) प्राणिमात्र के जीवन का एकमात्र उद्देश्य परोपकारी बनना होना चाहिए।
(घ) महात्मा गांधी जैसे महात्माओं ने कहा है कि मानव को परोपकार अवश्य करना चाहिए। परंतु यह निष्काम भावना से सम्पादित होना चाहिए। यदि परोपकार बदले की भावना से किया जाता है, तो उसका महत्त्व क्षीण हो जाता है।
(ङ) हमें परोपकारी बनना चाहिए।

उदाहरण 4.
ऐसा देखा जाता है कि अधिकांश लोग अपने बहुमूल्य समय को व्यर्थ में ही व्यतीत कर देते हैं। परंतु फिर तो वही बात कही जाती है “कि अब पछताए होत क्या जब चिड़िया चुग गई खेत”, आज हम लोग जितना समय व्यर्थ की बातों में नष्ट कर देते हैं, यदि उसके दशमांश का भी सदुपयोग करना सीख जाते तो हम अपने जीवन में असाधारण सफलताएँ प्राप्त कर सकते हैं। प्रत्येक सुंदर समय हमारे लिए वस्तुएँ लेकर आता है, किंतु हम उनसे कोई लाभ नहीं उठाते।

प्रश्न-
(क) उपर्युक्त गद्यांश का एक उचित शीर्षक दीजिए।
(ख) गद्यांश का सारांश अपने शब्दों में लिखिए।
उत्तर-
(क) ‘समय का सदुपयोग’
(ख) समय बीत जाने से पछताने के सिवा और कोई चारा नहीं रहता। मगर इससे कोई लाभ नहीं होता है। समय के सदुपयोग से हम अपने जीवन में असाधारण सफलताओं को प्राप्त कर सकते हैं।

II. पद्यांश

उदाहरण-

रण-बीच चौकड़ी भर-भर कर,
चेतक बन गया निराला था।
राणा प्रताप के घोड़े का,
(पड़ गया हवा से पाला था)
गिरता न कभी चेतक तन पर,
राणा प्रताप का घोड़ा था।
(वह दौड़ रहा अरि मस्तक पर)
या आसमान पर घोड़ा था।

प्रश्न-
(क) पद्यांश का उपयुक्त शीर्षक लिखिए।
(ख) इस पद्यांश का भावार्थ लिखिए।
(ग) कोष्ठांकित शब्दों का अर्थ स्पष्ट कीजिए।
उत्तर-
(क) शीर्षक-‘चेतक’
(ख) महाराणा प्रताप के घोड़े का नाम चेतक था जो बड़ा ही अनोखा था। वह हल्दीघाटी के मैदान में तीव्र गति से दौड़ रहा था। उसे दौड़ाने के लिए कोड़ा न मारना पड़ता था। वह इतना समझदार था कि राणा का संकेत पाते ही मुड़ जाता था और शत्रुओं के मस्तक पर पैर रखता हुआ दौड़ पड़ता था।
(ग) पड़ गया हवा से पाला था-राणा प्रताप के घोड़े की तीव्र गति को देखकर ऐसा प्रतीत होता था मानो वायु भी उसकी गति से हार मान गई है।
वह दौड़ रहा अरि मस्कक पर-राणा प्रताप का घोड़ा निर्भय होकर शत्रुओं के मस्तकों को कुचलता हुआ दौड़ जाता था।

अभ्यास के लिए अपठित गद्यांश

(1) प्रत्येक मनुष्य, चाहे वह स्थिति में कितना ही छोटा हो, ऊपर उठ सकता है। प्रत्येक मनुष्य अपनी शक्तियों का विकास कर सकता है। प्रत्येक मनुष्य अपने लक्ष्य को प्राप्त कर सकता है अथवा उसे बहुत निकट ला सकता है। आवश्यकता इतनी है कि वह भूल जाय कि वह तुच्छ है, पंगु है, कुछ नहीं कर सकता। निराशा का बीज बड़ा घातक होता है। वह जब कलेजे की भूमि में घुस जाता है, तो उसे फोड़कर अपना विस्तार करता है। निराशा से अपने आपको बचाओ। निराशा जीवन के प्रकाश पर दुर्दिन की बदली की तरह छा जाती है। यह आत्मा के स्वर को क्षीण करती है और चेतना के स्थान पर जड़ता, निश्चेष्टता की प्रतिष्ठा करती है।

(क) उपर्युक्त गद्यांश का सारांश लिखिए।
(ख) इस गद्यांश का उचित शीर्षक लिखिए।
(ग) रेखाकित अंशों को स्पष्ट कीजिए।

(2) मस्तिष्क की शक्ति से ही हम गिरते और उठते हैं; बड़े होते और चलते हैं। विचार की तीव्र शक्ति से ही सब काम होते हैं। जो अपने विचारों के स्रोत को नियंत्रित कर सकता है, वह अपने मनोवेग पर भी शासन कर सकता है। ऐसा व्यक्ति. अपने संकल्प से वृद्धावस्था को यौवन में बदल सकता है, रोगी को नीरोग कर सकता है। विचार-शक्ति संसार को चेतना प्रदान करती और चलाती है। शुभ, उन्नत और कल्याणकारी विचारों से मानव-शरीर अधिक सक्षम एवं नीरोग रहता है।

(क) उपर्युक्त गद्यांश का सारांश लिखिए।
(ख) इस गद्यांश का उचित शीर्षक लिखिए।
(ग) रेखांकित अंशों का भाव स्पष्ट कीजिए।

(3) राष्ट्रीय एकता, प्रत्येक स्वतंत्र राष्ट्र के लिए नितांत आवश्यक है। जब भी धार्मिक या जातीय आधार पर राष्ट्र से अलग होने की कोई कोशिश होती है, तब हमारी राष्ट्रीय एकता के खंडित होने का खतरा बढ़ जाता है। यह एक सुनिश्चित सत्य है कि राष्ट्र का स्वरूप निर्धारित करने में वहाँ विकास करने वाले जन एक अनिवार्य तत्त्व होते हैं। राष्ट्र के निवासियों के मन में राष्ट्रहित की दृष्टि से भावनात्मक स्तर पर स्नेह-संबंध, सहिष्णुता, पारस्परिक सहयोग एवं उदार मनोवृत्ति के माध्यम से राष्ट्रीय एकता की अभिव्यक्ति होती है। राष्ट्र को केवल भूखण्ड मानकर उसके प्रति अपने कर्तव्यों से उदासीन होने वाले राष्ट्रीय एकता स्थापित करने में कदापि सहायक नहीं हो सकते। वस्तुतः राष्ट्रीय एकता के आदर्श को व्यवहार में अवतरित करके ही राष्ट्र के निवासी अपने राष्ट्र की उन्नति और प्रगति में सच्चे सहायक सिद्ध हो सकते हैं।

(क) उपर्युक्त गद्यांश का सारांश लगभग 40 शब्दों में लिखिए।
(ख) इस गद्यांश का उचित शीर्षक लिखिए।

(4) आत्मविश्वास श्रेष्ठ जीवन के लिए पहली आवश्यकता है। तन्मयता से आत्मविश्वास का जन्म होता है। संसार का इतिहास उन लोगों की कीर्तिकथाओं से भरा पड़ा है, जिन्होंने अंधकार और विपत्ति की घड़ियों में आत्मविश्वास के प्रकाश में जीवन की यात्रा की और परिस्थितियों से ऊपर उठ गए। उनसे भी अधिक संख्या उन वीरों की है, जिन्हें इतिहास आज भूल गया है पर जिन्होंने मानवता के निर्माण में, उसे उठाने में नींव का काम किया है। केवल आत्म-विश्वास और आशा के बल पर वे जिए और उसी के साथ उच्च उद्देश्य के लिए प्राण समर्पण करने में भी न चूके। जैसे तूफान के समय नाविक के लिए दिग्दर्शक यंत्र का उपयोग है, वैसे ही जीवन-यात्रा में आशा और आत्मविश्वास का महत्त्व है।

(क) उपर्युक्त गद्यांश का सारांश एक-तिहाई भाग में लिखिए।
(ख) इस गद्यांश का उचित शीर्षक दीजिए।

(5) यूरोप और अमेरिका में जिन अनेक नए शास्त्रों की खोज हुई है, उन सबसे हमें बहुत कुछ सीखना है। लेकिन भारत की अपनी भी कुछ विद्याएँ हैं और कुछ शास्त्र यहाँ पर भी प्राचीनकाल से विकसित हैं। वेद भगवान ने हमें आज्ञा दी है-आ नो भद्राः कृतवो यन्तु विश्वतः, अर्थात् दुनिया भर से मंगल विचार हमारे पास आएँ। हम सब विचारों का स्वागत करते हैं और यह नहीं समझते कि यह विचार स्वदेशी है या परदेशी, पुराना है या नया। हम इतना ही सोचते हैं कि वह ठीक है या गलत। जो विचार ठीक है, वह पुराना भी हो तो भी अपनाया जाय। इसमें कोई शक नहीं कि हमको बहुत लेना है। लेकिन जो अपने पास है, उसे भी पहचानना चाहिए। यह इसलिए भी जरूरी है कि जो यहाँ का होता है, वह यहाँ की परिस्थिति और चारित्र्य के लिए अनुकूल होता है। वह हमारे स्वभाव के अनुकूल होने के कारण हमें काफी मदद दे सकता है।

(क) इस अवतरण का सारांश लिखिए।
(ख) गद्यांश के लिए उचित शीर्षक लिखिए।

(6) भारत हम सभी का घर है और हम सभी इस घर के सदस्य हैं। हमें आपस में मिल-जुलकर रहना चाहिए। यदि घर में एकता नहीं होगी तो आपस में कलह और द्वेष बढ़ेगा। जिस घर में फूट हो, उस घर की कोई इज्जत नहीं करता। इतिहास इस बात का साक्षी है कि जब-जब हममें एकता का अभाव हुआ, तब-तब हम पराधीन हो गए। जयचंद के कारण भारत पराधीन हुआ। एकता के अभाव के कारण ही सन् 1857 का स्वतंत्रता का संग्राम असफल हुआ। आपस की फूट के कारण ही सन् 1947 में देश का विभाजन हुआ। स्वतंत्रता प्राप्ति के बाद आज फिर फूट डालने वाली शक्तियाँ सिर उठा रही हैं। यदि हम सभी आपस में संगठित रहेंगे तो कोई भी देश हमारा बाल बाँका नहीं कर सकता। संगठन में बड़ी शक्ति होती है। पानी की एक-एक बूंद से बड़ी नदी बन जाती है। अनेक धागे निकलकर जब रस्सी बनाते हैं तो बड़े-बड़े हाथी भी उससे बाँधे जा सकते हैं। आग की छोटी-छोटी चिनगारियाँ मिलकर महाज्वाला बनती हैं और बड़े-बड़े जंगलों और भवनों को स्वाहा कर डालती हैं।

(क) इस अवतरण का उचित शीर्षक लिखिए।
(ख) गद्यांश का सारांश एक-तिहाई भाग में लिखिए।
(ग) आपस की फूट के कारण क्या हानियाँ होती हैं?

(7) यदि सभी लोग अपने-अपने धर्म का पालन करें तो सभी सुखी और समृद्ध हो सकते हैं, परन्तु आज ऐसा नहीं है। धर्म का स्थान छोटा होने से सुख-समृद्धि गूलर का फूल हो गई है। यदि एक सुखी और संपन्न है तो पचास दुखी और दरिद्र हैं। साधनों की कमी नहीं है, परंतु धर्मबुद्धि के विकसित न होने से उनका उपयोग नहीं हो रहा है। कुछ स्वार्थी प्रकृति के प्राणी तो समाज में सभी कालों में रहे हैं और रहेंगे। परंतु आजकल ऐसी व्यवस्था है कि ऐसे लोगों को अपनी प्रवृत्ति के अनुसार काम करने का खुला अवसर प्राप्त हो जाता है और उनकी सफलता दूसरों को उनका अनुगामी बना देती है। दूसरी ओर जो सचमुच सदाचारी हैं, उनके मार्ग में बड़ी-बड़ी अड़चनें

(क) उपर्युक्त गद्यांश का शीर्षक लिखो।
(ख) दुखी और दरिद्र लोगों की संख्या अधिक क्यों है?
(ग) इस गद्यांश का सारांश 25 शब्दों में लिखिए।

(8) साम्प्रदायिक सद्भाव और सौहार्द्र बनाए रखने के लिए यह आवश्यक है कि हम दूसरे धर्मावलंबियों के विचारों को समझें और उनका सम्मान करें। हमारा ही धर्म सर्वश्रेष्ठ है, इस विचार को मन में जमने दें। हमें यह हमेशा याद रखना चाहिए कि प्रेम से प्रेम और विश्वास से विश्वास उत्पन्न होता है और यह भी नहीं भूलना चाहिए कि घृणा से घृणा का जन्म होता है, जो दावाग्नि की तरह सबको जलाने का काम करती है। भगवान बुद्ध, महात्मा ईसा, महात्मा गांधी सभी घृणा को प्रेम से जीतने में विश्वास करते थे। गांधीजी ने सर्वधर्म संभव द्वारा साम्प्रदायिक घृणा को मिटाने का आजीवन प्रयत्न किया। हिन्दू और मुसलमान दोनों की धार्मिक भावनाओं को समान आदर की दृष्टि से देखा। सभी धर्म आत्मा की शांति के लिए भिन्न-भिन्न उपाय और साधन बताते हैं। धर्मों में छोटे-बड़े का कोई भेद नहीं है। सभी धर्म सत्य, प्रेम, समता, सदाचार और नैतिकता पर बल देते हैं, इसलिए धर्म के मूल में पार्थक्य या भेद नहीं है।

(क) उपर्युक्त गद्यांश का शीर्षक लिखो।
(ख) सर्वधर्म समभाव से क्या तात्पर्य है।
(ग) इस गद्यांश का सार लगभग 30-40 शब्दों में लिखिए।

(9) नैतिक का अर्थ है, उचित और अनुचित की भावना। यह भावना हमें कुछ कार्य तथा व्यवहार करने की अनुमति देती है। प्रत्येक समाज की अपनी नैतिकता पृथक्-पृथक् होती है, परंतु इससे समस्त समाज नियंत्रित रहता है। नैतिकता से नियम प्रत्येक देश या समाज के सांस्कृतिक आदर्शों पर आधारित रहते हैं। उदाहरण के लिए भारतीय समाज में सत्य, अहिंसा, न्याय, समानता, दया, वृद्धों के प्रति श्रद्धा आदि कुछ ऐसे नियम हैं, जिनसे सभी व्यक्तियों के आचरण प्रभावित होते हैं। इन नियमों को मारने के लिए कोई दबाव नहीं डाला जाता, बल्कि ये हमारी आत्मा से संबंधित

(क) इस अंश का सारांश लिखिए।
(ख) गद्यांश के लिए उचित शीर्षक लिखिए।

अभ्यास के लिए अपठित पद्यांश :

1. चाह नहीं मैं सुरबाला के गहनों में गूंथा जाऊँ।
चाह नहीं प्रेमी बाला में बिंध प्यारी को ललचाऊँ।
चाह नहीं सम्राटों के शव पर हे हरि डाला जाऊँ .
चाह नहीं देवों के सिर पर चर्दै भाग्य पर इठलाऊँ।

प्रश्न-
(क) उपर्युक्त पयांश का शीर्षक लिखिए।
(ख) मोटे छपे (काले) शब्दों का अर्थ स्पष्ट कीजिए।
(ग) इस पद्यांश का भावार्थ लिखिए।

2. सीस पगा न झगा तन पै प्रभु! जानै को आहि बसै केहि ग्रामा।
धोती फटी सी लटी दुपटी, अरु पाँय उपानहु को नहीं सामा॥
द्वार खड़े द्विज दुर्बल देखि रह्यो चकि सों बसुधा अभिरामा।
पूछत दीनदयाल को धाम, बतावत अपनो नाम सुदामा।।

प्रश्न-
(क) उपर्युक्त पद्यांश का उपयुक्त शीर्षक लिखिए।
(ख) इस पद्यांश का भावार्थ अपने शब्दों में लिखिए।

3. गाँवों में संकुचित विचार, अन्धविश्वास, कुरीतियाँ और व्यर्थ व्यय का बोलबाला है। पंचायतों को चाहिए कि गाँवों में बच्चों के लिए पाठशाला खोलें और उनकी पढ़ाई का प्रबन्ध करें। जब लोग पढ़-लिख जायें तब ग्रामीणों की बुरी आदतें स्वतः ही समाप्त हो जायेंगी।

प्रश्न-
(क) उपर्युक्त गद्यांश का उपयुक्त शीर्षक लिखिए।
(ख) उपयुक्त गद्यांश का सारांश लिखिए।
(ग) मोटे छपे (काले) शब्दों के अर्थ स्पष्ट कीजिए।

MP Board Class 10th Hindi Solutions

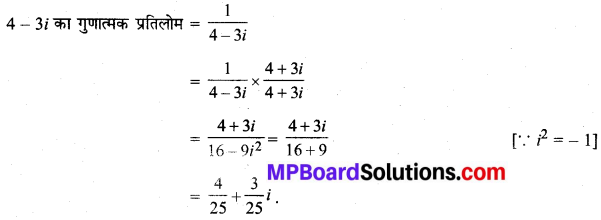
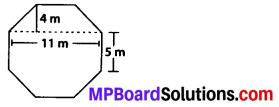
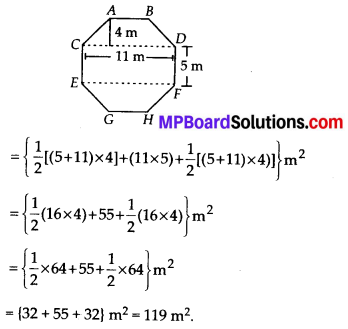
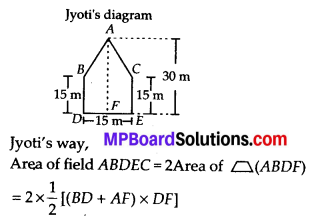
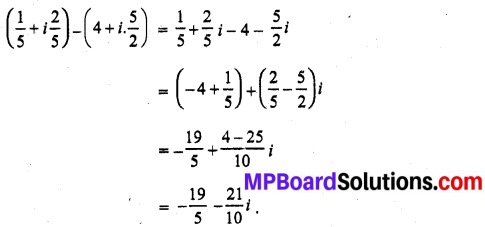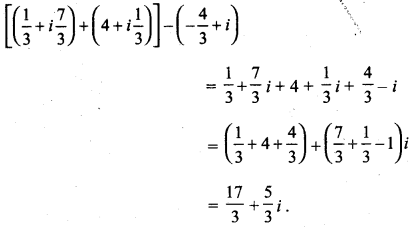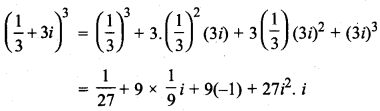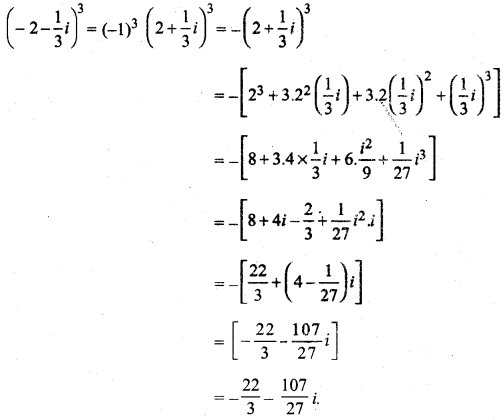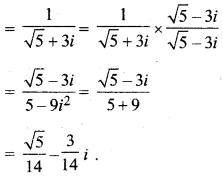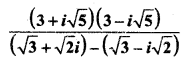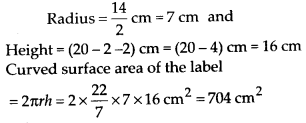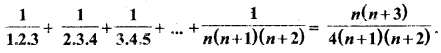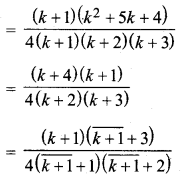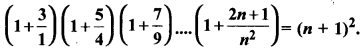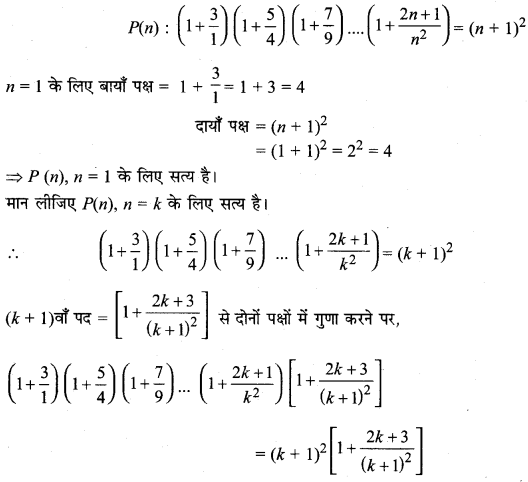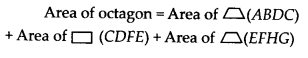MP Board Class 10th General Hindi व्याकरण मुहावरे एवं लोकोक्तियाँ

(क) मुहावरे

‘मुहाविरा’ अरबी भाषा का शब्द है, जिसका अर्थ है ‘अभ्यास’। वह वाक्यांश, जिसका साधारण शब्दार्थ न लेकर कोई विशेष अर्थ ग्रहण किया जाए, मुहावरा कहलाता-

1. महावरे वाक्यांश होते हैं। इनका प्रयोग वाक्यों के बीच में ही होता है. स्वतंत्र रूप से नहीं होता।
2. मुहावरों के प्रयोग से भाषा में सजीवता और रोचकता आ जाती है।
3. मुहावरा अपना असली रूप कभी नहीं बदलता। उसमें प्रयुक्त शब्दों को उनके पर्यायवाची शब्दों से भी नहीं बदला जा सकता। ‘गाल बजाना’ के स्थान पर ‘कपोल बजाना’ हास्यास्पद है।
4. मुहावरे का शब्दार्थ नहीं लेना चाहिए, बल्कि प्रसंग के अनुसार उसका अर्थ लेना चाहिए। ‘छाती पर पत्थर रखना’ का यदि शब्दार्थ लिया जाए तो उसका अर्थ बिल्कुल भिन्न होगा, जबकि मुहावरे के रूप में प्रयोग करने पर इसका अर्थ होगा ‘चुपचाप सहना’।
5. मुहावरे समय के साथ बनते – बिगड़ते रहते हैं।

यहाँ कुछ बहुप्रचलित मुहावरों के अर्थ और उनका वाक्यों में प्रयोग दिया जा रहा है –

1. अक्ल पर पत्थर पड़ना=बुद्धि मारी जाना।
प्रयोग – तुम्हारी अक्ल पर क्या पत्थर पड़ गए थे तो तुम बच्चे को अकेला छोड़ आए?

2. अंकुश लगाना=नियंत्रण करना।
प्रयोग – सुरेश! तुम अपने बेटे पर अंकुश लगाओ, नहीं तो आगे बहुत पछताओगे।

3. अपना उल्लू सीधा करना स्वार्थ पूरा करना।
प्रयोग – आज के राजनीतिज्ञ जनता की सेवा नहीं करते अपना उल्लू सीधा करते हैं।

4. अपनी खिचड़ी अलग पकाना सबसे अलग।
प्रयोग – मिलजुलकर काम करो, अपनी खिचड़ी अलग पकाने से कोई लाभ नहीं।

5. अपने पैरों पर खड़ा होना स्वावलम्बी होना।
प्रयोग – मैं तुम लोगों का बोझ कब तक उठाऊँगा अपने पैरों पर खड़े होने का प्रयास करो।

6. अपने पैरों कुल्हाड़ी मारना – अपने ही हाथों अपना अहित करना।
प्रयोग – तुमने शर्माजी का कहा न मानकर अपने पैरों पर कुल्हाड़ी मार ली है।

7. आँखों में धूल झोंकना धोखा देना।
प्रयोग – तुम यह सड़ी – गली सब्जी देकर मेरी आँखों में धूल झोंकना चाहते हो।

8. आँख खुलना – समझ आ जाना।
प्रयोग – उसका व्यवहार देखकर मेरी आँखें खुल गईं।

9. आँख दिखाना – धमकाना।
प्रयोग – माताजी ने ज्यों ही आँखें दिखाईं त्यों ही बालक ने मिठाई लेने से इन्कार कर दिया।

10. आटे – दाल का भाव मालूम होना वास्तविकता का ज्ञान होना।
प्रयोग – आठ सौ – नौ सौ रुपये में घर का सब खर्च चलाओगे तब आटे – दाल का भाव मालूम होगा।

11. आस्तीन का साँप होना विश्वासघाती सिद्ध होना।
प्रयोग – जिसे हमने अपना परम मित्र समझा था, वह आस्तीन का साँप सिद्ध हुआ।

12. ईंट से ईंट बजाना नष्ट कर देना।
प्रयोग – मानसिंह ने राणा प्रताप से कहा, “मैं मेवाड़ की ईंट से ईंट बजा दूंगा।”

13. उँगली उठाना=दोषारोपण करना।
प्रयोग – ऐसा काम करना कि कोई उँगली न उठा सके।

14. कमर कसना कार्य करने को तैयार होना।
प्रयोग – नौजवानों को देश के सम्मान की रक्षा के लिए कमर कस लेनी चाहिए।

15. कमर टूटना – दुःखदायक स्थिति बनना।
प्रयोग – व्यापार में बहुत हानि होने से उसकी तो कमर ही टूट गई।

16. काठ का उल्लू – महान् मूर्ख।
प्रयोग – उसे क्या समझते हो, वह तो निरा काठ का उल्लू है।

17. कान भरना – चुगली करना, भड़काना।
प्रयोग – शर्माजी अन्य अध्यापकों के खिलाफ प्रिंसिपल साहब के कान भरते रहते हैं।

18. कान का कच्चा होना दूसरों की बात पर शीघ्र विश्वास कर लेना।
प्रयोग – जो अधिकारी कान का कच्चा होता है, उससे न्याय की आशा कैसे की जा सकती है।

19. खरी – खोटी सुनाना भला – बुरा कहना।
प्रयोग – मेरी कोई गलती नहीं थी, फिर भी प्रिंसिपल साहब ने मुझे खरी – खोटी सुना दी।

20. खून खौलना=बहुत क्रुद्ध होना।
प्रयोग – द्रोपदी को लज्जित होते देख भीम का खून खौलने लगा।

21. खाक में मिलना बर्बाद हो जाना।
प्रयोग – रावण की हठधर्मी से सोने की लंका खाक में मिल गई।

22. गड़े मुर्दे उखाड़ना=पुरानी बातें दोहराना।
प्रयोग – इतिहास में तो गड़े मुर्दे ही उखाड़े जाते हैं।

23. गले का हार – अत्यंत प्रिय।
प्रयोग – रामचरितमानस भक्तों के गले का हार है।

24. गाल बजाना बढ़ – चढ़कर बातें करना।
प्रयोग – धीरेन्द्र की बात पर यकीन न करना, उसे गाल बजाने की आदत है।

25. गुदड़ी का लाल=निर्धनता में उत्पन्न प्रतिभाशाली व्यक्ति।
प्रयोग – लाल बहादुर शास्त्री गुदड़ी के लाल थे।

26. घाव पर नमक छिड़कना – दुखी को और दुखी करना।
प्रयोग – एक तो उसका नुकसान हुआ, अब ताने देकर उसके घाव पर नमक मत छिड़को।

27. चंगुल में फँसना काबू में कर लेना।
प्रयोग – भोले – भाले लोग धूर्तों के चंगुल में फँस जाते हैं।

28. चकमा देना – धोखा देना।
प्रयोग – चोर पुलिस को चकमा देकर भाग निकला।

29. चार दिन की चाँदनी थोड़े समय की सम्पन्नता।
प्रयोग – लक्ष्मी चंचल है, चार दिन की चाँदनी पर गर्व मत करो।

30. चिकना घड़ा जिस पर किसी बात का असर न हो।
प्रयोग – वह तो चिकना घड़ा है, तुम्हारी बातों का उस पर कोई असर नहीं पड़ेगा।

31. छप्पर फाड़कर देना=भाग्य के बल पर लाभ होना।
प्रयोग – भगवान ने उसे छप्पर फाड़कर धन दिया।

32. छोटे मुँह बड़ी बात अपनी मर्यादा से अधिक बोलना।
प्रयोग – छोटे मुँह बड़ी बात करके तुमने समझदारी का काम नहीं किया।

33. जान के लाले पड़ना=संकट में पड़ना।
प्रयोग – सारा गाँव बाढ़ की चपेट में आ गया; लोगों को जान के लाले पड़ गए।

34. जले पर नमक छिड़कना दुखी के दुख को और अधिक बढ़ाना।
प्रयोग – सुरेश तो परीक्षा में अनुत्तीर्ण होने पर वैसे ही दुखी था, तुमने उसका उपहास करके जले पर नमक छिड़क दिया।

35. टका – सा जवाब देना – साफ इन्कार कर देना।
प्रयोग – इस बार भी जब चंदा देने की बात उठी तो उसने टका – सा जवाब दे दिया।

36. टाँग अड़ाना रुकावट डालना।
प्रयोग – मेरी उसकी बात हो रही है, तुम क्यों बीच में टाँग अड़ाते हो?

37. टेढ़ी खीर कठिन कार्य।
प्रयोग – कक्षा में प्रथम आना टेढ़ी खीर है।

38. डंके की चोट सबके सामने।
प्रयोग – उसने डंके की चोट पे समाज से बाहर शादी की।

39. तलवे चाटना – चापलूसी करना।
प्रयोग – वे कोई और होंगे जो आपके तलवे चाटते हैं, मुझसे आशा न करना

40. तिनके का सहारा थोड़ा – सा आश्रय।
प्रयोग – डूबते को तिनके का सहारा होता है।

41. तूती बोलना धाक जमना।
प्रयोग – वे दिन गए, जब जमींदारों की तूती बोलती थी।

42. दंग रह जाना आश्चर्यचकित होना।
प्रयोग – बालक के करतब देखकर दर्शक दंग रह गए।

43. दाँत खट्टे करना=पराजित करना।
प्रयोग – भारत ने अनेक बार दुश्मनों के दाँत खट्टे किए हैं।

44. दाल. में काला होना=संदेहजनक बात होना।
प्रयोग – आपकी बातों से लगता है कि दाल में कुछ काला है।

45. दाल न गलना=चाल सफल न होना।
प्रयोग – पिताजी को पता लग गया है, अब तुम्हारी दाल नहीं गलेगी।

46. दुम दबाकर भागना डरकर भाग जाना।
प्रयोग – दुम दबाकर भागना तो कायरों का काम है।

47. दो टूक बात कहना – साफ – साफ बात कहना।
प्रयोग – मुझे कुछ लेना – देना नहीं है, मैंने दो टूक बात कह दी।

48. नमक खाना – पालन – पोषण होना।
प्रयोग – मैंने इस घर का नमक खाया है, इसे बरबाद न होने दूंगा।

49. नाक कटना – बदनामी होना।
प्रयोग – भारतीय टीम तीनों मैच हार गई, उसकी तो नाक कट गई।

50. नाक में दम करना परेशान करना।
प्रयोग – मच्छरों ने तो नाक में दम कर रखी है, रात भर सोने नहीं देते।

51. नाक रगड़नाखुशामद करना।
प्रयोग – पहले तो बहुत ताव दिखा रहे थे, अब क्यों नाक रगड़ते हो?

52. नाक – भौं सिकोड़ना – नफरत प्रकट करना।
प्रयोग – नाक – भौं मत सिकोड़ो, जो कुछ परोसा गया है, वह खा लो।

53. पत्थर की लकीर अमिट।
प्रयोग – मेरी बात पत्थर की लकीर मानो, शहर में दंगा होनेवाला है।

54. परदा डालना कोई बात छिपाना।
प्रयोग – अपने पापों का प्रायश्चित करो, उन पर पर्दा मत डालो। प्रमा

55. पहाड़ टूटना अत्यधिक विपत्ति आ जाना।
प्रयोग – अवधेश के निधन से पूरे परिवार पर पहाड़ टूट पड़ा।

56. पानी – पानी होना अधिक शर्मिन्दा होना।
प्रयोग – बद्रीसिंह को जब प्रिंसिपल साहब ने डाँटा तो वह पानी – पानी हो गया।

57. पाँचों उँगलियाँ घी में होना सभी प्रकार का सुख होना।
प्रयोग – तुम्हारे भाई एम.एल.ए. हो गए हैं, अब तो तुम्हारी पाँचों उँगलियाँ घी में हैं।

58. पीठ दिखाना कायरता दिखाना।
प्रयोग – युद्ध में पीठ दिखाना क्षत्रिय को शोभा नहीं देता।

59. पेट में चूहे कूदना – बहुत भूखा होना।
प्रयोग – पेट में चूहे कूद रहे हैं, अब काम – धाम नहीं हो सकता।

60. पौ बारह होना बहुत लाभ होना।
प्रयोग – मंत्रीजी का हाथ सिर पर है; अब तो तुम्हारे पौ बारह हैं।

61. फूंक – फूंककर कदम रखना सावधानी बरतना।
प्रयोग – वह एक बार धोखा खा चुका है, इसलिए फूंक – फूंककर कदम रखता

62. बाल की खाल निकालना – अनावश्यक रूप से दोष निकालना।
प्रयोग – बाल की खाल निकालना उसका स्वभाव बन गया है।

(ख) लोकोक्ति

लोकोक्ति का अर्थ है – लोक में प्रचलित उक्ति। किसी महापुरुष, किसी कवि या लेखक की उक्ति कहावत बन जाती है। कहावतों में एक अनुभूत सत्य छिपा रहता है। लोकोक्ति एक स्वतंत्र वाक्य की तरह भाषा में प्रयुक्त होती है। इसका प्रयोग किसी कथन की पूर्ति में उदाहरण के रूप में किया जाता है। लोकोक्ति का क्षेत्र मुहावरे की अपेक्षा अधिक व्यापक है। इसमें स्वयं एक स्वतंत्र अर्थ ध्वनित करने की क्षमता होती है। ‘सुनिए सबकी, करिए मन की’ यह एक लोकोक्ति है। इसका अर्थ है, ‘सबकी बात सुनकर जो मन को अच्छा लगे, वही करना चाहिए। इस प्रकार इस लोकोक्ति में एक वाक्य के सभी आवश्यक तत्त्व विद्यमान हैं।

मुहावरे और लोकोक्ति में अंतर है। मुहावरा वाक्यांश है, जबकि कहावत स्वतंत्र वाक्य है। मुहावरे का स्वतंत्र रूप में प्रयोग नहीं हो सकता, उसे किसी वाक्य का अंग बनना पड़ता है, कहावत का एक वाक्य की तरह प्रयोग किया जाता है।

लोकोक्ति किसी कथा या चिर- सत्य से संबद्ध रहती है। यहाँ कुछ लोकोक्तियों के अर्थ और उनका वाक्यों में प्रयोग दिया जा रहा है –

1. अधजल गगरी छलकत जाय=गुणहीन व्यक्ति अपने गुणों का अधिक प्रदर्शन करता है।
प्रयोग – किशोर एक साधारण क्लर्क है। घूसखोरी में उसने कुछ धन कमा लिया है तो उसके दिमाग नहीं मिलते। सच है – अधजल गगरी छलकत जाय।

2. अपनी करनी पार उतरे – अपने सुकर्मों से ही अच्छा फल मिलता है।
प्रयोग – अगर पढ़ाई में मन लगाओगे और मेहनत करोगे तो अच्छे नंबरों से पास हो जाओगे, नहीं पढ़ोगे तो फेल हो जाओगे। अपनी करनी पार उतरे।

3. अक्ल बड़ी कि भैंस – शारीरिक शक्ति से बौद्धिक शक्ति बड़ी होती है।
प्रयोग – भीमसिंह देखने में हाथी जरूर है, लेकिन उसकी बुद्धि मोटी है। वह वाद – विवाद में तुम्हारी बराबरी नहीं कर सकता। अक्ल बड़ी कि भैंस कहावत तुमने सुनी ही होगी।

4. अपना हाथ जगन्नाथ अपना काम स्वयं करना चाहिए।
प्रयोग – सत्यम् ने अलमारी खोलकर लड्डू निकाला और खा लिया। फिर वह बोला, “अपना हाथ, जगन्नाथ”।

5. अंधा पीसे, कुत्ता खाय – ठीक न्याय न होना।
प्रयोग – आज न्याय तो कहीं रहा ही नहीं। भ्रष्टाचारी और चापलूस लोगों का बोलबाला है। स्थिति तो यह है कि अंधा पीसे, कुत्ता खाय।

6. अंधेर नगरी, चौपट राजा – जहाँ कोई व्यवस्था या न्याय न हो।
प्रयोग – बिहार की बात मत पूछो। वहाँ तो अंधेर नगरी चौपट राजा की बात चरितार्थ हो रही है।

7. अपनी – अपनी ढपली, अपना – अपना राग – अपनी – अपनी बात को महत्त्व देना।
प्रयोग – चौदह पार्टियों की सरकार में सब अपनी – अपनी हाँकते हैं। इसीलिए इस सरकार के कार्यकलापों पर लोग कहते हैं – अपनी – अपनी ढपली, अपना – अपना राग।

8. अपनी गली में कुत्ता भी शेर अपने घर पर कमजोर भी अपने आपको बहुत ताकतवर समझता है।।
प्रयोग – जसवीर अपने घर पर खड़ा होकर उदयन को गालियाँ दे रहा था। उदयन ने कहा, “जसवीर अपनी गली में कुत्ता भी शेर होता है, अगर हिम्मत हो तो बाहर निकल आओ।”

9. अंधों में काना राजा मूर्तों के बीच में कोई साधारण समझदार।
प्रयोग – गाँव के अशिक्षितों के बीच वहाँ का पटवारी ही अंधों में काना राजा होता है।’

10. अब पछताये होत का जब चिड़ियाँ चुग गईं खेत – समय निकल जाने पर पछताने से कोई लाभ नहीं।
प्रयोग – साल भर से तुम्हें समझा रहे थे कि पढ़ाई में ध्यान लगाओ, लेकिन तुमने एक न सुनी। अब फेल हो गए तो रोते हो। यह बेकार है, क्योंकि अब पछताये होत क्या जब चिड़ियाँ चग गई खेत।।

11. अंधा बाँटे रेवड़ी, फिरि – फिरि अपने को देय अपने सगे – सम्बन्धियों को लाभ पहुँचाना।
प्रयोग – यादवजी मंत्री हो गए हैं, वे सरकारी नौकरी में यादवों को ही भर रहे हैं। सच है – अंधा बाँटे रेवड़ी, फिर – फिर अपने को देय।

12. आँखों का अंधा नाम नयनसुख नाम और गुण में विरोध।
प्रयोग – नाम तो है सुशील, लेकिन काम है चरित्रहीनों का। ऐसे ही लोगों के लिए यह कहावत कही जाती है – आँखों का अंधा नाम नयनसुख।

13. आम के आम गुठलियों के दाम दोहरा लाभ।
प्रयोग – हम तो अखबार खरीदते हैं, हमारी बीवी रद्दी अखबारों के लिफाफे बनाकर बेच देती है। आम के आम गुठलियों के दाम।

14. आप भला तो जग भगाभले के लिए सब भले होते हैं।
प्रयोग – छोटे भैया तो यथाशक्ति सबकी सहायता करते हैं और सबसे अच्छी तरह से मिलते हैं, इसलिए सब लोग आदर करते हैं। सच है – आप भला तो जग भला।

15. आगे नाथ न पीछे पगहा – आगे – पीछे कोई न होना।
प्रयोग – पता नहीं अमरनाथ इतने धन का क्या करेगा, उसके आगे नाथ न पीछे पगहा।

16. उल्टे बाँस बरेली का उल्टा काम करना।
प्रयोग – भोपाल से पेठा लेकर आगरा जा रहे हो। दिमाग तो ठीक है. उल्टे बाँस बरेली को।

17. ऊँची दुकान, फीका पकवान बाहरी दिखावा।
प्रयोग – होटल का नाम तो है ग्राण्ड होटल, लेकिन वहाँ कोई विशेष सुविधाएँ नहीं हैं। ऊँची दुकान फीका पकवान की कहावत चरितार्थ होती है।

18. ऊँट के मुँह में जीरा आवश्यकता से बहुत कम वस्तु।
प्रयोग – शर्मा जी के लिए चार पूड़ियाँ तो ऊँट के मुँह में जीरा साबित होंगी।

19. एक अनार सौ बीमार – वस्तु कम, माँग अधिक।
प्रयोग – पिताजी ने आइसक्रीम मँगाई चार और खानेवाले इकट्ठे हो गए चौदह। यह तो एक अनार सौ बीमार वाली कहावत हो गई।

20. ओखली में सिर दिया तो मूसलों से क्या डर कठिन काम शुरू करके कठिनाइयों से क्या डरना।
प्रयोग – बंजर जमीन खरीदकर उसे जोतना शुरू किया है तो उसमें कठिनाइयाँ तो आएँगी ही। ओखली में सिर दिया तो मूसलों से क्या डर?

21. कहाँ राजा भोज, कहाँ गंगू तेली – दो ऐसे असमान व्यक्ति जिनकी आपस में कोई तुलना न हो।
प्रयोग – कहाँ परमानन्द जैसा संत पुरुष और कहाँ रवीन्द्र जैसा स्वार्थी व्यक्ति। आप भी क्या समानता दिखा रहे हैं? कहाँ राजा भोज कहाँ गंगू तेली।

22. काला अक्षर भैंस बराबर – निरक्षर व्यक्ति।
प्रयोग – राम से पत्र पढ़वाने जा रहे हो। अरे भाई उसके लिए तो काला अक्षर भैंस बराबर है।

23. का वर्षा जब कृषी सुखानी – अवसर निकल जाने पर प्रयत्न करना व्यर्थ है।
प्रयोग – परीक्षा के पहले पुस्तकें खरीदने को रुपये मँगाए थे, वह पिताजी ने भेजे नहीं। अब परीक्षा समाप्त होने पर मनीआर्डर आया है। अब रुपये किस काम के। ठीक ही कहा है – का वर्षा जब कृषी सुखानी।

24. खरबूजे को देखकर खरबूजा रंग बदलता है – संगति का प्रभाव पड़ता है।
प्रयोग – उमेश का बड़ा लड़का कामचोर है, छोटे लड़के पर भी उसका प्रभाव पड़ा है। वह भी कामधाम नहीं करता। सच ही तो है – खरबूजे को देखकर खरबूजा रंग बदलता है।

25. खिसियानी बिल्ली खम्भा नोचे लज्जित होने पर निरपराध पर क्रोधित होना।
प्रयोग – जब ऊषा को उसके पिताजी ने डांट दिया तो वह अपनी छोटी बहिन पर बिगड़ी। तब उसके भाई ने कहा ‘खिसियानी बिल्ली खम्भा नोचे।’

26. खोदा पहाड़ निकली चुहिया=बहुत प्रयास करने का थोड़ा फल मिलना।
प्रयोग – सेन्ट्रल लायब्रेरी में मैथिलीशरण जी की पुस्तकें तलाश करने गया था, लेकिन मिली एक पंचवटी। मन ही मन कहा – खोदा पहाड़ निकली चुहिया।

27. गेहूँ के साथ घुन भी पिसता है बड़ों के साथ रहने वालों को भी उनके साथ कष्ट उठाना पड़ता है।
प्रयोग – जसवीर और परमवीर आपस में लड़ रहे थे, विजय दोनों को समझा रहा था। प्रिंसिपल साहब ने तीनों को बुलाकर मार लगाई। गेहूँ के साथ घुन भी पिस गया।

28. घर का जोगी जोगड़ा आन गाँव का सिद्ध – स्वयं के स्थान पर सम्मान नहीं मिलता।
प्रयोग – बनवारीलालजी गाँव के बहुत अच्छे वैद्य हैं, लेकिन गाँववाले डिस्पेन्सरी के कम्पाउण्डर से दवाइयाँ लेते हैं। ठीक ही है – घर का जोगी जोगड़ा आन गाँव का सिद्ध।

29. घर का भेदी लंका ढावै आपसी फूट का फल बुरा होता है।
प्रयोग – जयचन्द ने मुहम्मद गोरी से मिलकर पृथ्वीराज के खिलाफ युद्ध लड़ा। ठीक ही कहा है – घर का भेदी लंका ढावै।

30. चार दिन की चाँदनी, फिर अँधेरी रात – थोड़े समय का सुख।
प्रयोग – धन – संपत्ति का गर्व न करना; यह तो आती – जाती रहती है, चार दिन। की चाँदनी फिर अंधेरी रात कहावत को याद रखो।

31. चोर – चोर मौसेरे भाई एक जैसी मनोवृत्ति वाले लोग।
प्रयोग – विकास और प्रयास दोनों में से किसी पर विश्वास मत करना, दोनों चोर – चोर मौसेरे भाई हैं।

32. चोर की दाढ़ी में तिनका – अपराधी की चेष्टा से उसका अपराध प्रकट हो जाता
प्रयोग – कक्षाध्यापक ने जब चार अपराधी प्रवृत्ति के लड़कों को शीशा तोड़ने के जुर्म में प्रिंसिपल साहब के सामने खड़ा किया तो एक ने चिल्लाकर कहा, “मैं तो कल आया ही नहीं था। इसी को कहते हैं चोर की दाढ़ी में तिनका।”

33. जहाँ चाह वहाँ राह – दृढ़ इच्छाशक्ति से सब काम हो सकते हैं।
प्रयोग – हिम्मत हारकर मत बैठो, प्रयत्न करो – जहाँ चाह वहाँ राह।

34. जिसकी लाठी उसकी भैंस बलवान की ही जीत होती है।
प्रयोग – बद्रीप्रसाद अदालत से तो जीत गए, लेकिन खेत तो अभी भी पहलवान सिंह जोत रहा है। आजकल तो जिसकी लाठी उसकी भैंस है।

35. जैसे नागनाथ, वैसे साँपनाथ दोनों एक समान।
प्रयोग – क्या सुधीर और क्या मधुर’ दोनों में से किसी से सहायता की उम्मीद न करना। जैसे नागनाथ, वैसे साँपनाथ।

36. थोथा चना बाजे घना कम जाननेवाला अधिक बुद्धिमान होने का प्रदर्शन करता
प्रयोग – किशोर एक साधारण ठेकेदार है लेकिन बातें करोड़ों की करता है। सच है – थोथा चना बाजे घना।

37. दूर के ढोल सुहावने होते हैं दूर की चीजें अच्छी लगती हैं।
प्रयोग – सुना था कि कृष्ण जहाँ रासलीला करते थे, वहाँ बड़े सुंदर कुल हैं किंतु जाकर देखा तो सब वीरान दिखा। ठीक ही कहा है – दूर के ढोल सुहावने होते हैं।

38. धोबी का कुत्ता घर का न घाट का=दोनों तरफ की साधने वाले को कहीं सफलता नहीं मिलती।
प्रयोग – हरीश ने कम्प्यूटर की कक्षा में प्रवेश लिया और एम.बी.ए. की भी तैयारी की। दोनों ओर दिमाग रहने से कहीं भी सफलता नहीं मिली। उसके मित्रों ने कहा – धोबी का कुत्ता घर का न घाट का।

39. न रहेगा बाँस, न बजेगी बाँसुरीन कारण होगा, न कार्य होगा।
प्रयोग – सत्यम और संकेत कैरम के लिए लड़ते रहते थे। एक दिन उनकी माँ ने कहा, “मैं कैरम उठाके रखे देती हूँ। न रहेगा बाँस, न बजेगी बाँसुरी।”

40. नाच न जाने आँगन टेढ़ा – स्वयं की अयोग्यता को छिपाकर साधनों को दोष देना।
प्रयोग – सुरेश को चित्र बनाना आता तो नहीं, लेकिन वह कहता था कि ब्रुश खराब था, इसलिए चित्र अच्छा नहीं बना। इसी को नाच न जाने आँगन टेढ़ा कहते हैं।

MP Board Class 10th Hindi Solutions

MP Board Class 8th Maths Solutions Chapter 11 Mensuration Ex 11.4

Question 1.
Given a cylindrical tank, in which situation will you find surface area and in which situation volume.
(a) To find how much it can hold.
(b) Number of cement bags required to plaster it.
(c) To find the number of smaller tanks that can be filled with water from it.
Solution:
(a) To find how much a cylinder can hold, we need to find the volume of the cylindrical tank.
(b) To find the number of cement bags required to plaster the tank, we need to find the surface area of the cylindrical tank.
(c) To find the number of smaller tanks that can be filled with water from the bigger tank, we need to find the volume of the big cylindrical tank and one small tank.

Question 2.
Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater ? Verify it by finding the volume of both the cylinder. Check whether the cylinder with greater volume also has greater surface area?

Solution:
∵ Volume of cylinder = πr²h
Now, radius of cylinder B is double the radius of cylinder A and height of cylinder B is half the height of A. Due to the square of radius, the radius will assert greater impact in the volume of cylinder than the height. So, volume of cylinder B will be greater.

Hence, cylinder B has both, greater volume and greater surface area.

Question 3.
Find the height of a cuboid whose base area is 180 cm² and volume is 900 cm³ ?
Solution:
We have, base area = 180 cm²,
Volume = 900 cm³
To find, height of a cuboid = h cm, say
We know, Volume = Base area × Height of a cuboid
⇒ 900 = 180 × h ⇒ h = 5 cm.

Question 4.
A cuboid is of dimensions 60 cm × 54 cm × 30 cm. How many small cubes with side 6 cm can be placed in the given cuboid?
Solution:
We have,
Big cuboid dimensions = 60 cm × 54 cm × 30 cm
Side of a small cube = 6 cm
Number of cubes that can be placed in the given cuboid

Question 5.
Find the height of the cylinder whose volume is 1.54 m³ and diameter of the base is 140 cm?
Solution:
We have, volume of the cylinder = 1.54 m³ = 1.54 × 106 cm³
Diameter = 140 cm,
Radius = 140 ÷ 2 = 70 cm
∵ volume of the cylinder = πr²h

⇒ 100 cm = h
∴ Height of the cylinder is 100 cm.

Question 6.
A milk tank is in the form of cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in litres that can be stored in the tank?
Solution:
We have, radius of the cylindrical tank = 1.5 m and length = 7 m
∴ Volume of tank = πr²h = π(1 .5)² × 7
= 49.5 m³ = 49500 litres. [∵ 1 m³ = 1000 L]

Question 7.
If each edge of a cube is doubled,
(i) how many times will its surface area increase?
(ii) how many times will its volume increase?
Solution:
Let the edge of the cube be a cm.
After doubling the length, the edge becomes 2a cm.
Surface area of old cube = 6a² and volume of old cube = a³
Surface area of new cube = 6(2a)² = 24 a² and volume of new cube = (2a)³ = 8a³
Hence, surface area increases 4 times and volume increases 8 times if the edge of a cube is doubled.

Question 8.
Water is pouring into a cuboidal reservoir at the rate of 60 litres per minute. If the volume of reservoir is 108 m3, find the number of hours it will take to fill the reservoir.
Solution:
We have,
volume of reservoir = 108 m³ = 108 × 103 L
[∵ 1 m³ = 103 L]
Rate of pouring water = 60 L/minute
Time to fill the reservoir

= 1.8 × 10³ min. = 1800 min.= 30 hrs.

MP Board Class 8th Maths Solutions

MP Board Class 11th Maths Solutions Chapter 5 सम्मिश्र संख्याएँ और द्विघातीय समीकरण Ex 5.1

प्रश्न 1 से 10 तक की सम्मिश्र संख्याओं में प्रत्येक को a + ib के रूप में व्यक्त कीजिए।
प्रश्न 1.
\((5 i)\left(-\frac{3}{5} i\right)\)
हलः
\((5 i)\left(-\frac{3}{5} i\right)\) = -5 × \(\frac{3}{5}\) × i × i
= -3i² = 3 [∵ i² = i]

प्रश्न 2.
i⁹ + i¹⁹
हल:
i⁹ + i¹⁹ = i⁸.i + i¹⁸.i.
= [i²]⁴.i + [i²]⁹. i
= (-1)⁹ i + (-1)⁹ i = i – i = 0.

प्रश्न 3.
i^-39
हल:

प्रश्न 4.
3(7 + i7) + i (7 + i7).
हल:
3(7 + i7) + i (7 + i7) = 21 + 21i + 7i + 7i²
= 21 + 28i + 7(-1) [∵ i² = -1]
= 21 – 7 + 28i
= 14 + 28i.

प्रश्न 5.
(1 – i) – (-1 + i6).
हल:
(1 – i) – (-1 + i6) = (1 – i) + (1 – 6i)
= 1 – i + 1 – 6i
= 2 – 7i.

प्रश्न 6.
\(\left(\frac{1}{5}+i \frac{2}{5}\right)-\left(4+i \frac{5}{2}\right)\)
हल:

प्रश्न 7.
\(\left[\left(\frac{1}{3}+i \frac{7}{3}\right)+\left(4+i \frac{1}{3}\right)\right]-\left(-\frac{4}{3}+i\right)\)
हल:

प्रश्न 8.
(1 – i)⁴.
हल:
(1 – i)² = [(1 – i)²]²
= [1 – 2i + i²]²
= [1 – 2i – 1]²2 [∵ i² = -1]
= (- 2i)²
= – 2i × -2i
= 4i² = 4(-1) = -4.

प्रश्न 9.
\(\left(\frac{1}{3}+3 i\right)^{3}\).
हल:

प्रश्न 10.
\(\left(-2-\frac{1}{3} i\right)^{3}\)
हल:

प्रश्न 11 से 13 तक की सम्मिश्र संख्याओं में प्रत्येक का गुणात्मक प्रतिलोम ज्ञात कीजिए।
प्रश्न 11.
हल:

प्रश्न 12.
\( \sqrt{{5}} \) + 3i.
हल:
\( \sqrt{{5}} \) + 3i का गुणात्मक प्रतिलोम

प्रश्न 13.
– i.
हल:
– i का गुणात्मक प्रतिलोम
= \(\frac{1}{-i}=\frac{1}{-i} \times \frac{i}{i}=-\frac{i}{i^{2}}=-\frac{i}{-1}\) = -i

प्रश्न 14.
निम्नलिखित व्यंजक को a + ib के रूप में व्यक्त कीजिए :

हल:

MP Board Class 11th Maths Solutions

MP Board Class 8th Maths Solutions Chapter 11 Mensuration Ex 11.3

Question 1.
There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?

Solution:
Surface area of box (a) = 2(lb + bh + hl)
= 2(60 × 40 + 40 × 50 + 50 × 60)
= 2(2400 + 2000 + 3000)
= 2 × 7400 = 14800 cm²
Surface area of box (b) = 6 × (side)² = 6 × 50² = 15000 cm²
Hence, box (a) required less amount of material than box (b) to make.

Question 2.
A suitcase with measures 80 cm × 48 cm × 24 cm is to be covered with a trapaulin cloth. How many metres of trapaulin of width 96 cm is required to cover 100 such suitcases?
Solution:
Let l, b and h be the length and breadth and height of the suitcase respectively.
⇒ l = 80 cm, b = 48 cm, h = 24 cm
Total surface area of suitcase = 2(lb + bh + hl)
= 2(80 × 48 + 48 × 24 + 24 × 80)
= 2(3840 + 1152 + 1920) cm² = 2(6912) cm² = 13824 cm²
Area of cloth required for 1 suitcase = Area of 1 suitcase
⇒ l × 96 = 13824

Length required for 100 suitcases

Question 3.
Find the side of a cube whose surface area is 600 cm².
Solution:
Surface area of cube = 6 × (side)²

Question 4.
Rukhsar painted the outside of the cabinet of measure 1 m × 2 m × 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet.

Solution:
Rukhsar painted all the cabinet except the bottom means she painted 4 walls and 1 top. Let l = 1 m, b = 2 m, h = 1.5 m be the length, breadth and height of cabinet respectively.
Area of painted cabinet
= (lb + bh + bh + lh + lh)
= [l × 2 + 2 × 1.5 + 2 × 1.5 + l × 1.5 + l × 1.5]m²
= [2 + 3.0 + 3.0 +1.5 +1.5] m² = 11 m².

Question 5.
Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth and height of 15 m, 10 m and 7 m respectively. From each can of paint 100 m² of area is painted. How many cans of paint will she need to paint the room?
SOlution:
Daniel is painting 4 walls and 1 ceiling.
∴ Total painted area = Area of 4 walls + Area of ceiling
Let l = 15, b = 10 and h = 7 be the length, breadth and height of the hall respectively. = 2 × h(l + b) + lb = {2 × 7 (15 +10) + (15 × 10)} m2
= {14 (25) +150} m² = {350 +150} m² = 500 m²
If 100 m² of area is painted with one can

Question 6.
Describe how the two figures given below are alike and how they are different. Which box has larger lateral surface area?

Solution:
Alike: They both have same height. Different: Their shapes are different one is cylinderical and other is cubical box.
Let r and h be the radius and height of the cylinder.

Let the side of cube be a = 7 cm
⇒ Lateral surface area = 4(a)² = 4(7)² cm² = 196 cm²
∴ Cubical box has larger lateral surface area.

Question 7.
A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How much sheet of metal is required ?
Solution:
Let r and h be the radius and height of the closed cylinder.
Total surface area = 2πr(r + h)

Question 8.
The lateral surface area of a hollow cylinder is 4224 cm². It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of rectangular sheet ?
Solution:
Let r and h be the radius and height of the hollow cylinder and l be its lateral surface area.

Question 9.
A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length is 1 m.
Solution:
Area covered in 1 revolution = curved surface area of cylinder

∴ Area covered in 750 revolutions = 2.64 × 750 m² = 1980 m²

Question 10.
A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in figure). If the label is placed 2 cm from top and bottom, what is the area of the label.

Solution:

MP Board Class 8th Maths Solutions