Bhagya

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.2

बिना प्रसरण किए और सारणिकों के गुणधर्मों का प्रयोग करके निम्नलिखित प्रश्न 1 से 5 को सिद्ध कीजिए-
प्रश्न 1.

हल:

प्रश्न 2.

हल:

प्रश्न 3.

हल:

प्रश्न 4.

हल:

प्रश्न 5.

हल:

सारणिकों के गुणधर्मों का प्रयोग करके प्रश्न 6 से 14 तक को सिद्ध कीजिए-
प्रश्न 6.

हल:

= 0 – a(0 + bc) – b(-ac + 0)
= -abc + abc
= 0
= R.H.S.

प्रश्न 7.

हल:

प्रश्न 8.

हल:

प्रश्न 9.
\(\left|\begin{array}{lll}{x} & {x^{2}} & {y z} \\ {y} & {y^{2}} & {z x} \\ {z} & {z^{2}} & {x y}\end{array}\right|\) = (x – y) (y – z)(z – x) (xy + yz + zx)
हल:


= (x – y)(y – z)(z – x)[(z² – xy) – z(x + y + z)]
= (x – y)(y – z)(z – x)[z² – xy – xz – zy –z²]
= (x – y)(y – z)(z – x)[-(xy + yz + zx)]
= -(x – y)(y – z)(z – x)(xy + yz + zx)= R.H.S.

प्रश्न 10.

हल:

प्रश्न 11.

हल:

प्रश्न 12.

हल:


= (1 – x)² (1 + x + x²)[1 + x(1 + x)]
= (1 – x)² (1 + x + x² )[1 + x + x²]
= (1 – x)² (1 + x + x²)²
= [(1 – x)(1 + x + x²)]²
= (1 – x³)² = R.H.S.

प्रश्न 13.

हल:

प्रश्न 14.

हल:

R₁ के अनुदिश प्रसरण करने पर
∆ = (a² + 1)[(b² + 1)(c² + 1) – bc.cb] – ab [ab (c² + 1) – bc.ca] + ac[ab. cb – ac.b² + 1]
= (a² + 1)[b²c² + b² + c² + 1 – b²c²] – ab[abc² + ab – abc] + ac[ab²c – acb² – ac]
= (a² + 1)(b² + c² + 1) – ab (ab) – ac (ac)
=a²b² + a²c² + a² + b² + c² + 1 – a²b² – a²c²
= 1 + a² + b² + c²

प्रश्न संख्या 15 तथा 16 में सही उत्तर चुनिए।
प्रश्न 15.
यदि A एक 3 × 3 कोटि का वर्ग आव्यूह है तो |KA| का मान होगा-
(A) K|A|
(B) k²|A|
(C) k³|A|
(D) 3k|A|
हल:
|kA | को |A | के पद में व्यक्त करना

अतः विकल्प (C) सही है।

प्रश्न 16.
निम्नलिखित में से कौन-सा कथन सही है?
(A) सारणिक एक वर्ग आव्यूह है।
(B) सारणिक एक आव्यूह से सम्बद्ध एक संख्या है।
(C) सारणिक एक वर्ग आव्यूह से सम्बद्ध एक संख्या है।
(D) इनमें से कोई नहीं।
हल:
सारणिक एक वर्ग आव्यूह से सम्बद्ध एक संख्या है।
अतः विकल्प (C) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.6 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 4 सारणिक Ex 4.6

निम्नलिखित प्रश्नों में 1 से 6 तक दी गई समीकरण निकायों का संगत अथवा असंगत के रूप में वर्गीकरण कीजिए।
प्रश्न 1.
x + 2y = 2
2x + 3y = 3
हल:
दिए गये समीकरण निकाय को हम इस प्रकार से लिख सकते हैं।
AX = B

प्रश्न 2.
2x – y = 5
x + y = 4
हल:
दिया गया समीकरण निकाय
2x – y = 5
x + y = 4

प्रश्न 3.
x + 3y = 5
2x + 6y = 8
हल:
दिए गए समीकरण निकाय को हम इस प्रकार से लिख सकते हैं।
AX = B

प्रश्न 4.
x + y + = 1
2x + 3y + 2z = 2
ax + ay + 2az =4
हल:
दिया गया समीकरण निकाय
x + y + z = 1
2x + 3y + 2z = 2
ax + ay + 2az = 4

= a[1(6 – 2) – 1(4 – 2) + 1(2 – 3)]
= a [1 × 4 – 1 × 2 + 1(-1)]
= a[4 – 2 – 1] = a × 1 = a ≠ 0
अतः दिया गया समीकरण निकाय संगत है।

प्रश्न 5.
3x – y – 2z = 2
2y – z = -1
3x – 5y = 3
हल:
3x – y – 2z = 2
2y – z = -1
3x – 5y = 3

प्रश्न 6.
5x – y + 4z = 5
2x + 3y + 5z = 2
5x – 2y + 6z = -1
हल:
दिए गए समीकरण निकाय को निम्न प्रकार से लिख सकते हैं
AX = B

= 5(18 + 10) + 1(12 – 25) + 4(-4 – 15)
= 140 – 13 – 76
= 51 ≠ 0
अतः समीकरण निकाय संगत है।

निम्नलिखित प्रश्न 7 से 14 तक प्रत्येक समीकरण निकाय को आव्यूह विधि से हल कीजिए।
प्रश्न 7.
5x + 2y = 4
7x + 3y = 5
हल:
दिया गया समीकरण निकाय
5x + 2y = 4
7x + 3y = 5

प्रश्न 8.
2x – y = -2
3x + 4y = 3
हल:
दी गई समीकरण निकाय
2x – y = -2
3x + 4y = 3
उपरोक्त समीकरणों को निम्न प्रकार से लिख सकते हैं-
AX = B

प्रश्न 9.
4x – 3y = 3
3x – 5y = 7
हल:
दिया गया समीकरण निकाय
4x – 3y = 3
3x – 5y = 7
समीकरण निकाय AX = B के रूप में लिखा जा सकता है, जहाँ

प्रश्न 10.
5x + 2y = 3
3x + 2y = 3
हल:
दिया गया समीकरण निकाय
5x + 2y = 3
3x + 2y = 5
समीकरण निकाय AX = B के रूप में लिखा जा सकता है, जहाँ

प्रश्न 11.
निम्नलिखित समीकरण निकाय को आव्यूह विधि से हल कीजिए
2x + y + z = 1
x – 2y -2z = 3/2
3y – 5z = 9
हल:
दी गई समीकरण निकाय को निम्न प्रकार से लिख सकते हैं-
AX = B

प्रश्न 12.
x – y + z = 4
2x + y – 3z = 0
x + y + z = 2
हल:
दिया गया समीकरण निकाय
x – y + z = 4
2x + y – 3z = 0
x + y + z = 2
समीकरण निकाय AX = B के रूप में लिखा जा सकता है, जहाँ,

प्रश्न 13.
2x + 3y + 3z = 5
x – 2y + 2 = -4
3x – y – 2z = 3
हल:
दिया गया समीकरण निकाय
2x + 3y + 3z = 5
x – 2y + z = -4
3x – y – 2z = 3
समीकरण निकाय को AX = B के रूप में लिखा जा सकता है, जहाँ

प्रश्न 14.
x – y + 2z = 7
3x + 4y – 5z = -5
2x – y + 3z = 12
हल:
दिया गया समीकरण निकाय
x – y + 2z = 7
3x + 4y – 5z = -5
2x – y + 3z = 12
समीकरण निकाय को AX = B के रूप में लिखा जा सकता है, जहाँ

प्रश्न 15.
यदि A = \(\left[\begin{array}{ccc}{2} & {-3} & {5} \\ {3} & {2} & {-4} \\ {1} & {1} & {-2}\end{array}\right]\) है तो A^-1 ज्ञात कीजिए। A^-1 का प्रयोग करके निम्नलिखित समीकरण निकाय को हल कीजिए।
2x – 3y + 5z = 11
3x + 2y – 4z = -5
x + y – 2z = -3
हल:

प्रश्न 16.
4 kg प्याज, 3 kg गेहूँ और 2 kg चावल का मूल्य Rs. 60 है। 2 kg प्याज, 4kg गेहूँ और 6 kg चावल का मूल्य Rs. 90 है। 6 kg प्याज, 2 kg गेहूँ और 3 kg चावल का मूल्य Rs. 70 है। आव्यूह विधि द्वारा प्रत्येक का मूल्य प्रति kg ज्ञात कीजिए।
हल:
माना प्याज, गेहूँ तथा चावल का मूल्य प्रति किग्रा क्रमश: x रु०, ५ रु० तथा 2 रु० है।
4 किग्रा प्याज 3 किया गेहूँ तथा 2 किग्रा चावल का मूल्य = 60 रुपये
∴ 4x + 3y + 2z = 60 …(1)
2 किग्रा प्याज, 4 किग्रा गेहूँ तथा 6 किग्रा चावल का मूल्य = 90 रु०
∴ 2x + 4y + 6z = 90 …(2)
6 किया प्याज, 2 किग्रा गेहूँ तथा 3 किग्रा चावल का मूल्य = 70 रु०
∴ 6x + 2y + 3z = 70 ….(3)
अब समीकरण निकाय
4x + 3y + 2z = 60
2x + 4y + 6z = 90
या x + 2y + 32 = 45
6x + 2y + 3z = 70
इसे AX = B के रूप में लिख सकते हैं, जबकि



अत: प्याज, गेहूँ तथा चावल का मूल्य प्रति किग्रा क्रमश: 5 रु०,8 रु०, तथा 8 रु० है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन Ex 2.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन Ex 2.1

निम्नलिखित के मुख्य मानों को ज्ञात कीजिए :
प्रश्न 1.
sin^-1\(\left(-\frac{1}{2}\right)\)
हल :
माना y = in^-1\(\left(-\frac{1}{2}\right)\)

प्रश्न 2.
cos^-1\(\frac{\sqrt{3}}{2}\)
हल :
माना y = cos^-1\(\frac{\sqrt{3}}{2}\)
⇒ cos y = \(\frac{\sqrt{3}}{2}\)
⇒ cos y = cos\(\frac{\pi}{6}\)
∵ cos^-1 की मुख्य शाखा का परिसर [0, π] होता है तथा cos \(\frac{\pi}{6}=\frac{\sqrt{3}}{2}\)
∴ cos\(\frac{\sqrt{3}}{2}\) का मुख्य मान \(\frac{\pi}{6}\) है।

प्रश्न 3.
cosec^-1(2)
हल :
माना y = cosec^-1 (2)
⇒ cosec y = 2
cosec y = cosec \(\frac{\pi}{6}\)
⇒ cosec^-1(cosec y) = \(\frac{\pi}{6}\)
y =\(\frac{\pi}{6}\)
अतः cosec^-1 (2) का मुख्य मान = \(\frac{\pi}{6}\)

प्रश्न 4.
tan^-1 (-\( \sqrt{{3}} \))
हल :
माना y = tan^-1(-\( \sqrt{{3}} \))
⇒ tan y = –\( \sqrt{{3}} \)
tan y = tan\(\left(-\frac{\pi}{3}\right)\)
∵ tan^-1 की मुख्य शाखा का परिसर \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\) और tan\(\tan \left(-\frac{\pi}{3}\right)=-\sqrt{3}\)
अत: tan^-1(-\( \sqrt{{3}} \))का मुख्य मान = \(\frac{-\pi}{3}\)

प्रश्न 5.
cos^-1\(\left(-\frac{1}{2}\right)\)
हल :
माना y = cos^-1\(\left(-\frac{1}{2}\right)\)

प्रश्न 6.
tan^-1(-1)
हल :
माना y = tan^-1(1)
⇒ tan y = -1
tany = tan\(\left(-\frac{\pi}{4}\right)\)
अत: tan^-1(-1) का मुख्य मान = \(-\frac{\pi}{4}\)

प्रश्न 7.
sec^-1\(\left(\frac{2}{\sqrt{3}}\right)\)
हल :
माना y = sec^-1\(\left(\frac{2}{\sqrt{3}}\right)\)

प्रश्न 8.
cot^-1\(\sqrt{3}\)
हल :
माना y = cot^-1\(\sqrt{3}\)
= cot y = (\(\sqrt{3}\)) = cot \(\frac{\pi}{6}\)
फलन cot^-1x का मुख्य मान शाखा का परिसर = (0, π) है। अतः cot^-1 (\(\sqrt{3}\)) = \(\frac{\pi}{6}\) है।

प्रश्न 9.
cos^-1\(\left(-\frac{1}{\sqrt{2}}\right)\)
हल :
माना y = cos^-1\(\left(-\frac{1}{\sqrt{2}}\right)\)

प्रश्न 10.
cosec^-1\(-\sqrt{2}\)
हल :
माना y = cosec^-1\(-\sqrt{2}\)
⇒ cosec y = –\(\sqrt{2}\) = -cosee \(\frac{\pi}{4}\) = cosee \(\left(-\frac{\pi}{4}\right)\)
फलन cosec^-1x का मुख्य मान शाखा का परिसर = \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) – [0]
अतः cosec^-1(-\( \sqrt{{2}} \)) = –\(-\frac{\pi}{4}\) है।

प्रश्न 11.
निम्नलिखित के मान ज्ञात कीजिए
tan^-1(1) + cos^-1\(\left(-\frac{1}{2}\right)\) + sin^-1\(\left(-\frac{1}{2}\right)\)
हल :

प्रश्न 12.
cos^-1\(\left(\frac{1}{2}\right)\) + 2sin^-1\(\left(\frac{1}{2}\right)\)
हल :

प्रश्न 13.
यदि sin^-1 x = y तो

हल :

प्रश्न 14.
tan^-1\( \sqrt{{3}} \)– sec^-1(-2) का मान बराबर है-
(A) π
(B) \(-\frac{\pi}{3}\)
(C) \(\frac{\pi}{3}\)
(D) \(\frac{2 \pi}{3}\)
हल:
माना y = tan^-1\( \sqrt{{3}} \)– sec^-1(-2)

अतः विकल्प (B) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन Ex 2.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन Ex 2.2

निम्नलिखित को सिद्ध कीजिए-
प्रश्न 1.
3 sin^-1 x = sin^-1(3x – 4x³), x ϵ \(\left[-\frac{1}{2}, \frac{1}{2}\right]\)
हल:
माना sin^-1x = y
⇒ x = sin y
R.H.S. = sin^-1 (3x – 4x³)
= sin^-1(3 sin y – 4 sin³ y)
= sin^-1 (sin 3y)
(∵ sin 3y = 3 sin y – 4 sin³y)
= 3y (∵ sin^-1 sin x = x)
= 3 sin^-1 x
= L.H.S.
अत: 3 sin^-1x = sin^-1(3x – 4x³)

प्रश्न 2.
3 cos^-1 x = cos^-1 (4x³ – 3x), x ϵ \(\left[\frac{1}{2}, 1\right]\)
हल:
सिद्ध करना है
3cos^-1 x = cos^-1 (4x³ – 3x) …(1)
माना cos^-1 = y
⇒ x = cosy
∴ समी० (1) का RH.S.
=cos^-1(4x³ – 3x)
= cos^-1 (4cos³ y – 3cos y)
=cos^-1 (cos 3y)
= 3y
= 3cos^-1x (∵ cos^-1 x = y)
अत: 3cos^-1 = cos^-1 (4x³ – 3x)

प्रश्न 3.
tan^-1\(\frac{2}{11}\) + tan^-1\(\frac{7}{24}\) = tan^-1\(\frac{1}{2}\)
हल:
हम जानते हैं कि

प्रश्न 4.
2 tan^-1\(\frac{1}{2}\) + tan^-1\(\frac{1}{7}\) = tan^-1\(\frac{31}{17}\)
हल:
2 tan^-1\(\frac{1}{2}\) + tan^-1\(\frac{1}{7}\) = tan^-1\(\frac{31}{17}\)

निम्नलिखित फलनों को सरलतम रूप में लिखिए-
प्रश्न 5.
tan-1 \(\frac{\sqrt{1+x^{2}}-1}{x}\), x ≠ 0
हल:
माना x = tan θ ⇒ θ = tan^-1x

प्रश्न 6.
tan^-1\(\frac{1}{\sqrt{x^{2}-1}}\), |x| > 1.
हल:
माना x = secθ ⇒ θ = sec^-1x

प्रश्न 7.
tan^-1\((\sqrt{\frac{1-\cos x}{1+\cos x}})\), 0 < x < π
हल:

प्रश्न 8.
tan^-1\(\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right), \frac{-\pi}{4}<x<\frac{3 \pi}{4}\)
हल:

प्रश्न 9.
tan^-1\(\frac{x}{\sqrt{a^{2}-x^{2}}}\), |x| < a
हल:
माना x = a sin θ ⇒ \(\frac{x}{a}\) = sin θ

प्रश्न 10.

हल:
माना x = a tan θ ⇒ \(\frac{x}{a}\) = tan θ

निम्नलिखित में से प्रत्येक का मान ज्ञात कीजिए
प्रश्न 11.
tan^-1[2cos (2sin^-1\(\frac{1}{2}\))]
हल:

प्रश्न 12.
cot (tan^-1 a + cot^-1 a)
हल:
माना y = cot (tan^-1a + cot^-1a)
= cot\(\frac{\pi}{2}\) [∵ tan^-1a + cot^-1a = \(\frac{\pi}{2}\)]
= 0 [∵ cot \(\frac{\pi}{2}\) = 0]

प्रश्न 13.

|x| < 1, y > 0 तथा xy < 1
हल:
माना

प्रश्न 14.
यदि sin(sin^-1\(\frac{1}{5}\) + cos^-1x) = 1, तो x का मान ज्ञात कीजिए।
हल:

प्रश्न 15.
यदि tan^-1 \(\frac{x-1}{x-2}\) + tan^-1\(\frac{x+1}{x+2}=\frac{\pi}{4}\), तो x का मान ज्ञात कीजिए।
हल:

प्रश्न संख्या 16 से 18 में दिए गए प्रत्येक व्यंजक का मान ज्ञात कीजिए-
प्रश्न 16.
sin^-1 (sin\(\frac{2 \pi}{3}\))
हल:
माना y = sin^-1 (sin\(\frac{2 \pi}{3}\)), तब

प्रश्न 17.
tan^-1 (tan\(\frac{3 \pi}{4}\))
हल:
माना y = tan^-1 (tan\(\frac{3 \pi}{4}\))

प्रश्न 18.
tan (sin^-1\(\frac{3}{5}\) + cot^-1\(\frac{3}{2}\))
हल:
tan (sin^-1\(\frac{3}{5}\) + cot^-1\(\frac{3}{2}\))

प्रश्न 19.
cos^-1(cos \(\frac{7 \pi}{6}\)) का मान बराबर है-

हल:
cos^-1[cos \(\frac{7 \pi}{6}\)]
cos^-1 की मुख्य मान शाखा [0, π] है।

अत: विकल्प (B) सही है।

प्रश्न 20.
sin [\(\frac{\pi}{3}\) – sin^-1(\(-\frac{1}{2}\))] का मान है-

हल:

अत: विकल्प (D) सही है।

प्रश्न 21.
tan^-1\( \sqrt{{3}} \) – cot^-1 (-\( \sqrt{{3}} \)) का मान है
(A) π
(B) \(-\frac{\pi}{2}\)
(C) 0
(D) 2\( \sqrt{{3}} \)
हल:

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 3 आव्यूह Ex 3.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 3 आव्यूह Ex 3.3

प्रश्न 1.
निम्नलिखित आव्यूहों में से प्रत्येक का परिवर्त ज्ञात कीजिए-

हल:
यहाँ पंक्तियों को स्तम्भों में, स्तम्भों को पंक्तियों में बदलने पर,

प्रश्न 2.
यदि A = \(\left[\begin{array}{ccc}{-1} & {2} & {3} \\ {5} & {7} & {9} \\ {2} & {1} & {1}\end{array}\right]\) तथा B = \(\left[\begin{array}{ccc}{-4} & {1} & {-5} \\ {1} & {2} & {0} \\ {1} & {3} & {1}\end{array}\right]\) हैं तो सत्यापित कीजिए कि-
(i) (A + B)’ = A’ + B’
(ii) (A – B) = A’ – B’
हल:
यहाँ A = \(\left[\begin{array}{ccc}{-1} & {2} & {3} \\ {5} & {7} & {9} \\ {2} & {1} & {1}\end{array}\right]\), B = \(\left[\begin{array}{ccc}{-4} & {1} & {-5} \\ {1} & {2} & {0} \\ {1} & {3} & {1}\end{array}\right]\)


अतः (A – B)’ = A’ – B’

प्रश्न 3.
यदि A = \(\left[\begin{array}{rr}{3} & {4} \\ {-1} & {2} \\ {0} & {1}\end{array}\right]\) तथा B = \(\left[\begin{array}{rrr}{-1} & {2} & {1} \\ {1} & {2} & {3}\end{array}\right]\) हैं तो सत्यापित कीजिए कि-
(i) (A + B)’ = A’ + B’
(ii) (A – B)’ = A’ – B’
हल:

प्रश्न 4.
यदि A’ = \(\left[\begin{array}{rr}{-2} & {3} \\ {1} & {2}\end{array}\right]\) तथा B = \(\left[\begin{array}{rr}{-1} & {0} \\ {1} & {2}\end{array}\right]\) हैं तो (A + 2B)’ ज्ञात कीजिए।
हल:

प्रश्न 5.
A तथा B आव्यूहों के लिए सत्यापित कीजिए कि (AB)’ = B’A’, जहाँ

हल:

प्रश्न 6.
(i) यदि A = \(\left[\begin{array}{cc}{\cos \alpha} & {\sin \alpha} \\ {-\sin \alpha} & {\cos \alpha}\end{array}\right]\) हो तो सत्यापित कीजिए कि A’A = I
(ii) यदि B = \(\left[\begin{array}{cc}{\sin \alpha} & {\cos \alpha} \\ {-\cos \alpha} & {\sin \alpha}\end{array}\right]\) हो तो सत्यापित कीजिए कि A’A = I
हल:

प्रश्न 7.
(i) सिद्ध कीजिए कि आव्यूह A = \(\left[\begin{array}{ccc}{\mathbf{1}} & {-\mathbf{1}} & {\mathbf{5}} \\ {-\mathbf{1}} & {\mathbf{2}} & {\mathbf{1}} \\ {\mathbf{5}} & {\mathbf{1}} & {\mathbf{3}}\end{array}\right]\) एक सममित आव्यूह है।
(ii) सिद्ध कीजिए कि आव्यूह A = \(\left[\begin{array}{ccc}{\mathbf{0}} & {\mathbf{1}} & {-\mathbf{1}} \\ {-\mathbf{1}} & {\mathbf{0}} & {\mathbf{1}} \\ {\mathbf{1}} & {-\mathbf{1}} & {\mathbf{0}}\end{array}\right]\) एक विषम सममित आव्यूह है।
हल:

अतः आव्यूह A एक विषम सममित आव्यूह है।

प्रश्न 8.
आव्यूह A = \(\left[\begin{array}{ll}{1} & {5} \\ {6} & {7}\end{array}\right]\) के लिए सत्यापित कीजिए कि –
(i) (A + A’) एक समित आव्यूह है।
(ii) (A – A’) एक विषम सममित आव्यूह है।
हल:


अतः (A – A’) एक विषम सममित आव्यूह है।

प्रश्न 9.
यदि A = \(\left[\begin{array}{ccc}{\mathbf{0}} & {\boldsymbol{a}} & {\boldsymbol{b}} \\ {-\boldsymbol{a}} & {\boldsymbol{0}} & {\boldsymbol{c}} \\ {-\boldsymbol{b}} & {-\boldsymbol{c}} & {\boldsymbol{0}}\end{array}\right]\) तो \(\frac{1}{2}\)(A + A’) तथा \(\frac{1}{2}\)(A – A’) ज्ञात कीजिए।
हल:

प्रश्न 10.
निम्नलिखित आव्यूहों को एक सममित आव्यूह तथा एक विषम सममित आव्यूह के योगफल के रूप में व्यक्त कीजिए-

हल:

प्रश्न संख्या 11 तथा 12 में सही उत्तर चुनिए-
प्रश्न 11.
यदि A तथा B समान कोटि के सममित आव्यूह हैं तो AB – BA एक
(A) विषम सममित आव्यूह है
(B) सममित आव्यूह है
(C) शून्य आव्यूह है
(D) तत्समक आव्यूह है
हल:
A और B समान कोटि की सममित आव्यूह है।
∴ A = A, B’ = B
(AB – BA)’ = (AB)’ – (BA) = BA’ – A’B’
= BA – AB [∵ B’ = B, A’ = A]
= -(AB – BA)
⇒ AB – BA विषम सममित आव्यूह है।
अतः विकल्प (A) सही है।

प्रश्न 12.
यदि A = \(\left[\begin{array}{cc}{\cos \alpha} & {-\sin \alpha} \\ {\sin \alpha} & {\cos \alpha}\end{array}\right]\) तथा A’ + A = I, तो α का मान है-
(A) \(\frac{\pi}{6}\)
(B) \(\frac{\pi}{3}\)
(C) π
(D) \(\frac{3 \pi}{2}\)
हल:

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन विविध प्रश्नावली Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन विविध प्रश्नावली

प्रश्न 1.
मान लीजिए कि f: R → R, f(x) = 10x + 7 द्वारा परिभाषित फलन है। एक ऐसा फलन g: R → R ज्ञात कीजिए, जिसके लिए gof = fog = I_R हो।
हल:
यहाँ f: R → R इस प्रकार है कि f(x) = 10x + 7
माना y = 10x + 7

अतः f व्युत्क्रमणीय है, जो g : Y → X, g(y) = \(\frac{y – 7}{10}\) से परिभाषित है।

प्रश्न 2.
मान लीजिए कि f: W → W, f(n) = n – 1, यदि ॥ विषम है तथा f (n) = n + 1, यदि n सम है, द्वारा परिभाषित है। सिद्ध कीजिए कि f व्युत्क्रमणीय है। f का प्रतिलोम ज्ञात कीजिए। यहाँ के समस्त पूर्णांकों का समुच्चय
हल:
दिया है : f: W → W को

यदि n₁ विषम n₂ दोनों सम हों तो
f(n₁) = f(n₂) ⇒ n₁ – 1 = n₂ + 1
या n₁ – n₂ = 2, जो सम्भव नहीं है।
यदि n₁ और n₂ विषम हों तो
f(n₁)= f(n₂) ⇒ n₁ – 1 = n₂ – 1
⇒ n₁ = n₂
यदि n₁ और n₂ दोनों सम हों, तो
n₁ + 1 = n₂ + 1 ⇒ n₁ = n₂
अतः f एकैकी भी है।
सहप्रान्त में प्रत्येक अवयव 2r + 1, प्रान्त का 2 प्रतिबिम्ब है। इसी प्रकार कोई भी सम संख्या प्रान्त का 2r + 1 का प्रतिबिम्ब है।
इस प्रकार सहप्रान्त का प्रत्येक अवयव प्रान्त के किसी – न – किसी अवयव का प्रतिबिम्ब है।
∴ f आच्छादक तथा व्युत्क्रमणीय है।
अतः f ^{– 1}(y) = g(y) इस प्रकार है कि

अतः का प्रतिलोम स्वयं है।

प्रश्न 3.
यदि f : R → R जहाँ f(x) = x² – 3x + 2 द्वारा परिभाषित है तो fIf (x)] ज्ञात कीजिए।
हल:
यहाँ f: R → R, f(x) = x² – 3x + 2 द्वारा परिभाषित है।
∴ [f(x)] = f(x² – 3x + 2)
= (x² – 3x + 2)² – 3(x² – 3x + 2) + 2
= (x⁴ + 9x² + 4 – 6x³ – 12x + 4x²) + (- 3x² + 2x – 6) + 2
= x⁴ – 6x³ + 10x² – 3x

प्रश्न 4.
सिद्ध कीजिए कि
f: R → {x ϵ R: – 1 < x < 1} जहाँ f(x) = \(\frac{x}{1+|x|}\), x ϵ R द्वारा परिभाषित फलन एकैकी तथा आच्छादक है।
हल:
यहाँ f: R → {x ϵ R : – 1 < x < 1} तथा f(x)= \(\frac{x}{1+|x|}\) द्वारा परिभाषित है।
(a) माना x ≥ 0, |x| = x

उत्तर
⇒ x₁(1 + x₂) = x₂(1 + x₁)
या x₁ + x₁x₂ = x₂ + x₂x₁
जब x < 0 |x| = – x, f(x) = \(\frac{x}{1-x}\)
f(x₁) = f(x₂) ⇒ \(\frac{x_{1}}{1-x_{1}}=\frac{x_{2}}{1-x_{2}}\)
⇒ x₁ (1 – x₂) = x₂(1 – x₁)
⇒ x₁ – x₁x₂ = x₂ – x₂x₁
∴ x₁ = x₂
अतः f एकैकी है।

अतः दोनों ही अवस्था में सहप्रान्त का प्रत्येक अवयव प्रान्त के किसी – न – किसी अवयव का प्रतिबिम्ब है।
∴ f आच्छादक है।
अत: f एकैकी तथा आच्छादक है।

प्रश्न 5.
सिद्ध कीजिए कि f(x) = x³ द्वारा प्रदत्त फलन f: R → R एकैक (Injective) है।
हल:
यहाँ f: R → R, f(x) = x³ द्वारा परिभाषित है।
f(x₁) = f(x₂) ⇒ x₁³ x₂³
⇒ x₁ = x₁
अतः f एकैकी है।

प्रश्न 6.
दो फलनों f: N → Z तथा g : Z → Z के उदाहरण दीजिए जो इस प्रकार हों कि gof एकैक है परन्तु g एकैक नहीं है।
हल:
(i) यहाँ f: N → Z तथा g: Z → Z द्वारा परिभाषित है।
f(x) = – x, g(x) = |x| से,
g(x)= |x|, – 1, 1 दोनों का प्रतिबिम्ब 1 है। .
∴ g एकैक नहीं है।
परन्तु g[f(x)] =g (- x) = |-x| = |x|
x ϵ N, g[(fx)] = |x|x = x
अतः gof एकैकी है।

(ii) f(x) = -2x, g(x) = |2x|

प्रश्न 7.
दो फलनों f: N → N तथा g: N → N के उदाहरण दीजिए, जो इस प्रकार हों कि gof आच्छादक है किन्तु f आच्छादक नहीं है।
हल:
(i) यहाँ f : N → N तथा g : N → N

f(x) = y = x + 1
∴ x = y – 1
यदि y – 1, x = 0 जो कि प्राकृत संख्या नहीं है।
अतः f आच्छादक नहीं है।
यदि x > 1,
gof (x) = g[f(x)] =g (x + 1) = (x + 1) – 1 = x
अतः gof आच्छादक है।

प्रश्न 8.
एक अरिक्त समुच्चय X दिया हुआ है। P(X) जो कि के समस्त उपसमुच्चयों का समुच्चय है, पर विचार कीजिए। ‘निम्नलिखित तरह से P(X) में एक सम्बन्ध R परिभाषित कीजिए-
P(x) में उपसमुच्चयों, A, B के लिए ARB, यदि और केवल यदि A⊂B है। क्या R,P(X) में एक तुल्यता सम्बन्ध है? अपने उत्तर का औचित्य भी लिखिए।
हल:
(i) यहाँ A ⊂ A ⇒ R स्वतुल्य है। .
(ii) A ⊂ B, B ⊄ A ⇒ R सममित नहीं है।
(iii) A ⊂ B, B ⊂ C ⇒ A ⊂ C ⇒ R संक्रामक है।
अतः R तुल्यता सम्बन्ध नहीं है।

प्रश्न 9.
किसी प्रदत्त अरिक्त समुच्चय x के लिए एक द्विआधारी संक्रिया* : P(X) × P(X) → P(X) पर विचार कीजिए, जो A * B = A ∩ B, ∀ A, B ϵ P(X) द्वारा परिभाषित है, जहाँ P(X) समुच्चय x का घात समुच्चय (Power set) है। सिद्ध कीजिए कि इस संक्रिया का तत्समक अवयव X है तथा संक्रिया के लिए P(X) में केवल x व्युत्क्रमणीय अवयव है।
हल:
दिया है : P(X) × P(X) → P(X)
तथा A * B = A ∩ B
∴ X * A = X ∩ A = A, सभी A के लिए
इसी प्रकार A * X = A ∩ X = A.
∴X एक तत्समक अवयव है तथा व्युत्क्रमणीय अवयव है। माना I एक दूसरा तत्समक अवयव है।
∴ I ∩ A = A सभी A के लिए
तथा x ϵ X, I ∩ {x} = {x}
⇒ x ϵ I ⇒ x ⊂ I और I ⊂ x
∴ I = X

प्रश्न 10.
समुच्चय {1, 2, 3,…., n} से स्वयं तक के समस्त आच्छादक फलनों की संख्या ज्ञात कीजिए।
हल:
माना Y : 1 2 3….n
तथा X : 1 2 3…..n
समुच्चय – Y का प्रत्येक अवयव समुच्चय X में किसी – न – किसी अवयव का प्रतिबिम्ब है।
इस प्रकार x और Y के अवयवों में सम्बन्ध
n (n – 1)(n – 2)… 3 2 1 = n! तरीकों से हो सकता है।
अतः द्विआधारी संक्रियाओं की संख्या n! है।

प्रश्न 11.
मान लीजिए कि S = {a, b, c} तथा T = {1, 2, 3} है। S से T तक के निम्नलिखित फलनों F के लिए F^-1 ज्ञात कीजिए, यदि उसका अस्तित्व है :
(i) F = {(1, 3), (b, 2), (c, 1)}
(ii) F = {(a, 2), (b, 1), (c, 1)}
हल:
(i) यहाँ S = {a, b, c},T = {1, 2, 3}
तथा F = {(a, 3), (b, 2), (c, 1)}
F(a)= 3, F(b)= 2, F(c)=1
∴ F^-1(3)= a, F^-1 (2) = F^-1 (1) = c
∴ F^-1 = {(3, a),(2, b), (1, c)}
(ii) F = {(a, 2),(b, 1), (c, 1)}
फलन F में b तथा c का प्रतिबिम्ब 1 है।
∴ यह एकैकी नहीं है।
अत: यह फलन व्युत्क्रमणीय नहीं है।

प्रश्न 12.
a * b=|a – b| तथा a o b = a, ∀ a, b ϵ R द्वारा परिभाषित द्विआधारी संक्रियाओं* : R × R → R तथा 0: R × R → R पर विचार कीजिए। सिद्ध कीजिए कि * क्रमविनिमेय है परन्तु साहचर्य नहीं है, . साहचर्य है परन्तु क्रमविनिमेय नहीं है। पुनः सिद्ध कीजिए कि सभी a, b, c ϵ R के लिए a * (b o c) = (a * b) o (a * c) है। [यदि ऐसा होता है तो हम कहते हैं कि संक्रिया * संक्रिया o पर वितरित (Distributes) होती है। क्या o संक्रिया * पर वितरित होती है? अपने उत्तर का औचित्य भी बतलाइए।
हल:
दिया है : a * b = |a – b| और a o b = a
(i) (a) a * b = |a – b|, |b * a| = |b – a| = |a – b|
अतः यह क्रमविनिमेय संक्रिया है।
(b) a * b = |a – b|, b * c = |b – c|
⇒ a * c ≠ |a – c|
अत: यह साहचर्य संक्रिया नहीं है।

(ii) (a) a o b = a, b o a = b ⇒ a ≠ b
अतः o क्रमविनिमेय संक्रिया नहीं है।
a o b = a, b o c = b, a o c = a
अतः o एक साहचर्य संक्रिया है।

(iii) सिद्ध करना है :
a * (boc)= (a * b) 0 (b * c)
L.H.S. = a * (boc)= a * b = |a – b|
R.H.S. = (a * b) 0 (b * c)
= |a – b| o |b – c| = |a – b|
∴ L.H.S. = R..S.
अतः A * (boc)= (a * b) o (b * c)

(iv) क्या a o (b * c) और (a o b) * (a0c) बराबर है?
L.H.S. = a 0 * (b * c) = ao |b – c| = a
R.H.S. = (aob) * (aoc) = a * a = |a – a|= 0
∴ L.H.S. ≠ R.H.S.
अतः संक्रिया o संक्रिया * पर वितरण संक्रिया नहीं है।

प्रश्न 13.
किसी प्रदत्त अरिक्त समुच्चय x के लिए मान लीजिए कि * : P(X) × P(X) → P(X), जहाँ A * B = (A – B) ∪ (B – A), ∀A, B ϵ P(X) द्वारा परिभाषित है। सिद्ध कीजिए कि रिक्त समुच्चयक ϕ, संक्रिया * का तत्समक है तथा P(X) के समस्त अवयव A व्युत्क्रमणीय हैं, इस प्रकार कि A^-1 = A.
हल:
यहाँ * : P(X) × P(X) → P(X) जो इस प्रकार परिभाषित है।
A * B = (A – B) ∪ (B – A)
दिया है : A * B = (A – B) ∪ (B – A)
जब B = ϕ क रखने पर,
A * ϕ = (A – ϕ) ∪ (ϕ – A)
= A ∪ ϕ = A
ϕ * A = (ϕ – A) ∪ (A – ϕ) = ϕ ∪ A = A
⇒ A * ϕ = ϕ * A = A
अतः ϕ तत्समक अवयव है।

(ii) A * A = (A – A) ∪ (A – A) = ϕ
A * A = ϕ = A^-1 = A

प्रश्न 14.
निम्नलिखित प्रकार से समुच्चय {0, 1, 2, 3, 4, 5} में एक द्विआधारी संक्रिया * परिभाषित कीजिए।

सिद्ध कीजिए कि शून्य (0) इस संक्रिया का तत्समक है तथा समुच्चय का प्रत्येक अवयव a ≠ 0 व्युत्क्रमणीय है, इस प्रकार कि 6 – c, a का प्रतिलोम है।
हल:
यहाँ संक्रिया समुच्चय A = {0, 1, 2, 3, 4, 5} पर

(i) e तत्समक अवयव है, यदि a * e = e * a = a
अब, माना e = 0, a * e = a + 0 = a
e* a = 0 + a = a
∴ a * e = e * a = a
अतः O तत्समक अवयव है।

(ii) b अवयव a का व्युत्क्रम है, यदि a * b = b * a = e
a * (6 – a)= a + (6 – a) – 6 = a + 6 – a – 6 = 0
(6 – a) * a = (6 – a) + a – 6 = 0
∴ a * (6 – a) = (6 – a) * a = 0
अतः A के प्रत्येक अवयव a का 6 – a व्युत्क्रम है।

प्रश्न 15.
मान लीजिए कि A ={ – 1, 0, 1, 2}, B = { – 4, – 2, 0, 2} और f, g: A → B, क्रमशः f(x) = x² – x, x ϵ A तथा g(x) = 2x\(\left|x-\frac{1}{2}\right|\) – 1. x ϵ A द्वारा परिभाषित फलन हैं क्या है तथा g समान हैं? अपने उत्तर का औचित्य भी बताइए।
हल:
यहाँ, यदि A = { – 1, 0, 1, 2) B = { – 4, – 2, 0, 2}
और f, g . A → B फलन की f(x) = x² – x, x ϵ A और g(x)= \(\left|x-\frac{1}{2}\right|\) . 1, x ϵ A द्वारा परिभाषित है।

प्रश्न 16.
यदि A = {1, 2, 3} हो तो ऐसे सम्बन्ध जिनमें अवयव (1, 2) तथा (1, 3) हों और जो स्वतुल्य तथा सममित हैं किन्तु संक्रामक नहीं है, की संख्या है
(A) 1
(B) 2
(C) 3
(D) 4
हल:
यहाँ, A = {1, 2, 3}
वह सम्बन्ध जिसमें (1, 2) और (1, 3) हों तथा सम्बन्ध स्वतुल्य व सममित हो तथा संक्रामक न हो,
{(1, 2), (1, 3), (1, 1), (2, 2), (3, 3), (2, 1), (3, 1)}
∴ ऐसा एक ही सम्बन्ध है।
अतः विकल्प (A) सही है।

प्रश्न 17.
यदि A= {1, 2, 3} हो तो अवयव (1, 2) वाले तुल्यता सम्बन्धों की संख्या है
(A) 1
(B) 2
(C) 3
(D) 4
हल:
यहाँ, A = {1, 2, 3}
तुल्यता सम्बन्ध जिसमें (1, 2) सम्मिलित हो ऐसे 2 सम्बन्ध हो सकते हैं।
अतः विकल्प (B) सही है।

प्रश्न 18.
मान लीजिए कि f :R → R है तब निम्नलिखित प्रकार से परिभाषित चिह्न फलन (signum Function) है।

तथा g : R → R, g(x) = [x] द्वारा प्रदत्त महत्तम पूर्णांक फलन है, जहाँ [x], x से कम या x के बराबर पूर्णांक है तो क्या fog तथा gof, अन्तराल [0, 1] में सम्पाती (coincide) हैं?
हल:
यहाँ f: R → R, जो

तथा g: R → R जो g(x) = [x] से परिभाषित है।
∴ x ϵ [0, 0, f(x) = 1, g(x) = 0.
gof (x) = g [f(x)] = g(1) = 1
तथा fog(x) = f(0)= 0
इस प्रकार fog ≠ gof
अतः अन्तराल (0, 1) में fog तथा gof सम्पाती नहीं हैं।

प्रश्न 19.
समुच्चय {a, b} में द्विआधारी संक्रियाओं की संख्या है
(A) 10
(B) 16
(C) 20
(D) 8
हल:
यहाँ समुच्चय {a, b}
समुच्चय A में 2 अवयव हैं।
द्विआधारी संक्रियाओं की संख्या = 2⁴ = 16
अतः विकल्प (B) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन विविध प्रश्नावली Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 2 प्रतिलोम त्रिकोणमितीय फलन विविध प्रश्नावली

निम्नलिखित के मान ज्ञात कीजिए-
प्रश्न 1.
cos^-1(cos\(\frac{13 \pi}{6}\))
हल:
माना y = cos^-1(cos\(\frac{13 \pi}{6}\))
cos^-1 की मुख्य मान शाखा का परिसर [0, π] है।

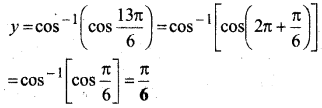
प्रश्न 2.
tan^-1(tan\(\frac{7 \pi}{6}\))
हल:
माना y = tan^-1(tan\(\frac{7 \pi}{6}\))
tan^-1 की मुख्य मान शाखा का परिसर \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) है।

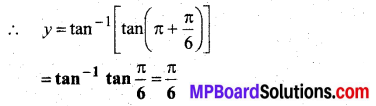
प्रश्न 3.
सिद्ध कीजिए-
2 sin^-1\(\frac{3}{5}\) = tan^-1 \(\frac{24}{7}\)
हल:
2 sin^-1\(\frac{3}{5}\) = tan^-1 \(\frac{24}{7}\)

प्रश्न 4.
सिद्ध कीजिए
sin^-1\(\frac{8}{17}\) + sin^-1\(\frac{3}{5}\) = tan^-1\(\frac{77}{36}\)
हल:
यहाँ sin^-1\(\frac{8}{17}\) + sin^-1\(\frac{3}{5}\) = tan^-1\(\frac{77}{36}\)

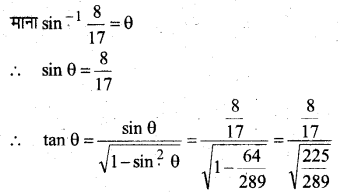
प्रश्न 5.
सिद्ध कीजिए-
cos^-1\(\frac{4}{5}\) + cos^-1\(\frac{12}{13}\) = cos^-1\(\frac{33}{65}\)
हल:
cos^-1\(\frac{4}{5}\) + cos^-1\(\frac{12}{13}\) = cos^-1\(\frac{33}{65}\)

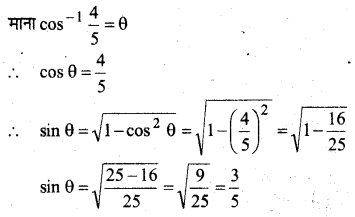
प्रश्न 6.
सिद्ध कीजिए-
cos^-1\(\frac{12}{13}\) + sin^-1\(\frac{3}{5}\) = sin^-1\(\frac{56}{65}\)
हल:
cos^-1\(\frac{12}{13}\) + sin^-1\(\frac{3}{5}\) = sin^-1\(\frac{56}{65}\)

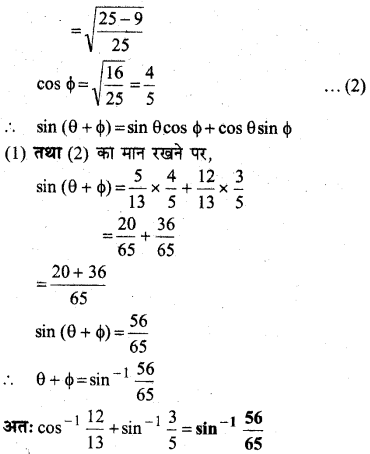
प्रश्न 7.
सिद्ध कीजिए-
tan^-1\(\frac{63}{16}\) = sin^-1\(\frac{5}{13}\) + cos^-1\(\frac{3}{5}\)
हल:
R.H.S. = sin^-1\(\frac{5}{13}\) + cos^-1\(\frac{3}{5}\)

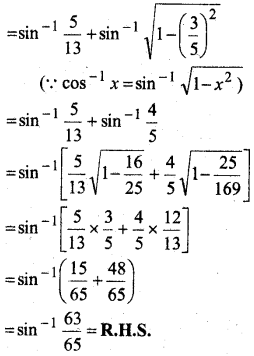
प्रश्न 8.
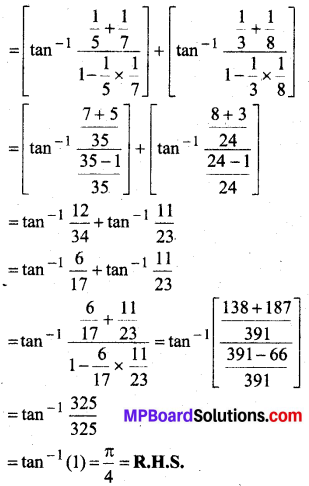
सिद्ध कीजिए-
tan^-1\(\frac{1}{5}\) + tan^-1\(\frac{1}{7}\) + tan^-1\(\frac{1}{3}\) + tan^-1\(\frac{1}{8}\) = \(\frac{\pi}{4}\)
हल:
L.H.S.
(tan^-1\(\frac{1}{5}\) + tan^-1\(\frac{1}{7}\)) + (tan^-1\(\frac{1}{3}\) + tan^-1\(\frac{1}{8}\))

सिद्ध कीजिए
प्रश्न 9.
tan^-1\( \sqrt{{x}} \) = \(\frac{1}{2} \) cos^-1\(\left(\frac{1-x}{1+x}\right)\), x ϵ [0, 1]
हल:
माना x = tan²θ ⇒ θ = tan^-1\( \sqrt{{x}} \)

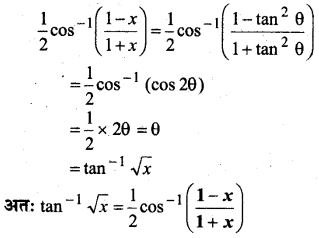
प्रश्न 10.

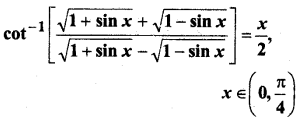
हल:

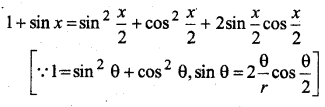
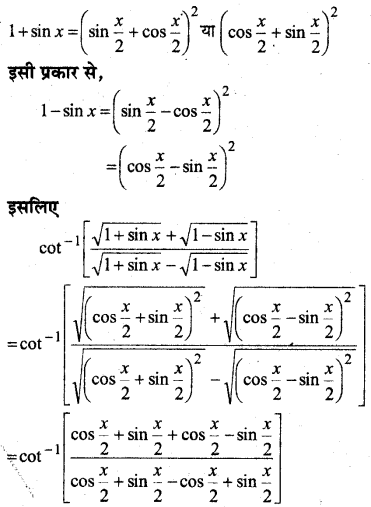
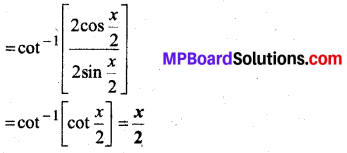
प्रश्न 11.

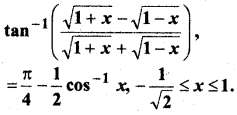
हल:

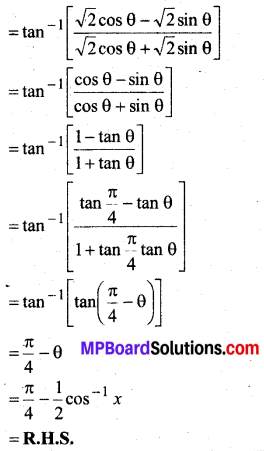
प्रश्न 12.

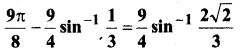
हल:

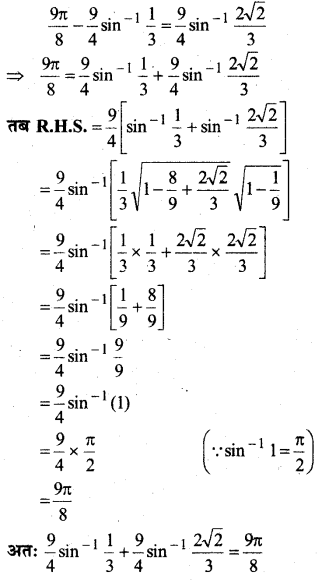
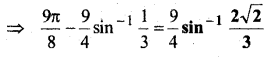
निम्नलिखित समीकरणों को सरल कीजिए।
प्रश्न 13.
2 tan^-1(cosx) = tan^-1(2cosec x)
हल:
2 tan^-1(cosx) = tan^-1(2 cosecx)

प्रश्न 14.
tan^-1\(\frac{1-x}{1+x}=\frac{1}{2}\)tan^-1 x, (x > 0)
हल:

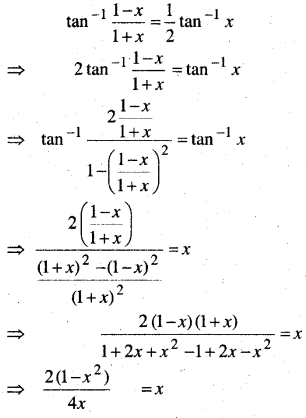
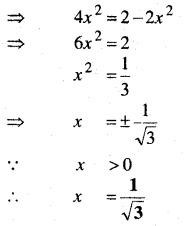
प्रश्न 15.
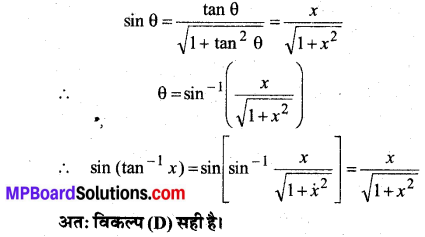
sin (tan^-1x), |x| < 1 बराबर होता है-

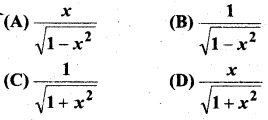
हल:
sin (tan^-1x)
माना tan^-1x = θ
x = tanθ

प्रश्न 16.
यदि sin^-1(1 – x) – 2 sin^-1 x = \(\frac{\pi}{2}\), तो x का मान बराबर है-
(A) 0, \(\frac{1}{2}\)
(B) 1, \(\frac{1}{2}\)
(C) 0
(D) \(\frac{1}{2}\)
हल:
sin^-1(1 – x) – 2sin^-1 x = \(\frac{\pi}{2}\)
हम जानते हैं, \(\frac{\pi}{2}\) = sin^-1(1 – x) + cos^-1(1 – x)
∴ sin^-1 (1 – x) – 2sin^-1 x = sin^-1 (1 – x) + cos^-1 (1 – x)
⇒ -2sin^-1 x = cos^-1 (1 – x) … (1)
माना sin^-1x = θ
∴ x = sin θ
∴ cos 2θ = 1 – 2sin² θ = 1 – 2x²
cos (-2θ) = 1 – 2x²
-2θ = cos^-1 (1 – 2x²)
-2sin^-1 x = cos^-1 (1 – 2x²) …(2)
समीकरण (1) व (2) से,
cos^-1(1 – 2x²) = cos^-1 (1 – x)
1 – 2x² = 1 – x
x² – 2x² = 0
x(1 – 2x²) = 0 = x = 0, x = \(\frac{1}{2}\)
x = \(\frac{1}{2}\) समीकरण को सन्तुष्ट नहीं करता है।
∴ x = 0
अतः विकल्प (C) सही है।

प्रश्न 17.
tan^-1\(\left(\frac{x}{y}\right)\) – tan^-1\(\frac{x-y}{x+y}\) का मान है-

हल:

In this article, we share MP Board Class 10th Maths Book Solutions Chapter 1 संबंध एवं फलन Ex 1.3 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन Ex 1.3

प्रश्न 1.
मान लीजिए कि f:{1, 3, 4} → {1, 2, 5} तथा g:{1, 2, 5} → {1, 3}, f = {(1, 2), (3, 5), (4, 1)} तथा g = {(1, 3), (2, 3), (5, 1)} द्वारा प्रदत्त है।g of ज्ञात कीजिए।
हल:
दिया है:
f = {(1, 2), (3, 5)(4, 1)}
तथा g = {(1, 3),(2, 3), (5, 1)}
∴ gof(1) = g (f (1))
= g(2)
= 3
gof(3) = g(f (3))
= g(5)
= 1
तथा g of(4) = g(f(4))
= g(1)
= 3
∴ gof = {(1, 3), (3, 1), (4, 3)}

प्रश्न 2.
मान लीजिए कि f,g तथा h, R से R तक दिए फलन हैं। सिद्ध कीजिए कि
(f + g)oh = foh + goh
(f.g)oh = (foh).(goh)
हल:
दिया है:
f: R → R, g: R → R, h: R → R
∴ (fog)oh(x) = (g + g)(h (x))
= g(h (x)) + g (h (x))
= (foh) (x) + (goh) (x)
= (foh + goh) (x)
∴ f(f + g) oh = foh + goh
पुनः (f.g) oh(x) = (f.g)(h (x))
= f (h (x)).g(h (x))
= (foh)x (goh) (x)
= [(goh) (goh)](x)
∴ (f.g)oh = (foh) (goh)

प्रश्न 3.
gof तथा fog ज्ञात कीजिए, यदि
(i) f(x) = |x| तथा g(x) = |5x – 2|
(ii) f(x) = 8x³ तथा g(x) = x^1/3
हल:
(i) ∵ f(x) = |x|
तथा g(x) = [5x – 2||
∴ gof(x) = g[f (x)]
= g[/x]
= |5 |x – 2|
तथा fog (x) = f|g(x)|
= f (|5x – 2|)
= |5x – 2|
= |5x – 2|

(ii) ∵ f(x) = 8x³
तथा g(x) = x^1/3
∴ gof(x) = g[f (x)]
= g(8x³)
= (8x³)^1/3
= 2x
तथा fog(x) = f[g(x)]
= f(x^1/3)
= 8(x^1/3)³
= 8x

प्रश्न 4.
यदि f(x) = \(\frac{(4 x+3)}{6 x – 4}\), x ≠ \(\frac{2}{3}\), तो सिद्ध कीजिए कि सभी x ≠ \(\frac{2}{3}\) के लिए f0f(x) = x है। का प्रतिलोम फलन क्या है?
हल:
दिया है :

⇒ y (6x – 4) = 4x + 3
⇒ 6xy – 4y = 4x + 3
⇒ 6xy – 4x = 4y + 3
⇒ 6xy – 4x = 4y + 3
⇒ x = \(\frac{4 y+3}{6 y-4}\)
⇒ g(y) = f^-1(y) = \(\frac{4 y+3}{6 y-4}\)
अतः f का प्रतिलोम f ही है।

प्रश्न 5.
कारण सहित बतलाइए कि क्या निम्नलिखित फलनों के प्रतिलोम हैं-
(i) f:{1, 2, 3, 4} → {10} जहाँ
f = {(1, 10), (2, 10), (3, 10), (4, 10)}
(ii) g : {5, 6, 7, 8} → {1, 2, 3, 4} जहाँ
g = {(5, 4), (6, 3), (7, 4),(8, 2}}
(iii) h: {2, 3, 4, 5} → {7, 9, 11, 13} जहाँ
h = {(2, 7), (3, 9), (4, 11), (5, 13)}
हल:
(i) दिया है : f :{1, 2, 3, 4} → {10) जहाँ
f = {(1, 10),(2, 10), (3, 10),(4, 10)}
∵ f(1) = 10, f(2) = 10, f(3) = 10, f(4) = 10
⇒ f(1) = f(2) = f(3) = f(4)
∴ f एकैक नहीं है।
अतः दिए गये फलन का प्रतिलोम नहीं है।

(ii) g = {5, 6,7, 8} → 1, 2, 3, 4) जहाँ
g = {(5, 4), (6, 3),(7, 4), (8, 2)}
∴ g (5) = 4 तथा g (7) = 4
∵ (5) = g (7) = 4
∴ एकैक नहीं है।
अतः दिये गये फलन का प्रतिलोम नहीं है।

(iii) h : {2, 3, 4, 5} → {7, 11, 13} जहाँ
h = {(2, 7),(3, 9),(4, 11), (5, 13)}
∴ h (2) = 7, h (3) = 9, h (4) = 11 तथा h (5) = 13
∴ h एकैक है
अतः दिए गए फलन (h) का प्रतिलोम है।

प्रश्न 6.
सिद्ध कीजिए कि f:[- 1, 1] → R, f(x) = \(\frac{x}{x+2}\), द्वारा प्रदत्त फलन एकैकी है। फलन f: [- 1, 1] → (f का परिसर), का प्रतिलोम फलन ज्ञात कीजिए।
हल:
यदि f(x₁) = f(x₂) तब,

प्रश्न 7.
f(x) = 4x + 3 द्वारा प्रदत्त फलन f : R → R पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है। का प्रतिलोम फलन ज्ञात कीजिए।
हल:
फलन f : R → R निम्न द्वारा परिभाषित है
f(x) = 4x + 3
यदि f(x₁) = f(x₂)
⇒ 4x₁ + 3 = 4x₂ + 3
⇒ x₁ = x₂
∴ f एकैक है।
तथा माना f(x) = y = 4x + 3
⇒ 4x = y – 3
⇒ x = \(\frac{y-3}{4}\) = g(y)
सहप्रान्त (Co – domain) प्रत्येक अवयव yE R का प्रान्त (do main) में पूर्व प्रतिबिम्ब (pre image) है।
∴ f आच्छादक (onto) है
अतः f एकैक और आच्छादक है।
अत: f व्युत्क्रमणीय है।
∴ f का प्रतिलोम फलन
f^-1 (y) = g(y)
= \(\frac{y-3}{4}\)

प्रश्न 8.
f(x) = x² + 4 द्वारा प्रदत्त फलन f : R → [4, ∞) पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है तथा f का प्रतिलोम f^-1, f^-1(y) = \(\sqrt{y-4}\), द्वारा प्राप्त होता है, जहाँ R सभी ऋणेत्तर वास्तविक संख्याओं का समुच्चय है।
हल:
यदि f (x₁) = f(x₂)
⇒ x₁² + 4 = x₁² + 4
⇒ x₁² = x₁² = x₁ = x₂
( ∵ x ϵ R₊
∴ x > 0)
∴ f एकैक है।
माना y = f(x) = x² + 4
= x² + 4 = y
x² = y – 4 = x = ±\(\sqrt{y-4}\)
लेकिन x धनात्मक है।
∴ x = \(\sqrt{y-4}\)
∴ f आच्छादक है।
अतः फलन f व्युत्क्रमणीय है।
∴ f का प्रतिलोम फलन
f^-1(y) = g(y)
= \(\sqrt{y-4}\) , y ≥ 4
∀ y ≥ 4, 8 (y) एक धनात्मक मान है।
अतः f का प्रतिलोम फलन = \(\sqrt{y-4}\)

प्रश्न 9.
f(x) = 9x² + 6x – 5 द्वारा प्रदत्त फलन f: R → [ – 5, ∞) पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है तथा f^-1 = \(\left(\frac{(\sqrt{y+6}-1)}{3}\right)\) है।
हल:
दिया है : f(x) = 9x² + 6x – 5 तथा f: R → [ – 5, ∞)
माना y = 9x² + 6x – 5
= (3x + 1)² – 6
⇒ y + 6 = (3x + 1)² ⇒ 3x + 1 = \(\sqrt{y+4}\)

प्रश्न 10.
मान लीजिए कि f: x → y व्युत्क्रमणीय फलन है। सिद्ध कीजिए कि f का प्रतिलोम फलन अद्वितीय (unique) है।
हल:
∵ यदि f एक व्युत्क्रमणीय है।
∴ gof (x) = I_x और fog (y) = I_y
⇒ f एकैक तथा आच्छादक है।
माना g₁ व g₂, f के दो प्रतिलोम फलन हैं।
∴ fog₁ (y) = I_y तथा g0g₂(y) = I_y
I_y दिए गये फलन f के लिए अद्वितीय है
∴ g₁(9) = g₂ (y) ⇒ f एकैक और आच्छादक है
अतः f का प्रतिलोम फलन अद्वितीय है।

प्रश्न 11.
f: {1, 2, 3} → {a, b, c}, f(1) = a, f(2) = b तथा f(3) = c द्वारा प्रदत्त फलन पर विचार कीजए। f^-1 ज्ञात कीजिए और सिद्ध कीजिए कि (f^-1)^-1 = f है।
हल:
दिया है :
f: {1, 2, 3} → a, b, d
तथा f(1) = a, f(2) = b, f (3) = c
माना x = {1, 2, 3} तथा y = {a, b, c}
इसलिए f: X → Y
∴ f^-1 : Y → X
= f^-1(a) = 1, f^-1(b) = 2, f^-1(c) = 3
इस फलन का प्रतिलोम फलन हम इस प्रकार से भी लिख सकते हैं
(f^-1)^-1 : x → y
⇒ (f^-1)^-1(1) = a, (f^-1)^-1
(2) = b, (f^-1)^-1(3) = c
इसलिए,
f: x → y
f(1) = a, f(2) = b, f(3) = c
अतः (f^-1)^-1 = f

प्रश्न 12.
मान लीजिए कि f:x → Y एक व्युत्क्रमणीय फलन है सिद्ध कीजिए कि f^-1 का प्रतिलोम f, है अर्थात् (f^-1)^-1 = f है।
हल:
f:x → Y एक व्युत्क्रमणीय फलन है।
∴ f एकैक तथा आच्छादक है।
⇒ g: y → x, जहाँ भी एकैक और आच्छादक है
∴ gof (x) = I_x तथा fog (y) = I_y
⇒ g = f
अतः f^-1 o(f^-1)^-1 = I
fo[f^-1 o(f^-1)^-1] = foI
⇒ (f of^-1) o(f^-1)^-1 = f
Io(f^-1)^-1 = f
⇒ (f^-1)^-1 = f

प्रश्न 13.
यदि f :R → R, f(x) = (3 – x³)^1/3, द्वारा प्रदत्त है तो fof(x) बराबर है.
(A) x^1/3
(B) x³
(C) x
(D) (3 – x³)
हल:
दिया है : f(x) = (3 – x³)^1/3 तथा f: R → R
∴ fof(x) = f[f(x)] = [[(3 – x²)^1/3]
= [3 – {(3 – x³ )^1/3}³}]^1/3
= [3 – (3 – x³)]^1/3 = x
अतः विकल्प (C) सही है।

प्रश्न 14.
मान लीजिए कि f(x) = \(\frac{4 x}{3 x+4}\) द्वारा परिभाषित एक फलन f: R – 1 – \(\left\{-\frac{4}{3}\right\}\) → R है। f का प्रतिलोम, अर्थात् प्रतिचित्र (Map) g : परिसर f → R – \(\left\{-\frac{4}{3}\right\}\), निम्नलिखित में से किसके द्वारा प्राप्त होगा-

हल:
दिया है : f(x) = \(\frac{4 x}{3 x+4}\) तथा f: R – \(\left\{-\frac{4}{3}\right\}\) → R
माना y = \(\frac{4 x}{3 x+4}\)
∴ y(3x + 4) = 4x या 3xy + 4y = 4x
⇒ x(3y – 4) + 4y = 0
⇒ x = \(\frac{4 y}{4-3 y}\) = g(y)
अतः विकल्प (B) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन Ex 1.1 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Solutions Chapter 1 संबंध एवं फलन Ex 1.1

प्रश्न 1.
निर्धारित कीजिए कि क्या निम्नलिखित सम्बन्धों में से प्रत्येक स्वतुल्य, सममित तथा संक्रामक हैं –
(i) समुच्चय A = {1, 2, 3,….13, 14} में सम्बन्ध R, इस प्रकार परिभाषित है कि
R= {(x, y): 3x – y = 0}
(ii) प्राकृत संख्याओं के समुच्चय N में R = {(x, y): y = x + 5 तथा x < 4} द्वारा परिभाषित सम्बन्ध R.
(iii) समुच्चय A = {1, 2, 3, 4, 5, 6} में R = {(x, y) : y भाज्य है x से} द्वारा परिभाषित सम्बन्ध R है।
(iv) समस्त पूर्णांकों के समुच्चय z में R = {(x, y): x – y एक पूर्णांक है } द्वारा परिभाषित सम्बन्ध R.
(v) किसी विशेष समय पर किसी नगर के निवासियों के समुच्चय में निम्नलिखित सम्बन्ध R.
(a) R = {(x, y): x तथा y एक ही स्थल पर कार्य करते
(b) R = {(x, y): x तथा ‘एक ही मोहल्ले में रहते हैं।}
(c) R = {(x, y) : x, y से ठीक – ठीक 7 सेमी लम्बा है।}
(d) R = {(x, y): x, y की पत्नी है।।
(e) R = {(x, y): x, y के पिता हैं।}
हल:
(i) दिया है : A = {1, 2, 3,….13, 14}
तथा R = {(x, y) : 3x – y = 0}
(a) y = x रखने पर,
3x – x ≠ 0 [∵x ≠ 0]
इसलिए R स्वतुल्य नहीं है।
(b) x और y को आपस में बदलने पर,
यदि 3x – y = 0, 3y – x ≠ 0
इसलिए R सममित नहीं है।
(c) यदि 3x – y = 0, 3y – z = 0 तब 3y – z ≠ 0.
इसलिए R संक्रामक नहीं है।
अतः R स्वतुल्य सममित तथा संक्रामक नहीं है।

(ii) प्राकृत संख्याओं का समुच्चय A = {1, 2, 3, 4,….}
R = {(x, y): y= x + 5, x < 4}
= {(1, 6), (2, 7), (3, 8)}
स्पष्ट है यह सम्बन्ध स्वतुल्य, सममित तथा संक्रामक नहीं है।

(iii) दिया है :
A = {1, 2, 3, 4, 5, 6 8}
R = {(x, y) : y संख्या x से भाज्य है।
= {1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6) (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4) (5, 5), (6, 6)}
(a) (1, 2), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6) ϵ R
इसलिए R स्वतुल्य है।

(b) यदि ” संख्या x से भाज्य है तो x संख्या ” से भाज्य नहीं है।
जैसे – (1, 2) ϵ R परन्तु (2, 1) ∉ R
इसलिए R सममित नहीं है।

(c) (1, 2), (2, 4) ϵ R, (1, 4) भी R में है।
इसी प्रकार (1, 3), (3, 6) ϵ R तब (1, 6) ϵ R
इसलिए, R संक्रामक है।
अतः R स्वतुल्य तथा संक्रामक है परन्तु सममित नहीं है।

(iv) A = पूर्णांकों का समुच्चय
{… – 3, – 2, – 1, 0, 1, 2, 3,…}
तथा R = {(x, y) : x – y एक पूर्णांक है}
(a) y = x रखने पर,
x – x = 0, एक पूर्णांक है। एक
इसलिए R स्वतुल्य है।

(b) x – y और y – x दोनों ही पूर्णांक हैं।
इसलिए R सममित नहीं है।

(c) x – y और y – z दोनों ही पूर्णांक हैं तथा x – z भी पूर्णांक हैं।
इसलिए R संक्रामक है।
अतः R स्वतुल्य, सममित तथा संक्रामक है। उत्तर

(v) माना A = किसी विशेष समय पर किसी नगर में रहने – वालों का समुच्चय
(a) R = {(x, y) : x तथा y एक ही स्थान पर कार्य करते हैं।
∴ R स्वतुल्य है, क्योंकि प्रत्येक व्यक्ति उस नगर में उस विशेष समय पर कार्यरत है।
R सममित है, क्योंकि x, y एक ही स्थान पर एक समय पर _ कार्यरत हैं तो y, z भी उसी स्थान पर उस समय कार्यरत हैं।
R संक्रामक है, क्योंकि x, y तथा y, एक नगर में एक ही समय पर कार्यरत हैं तो उस नगर में उसी समय x, z भी कार्यरत
अतः स्वतुल्य, सममित तथा संक्रामक है।

(b) R = {(x, y) : x तथा y एक ही मोहल्ले में रहते हैं।
R स्वतुल्य है, क्योंकि उस स्थान का प्रत्येक व्यक्ति वहीं पर रहता है।
R सममित है, क्योंकि और एक स्थान पर रहते हैं तो उसी स्थान पर y और x भी रहते हैं।
R संक्रामक है, क्योंकि x, y तथा y, z एक स्थान पर रहते हैं तो x, z भी उसी स्थान पर रहते हैं।
अतः R स्वतुल्य, सममित तथा संक्रामक है।

(c) R = {(x, y}): z, y से ठीक – ठीक 7 सेमी लम्बा है}.
R स्वतुल्य नहीं है, क्योंकि कोई भी व्यक्ति अपने से 7 सेमी अधिक लम्बा नहीं हो सकता।
R सममित नहीं है, क्योंकि y, x से ठीक 7 सेमी अधिक लम्बा हो तो x, y से 7 सेमी लम्बा नहीं हो सकता।
R संक्रामक नहीं है, क्योंकि x, y से तथा y, x से ठीक 7 सेमी लम्बे तो x, 2 से ठीक 7 सेमी अधिक लम्बे नहीं हैं।
अतः R स्वतुल्य, सममित तथा संक्रामक में से कोई भी नहीं है।

(d) R = {(x, y}) : x, y की पत्नी है।
R स्वतुल्य नहीं है, क्योंकि x अपनी ही पत्नी नहीं हो सकती हैं।
R सममित नहीं है, क्योंकि यदि x, y की पत्नी है तो y, x की पत्नी नहीं हो सकती।
R संक्रामक नहीं है, क्योंकि यदि x, y की पत्नी है तो y किसी की भी पत्नी नहीं है।
अतः R स्वतुल्य, सममित तथा संक्रामक नहीं है।

(e) R = {(x, y) : x, y के पिता हैं।
R स्वतुल्य नहीं है, क्योंकि x अपना ही पिता नहीं हो सकता।
R सममित नहीं है, क्योंकि x, y का पिता है तो y, x का पिता नहीं हो सकता।
R संक्रामक नहीं है, क्योंकि x, y का y, z का पिता है तो x, z का पिता नही हो सकता।
अतः R स्वतुल्य, सममित तथा संक्रामक नहीं है।

प्रश्न 2.
सिद्ध कीजिए कि वास्तविक संख्याओं के समुच्चय R में R = {(a, b):a ≤ b² }, द्वारा परिभाषित संबंध R, न तो स्वतुल्य है, न सममित है और न ही संक्रामक है।
हल:
(i) ∵ a ≰ a², समस्त a ϵ R जैसे \(\frac{1}{2}, \frac{1}{4}\) से छोटा नहीं हो सकता है।
अतः R स्वतुल्य नहीं है।
(ii) R सममित भी नहीं है क्योंकि यदि a ≤ b² तब, b, a² से छोटा अथवा बराबर नहीं हो सकता है। जैसे 2 < 7² लेकिन 7 ≰ 2²
(iii) R न ही संक्रामक क्योंकि
यदि a ≤ b², b ≤ c² तब a, c² से छोटा नहीं है जैसे 5 < 3², 3 < 2² लेकिन 5, 2² से छोटा नहीं है।

प्रश्न 3.
जाँच कीजिए कि क्या समुच्चय {1, 2, 3, 4, 5, 6} में R = {(a, b): b = a + 1} द्वारा परिभाषित संबंध R स्वतुल्य, सममित या संक्रामक है।
हल:
∵ a ≠ a + 1
∴ R स्वतुल्य नहीं है।
R सममित नहीं है क्योंकि यदि b = a + 1, तब a ≠ b + 1
R संक्रामक भी नहीं है क्योंकि यदि b = a + 1, c = b + 1, तब c = (a + 1) + 1 # a + 1

प्रश्न 4.
सिद्ध कीजिए कि R में R= {(a, b): a ≤ b}, द्वारा परिभाषित संबंध R स्वतुल्य तथा संक्रामक है किन्तु सममित नहीं है।
हल:
दिया है R = {(a, b): a ≤ b}
b के स्थान पर a रखने पर,
a ≤ a ⇒ a = a
सत्य है अतः R स्वतुल्य है।
पुनः यदि a ≤ b, लेकिन b ≤ a सत्य नहीं है
जैसे 2 < 3 लेकिन 3 ≮ 2 अतः R सममित नहीं है।
पुनः यदि a ≤ b और b ≤ c तब a ≤ c
जैसे 2 < 5, 5 < 8 ⇒ 2 < 8 इसलिए R संक्रामक है
अतः R स्वतुल्य तथा संक्रामक है किन्तु सममित नहीं है।

प्रश्न 5.
जाँच कीजिए कि क्या R में R= {(a, b): a ≤ b³} द्वारा परिभाषित संबंध स्वतुल्य, सममित अथवा संक्रामक है?
हल:
(i) ∵ a ≤ a³ सत्य नहीं है जैसे \(\frac{1}{3}\) ≮ \(\left(\frac{1}{3}\right)^{3}\)
∴ R स्वतुल्य नहीं है।
(ii) यदि a ≤ b³, लेकिन b ≰ a³; जैसे 2 ≤ 9³, लेकिन 9 ≰ 2³
∴ R सममित नहीं है।
(iii) यदि a ≤ b³ और b ≤ cv लेकिन यह आवश्यक नहीं है कि a,c से छोटा होगा।
∴ R संक्रामक नहीं है।

प्रश्न 6.
सिद्ध कीजिए कि समुच्चय {1, 2, 3} में R={(1, 2), (2, 1)} द्वारा प्रदत्त संबंध R सममित है किंतु न तो स्वतुल्य है और न संक्रामक है।
हल:
(i) (1, 1), (2, 2), (3, 3) ∉ R
∴ R स्वतुल्य नहीं है।
(ii) ∵ (1, 2), (2, 1) ϵ R
∴ R सममित है।
(iii) ∵ (1, 2) और (2, 1) ϵ R, परन्तु (1, 1) ∉ R
∴ R संक्रामक नहीं है।

प्रश्न 7.
सिद्ध कीजिए कि किसी कॉलेज के पुस्तकालय की समस्त पुस्तकों के समुच्चय A में R = {(x, y): x तथा y में पेंजों की संख्या समान है} द्वारा प्रदत्त सम्बन्ध र एक तुल्यता सम्बन्ध है।
हल:
A = किसी कॉलेज के पुस्तकालय की समस्त पुस्तको का समुच्चय
तथा R = {(x, y}): x तथा y में पेजों की संख्या समान है।
(i) R स्वतुल्य है, क्योंकि बराबर पृष्ठों वाली प्रत्येक पुस्तक में उतने ही पृष्ठ होंगे।
(ii) R सममित है, क्योंकि x, y पुस्तकों में पृष्ठ बराबर हैं तो y,x पुस्तकों में भी पृष्ठ बराबर होंगे।
(iii) R संक्रामक है, क्योंकि x, y तथा y, z पुस्तकों में पृष्ठ बराबर हैं तो x, z पुस्तकों में भी पृष्ठ बराबर होंगे।
अतः R तुल्यता सम्बन्ध है।

प्रश्न 8.
सिद्ध कीजिए कि A = {1, 2, 3, 4, 5} में, R= {(a, b):|a – b| सम है} द्वारा प्रदत्त संबंध R एक तुल्यता संबंध है। प्रमाणित कीजिए कि {1, 3, 5} के सभी अवयव एक दूसरे से संबंधित हैं और समुच्चय {2, 4} के सभी अवयव एक – दूसरे से संबंधित हैं परन्तु {1, 3, 5} का कोई भी अवयव {2, 4} के किसी अवयव से संबंधित नहीं है।
हल:
A = {1, 2, 3, 4, 5) तथा R = {(a, b):|a – b| सम है}
माना अवयव a, समुच्चय A का अवयव है
तब |a – a| = 0 सम है।
∴ R स्वतुल्य है।
यदि |a – b| सम है
तब, |b – a| भी सम होगा।
∴ R सममित है
पुनः a – c = a – b + b – c
यदि |a – b| तथा | b – सम हो तब,
उनका योग |a – b + b – c| भी सम होगा।
a |a – c| सम होगा।
∴ R संक्रामक है
अत: R एक तुल्यता संबंध है।
∵ |1 – 3| = |3 – 1| = 2
|3 – 5| = |5 – 3| = 2
तथा |1 – 5| = |5 – 1| = 4
जो कि सभी सम संख्याएँ हैं
इसलिए {1, 3, 5} के सभी अवयव एक दूसरे से संबंधित हैं।
इसी प्रकार {2, 4} के अवयव भी एक – दूसरे से संबंधित हैं। अब |1 – 2| = 1 जो कि सम संख्या नहीं है।
अतः {1, 3, 5) के अवयव {2, 4} से संबंधित नहीं है।

प्रश्न 9.
सिद्ध कीजिए कि समुच्चय A = {x ϵ z : 0 ≤ x ≤ 12}, में दिए गए निम्नलिखित संबंधों R में से प्रत्येक एक तुल्यता संबंध है :
(i) R = {(a, b): |a – b|, 4 का एक गुणज है}
(ii) R = {(a,b): a = b};
प्रत्येक दशा में 1 से संबंधित अवयवों को ज्ञात कीजिए।
हल:
दिया है समुच्चय
A = {x ϵ z : 0 ≤ x ≤ 12}
= {0, 1, 2,…12}
(i) R = {(a, b): |a – b, 4 का गुणज है।
(a) a – a = 0 = 4k, जहाँ k = 0 ⇒ (a, a) ϵ R
∴ R स्वतुल्य है।

(b) यदि |a – b| = 4k
तब |b – a| = 4k
⇒ (a, b) तथा (b, a) दोनों R से संबंध है
इसलिए R सममित है।
पुनः a – c = a – b + b – c
जब a – b तथा b – c दोनो के 4 के गुणज है।
तब, a – c भी 4 का गुणज होगा।
⇒ यदि (a, b), (b, c) ϵ R तब, (a – c) ϵ R
इसलिए R,संक्रामक है।
अतः R एक तुल्यता संबंध है।
अतः समुच्चय {1, 5, 9}, 1 से संबंधित है।

(ii) R = {(1, b): a = b}
∴ R = {(0, 0), (1, 1), (2, 2) … (12, 12)}
(a) a = a ⇒ (a, a) ϵ R
∴ R एक स्वतुल्य है।
(b) पुनः यदि (a, b) ϵ R
⇒ a = b ⇒ b = a, तब (b, a) ϵ R
∴ R सममित है।
पुनः यदि (a, b) ϵ R तथा (b, c) ϵ R
⇒ a = b = c
इसलिए a = c ⇒ (a, c) ϵ R
∴ R संक्रामक है।
अत: R एक तुल्यता संबंध R जो प्रत्येक दशा में 1 से संबंधित है।

प्रश्न 10.
ऐसे सम्बन्ध का उदाहरण दीजिए, जो
(i) सममित हो परन्तु न तो स्वतुल्य हो और न संक्रामक हो।
(ii) संक्रामक हो परन्तु न तो स्वतुल्य हो और न सममित हो।
(iii) स्वतुल्य तथा सममित हो किन्तु संक्रामक न हो।
(iv) स्वतुल्य तथा संक्रामक हो किन्तु सममित न हो।
(v) सममित तथा संक्रामक हो किन्तु स्वतुल्य न हो।
हल:
(i) माना A = एक समतल में सरल रेखाओं का समुच्चय तथा R = {(a, b): a, b पर लम्ब है} रेखा a, b पर लम्ब है तो b रेखा a पर लम्ब है।
(1) R सममित सम्बन्ध है।
(2) R स्वतुल्य नहीं है, क्योंकि रेखा a अपने आप ही लम्ब नहीं हो सकती है।
(3) R संक्रामक नहीं है, यदि रेखा b पर लम्ब है, b रेखा c पर लम्ब है परन्तु a रेखा c पर लम्ब नहीं है।

(ii) माना A = वास्तविक संख्याओं का समुच्चय – तथा R = {(a, b): a > b}
(1) R संक्रामक है, यदि a > b और b > c ⇒ a > c
(2) R स्वतुल्य नहीं है, यदि a अपने आप से बड़ी संख्या नहीं है।
(3) R सममित नहीं है, यदि a> b तो b,a से बड़ा नहीं है।

(iii) माना A = {1, 2, 3} तथा R = {(a, b): a + b ≤ 4}.
= {(1, 1), (1, 2), (1, 3),(2, 1),(2, 2), (3, 1)
(1) R स्वतुल्य है, यदि (1, 1), (2, 2) ϵ R.
(2) R सममित है, यदि (1, 2), (2, 1) ϵ R (1, 3), (3, 1) ϵ R
(3) R संक्रामक नहीं है, यदि (2, 1) ϵ R, (1, 3) ϵ R किन्तु (2, 3) ϵ R.

(iv) माना A = {1, 2, 3}
तथा R = {(a, b): a < b}
= {(1, 1), (2, 3), (3, 3), (1, 2), (1, 3),(2, 3)}
(1) R स्वतुल्य है, यदि (1, 1), (2, 2), (3, 3) ϵ R
(2) R संक्रामक है, यदि (1, 2), (2, 3) ϵ R ⇒ (1, 3) ϵ R
(3) R सममित नहीं है, यदि a < b परन्तु b, a से कम नहीं है।

(v) माना A = {1, 2, 3}
तथा R = {(1, b): 0 < |a – b| ≤ 2}
= {(1, 2), (1, 3), (2, 3), (3, 1), (2, 1), (3, 2)}
(1) R सममित है, यदि (1, 2) ϵ R, (2, 1) ϵ R इसी प्रकार (1, 3) ϵ R, (3, 1) ϵ R
(2) R संक्रामक है, यदि (1, 2), (2, 3) ϵ R c (1, 3) ϵ R
(3) R स्वतुल्य नहीं है, यदि (1, 1), (2, 2), (3, 3) R में नहीं है।

प्रश्न 11.
सिद्ध कीजिए कि किसी समतल में स्थित बिन्दुओं में R : {{P, Q) : बिन्दु P की मूल बिन्दु से दूरी, बिन्दु Q की मूल बिन्दु से दूरी के समान है} द्वारा प्रदत्त सम्बन्ध र एक तुल्यता सम्बन्ध है। पुनः सिद्ध कीजिए कि बिन्दु P ≠ (0, 0) से सम्बन्धित सभी बिन्दुओं का समुच्चय P से होकर जाने वाले एक ऐसे वृत्त को निरूपित करता है, जिसका केन्द्र मूलबिन्दु पर
हल:
माना A = समतल में बिन्दुओं का समुच्चय
तथा R = {(P, Q): मूल बिन्दु से P तथा Q की दूरी समान है}
= {(P, Q) : OP = OQ}
(i) R स्वतुल्य है, क्योंकि OP अपने ही बराबर है।
(ii) R सममित है, यदि OP = OQ ⇒ OQ =OP
(iii) R संक्रामक है, यदि OP = OQ, OQ = QR ⇒ OP = OR
अतः R तुल्यता सम्बन्ध है।
माना OP =K ⇒ बिन्दु P एक वृत्त पर रहता है जो O से K दूरी पर है।

प्रश्न 12.
सिद्ध कीजिए कि समस्त त्रिभुजों के समुच्चय A में, R = {(T₁, T₂) : T₁, T₂ के समरूप है} द्वारा परिभाषित सम्बन्ध र एक तुल्यता सम्बन्ध है। भुजाओं 3, 4, 5 वाले समकोण त्रिभुज T₁, भुजाओं 5, 12, 13 वाले समकोण त्रिभुज T₂ तथा भुजाओं 6, 8, 10 वाले समकोण त्रिभुज T₃ पर विचार कीजिए। T₁, T₂ और T₃ में से कौन – से त्रिभुज परस्पर सम्बन्धित हैं?
हल:
माना A = एक समतल में त्रिभुजों का समुच्चय
तथा R = {(T₁, T₂) : T₁ और T₂ समरूप त्रिभुज है।
(i) (a) R स्वतुल्य है, क्योंकि प्रत्येक त्रिभुज अपने समरूप है।
(b) R सममित है, यदि त्रिभुज T₁, T₂ के समरूप हैं तो त्रिभुज T₂, T₁ के भी समरूप हैं।
(c) R संक्रामक है, यदि त्रिभुज T₁, T₂ और त्रिभुज T,,T, समरूप हैं तो त्रिभुज T₂, T₃ भी समरूप हैं।
अतः R तुल्यता सम्बन्ध है।

(ii) त्रिभुज T₁ की भुजाएँ 3, 4, 5 हैं त्रिभुज T₂ की भुजाएँ 5, 12, 13 हैं तथा त्रिभुज T, की भुजाएँ 6, 8, 10 हैं।
::त्रिभुज T₁ तथा T₃ की भुजाएँ समानुपाती हैं। इसलिए यह समरूप है। अतः त्रिभुज T₁तथा T₃ आपस में सम्बन्धित है।

प्रश्न 13.
सिद्ध कीजिए कि समस्त बहुभुजों के समुच्चय A में, R = {(P₁, P₂) : P₁ तथा P₂ की भुजाओं की संख्या समान है} प्रकार से परिभाषित संबंध R एक तुल्यता संबंध है। 3, 4 और 5 लम्बाई की भुजाओं वाले समकोण त्रिभुज से संबंधित समुच्चय A के सभी अवयवों का समुच्चय ज्ञात कीजिए।
हल:
माना बहुभुज P में भुजाओं की संख्या n है।
R = {(P₁, P₂) : P₁ तथा P₂ भुजाओं वाले बहुभुज हैं}
(i) ∴ प्रत्येक बहुभुज की n भुजाएँ हैं
∴ R स्वतुल्य है।

(ii) यदि P₁ तथा P₂ n भुजाओं वाले बहुभुज हों तब P₂ तथा P₁ भी n भुजाओं वाले बहुभुज होंगे।
∴ R सममित है।

(iii) माना P₁, P₂ तथा P₃ n भुजाओं वाले बहुभुज हैं
तब P₁ तथा P₂ भी n भुजाओं वाले बहुभुज हैं।
∴ R संक्रामक है।
अतः R एक तुल्यता संबंध है तथा समुच्चय A एक ही में स्थित सभी त्रिभुजों का समुच्चय

प्रश्न 14.
मान लीजिए कि XY – तल में स्थित समस्त रेखाओं का समुच्चय L है और L में R = {(L₁, L₂) : L₁ समान्तर है L₂ के} द्वारा परिभाषित संबंध R है। सिद्ध कीजिए कि R एक तुल्यता संबंध है। रेखा y = 2x + 4 से संबंधित समस्त रेखाओं का समुच्चय ज्ञात कीजिए।
हल:
L = XY – तल में स्थित सभी रेखाओं का समुच्चय
R = {(L₁, L₂) : L₁ ||L₁
∵ L₁ ||L₁
∴ R स्वतुल्य है।
पुनः L₁|| L₂ ⇒ L₂|| L₁
∴ R सममित है ।
माना L₁ || L₂ तथा L₂ || L₃
⇒ L₁ || L₃
∴ R एक संक्रामक है।
अतः R एक तुल्यता संबंध है।
रेखा y = 2x + 4 से संबंधित समस्त रेखाओं का समुच्चय
y=2x + C, C ϵ R

प्रश्न 15,
मान लीजिए कि समुच्चय {1, 2, 3, 4} में, R={(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)} द्वारा – परिभाषित सम्बन्ध R है। निम्नलिखित में से सही उत्तर चुनिए।
(A) R स्वतुल्य तथा सममित है किन्तु संक्रामक नहीं है।
(B) R स्वतुल्य तथा संक्रामक है किन्तु सममित नहीं है।
(C) R सममित तथा संक्रामक है किन्तु स्वतुल्य नहीं है।
(D) R एक तुल्यता सम्बन्ध है।
हल:
माना A = {(1, 2, 3, 4}
तथा R = {(1, 2),(2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}
(i) R स्वतुल्य है, यदि (1, 1), (2, 2), (3, 3),(4, 4) ϵ R
(ii) R सममित नहीं है, यदि (1, 2) ϵ R परन्तु (2, 1) ϵ R
(iii) R संक्रामक है, यदि (1 ,3) ϵ R, (3, 2) R तथा (1, 2) ϵ R
अतः R स्वतुल्य, संक्रामक है परन्तु सममित नहीं है।
अतः विकल्प (B) सही है।

प्रश्न 16.
मान लीजिए कि समुच्चय N में, R = {(a, b): a = b – 2, b > 6} द्वारा प्रदत्त सम्बन्ध R है। निम्नलिखित में से सही उत्तर चुनिए-
(A) (2, 4) ϵ R
(B) (3, 8) ϵ R
(C) (6, 8) ϵ R
(D) (8, 7) ϵ R
हल:
माना A = N, प्राकृत संख्याओं का समुच्चय है।
तथा R = {(a, b): a = b – 2, b > 6}
a = b – 2, b > 6
b= 8 रखने पर, a = 8 – 2 = 6 ⇒ (6, 8) ϵ R
अतः विकल्प (C) सही है।

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन Ex 1.2 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 1 संबंध एवं फलन Ex 1.2

प्रश्न 1.
सिद्ध कीजिए कि f(x) = \(\frac{1}{x}\) द्वारा परिभाषित फलन f : R_* → R_* एकैकी तथा आच्छादक है, जहाँ R_* सभी ऋणेत्तर वास्तविक संख्याओं का समुच्चय है। यदि प्रांत R_* को N से बदल दिया जाए, जब कि सहप्रांत पूर्ववत R. ही रहे, तो भी क्या यह परिणाम सत्य होगा?
हल:
दिया है फलन f(x) = \(\frac{1}{x}\)
यदि f(x₁) = f(x₂)

इसलिए f आच्छादक है।
अतः f : R_* →R_*, एकैकी व आच्छादक है।
यदि R_* को N से बदल दिया जाए तथा सहप्रांत (co – domain) पूर्वत: R_* है तब,
f : N →R_*
माना f(n₁) = f(n₂)
⇒ \(\frac{1}{n_{1}} = \frac{1}{n_{2}} \Rightarrow n_{1} = n_{2}\) (जहाँ n₁, n₂ % N)
∴ f एकैक है
परन्तु R_* में प्रत्येक वास्तविक संख्या का पूर्वत प्रतिबिम्ब (Preimage) प्रांत N में नहीं होगा
जैसे- \(\frac{1}{5 / 7} = \frac{7}{5} \notin N\)
∴ f आच्छादक (onto) नहीं है।
अतः परिणाम सत्य नहीं होगा।

प्रश्न 2.
निम्नलिखित फलनों की एकैक (Injective) तथा आच्छादी (Surjective) गुणों की जाँच कीजिए :
(i) f (x) = x² द्वारा प्रदत्त f: N →N फलन है।
(ii) f (x) = x² द्वारा प्रदत्त f: Z → Z फलन है।
(iii) f (x) = x² द्वारा प्रदत्त f: R → R फलन है।
(iv) f (x) = x³ द्वारा प्रदत्त f: N →N फलन है।
(v) f(x) = x³ द्वारा प्रदत्त f: Z → Z फलन है।
हल
(i) यहाँ f (x) = x² और f : N → N
(a) f(x¹) = f(x²) ⇒ x²₁ = x²₂ ⇒ x₁ = x₂, x₂ % N
∴ f एकैकी है।
(b) परन्तु सहप्रान्त में ऐसे अवयव हैं जो प्रान्त के किसी भी अवयव का प्रतिबिम्ब नहीं है। जैसे, माना 3 सहप्रान्त में है तो 3 प्रान्त के किसी भी अवयव का प्रतिबिम्ब नहीं है।
∴ f आच्छादक नहीं है। अतः । एकैकी है परन्तु आच्छादक नहीं है।

(ii) f: Z → Z, जबकि f(x) = x²
(a) f(-1) = f(1) = 1 ⇒ -1 और 1 का प्रतिबिम्ब भिन्न नहीं है।
∴ f एकैकी नहीं है।
(b) सहप्रान्त में ऐसे अवयव हैं जो प्रान्त के किसी अवयव में प्रतिबिम्ब नहीं हैं। जैसे-3 सहप्रान्त के, 3 प्रान्त के किसी अवयव का प्रतिबिम्ब नहीं है।
∴ f आच्छादक नहीं है।
अतः एकैकी नहीं है और न ही आच्छादक है।

(iii) f: R →R, यदि f(x) = x²
(a) (-1)² = 1 ⇒ f(-1) = f(1)
अतः -1 और -1 का प्रतिबिम्ब 1 है।
∴ एकैकी नहीं है।
(b) -2 सहप्रान्त में है परन्तु यह प्रान्त के किसी भी अवयव का प्रतिबिम्ब नहीं है।
अतः f आच्छादक नहीं है।
∴ f तो एकैकी है और न ही आच्छादक है।

(iv) f: N → N, यदि f(x) = x³
(a) f(x₁) = f(x₂) ⇒ x₁³ = x₂³ ⇒ x₁ = x₂
प्रत्येक x % N का एक प्रतिबिम्ब है।
∴ f एकैकी है।

(b) सहप्रान्त के बहुत से ऐसे अवयव हैं जिनमें प्रान्त के किसी भी अवयव के प्रतिबिम्ब नहीं हैं। जैसे-2, 3, 4, …… ये प्रान्त के किसी भी अवयव के प्रतिबिम्ब नहीं हैं।
∴ f आच्छादक नहीं है।
अतः f एकैकी है, परन्तु आच्छादक नहीं है।

(v) f: Z → Z, यदि f(x) = x³
(a) f(x₁) = f(x₂) ⇒ x₁³ = x₂³ ⇒ x₁ = x₂
∴ f एकैकी है।

(b) f के सहप्रान्त में बहुत से अवयव हैं जो प्रान्त में किसी भी अवयव का प्रतिबिम्ब नहीं हैं। जैसे–2, 3,
∴ f आच्छादक नहीं है।
अतः f एकैकी है परन्तु आच्छादक नहीं है।

प्रश्न 3.
सिद्ध कीजिए कि f(x) = [x] द्वारा प्रदत्त महत्तम पूर्णांक फलन f : R → R_* , न तो एकैकी है और न आच्छादक है, जहाँ [x], x से कम या उसके बराबर महत्तम पूर्णांक को निरूपित करता है।
हल
फलन f : R → R इस प्रकार परिभाषित है कि f(x) = [x]
यदि x = 1.1 तो f(1.1) = 1 (∵ 1, 1.1 कम पूर्णांक है)
तथा f(1.3) = 1
∵ 1.1 व 1.3 के प्रतिबिम्ब बराबर हैं।
∴ f एकैकी नहीं है।
x % R के लिए प्रान्त (domain) की प्रत्येक अवयव का सहडोमेन (Co-domain) में प्रतिबिम्ब होगा परन्तु सह प्रान्त के प्रत्येक अवयव का पूर्व प्रतिबिम्ब (Pre image), प्रान्त में नहीं होगा।
इसलिए । आच्छादक नहीं है।
अतः f न तो एकैकी है और न ही आच्छादक है।

प्रश्न 4.
सिद्ध कीजिए कि f(x) = |x| द्वारा प्रदत्त मापांक फलन f : R → R, न तो एकैकी है और न आच्छादक है, जहाँ |x| बराबर x, यदि धन या शून्य है तथा| |x| बराबर -x, यदि x ऋण है।
हल
दिया है
f : R → R तथा f(x) = |x|
यदि x = 1 तथा f(1) = 1
यदि x = -1 तब f(-1) = 1
∵ 1 और -1 दोनों का प्रतिबिम्ब 1 है।
∴ f एकैकी नहीं है।
∵ सहडोमेन (Co-domain) के ऋणात्मक अवयव का कोई भी पूर्व प्रतिबिम्ब (Pre image) डोमेन (domain) में नहीं है।
∴ f आच्छादक नहीं है।
अतः f न तो एकैकी और न ही आच्छादक है।

प्रश्न 5.
सिद्ध कीजिए कि

द्वारा प्रदत्त चिन्ह फलन न तो एकैकी है और न आच्छादक है।
हल:
f : R → R इस प्रकार परिभाषित है कि

∴ f(1) = 1 तथा f(2) = 1
∵ 1 व 2 का प्रतिबिम्ब समान (1) है।
पुनः x > 0 के लिए
f(x₁) = f(x₂) = 1 जहाँ x₁ ≠ x₂
इसी प्रकार x < 0 के लिए
f(x₁) = f(x₂) = -1 जहाँ x₁ ≠ x₂
∴ f एकैकी नहीं है।
सहप्रान्त (Co-domain) के अवयव -1, 0, 1 का पूर्व प्रतिबिम्ब (Pre image) डोमेन (domain) में नहीं है।
∴ f आच्छादक नहीं है।
अतः f न तो एकैकी है और न ही आच्छादक है।

प्रश्न 6.
मान लीजिए कि A = {1, 2, 3}, B = {4, 5, 6, 7} तथा f = {(1, 4),(2, 5),(3, 6)}A से B तक एक फलन है। सिद्ध कीजिए कि f एकैकी है।
हल
A = {1, 2, 3}, B = {4, 5, 6, 7}
तथा f = {(1, 4),(2, 5), (3, 6)}
चित्र के अनुसार A के प्रत्येक अवयव का प्रतिबिम्ब B में है।
इसलिए f एकैकी है।

प्रश्न 7.
निम्नलिखित में से प्रत्येक स्थिति में बतलाइए कि क्या दिए हुए फलन एकैकी, आच्छादक अथवा एकैकी आच्छादी (bijective) हैं। अपने उत्तर का औचित्य भी बतलाइए।
(i) f(x) = 3 – 4x द्वारा परिभाषित फलन f : R → R है।
(ii) f(x) = 1+ x² द्वारा परिभाषित फलन f: R →R है।
हल
(i) यहाँ f: R → R, यदि f(x) = 3 – 4x
(a) f(x₁) = f(x₂) ⇒ 3 – 4x₁ = 3 – 4x₂ = x₁ ⇒ x₂
अत: f एकैकी है।
(b) f(x) = y = 3 – 4x
∴ x = \(\frac{3-y}{4}\)
y के प्रत्येक मान के लिए एक ही मान है।
सहप्रान्त में प्रत्येक प्रान्त के एक अवयव का प्रतिबिम्ब है।
∴ f आच्छादक है।
अतः f एकैकी तथा आच्छादक है।

(ii) f : R → R, यदि f(x) = 1 + x²
(a) f(-1) = 1 + 1 = 2 f(1) = 1 + 1 = 2
f(-1) = f(1)
-1 और 1 दोनों का एक प्रतिबिम्ब है।
∴ f एकैकी नहीं है।..
(b) सहप्रान्त की कोई भी ऋणात्मक संख्या प्रान्त के किसी भी अवयव का प्रतिबिम्ब नहीं है।
∴ f आच्छादक नहीं है।
अतः एकैकी तथा आच्छादक नहीं है।

प्रश्न 8.
मान लीजिए कि A तथा B दो समुच्चय हैं। सिद्ध कीजिए कि f: A × B → B × A, इस प्रकार हैं कि f (a, b) = (b, a) एक एकैकी आच्छादी (bijective) फलन है।
उत्तर
हल
यहाँ f = (A × B)→ (B × A), यदि f(a, b) = (b, a)
(a) f(a₁, b₁) = f(a₂, b₂) ⇒ (b₁, a₁) = (b₂, a₂)
∴ b₁ = b₂, और a₁ = a₂
अत: f एकैकी है।

(b) सहप्रान्त का सदस्य (p, q) प्रान्त में (g, p) का प्रतिबिम्ब है।
∴ f आच्छादक है।
अतः f एकैकी तथा आच्छादक है।

प्रश्न 9.
मान लीजिए कि समस्त n % N के लिए,

द्वारा परिभाषित एक फलन f: N → N है। बतलाइए कि क्या फलन f एकैकी आच्छादी है। अपने उत्तर का औचित्य भी बतलाइए।
हल
फलन f: N → N इस प्रकार परिभाषित है कि

∵ प्रान्त में स्थित अवयव 1 व 2 के प्रतिबिम्ब सहप्रान्त में एक ‘1’ ही है।
∴ f एकैक नहीं है।
इसलिए f आच्छादी नहीं है।
पुनः सह प्रान्त के प्रत्येक अवयव की Pre image प्रान्त में स्थित है।
इसलिए f आच्छादक है।
अतः f एकैक नहीं है परन्तु आच्छादक है। इसलिए f एकैकी आच्छादती (bijective) नहीं है।

प्रश्न 10.
मान लीजिए कि A = R – {3} तथा B = R – {1} है f(x) = \(\left(\frac{x-2}{x-3}\right)\) द्वारा परिभाषित फलन f: A → B पर विचार कीजिए। क्या एकैकी तथा आच्छादक है? अपने उत्तर का औचित्य भी बतलाइए।
हल
f: A → B, जहाँ A = R – {3}, B = R – {1},
f इस प्रकार परिभाषित है कि

⇒ y के प्रत्येक मान के लिए प्रांत (domain) में Pre image x = \(\frac{3 y-2}{y-1}\) स्थित है।
इसलिए f आच्छादक है।
अतः f एकैक तथा आच्छादक है।

प्रश्न 11.
मान लीजिए f: R → R; f (x) = x⁴ द्वारा परिभाषित है। सही उत्तर का चयन कीजिए।
(A) f एकैकी आच्छादक है। (B) f बहुएक आच्छादक है
(C) f एकैकी है किन्तु आच्छादक नहीं है, (D) f न तो एकैकी है और न आच्छादक है।
हल
यहाँ f: R → R, यदि f (x) = x⁴
(a) f(-1) = (-1)⁴ = 1, f(1) = 1⁴ = 1
f(-1) = f(1)
-1 और 1 का प्रतिबिम्ब 1 है।
∴ f एकैकी नहीं है।

(b) सहप्रान्त का -1 प्रान्त के किसी भी सदस्य का प्रतिबिम्ब नहीं है।
∴ f आच्छादक नहीं है।
अत: f एकैकी और आच्छादक नहीं है।
अतः विकल्प (D) सही है।

प्रश्न 12.
मान लीजिए कि f (x) = 3x द्वारा परिभाषित फलन f: R → R है। सही उत्तर चुनिए :
(A) f एकैकी आच्छादक है
(B) f बहुएक आच्छादक है
(C) f एकैकी है परन्तु आच्छादक नहीं है
(D) f न तो एकैकी है और न आच्छादक है
हल
यहाँ f :R → R, f(x) = 3x द्वारा परिभाषित किया गया है।
(a) f(x₁) = f(x₂) = 3x₁ = 3x₂
∴ x₁ = x₂
अतः f एकैकी है।

(b) माना y = 3x
∴ x = \(\frac{y}{3}\)
y के प्रत्येक मान के लिए x का मान निम्न है।
∴ आच्छादक है।
अतः f एकैकी तथा आच्छादक है।
अतः विकल्प (A) सही है।