MP Board Class 9th Maths Solutions Chapter 7 Triangles Ex 7.3

MP Board Class 9th Maths Solutions Chapter 7 Triangles Ex 7.3

Question 1.
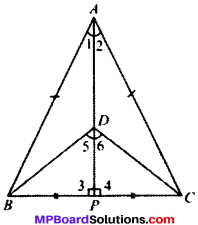
∆ABC and ∆DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. below). If AD is extended to intersect BC at P, show that

1. ∆ABD = ∆ACD
2. ∆ABP = ∆ACP
3. AP bisects ∠A as well as ∠D.
4. AP is the perpendicular bisector of BC.

Solution:
Given
AB = AC
DB = DC
To prove:

1. ∆ABD = ∆ACD
2. ∆ABP = ∆ACP
3. ∠1 = ∠2 and ∠5 = ∠6
4. ∠3 = ∠4 = 90° and BP = PC

Proof
1. In ∆ABD and ∆ACD
AB = AC (given)
BD = CD (given)
AD =AD (common)
∆ABD = ∆ACD (by SSS)
and so ∠1 = ∠2 (by CPCT)

2. In ∆ABP and ∆ACP
AB = AC (given)
∠1 = ∠2 (proved)
AP = AP (common)
∆ABP ≅ ∆ACP (by SAS)
and so ∠3 = ∠4
and BP = CP (by CPCT)

∠1 = ∠2 AP bisects ∠A

3. In ∆DBP and ∆DCP
BP = CP (proved)
∠3 = ∠4 (proved)
DP = DP (common)

∆DBP ≅ ∆DCP (by SAS)
and so ∠5 = ∠6 (by CPCT)
∴ AP bisects ∠D.

4. BP = CP (proved)
∠3 = ∠4 (proved)
∠3 + ∠4 = 180° (LPA’s)
∠3 + ∠3 = 180° (∠3 = ∠4)
2∠3 = 180°
∠3 = 90°
∠3 = ∠4 (each 90°)
and therefore, AP is the perpendicular bisector of BC

Question 2.
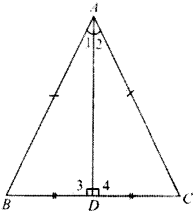
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that

1. AD bisects BC
2. AD bisects ∠A.

Solution:
Given
AB = AC and AD ⊥ BC
To prove
∠1 = ∠2 and
BD = CD
Proof:
In ∆ABD and ∆ACD
AB = AC
AD = AD
∠3 = ∠4
∆ABD = ∆ADC
and so BD = CD and ∠1 = ∠2

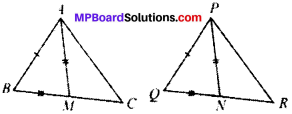
Question 3.
Two sides AS and BC and median AM on one triangle ABC are respectively equal to sides PQ and QR and median PN of ∆PQR (see-Fig. below). Show that:

1. ∆ABM ≅ ∆PQN
2. ∆ABC ≅ ∆PQR

Solution:
Given
AB = PQ
BC = QR
AM = PN
To prove:

1. ∆ABM ≅ ∆PQN
2. ∆ABC ≅ ∆PQR

Proof:
BC = QR (given)
\(\frac{1}{2}\) BC = \(\frac{1}{2}\)QR
BM = QN

1. In ∆ABM and ∆PQN
AB = PQ (given)
BM = QN (proved)
AM = PN (given)
∆ABM ≅ ∆PQN (by SSS)
and so ∠ABC = ∠PQR (by CPCT)

2. In ∆ABC and ∆PQR
AB = PQ (given)
BC = QR (given)
∠B = ∠Q (proved)
∆ABC ≅ ∆PQR by (SAS)

Question 4.
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that triangle ABC is isosceles.

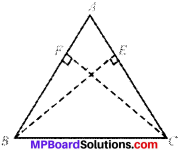
Solution:
Given
∠E = ∠F
BE = CF
To prove
AB = AC
Proof:
In ∆FBC and ∆ECB
BE = CF (given)
∠F = ∠E (each 90°)
BC = CB (common)
∴ ∆FBC = ∆ECB (by RHS)
and so ∠B = ∠C (by CPCT)
In ∆ABC, ∠B = ∠C
AB = AC
(sides opposite to equal angles of a A are equal)
and so ABC is isosceles.

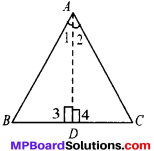
Question 5.
ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
Solution:
Given
AB = AC
∠APB = ∠APC = 90°
To prove:
∠B = ∠C

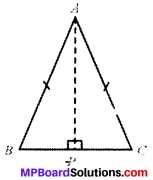
Proof:
In ∆ABP and ∆ACP
AP = AP (common)
∠APB = ∠APC (each 90°)
AB = AC (given)
∴ ∆ABP = ∆ACP (by RHS)
and ∠B = ∠C (by CPCT)

Theorem 7.6.
If two angles of a triangle are equal, then the sides opposite to them are also equal.
Given
In ∆ABC, ∠C = ∠B

To prove: AB = AC
Construction:
Draw the bisector of ∠A and let it meet BC an D
Proof:
In ∆s ABD and ACD, we have ∠B = ∠C (Given)
∠BAD = ∠CAD (Construction)
AD = AD (Common)
∴ ∆ABD ≅ ∆ACD (AAS Cong. Criterion)
Hence, AB = AC (CPCT)

Theorem 7.7.
If two sides of a triangle are unequal, the longest side has greater angle opposite to it.
Given:
In ∆ABC; AC > AB
To prove: ∠ABC > ∠ACB.

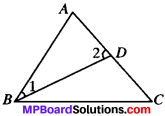
Construction:
Mark point D on AC such that AB = AD. Join BD.
Proof:
In ∆ABD,
AB = AD
∴ ∠1 = ∠2 (Const. As opp. equal sides) ….(1)
But ∠2 is an exterior angle of ABCD.
∠2 > ∠ACB (Exterior Angle Theorem) …(2)
From (1) and (2), we have
∠1 > ∠ACB (Const.)
But ∠ABC > ∠1
∴ ∠ABC > ∠ACB

Theorem 7.8. (Converse of Theorem 7.7)
In a triangle the greater angle has the longer side opposite to it.
Given:
In ∆ABC, ∠ABC > ∠ACB
To prove: AC > AB

Proof:
For ∆ABC, there are only three possibilities of which exactly one must be true.

1. AC = AB
2. AC < AB (iii) AC > AB.

Case 1:
If AC = AB, then ∠ABC = ∠ACB, which is contrary to what is given.
AB ≠ AC

Case 2:
If AC < AB, the longer side has the greater angle opposite to it.
∴ ∠ACB > ∠ABC.
This is also contrary to what is given.

Case 3:
We are left with the only possibility, namely AC > AB which is true.
AC > AB.

MP Board Class 9th Maths Solutions