MP Board Class 8th Maths Solutions Chapter 4 Practical Geometry Ex 4.5
Question 1.
Draw the following.
(i) The square READ with RE = 5.1 cm.
(ii) A rhombus whose diagonals are 5.2 cm and 6.4 cm long.
(iii) A rectangle with adjacent sides of lengths 5 cm and 4 cm.
(iv) A parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm.
Solution:
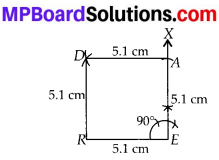
(i) Since, all 4 sides of a square are equal and each of 4 angles is equal to 90°.
Steps of Construction:
Step-1: Draw RE = 5.1 cm.
Step-2 : Draw ∠REX = 90°.
Step-3 : Cut off EA = 5.1 cm on \(\overrightarrow{E X}\)
Step-4: With R as centre and radius equal to 5.1 cm, draw an arc.
Step-5 : With A as centre and radius equal to 5.1 cm, cut off another arc on the arc drawn in step-4 at point D.
Step-6 : Join DA and DR.
Hence, READ is the required square.
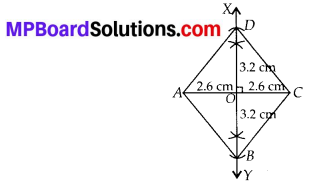
(ii) We know that diagonals of a rhombus bisect each other at right angles. Let AC = 5.2 cm and BD = 6.4 cm.
Steps of Construction:
Step-1: Draw AC = 5.2 cm.
Step-2 : Draw perpendicular bisector XY of AC which cut AC at point O.
Step-3 : Cut off OD = 3.2 cm on OX and OB = 3.2 cm on \(\overrightarrow{O Y}\).
Step-4 : Join AD, CD, AB and CB.
Hence, ABCD is the required rhombus.
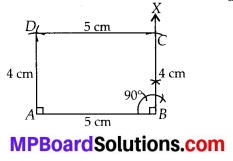
(iii) In a rectangle, opposite sides are equal and each of 4 angles is equal to 90°.
Let AB = 5 cm and BC = 4 cm
∴ AB = DC = 5 cm and BC = AD = 4 cm.
Also, ∠A = ∠B = ∠C = ∠D = 90°.
Steps of Construction:
Step-1: Draw AB = 5 cm.
Step-2 : Draw ∠ABX = 90°.
Step-3 : Cut off BC = 4 cm on BX .
Step-4: With A as centre and radius equal to 4 cm, cut off an arc.
Step-5 : With C as centre and radius equal to 5 cm cut off another arc on the arc drawn in step-4 at point D.
Step-6 : Join AD and CD.
Hence, ABCD is the required rectangle.
(iv) Here, data given is incomplete. Since we know that to draw a quadrilateral at least five parts are necessary. In the present case, OK = 5.5 cm & KA = 4.2 cm is given.
We know that opposite sides of a parallelogram are equal.
∴ OK = YA = 5.5 cm and KA = OY = 4.2 cm
Here, only four parts are given. This means that one more part is necessary.
So, either one angle or diagonal of a parallelogram is required to construct it.
Hence, parallelogram OKAY cannot be drawn.