MP Board Class 8th Maths Solutions Chapter 3 Understanding Quadrilaterals Ex 3.1
Question 1.
Given here are some figures.
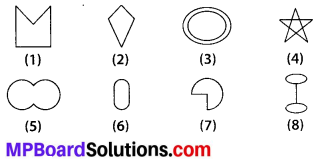
Classify each of them on the basis of the following.
(a) Simple curve
(b) Simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon
Solution:
(a) Simple curve : It is a curve that does not intersect itself. (1), (2), (5), (6) and (7) are simple curve.
(b) Simple closed curve : A closed curve if it does not pass through one point more than once (1), (2), (5), (6) and (7) are simple closed curve.
(c) Polygon : A simple closed curve made up of only line segments is called a polygon.
(1) and (2) are polygons.
(d) Convex polygon : A polygon that has all its interior angles less than 180°.
(2) is a convex polygon.
(e) Concave polygon – A polygon that has at least one interior angle greater than 180°. (1) is a concave polygon.
Question 2.
How many diagonals does each of the following have?
(a) A convex quadrilateral
(b) A regular hexagon
(c) A triangle
Solution:
A diagonal is a line segment joining two non consecutive vertices.
(a) Convex quadrilateral : Convex quadrilateral has 2 diagonals.
(b) A regular hexagon : A regular hexagon has 9 diagonals.
(c) A triangle : It has 0 diagonal, i.e., no diagonal.
![]()
Question 3.
What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!
Solution:
Sum of measures of four angles of a convex quadrilateral is 360°.
Example : Draw a figure given below and divide it into two triangles by joining AB, named CAB and DBA.
Now in ∆DBA, we have

Which shows that a quadrilateral which is not convex also have sum of measure of its angles is 360°.
![]()
Question 4.
Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that).
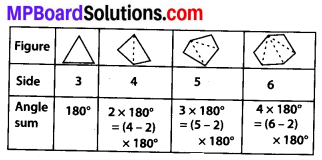
What can you say about the angle sum of a convex polygon with number of sides?
(a) 7
(b) 8
(c) 10
(d) n
Solution:
(a) If a convex polygon has 7 Sides, then angle sum = (7 – 2) × 180°
= 5 × 180° =900°.
(b) If a convex polygon has 8 sides, then angle sum = (8 – 2) × 180°
= 6 × 180° = 1080°.
(c) If a convex polygon has 10 sides, then angle sum = (10 – 2) × 180°
= 8 × 180° = 1440°.
(d) If a convex polygon has n sides, then angle sum = (n – 2) × 180°.
![]()
Question 5.
What is a regular polygon? State the name of a regular polygon of
(i) 3 sides
(ii) 4 sides
(iii) 6 sides
Solution:
Regular polygon- A polygon, which has all sides of equal length and angles of equal measure is called a regular polygon.
(i) An equilateral triangle, as all 3 sides are equal and all 3 angles are also equal (= 60°).
(ii) A square, as it has all 4 sides equal and all 4 angles are also equal (= 90°).
(iii) A regular hexagon, as it has all 6 sides equal and all 6 angles equal (= 120°).
Question 6.
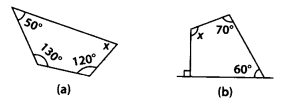
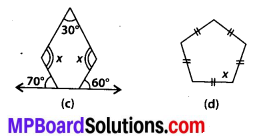
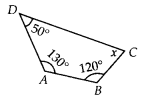
Find the angle measure x in the following figures.
Solution:
(a) Let ABCD be a given quadrilateral.
∵ Sum of all angles of a quadrilateral is 360°
∴ m∠A + m∠B + m∠C + m∠D = 360°
⇒ 130° + 120° + x + 50° = 360°
⇒ 300° + x = 360°
⇒ x = 360° – 300°
⇒ x = 60°.
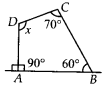
(b) Let ABCD be a given quadrilateral.
Sum of all angles of a quadrilateral is 360°.
∴ m∠A + m∠B + m∠C + m∠D = 360°
⇒ 90° + 60° + 70°’+ x = 360°
⇒ 220° + x = 360° D
⇒ x = 360° – 220°
⇒ x = 140°.
(c) Let ABCDE be a given polygon, which has 5 sides.

Now, sum of angles = (5 – 2) × 180°
= 3 × 180° = 540°.
Also, m∠1 = 180° – 70° = 110° [By linear pair] and m∠Z = 180° – 60° = 120° [By linear pair]
Thus m∠1 + m∠2 + m∠3 + m∠4 + m∠5 = 540°
⇒ 110° + 120° + x + x + 30° = 540°
⇒ 260° + 2x = 540°
⇒ 2x = 540° – 260°
⇒ 2x = 280° ∴ x = 140°.
(d) Let ABCDE be a given pentagon.

∴ Sum of angles of a given pentagon
ABODE = (5 – 2) × 180° = 540°.
∴ m∠1 + m∠2 + m∠3 + m∠4 + m∠5 = 540°
⇒ x + x + x + x + x = 540°
⇒ 5x = 540° ⇒ x = 108°.
![]()
Question 7.
(a) Find x + y + z.
(b) Find x + y + z + w.
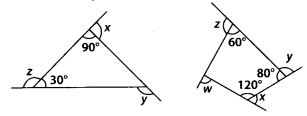
Solution:
(a) Let ABC be a given triangle.
Sum of angles of a triangle is 180°.
m∠A + m∠B + m∠C = 180°
⇒ 30° + m∠B + 90° = 180°
⇒ m∠B + 120° = 180°
⇒ m∠B = 180° – 120° = 60°
⇒ m∠B = 60° …(i)
Clearly, x + 90° = 180° [By linear pair]
⇒ x = 180° – 90° ⇒ x = 90° …… (ii)
Also z + 30° = 180° [By linear pair]
⇒ z = 180° – 30° ⇒ z = 150° …….. (iii)
and y + 60° = 180° [By linear pair]
⇒ y = 180° – 60° => y = 120° ……. (iv)
∴ By using (ii), (iii) and (iv), we get
x + y + z = 90° + 120° + 150°
⇒ x + y + z = 360°.
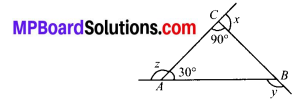
(b) Let ABCD be a given quadrilateral.

Sum of angles of a quadrilateral is 360°.
∴ m∠1 + m∠2 + m∠3 + m∠4 = 360°
⇒ m∠1 + 120° + 80° + 60° = 360° ⇒ m∠1 + 260° = 360°
⇒ m∠1 = 360° – 260° ⇒ m∠l = 100°
Clearly, w + 100° = 180° [By linear pair] ⇒ w = 180° – 100° = 80° ….(i)
x + 120° = 180° [By linear pair]
⇒ x = 180° – 120° = 60° y + 80° = 180°
⇒ y = 180° – 80° = 100° Also, z + 60° = 180°
⇒ z = 180° – 60° ⇒ z = 120° ….(iv)
Thus by (i), (ii), (iii) & (iv), we get
w + x + y + z = 80° + 60° + 100° + 120° = 360°