MP Board Class 8th Maths Solutions Chapter 2 Linear Equations in One Variable Ex 2.3
Solve the following equations and check your results.
Question 1.
3x = 2x + 18
Solution:
We have, 3x = 2x + 18
Transposing 2x to L.H.S., we get
3x – 2x = 18 ⇒ x = 18
Checking: L.H.S. = 3 × 18 = 54
R.H.S. = 2x + 18 = 2 × 18 + 18 = 36 + 18 = 54
Thus, L.H.S. = R.H.S.
Question 2.
5t – 3 = 3t – 5
Solution:
We have, 5t – 3 = 3t – 5
Transposing 3t to L.H.S., we get
5t – 3 – 3t = – 5
⇒ 2t – 3 = – 5
Transposing – 3 to R.H.S., we get
2t = -5 + 3
⇒ 2t = – 2
Dividing both sides by 2, we get
![]()
Checking : L.H.S. = 5t – 3 = 5 × (-1) – 3 = -5 – 3 = -8
R.H.S. = 3t – 5 = 3 × (-1) – 5 = -3 – 5 = -8
Thus, L.H.S. = R.H.S.
Question 3.
5x + 9 = 5 + 3x
Solution:
We have, 5x + 9 = 5 + 3x
Transposing 3x to L.H.S., we get
5x + 9 – 3x = 5
⇒ 2x + 9 = 5
Now, transposing 9 to R.H.S., we get
2x = 5 – 9 = 4 ⇒ 2x = – 4
Dividing both sides by 2, we get \(\frac{2 x}{2}=\frac{-4}{2}\)
Checking: L.H.S. = 5x + 9 = 5 × (-2) + 9 = -10 + 9 = -1
R.H.S. = 5 + 3x = 5 + 3 (-2) = 5 – 6 = – 1.
Thus, L.H.S. = R.H.S.
Question 4.
4z + 3 = 6 + 2z
Solution:
We have, 4z + 3 = 6 + 2z
Transposing 2z to L.H.S., we get
4z + 3-2z = 6 ⇒ 2z + 3 = 6
Transposing 3 to R.H.S., we get
2z = 6 – 3 ⇒ 2z = 3

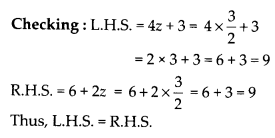
Question 5.
2x – 1 = 14 – x
Solution:
We have, 2x -1 = 14 – x
Transposing – x to L.H.S., we get
2x – 1 + x = 14 ⇒ 3x – 1 = 14
Transposing – 1 to R.H.S., we get
3x = 14 + 1 ⇒ 3x = 15
Dividing both sides by 3, we get \(\frac{3 x}{3}=\frac{15}{3}\)
⇒ x = 15
Checking: L.H.S. = 2x – 1 = 2 × 5 – 1 = 10 – 1 = 9
R.H.S. = 14 – x = 14 – 5 = 9
Thus, L.H.S. = R.H.S.
Question 6.
8x + 4 = 3(x – 1) + 7
Solution:
We have, 8x + 4 = 3(x – 1) + 7
⇒ 8x + 4 = 3x – 3 + 7 ⇒ 8x + 4 = 3x + 4
Transposing 3x to L.H.S., we get
8x + 4 – 3x = 4 ⇒ 5x + 4 = 4
Transposing 4 to R.H.S., we get
⇒ 5x = 4 – 4 ⇒ 5x = 0
Dividing both sides by 5, we get
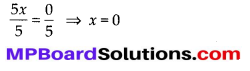
Checking: L.H.S. = 8x + 4 = 8 × 0 + 4 = 4
R.H.S. = 3(x – 1) + 7 = 3(0 – 1) + 7 = -3 + 7 = 4
Thus, L.H.S. = R.H.S.
Question 7.
x = \(\frac{4}{5}\)(x + 10)
Solution:
We have, x = \(\frac{4}{5}\)(x + 10)
Multiplying both sides by 5, we get
5x = 4(x + 10) ⇒ 5x = 4x + 40
Transposing 4x to L.H.S., we get 5x – 4x = 40 ⇒ x = 40
Checking : L.H.S. = x = 40
![]()
Thus, L.H.S. = R.H.S.
Question 8.
\(\frac{2 x}{3}+1=\frac{7 x}{15}+3\)
Solution:

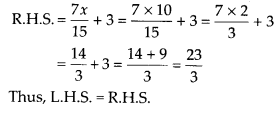
Question 9.
\(2 y+\frac{5}{3}=\frac{26}{3}-y\)
Solution:

Question 10.
3m = 5m – \(\frac{8}{5}\)
Solution:
