MP Board Class 8th Maths Solutions Chapter 13 सीधा और प्रतिलोम समानुपात Ex 13.2
प्रश्न 1.
निम्नलिखित में से कौन प्रतिलोम अनुपात में हैं?
- किसी कार्य पर लगे व्यक्तियों की संख्या और उस कार्य को पूरा करने में लगा समय।
- एक समान चाल से किसी यात्रा में लिया गया समय और दूरी।
- खेती की गई भूमि का क्षेत्रफल और काटी गई फसल।
- एक निश्चित यात्रा में लिया गया समय और वाहन की चाल।
- किसी देश की जनसंख्या और प्रति व्यक्ति भूमि का क्षेत्रफल।
उत्तर:
- प्रतिलोम अनुपात
- अनुक्रमानुपाती
- अनुक्रमानुपाती
- प्रतिलोम अनुपात
- प्रतिलोम अनुपात।
![]()
प्रश्न 2.
एक टेलीविजन गेम शो (game show) में ₹ 1,00,000 की पुरस्कार राशि विजेताओं में समान रूप से वितरित की जाती है। निम्नलिखित सारणी को पूरा कीजिए तथा ज्ञात कीजिए कि क्या एक व्यक्तिगत विजेता को दी जाने वाली पुरस्कार की धनराशि विजेताओं की संख्या के अनुक्रमानुपाती है या व्युत्क्रमानुपाती है?

हल:
स्पष्ट है कि विजेताओं की संख्या बढ़ने पर पुरस्कार की धनराशि कम हो जाएगी।
विजेताओं की संख्याओं के लिए धनराशि –
- 4 → ₹ 25,000
- 5 → ₹ 20,000
- 8 → ₹ 12,500
- 10 → ₹ 10,000
- 20 → ₹ 5,000
यहाँ, एक विजेता को दी गई धनराशि विजेताओं की संख्या के व्युत्क्रमानुपाती है।
प्रश्न 3.
रहमान तीलियों या डंडियों का प्रयोग करते हुए, एक पहिया बना रहा है। वह समान तीलियाँ इस प्रकार लगाना चाहता है कि किन्हीं भी क्रमागत तीलियों के युग्मों के बीच के कोण बराबर हैं।

निम्नलिखित सारणी को पूरा करके उसकी सहायता कीजिए –
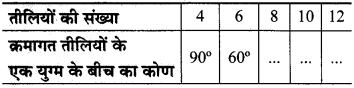
- क्या तीलियों की संख्या और क्रमागत तीलियों के किसी युग्म के बीच का कोण प्रतिलोम समानुपात में हैं?
- 15 तीलियों वाले एक पहिए के क्रमागत तीलियों के किसी युग्म का कोण परिकलित कीजिए।
- यदि क्रमागत तीलियों के प्रत्येक युग्म के बीच का कोण 40° है, तो आवश्यक तीलियों की संख्या कितनी होगी?
हल:
यहाँ यह स्पष्ट है कि तीलियों की संख्या अधिक होगी तो क्रमागत तीलियों के युग्मों के बीच कोण का माप कम होगी।
हम यहाँ यह भी देखते हैं कि –
4 x 90° = 6 x 60° = 360°
अतः यह प्रतिलोम समानुपात की स्थिति है।
इसलिए 8 × x = 360°; ∴ x = \(\frac{360}{8}\) = 45°
और 10 x y = 360°; ∴ y = \(\frac{360}{10}\) = 36°
और 12 x 2 = 360°; ∴ 2 = \(\frac{360}{12}\) = 30°
अतः 8 → 45%, 10 → 36°, 12 → 30°
1. हाँ, तीलियों की संख्या और क्रमागत तीलियों के किसी युग्म के बीच का कोण प्रतिलोम समानुपात में हैं। उत्तर
2. माना कि 15 तीलियों वाले एक पहिए के क्रमागत तीलियों के किसी युग्म का कोण = x है।
15 × x = 4 x 90°
x = \(\frac{4×90°}{15}\) = 9
अतः अभीष्ट कोण = 24°
3. माना कि तीलियों की संख्या = y है।
y = 40° = 4 x 90°
y = \(\frac{4×90°}{40°}\) = 9
अतः आवश्यक तीलियों की संख्या = 9
![]()
प्रश्न 4.
यदि किसी डिब्बे की मिठाई को 24 बच्चों में बाँटा जाए, तो प्रत्येक बच्चे को 5 मिठाइयाँ मिलती हैं। यदि बच्चों की संख्या में 4 की कमी हो जाए, तो प्रत्येक बच्चे को कितनी मिठाइयाँ मिलेंगी?
हल:
क्योंकि बच्चों की संख्या में 4 की कमी हो जाती है, तो
बच्चों की संख्या = 24 – 4 = 20
माना कि अब प्रत्येक को x मिठाइयाँ मिलती हैं,
अब, सूचना को सारणी के रूप में रखने पर,
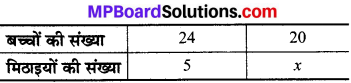
बच्चों की संख्या कम होने से बच्चों को अधिक मिठाइयाँ मिलेंगी।
अत: यह एक व्युत्क्रमानुपात की स्थिति हैं।
24 x 5 = 20 × x
x = \(\frac{24×5}{20}\) = 6
इसलिए, प्रत्येक बच्चे को 6 मिठाइयाँ मिलेंगी।
प्रश्न 5.
एक किसान की पशुशाला में 20 पशुओं के लिए 6 दिन का पर्याप्त भोजन है। यदि इस पशुशाला में 10 पशु और आ जाएँ, तो यह भोजन कितने दिन तक पर्याप्त रहेगा?
हल:
अब,पशुओं की संख्या = 20 + 10 = 30
मानाकि भोजन 30 पशुओं के दिन तक पर्याप्त रहेगा। हम निम्न सारणी प्राप्त करते हैं –

जितने पशु अधिक होंगे उतने ही कम समय में भोजन समाप्त हो जाएगा।
अतः यह एक प्रतिलोम समानुपात की स्थिति है।
इसलिए 20 x 6 = 30 x y
या y = \(\frac{20×6}{30}\) = 4 दिन
अतः भोजन 4 दिन तक पर्याप्त रहेगा।
प्रश्न 6.
एक ठेकेदार यह आकलन करता है कि जसमिंदर के घर में पुनः तार लगाने का कार्य 3 व्यक्ति 4 दिन में कर सकते हैं। यदि वह तीन के स्थान पर चार व्यक्तियों को इस काम पर लगाता है, तो यह कार्य कितने दिन में पूरा हो जाएगा?
हल:
व्यक्तियों की संख्या अधिक होने पर कार्य जल्दी समाप्त हो जाएगा।
माना कार्य x दिन में समाप्त हो जाएगा। अतः यह एक प्रतिलोम समानुपात की स्थिति है।
3 व्यक्ति : 4 व्यक्ति = x दिन : 4 दिन
x = \(\frac{3×4}{4}\) = 3 दिन
अतः कार्य 3 दिन में समाप्त हो जाएगा।
प्रश्न 7.
बोतलों के एक बैच (Batch) को 25 बक्सों में रखा जाता है, जबकि प्रत्येक बक्स में 12 बोतलें हैं। यदि इसी बैच की बोतलों को इस प्रकार रखा जाए कि प्रत्येक बक्स में 20 बोतलें हों, तो कितने बक्स भरे जाएँगे?
हल:
माना कि बक्स में 20 बोतलें रखने पर x बक्सों की आवश्यकता होती है, तब

प्रत्येक बक्स में बोतलों की संख्या अधिक रखने पर कम बक्सों की आवश्यकता होगी।
अतः यह एक प्रतिलोम समानुपात की स्थिति है।
इसलिए 25 x 12 =xx 20
x = \(\frac{25×12}{20}\)
= 15 बक्से
अतः 15 बक्से भरे जायेंगे।
![]()
प्रश्न 8.
एक फैक्ट्री को कछ वस्तएँ 63 दिन में बनाने के लिए 42 मशीनों की आवश्यकता होती है। उतनी ही वस्तुएँ 54 दिन में बनाने के लिए, कितनी मशीनों की आवश्यकता होगी?
हल:
मानाकि x मशीनों की आवश्यकता होती है। तब

दिनों की संख्या कम करने पर अधिक मशीनों की आवश्यकता होगी।
अतः यहाँ प्रतिलोम समानुपात की स्थिति है।
इसलिए 42 x 63 = x x 54
या x = \(\frac{42×63}{54}\) = 49
अतः आवश्यक मशीनों की संख्या = 49
प्रश्न 9.
एक कार एक स्थान तक पहुँचने में 60 km/h की चाल से चलकर 2 घण्टे का समय लेती है। 80 km/h की चाल से उस कार को कितना समय लगेगा?
हल:
मानाकि कार को 80 km/h की चाल से चलने पर x घण्टे लगते हैं, तब

कार की चाल अधिक हो जाने पर उसे कम समय लगेगा।
अतः यह प्रतिलोम समानुपात की स्थिति है।
इसलिए 60 x 2 = 80 × x
या x = \(\frac{60×2}{80}\)
x = \(\frac{3}{2}\)
= 3 घण्टे
अत: कार को 11 घण्टा लगेगा।
प्रश्न 10.
दो व्यक्ति एक घर में नई खिड़कियाँ 3 दिन में लगा सकते हैं।
- कार्य प्रारम्भ होने से पहले, एक व्यक्ति बीमार पड़ जाता है। अब यह कार्य कितने दिन में पूरा हो पाएगा?
- एक ही दिन में खिड़कियाँ लगवाने के लिए, कितने व्यक्तियों की आवश्यकता होगी?
हल:
1. माना कि खिड़कियाँ लगाने में x दिन लगते हैं, तब
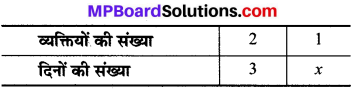
व्यक्तियों की संख्या कम होने से खिड़कियाँ लगाने में अधिक दिन लगेंगे।
अतः यह प्रतिलोम समानुपात की स्थिति है।
इसलिए 2 x 3 = 1 × x
x = \(\frac{2×3}{1}\)
= 6 दिन
अतः 1 व्यक्ति 6 दिन में कार्य पूरा करेगा।
2. माना कि 1 दिन में खिड़कियाँ लगाने के लिएx व्यक्तियों की आवश्यकता होगी, तब
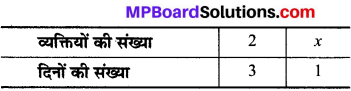
दिनों की संख्या कम हो जाने से अधिक व्यक्तियों की आवश्यकता होगी।
अतः यह एक प्रतिलोम समानुपात की स्थिति है।
इसलिए 2 x 3 = x × 1
x = \(\frac{2×3}{1}\) = 6 व्यक्ति
अतः 1 दिन में खिड़कियाँ लगवाने के लिए आवश्यक व्यक्तियों की संख्या =6
प्रश्न 11.
किसी स्कूल में, 45 मिनट अवधि के 8 कालांश होते हैं। यह कल्पना करते हुए कि स्कूल का कार्य समय उतना ही रहता है, यदि स्कूल में बराबर अवधि के 9 कालांश हों, तो प्रत्येक कालांश कितने समय का होगा?
हल:
माना कि कालांश का समय x मिनट है, तब

कालांश अधिक हो जाने पर समय अवधि कम हो जाएगी।
अतः यह एक प्रतिलोम समानुपात की स्थिति है।
इसलिए 8 x 45 = 9 × x
x = \(\frac{8×45}{9}\) = 40 मिनट
अतः प्रत्येक कालांश का समय 40 मिनट होगा।
पाठ्य-पुस्तक पृष्ठ संख्या # 223
![]()
इन्हें कीजिए (क्रमांक 13.5)
प्रश्न 1.
एक कागज की शीट लीजिए। उसे आकृति में दर्शाए अनुसार मोड़िए। प्रत्येक स्थिति में, भागों की संख्या तथा एक भाग का क्षेत्रफल लिखिए।

अपने प्रेक्षण की सारणी बनाइए और उसकी अपने मित्रों से चर्चा कीजिए। क्या यह एक प्रतिलोम समानुपात की स्थिति है? क्यों?
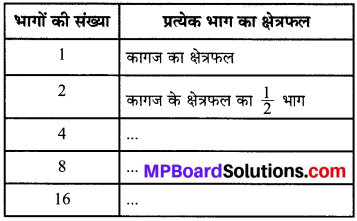
हल:
- 4 → कागज के क्षेत्रफल का \(\frac{1}{4}\) भाग
- 8 → कागज के क्षेत्रफल का \(\frac{1}{8}\) भाग
- 16 → कागज के क्षेत्रफल का \(\frac{1}{16}\) भाग
यहाँ, 1 x 1 = 2 x \(\frac{1}{2}\) = 4 x 1 = 8 x \(\frac{1}{8}\)
= 16 x \(\frac{1}{16}\) = 1 (अचर)
अतः यहाँ एक प्रतिलोम समानुपात की स्थिति है।
क्योंकि भागों की संख्या बढ़ने पर क्षेत्रफल में कमी हो जाती है।
प्रश्न 2.
वृत्तीय आधार वाले विभिन्न मापों के कुछ बर्तन लीजिए। प्रत्येक बर्तन में पानी की समान मात्रा भरिए। प्रत्येक बर्तन का व्यास और उस बर्तन में पानी किस ऊँचाई तक है उसे मापकर लिखिए। अपने प्रेक्षणों की एक सारणी बनाइए। क्या यह एक प्रतिलोम समानुपात की स्थिति है?
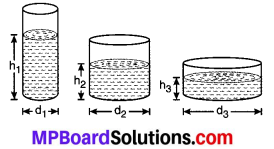
हल:
सारणी

माना कि इनके पानी का आयतन क्रमशः V1, V2 तथा V3 हैं।
इसलिए, आयतन V1 = π(\(\frac { d_{ 1 } }{ 2 } \))2h1
V2 = π(\(\frac { d_{ 2 } }{ 2 } \))2h2
V3 = π(\(\frac { d_{ 3 } }{ 2 } \))2h3
परन्तु V1 = V2 = V3 (पानी की मात्रा समान है)
इसलिए π(\(\frac { d_{ 1 } }{ 2 } \))2h1 = π(\(\frac { d_{ 2 } }{ 2 } \))2h2 = π(\(\frac { d_{ 3 } }{ 2 } \)) 2h3
d12h1 = d22h2 = d32h3
परन्तु d1h1 ≠ d2h2 ≠ d3h3
अतः यह एक प्रतिलोम समानुपात की स्थिति नहीं है।