MP Board Class 7th Maths Solutions Chapter 14 Symmetry Ex 14.1
Question 1.
Copy the figures with punched holes and find the axes of symmetry for the following:
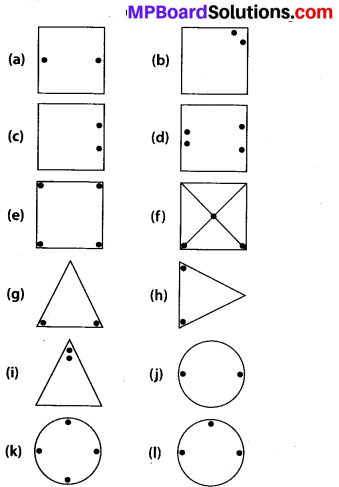
Solution:
The axes of symmetry in the given figures are as follows :
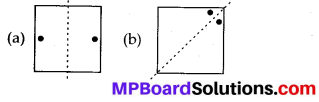
Question 2.
Given the line(s) of symmetry, find the other hole(s).
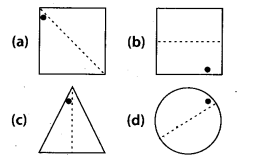
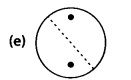
Solution:
Question 3.
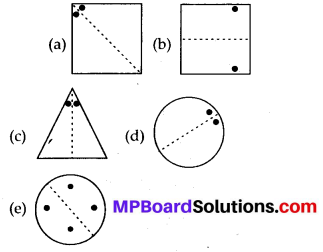
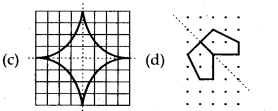
In the following figures, the mirror line (f.e., the line of symmetry) is given as a dotted line. Complete each figure performing reflection in the dotted (mirror) line. (You might perhaps place a mirror along the dotted line and look into the mirror for the image). Are you able to recall the name of the figure you complete?
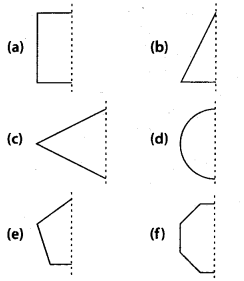
Solution:
The given figures can be completed as follows :
(a) It will be a square
(b) It will be a triangle

(c) It will be a rhombus
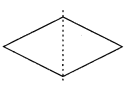
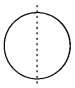
(d) It will be a circle
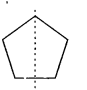
(e) It will be a pentagon
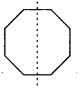
(f) It will be a octagon
![]()
Question 4.
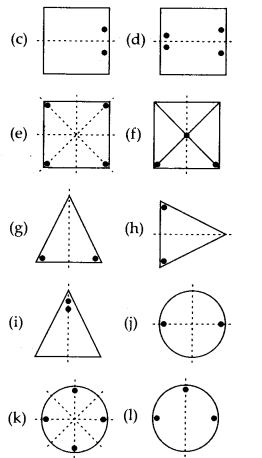
The following figures have more than one line of symmetry. Such figures are said to have multiple lines of symmetry.
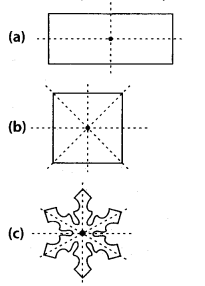
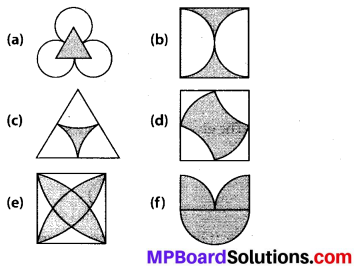
Identify multiple lines of symmetry, if any, in each of the following figures:
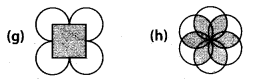
Solution:
(a) The given figure has 3 lines of symmetry.
Hence, it has multiple lines of symmetry,
(b) The given figure has 2 lines of symmetry.
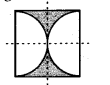
Hence, it has multiple lines of symmetry,
(c) The given figure has 3 lines of symmetry.
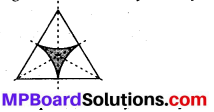
Hence, it has multiple lines of symmetry,
(d) The given figure has 2 lines of symmetry.

Hence, it has multiple lines of symmetry,
(e) The given figure has 4 lines of symmetry.
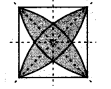
Hence, it has multiple lines of symmetry.
(f) The given figure has only 1 line of symmetry.
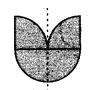
(g) The given figure has 4 lines of symmetry.
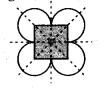
Hence, it has multiple lines of symmetry.
(h) The given figure has 6 lines of symmetry.
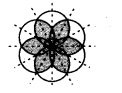
Hence, it has multiple lines of symmetry.
Question 5.
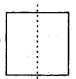
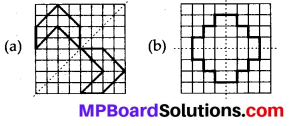
Copy the figure given here.

Take any one diagonal as a line of symmetry and shade a few more squares to make the figure symmetric about a diagonal. Is there more than one way to do that? Will the figure be symmetric about both the diagonals?
Solution:
We can shade a few more squares so as to make the given figure symmetric about any of its diagonals.
Yes, the figure is symmetric about both the diagonals. There is more than one way so as to make the figure symmetric about a diagonal as we can choose any of its 2 diagonals.
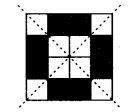
Question 6.
Copy the diagram and complete each shape to be symmetric about the mirror line(s).

Solution:
The given figures can be completed about the given mirror lines as follows :
![]()
Question 7.
State the number of lines of symmetry for the following figures.
(a) An equilateral triangle
(b) An isosceles triangle
(c) A scalene triangle
(d) A square
(e) A rectangle
(f) A rhombus
(g) A parallelogram
(h) A quadrilateral
(i) A regular hexagon
(j) A circle
Solution:
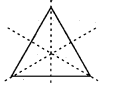
(a) There are 3 lines of symmetry in an equilateral triangle.
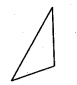
(b) There is only 1 line of symmetry in an isosceles triangle.

(c) There is no line of symmetry in a scalene triangle.
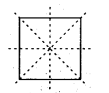
(d) There are 4 lines of symmetry in a square.
(e) There are 2 lines of symmetry in a rectangle.

(f) There are 2 lines of symmetry in a rhombus.
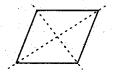
(g) There is no line of symmetry in a parallelogram.

(h) There is no line of symmetry in a quadrilateral.
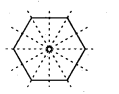
(i) There are 6 lines of symmetry in a regular hexagon.
(j) There are infinite lines of symmetry in a circle. Some of these are represented as follows.
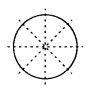
Question 8.
What letters of the English alphabet have reflectional symmetry (i.e., symmetry related to mirror reflection) about
(a) a vertical mirror
(b) a horizontal mirror
(c) both horizontal and vertical mirrors
Solution:
(a) A, H, I, M, O, T, U, V,-W, X, Y are the letters having reflectional symmetry about a vertical mirror.
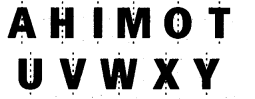
(b) B, C, D, E, H, I, K, O, X are the letters having reflection symmetry about a horizontal mirror.

(c) H, I, O, X are the letters having reflectional symmetry about both horizontal and vertical mirrors.
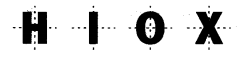
![]()
Question 9.
Give three examples of shapes with no line of symmetry.
Solution:
A scalene triangle, a parallelogram and a trapezium do not have any line of symmetry.

Question 10.
What other name can you give to the line of symmetry of
(a) an isosceles triangle?
(b) a circle?
Solution:
(a) An isosceles triangle has only 1 line of symmetry.
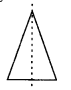
Which divides the triangle into two equal parts.
Therefore, this line of symmetry is the median and also the altitude of isosceles triangle.
(b) There are infinite lines of symmetry in a circle. Some of these are represented as follows.
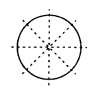
It can be concluded that each line of symmetry is the diameter of the circle.