MP Board Class 7th Maths Solutions Chapter 11 Perimeter and Area Ex 11.2

MP Board Class 7th Maths Solutions Chapter 11 Perimeter and Area Ex 11.2

Question 1.
Find the area of each of the following parallelograms:

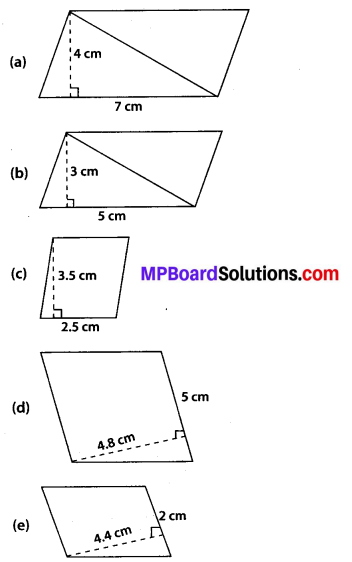
Solution:
Area of parallelogram = Base × Height
(a) Height = 4 cm, Base = 7 cm
Area of parallelogram = 7 × 4 = 28 cm²

(b) Height = 3 cm, Base = 5 cm
Area of parallelogram = 5 × 3 = 15 cm²

(c) Height = 3.5 cm, Base = 2.5 cm
Area of parallelogram = 2.5 × 3.5 = 8.75 cm²

(d) Height = 4.8 cm, Base = 5 cm
Area of parallelogram = 5 × 4.8 = 24 cm²

(e) Height = 4.4 cm, Base = 2 cm
Area of parallelogram = 2 × 4.4 = 8.8 cm²

Question 2.
Find the area of each of the following triangles:


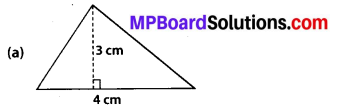
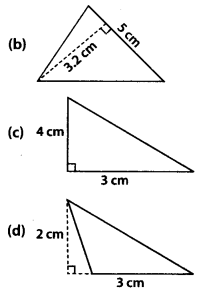
Solution:
Area of triangle = \(\frac{1}{2}\) × Base × Height
(a) Base = 4 cm, height = 3 cm
Area = \(\frac{1}{2}\) × 4 × 3 = 6 cm²

(b) Base = 5 cm, height = 3.2 cm
Area = \(\frac{1}{2}\) × 5 × 3.2 = 8 cm²

(c) Base = 3 cm, height = 4 cm
Area = \(\frac{1}{2}\) × 3 × 4 = 6cm²

(d) Base = 3 cm, height = 2 cm
Area = \(\frac{1}{2}\) × 3 × 2 = 3 cm²

Question 3.
Find the missing values:

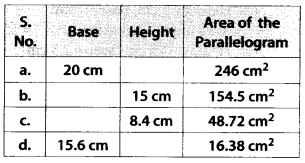
Solution:
Area of parallelogram = Base × Height
(a) Base = 20 cm
Let height = h
Area of parallelogram = 246 cm²
∴ 20 × h = 246
⇒ h = \(\frac{246}{20}\) = 12.3 cm
Therefore, the height of parallelogram is 12.3 cm.

(b) Let base = b
Height = 15 cm
Area of parallelogram = 154.5 cm²
∴ b × 15 = 154.5
⇒ b = \(\frac{154.5}{15}\) = 10.3 cm
Therefore, the base of parallelogram is 10.3 cm.

(c) Let base = b
Height = 8.4 cm
Area of parallelogram = 48.72 cm²
∴ b × 8.4 = 48.72
⇒ b = \(\frac{48.72}{8.4}\) = 5.8 cm
Therefore, the base of parallelogram is 5.8 cm.

(d) Base = 15.6 cm
Let height = h
Area of parallelogram = 16.38 cm²
∴15.6 × h = 16.38
⇒ h = \(\frac{16.38}{15.6}\) = 1.05 cm
Therefore, the height of parallelogram is 1.05 cm.

Question 4.
Find the missing values:

Solution:
Area of triangle = \(\frac{1}{2}\) × Base × Height
Let b be the base of triangle and h be the height of triangle.
(i) b = 15 cm

Therefore, the height of triangle is 11.6 cm.

(ii) h = 31.4 mm
Area = \(\frac{1}{2}\) × b × h = 1256 mm²

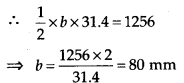
Therefore, the base of triangle is 80 mm.

(iii) b = 22 cm

Therefore, the height of triangle is 15.5 cm.

Question 5.
PQRS is a parallelogram (see the given figure). QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:
(a) the area of the parallelogram PQRS
(b) QN, if PS = 8 cm

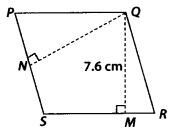
Solution:
(a) Area of parallelogram = Base × Height
= SR × QM
= 12 × 7.6 = 91.2 cm²

(b) PS = 8 cm
Area of parallelogram = Base × Height
= PS × QN = 91.2 cm²
⇒ 8 × QN = 91.2
⇒ QN = \(\frac{91.2}{8}\) = 11.4 cm

Question 6.
DL and BM are the heights on sides AB and AD respectively of parallelogram ABCD (see the given figure).

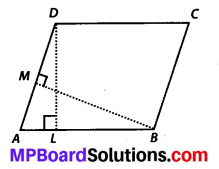
If the area of the parallelogram is 1470 cm², AB = 35 cm and AD = 49 cm, find the length of BM and DL.
Solution:
Area of parallelogram = Base × Height
= AB × DL
⇒ 1470 = 35 × DL
⇒ DL = \(\frac{1470}{35}\) = 42 cm
Also, area of parallelogram = AD × BM
⇒ 1470 = 49 × BM
∴ BM = \(\frac{1470}{49}\) = 30 cm

Question 7.
∆ABC is right angled at A (see the given figure). AD is perpendicular to BC. If AB = 5 cm, BC – 13 cm and AC = 12 cm, find the area of ∆ABC. Also find the length of AD.

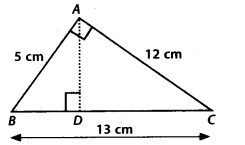
Solution:

Question 8.
∆ABC is isosceles with AB = AC= 7.5 cm and BC = 9 cm (see the given figure). The height AD from A to BC, is 6 cm. Find the area of ∆ABC. What will be the height from C to AB i. e., CE?

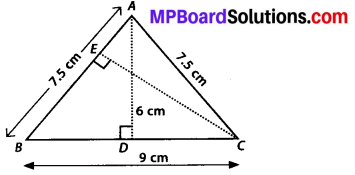
Solution:

MP Board Class 7th Maths Solutions