MP Board Class 7th Maths Solutions Chapter 10 Practical Geometry Ex 10.1
Question 1.
Draw a line, say AB, take a point C outside it. Through C, draw a line parallel to AB using ruler and compasses only.
Solution:
Step of Construction :
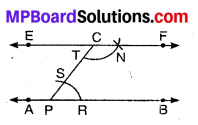
1. Take any point P on line AB.
2. Take any point C (Given) outside AB and join PC.
3. With P as centre and a convenient radius, draw an arc cutting line AB at R and PC at S.
4. Now with C as centre and the same radius as in Step 3, draw an arc intersecting PC at T.
5. With T as centre and radius equal to R draw an arc intersecting the previous arc at N.
6. Now, join CN and produce it on both sides to form a line EF.
Thus, EF is the required line parallel to AB and passing through the given point C.
Question 2.
Draw a line l. Draw a perpendicular to l at a xy n point on l. On this perpendicular choose a point X, 4 cm away from l. Through X, draw a line m parallel to l.
Solution:
Steps of Constructions :
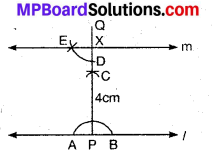
1. Draw a line l and take any point P on it.
2. With P as centre and any suitable radius draw an arc intersecting line l at A and B.
3. With A as centre and radius equal to more than AP draw an arc.
4. Again with B as centre and same radius as in Step 3 draw another arc to intersects the previous arc at C.
5. Join PC and produce it to Q.
Then PQ is the required perpendicular.
6. Now with P as centre and radius equal to 4 cm, draw an arc to intersect PQ at X, such that PX = 4 cm.
7. With X as centre and a convenient radius draw an arc intersecting PQ at D.
8. Again with D as centre and same radius as in Step 7 draw an arc to intersect the previous arc at E.
9. Join XE and produce if to form a line m.
Thus, m is the required line.
![]()
Question 3.
Let l be a line and P be a point not on l. Through P, draw a line m parallel to l. Now join P to any point Q on l. Choose any other point R on m. Through R, draw a line parallel to PQ. Let this meet l at S. What shape do the two sets of parallel lines enclose?
Solution:
Steps of Construction :
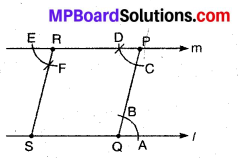
1. Draw a line l and take any point P outside it.
2. Take any point Q on line l
3. Join QP.
4. With Q as centre and any suitable radius, draw an arc intersecting line l and QP at A and B respectively.
5. Now with P as centre and same radius as in Step 4, draw an arc on the opposite side of PQ to intersect PQ at C.
6. Again with C as centre and radius equal to AB, draw an arc to intersect the previous arc at D.
7. Join PD and produce it in both directions to obtain the required line m.
8. Further take any point R on m.
9. Through R, draw a line RS || PQ by following the steps explained above.
The shape of the figure enclosed by these lines is a parallelogram QPRS.