MP Board Class 12th Physics Solutions Chapter 6 वैद्युत चुम्बकीय प्रेरण
वैद्युत चुम्बकीय प्रेरण NCERT पाठ्यपुस्तक के अध्याय में पाठ्यनिहित प्रश्न एवं उनके उत्तर
प्रश्न 1.
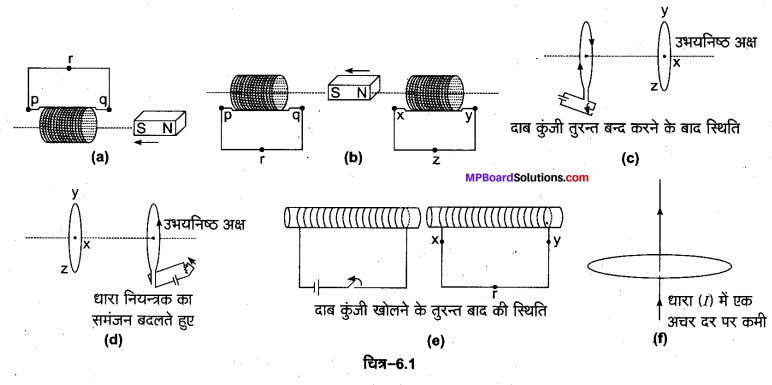
चित्र 6.1 (a) से (f) में वर्णित स्थितियों के लिए प्रेरित धारा की दिशा की प्रागुक्ति (predict) कीजिए।
उत्तर :
(a) लेन्ज के नियम के अनुसार कुंडली का चुम्बक के दक्षिण ध्रुव के सामने वाला पृष्ठ, चुम्बक की गति का विरोध करेगा अर्थात् यह पृष्ठ दक्षिणी ध्रुव बनेगा। इसके लिए प्रेरित धारा qrpq मार्ग का अनुसरण करेगी।
(b) कुंडली pq का, चुम्बक के दक्षिणी ध्रुव के सामने का पृष्ठ, दक्षिणी ध्रुव के पास आने का विरोध करेगा अर्थात् यह सिरा दक्षिणी ध्रुव बनेगा। इसके लिए प्रेरित धारा prqp मार्ग का अनुसरण करेगी। कुंडली xy का, चुम्बक के उत्तरी ध्रुव के सामने वाला पृष्ठ, उत्तरी ध्रुव के दूर जाने का विरोध करेगा अर्थात् दक्षिणी ध्रुव बनेगा। इसके लिए कुंडली
xy में धारा xyzx मार्ग का अनुसरण करेगी।
(c) जब प्रथम कुंडली से जुड़ी कुंजी दबाते हैं तो इसमें धारा शून्य से महत्तम मान की ओर बढ़ती है। इस बढ़ती हुई धारा के कारण समीपस्थ कुंडली में विपरीत दिशा में धारा प्रेरित होती है। __ अतः समीपस्थ कुंडली में धारा xyzx मार्ग का अनुसरण करेगी।
(d) इंगित दिशा में धारा नियन्त्रक का समंजन बदलने पर परिपथ का प्रतिरोध घटेगा तथा कुंडली में धारा बढ़ेगी। यह बढ़ती हुई धारा समीपस्थ कुंडली में विपरीत दिशा में धारा प्रेरित करेगी। अतः प्रेरित धारा xzyx मार्ग का अनुसरण करेगी।
(e) लेन्ज के नियम के अनुसार कुंजी छोड़ने पर दूसरी कुंडली में धारा की दिशा वही होगी जो कि कुंजी छोड़ने से पूर्व प्रथम कुंडली में थी। अतः प्रेरित धारा xryx मार्ग का अनुसरण करेगी।
(f) तार में प्रवाहित धारा के कारण चुम्बकीय क्षेत्र रेखाएँ, लूप के तल के समान्तर हैं। अत: धारा परिवर्तन के कारण लूप से गुजरने वाले फ्लक्स में कोई परिवर्तन नहीं होगा, अत: लूप में कोई धारा प्रेरित नहीं होगी।
प्रश्न 2.
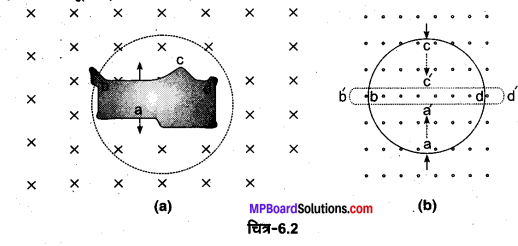
चित्र 6.2 में वर्णित स्थितियों के लिए लेन्ज के नियम का उपयोग करते हुए प्रेरित विद्युत धारा की दिशा ज्ञात कीजिए।
(a) जब अनियमित आकार का तार वृत्ताकार लूप में बदल रहा हो;
(b) जब एक वृत्ताकार लूप एक सीधे तार में विरूपित किया जा रहा हो।.
उत्तर :
(a) क्रॉस (x) द्वारा एक ऐसे चुम्बकीय क्षेत्र को प्रदर्शित किया गया है जिसकी दिशा कागज के तल के लम्बवत् भीतर की ओर है अनियमित आकार के लूप को वृत्तीय रूप में खींचने पर इससे गुजरने वाला फ्लक्स बढ़ेगा। अत: लूप में प्रेरित धारा इस प्रकार की होगी कि वह निम्नगामी फ्लक्स को बढ़ने से रोकेगी। प्रेरित धारा कागज के तल के लम्बवत् ऊपर की ओर चुम्बकीय क्षेत्र उत्पन्न करेगी। अत: धारा की दिशा adcba मार्ग का अनुसरण करेगी।
(b) चुम्बकीय क्षेत्र कागज के तल के लम्बवत् बाहर की ओर है। लूप के आकार को बदलने पर उससे गुजरने वाला ऊर्ध्वमुखी फ्लक्स घटेगा। अत: लूप में प्रेरित धारा ऊर्ध्वमुखी चुम्बकीय क्षेत्र उत्पन्न करेगी। इसके लिए धारा a’ d’ c b’a’ मार्ग का अनुसरण करेगी।
![]()
प्रश्न 3.
एक लम्बी परिनालिका के इकाई सेन्टीमीटर लम्बाई में 15 फेरे हैं। उसके अन्दर 2.0 सेमी का एक छोटा-सा लूप परिनालिका की अक्ष के लम्बवत् रखा गया है। यदि परिनालिका में बहने वाली धारा का मान 0.1सेकण्ड में 2.0 ऐम्पियर से 4.0 ऐम्पियर कर दिया जाए तो धारा परिवर्तन के समय प्रेरित विद्युत वाहक बल कितना होगा?
हल :
परिनालिका में फेरों की संख्या N = 15, लम्बाई 1 = 1 सेमी = 0.01 मीटर, i1 = 2.0 ऐम्पियर, i2 = 4.0 ऐम्पियर, ∆t = 0.1 सेकण्ड, लूप का क्षेत्रफल A = 2.0 सेमी2 = 2.0 × 10-4 मीटर2
लूप में प्रेरित वैद्युत वाहक बल

जबकि परिनालिका के अक्ष पर चुम्बकीय क्षेत्र में परिवर्तन

प्रश्न 4.
एक आयताकार लूप जिसकी भुजाएँ 8 सेमी एवं 2 सेमी हैं, एक स्थान पर थोड़ा कटा हुआ है। यह लूप अपने तल के अभिलम्बवत् 0.3 टेस्ला के एकसमान चुम्बकीय क्षेत्र से बाहर की ओर निकल रहा है। यदि लूप के बाहर निकलने का वेग 1 सेमी सेकण्ड-1 है तो कटे भाग के सिरों पर उत्पन्न वैद्युत वाहक बल कितना होगा, जब लूप की गति अभिलम्बवत् हो (a) लूप की लम्बी भुजा के, (b) लूप की छोटी भुजा के। प्रत्येक स्थिति में उत्पन्न प्रेरित वोल्टता कितने समय तक टिकेगी?
हल :
लम्बी भुजा की लम्बाई l1 = 0.08 मीटर, छोटी भुजा की लम्बाई l2 = 0.02 मीटर
B= 0.3 टेस्ला, υ = 1 सेमी सेकण्ड-1 = 0.01 मीटर सेकण्ड-1
(a) जब लूप लम्बी भुजा के लम्बवत् दिशा में गति कर रहा है तो वैद्युत वाहक बल इसी भुजा के सिरों के बीच उत्पन्न होगा।
∴ वैद्युत वाहक बल e = Bυl1 = 0.3 × 0.01 × 0.08
= 2.4 × 10-4 वोल्ट = 0.24 मिलीवोल्ट
यह वैद्युत वाहक बल तभी तक प्रेरित रहेगा जब तक कि लूप पूर्णतः चुम्बकीय क्षेत्र से बाहर नहीं निकल जाता। लगा समय

(b) इस बार वैद्युत वाहक बल छोटी भुजा के सिरों के बीच प्रेरित होगा।
∴ वैद्युत वाहक बल e = Bυl2 = 0.3x 0.01 x 0.02
= 0.6 × 10-4 वोल्ट
= 0.06 मिलीवोल्ट।
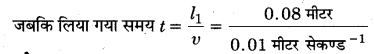
= 8 सेकण्ड।
![]()
प्रश्न 5.
1.0 मीटर लम्बी धातु की छड़ उसके एक सिरे से जाने वाले अभिलम्बवत् अक्ष के परितः 400 रेडियन सेकण्ड-1 की कोणीय आवृत्ति से घूर्णन कर रही है। छड़ का दूसरा सिरा एक धात्विक वलय से सम्पर्कित है। अक्ष के अनुदिश सभी जगह 0.5 टेस्ला का एकसमान चुम्बकीय क्षेत्र उपस्थित है। वलय तथा अक्ष के बीच स्थापित वैद्युत वाहक बल की गणना कीजिए।
हल :
छड़ की लम्बाई l = 1.0 मीटर, ω = 400 रेंडियन सेकण्ड-1, B= 0.5 टेस्ला
अक्ष O से x दूरी पर स्थित छड़ के अल्पशि PQ = dx पर विचार कीजिए।
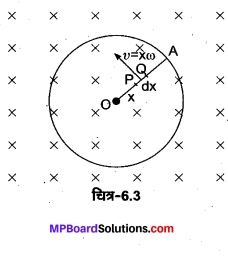
इस अल्पांश का रेखीय वेग υ = xω
∴ इस अल्पांश का विभवान्तर
de = Bυdx = Bxω dx
∴ वलय तथा अक्ष के बीच प्रेरित वैद्युत वाहक बल
e = छड़ के सिरों O तथा A के बीच प्रेरित वैद्युत वाहक बल

प्रश्न 6.
एक वृत्ताकार कुंडली जिसकी त्रिज्या 8.0 सेमी तथा फेरों की संख्या 20 है अपने ऊर्ध्वाधर व्यास के परितः 50 रेडियन सेकण्ड-1 की कोणीय आवृत्ति से 3.0 × 10-2 टेस्ला के एकसमान चुम्बकीय क्षेत्र में घूम रही है। कुंडली में उत्पन्न अधिकतम तथा औसत प्रेरित वैद्युत वाहक बल का मान ज्ञात कीजिए। यदि कुंडली 10Ω प्रतिरोध का एक बन्द लूप बनाए तो कुंडली में धारा के अधिकतम मान की गणना कीजिए। जूल ऊष्मन के कारण क्षयित औसत शक्ति की गणना कीजिए। यह शक्ति कहाँ से प्राप्त होती है?
हल :
त्रिज्या r = 0.08 मीटर, N = 20, ω = 50 रेडियन सेकण्ड, B= 3.0 × 10-2 टेस्ला, emax = ?,
eaυ = ?
यदि R= 10Ω तब imax= ?
औसत शक्ति क्षय Paυ = ?
जब कुंडली चुम्बकीय क्षेत्र में घूमती है तो उसके सिरों के बीच प्रत्यावर्ती वैद्युत वाहक बल उत्पन्न होता है। वै० वा० बल का महत्तम मान
emax = NBAω
= 20 × 3.0 × 10-2 × [r × (0.08)2] × 50
⇒ emax = 0.603 वोल्ट।
जबकि एक पूर्ण चक्र के लिए प्रत्यावर्ती वैद्युत वाहक बल का औसत मान शून्य होगा।
⇒ eaυ = 0
परिपथ में महत्तम धारा
\(i_{\max }=\frac{e_{\max }}{R}=\frac{0.603}{10}\)
= 0.0603 ऐम्पियर।
परिपथ में औसत शक्ति क्षय
Paυ = \(\frac{1}{2}\) × emax × imax =x emax ximar
= \(\frac{1}{2}\) × 0.603 × 0.0603
= 0.018 वाट।
यह शक्ति कुंडली को घुमाने वाले बाह्य स्रोत के द्वारा किए गए कार्य से प्राप्त होती है।
प्रश्न 7.
पूर्व से पश्चिम दिशा में विस्तृत एक 10 मीटर लम्बा क्षैतिज सीधा तार 0.30 × 10-4 वेबर मीटर-2 तीव्रता वाले पृथ्वी के चुम्बकीय क्षेत्र के क्षैतिज घटक के लम्बवत् 5.0 मीटर सेकण्ड-1 की चाल से गिर रहा है।
(a) तार में प्रेरित वैद्युत वाहक बल का तात्क्षणिक मान क्या होगा?
(b) वैद्युत वाहक बल की दिशा क्या है?
(c) तार का कौन-सा सिरा उच्च विद्युत विभव पर है?
हल :
तार की लम्बाई l = 10 मीटर, υ = 5.0 मीटर सेकण्ड-1,
चुम्बकीय क्षेत्र BH = 0.30 × 10-4 वेबर मीटर-2
(a) तार में प्रेरत वैद्युत वाहक बल का तात्क्षणिक मान
e = BHU = 0.30 × 10-4 × 5.0 × 10
= 1.5 × 10-3 वोल्ट
= 1.5 मिलीवोल्ट।
(b) फ्लेमिंग के दाएँ हाथ के नियम से, वैद्युत वाहक बल की दिशा पश्चिम से पूर्व की ओर होगी।
(c) यह तार जब वैद्युत वाहक बल के स्रोत की भाँति कार्य करेगा तो पूर्वी सिरा उच्च विद्युत विभव पर होगा।
![]()
प्रश्न 8.
किसी परिपथ में 0.1 सेकण्ड में धारा 5.0 ऐम्पियर से 0.0 ऐम्पियर तक गिरती है। यदि औसत प्रेरित वैद्युत वाहक बल 200 वोल्ट है तो परिपथ में स्वप्रेरकत्व का आकलन कीजिए।
हल :
i1 = 5.0 ऐम्पियर, i2 = 0.0 ऐम्पयर, ∆t = 0.1 सेकण्ड
|e | = 200 वोल्ट, स्वप्रेरकत्व L = ?
सूत्र | e |= \(L \frac{d i}{d t}\)
स्वप्रेरकत्व \(L=\frac{|e|}{d i / d t}=\frac{200}{(5.0-0.0) / 0.1}=\frac{200 \times 0.1}{5.0} \) हेनरी
प्रश्न 9.
पास-पास रखे कुंडलियों के एक युग्म का अन्योन्य प्रेरकत्व 1.5 हेनरी है। यदि एक कुंडली में 0.5 सेकण्ड में धारा 0 से 20 ऐम्पियर परिवर्तित हो तो दूसरी कुंडली की फ्लक्स बंधता में कितना परिवर्तन होगा?
हल :
दिया है : M = 1.5 हेनरी, ∆i = 20 ऐम्पियर – 0 ऐम्पियर = 20 ऐम्पियर, ∆t = 0.5 सेकण्ड दूसरी कुंडली में फ्लक्स बन्धता में परिवर्तन
∆Φ = M∆i = 1.5 × 20 = 30 वेबर।
प्रश्न 10.
एक जेट प्लेन पश्चिम की ओर 1800 किमी/घण्टा वेग से गतिमान है। प्लेन के पंख 25 मीटर लम्बे हैं। इनके सिरों पर कितना विभवान्तर उत्पन्न होगा? पृथ्वी के चुम्बकीय क्षेत्र का मान उस स्थान पर 5 × 10-4 टेस्ला तथा नति कोण (dip angle) 30° है।
हल :
दिया है : वेग υ = 1800 किमी/घण्टा = 1800 × \(\frac{5}{18}\)
= 500 मीटर सेकण्ड-1
पंखों की लम्बाई 1 = 25 मीटर,
B= 5 × 10-4 टेस्ला, नति कोण δ = 30°
∵ प्लेन क्षैतिज दिशा में गतिमान है, अत: प्लेन के पंख पृथ्वी के क्षेत्र के ऊर्ध्व घटक को काटेंगे।
ऊर्ध्व घटक BV = B sin δ = 5 × 10-4 × \(\frac{1}{2}\) = 2.5 × 10-4 टेस्ला
∴ पंखों के सिरों के बीच प्रेरित वैद्युत वाहक बल
e = BVυl = 2.5 × 10-4 × 500 × 25
= 3.125 वोल्ट
= 3.1 वोल्ट।
प्रश्न 11.
मान लीजिए कि प्रश्न 4 में उल्लिखित लूप स्थिर है किन्तु चुम्बकीय क्षेत्र उत्पन्न करने वाले वैद्युत चुम्बक में धारा का मान कम किया जाता है जिससे चुम्बकीय क्षेत्र का मान अपने प्रारम्भिक मान 0.3 टेस्ला से 0.02 टेस्ला सेकण्ड-1 की दर से घटता है। अब यदि लूप का कटा भाग जोड़ दें जिससे प्राप्त बन्द लूप का प्रतिरोध 1.6Ω हो तो इस लूप में ऊष्मन के रूप में शक्ति ह्रास क्या है? इस शक्ति का स्रोत क्या है?
हल :
लूप का क्षेत्रफल A = 8 × 2 सेमी2 = 16 × 10-4 मीटर2
\(\frac{d B}{d t}\) = 0.02 टेस्ला सेकण्ड-1, R = 1.6Ω
प्रेरित वैद्युत वाहक बल \(e=\frac{d \phi}{d t}=\frac{d}{d t}(B A)=A \frac{d B}{d t}\)
⇒ e = 16 × 10-4 × 0.02
= 3.2 × 10-5 वोल्ट।
∴ प्रेरित धारा: \(\frac{e}{R}=\frac{3.2 \times 10^{-5}}{1.6}\)
= 2.0 × 10-5 ऐम्पियर।
∴ शक्ति ह्रास P = e × i
= 3.2 × 10-5 × 2.0 × 10-5
= 6.4 × 10-10 वाट।
यह शक्ति, चुम्बकीय क्षेत्र में परिवर्तन करने वाले बाह्य स्रोत द्वारा प्रदान की जाती है।
प्रश्न 12.
12 सेमी भुजा वाला वर्गाकार लूप जिसकी भुजाएँ x एवं Y अक्षों के समान्तर हैं, –दिशा में 8 सेमी सेकण्ड-1 की गति से चलाया जाता है। लूप तथा उसकी गति का परिवेश धनात्मक –दिशा के चुम्बकीय क्षेत्र का है। चुम्बकीय क्षेत्र न तो एकसमान है और न ही समय के साथ नियत है। इस क्षेत्र की ऋणात्मक दिशा में प्रवणता 10-3 टेस्ला सेकण्ड-1 है (अर्थात् ऋणात्मक x-अक्ष की दिशा में इकाई सेन्टीमीटर दूरी पर क्षेत्र के मान में 10-3 टेस्ला सेकण्ड-1 की वृद्धि होती है) तथा क्षेत्र के मान में 10-3 टेस्ला सेकण्ड-1 की दर से कमी भी हो रही है। यदि कुंडली का प्रतिरोध 4.50 मिलीओम हो तो प्रेरित धारा का परिमाण एवं दिशा ज्ञात कीजिए।
हल :
लूप का प्रतिरोध R = 4.50 × 10-3Ω, लूप की भुजा a = 12 सेमी
\(\frac{\partial B}{\partial x}\) = – 10-3 टेस्ला मीटर-1 = – 10-1 टेस्ला मीटर-1
= – 0.1 टेस्ला मीटर-1 [X-अक्ष की ऋणात्मक दिशा में]
thada \(\frac{\partial x}{\partial t}\) = 8 सेमी सेकण्ड-1 = 0.08 मीटर सेकण्ड-1.
\(\frac{\partial B}{\partial t}\) = – 10-3 टेस्ला सेकण्ड-1
\(\frac{\partial B}{\partial x}\) तथा \(\frac{\partial B}{\partial t}\) दोनों का चिह्न ऋणात्मक लिया गया है क्योंकि x तथा t दोनों के बढ़ने के साथ चुम्बकीय क्षेत्र घट रहा है।
माना लूप की भुजा की लम्बाई ‘a’ है। x दूरी पर स्थित dx चौड़ाई की एक पट्टी ४ पर विचार कीजिए।
माना इस पट्टी पर चुम्बकीय क्षेत्र B(x, t) है तथा इस पट्टी का क्षेत्रफल dA = adx है।
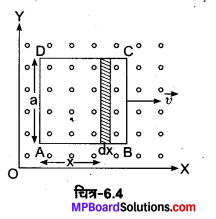
∴ इस पट्टी से बद्ध चुम्बकीय फ्लक्स
dΦ = BdA = B(x, t) adx
∴ लूप से बद्ध कुल फलक्स

धारा की दिशा ऐसी होगी जो z-दिशा में चुम्बकीय फ्लक्स के घटने का विरोध करेगी। इसके लिए धारी वामावर्त दिशा में प्रवाहित होगी।
![]()
प्रश्न 13.
एक शक्तिशाली लाउडस्पीकर के चुम्बक के ध्रुवों के बीच चुम्बकीय क्षेत्र की तीव्रता के परिमाण का मापन किया जाना है। इस हेतु एक छोटी चपटी 2 सेमी क्षेत्रफल की अन्वेषी कुंडली (search coil) का प्रयोग किया गया है। इस कुंडली में पास-पास लिपंटे 25 फेरे हैं तथा इसे चुम्बकीय क्षेत्र के लम्बवत् व्यवस्थित किया गया है और तब इसे द्रुत गति से क्षेत्र के बाहर निकाला जाता है। तुल्यतः एक अन्य विधि में अन्वेषी कुंडली को 90° से तेजी से घुमा देते हैं जिससे कुंडली का तल चुम्बकीय क्षेत्र के समान्तर हो जाए। इन दोनों घटनाओं में कुल 7.5 मिलीकूलॉम आवेश का प्रवाह होता है (जिसे परिपथ में प्रक्षेप धारामापी (ballistic galvanometer) लगाकर ज्ञात किया जा सकता है)। कुंडली तथा धारामापी का संयुक्त प्रतिरोध 0.502 है। चुम्बक की क्षेत्र की तीव्रता का आकलन कीजिए। •
हल :
A = 2 × 10-4 मीटर2, N= 25 फेरे, प्रेरित आवेश q = 7.5×10-3 कूलॉम
परिपथ का प्रतिरोध R = 0.50Ω
माना चुम्बकीय क्षेत्र की तीव्रता = B.
प्रारम्भिक फ्लक्स Φ1 = NBA cos 0° = NBA
अन्तिम फ्लक्स Φ2 = 0
∴ प्रेरित वैद्युत वाहक बल e = \(-\frac{d \phi}{d t}\)

प्रश्न 14.
चित्र 6.5 में एक धातु की छड़ PQ को दर्शाया गया है जो पटरियों AB पर रखी हैं तथा एक स्थायी चुम्बक के ध्रुवों के मध्य स्थित है। पटरियाँ, छड़ एवं चुम्बकीय क्षेत्र परस्पर अभिलम्बवत् दिशाओं में हैं। एक गैल्वेनोमीटर (धारामापी) G को पटरियों से एक स्विच K की सहायता से संयोजित किया गया है। छड़ की लम्बाई = 15 सेमी, B= 0.50 टेस्ला तथा पटरियों, छड़ तथा धारामापी से बने बन्द लूप का प्रतिरोध = 9.0 मिली ओम है। . क्षेत्र को एकसमान मान लें।
(a) माना कुंजी K खुली (open) है तथा छड़ 12 सेमी सेकण्ड -1की चाल से दर्शायी गई दिशा में गतिमान है। प्रेरित वैद्युत वाहक बल का मान एवं ध्रुवणता (polarity) बताइए।
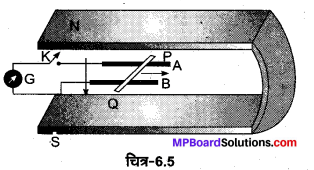
(b) क्या कुंजी K खुली होने पर छड़ के सिरों पर आवेश का आधिक्य हो जाएगा? क्या होगा यदि कुंजी K बंद (close) कर दी जाए।
(c) जब कुंजी K खुली हो तथा छड़ एकसमान वेग से गति में हो तब भी इलेक्ट्रॉनों पर कोई परिणामी बल कार्य नहीं करता यद्यपि उन पर छड़ की गति के कारण चुम्बकीय बल कार्य करता है। कारण स्पष्ट कीजिए।
(d) कुंजी बन्द होने की स्थिति में छड़ पर लगने वाले अवमन्दन बल का मान क्या होगा?
(e) कुंजी बन्द होने की स्थिति में छड़ को उसी चाल (= 12 सेमी सेकण्ड-1) से चलाने हेतु कितनी शक्ति (बाह्य कारक के लिए) की आवश्यकता होगी?
(f) बन्द परिपथ में कितनी शक्ति का ऊष्मा के रूप में क्षय होगा? इस शक्ति का स्रोत क्या है?
(g) गतिमान छड़ में उत्पन्न वैद्युत वाहक बल का मान क्या होगा यदि चुम्बकीय क्षेत्र की दिशा पटरियों के लम्बवत् होने की बजाय उनके समान्तर हो?
हल :
दिया है : B= 0.50 टेस्ला , l = 0.15 मीटर, υ = 0.12 सेमी सेकण्ड-1, R= 9.0 × 10-3Ω
(a) छड़ में प्रेरित वैद्युत वाहक बल e = Bυl = 0.50 × 0.12 × 0.15
= 9 × 10-3 वोल्ट = 9.0 मिलीवोल्ट।
छड़ का सिरा P धनात्मक तथा Q ऋणात्मक होगा।
(b) हाँ, छड़ के Q सिरे पर इलेक्ट्रॉन एकत्र हो जाएँगे जबकि P सिरे पर धनावेश की अधिकता हो जाएगी।
यदि कुंजी K को बन्द कर दिया जाए तो Q सिरे पर एकत्र होने वाले इलेक्ट्रॉन बन्द परिपथ से होते हुए (G से होकर) सिरे P की ओर गति करने लगेंगे। इस प्रकार परिपथ में स्थायी धारा स्थापित हो जाएगी।
(c) जब कुंजी K खुली है तो P सिरा धनात्मक व Q सिरा ऋणात्मक हो जाता है। इससे छड़ के भीतर सिरे P से सिरे Q की ओर एक वैद्युत क्षेत्र स्थित हो जाता है। इस क्षेत्र के कारण इलेक्ट्रॉनों पर Q से P की ओर वैद्युत बल लगता है जो विपरीत दिष्ट चुम्बकीय बल को सन्तुलित कर लेता है।
इस प्रकार इलेक्ट्रॉनों पर कोई नेट बल कार्य नहीं करता है।
(d) कुंजी K बन्द होने की स्थिति में छड़ PQ से प्रवाहित धारा
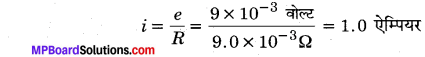
∴ छड़ PQ पर चुम्बकीय क्षेत्र के कारण कार्य करने वाला अवमन्दन बल
F = il B sin 90° = 1.0 × 0.15 × 0.50 .
= 75 × 10-3 न्यूटन = 0.075 न्यूटन।
(e) कुंजी K के बन्द होने पर छड़ को खींचते रहने के लिए व्यय की जाने वाली शक्ति
P = Fυ = 0.075 × 0.12 = 9 × 10-3 वाट।
(f) परिपथ में व्यय ऊष्मीय शक्ति
. P= i2R = (1.0)2 × 9.0 × 10-3 = 9 × 10-3 वाट।
इस शक्ति का स्रोत छड़ को एकसमान वेग से खींचते रहने के लिए बाह्य स्रोत द्वारा व्यय की गई शक्ति है।
(g) शून्य; इस स्थिति में छड़ चुम्बकीय बल रेखाओं को नहीं काटेगी। अतः कोई वैद्युत वाहक बल प्रेरित नहीं होगा।
प्रश्न 15.
वायु के क्रोड वाली एक परिनालिका में, जिसकी लम्बाई 30 सेमी तथा अनुप्रस्थ काट का क्षेत्रफल 25 सेमी तथा कुल फेरे 500 हैं, 2.5 ऐम्पियर धारा प्रवाहित हो रही है। धारा को 10-3 सेकण्ड के अल्पकाल में अचानक बन्द कर दिया जाता है। परिपथ में स्विच के खुले सिरों के बीच उत्पन्न औसत वैद्युत वाहक बल का मान क्या होगा? परिनालिका के सिरों पर चुम्बकीय क्षेत्र के परिवर्तन की उपेक्षा कर सकते हैं?
हल :
फेरों की संख्या N = 500, लम्बाई 1 = 0.30 मीटर, क्षेत्रफल A = 25 × 10-4 मीटर2,
i1 = 2.5 ऐम्पियर, i2 = 0, dt = 103 सेकण्ड
अक्ष पर चुम्बकीय क्षेत्र को एकसमान मानते हुए प्रारम्भिक चुम्बकीय क्षेत्र \(B_{1}=\mu_{0} \frac{N}{l} i_{1}\)
तथा अन्तिम चुम्बकीय क्षेत्र B_{2}=\mu_{0} \frac{N}{l} i_{2}=0
∴ परिनालिका से बद्ध फ्लक्स बन्धुता में परिवर्तन
dΦ = NB2A – NB1A –
= 0 – 500 × 4 π × 10-7 × \(\frac{500}{0.30}\) × 25 × 10-4
= – 65.45 × 10-4 वेबर
अतः स्विच के सिरों के बीच प्रेरित औसत वैद्युत वाहक बल
\(e=-\frac{d \phi}{d t}=\frac{65.45 \times 10^{-4}}{10^{-3}}\)
= 6.545 वोल्ट = 6.5 वोल्ट।
प्रश्न 16.
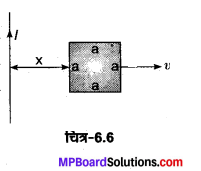
(a) चित्र 6.6 में दर्शाए अनुसार एक लम्बे, सीधे तार तथा एक वर्गाकार लूप जिसकी एक भुजा की लम्बाई a है, के लिए अन्योन्य प्रेरकत्व का व्यंजक प्राप्त कीजिए।
(b) अब मान लीजिए कि सीधे तार में 50 ऐम्पियर की धारा प्रवाहित हो रही है तथा । लूप एक स्थिर वेग υ = 10 मीटर/सेकण्ड-1 से दायीं ओर को गति कर रहा है। लूप में प्रेरित वैद्युत वाहक बल का परिकलन उस क्षण पर कीजिए जब x= 0.2 मीटर हो। लूप के | लिए a = 0.1 मीटर लीजिए तथा यह मान लीजिए कि उसका प्रतिरोध बहुत अधिक है।
हल :
(a) यदि अन्योन्य प्रेरण गुणांक M है तो
Φ = Mi
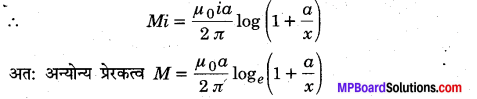
(b) लूप के भीतर तार से 2 दूरी पर स्थित dz चौड़ाई की एक ऐसी पट्टी पर विचार कीजिए जो कि तार के समान्तर है।
इस पट्टी का क्षेत्रफल dA = adz
तार के कारण पट्टी पर चुम्बकीय क्षेत्र \(B=\frac{\mu_{0}}{2 \pi} \cdot \frac{i}{z}\)
यह क्षेत्र पट्टी के तल के लम्बवत् भीतर की ओर है।
∴ पट्टी से बद्ध चुम्बकीय फ्लक्स dΦ = BdA = \(\frac{\mu_{0}}{2 \pi} \cdot \frac{i}{z}\) .adz
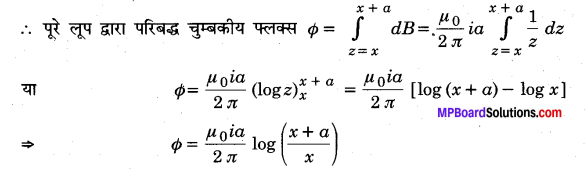
दिया है : i = 50 ऐम्पियर, υ = 10 मीटर/सेकण्ड-1, e= ?, जबकि x = 0.2 मीटर, a = 0.1 मीटर
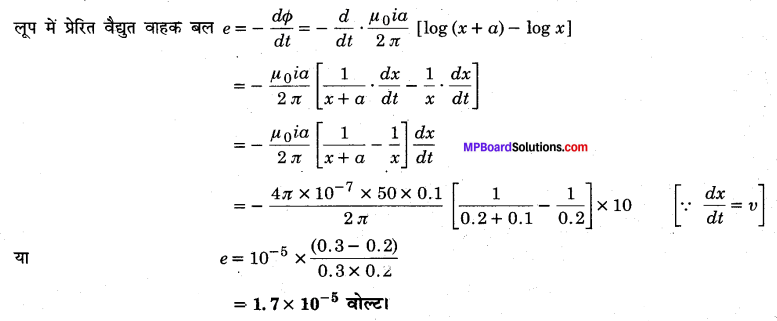
![]()
प्रश्न 17.
किसी M द्रव्यमान तथा R त्रिज्या वाले एक पहिये के किनारे (rim) पर एक रैखिक आवेश स्थापित किया गया है जिसकी प्रति इकाई लम्बाई पर आवेश का मान λ है। पहिये के स्पोक (spoke) हल्के एवं कुचालक हैं तथा वह अपनी अक्ष के परितः घर्षण रहित घूर्णन हेतु स्वतन्त्र है जैसा कि चित्र 6.8 में दर्शाया गया है। पहिये के वृत्तीय भाग पर रिम, के अन्दर एकसमान चुम्बकीय क्षेत्र विस्तरित है। इसे इस प्रकार परिभाषित किया गया है –
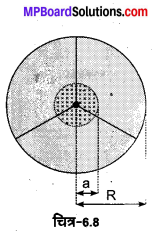

चुम्बकीय क्षेत्र को अचानक ‘ऑफ’ (switched off) करने के पश्चात्, पहिये का कोणीय वेग ज्ञात कीजिए।
हल :
माना चुम्बकीय क्षेत्र को स्विच ऑफ करने पर E वैद्युत क्षेत्र उत्पन्न होता है (Note) तथा पहिया ω कोणीय वेग से घूमना प्रारम्भ करता है।
यदि पहिये पर कुल आवेश q है तो एक पूर्ण चक्र के दौरान वैद्युत क्षेत्र द्वारा आवेश को घुमाने में कृत कार्य
w = F x s = qE x 2 1 R

वैद्युत चुम्बकीय प्रेरण NCERT भौतिक विज्ञान प्रश्न प्रदर्शिका (Physics Exemplar Problems) पुस्तक से चयनित महत्त्वपूर्ण प्रश्नों के हल
वैद्युत चुम्बकीय प्रेरण बहुविकल्पीय प्रश्नोत्तर
प्रश्न 1.
x- y तल के किसी प्रदेश में, जहाँ चुम्बकीय क्षेत्र \(B=B_{0}(2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}+4 \hat{\mathrm{k}}) \mathrm{T}\) है, (यहाँ B0 कोई नियतांक है), L मीटर भुजा का कोई वर्ग रखा है। इस वर्ग से गुजने वाले फ्लक्स का परिमाण है –
(a) 2B0L2 wb
(b) 3B0L2 Wb
(c) 4B0L2 Wb
(d) 29 BoL2 Wb.
उत्तर :
(c) 4B0L2 Wb
![]()
प्रश्न 2.
किसी बेलनाकार छड़ चुम्बक को उसके अक्ष के परित: (चित्र 6.9) घूर्णन कराया जाता है। किसी अ क्ष
तार को इसके अक्ष से संयोजित करके इसके बेलनाकार पृष्ठ से किसी सम्पर्क द्वारा स्पर्श कराया गया है, तब –
(a) ऐमीटर A से दिष्ट धारा प्रवाहित होती है।
(b) ऐमीटर A से दिष्ट धारा प्रवाहित नहीं होती है
(c) ऐमीटर A से आवर्तकाल \(T=\frac{2 \pi}{\omega}\) की प्रत्यावर्ती ज्वावक्रीय धारा प्रवाहित होती है ।
(d) ऐमीटर A से काल परिवर्तित धारा प्रवाहित होती है जो ज्यावक्रीय नहीं होती।
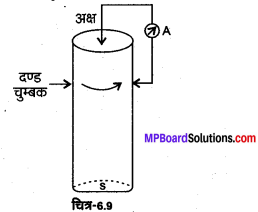
उत्तर :
(a) ऐमीटर A से दिष्ट धारा प्रवाहित होती है।
प्रश्न 3.
चित्र 6.10 में दर्शाए अनुसार A तथा B दो कुण्डलियाँ हैं। जब A को B की ओर गति कराते हैं तो B में चित्र में दर्शाए अनुसार धारा प्रवाहित होने लगती है तथा A के रुकने पर A धारा प्रवाहित होना बन्द हो जाती है। B में धारा वामावर्ती है। जब A गति करता है तो B को स्थिर रखा जाता है तो हम यह निष्कर्ष निकाल सकते हैं कि –
(a) A में दक्षिणावर्ती दिशा में नियत धारा है
(b) A में परिवर्ती धारा है
(c) A में कोई धारा नहीं है
(d) A में वामावर्ती दिशा में नियत धारा है।
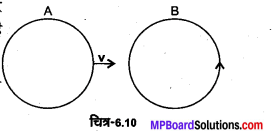
उत्तर :
(d) A में वामावर्ती दिशा में नियत धारा है।
![]()
प्रश्न 4.
इस प्रश्न में भी स्थिति प्रश्न 6.10 की भाँति है। अन्तर केवल यह है कि अब कुण्डली A को ऊर्ध्वाधर अक्ष के परितः घूर्णन कराया गया है (चित्र-6.11)। यदि A विराम में है तो B में कोई धारा प्रवाहित नहीं होती। जब B में (t = 0 पर) धारा वामावर्ती दिशा में है तथा इस क्षण, t = 0, पर कुंडली A दर्शाए अनुसार है तब कुंडली A में प्रवाहित होती है?
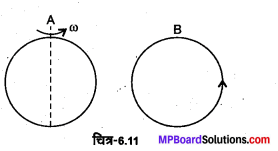
(a) दक्षिणावर्त नियत धारा
(b) दक्षिणावर्त परिवर्ती धारा
(c) वामावर्त परिवर्ती धारा
(d) वामावर्त नियत धारा।
उत्तर :
(a) दक्षिणावर्त नियत धारा
प्रश्न 5.
किसी अनुप्रस्थ काट के क्षेत्रफल A तथा नियत फेरों की संख्या N वाली l लम्बाई की परिनालिका का स्वप्रेरकत्व L बढ़
जाता है –
(a) l तथा A में वृद्धि के साथ
(b) l में कमी तथा A में वृद्धि के साथ
(c) l में वृद्धि तथा A में कमी के साथ
(d) l तथा A में कमी के साथ।
उत्तर :
(b) l में कमी तथा A में वृद्धि के साथ
वैद्युत चुम्बकीय प्रेरण अति लघु उत्तरीय प्रश्नोत्तर
प्रश्न 1.
किसी ऐसे चुम्बक पर विचार कीजिए जो एक ऑन/ऑफ स्विच लगे तार के लूप से घिरा है। यदि स्विच को ऑफ स्थिति (खुले परिपथ) से ऑन स्थिति (बन्द परिपथ) पर लाया जाए तो क्या परिपथ में कोई धारा प्रवाहित होगी?
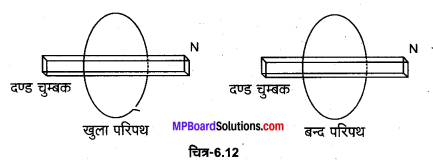
उत्तर :
तार का कोई भी भाग गतिमान नहीं है, अत: कोई गतिक वैद्युत वाहक बल उत्पन्न नहीं होगा। चुम्बक भी स्थिर है, अत: समय के साथ चुम्बकीय क्षेत्र परिवर्तित नहीं होगा। अत: कोई प्रेरित वैद्युत वाहक बल भी उत्पन्न नहीं होगा। अत: परिपथ में कोई धारा प्रवाहित नहीं होगी।
प्रश्न 2.
कसकर लिपटी परिनालिका के रूप में कोई तार किसी दिष्ट धारा स्रोत से संयोजित है और इसमें विद्युत धारा प्रवाहित हो रही है। यदि कुंडली को इस प्रकार से खींचा जाए कि सर्पिलाकार कुंडली के क्रमागत लपेटों के बीच अन्तराल हो जाए, तो क्या विद्युत धारा बढ़ेगी अथवा घटेगी, स्पष्ट कीजिए।
उत्तर :
कुंडली को खींचकर उसके क्रमागत लपेटों के बीच अन्तराल आ जाने पर इन रिक्त स्थानों से चुम्बकीय फ्लक्स की हानि होगी। अत: लेन्ज के नियमानुसार परिनालिका में एक प्रेरित धारा बहेगी जो चुम्बकीय फ्लक्स में कमी का विरोध करेगी। अतः परिनालिका में प्रवाहित विद्यत धारा बढ़ेगी।
प्रश्न 3.
कोई परिनालिका किसी बैटरी से संयोजित है जिसके कारण उसमें अपरिवर्तित धारा प्रवाहित हो रही है। यदि इस परिनालिका के भीतर कोई लोह क्रोड रख दिया जाए तो विद्युत धारा घटेगी अथवा बढ़ेगी? स्पष्ट कीजिए।
उत्तर :
परिनालिका के भीतर कोई लौह क्रोड रख देने पर चुम्बकीय क्षेत्र में वृद्धि के कारण चुम्बकीय फ्लक्स में वृद्धि हो जाएगी। अत: लेन्ज के नियमानुसार परिनालिका में एक प्रेरित वैद्युत वाहक बल एवं प्रेरित धारा उत्पन्न होगी जोकि फ्लक्स वृद्धि का विरोध करेगी। अतः परिनालिका में प्रवाहित धारा घटेगी।
प्रश्न 4.
धातु के किसी ऐसे छल्ले पर विचार कीजिए जो किसी ऊर्ध्वाधरतः रखी स्थिर परिनालिका (जैसे–कार्ड बोर्ड में जड़ी) के शीर्ष पर रखा है (चित्र 6.13)। छल्ले का केन्द्र परिनालिका के अक्ष के सम्पाती है। यदि अचानक स्विच ऑन करके परिनालिका में धारा प्रवाहित कराएँ तो धातु का छल्ला ऊपर उछलता है। स्पष्ट कीजिए।
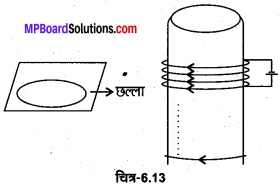
उत्तर :
प्रारम्भ में धातु के छल्ले से बद्ध चुम्बकीय फ्लक्स शून्य है। अचानक स्विच ऑन करने पर छल्लों से चुम्बकीय फ्लक्स गुजरता है। लेज के नियमानुसार धातु के छल्ले में एक प्रेरित वैद्युत वाहक बल उत्पन्न होता है जो इस चुम्बकीय फ्लक्स में वृद्धि का विरोध करता है। यह केवल तभी सम्भव है जब छल्ला परिनालिका से दूर अर्थात् ऊपर की ओर गति करे। अत: छल्ला ऊपर की ओर उछलता है।
![]()
प्रश्न 5.
1 सेमी आन्तरिक त्रिज्या के किसी धातु के पाइप पर विचार कीजिए। यदि 0.8 सेमी त्रिज्या का कोई बेलनाकार छड़ चुम्बक इस पाइप में गिराया जाए तो वह नीचे गिरने में किसी प्रकार की अचुम्बकित बेलनाकार लौह छड़ की तुलना में अधिक समय लेता है। स्पष्ट कीजिए।
उत्तर :
जब बेलनाकार छड़ चुम्बक को धातु के पाइप में गिराया जाता है तो पाइप में भँवर धाराएँ उत्पन्न होगी, जोकि चुम्बक की गति का विरोध करेंगी। अतः इसकी गति का त्वरण, गुरुत्वीय त्वरण से कम हो जाता है। अचुम्बकित बेलनाकार छड़ को पाइप में गिराने पर, पाइप में भँवर धाराएँ उत्पन्न नहीं होंगी और वह गुरुत्वीय त्वरण से नीचे गिरेंगी। अतः बेलनाकार छड़ चुम्बक पाइप में गिरने में, किसी अचुम्बकित बेलनाकार छड़ से अधिक समय लेती है।