MP Board Class 12th Physics Solutions Chapter 2 स्थिरवैद्युत विभव तथा धारिता
स्थिरवैद्युत विभव तथा धारिता NCERT पाठ्यपुस्तक के अध्याय में पाठ्यनिहित प्रश्न एवं उनके उत्तर
प्रश्न 1.
5 × 10-8 कूलॉम तथा – 3× 10-8 कूलॉम के दो आवेश 16 सेमी दूरी पर स्थित हैं। दोनों आवेशों को मिलाने वाली रेखा के किस बिन्दु पर विद्युत विभव शून्य होगा? अनन्त पर विभव शून्य लीजिए।
COMMON ERRORS
दो विपरीत प्रकृति के आवेशों के कारण वैद्युत विभव केवल एक बिन्दु पर शून्य न होकर दो बिन्दुओं पर शून्य
होता है। पहला बिन्दु दोनों आवेशों के बीच में होगा तथा दूसरा बिन्दु आवेशों से बाहर छोटे परिमाण के आवेश के निकट होगा।
हल :
प्रथम दशा : माना बिन्दु आवेश qA = 5 × 10-8 कूलॉम से दूसरे आवेश की ओर दूरी पर 0 बिन्दु पर विद्युत विभव शून्य है,

अत: प्रथम आवेश से दूसरे आवेश की ओर 10 सेमी दूरी पर विद्युत विभव शून्य है।
द्वितीय दशा : माना प्रथम आवेश से दूसरे आवेश की ओर r दूरी पर (दूसरे आवेश से बाहर r > 0.16 मीटर) विद्युत विभव शून्य है।
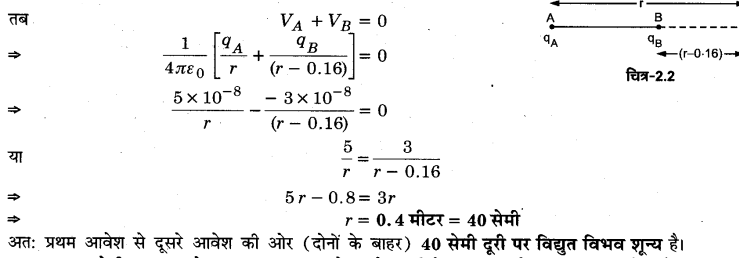
![]()
प्रश्न 2.
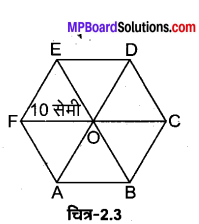
10 सेमी भुजा वाले एक सम-षट्भुज के प्रत्येक शीर्ष पर 5 माइक्रोकूलॉम का आवेश है। षट्भुज के केन्द्र पर विभव परिकलित कीजिए।
हल :
प्रत्येक आवेश q = 5 माइक्रोकूलॉम
प्रत्येक आवेश की केन्द्र O से दूरी r = 0.1 मीटर
∴ केन्द्र O पर परिणामी विभव V =\(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 × 109 × 6 × \(\frac{q}{r}\)
= 9 × 109 × 6 × \(\frac{5 \times 10^{-6}}{0.1}\)
= 2.7 × 106 वोल्ट।
प्रश्न 3.
6 सेमी की दूरी पर अवस्थित दो बिन्दुओं A एवं B पर दो आवेश 2 माइक्रोकूलॉम तथा – 2माइक्रोकूलॉम रखे हैं।
(a) निकाय के सम विभव पृष्ठ की पहचान कीजिए।
(b) इस पृष्ठ के प्रत्येक बिन्दु पर विद्युत क्षेत्र की दिशा क्या है?
हल :
(a) चूँकि दोनों वेश समान परिमाण के परन्तु विपरीत चिह्न के हैं। अतः समविभव पृष्ठ दोना आवेशों को मिलाने वाली रेखा AB के लम्बवत् होगा तथा उसके मध्य-बिन्दु से जाएगा।
(b) विद्युत क्षेत्र की दिशा समविभव पृष्ठ के लम्बवत् धनावेश से ऋणावेश की ओर (AB की दिशा में) होगी।
प्रश्न 4.
12 सेमी त्रिज्या वाले एक गोलीय चालक के पृष्ठ पर 1.6 × 10-7कूलॉम पर आवेश एकसमान रूप से वितरित है।
(a) गोले के अन्दर
(b) गोले के ठीक बाहर
(c) गोले के केन्द्र से 18 सेमी पर अवस्थित, किसी बिन्दु पर विद्युत क्षेत्र क्या होगा?
हल :
(a) ∵ आवेश चालक के पृष्ठ पर वितरित है; अतः गोले के भीतर विद्युत क्षेत्र शून्य होगा।
(b) दिया है : गोले की त्रिज्या R= 0.12 मीटर
गोले. पर आवेश q= 1.6 × 10-7 कूलॉम
∴ गोले के पृष्ठ के ठीक बाहर विद्यत क्षेत्र \(E=\frac{1}{4 \pi \varepsilon_{0}} \frac{q}{R^{2}}=9 \times 10^{9} \times \frac{1.6 \times 10^{-7}}{0.12 \times 0.12}\)
= 105 न्यूटन कूलॉम-1।
(c) बिन्दु की गोले के केन्द्र से दूरी r = 0.18 मीटर
∵ r > R; अतः बिन्दु गोले के पृष्ठ के बाहर है।
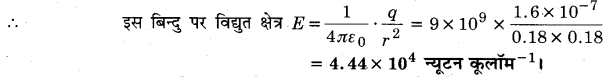
![]()
प्रश्न 5.
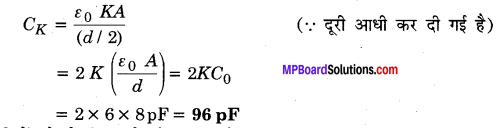
एक समान्तर पट्टिका संधारित्र, जिसकी पट्टिकाओं के बीच वायु है, की धारिता 8 pF (1 pF = 10-12 फैरड) है। यदि पट्टिकाओं के बीच की दूरी को आधा कर दिया जाए और इनके बीच के स्थान में 6 पराविद्युतांक का एक पदार्थ भर दिया जाए तो इसकी धारिता क्या होगी?
हल :
दिया है : वायु संधारित्र की धारिता Co = 8 pF = \(\frac{\varepsilon_{0} A}{d}\)
पदार्थ का पराविद्युतांक K = 6
∴ पराविद्युत पदार्थ भरने पर संधारित्र की धारिता
प्रश्न 6.
9 pF धारिता वाले तीन संधारित्रों को श्रेणीक्रम में जोड़ा गया है।
(a) संयोजन की कुल धारिता क्या है?
(b) यदि संयोजन को 120 वोल्ट के संभरण (सप्लाई) से जोड़ दिया जाए, तो प्रत्येक संधारित्र पर क्या विभवान्तर होगा?
स्थिर वैद्युत विभव तथा धारिता । 69
हल :
दिया है : C1 = C2 = C3 = 9 pF
श्रेणी संयोजन का विभवान्तर V = 120 वोल्ट
कुल धारिता = ?
प्रत्येक संधारित्र का विभवान्तर = ?
(a) श्रेणी संयोजन के सूत्र से,
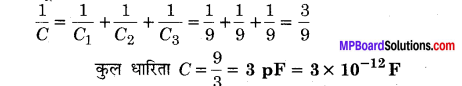
![]()
(b) संयोजन पर कुल आवेश q = CV = 3 × 10-12 × 120 = 360 × 10-12 कूलॉम
श्रेणी संयोजन में प्रत्येक संधारित्र पर इतना ही आवेश होगा।
∴ प्रत्येक संधारित्र का विभवान्तर V1 = V2 = V3 = \(\frac{q}{C_{1}}\)
(∵ सब की धारिताएँ समान हैं)
=\(\frac{360 \times 10^{-12}}{9 \times 10^{-12}}\) = 40 वोल्ट।
अन्य विधि : माना तीनों के विभवान्तर क्रमश: V1, V2 व V3 हैं।
तब, V1+ V2 + V3 = 120
∵ श्रेणी संयोजन में विभवान्तर धारिताओं के व्युत्क्रमानुपाती होते हैं।
∵ तीनों की धारिताएँ समान हैं। अत: विभवान्तर भी समान होंगे।
V3 = V2 = V1
अतः
3V1= 120 ⇒ V1 = 40 वोल्ट
अतः प्रत्येक संधारित्र का विभवान्तर 40 वोल्ट है।
प्रश्न 7.
2 pF, 3 pF और 4 pF धारिता वाले तीन संधारित्र पार्श्वक्रम में जोड़े गए हैं।
(a) संयोजन की कुल धारिता क्या है?
(b) यदि संयोजन को 100 वोल्ट के संभरण से जोड़ दें तो प्रत्येक संधारित्र पर आवेश ज्ञात कीजिए।
हल :
दिया है : C1 = 2 pF, C2 = 3 pF, C3 = 4 pF
पार्श्वक्रम का विभवान्तर V = 100 वोल्ट
कुल धारिता = ?, प्रत्येक संधारित्र पर आवेश = ?
(a) पार्श्वक्रम में कुल धारिता C = C1 + C2 + C3 = 2+ 3+ 4 = 9 pF
(b) पार्श्वक्रम में सभी का विभवान्तर संयोजन के विभवान्तर के बराबर होता है।
∴ V1 = V2 = V3 = 100 वोल्ट
प्रथम संधारित्र पर आवेश q1 = C1V1 = 2 × 10-12 × 100 = 2 × 10-10 कूलॉम।
दूसरे संधारित्र पर आवेश q2 = C2V2 = 3 × 10-12 × 100 = 3 × 10-10 कूलॉम।
तीसरे संधारित्र पर आवेश q3 = C3V3 = 4 × 10-12 × 100 = 4 × 10-10 कूलॉम।
![]()
प्रश्न 8.
पट्टिकाओं के बीच वायु वाले समान्तर पट्टिका संधारित्र की प्रत्येक पट्टिका का क्षेत्रफल 6x 10-3 मीटर तथा उनके बीच की दूरी 3 मिमी है। संधारित्र की धारिता को परिकलित कीजिए। यदि इस संधारित्र को 100 वोल्ट के संभरण से जोड़ दिया जाए तो संधारित्र की प्रत्येक पट्टिका पर कितना आवेश होगा?
हल :
दिया है : प्लेट क्षेत्रफल A = 6 × 10-3 मीटर2, V = 100 वोल्ट,
बीच की दूरी d = 3 मिमी = 3 × 10-3 मीटर
धारिता C = ?, प्रत्येक पट्टी पर आवेश = ?
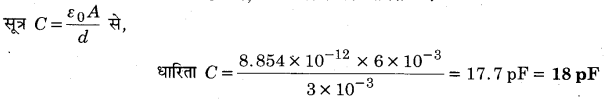
संधारित्र पर आवेश q = CV = 17.7 × 10-12 x 100 = 17.7 × 10-10 कूलॉम
∴ एक पट्टी पर आवेश = + 17.7 × 10-10 कूलॉम।
दूसरी पट्टी पर आवेश = – 17.7 × 10-10 कूलॉम।
प्रश्न 9.
प्रश्न 8 में दिए गए संधारित्र की पट्टिकाओं के बीच यदि 3 मिमी मोटी अभ्रक की एक शीट (पत्तर) (पराविद्युतांक = 6) रख दी जाती है तो स्पष्ट कीजिए कि क्या होगा जब
(a) विभव (वोल्टेज) संभरण जुड़ा ही रहेगा?
(b) संभरण को हटा लिया जाएगा?
हल :
प्रश्न 8 के परिणाम से, V = 100 वोल्ट, q = 18 × 10-10 कूलॉम ।
अब माध्यम का पराविद्युतांक K = 6
पराविद्युत की मोटाई t = 3 मिमी = 3 × 10-3 मीटर
t= d; अतः संधारित्र पूर्णतः परावैद्युत द्वारा भरा है।
EXTRA SHOTS
- संधारित्र के आवेशित हो जाने के बाद, उसे आवेशित करने वाली बैटरी हटा लेने पर उसकी प्लेटों पर आवेश अपरिवर्तित रहता है।
- संधारित्र के आवेशित हो जाने के बाद भी बैटरी, संधारित्र से जुड़ी रहे तब उसकी प्लेटों के बीच विभवान्तर नियत रहता है।
∴ संधारित्र की नई धारिता C = KC = 6 × 18 pF [∵ Co = 18pF]
= 108pF
(a) ∵ विभव संभरण जुड़ा हुआ है। अत: संधारित्र का विभवान्तर नियत अर्थात् 100 वोल्ट रहेगा।
संधारित्र पर नया आवेश q = CV = 108 × 10-12 × 100
= 1.08 × 10-8 कूलॉम
अतः इस स्थिति में, C = 108 pF, V = 100 वोल्ट,
q= 1.08 × 10-8 कूलॉम ।
(b) ∵ विभव संभरण हटा लिया गया है। अत: संधारित्र पर आवेश q= 18 × 10-10 कूलॉम नियत रहेगा।
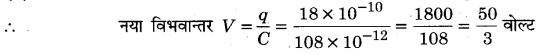
अतः C = 108 pF, \(V=\frac{50}{3}\) वोल्ट = 16.6 वोल्ट,
q= 1.8 × 10-9 कूलॉम।।
प्रश्न 10.
12 pF का एक संधारित्र 50 वोल्ट की बैटरी से जुड़ा है। संधारित्र में कितनी स्थिर विद्युत ऊर्जा . संचित होगी?
हल :
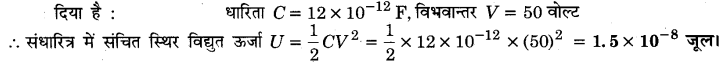
प्रश्न 11.
200 वोल्ट संभरण (सप्लाई) से एक 600 pF से संधारित्र को आवेशित किया जाता है। फिर इसको संभरण से वियोजित कर देते हैं तथा एक अन्य 600 pF वाले अनावेशित संधारित्र से जोड़ देते हैं। इस प्रक्रिया में कितनी ऊर्जा का ह्रास होता है?
हल :
दिया है : धारिताएँ C1 = 600 × 10-12F, C2 = 600 × 10-12F
विभवान्तर V1 = 200 वोल्ट, V2 = 0 वोल्ट
प्रक्रिया में ऊर्जा का ह्रास ∆U = ?
∵ आवेश के बाद संभरण को हटा दिया जाता है; अत: निकाय पर कुल आवेश नियत रहेगा।(Note)
माना संधारित्रों को जोड़ने पर उनका उभयनिष्ठ विभव V है,.
q= C1V1+ C2V2 = (C1 + C2)V
600 × 10-12 × 200 + 0 = [600+ 600] × 10-12 × v
∴ \(V=\frac{600 \times 200}{1200}\) वोल्ट
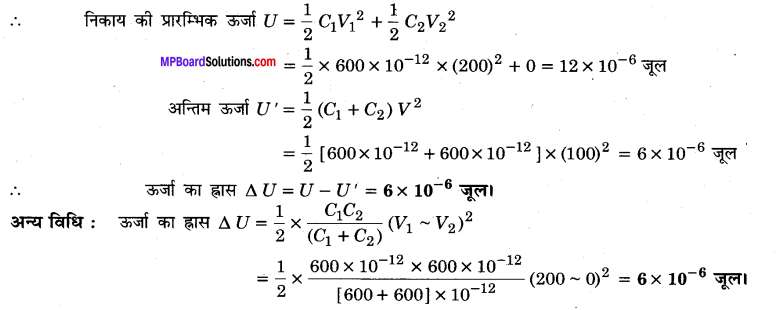
![]()
प्रश्न 12.
मूलबिन्दु पर एक 8 माइक्रोकूलॉम का आवेश अवस्थित है। – 2x 10-9 कूलॉम के एक छोटे से आवेश को बिन्दु P(0, 0, 3 सेमी) से, बिन्दु R (0, 6 सेमी, 9 सेमी) से होकर, बिन्दु Q (0, 4 सेमी, 0) तक ले जाने में किया गया कार्य परिकलित कीजिए।
हल :
मूलबिन्दु पर आवेश Q = 8 × 10-3 कूलॉम
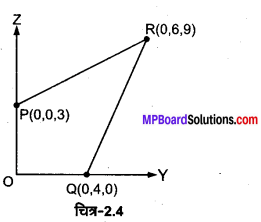
दूसरा आवेश q= – 2 × 10-9 कूलॉम
∵ स्थिर विद्युत क्षेत्र में किसी आवेश को एक बिन्दु से दूसरी बिन्दु तक ले जाने में | किया जाने वाला कार्य मार्ग के स्थान पर अन्त्य बिन्दुओं पर निर्भर करता है।
∴ आवेश q को बिन्दु P से Q तक ले जाने में किया गया कार्य
w = q (VQO – VP)
यहाँ बिन्दु Q की मूलबिन्दु से दूरी rQ = OQ = 0.04 मीटर
Q(0,4,0) तथा बिन्दु P की मूलबिन्दु से दूरी rP = OP = 0.03 मीटर
∴ मूलबिन्दु पर स्थित आवेश Q के कारण Q व P के बीच विभवान्तर
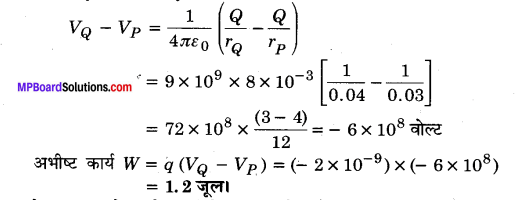
प्रश्न 13.
b भुजा वाले एक घन के प्रत्येक शीर्ष पर 4 आवेश है। इस आवेश विन्यास के कारण घन के केन्द्र पर विद्युत विभव तथा विद्युत क्षेत्र ज्ञात कीजिए।
हल :

(b) ∵ सभी शीर्षों पर आवेश समान हैं। अत: विपरीत शीर्षों के कारण केन्द्र पर उत्पन्न विद्युत क्षेत्र परिमाण में बराबर तथा दिशा में विपरीत होंगे।
अतः केन्द्र पर नैट विद्युत क्षेत्र शून्य होगा।
प्रश्न 14.
1.5 माइक्रोकूलॉम और 2.5 माइक्रोकूलॉम आवेश वाले दो सूक्ष्म गोले 30 सेमी दूर स्थित हैं। (a) दोनों आवेशों को मिलाने वाली रेखा के मध्य-बिन्दु पर और
(b) मध्य-बिन्दु से होकर जाने वाली रेखा के अभिलम्ब तल में मध्य बिन्दु से 10 सेमी दूर स्थित किसी बिन्दु पर विभव और विद्युत क्षेत्र ज्ञात कीजिए।
हल :
(a) मध्य-बिन्दु की प्रत्येक आवेश से दूरी rA = rB = 0.15 मीटर



प्रश्न 15.
आन्तरिक त्रिज्या r1 तथा बाह्य त्रिज्या r2 वाले एक गोलीय चालक खोल (कोश) पर Q आवेश है।
(a) खोल के केन्द्र पर एक आवेश q रखा जाता है। खोल के भीतरी और बाहरी पृष्ठों पर पृष्ठ आवेश घनत्व क्या है?
(b) क्या किसी कोटर (जो आवेशविहीन है) में विद्युत क्षेत्र शून्य होता है, चाहे खोल गोलीय न होकर किसी भी अनियमित आकार का हो? स्पष्ट कीजिए।
हल :
(a) जब चालक को केवल Q आवेश दिया गया है तो यह पूर्णत: चालक के बाह्य पृष्ठ पर रहता है।
हम जानते हैं कि एक चालक के भीतर नैट आवेश शून्य रहता है। अत: खोल के केन्द्र पर 4 आवेश रखने पर, q खोल की भीतरी सतह पर – q आवेश प्रेरित हो जाता है तथा बाहरी सतह पर अतिरिक्त + q आवेश आ जाता है।
अतः भीतरी सतह पर आवेश = – q
बाहरी सतह पर आवेश = Q+q

(b) हाँ, यदि कोटर आवेशविहीन है तो उसके अन्दर विद्युत क्षेत्र शून्य होगा।
इसके विपरीत कल्पना करें कि किसी चालक के भीतर एक अनियमित आकृति का आवेशविहीन कोटर है जिसके भीतर विद्युत क्षेत्र शून्य नहीं है। अब एक ऐसे बन्द लूप पर विचार करें जिसका कुछ भाग कोटर के भीतर क्षेत्र रेखाओं के समान्तर है तथा शेष भाग कोटर से बाहर परन्तु चालक के भीतर है। चूँकि चालक के भीतर विद्युत-क्षेत्र शून्य है। अत: यदि एकांक आवेश को इस बन्द लूप के अनुदिश ले जाया जाए तो क्षेत्र द्वारा किया गया नैट कार्य प्राप्त होगा। परन्तु यह स्थिति स्थिर विद्युत क्षेत्र के लिए सत्य नहीं है (बन्द लूप पर नैट कार्य शून्य होता है)। अत: हमारी परिकल्पना कि कोटर के भीतर विद्युत क्षेत्र शून्य नहीं है, गलत है।
अर्थात् चालक के भीतर आवेशविहीन कोटर के भीतर विद्युत क्षेत्र शून्य होगा।
![]()
प्रश्न 16.
(a) दर्शाइए कि आवेशित पृष्ठ के एक पार्श्व से दूसरे पार्श्व पर स्थिर विद्युत क्षेत्र के अभिलम्ब घटक में असांतत्य होता है, जिसे \(\left(\overrightarrow{\mathrm{E}}_{2}-\overrightarrow{\mathrm{E}}_{1}\right) \cdot \hat{\mathrm{n}}=\frac{\sigma}{\varepsilon_{0}}\) द्वारा व्यक्त किया जाता है। जहाँ \(\hat{\mathbf{n}}\) एक बिन्दु पर पृष्ठ के
अभिलम्ब एकांक सदिश है तथा σ उस बिन्दु पर पृष्ठ आवेश घनत्व है \(\hat{\mathbf{n}}\) की दिशा पार्श्व 1 से पार्श्व 2 की ओर
है)। अतः दर्शाइए कि चालक के ठीक बाहर विद्युत क्षेत्र \(\frac{\sigma \hat{\mathbf{n}}}{\varepsilon_{0}}\) है।
(b) दर्शाइए कि आवेशित पृष्ठ के एक पार्श्व से दूसरे पार्श्व पर स्थिर विद्युत क्षेत्र का स्पर्शीय घटक संतत है।
उत्तर :
(a) माना AB एक आवेशित पृष्ठ है जिस पर पृष्ठीय आवेश घनत्व σ है। पृष्ठ के समीप प्रत्येक बिन्दु पर विद्युत क्षेत्र \(\overrightarrow{\mathrm{E}}\) समान तथा पृष्ठ के लम्बवत् बाहर की ओर है।
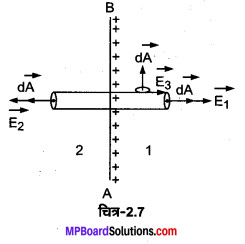
चित्र में एक बेलनाकार गाउसीय पृष्ठ को प्रदर्शित किया गया है। इस पृष्ठ 2 के वृत्ताकार परिच्छेदों पर अभिलम्ब सदिश \(\hat{\mathbf{n}}_{1} व 1\hat{\mathbf{n}}_{2}\) क्रमशः क्षेत्रों \(\overrightarrow{\mathrm{E}}_{1}\) व \(\overrightarrow{\mathrm{E}}_{2}\) के समदिश हैं जबकि वक्र पृष्ठ पर अभिलम्ब संगत क्षेत्र \(\overrightarrow{\mathrm{E}}_{3}\) के लम्बवत् हैं। ..
माना प्रत्येक वृत्तीय परिच्छेद का क्षेत्रफल Δ A है तब गाउसीय पृष्ठ से -गुजरने वाला विद्युत फ्लक्स
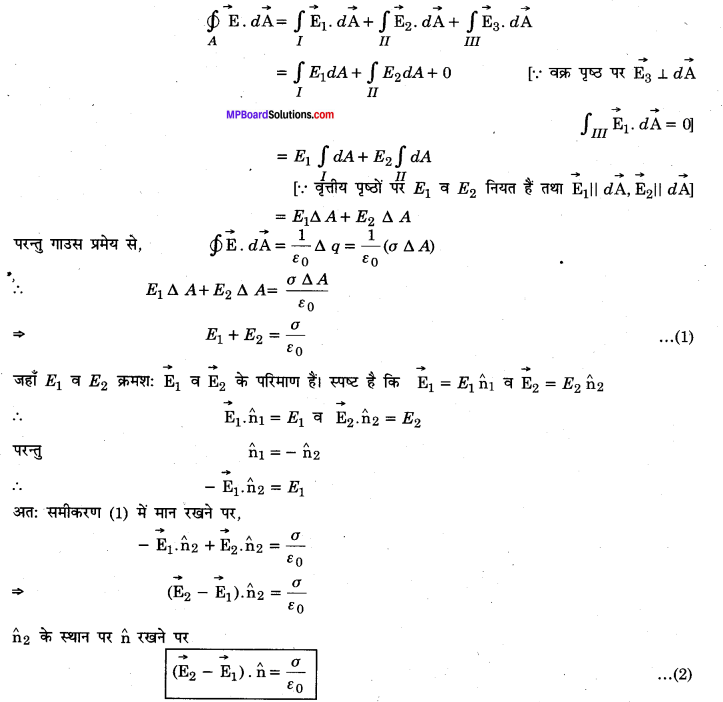
![]()
उपर्युक्त समीकरण (2) किसी आवेशित सतह के दोनों ओर स्थित विद्युत क्षेत्रों के बीच सम्बन्ध को व्यक्त करता है।
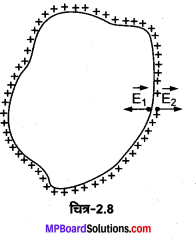
अब संलग्न चित्र में प्रदर्शित अनियमित आकृति के आवेशित चालक पर विचार के कीजिए। चालक का सम्पूर्ण आवेश उसकी बाह्य सतह पर फैला है। अत: चालक की। बाह्य सतह एक समविभव पृष्ठ है। आइए हम समीकरण (2) को इस चालक के बाहर विद्युत-क्षेत्र ज्ञात करने के लिए प्रयुक्त करते हैं।

(b) आवेशित पृष्ठ के एक ओर से दूसरी ओर जाने पर स्थिर विद्युत क्षेत्र का स्पर्श रेखीय घटक सतत (सर्वथा शून्य) होता है, अन्यथा पृष्ठ के विभिन्न बिन्दु अलग-अलग विभवों पर होंगे तथा धनावेश पृष्ठ के अनुदिश उच्च विभव से निम्न विभव के बिन्दुओं की ओर गति करता रहेगा।
प्रश्न 17.
रैखिक आवेश घनत्व λ वाला एक लम्बा आवेशित बेलन एक खोखले समाक्षीय चालक बेलन द्वारा घिरा है। दोनों बेलनों के बीच के स्थान में विद्युत क्षेत्र कितना है?
हल :
दोनों बेलनों के बीच r त्रिज्या तथा l लम्बाई के समाक्षीय बेलनाकार गाउसीय पृष्ठ पर विचार कीजिए।
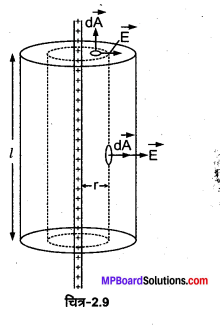
सममिति के कारण इस बेलन के वक्र पृष्ठ के प्रत्येक बिन्दु पर विद्युत क्षेत्र \(\overrightarrow{\mathrm{E}}\) सर्वत्र । समान तथा पृष्ठीय अल्पांश \(d \overrightarrow{\mathrm{A}}\) के समान्तर है जबकि वृत्तीय पृष्ठों पर \(\overrightarrow{\mathrm{E}}\) अल्पांश \(d \overrightarrow{\mathrm{A}}\) के लम्बवत् है। अतः
गाउसीय पृष्ठ से गुजरने वाला विद्युत फ्लक्स

![]()
प्रश्न 18.
एक हाइड्रोजन परमाणु में इलेक्ट्रॉन तथा प्रोटॉन लगभग 0.53 Å दूरी पर परिबद्ध हैं :
(a) निकाय की स्थितिज ऊर्जा का ev में परिकलन कीजिए, जबकि प्रोटॉन व इलेक्ट्रॉन के मध्य से अनन्त दूरी पर स्थितिज ऊर्जा को शून्य माना गया है।
(b) इलेक्ट्रॉन को स्वतन्त्र करने में कितना न्यूनतम कार्य करना पड़ेगा, यदि यह दिया गया है कि इसकी कक्षा में गतिज ऊर्जा (a) में प्राप्त स्थितिज ऊर्जा के परिमाण की आधी है?
(c) यदि स्थितिज ऊर्जा को 1.06 Å पृथक्करण पर शून्य ले लिया जाए तो, उपर्युक्त (a) और (b) के उत्तर
क्या होंगे?
हल : यहाँ q1 = – 1.6 x 10-19 कूलॉम,
q2= + 1.6 x 10-19 कूलॉम
r = 0.53Å = 5.3 x 10-11 मीटर
(a) इलेक्ट्रॉन-प्रोटॉन के निकाय की विद्युत स्थितिज ऊर्जा

(b) इलेक्ट्रॉन की स्थितिज ऊर्जा U = – 27.17 ev

U’ को शून्य मानने पर r = 0.53 Å दूरी पर स्थितिज ऊर्जा
U” = U – U’ = – 27.2 + 13.6 = – 13.6 ev
जबकि K = 13.6ev
∴ हाइड्रोजन परमाणु में इलेक्ट्रॉन की कुल ऊर्जा
E= K +U” = 0
अतः इलेक्ट्रॉन को मुक्त करने के लिए आवश्यक कार्य
W = E – U’ = 0- (- 13.6) = 13.6 ev
![]()
प्रश्न 19.
यदि H2 अणु के दो में से एक इलेक्ट्रॉन को हटा दिया जाए तो हमें हाइड्रोजन आण्विक आयन : (H2+) प्राप्त होगा। (H2+) की निम्नतम अवस्था (ground state) में दो प्रोटॉन के बीच दूरी लगभग 1.5A है
और इलेक्ट्रॉन प्रत्येक प्रोटॉन से लगभग 1Å की दूरी पर है। निकाय की स्थितिज ऊर्जा ज्ञात कीजिए। स्थितिज ऊर्जा की शून्य स्थिति के चयन का उल्लेख कीजिए।
हल :
प्रत्येक प्रोटॉन का आवेश q1 = q2 = + 1.6 x 10-19 कूलॉम
दोनों के बीच की दूरी r12 = 1.5 Å = 1.5 x 10-10 मीटर
इलेक्ट्रॉन का आवेश q3 = – 1.6 x 10-19 कूलॉम ।
r23 = r31 = 1A = 10-10 मीटर,
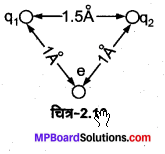

स्थितिज ऊर्जा का शून्य अनन्त पर लिया गया है।
प्रश्न 20.
a और । त्रिज्याओं वाले दो आवेशित चालक गोले एक तार द्वारा एक-दूसरे से जोड़े गए हैं। दोनों गोलों के पृष्ठों पर विद्युत क्षेत्रों में क्या अनुपात है? प्राप्त परिणाम को, यह समझाने में प्रयुक्त कीजिए कि किसी चालक के तीक्ष्ण और नुकीले सिरों पर आवेश घनत्व, चपटे भागों की अपेक्षा अधिक क्यों होता है?
हल :
माना इन गोलों पर आवेश क्रमशः 41 तथा 42 हैं।
:: दोनों गोले चालक तार द्वारा जुड़े हैं। अत: दोनों के पृष्ठीय विभव बराबर होंगे।

माना किसी आवेशित चालक के दो अलग-अलग भागों की वक्रता त्रिज्याएँ a तथा b हैं। माना चालक का प्रथम भाग दूसरे की तुलना में अधिक नुकीला है तब a यदि इन भागों पर q1 व q2 आवेश संचित हैं तो

अर्थात् कम वक्रता त्रिज्या वाले भाग (नुकीले भाग) का पृष्ठीय घनत्व अधिक वक्रता त्रिज्या वाले भाग की तुलना में अधिक होगा।
प्रश्न 21.
बिन्दु (0, 0, – a) तथा (0, 0, a) पर दो आवेश क्रमशः -q और +q स्थित हैं।
(a) बिन्दुओं (0, 0, z) और (x, y, 0) पर स्थिर विद्युत विभव क्या है?
(b) मूल बिन्दु से किसी बिन्दु की दूरी r पर विभव की निर्भरता ज्ञात कीजिए, जबकि \(\frac{r}{a}\) >> 1 है।
(c) X-अक्ष पर बिन्दु (5, 0, 0) से बिन्दु (- 7, 0,0) तक एक परीक्षण आवेश को ले जाने में कितना कार्य । करना होगा? यदि परीक्षण आवेश को उन्हीं बिन्दुओं के बीच X-अक्ष से होकर न ले जाएँ तो क्या उत्तर बदल जाएगा?
हल :
दिए गए बिन्दु आवेश एक विद्युत द्विध्रुव बनाते हैं।
आवेशों के बीच की दूरी = 2a
∴ विद्युत द्विध्रुव आघूर्ण \(\overrightarrow{\mathrm{p}}=q \times 2 \overrightarrow{\mathrm{a}}=2 q \overrightarrow{\mathrm{a}}\)
(a) बिन्दु (0, 0, z) द्विध्रुव की अक्ष पर स्थित है,
∴ इस बिन्दु पर विद्युत विभव \(V=\pm \frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{p}{\left(z^{2}-a^{2}\right)}\)
बिन्दु (x, y, 0) द्विध्रुव के विषुवत तल में स्थित है; अतः इस बिन्दु पर विद्युत विभव शून्य होगा।
(b) द्विध्रुव के कारण किसी बिन्दु पर विद्युत विभव :
माना कोई बिन्दु P, द्विध्रुव के केन्द्र (मूल बिन्दु) से 7 दूरी पर स्थित है। इस बिन्दु की बिन्दु आवेशों +q तथा । q से दूरियाँ क्रमश: r1 तथा r2 हैं।
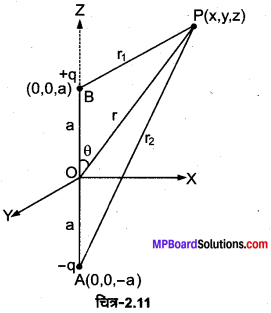
तब बिन्दु P पर द्विध्रुव के कारण विद्युत विभव
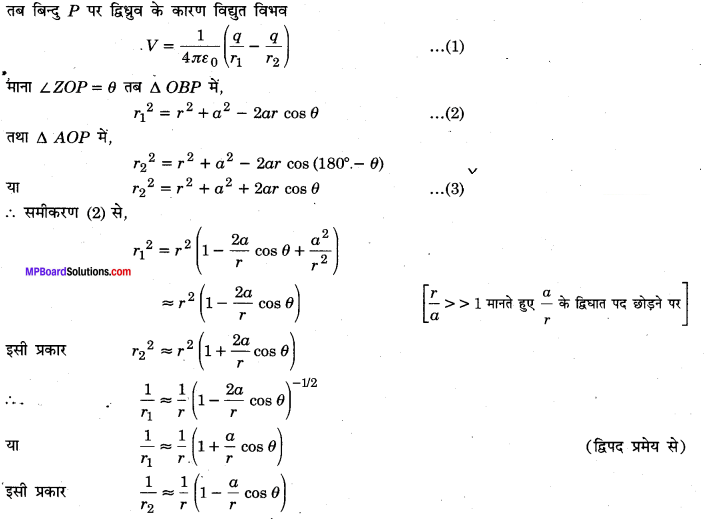

(c) बिन्दु P(5, 0, 0) तथा Q(- 7, 0, 0) द्विध्रुव के विषुवत तल में स्थित हैं। अत: इन दोनों बिन्दुओं पर विभव शून्य होगा।
∴ परीक्षण आवेश qo को बिन्दु P से Q तक ले जाने में किया गया कार्य
W = qo [V (Q)- V (P)] = 0 [∵ V (P) = V(Q)= 0]
विद्युत-क्षेत्र एक संरक्षी क्षेत्र है जिसमें किया गया कार्य केवल अन्त्य बिन्दुओं पर निर्भर करता है, न कि मार्ग पर। (Note)
अतः उत्तर में कोई परिवर्तन नहीं आएगा।
प्रश्न 22.
नीचे दिए गए चित्र-2.12 में एक आवेश विन्यास जिसे विद्युत चतुर्युवी कहा जाता है, दर्शाया गया है। चतुर्भुवी के अक्ष पर स्थित किसी बिन्दु के लिए r पर विभव की. a a . निर्भरता प्राप्त कीजिए जहाँ \(\frac{r}{a}\)>>11 अपने परिणाम की तुलना एक विद्युत द्विध्रुव व विद्युत एकल ध्रुव (अर्थात् किसी एकल आवेश) के लिए प्राप्त परिणामों से कीजिए।
हल :
माना P की विभिन्न आवेशों से दूरियाँ निम्नलिखित हैं –
r-a, r, r+a
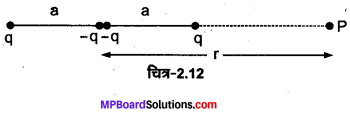

विद्युत द्विध्रुव के कारण अक्ष पर विभव दूरी के वर्ग के व्युत्क्रमानुपाती (\(V \propto \frac{1}{r^{2}}\) ) होता है। एकल ध्रुव के कारण यह दूरी के व्युत्क्रमानुपाती (\(V \propto \frac{1}{r}\) ) होता है। अतः चतुर्भुवी के कारण विभव, विद्युत द्विध्रुव तथा एकल ध्रुव की तुलना में अधिक तेजी से घटता है।
![]()
प्रश्न 23.
एक विद्युत टैक्नीशियन को 1 किलोवोल्ट विभवान्तर के परिपथ में 2 μF संधारित्र की आवश्यकता है। 1 μF के संधारित्र उसे प्रचुर संख्या में उपलब्ध हैं जो 400 वोल्ट से अधिक का विभवान्तर वहन नहीं कर सकते। कोई सम्भव विन्यास सुझाइए जिसमें न्यूनतम संधारित्रों की आवश्यकता हो।
हल :
माना हम प्रत्येक पंक्ति में n संधारित्र जोड़ते हैं तथा ऐसी m पंक्तियों को समान्तर क्रम में जोड़ते हैं। श्रेणीक्रम में, 1 kV = 1000 वोल्ट का विभवान्तर n संधारित्रों में बराबर बॅट जाएगा।

∵ n न्यूनतम पूर्णांक है। अत: n = 3
प्रत्येक पंक्ति की धारिता = \(\frac{1}{n}\) माइक्रोफैरड होगी।
समान्तर क्रम में जुड़ी ऐसी m पंक्तियों की धारिता
\(\frac{1}{n} +\frac{1}{n} + \frac{1}{n}\) + m पद – = 2μF
⇒ \(\frac{m}{n}\) = 2μF
⇒ m = 2n = 2×3 = 6 ,
∵ हमें 3-3 संधारित्रों को श्रेणीक्रम में जोड़कर इस प्रकार की 6 पंक्तियाँ बनानी होंगी। अब इन 6 पंक्तियों को समान्तर क्रम में जोड़ना होगा।
प्रश्न 24.
2F वाले एक समान्तर पट्टिका संधारित्र की पट्टिका का क्षेत्रफल क्या है, जबकि पट्टिकाओं का पृथकन 0.5 सेमी है?
हल :
दिया है : d = 0.5 सेमी = 5 x 10 -3मीटर, C = 2F, A = ?
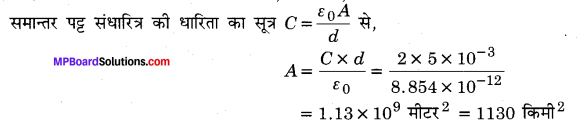
∴ पट्टिका का क्षेत्रफल 1.13x 10° मीटर’ या 1130 किमी है।
प्रश्न 25.
चित्र 2.13 के नेटवर्क (जाल) की तुल्य धारिता प्राप्त कीजिए। 300 वोल्ट संभरण (सप्लाई) के साथ प्रत्येक संधारित्र का आवेश व उसकी वोल्टता ज्ञात कीजिए।
हल :
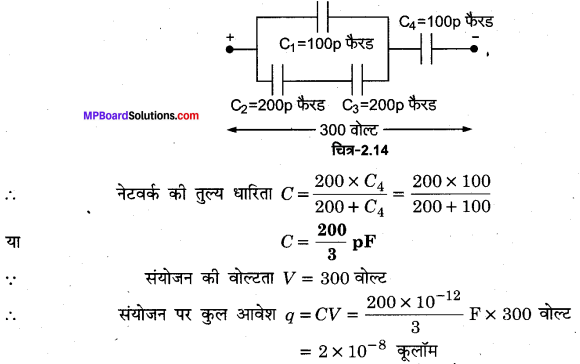
दिए गए नेटवर्क को चित्र 2.14 की भाँति व्यवस्थित किया जा सकता है
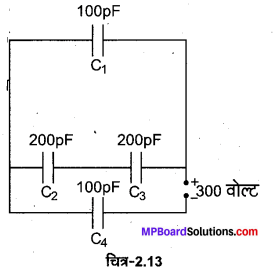
सर्वप्रथम C2 व C3 श्रेणीक्रम में जुड़े हैं, इनकी तुल्य धारिता
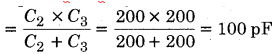
अब यह 100 pF की धारिता C1 के साथ समान्तर क्रम में जुड़ी है,
अतः तुल्य धारिता = 100 + 100 = 200 pF
पुन: यह 200 pF, C4 के साथ श्रेणीक्रम में जुड़ा है।
∵ C4 शेष संयोजन (धारिता 200 pF) के साथ श्रेणीक्रम में जुड़ा है,
अत: C4तथा शेष संयोजन, दोनों पर यही आवेश होगा।
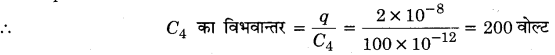
∴ शेष संयोजन का विभवान्तर V = 300 वोल्ट – 200 वोल्ट = 100 वोल्ट
∵ C1,C2 व C3 के श्रेणी संयोजन से समान्तर क्रम में जुड़ा है,
∴ C1 का विभवान्तर = 100 वोल्ट
तथा C2 व C3 के श्रेणी संयोजन का विभवान्तर = 100 वोल्ट
C1 पर आवेश q1 = C1V1= 100 x 10-12 फैरड x100 वोल्ट
= 10-8 कूलॉम.
∴ C = C3; अतः कुल विभवान्तर 100 V इन पर बराबर-बराबर बंटेगा।
प्रत्येक का विभवान्तर = 50 वोल्ट
प्रत्येक पर आवेश q2 = C2V2= 200 x 10-12
F x 50 वोल्ट = 10-8c
अतः संयोजन की धारिता \(C=\frac{200}{3}\) pF
C1 का विभवान्तर = 100 वोल्ट।
तथा आवेश = 10-8 कूलॉम
C2 का विभवान्तर = 50 वोल्ट ।
तथा आवेश = 10-8 कूलॉम
C3 का विभवान्तर = 50वोल्ट
तथा आवेश = 10-8 कूलॉम
C4 का विभवान्तर = 200 वोल्ट
तथा आवेश = 2 x 10-8 कूलॉम
![]()
प्रश्न 26.
किसी समान्तर पट्टिका संधारित्र की प्रत्येक पट्टिका का क्षेत्रफल 90 सेमी2 है और उनके बीच पृथक्न 2.5 मिमी है। 400 वोल्ट संभरण से संधारित्र को आवेशित किया गया है।
(a) संधारित्र कितना स्थिर विद्युत ऊर्जा संचित करता है?
(b) इस ऊर्जा को पट्टिकाओं के बीच स्थिर विद्युत क्षेत्र में संचित समझकर प्रति एकांक आयतन ऊर्जा u ज्ञात कीजिए। इस प्रकार, पट्टिकाओं के बीच विद्युत क्षेत्र E के परिमाण और u में सम्बन्ध स्थापित कीजिए।
हल :
दिया है : A = 90 सेमी2 = 9 x 10-3 मीटर2, d = 2.5 मिमी = 2.5 x 10-3 मीटर V= 400 वोल्ट, U = ?, एकांक आयतन में ऊर्जा u = ?
u व E के बीच सम्बन्ध = ?
(a)
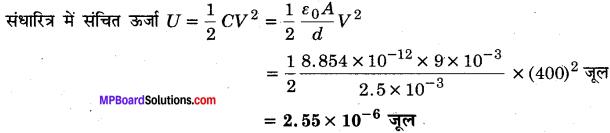
(b)

प्रश्न 27.
एक 4 माइक्रोफैरड के संधारित्र को 200 वोल्ट संभरण (सप्लाई) से आवेशित किया गया है। फिर संभरण से हटाकर इसे एक अन्य अनावेशित 2 माइक्रोफैरड के संधारित्र से जोड़ा जाता है। पहले संधारित्र की कितनी स्थिर विद्युत ऊर्जा का ऊष्मा और विद्युत चुम्बकीय विकिरण के रूप में ह्रास होता है ?
हल :
दिया है : C1 = 4 x 10-6 फैरड, V1 = 200 वोल्ट,
C2= 2 x 10-6 फैरड, V2 = 0 वोल्ट
माना जोड़ने के पश्चात् दोनों का उभयनिष्ठ विभव V है।
∵ जोड़ने से पूर्व संभरण को हटा लिया गया है। अत: कुल आवेश स्थिर रहेगा।


प्रश्न 28.
दर्शाइए कि एक समान्तर पट्टिका संधारित्र की प्रत्येक पट्टिका पर बल का परिमाण \(\frac{1}{2}\)QE है, जहाँ Q.संधारित्र पर आवेश है और E पट्टिकाओं के बीच विद्युत क्षेत्र का परिमाण है। घटक 1/2 के मूल को समझाइए।
हल :
माना दोनों पट्टिकाओं के बीच लगने वाला पारस्परिक आकर्षण बल F है तथा प्लेटों के बीच की दूरी x है। दूरी x में dx की वृद्धि करने पर आकर्षण बल F के विरुद्ध कृत कार्य
dW = F dx ………………….(1)
∵ प्लेटों के बीच विद्युत क्षेत्र E है। अत: संधारित्र के एकांक आयतन में संचित ऊर्जा
![]()
∵ प्लेटों का क्षेत्रफल A व बीच की दूरी x है। अत: संधारित्र की कुल ऊर्जा
![]()
∵ दूरी x में dx की वृद्धि करने पर ऊर्जा में वृद्धि
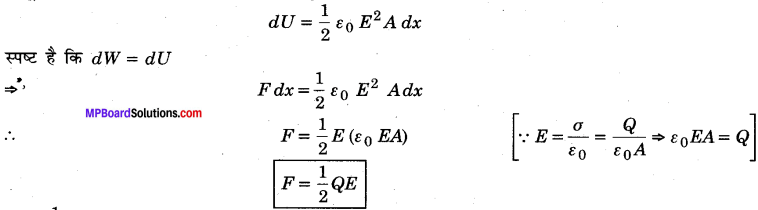
घटक \(\frac{1}{2}\) का मूल इस तथ्य में निहित है कि चालक प्लेट के बाहर विद्युत क्षेत्र E तथा प्लेट के भीतर शून्य होता है। अत: औसत विद्युत क्षेत्र \(\frac{E}{2}\) होता है, जिसके विरुद्ध प्लेट को खिसकाया जाता है।
![]()
प्रश्न 29.
दो संकेन्द्री गोलीय चालकों जिनको उपयुक्त विद्युतरोधी आवेश (+q) आलम्बों से उनकी स्थिति में रोका गया है, से मिलकर एक गोलीय संधारित्र बना है (चित्र 2.15)। दर्शाइए कि गोलीय संधारित्र की धारिता C इस प्रकार व्यक्त की जाती है :
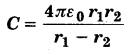
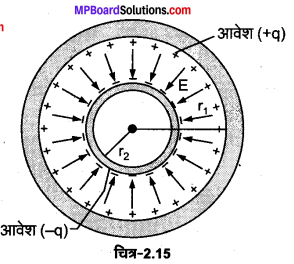
यहाँ r1 और r2 क्रमशः बाहरी तथा भीतरी गोलों की त्रिज्याएँ हैं।
हल :
गोलीय अथवा गोलाकार संधारित्र की धारिता (Capacitance . of Spherical Capacitor) का व्यंजक-माजा गोलीय संधारित्र धातु के आवेश (-q) दो समकेन्द्रीय खोखले गोलों A व B का बना है, जो एक-दूसरे को कहीं भी स्पर्श नहीं करते (चित्र 2.15)। जब गोले A को -q आवेश दिया जाता है तो प्रेरण द्वारा गोले B पर +q आवेश उत्पन्न हो जाता है। चूंकि गोले B का बाहरी तल पृथ्वी से जुड़ा है; अत: गोले B के बाहरी तल पर उत्पन्न -q आवेश पृथ्वी से आने वाले इलेक्ट्रॉनों से निरावेशित हो जाता है। इस प्रकार गोले B के आन्तरिक पृष्ठ पर + q आवेश रह जाता है। माना गोले A की त्रिज्या r2 तथा गोले B की त्रिज्या r1 है।

चूँकि गोले के भीतर प्रत्येक बिन्दु पर वही विभव होता है जो कि उसके पृष्ठ पर होता है।
अत: गोले B के अन्दर, +q आवेश के कारण विभव
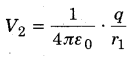
चूँकि विभव अदिश राशि है; अत: गोले A पर परिणामी विभव
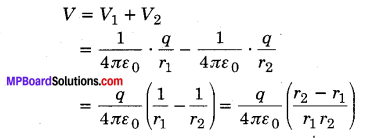
गोला B पृथ्वी से जुड़ा होने के कारण इस पर विभव शून्य है। अत: गोले A व B के बीच विभवान्तर

प्रश्न 30.
एक गोलीय संधारित्र के भीतरी गोले की त्रिज्या 12 सेमी है तथा बाहरी गोले की त्रिज्या 13 सेमी है। बाहरी गोला भू-सम्पर्कित है तथा भीतरी गोले पर 2.5 माइक्रोकूलॉम का आवेश दिया गया है। संकेन्द्री गोलों के बीच के स्थान में 32 पराविधुतांक का द्रव भरा है।
(a) संधारित्र की धारिता ज्ञात कीजिए।
(b) भीतरी गोले का विभव क्या है?
(c) इस संधारित्र की धारिता की तुलना एक 12 सेमी त्रिज्या वाले किसी वियुक्त गोले की धारिता से कीजिए। व्याख्या कीजिए कि गोले की धारिता इतनी कम क्यों है?
हल :
दिया है : r1 = 13 सेमी = 0.13 मीटर, r2 = 12 सेमी = 0.12 मीटर, K = 32, Q = 2.5x 10-6 कूलॉम

अर्थात् गोलीय संधारित्र की धारिता एकल गोले की धारिता से 416 गुनी अधिक है। इससे यह निष्कर्ष प्राप्त होता है कि एकल चालक के समीप एक अन्य भू-सम्पर्कित चालक रखकर उनके बीच के स्थान में पराविद्युत भरने से धारिता बहुत अधिक बढ़ जाती है।
प्रश्न 31.
सावधानीपूर्वक उत्तर दीजिए :
(a) दो बड़े चालक गोले जिन पर आवेश Q1 और Q2 हैं, एक-दूसरे के समीप लाए जाते हैं। क्या इनके बीच स्थिर विद्युत बल का परिमाण तथ्यत –
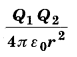
द्वारा दर्शाया जाता है, जहाँ r इनके केन्द्रों के बीच की दूरी है।
(b) यदि कूलॉम के नियम में \(\frac{1}{r^{3}}\) निर्भरता का समावेश (1/r2 के स्थान पर) हो तो क्या गाउस का नियम अभी भी सत्य होगा?
(c) स्थिर विद्युत क्षेत्र विन्यास में एक छोटा परीक्षण आवेश किसी बिन्दु पर विराम में छोड़ा जाता है। क्या यह उस बिन्दु से होकर जाने वाली क्षेत्र रेखा के अनुदिश चलेगा?
(d) इलेक्ट्रॉन द्वारा एक वृत्तीय कक्षा पूरी करने में नाभिक के क्षेत्र द्वारा कितना कार्य किया जाता है? यदि कक्षा दीर्घवृत्ताकार हो तो क्या होगा?
(e) हमें ज्ञात है कि एक आवेशित चालक के पृष्ठ के आर-पार विद्युत क्षेत्र असंतत होता है। क्या वहाँ विद्युत विभव भी असंतत होगा?
(f) किसी एकल चालक की धारिता से आपका क्या अभिप्राय है?
(g) एक सम्भावित उत्तर की कल्पना कीजिए कि पानी का पराविद्युतांक (= 80), अभ्रक के पराविद्युतांक (= 6) से अधिक क्यों होता है?
हल :
(a) यदि दोनों गोले एक-दूसरे से बहुत अधिक दूरी पर होंगे तभी वे बिन्दु आवेशों की भाँति कार्य करेंगे। कूलॉम का नियम केवल बिन्दु आवेशों के लिए सत्य है। अत: गोलों को समीप लाने पर कूलॉम का नियम लागू नहीं होगा।
(b) नहीं, गाउस का नियम केवल तभी तक सत्य है जब तक कि कूलॉम के नियम में निर्भरता (\(\frac{1}{r^{2}}\)) है; अतः कूलॉम के नियम में निर्भरता (\frac{1}{r^{3}}) होने पर गाउस का नियम लागू नहीं होगा।
(c) नहीं, यदि क्षेत्र रेखा एक सरल रेखा है, केवल तभी परीक्षण आवेश क्षेत्र रेखा के अनुदिश चलेगा।
(d) शून्य, स्थिर विद्युत क्षेत्र में बिन्दु आवेश के बन्द वक्र पर चलाने में किया गया कार्य शून्य होता है। यदि वक्र दीर्घवृत्ताकार है तो भी कार्य शून्य होगा।
(e) नहीं, चालकं की पूरी सतह पर विद्युत विभव सतत होता है। (1) एकल चालक की धारिता एक ऐसे संधारित्र की धारिता है, जिसकी दूसरी प्लेट अनन्त पर है।
(g) जल के अणुओं का अपना स्थायी द्विध्रुव आघूर्ण होता है। अत: जल का पराविद्युतांक उच्च होता है, इसके विपरीत अभ्रक के अणुओं का द्विध्रुव आघूर्ण शून्य होता है; अत: इसका पराविद्युतांक निम्न होता है।
प्रश्न 32.
एक बेलनाकार संधारित्र में 15 सेमी लम्बाई एवं त्रिज्याएँ 1.5 सेमी तथा 1.4 सेमी के दो समाक्ष बेलन हैं। बाहरी बेलन भू-सम्पर्कित है और भीतरी बेलन को 3.5 माइक्रोकूलॉम का आवेश दिया गया है। निकाय की धारिता और भीतरी बेलन का विभव ज्ञात कीजिए। अन्त्य प्रभाव (अर्थात् सिरों पर क्षेत्र रेखाओं का मुड़ना) की उपेक्षा कर सकते हैं।
हल :

![]()
प्रश्न 33.
पराविधुतांक तथा 107 वोल्ट मीटर-1 की पराविद्युत सामर्थ्य वाले एक पदार्थ से 1 किलोवोल्ट वोल्टता अनुमतांक के समान्तर पट्टिका संधारित्र की अभिकल्पना करनी है। [पराविद्युत सामर्थ्य वह अधिकतम विद्युत क्षेत्र है जिसे कोई पदार्थ बिना भंग हुए अर्थात् आंशिक आयनन द्वारा बिना विद्युत संचरण आरम्भ किए सहन कर सकता है। सुरक्षा की दृष्टि से क्षेत्र को कभी भी पराविद्युत सामर्थ्य के 10% से अधिक नहीं होना चाहिए।] 50pF धारिता के लिए पट्टिकाओं का कितना न्यूनतम क्षेत्रफल होना चाहिए?
हल :
दिया है : K = 3, पराविद्युत सामर्थ्य = 107 वोल्ट/मीटर,
C = 50 pF, न्यूनतम क्षेत्रफल A = ? V = 1000 वोल्ट
प्लेटों के बीच अधिकतम क्षेत्र Emax = पराविद्युत सामर्थ्य का 10%

प्रश्न 34.
व्यवस्थात्मकतः निम्नलिखित में संगत समविभव पृष्ठ का वर्णन कीजिए :
(a) Z-दिशा में अचर विद्युत क्षेत्र
(b) एक क्षेत्र जो एकसमान रूप से बढ़ता है, परन्तु एक ही दिशा (मान लीजिए 2-दिशा) में रहता है।
(c) मूलबिन्दु पर कोई एकल धनावेश और
(d) एक समतल में समान दूरी पर समान्तर लम्बे आवेशित तारों से बने एकसमान जाल।
उत्तर :
(a) x-y समतल के समान्तर समतल।
(b) समविभव पृष्ठ x-y समतल के समान्तर होंगे, परन्तु बढ़ते क्षेत्र के साथ, भिन्न-भिन्न नियत विभव वाले समतल एक-दूसरे के समीप होते जाएँगे।
(c) संकेन्द्रीय गोले जिनके केन्द्र मूलबिन्दु पर हैं।
(d) ग्रिड के समीप, समविभव पृष्ठों की आकृति समय के साथ बदलेगी परन्तु ग्रिड से दूर जाने पर समविभव . पृष्ठ ग्रिड (जाल) के अधिकाधिक समान्तर होते जाएँगे।
प्रश्न 35.
किसी वान डे ग्राफ प्रकार के जनित्र में एक गोलीय धातु कोश 15 x 106 वोल्ट का एक इलेक्ट्रोड बनाना है। इलेक्ट्रोड के परिवेश की गैस की पराविद्युत सामर्थ्य 5 x 107 वोल्ट मीटर-1 है। गोलीय कोश की आवश्यक न्यूनतम त्रिज्या क्या है?
हल :
दिया है : गोलीय कोश का विभव V = 15 x 106 वोल्ट
गैस की पराविद्युत सामर्थ्य Emax = 5 x 107 वोल्ट मीटर-1
माना कोश की न्यूनतम त्रिज्या r है, तब
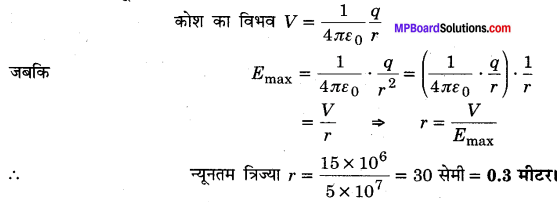
प्रश्न 36.
r1 त्रिज्या तथा q1 आवेश वाला एक छोटा गोला r2 त्रिज्या और q2 आवेश के गोलीय खोल (कोश) से घिरा है। दर्शाइए यदि q1 धनात्मक है तो (जब दोनों को एक तार द्वारा जोड़ दिया जाता है) आवश्यक रूप से आवेश, गोले से खोल की तरफ ही प्रवाहित होगा, चाहे खोल पर आवेश q2 कुछ भी हो।
हल :
हम जानते हैं कि किसी चालक का सम्पूर्ण आवेश उसके बाह्य पृष्ठ पर रहता है; अत: जैसे ही दोनों गोलों को चालक तार द्वारा जोड़ा जाएगा वैसे ही अन्दर वाले छोटे गोले का सम्पूर्ण आवेश तार से होकर बाहरी खोल की ओर प्रवाहित हो जाएगा, चाहे खोल पर आवेश q2 कुछ भी क्यों न हो।
प्रश्न 37.
निम्न का उत्तर दीजिए :
(a) पृथ्वी के पृष्ठ के सापेक्ष वायुमण्डल की ऊपर परत लगभग 400 किलोवोल्ट पर है, जिसके संगत विद्युतक्षेत्र ऊँचाई बढ़ने के साथ कम होता है। पृथ्वी के पृष्ठ के सापेक्ष विद्युत क्षेत्र लगभग 100 वोल्ट मीटर-1 है। तब फिर जब हम घर से बाहर खुले में जाते हैं तो हमें विद्युत आघात क्यों नहीं लगता? (घर को लोहे का पिंजरा मान लीजिए; अतः उसके अन्दर कोई विद्युत क्षेत्र नहीं है।)
(b) एक व्यक्ति शाम के समय अपने घर के बाहर 2 मीटर ऊँचा अवरोधी पट्ट रखता है जिसके शिखर पर एक 1 मीटर क्षेत्रफल की बड़ी ऐलुमिनियम की चादर है। अगली सुबह वह यदि धातु की चादर को छूता है तो क्या उसे विद्युत आघात लगेगा?
(c) वायु की थोड़ी-सी चालकता के कारण सारे संसार में औसतन वायुमण्डल में विसर्जन धारा 1800 ऐम्पियर मानी जाती है। तब यथासमय वातावरण स्वयं पूर्णतः निरावेशित होकर विद्युत उदासीन क्यों नहीं हो जाता? दूसरे शब्दों में, वातावरण को कौन आवेशित रखता है?
(d) तड़ित के दौरान वातावरण की विद्युत ऊर्जा, ऊर्जा के किन रूपों में क्षयित होती है?
हल :
(a) हमारा शरीर तथा पृथ्वी के समान विभव पर रहने के कारण हमारे शरीर से होकर कोई विद्युत धारा प्रवाहित नहीं होती इसीलिए हमें कोई विद्युत आघात नहीं लगता।
(b) हाँ, पृथ्वी तथा ऐलुमिनियम की चादर मिलकर एक संधारित्र बनाती हैं तथा अवरोधी पट्ट पराविद्युत का कार्य करता है। ऐलुमिनियम की चादर वायुमण्डलीय आवेश के लगातार गिरते रहने से आवेशित होती रहती है और उच्च विभव प्राप्त कर लेती है; अतः जब व्यक्ति इस चादर को छूता है तो उसके शरीर से होकर एक विद्युत धारा प्रवाहित होती है और इस कारण उस व्यक्ति को विद्युत आघात लगेगा।
(c) यद्यपि वायुमण्डल 1800 ऐम्पियर की औसत विसर्जन धारा के कारण लगातार निरावेशित होता रहता है परन्तु साथ ही यह तड़ित तथा झंझावात के कारण यह लगातार आवेशित भी होता रहता है और इन दोनों के बीच एक सन्तुलन बना रहता है जिससे कि वायुमण्डल कभी भी पूर्णत: निरावेशित नहीं हो पाता।
(d) तड़ित के दौरान वातावरण की विद्युत ऊर्जा, प्रकाश उर्जा, ध्वनि ऊर्जा तथा ऊष्मीय ऊर्जा के रूप में क्षयित होती है।
NCERT भौतिक विज्ञान प्रश्न प्रदर्शिका (Physics Exemplar LQ Problems) पुस्तक से चयनित महत्त्वपूर्ण प्रश्नों के हल
स्थिरवैद्युत विभव तथा धारिता बहुविकल्पीय प्रश्नोत्तर
प्रश्न 1.
चित्र में दर्शाए अनुसार परिपथ में 4 μF का संधारित्र संयोजित है। बैटरी का आन्तरिक प्रतिरोध 0.5Ω है। संधारित्र की प्लेटों पर आवेश की मात्रा होगी –
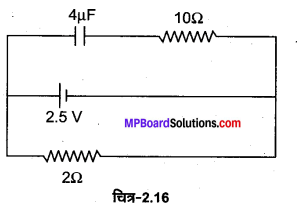
(a) 0
(b) 4 μc
(c) 16 μc
(d) 8 μc
उत्तर :
(d) 8 μc
प्रश्न 2.
किसी एक समान विद्युत क्षेत्र में किसी धनावेशित कण को मुक्त किया जाता है। आवेश की वैद्युत स्थितिज ऊर्जा
(a) नियत रहती है क्योंकि विद्युत क्षेत्र एकसमान है
(b) बढ़ जाती है क्योंकि आवेश विद्युत क्षेत्र के अनुदिश गति करता है
(c) घट जाती है क्योंकि आवेश विद्युत क्षेत्र के अनुदिश गति करता है
(d) घट जाती है क्योंकि आवेश विद्युत क्षेत्र के विपरीत गति करता है।
उत्तर :
(c) घट जाती है क्योंकि आवेश विद्युत क्षेत्र के अनुदिश गति करता है
![]()
प्रश्न 3.
कुछ आवेशों के एक समूह का कुल योग शून्य नहीं है। इससे अधिक दूरी पर बनने वाले समविभव पृष्ठ होंगे –
(a) गोले
(b) समतल
(c) परवलयज
(d) दीर्घवृत्तज।
उत्तर :
(a) गोले
प्रश्न 4.
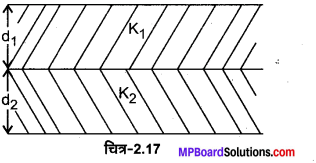
कोई समान्तर पट्टिका संधारित्र दो श्रेणीबद्ध परावैद्युत गुटकों से बना है। इनमें चित्र में दर्शाए अनुसार एक गुटके की मोटाई d1 तथा परावैद्युतांक K1 तथा दूसरे गुटके की मोटाई d25 तथा परावैद्युतांक K2 है।* इस व्यवस्था को एक ऐसा परावैद्युत गुटका माना जा सकता है जिसकी d) मोटाई d = (d1 + d2) तथा प्रभावी परावैद्युतांक K है। तब K का मान है –
(a)\(\frac{K_{1} d_{1}+K_{2} d_{2}}{d_{1}+d_{2}}\)
(b)\(\frac{K_{1} d_{1}+K_{2} d_{2}}{K_{1}+K_{2}}\)
(c)\(\frac{K_{1} K_{2}\left(d_{1}+d_{2}\right)}{\left(K_{1} d_{2}+K_{2} d_{1}\right)}\)
(d)\(\frac{2 K_{1} K_{2}}{\left(K_{1}+K_{2}\right)}\)
उत्तर :
(c)\(\frac{K_{1} K_{2}\left(d_{1}+d_{2}\right)}{\left(K_{1} d_{2}+K_{2} d_{1}\right)}\)
स्थिरवैद्युत विभव तथा धारिता अति लघु उत्तरीय प्रश्नोत्तर
प्रश्न 1.
R1 तथा R2 त्रिज्याओं (R1 > R2) के दो चालक गोलों पर विचार कीजिए। यदि दोनों गोले समान विभव पर हैं तो छोटे गोले की अपेक्षा बड़े गोले पर अधिक आवेश होता है। उल्लेख कीजिए, छोटे गोले का आवेश घनत्व बड़े गोले की तुलना में अधिक होगा अथवा कम?
उत्तर :
दोनों गोले समान विभव पर हैं। अत: V1 = V2 अथवा

अत: छोटे गोले (R2 त्रिज्या का) का आवेश पृष्ठ घनत्व, बड़े गोले की तुलना में अधिक होगा।
प्रश्न 2.
मुक्त इलेक्ट्रॉन उच्च विभव के क्षेत्र की ओर गमन करते हैं अथवा निम्न विभव के क्षेत्र की ओर?
उत्तर :
मुक्त इलेक्ट्रॉन उच्च विभव के क्षेत्र की ओर गमन करते हैं। .
प्रश्न 3.
समान आवेश वाले दो निकटवर्ती चालकों के बीच क्या कोई विभवान्तर हो सकता है?
उत्तर :
हाँ, यदि चालकों का आमाप भिन्न-भिन्न हों तब समान आवेश होते हुए भी उनके बीच विभवान्तर हो सकता है।
![]()
प्रश्न 4.
कोई परीक्षण आवेश q किसी बिन्दु आवेश Q के विद्युत क्षेत्र में दो भिन्न बन्द पथों पर गमन करता है (चित्रानुसार )। पहला पथ विद्युत क्षेत्र की रेखाओं के अनुदिश तथा लम्बवत् कोई भाग है। दूसरा पथ एक आयताकार पाश है जिसका क्षेत्रफल पहले पाश के बराबर है। इन दोनों प्रकरणों में किए गए कार्य की तुलना कीजिए।
उत्तर :
वैद्युत बल एक संरक्षी बल है, अत: इसके अन्तर्गत बन्द पथ में किया है गया कार्य दोनों स्थितियों में शून्य होगा।
स्थिरवैद्युत विभव तथा धारिता लघु उत्तरीय प्रश्नोत्तर
प्रश्न 1.
किसी संधारित्र की पट्टिकाओं के बीच कोई परावैद्युत है तथा यह संधारित्र किसी दिष्ट स्रोत से संयोजित है। अब बैटरी को हटाया जाता है और फिर परावैद्युत को हटा दिया जाता है। यह उल्लेख कीजिए कि ऐसा करने पर संधारित्र की धारिता उसमें संचित ऊर्जा, विद्युत क्षेत्र, संचित आवेश तथा वोल्टता में वृद्धि होगी, कमी होगी अथवा नियत रहेगी?
उत्तर :
संधारित्र की पट्टिकाओं से संयोजित दिष्ट स्रोत (बैटरी) को हटा लेने पर संधारित्र की प्लेटों पर आवेश नियत रहेगा।
संधारित्र की प्लेटों के बीच से परावैद्युत को हटा लेने पर उसकी धारिता कम हो जाएगी।
संधारित्र में संचित ऊर्जा \(E=\frac{\sigma}{\varepsilon_{0} K}\), धारिता C घट जाने के कारण अधिक हो जाएगी।
प्लेटों के बीच वैद्युत क्षेत्र \(V=\frac{q}{C}\), परावैद्युत हटा लेने पर बढ़ जाएगा।
प्लेटों के बीच वोल्टता \(V=\frac{q}{C}\), धारिता कम हो जाने के कारण (या V = E.d के अनुसार) बढ़ जाएगी।
स्थिरवैद्युत विभव तथा धारिता विस्तृत उत्तरीय प्रश्नोत्तर
प्रश्न 1.
R तथा 2R त्रिज्याओं के दो धातु के गोलों के पृष्ठीय आवेश घनत्व समान हैं। इन्हें सम्पर्क में लाकर पृथक कर दिया जाता है। इन दोनों पर नए पृष्ठीय आवेश घनत्व क्या होंगे?
हल :
धातु के गोलों पर आवेश q1 = σ 4πR2 तथा
q2 = σ4π(2R2)
4(σ4πR2) = 4q1

चालकों को परस्पर सम्पर्क में रखने पर, उन पर आवेशों का पुनर्वितरण उनकी धारिताओं के अनुपात में होता है। अतः