MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.6

In this article, we share MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.6 Pdf, These solutions are solved by subject experts from the latest MP Board books.

MP Board Class 12th Maths Book Solutions Chapter 9 अवकल समीकरण Ex 9.6

1 से 12 तक के प्रश्नों में, प्रत्येक अवकल समीकरण का व्यापक हल ज्ञात कीजिए-
प्रश्न 1.
\(\frac{d y}{d x}\) + 2y = sinx
हल:
यह \(\frac{d y}{d x}\) + 2y = Q के रूप का रैखिक अवकल समी० है, जहाँ
P = 2 तथा Q = sin x

प्रश्न 2.
\(\frac{d y}{d x}\) + 3y = e^-2x
हल:
\(\frac{d y}{d x}\) + 3y = e^-2x …(i)
यह \(\frac{d y}{d x}\)Py = Q के रूप का रैखिक अवकल समी० है यहाँ
P = 3 तथा Q = e^-2x

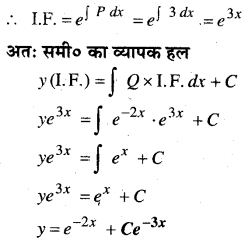
प्रश्न 3.
\(\frac{d y}{d x}+\frac{y}{x}\) = x²
हल:
\(\frac{d y}{d x}+\frac{y}{x}\) = x²
यह \(\frac{d y}{d x}+\frac{y}{x}\) + Py = Q के रूप का रैखिक अवकल समी० है
यहाँ

प्रश्न 4.
\(\frac{d y}{d x}\) + (sec x)y = tan x (0 ≤ x ≤ \(\frac{\pi}{2}\))
हल:
\(\frac{d y}{d x}\) + (sec x)y = tan x (0 ≤ x ≤ \(\frac{\pi}{2}\))
यह \(\frac{d y}{d x}\)Py = Q के रूप का रैखिक अवकल समी० है यहाँ
P = sec x तथा Q = tan x

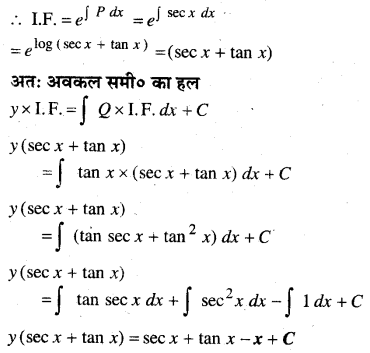
प्रश्न 5.
cos² x\(\frac{d y}{d x}\) + y = tan x(0 ≤ x ≤ \(\frac{\pi}{2}\))
हत्ल :
cos² x\(\frac{d y}{d x}\) + y = tan x(0 ≤ x ≤ \(\frac{\pi}{2}\))
cos² x से भाग करने पर

प्रश्न 6.
x\(\frac{d y}{d x}\) + 2y = x² logx
हल:
दिया गया समी०

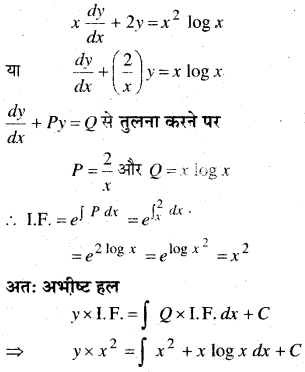
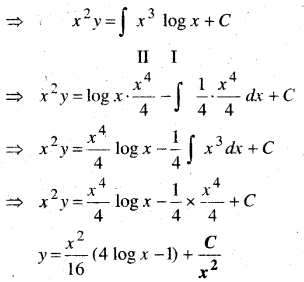
प्रश्न 7.
x log x \(\frac{d y}{d x}\) + y = \(\frac{2}{x}\) logx
हल:
दिया गया समी०

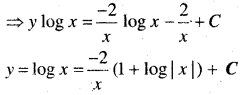
प्रश्न 8.
(1 + x²)dy + 2xy dx = cotx dx (x ≠ 0)
हल:
(1 + x²)dy + 2xy dx = cotx dx

प्रश्न 9.
x\(\frac{d y}{d x}\) + y – x + xy cot x = 0, (x ≠ 0)
हल:
दिया गया अवकल समी०

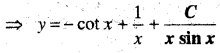
प्रश्न 10.
(x + y)\(\frac{d y}{d x}\) = 1
हल:
अवकल समीकरण,
(x + y)\(\frac{d y}{d x}\) = 1

यही अभीष्ट हल है।

प्रश्न 11.
y dx + (x – y²)dy = 0
हल:
y dx + (x – y²) dy = 0

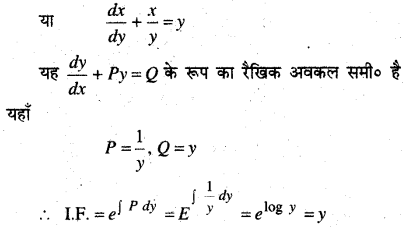
प्रश्न 12.
(x + 3y²)\(\frac{d y}{d x}\) = y, (y > 0)
हल:
(x + 3y²)\(\frac{d y}{d x}\) = y

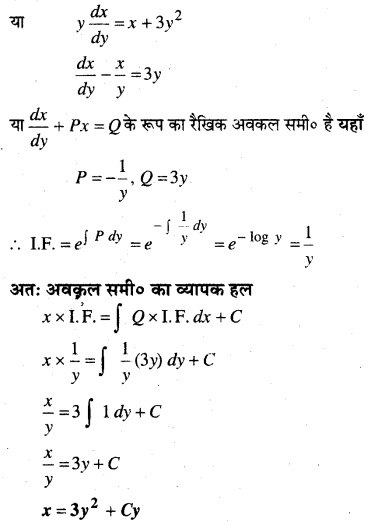
13 से 15 तक के प्रश्नों में प्रत्येक अवकल समीकरण के लिए दिए हुए प्रतिबन्ध को सन्तुष्ट करने वाला विशिष्ट हल ज्ञात कीजिए
प्रश्न 13.
\(\frac{d y}{d x}\) + 2y tan x = sin x; y = 0 यदि x = \(\frac{\pi}{3}\)
हल:
दिया गया समी०
\(\frac{d y}{d x}\) + 2y tan x = sin x …(i)
यह एक रैखिक अवकल समी० है

प्रश्न 14.
(1 + x²)\(\frac{d y}{d x}\) + 2xy = \(\frac{1}{1+x^{2}}\); y = 0 यदि x = 1
हल:
दिया गया समी०

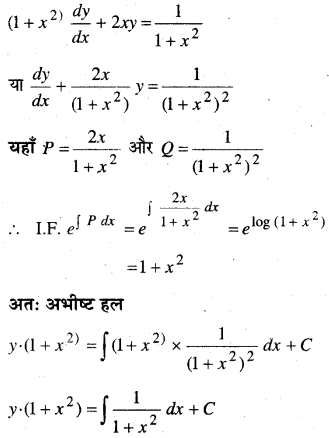
प्रश्न 15.
\(\frac{d y}{d x}\) – 3y cot x = sin 2x; y = 2 यदि x = \(\frac{\pi}{2}\)
हल:
दिया है
\(\frac{d y}{d x}\) – 3y cot x = sin 2x …(i)

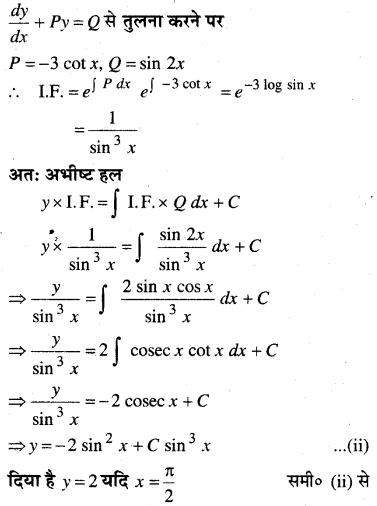
⇒ -2 + C
⇒ C = 4
C का यह मान समी० (ii) में रखने पर
y = 4 sin ³ – 2 sin²x

प्रश्न 16.
मूल बिन्दु से गुजरने वाले एक वक्र का समीकरण ज्ञात कीजिए यदि इस वक्र के किसी बिन्दु (x, y)पर स्पर्श रेखा की प्रवणता उस बन्दु के निर्देशांकों के योग के बराबर है।
हल:
बिन्दु (x, y) पर स्पर्श रेखा की प्रवणता = \(\frac{d y}{d x}\)
∴ दिए गए परवलय के अनुसार

∵ यह वक्र मूल बिन्दु से गुजरता है
∴ x = 0 तथा y = 0 समी० (ii) में रखने पर
⇒ 0 = -1 – 1 = Ce^° ⇒ C = 1
C का यह मान समी० (ii) में रखने पर
y = -x – 1 + e^x
या x + y + 1 = e^x

प्रश्न 17.
बिन्दु (0, 2) से गुजरने वाले वक्र का समीकरण ज्ञात कीजिए यदि इस वक्र के किसी बिन्दु के निर्देशांकों का योग उस बिन्दु पर खींची गई स्पर्श रेखा की प्रवणता के परिमाण से 5 अधिक है।
हल:
बिन्दु (x, y) से स्पर्श रेखा की प्रवणता \(\frac{d y}{d x}\) है।
तब प्रश्नानुसार


⇒ ye^-x = (x – 5) e^-x – e^x + C
⇒ y = -(x – 5) – 1 + Ce^x
⇒ y = 4 – x + Ce^x
∵ वक्र बिन्दु (0, 2) से गुजरता है, अतः
x = 0 तथा y = 2 समी० में रखने पर
⇒ 2 = 4 – 0 + Ce⁰
C = -2
C = -2 समी० (II) में रखने पर
y = 4 – x + (-2)e^x
y = 4 – x – 2e^x
Case-II
इसी प्रकार ऋण चिन्ह लेने पर,

ye^x = (5 – x) e^x + e^x + C
y = (5 – x) + 1 + Ce^-x
y = 6 – x + Ce^-x
यह वक्र बिन्दु (0, 2) से गुजरता है, अतः x = 0 तथा y = 2 लेने पर
2 = 6 – 0 + Ce⁰ ⇒ C = -4
मान प्रतिस्थापित करने पर
y = 6 – 4 – 4e^-x

प्रश्न 18.
अवकल समीकरण x\(\frac{d y}{d x}\) – y = 2x² का समाकलन गुणक है-
(A) e^-x
(B) e^-y
(C) \(\frac{1}{x}\)
(D) x
हल:
अवकल समीकरण है :

अतः विकल्प (C) सही है।

प्रश्न 19.
अवकल समीकरण (1 – y²)\(\frac{d y}{d x}\) + yx = ay (-1 < y < 1) का समाकलन गुणक है-

हल:
अवकल समीकरण है :


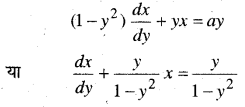
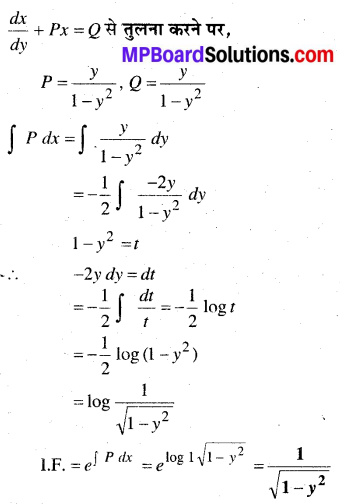
अतः विकल्प (D) सही है।